Comparative Analysis of Productivity Methods to Evaluate Thermal Comfort in Classrooms through Hierarchical Clustering
Abstract
:1. Introduction
2. Materials and Methods
2.1. PRISMA, Search Strategy and StArt
2.2. Model Performance Comparison
2.3. Hierarchical Cluster Analysis: Categorization of Models
- The first step is to create a proximity matrix between the variables. This matrix captures the measure of similarity between all possible combinations of variables using the squared Euclidean distance. Smaller values indicate more excellent proximity between the variables and vice versa.
- Subsequently, clusters are formed by evaluating the similarity measures between groups or individual variables. At each stage, it is checked whether the two groups have the highest level of similarity; if so, these groups are combined.
- In the next stage, the process continues by checking whether any groups can be included in the previous combination due to their high level of similarity.
- The stages continue until all the variables have been grouped into a single set.
3. Results
3.1. Initial Results from Academic Databases
3.2. Selected Models
3.3. Comparison of Model Performance
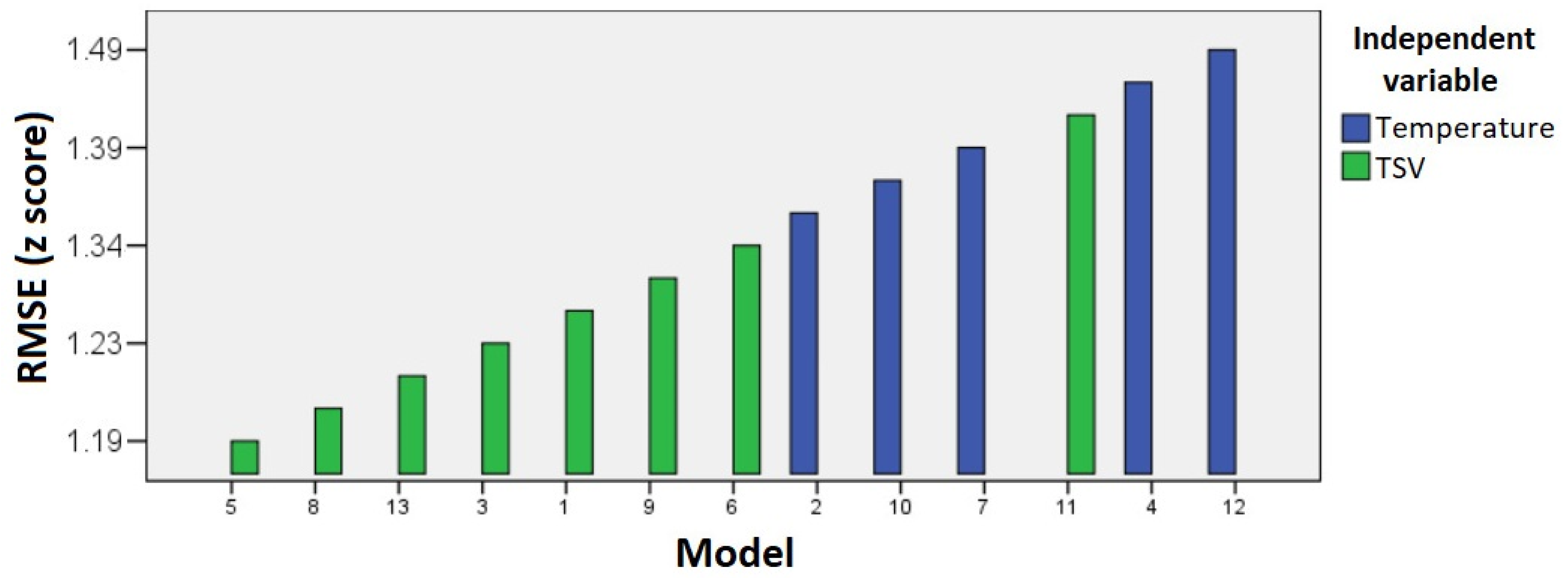
3.4. Model Performance and Root Mean Square Error
3.5. Hierarchical Cluster Analysis: Categorization of Models
- Clustering by the use of the temperature variable (cluster 1): Models 2, 10, and 7 share the use of this variable.
- Clustering by using TSV in studies with similar age groups (cluster 2): Models 3, 1, and 9 come from studies with participants in similar age ranges.
- Clustering by using TSV in studies with different age groups from the previous Cluster (cluster 3): Models 8 and 13 originate from studies with participants of different ages.
4. Discussion
4.1. Specific Aspects of Models and Their Contexts
4.2. Root Mean Square Error (RMSE) and Hierarchical Clustering
- Cluster 1 (Variable: Temperature):
- ○
- Models: 2, 10, and 7.
- ○
- Interpretation: These models share the use of the temperature variable in their methodologies or analyses. The clustering suggests that these models were developed to explore specific temperature-related effects. Therefore, they would have been development in order to investigate how temperature variation affects certain phenomena or results.
- Cluster 2 (TSV in similar age groups):
- ○
- Models: 3, 1, and 9.
- ○
- Interpretation: These models are grouped because they are derived from studies with participants in similar age groups. This suggests that TSV may significantly influence these specific age groups, and these models were developed to explore this relationship.
- Cluster 3 (TSV in different age groups from the previous Cluster):
- ○
- Models: 8 and 13.
- ○
- Interpretation: These models are grouped due to studies with participants of different ages compared to Cluster 2. This may indicate variations in the effects of TSV in other age groups. Analysis of these models may offer insights into how TSV influences different age groups.
- Cluster 4 (Model 11 as inferior performance):
- ○
- Model: 11
- ○
- Interpretation: Model 11 is placed in a later category, suggesting it performs less well than the other analyzed models. This may indicate that Model 11 may not fit as well as the others in terms of the use or influence of TSV. The mention of the impact of temperature variation on productivity also suggests that Model 11 may not be as effective in this specific study context.
4.3. Limitations of the Study
4.4. Gaps in Research and Future Trends
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASHRAE | American Society of Heating, Refrigerating, and Air Conditioning Engineers |
| BLR | Binary Linear Regression |
| HLM | Hierarchical Linear Model |
| IAQ | Indoor Air Quality |
| IE | Indoor Environmental Quality |
| OR | Ordinary Regression |
| PCA | Principal Component Analysis |
| PEC | Personal Environmental Control |
| PH | Variation in productivity for men |
| PKAS | Personalized Kitchen Air Supply |
| PM | Variation in productivity for women |
| PMV | Predicted Mean Vote |
| PPD | Predicted Percentage of Dissatisfied |
| PR | Polynomial Regression |
| PRISMA | Preferred Reporting Items for Systematic Reviews and Meta-Analyses |
| RMSE | Root Mean Square Error |
| RP | Relative performance |
| RVA | Regression and Variance Analysis |
| SEM | Structural Equation Modeling |
| StArt | State of the Art through Systematic Reviews |
| T | Temperature |
| TSV | Thermal Sensation Vote |
| UTCI | Universal Thermal Climate Index |
References
- Liu, F.; Chang-Richards, A.; Wang, K.I.-K.; Dirks, K.N. Effects of Indoor Environment Factors on Productivity of University Workplaces: A Structural Equation Model. Build. Environ. 2023, 233, 110098. [Google Scholar] [CrossRef]
- Lan, L.; Wargocki, P.; Lian, Z. Quantitative Measurement of Productivity Loss Due to Thermal Discomfort. Energy Build. 2011, 43, 1057–1062. [Google Scholar] [CrossRef]
- Parkinson, T.; Parkinson, A.; de Dear, R. Continuous IEQ Monitoring System: Performance Specifications and Thermal Comfort Classification. Build. Environ. 2019, 149, 241–252. [Google Scholar] [CrossRef]
- ASHRAE Standard 55-2020; Thermal Environmental Conditions for Human Occupancy. American Society of Heating, Refrigerating, and Air Conditioning Engineer ASHRAE: Atlanta, GA, USA, 2021.
- Fanger, O.P. Thermal Comfort: Analysis and Applications in Environmental Engineering; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Henriques, I.B.; Mady, C.E.K.; Oliveira Junior, S. Assessment of Thermal Comfort Conditions during Physical Exercise by Means of Exergy Analysis. Energy 2017, 128, 609–617. [Google Scholar] [CrossRef]
- Tarantini, M.; Pernigotto, G.; Gasparella, A. A Co-Citation Analysis on Thermal Comfort and Productivity Aspects in Production and Office Buildings. Buildings 2017, 7, 36. [Google Scholar] [CrossRef]
- Oh, S.; Song, S. Detailed Analysis of Thermal Comfort and Indoor Air Quality Using Real-Time Multiple Environmental Monitoring Data for a Childcare Center. Energies 2021, 14, 643. [Google Scholar] [CrossRef]
- Hu, G.; You, F. Multizone Building Control with Thermal Comfort Constraints under Disjunctive Uncertainty Using Data-Driven Robust Model Predictive Control. Adv. Appl. Energy 2023, 9, 100124. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, J.; Zhou, X.; Gao, J.; Cao, C.; Zeng, Y.; Li, J. Personalized Kitchen Air Supply for Reducing Individual Thermal Discomfort and Cooking Pollution Intake. Build. Environ. 2023, 245, 110921. [Google Scholar] [CrossRef]
- Favero, M.; Sartori, I.; Carlucci, S. Human Thermal Comfort under Dynamic Conditions: An Experimental Study. Build. Environ. 2021, 204, 108144. [Google Scholar] [CrossRef]
- Petegrosso, R.; Li, Z.; Kuang, R. Machine Learning and Statistical Methods for Clustering Single-Cell RNA-Sequencing Data. Brief. Bioinform. 2020, 21, 1209–1223. [Google Scholar] [CrossRef]
- Bueno, A.M.; Mendes da Luz, I.; Niza, I.L.; Broday, E.E. Hierarchical and K-Means Clustering to Assess Thermal Dissatisfaction and Productivity in University Classrooms. Build. Environ. 2023, 233, 110097. [Google Scholar] [CrossRef]
- Appel-Meulenbroek, R.; Clippard, M.; Pfnür, A. The Effectiveness of Physical Office Environments for Employee Outcomes: An Interdisciplinary Perspective of Research Efforts. J. Corp. Real Estate 2018, 20, 56–80. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; Chou, R.; et al. The PRISMA 2020 Statement: An Updated Guideline for Reporting Systematic Reviews. BMJ 2021, 71, n71. [Google Scholar] [CrossRef] [PubMed]
- Feng, W.; Liu, J. A Literature Survey of Local Climate Zone Classification: Status, Application, and Prospect. Buildings 2022, 12, 1693. [Google Scholar] [CrossRef]
- Romaszko, J.; Dragańska, E.; Jalali, R.; Cymes, I.; Glińska-Lewczuk, K. Universal Climate Thermal Index as a Prognostic Tool in Medical Science in the Context of Climate Change: A Systematic Review. Sci. Total Environ. 2022, 828, 154492. [Google Scholar] [CrossRef]
- Niza, I.L.; Broday, E.E. Thermal comfort conditions in Brazil: A discriminant analysis through the ASHRAE Global Thermal Comfort Database II. Build. Environ. 2022, 221, 109310. [Google Scholar] [CrossRef]
- Zamboni, A.; Thommazo, A.D.; Hernandes, E.C.M.; Fabbri, S.C.P.F. StArt Uma Ferramenta Computacional de Apoio à Revisão Sistemática. In Proceedings of the Brazilian Conference on Software: Theory and Practice-Tools Session, Salvador, Brazil, 23–27 September 2010; pp. 91–96. [Google Scholar]
- Kawakubo, S.; Sugiuchi, M.; Arata, S. Office Thermal Environment That Maximizes Workers’ Thermal Comfort and Productivity. Build. Environ. 2023, 233, 110092. [Google Scholar] [CrossRef]
- Geng, Y.; Ji, W.; Lin, B.; Zhu, Y. The Impact of Thermal Environment on Occupant IEQ Perception and Productivity. Build. Environ. 2017, 121, 158–167. [Google Scholar] [CrossRef]
- Jiang, J.; Wang, D.; Liu, Y.; Xu, Y.; Liu, J. A Study on Pupils’ Learning Performance and Thermal Comfort of Primary Schools in China. Build. Environ. 2018, 134, 102–113. [Google Scholar] [CrossRef]
- Wang, D.; Xu, Y.; Liu, Y.; Wang, Y.; Jiang, J.; Wang, X.; Liu, J. Experimental Investigation of the Effect of Indoor Air Temperature on Students’ Learning Performance under the Summer Conditions in China. Build. Environ. 2018, 140, 140–152. [Google Scholar] [CrossRef]
- Maroco, J. Análise Estatística: Com Utilização do SPSS; Edições Silabo, Lda: Lisbon, Portugal, 2003. [Google Scholar]
- Bridges, C.C. Hierarchical Cluster Analysis. Psychol. Rep. 1966, 18, 851–854. [Google Scholar] [CrossRef]
- Cui, W.; Cao, G.; Park, J.H.; Ouyang, Q.; Zhu, Y. Influence of Indoor Air Temperature on Human Thermal Comfort, Motivation and Performance. Build. Environ. 2013, 68, 114–122. [Google Scholar] [CrossRef]
- Kim, H.; Hong, T.; Kim, J.; Yeom, S. A Psychophysiological Effect of Indoor Thermal Condition on College Students’ Learning Performance through EEG Measurement. Build. Environ. 2020, 184, 107223. [Google Scholar] [CrossRef]
- Gnecco, V.M.; Pigliautile, I.; Pisello, A.L. Long-Term Thermal Comfort Monitoring via Wearable Sensing Techniques: Correlation between Environmental Metrics and Subjective Perception. Sensors 2023, 23, 576. [Google Scholar] [CrossRef] [PubMed]
- ISO 7730:2005; Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria. International Organization for Standardization: Geneva, Switzerland, 2005.
- Muhy Al-Din, S.S.; Ahmad Nia, H.; Rahbarianyazd, R. Enhancing Sustainability in Building Design: Hybrid Approaches for Evaluating the Impact of Building Orientation on Thermal Comfort in Semi-Arid Climates. Sustainability 2023, 15, 15180. [Google Scholar] [CrossRef]
- Pagano, R.R. Understanding Statistics in the Behavioral Sciences, 9th ed.; Cengage Learning: Belmont, CA, USA, 2009. [Google Scholar]
- Ruz, M.L.; Garrido, J.; Vázquez, F. Educational Tool for the Learning of Thermal Comfort Control Based on PMV-PPD Indices. Comput. Appl. Eng. Educ. 2018, 26, 906–917. [Google Scholar] [CrossRef]
- Nikolaou, T.G.; Kolokotsa, D.S.; Stavrakakis, G.S.; Skias, I.D. On the application of clustering techniques for office buildings’ energy and thermal comfort classification. IEEE Trans. Smart Grid 2012, 3, 2196–2210. [Google Scholar] [CrossRef]
- Virot, E.; Godet, J.; Khayath, N.; Ott, M.; Dazy, A.; de Blay, F. Cluster analysis of indoor environmental factors associated with symptoms of mite allergy. Ann. Allergy Asthma Immunol. 2019, 123, 280–283. [Google Scholar] [CrossRef]
- Zhang, D.; Ortiz, M.A.; Bluyssen, P.M. Clustering of Dutch school children based on their preferences and needs of the IEQ in classrooms. Build. Environ. 2019, 147, 258–266. [Google Scholar] [CrossRef]
- Feng, X.; Zainudin, E.B.; Wong, H.W.; Tseng, K.J. A Hybrid Ensemble Learning Approach for Indoor Thermal Comfort Predictions Utilizing the ASHRAE RP-884 Database. Energy Build. 2023, 290, 113083. [Google Scholar] [CrossRef]
- Qi, Y.; Wang, R.; Zhao, C.; Ding, C.; Du, C.; Zhang, J.; Zhang, X.; Chen, X.; Zhang, M.; Bie, Q.; et al. A Personalized Regression Model for Predicting Thermal Sensation Based on Local Skin Temperature in Moderate Summer Conditions. Energy Build. 2023, 301, 113719. [Google Scholar] [CrossRef]
- Zhou, B.; Huang, Y.; Nie, J.; Ding, L.; Sun, C.; Chen, B. Modification and Verification of the PMV Model to Improve Thermal Comfort Prediction at Low Pressure. J. Therm. Biol. 2023, 117, 103722. [Google Scholar] [CrossRef]
- Ahmad, S.A.; Zaki, S.A.; Azizan, A.; Md Taib, N.S. Performance of Machine Learning Algorithms Considering Spatial Effects Assessment for Indoor Personal Thermal Comfort in Air-Conditioned Workplace. E3S Web Conf. 2023, 396, 01064. [Google Scholar] [CrossRef]
- Karna, A.; Gibert, K. Automatic Identification of the Number of Clusters in Hierarchical Clustering. Neural Comput. Appl. 2022, 34, 119–134. [Google Scholar] [CrossRef]
- Zheng, G.; Wei, C.; Yue, X.; Li, K. Application of Hierarchical Cluster Analysis in Age Segmentation for Thermal Comfort Differentiation of Elderly People in Summer. Build. Environ. 2023, 230, 109981. [Google Scholar] [CrossRef]
- Bennetts, H.; Arakawa Martins, L.; van Hoof, J.; Soebarto, V. Thermal Personalities of Older People in South Australia: A Personas-Based Approach to Develop Thermal Comfort Guidelines. Int. J. Environ. Res. Public Health 2020, 17, 8402. [Google Scholar] [CrossRef]
- Li, B.; Tavakoli, A.; Wang, A.; Kaur, N.; Barnes, L.; Doryab, A.; Heydarian, A. Measuring Success, One Sensor at a Time: A Sensing Infrastructure for Longitudinal Workspace Behavior Monitoring. In Proceedings of the 10th ACM International Conference on Systems for Energy-Efficient Buildings, Cities, and Transportation, Istanbul, Turkey, 15–16 November 2023; ACM: New York, NY, USA, 2023. [Google Scholar]
- Marigo, M.; Carnieletto, L.; Moro, C.; Arcelli, T.; Ciloni, C.; Turchi, G.P.; De Carli, M.; Di Bella, A. Thermal Comfort and Productivity in a Workplace: An Alternative Approach Evaluating Productivity Management inside a Test Room Using Textual Analysis. Build. Environ. 2023, 245, 110836. [Google Scholar] [CrossRef]
- Latha, P.K.; Shanmugam, R.; Krishnamoorthy, M.; Venugopal, V. Rising Temperatures and Its Impacts on Thermal Comfort and Productivity—A Case Study from Select Workplaces in Southern India. In Lecture Notes in Civil Engineering; Springer Nature: Singapore, 2022; pp. 763–771. ISBN 9789811903038. [Google Scholar]
- Huang, S.; Zhou, F.; Liu, J.; Zhang, X. Comparison of Various Dual-Temperature Zones Space Heating Systems Based on Energy Cascade Utilization Principle. Appl. Therm. Eng. 2024, 236, 121606. [Google Scholar] [CrossRef]
- Xie, K.; Lee, M.; Khalid, R.; Zakka, V.G. The Impact of Personal Environmental Control on the Performance of Thermal Systems: Building Energy Consumption, Occupant Thermal Comfort, and Productivity. Energy Build. 2023, 298, 113552. [Google Scholar] [CrossRef]
- Siriwardhana, S.; Moehler, R.C. Enabling Productivity Goals through Construction 4.0 Skills: Theories, Debates, Definitions. J. Clean. Prod. 2023, 425, 139011. [Google Scholar] [CrossRef]



| Inclusion Criteria | Exclusion Criteria |
|---|---|
| Articles published in English | Articles published in other languages |
| Articles published over the years, with no time frame | Duplicate articles, conference papers, book chapters, conference reviews, books, editorials, or short articles |
| Articles published only in journals | Articles with missing data (title, abstract, keywords, author, or year of publication) |
| Articles published with thermal comfort models related to productivity, which considered parameters such as air and mean radiant temperature, relative humidity, clothing insulation, air velocity, and Predicted Percentage of Dissatisfied (PPD) | Published articles that do not address the research topic |
| Ref. | Model | Original | Adapted |
|---|---|---|---|
| [20] | 5 | ||
| 6 |
| Ref. | Order (Models) | Models | Evaluation Method | Location | Country |
|---|---|---|---|---|---|
| [26] | 1 | BLR | Climate chamber (classroom) | China | |
| [21] | 2 | RVA | Office | China | |
| [21] | 3 | RVA | Office | China | |
| [22] | 4 | RVA | Classroom | China | |
| [20] | 5 | OR/HLM | Office | Japan | |
| [20] | 6 | HLM | Office | Japan | |
| [27] | 7 | PR | Climate chamber (classroom) | South Korea | |
| [27] | 8 | PR | Climate chamber (classroom) | South Korea | |
| [2] | 9 | PR | Office | China | |
| [1] | 10 | SEM | Classroom | China | |
| [1] | 11 | SEM | Classroom | China | |
| [23] | 12 | RVA | Classroom | China | |
| [23] | 13 | RVA | Classroom | China |
| Models | Applicable Data | Mean (Standard Deviation) | RMSE | ||
|---|---|---|---|---|---|
| Productivity Observed (%) | Percentage Predicted (%) | Non-Standardized Data (%) | Standardized Data (z-Score) | ||
| 1 | 519 | 59.68 (15.27) | 099.12 (0.91) | 42.23 | 1.25 |
| 2 | 519 | 59.68 (15.27) | 102.41 (4.70) | 45.55 | 1.38 |
| 3 | 519 | 59.68 (15.27) | 101.44 (1.60) | 44.39 | 1.23 |
| 4 | 231 | 59.31 (15.53) | 100.73 (7.35) | 45.00 | 1.46 |
| 5 | 167 | 56.89 (16.63) | 094.41 (1.48) | 40.88 | 1.19 |
| 6 | 352 | 61.00 (14.42) | 100.87 (0.10) | 42.37 | 1.34 |
| 7 | 519 | 59.68 (15.27) | 096.47 (3.77) | 39.97 | 1.39 |
| 8 | 519 | 59.68 (15.27) | 099.23 (1.12) | 42.30 | 1.22 |
| 9 | 519 | 59.68 (15.27) | 099.51 (0.57) | 42.62 | 1.27 |
| 10 | 519 | 59.68 (15.27) | 095.69 (4.99) | 39.37 | 1.39 |
| 11 | 519 | 59.68 (15.27) | 099.61 (0.10) | 42.76 | 1.41 |
| 12 | 184 | 60.01 (14.17) | 102.23 (2.70) | 44.70 | 1.49 |
| 13 | 519 | 59.68 (15.27) | 101.52 (2.22) | 44.41 | 1.23 |
| Cases | Original Data | Model 1 | Model 2 | Model 3 | Model 7 | Model 8 | Model 9 | Model 10 | Model 11 | Model 13 |
|---|---|---|---|---|---|---|---|---|---|---|
| Original data | 0 | 806.37 | 990.00 | 790.13 | 1005.63 | 772.10 | 833.66 | 1003.13 | 1029.29 | 780.54 |
| Model 1 | 806.37 | 0 | 744.72 | 010.63 | 773.20 | 145.63 | 029.32 | 767.75 | 675.01 | 336.53 |
| Model 2 | 990.00 | 744.72 | 0 | 718.03 | 035.24 | 679.47 | 802.05 | 025.54 | 1124.86 | 690.71 |
| Model 3 | 790.13 | 010.63 | 718.03 | 0 | 737.92 | 079.10 | 070.94 | 733.61 | 797.39 | 235.12 |
| Model 7 | 1005.63 | 773.20 | 035.24 | 737.92 | 0 | 674.24 | 841.73 | 000.79 | 1180.09 | 667.12 |
| Model 8 | 772.10 | 145.63 | 679.47 | 079.10 | 674.24 | 0 | 282.84 | 673.45 | 1150.49 | 046.27 |
| Model 9 | 833.66 | 029.32 | 802.05 | 070.94 | 841.73 | 282.84 | 0 | 834.89 | 456.61 | 508.67 |
| Model 10 | 1003.13 | 767.75 | 025.54 | 733.61 | 000.79 | 673.45 | 834.89 | 0 | 1172.37 | 669.07 |
| Model 11 | 1029.29 | 675.01 | 1124.86 | 797.39 | 1180.09 | 1150.49 | 456.61 | 1172.37 | 0 | 1363.08 |
| Model 13 | 780.54 | 336.53 | 690.71 | 235.12 | 667.12 | 046.27 | 508.67 | 669.07 | 1363.08 | 0 |
| Stage | Combination | Coefficients | The First-Stage Cluster is Displayed First | Next Stage | ||
|---|---|---|---|---|---|---|
| Cluster 1 | Cluster 2 | Cluster 1 | Cluster 2 | |||
| 1 | 7 | 10 | 000.79 | 0 | 0 | 3 |
| 2 | 1 | 3 | 010.63 | 0 | 0 | 4 |
| 3 | 2 | 7 | 020.52 | 0 | 1 | 9 |
| 4 | 1 | 9 | 036.96 | 2 | 0 | 6 |
| 5 | 8 | 13 | 046.27 | 0 | 0 | 6 |
| 6 | 1 | 8 | 174.50 | 4 | 5 | 7 |
| 7 | OBS | 1 | 381.86 | 0 | 6 | 8 |
| 8 | OBS | 11 | 533.32 | 7 | 0 | 9 |
| 9 | OBS | 2 | 638.78 | 8 | 3 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendes da Luz, I.; Lourenço Niza, I.; Broday, E.E. Comparative Analysis of Productivity Methods to Evaluate Thermal Comfort in Classrooms through Hierarchical Clustering. Buildings 2024, 14, 698. https://doi.org/10.3390/buildings14030698
Mendes da Luz I, Lourenço Niza I, Broday EE. Comparative Analysis of Productivity Methods to Evaluate Thermal Comfort in Classrooms through Hierarchical Clustering. Buildings. 2024; 14(3):698. https://doi.org/10.3390/buildings14030698
Chicago/Turabian StyleMendes da Luz, Inaiele, Iasmin Lourenço Niza, and Evandro Eduardo Broday. 2024. "Comparative Analysis of Productivity Methods to Evaluate Thermal Comfort in Classrooms through Hierarchical Clustering" Buildings 14, no. 3: 698. https://doi.org/10.3390/buildings14030698






