Evaluating Airborne Sound Insulation in Dwellings Constructed with Hollow Ceramic Blocks under Brazilian Housing Policies
Abstract
1. Introduction
- Provide essential information for the construction sector to discourage the use of single-leaf partition walls constructed with vertical hollow ceramic blocks from an acoustical point of view.
- Examine the use of existing prediction models that rely on analytical equations and introduce a new approach by taking into account the dynamic modulus of stiffness in the calculations.
2. Materials and Methods
2.1. Composition of the Buildings
2.2. Acoustical Properties and Prediction Models
2.2.1. Physical and Mechanical Properties
2.2.2. Prediction Model for Orthotropic Behavior
2.2.3. Prediction Model according to ISO 12354-1
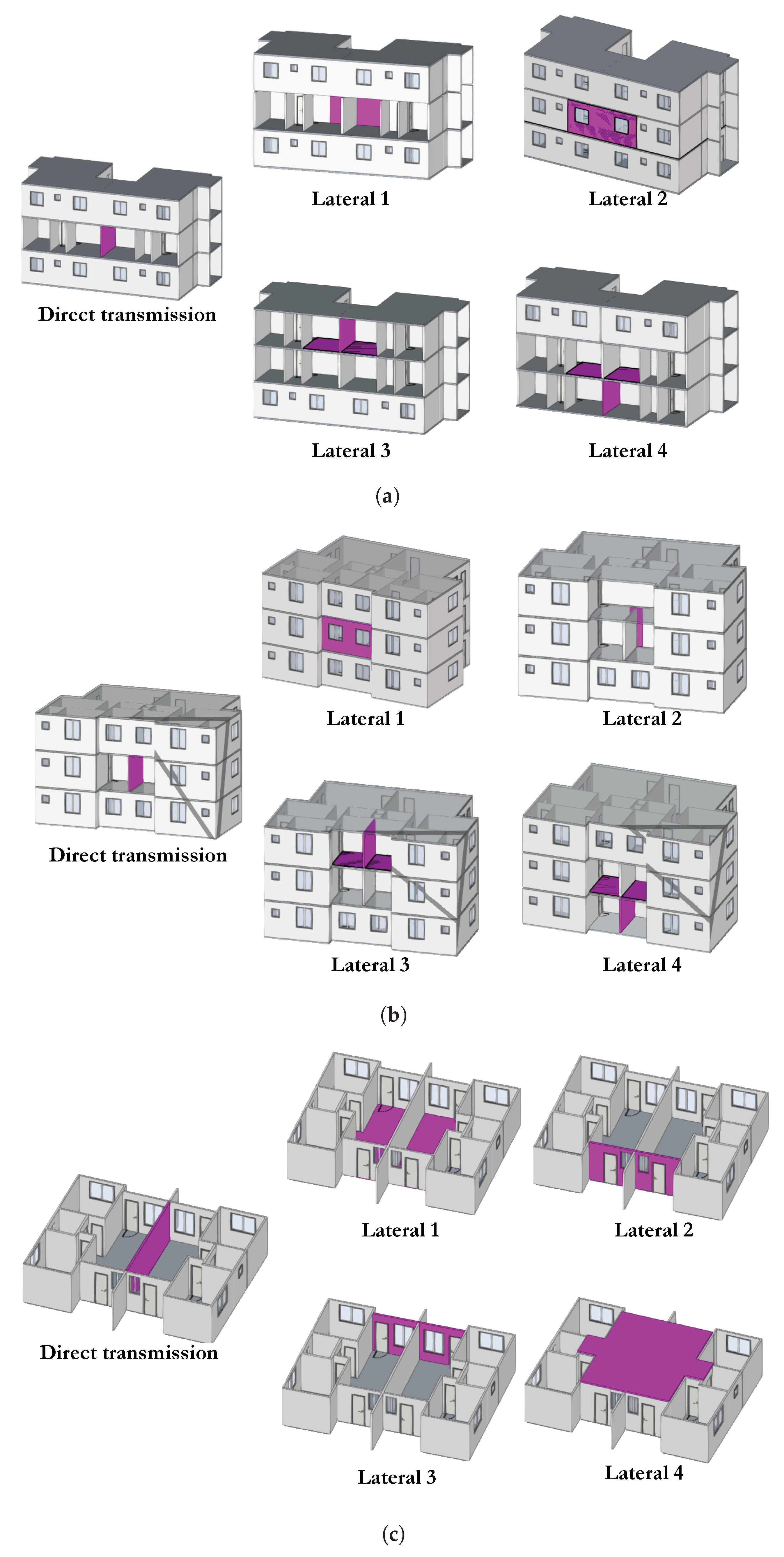
2.3. Acoustical Simulations
2.4. Acoustical Measurements
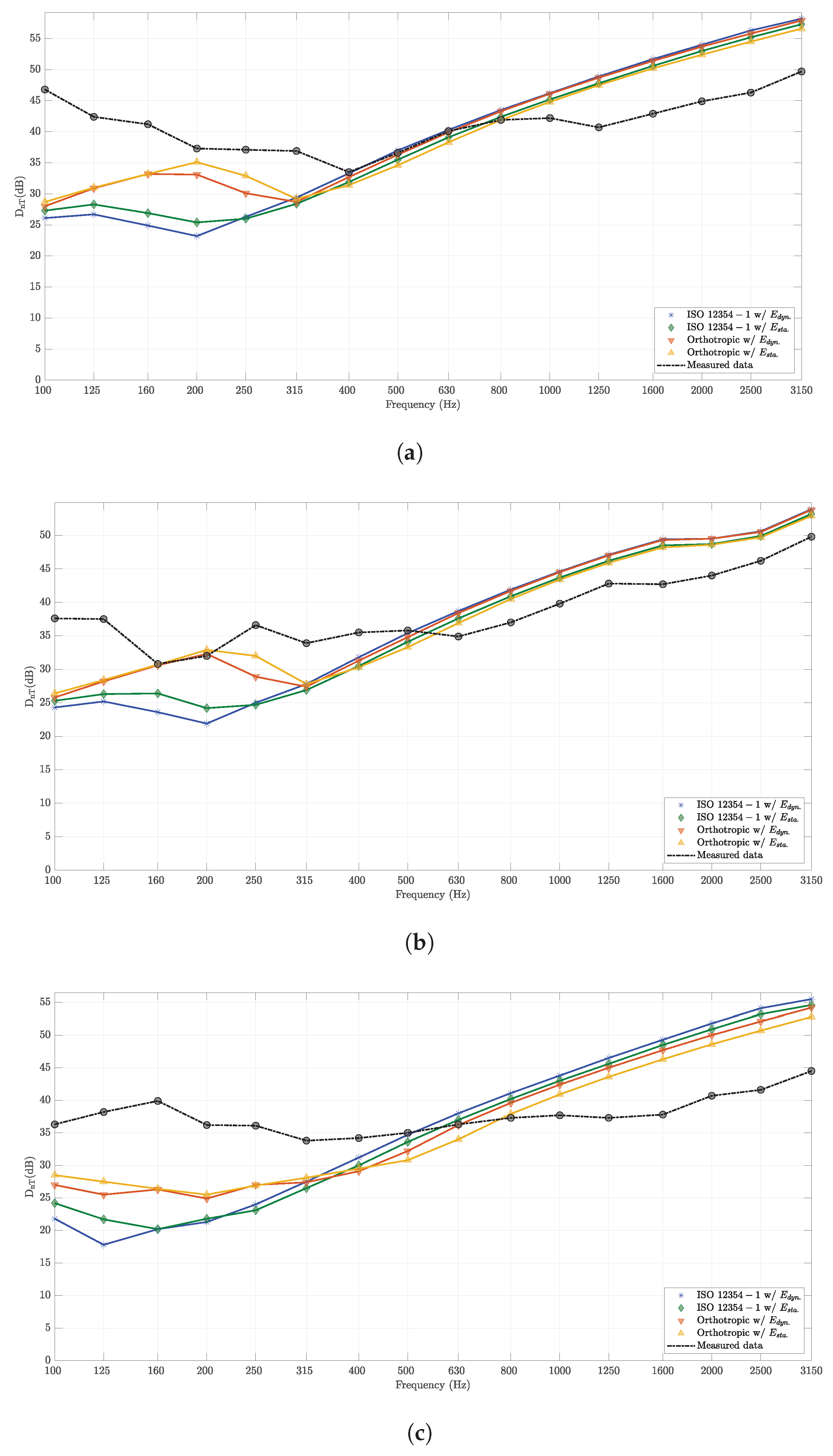
3. Results and Discussion
3.1. Sound Reduction Indices
3.2. Overall Levels
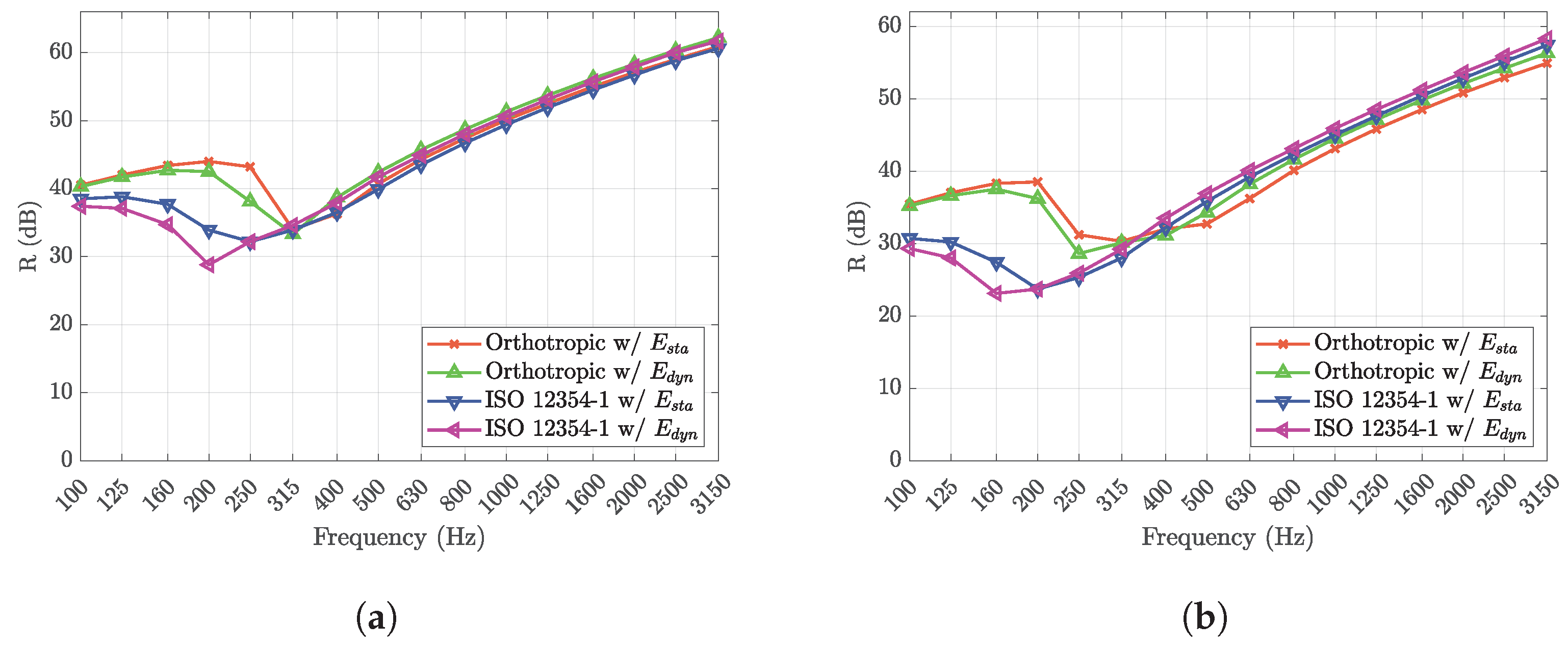
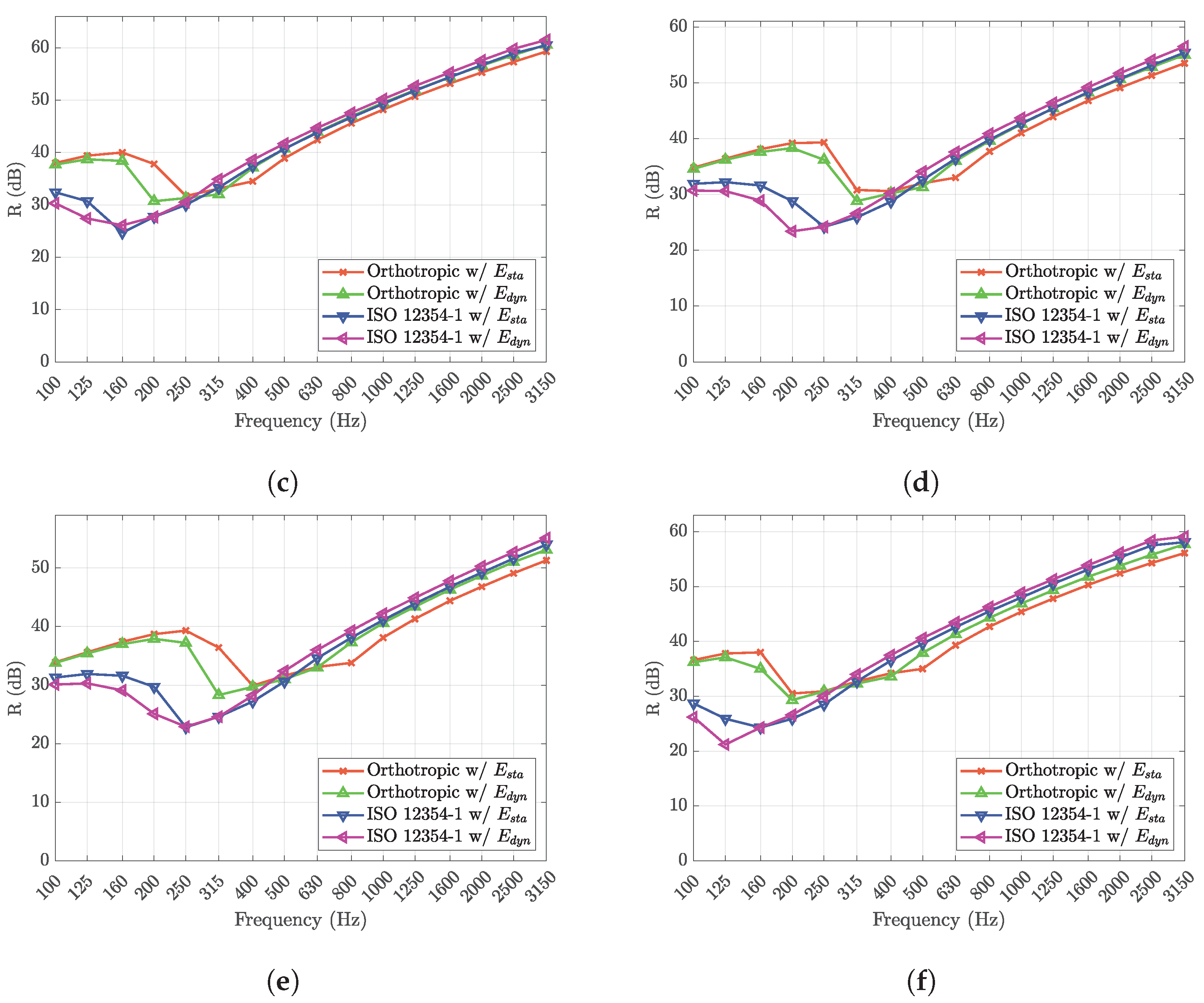
3.3. Spectral Analysis
3.4. Limitations of the Prediction Models
- The selected predictive models utilized elastic moduli from literature sources for both the coating system and joints, along with compressive resistance and densities. Construction companies controlled the thicknesses of the applied coatings in the buildings, which could vary due to slight deviations in the walls.
- Analytical expressions, sourced from the literature, were employed to calculate equivalent elastic moduli. However, for enhanced accuracy, it is recommended to measure this value through a comprehensive mechanical characterization of the sample. To accommodate variations in coating thicknesses and types of hollow blocks, the authors opted to calculate these factors separately.
- Assumptions were made regarding the impedance of the air (412 Ns/m2), the speed of sound in air (343 m/s), and the air density (1.29 kg/m3). Altering these values will yield different outcomes in the predicted models.
- The orthotropic model with demonstrates high accuracy in the mid-frequency range (e.g., 400–800 Hz) for hollow blocks featuring single-spaced holes, akin to those utilized in Wall Type A. However, for blocks with larger holes, as found in wall types B to F, it is necessary to conduct additional studies to fine-tune all prediction models and minimize deviations across lower and higher frequencies.
- According to Granzotto et al. (2020) [19], their model fails to forecast thickness resonances beyond the high-frequency spectrum (e.g., >2500 Hz) and this phenomenon cannot be feasibly derived through analytical calculations.
- Care should be exercised when making comparisons within the low-frequency range (from 100 to 250 Hz), as this interval contains the greatest uncertainties in the measured data [53].
- As described by Rindel (2017) [15], sound insulation computation programs typically suffer from the limitation that their outcomes represent the maximum achievable values, assuming ideal workmanship and acoustically flawless building details—conditions rarely met in practice.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- João Pinheiro Foundation. Brazilian Housing Shortage—2016–2019; João Piheiro Foundation: Belo Horizonte, Brazil, 2020. [Google Scholar]
- King, R.; Orloff, M.; Virsilas, T.; Pande, T. Confronting the Urban Housing Crisis in the Global South: Adequate, Secure, and Affordable Housing; Working Paper; World Resources Institute: Washington, DC, USA, 2017. [Google Scholar]
- de Souza, L.E.P.F.; de Barros, R.D.; Barreto, M.L.; Katikireddi, S.V.; Hone, T.V.; de Sousa, R.P.; Leyland, A.; Rasella, D.; Millett, C.J.; Pescarini, J. The potential impact of austerity on attainment of the Sustainable Development Goals in Brazil. BMJ Glob. Health 2019, 4, e001661. [Google Scholar] [CrossRef] [PubMed]
- NBR 15575; Residential Buildings—Performance. Technical Report. Brazilian National Standards Organization ABNT: Rio de Janeiro, Brazil, 2021.
- Hippert, M.A.S.; Longo, O.C. The performance standard—NBR 15575 and the architectural and structural designs. In Structures and Architecture—Bridging the Gap and Crossing Borders, Proceedings of the Fourth International Conference on Structures and Architecture (ICSA 2019), Lisbon, Portugal, 24–26 July 2019, 1st ed.; CRC Press: Lisbon, Portugal, 2019; p. 8. [Google Scholar]
- Lazzarini, S.; Hippert, M.A.S. Diretrizes para controle de informação documentada gerada pela implantação da NBR 15575: Edificações habitacionais: Desempenho em empresas construtoras. Ambiente Construído 2021, 21, 181–196. [Google Scholar] [CrossRef]
- NBR 15575-4; Residential buildings—Performance. Part 4: Requirements for Internal and External Wall Systems. Technical Report. Brazilian Association for Technical Standards ABNT: Rio de Janeiro, Brazil, 2021.
- ISO 16283-1; Acoustics—Field Measurement of Sound Insulation in Buildings and of Building Elements—Part 1: Airborne Sound Insulation. Technical Report. International Organization for Standardization ISO: Geneva, Switzerland, 2014.
- Andargie, M.S.; Touchie, M.; O’Brien, W.; Müller-Trapet, M. A field study of the relationship between sound insulation and noise annoyance, activity disturbance and wellbeing in multi-unit residences. Appl. Acoust. 2023, 206, 109291. [Google Scholar] [CrossRef]
- E336-20; Standard Test Method for Measurement of Airborne Sound Attenuation between Rooms in Buildings. Technical Report. ASTM (American Society for Testing and Materials): West Conshohocken, PA, USA, 2020. [CrossRef]
- Rauscher, T.; Neubauer, R.O.; Zaglauer, M.; Leistner, P. Single-number values versus subjective judgment of airborne sound insulation in dwellings. Build. Acoust. 2023, 30, 91–101. [Google Scholar] [CrossRef]
- ISO 12354-1; Building Acoustics—Estimation of Acoustic Performance of Buildings from the Performance of Elements. Part 1: Airborne Sound Insulation between Rooms. Technical Report. International Organization of Standardization ISO: Geneva, Switzerland, 2017.
- Muneron, L.M.; Hammad, A.W.; Najjar, M.K.; Haddad, A.; Vazquez, E.G. Comparison of the environmental performance of ceramic brick and concrete blocks in the vertical seals’ subsystem in residential buildings using life cycle assessment. Clean. Eng. Technol. 2021, 5, 100243. [Google Scholar] [CrossRef]
- Hopkins, C. Sound Insulation; Routledge: Burlington, VT, USA, 2007. [Google Scholar]
- Rindel, J.H. Sound Insulation in Buildings; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- ISO 10140-4; Acoustics—Laboratory Measurement of Sound Insulation of Building Elements—Part 4: Measurement Procedures and Requirements. Technical Report. International Organization for Standardization: Geneva, Switzerland, 2021.
- Santoni, A.; Fausti, P.; Bonfiglio, P. Building materials: Influence of physical, mechanical and acoustic properties in sound prediction models. Build. Acoust. 2019, 26, 3–20. [Google Scholar] [CrossRef]
- Fabio, S.; Giovanni, D.N.; Mariano, P. Airborne sound insulation prediction of masonry walls using artificial neural networks. Build. Acoust. 2021, 28, 391–409. [Google Scholar] [CrossRef]
- Granzotto, N.; Bella, A.D.; Piana, E.A. Prediction of the sound reduction index of clay hollow brick walls. Build. Acoust. 2020, 27, 155–168. [Google Scholar] [CrossRef]
- CYPE Ingenieros S.A. AcouBAT by CYPE, version 2024.b; CYPE: Alicante, Spain, 2024. [Google Scholar]
- NBR 8545; Masonry Execution without Structural Function Using Ceramic Bricks and Blocks. Technical Report. Brazilian Association for Technical Standards ABNT: Rio de Janeiro, Brazil, 1984.
- NBR 16868-2; Structural Masonry. Part 2: Execution ant Site Control. Technical Report. Brazilian Association for Technical Standards ABNT: Rio de Janeiro, Brazil, 2020.
- Castro, L.O.; Alvarenga, R.C.S.S.; Silva, R.M.; Ribeiro, J.C.L. Experimental evaluation of the interaction between strength concrete block walls under vertical loads. Rev. IBRACON Estruturas Mater. 2016, 9, 643–681. [Google Scholar] [CrossRef]
- NBR 15270-2; Ceramic Components—Hollow and Bricks for Masonry. Part 2: Test Method. Technical Report. Brazilian Association for Technical Standards ABNT: Rio de Janeiro, Brazil, 2023.
- NBR 6118; Design of Concrete Structures. Technical Report. Brazilian Association for Technical Standards ABNT: Rio de Janeiro, Brazil, 2023.
- Gidrão, G.d.M.S. Propriedades Dinâmicas do Concreto e Relações com sua Microestrutura. Ph.D. Thesis, Universidade de São Paulo, São Paulo, Brazil, 2015. [Google Scholar]
- NBR 6120; Design Loads for Structure. Technical Report. Brazilian Association for Technical Standards ABNT: Rio de Janeiro, Brazil, 2019.
- Santos, T.; Gomes, M.I.; Silva, A.S.; Ferraz, E.; Faria, P. Comparison of mineralogical, mechanical and hygroscopic characteristic of earthen, gypsum and cement-based plasters. Constr. Build. Mater. 2020, 254, 119222. [Google Scholar] [CrossRef]
- Moayedian, S.M.; Hejazi, M. Effect of scale on compressive strength of brick masonry with gypsum mortar. Measurement 2021, 172, 108932. [Google Scholar] [CrossRef]
- Coquard, P.; Boistelle, R.; Amathieu, L.; Barriac, P. Hardness, elasticity modulus and flexion strength of dry set plaster. J. Mater. Sci. 1994, 29, 4611–4617. [Google Scholar] [CrossRef]
- Haach, V.G.; Carrazedo, R.; Oliveira, L.M.; Corrêa, M.R. Application of acoustic tests to mechanical characterization of masonry mortars. NDT Int. 2013, 59, 18–24. [Google Scholar] [CrossRef]
- Ribeiro, R.S.; de Sousa, R.P.; Amarilla, R.S.D.; Sant’Ana, L.H.; Avelar, M.; Catai, R.E.; Matoski, A. Sound insulation of a hollow concrete blocks wall made with construction and demolition waste and wood-based panels as linings. Build. Acoust. 2021, 28, 423–442. [Google Scholar] [CrossRef]
- Eurocode 6; Design of Masonry Structures. Part 1-1: General Rules for Reinforced and Unreinforced Masonry Structures. Technical Report. European Committee for Standardization: Brussels, Belgium, 2005.
- Broyles, J.M.; Shepherd, M.R.; Brown, N.C. Evaluation of the dynamic response for scaled models of shaped concrete floor slabs. Build. Acoust. 2023, 30, 143–163. [Google Scholar] [CrossRef]
- Gidrao, G.d.M.S.; Carrazedo, R.; Bosse, R.M.; Silvestro, L.; Ribeiro, R.; de Souza, C.F.P. Numerical Modeling of the Dynamic Elastic Modulus of Concrete. Materials 2023, 16, 3955. [Google Scholar] [CrossRef]
- Makoond, N.; Cabané, A.; Pelà, L.; Molins, C. Relationship between the static and dynamic elastic modulus of brick masonry constituents. Constr. Build. Mater. 2020, 259, 120386. [Google Scholar] [CrossRef]
- Messali, F.; Metelli, G.; Plizzari, G. Experimental results on the retrofitting of hollow brick masonry walls with reinforced high performance mortar coatings. Constr. Build. Mater. 2017, 141, 619–630. [Google Scholar] [CrossRef]
- Lucchini, S.S.; Facconi, L.; Minelli, F.; Plizzari, G. Retrofitting unreinforced masonry by steel fiber reinforced mortar coating: Uniaxial and diagonal compression tests. Mater. Struct. 2020, 53, 144. [Google Scholar] [CrossRef]
- Hill, R. A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Piattoni, Q.; Quagliarini, E.; Lenci, S. Experimental analysis and modelling of the mechanical behaviour of earthen bricks. Constr. Build. Mater. 2011, 25, 2067–2075. [Google Scholar] [CrossRef]
- Santoni, A.; Bonfiglio, P.; Mollica, F.; Fausti, P.; Pompoli, F.; Mazzanti, V. Vibro-acoustic optimisation of Wood Plastic Composite systems. Constr. Build. Mater. 2018, 174, 730–740. [Google Scholar] [CrossRef]
- Nilsson, A.; Liu, B. Vibro-Acoustics; Science Press: Beijing, China, 2015; Volume 1. [Google Scholar]
- Vigran, T.E. Building Acoustics, 1st ed.; Taylor & Francis: Abingdon, UK, 2008. [Google Scholar]
- CYPE Ingenieros S.A. CYPE Architecture Software, version 2024.b; CYPE: Alicante, Spain, 2024. [Google Scholar]
- CYPE Ingenieros S.A. CYPE Open BIM Analytical Model, version 2024.b; CYPE: Alicante, Spain, 2024. [Google Scholar]
- ISO 3382-2; Acoustics—Measurement of Room Acoustic Parameters—Part 2: Reverberation Time in Ordinary Rooms. Technical Report. International Organization for Standardization ISO: Geneva, Switzerland, 2008.
- Berzborn, M.; Bomhardt, R.; Klein, J.; Richter, J.G.; Vorländer, M. The ITA-Toolbox: An Open Source MATLAB Toolbox for Acoustic Measurements and Signal Processing. In Proceedings of the 43th Annual German Congress on Acoustics, Kiel, Germany, 6–9 March 2017. [Google Scholar]
- ISO 717-1; Acoustics—Rating of Sound Insulation in Buildings and of Building Elements. Part 1: Airborne Sound Insulation. Technical Report. International Organization for Standardization ISO: Geneva, Switzerland, 2020.
- ISO 12999-1; Acoustics—Determination and Application of Measurement Uncertainties in Building Acoustics—Part 1: Sound Insulation. Technical Report. International Organization for Standardization ISO: Geneva, Switzerland, 2020.
- Fringuellino, M.; Smith, R. Sound Transmission through Hollow Brick Walls. Build. Acoust. 1999, 6, 211–224. [Google Scholar] [CrossRef]
- Klippel, S.; Labres, H.S.; Pacheco, F.; Oliveira, M.F.d.; Tutikian, B.F. Influência da espessura de revestimentos de argamassa no desempenho acústico de alvenarias de blocos cerâmicos. Ambiente Construído 2019, 19, 145–156. [Google Scholar] [CrossRef]
- Garg, N.; Saxena, T.; Kumar, A.; Maji, S. Uncertainty evaluation and implications of spectrum adaption terms in determining the airborne sound insulation in building elements. Noise Control Eng. J. 2014, 62, 333–343. [Google Scholar] [CrossRef]
- Scrosati, C.; Scamoni, F.; Bassanino, M.; Mussin, M.; Zambon, G. Uncertainty analysis by a Round Robin Test of field measurements of sound insulation in buildings: Single numbers and low frequency bands evaluation—Airborne sound insulation. Noise Control Eng. J. 2013, 61, 291–306. [Google Scholar] [CrossRef]
- Gajjar, P.N.; Ali, M.; Sayet, T.; Gasser, A.; Blond, E.; Pereira, J.M.; Lourenço, P.B. Numerical study on the nonlinear thermomechanical behaviour of refractory masonry with dry joints. Eng. Struct. 2023, 291, 116468. [Google Scholar] [CrossRef]
- Arroyo, F.; Christoforo, A.; Salvini, V.; Pelissari, P.; Pandolfelli, V.; Luz, A.; Cardoso, C. Development of plaster foam for thermal and acoustic applications. Constr. Build. Mater. 2020, 262, 120800. [Google Scholar] [CrossRef]
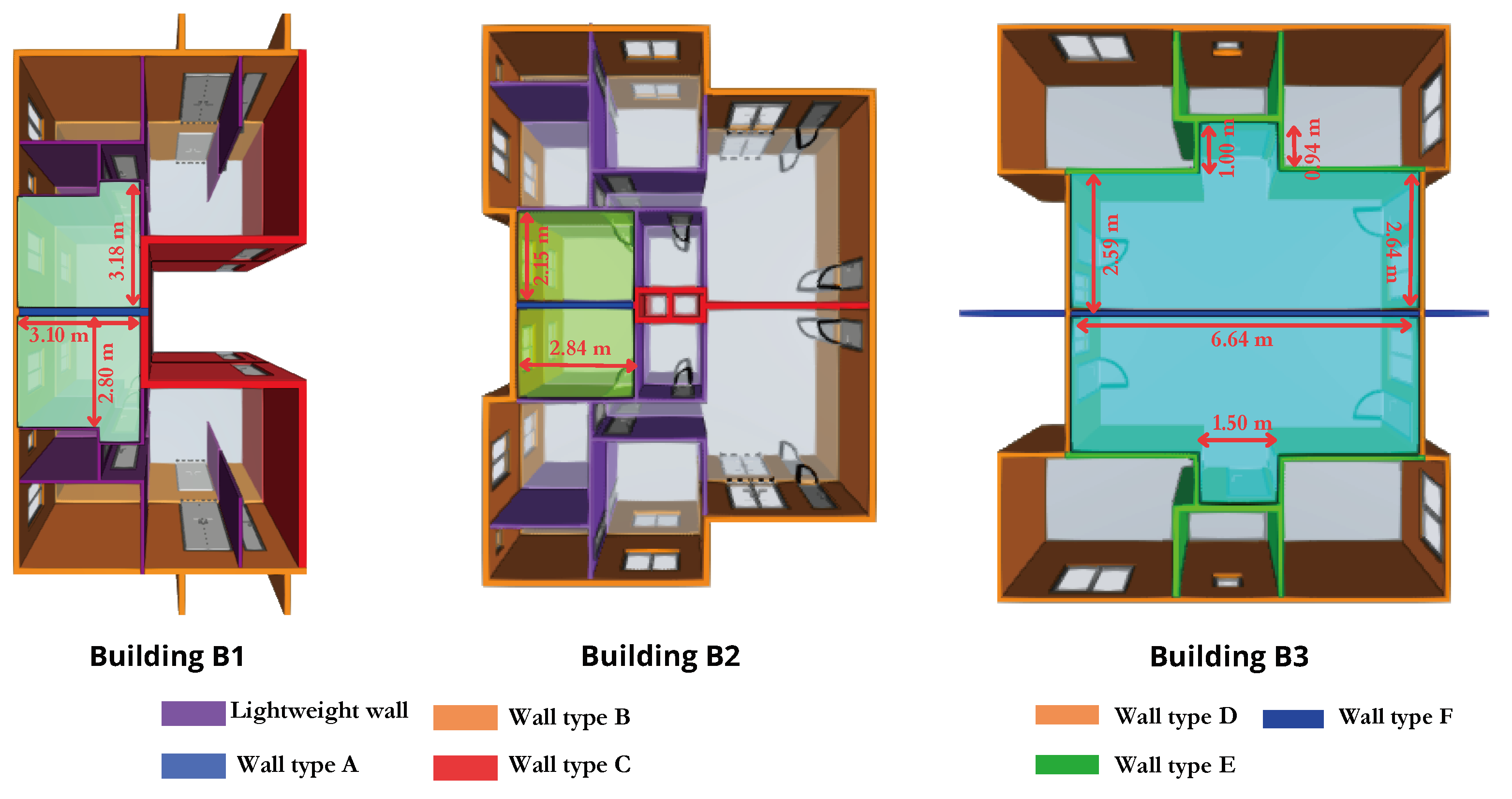


| Element | Detailing (cm) | m (kg/m2) | or (MPa) | (MPa) |
|---|---|---|---|---|
| Wall type A | 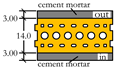 | 271.2 | 3.26 | 1.88 |
| Wall type B | 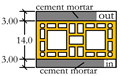 | 151.0 | 5.62 | 0.34 |
| Wall type C | 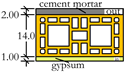 | 212.0 | 5.62 | 0.34 |
| Wall type D | 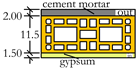 | 159.5 | 4.05 | 0.26 |
| Wall type E | 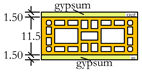 | 144.0 | 4.05 | 0.26 |
| Wall type F | 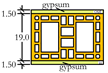 | 181.5 | 5.83 | 0.38 |
| Floor type A | 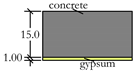 | 375.0 | 20.0 | — |
| Floor type B | 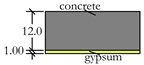 | 303.0 | 20.0 | — |
| Floor type C | 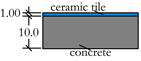 | 240.0 | 20.0 | — |
| Material | Density (kg/m3) | (GPa) | (GPa) |
|---|---|---|---|
| Gypsum mortar | 1500.0 [27] | 4.00 [28] | 2.00 [29,30] |
| Lime cement mortar | 1900.0 [27] | 7.40 [31] | 5.08 [31] |
| Concrete | 2400.0 [27] | 34.7 [26] | 30.0 [25] |
| (dB) | |||
|---|---|---|---|
| B1 | B2 | B3 | |
| Measured value (dB) | 42 (−1;−2) | 40 (−1;−2) | 38 (0;−1) |
| ISO 12354-1 model with (dB) | 40 (−2;−6) | 38 (−1;−5) | 37 (−2;−6) |
| ISO 12354-1 model with (dB) | 39 (−1;−4) | 38 (−1;−5) | 36 (−1;−5) |
| Orthotropic behavior with (dB) | 42 (−2;−5) | 40 (−1;−4) | 38 (−1;−5) |
| Orthotropic behavior with (dB) | 41 (−1;−4) | 40 (−2;−4) | 37 (−1;−4) |
| ID | Emission Room V (m3) | Reception Room V (m3) | Required (dB) | Measured (dB) | Equation (27) |
|---|---|---|---|---|---|
| B1 | 23.1 m3 | 23.1 m3 | 45 | 42 | Not applicable |
| B2 | 20.3 m3 | 20.3 m3 | 45 | 40 | Not applicable |
| B3 | 48.7 m3 | 48.7 m3 | 40 | 38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scoczynski Ribeiro, R.; Arnela, M.; Braz-César, M.T.; Bosse, R.M.; Silvestro, L.; Gidrão, G.d.M.S.; Kempka, M.; Silva, D.A.; Farias Czap, M.M. Evaluating Airborne Sound Insulation in Dwellings Constructed with Hollow Ceramic Blocks under Brazilian Housing Policies. Buildings 2024, 14, 813. https://doi.org/10.3390/buildings14030813
Scoczynski Ribeiro R, Arnela M, Braz-César MT, Bosse RM, Silvestro L, Gidrão GdMS, Kempka M, Silva DA, Farias Czap MM. Evaluating Airborne Sound Insulation in Dwellings Constructed with Hollow Ceramic Blocks under Brazilian Housing Policies. Buildings. 2024; 14(3):813. https://doi.org/10.3390/buildings14030813
Chicago/Turabian StyleScoczynski Ribeiro, Rodrigo, Marc Arnela, Manuel Teixeira Braz-César, Rúbia Mara Bosse, Laura Silvestro, Gustavo de Miranda Saleme Gidrão, Mariane Kempka, Dyorgge Alves Silva, and Marcela Maier Farias Czap. 2024. "Evaluating Airborne Sound Insulation in Dwellings Constructed with Hollow Ceramic Blocks under Brazilian Housing Policies" Buildings 14, no. 3: 813. https://doi.org/10.3390/buildings14030813
APA StyleScoczynski Ribeiro, R., Arnela, M., Braz-César, M. T., Bosse, R. M., Silvestro, L., Gidrão, G. d. M. S., Kempka, M., Silva, D. A., & Farias Czap, M. M. (2024). Evaluating Airborne Sound Insulation in Dwellings Constructed with Hollow Ceramic Blocks under Brazilian Housing Policies. Buildings, 14(3), 813. https://doi.org/10.3390/buildings14030813






