Double Drainage Consolidation Theory of Vertical Drains Based on Continuous Drainage Boundary Conditions
Abstract
:1. Introduction
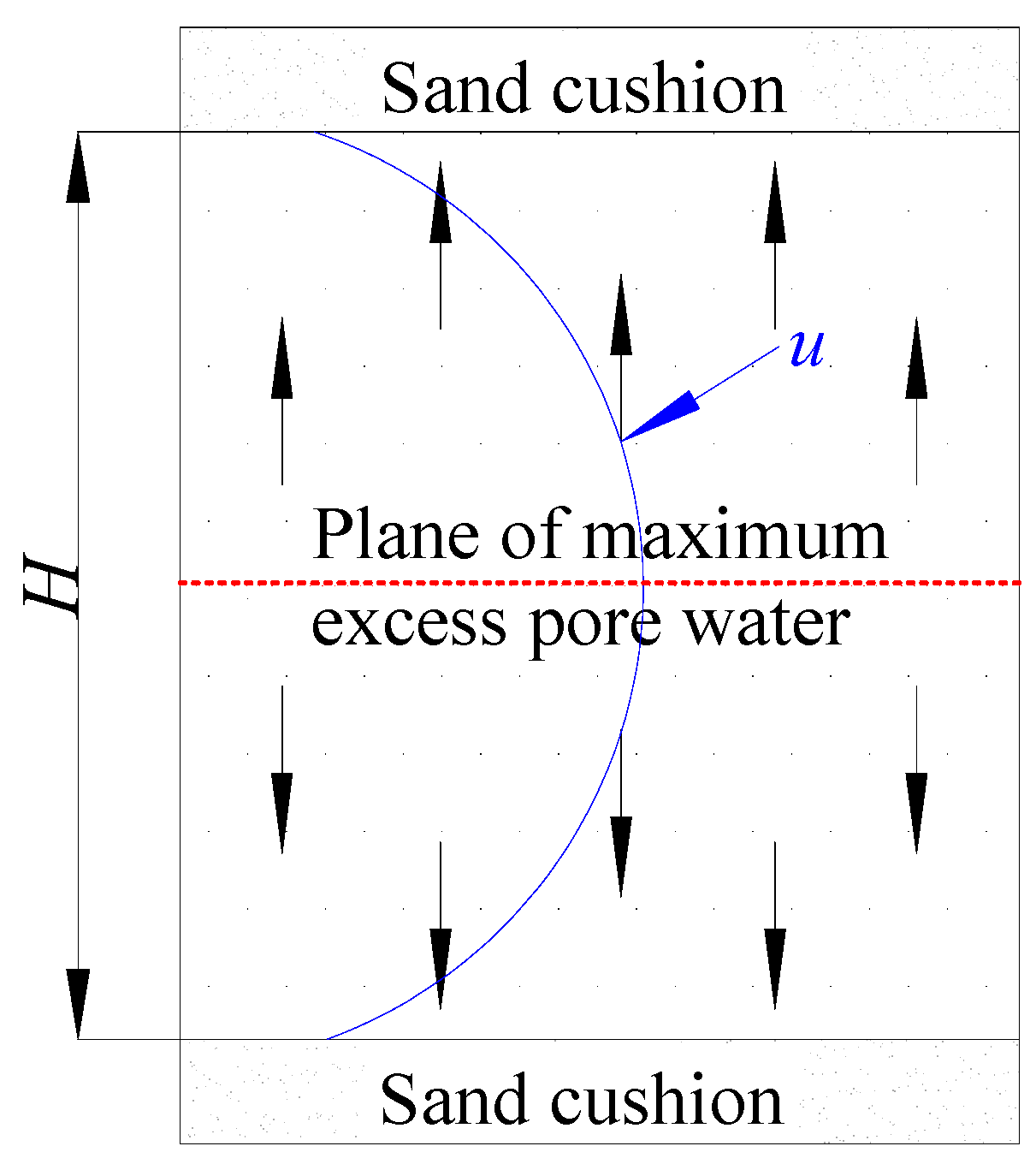
2. Drainage Boundary Condition
- (1)
- At the initial time (t = 0), the excess pore water pressure at any depth cannot dissipate, which means ;
- (2)
- As time goes by, the excess pore water pressure at the boundary decreases monotonously;
- (3)
- When the consolidation time is sufficiently long, the excess pore water pressure in the soil is completely dissipated, that is, when , u = 0.
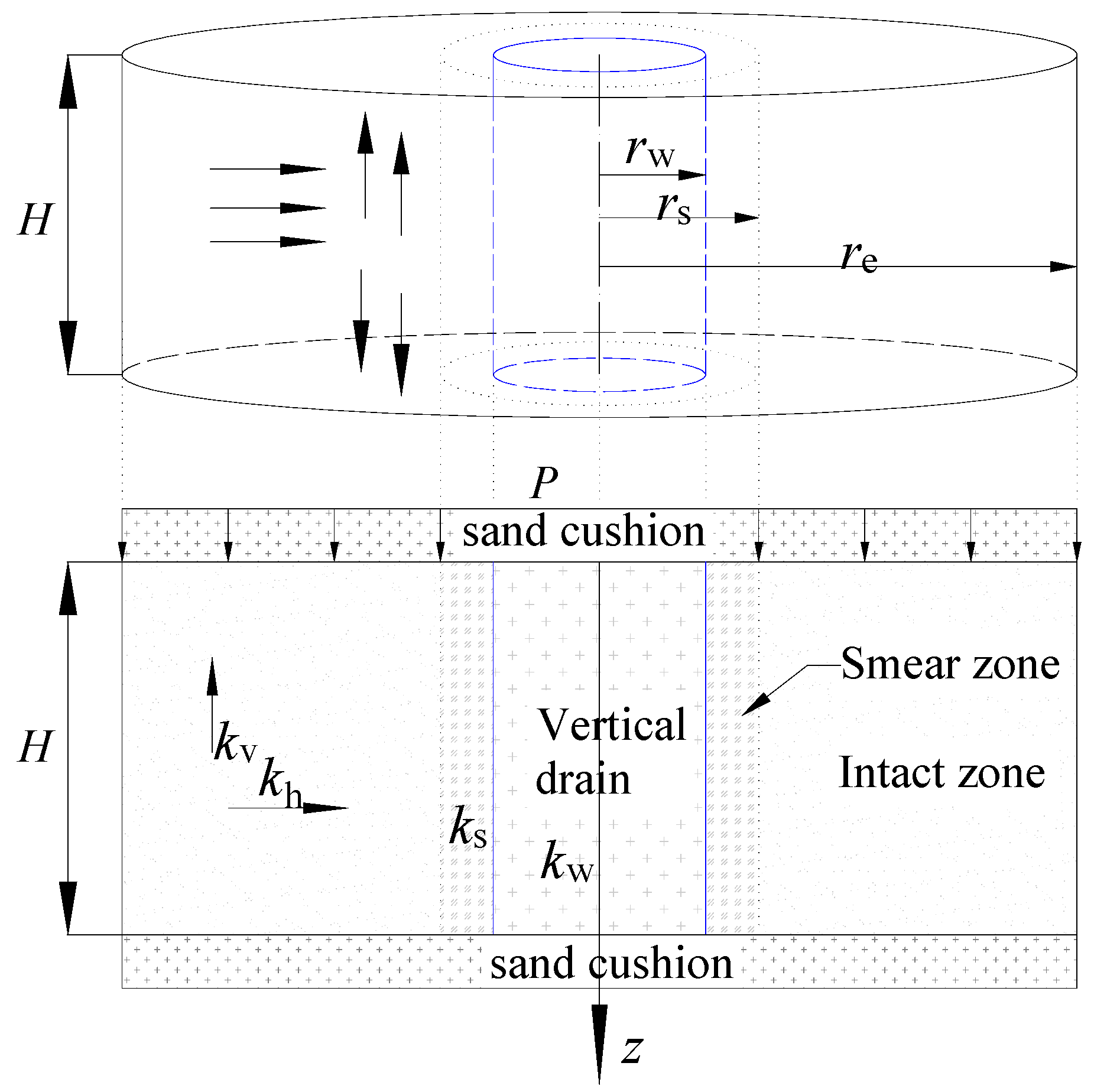
3. Double Drainage Consolidation for Vertical Drains
3.1. Assumptions
- (1)
- The equal strain hypothesis is adopted as the surcharge load is uniformly distributed over the large ground surface, and the seepage flow can be described by Darcy’s law;
- (2)
- At any time, the amount of water flowing into the vertical drain from the surrounding soil is equal to the amount that is discharged at drainage boundaries from the vertical drain;
- (3)
- During the process of consolidation, the permeability and compression coefficients remain unchanged;
- (4)
- The contribution of the soil’s self-weight to the consolidation process is ignored.
3.2. Derivation of Governing Equation
- (1)
- Strain equilibrium
- (2)
- Seepage flow continuity
3.3. Derivation of Analytical Solution
3.4. Evaluation of the Proposed Solution
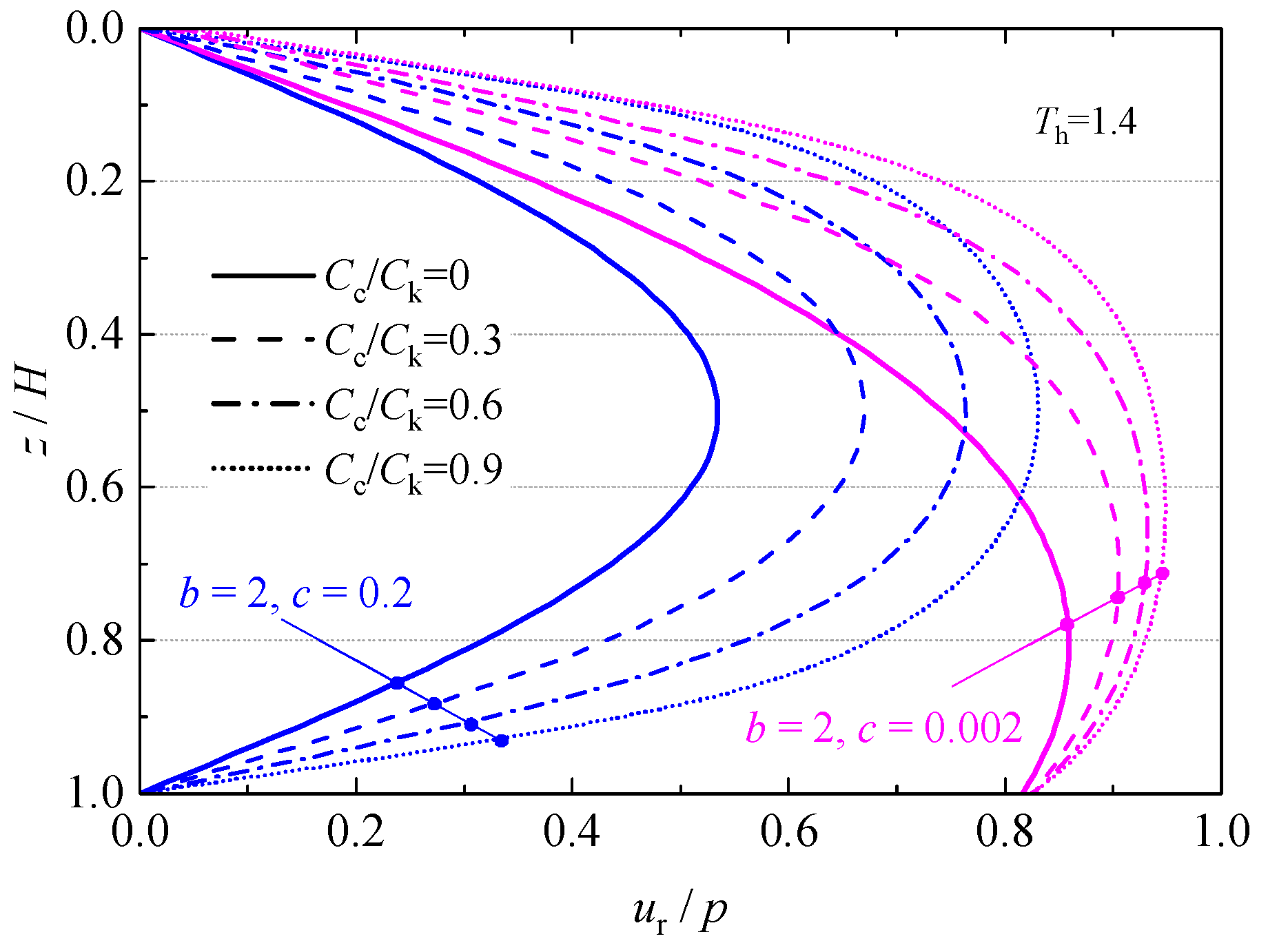
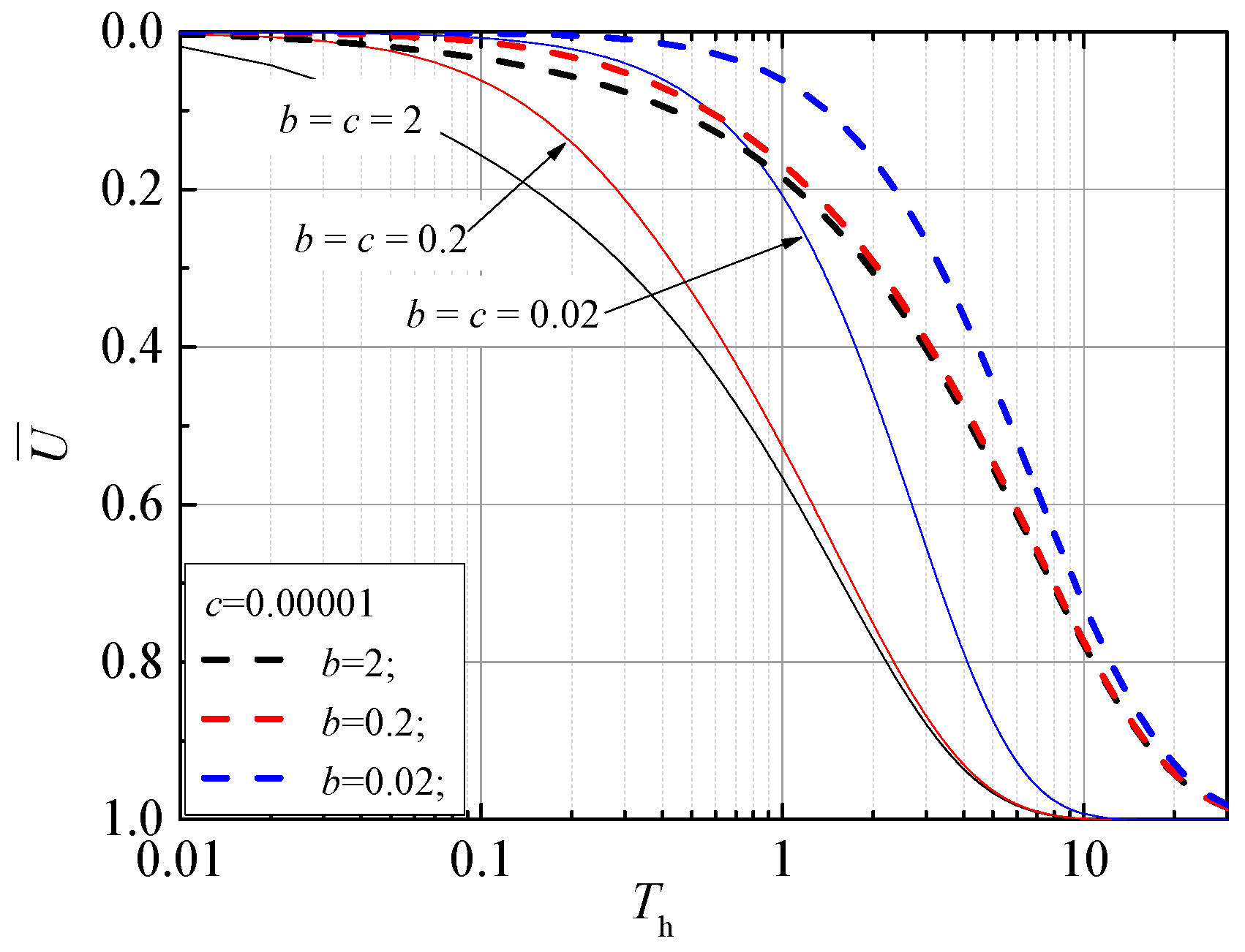
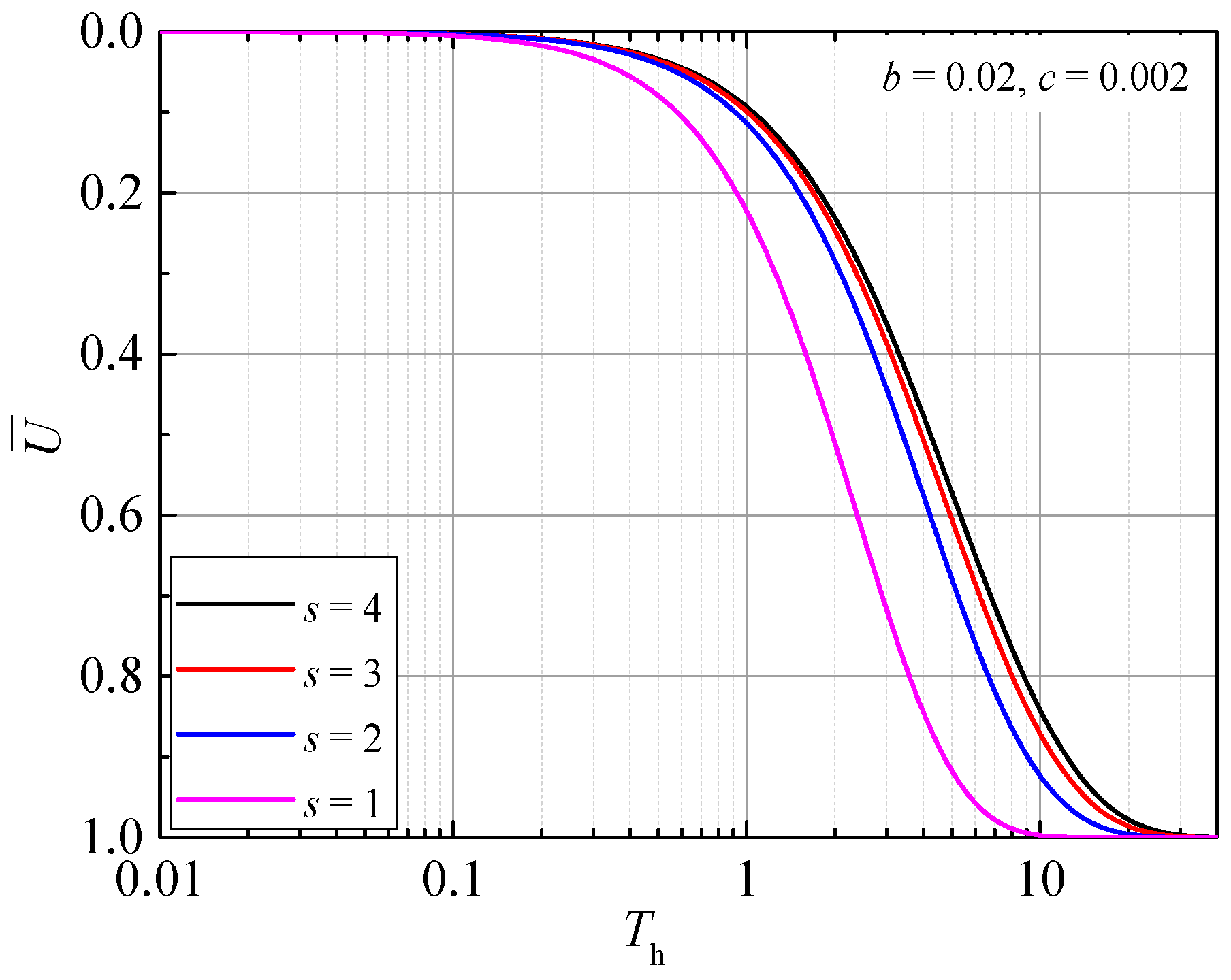
4. Parametric Analysis
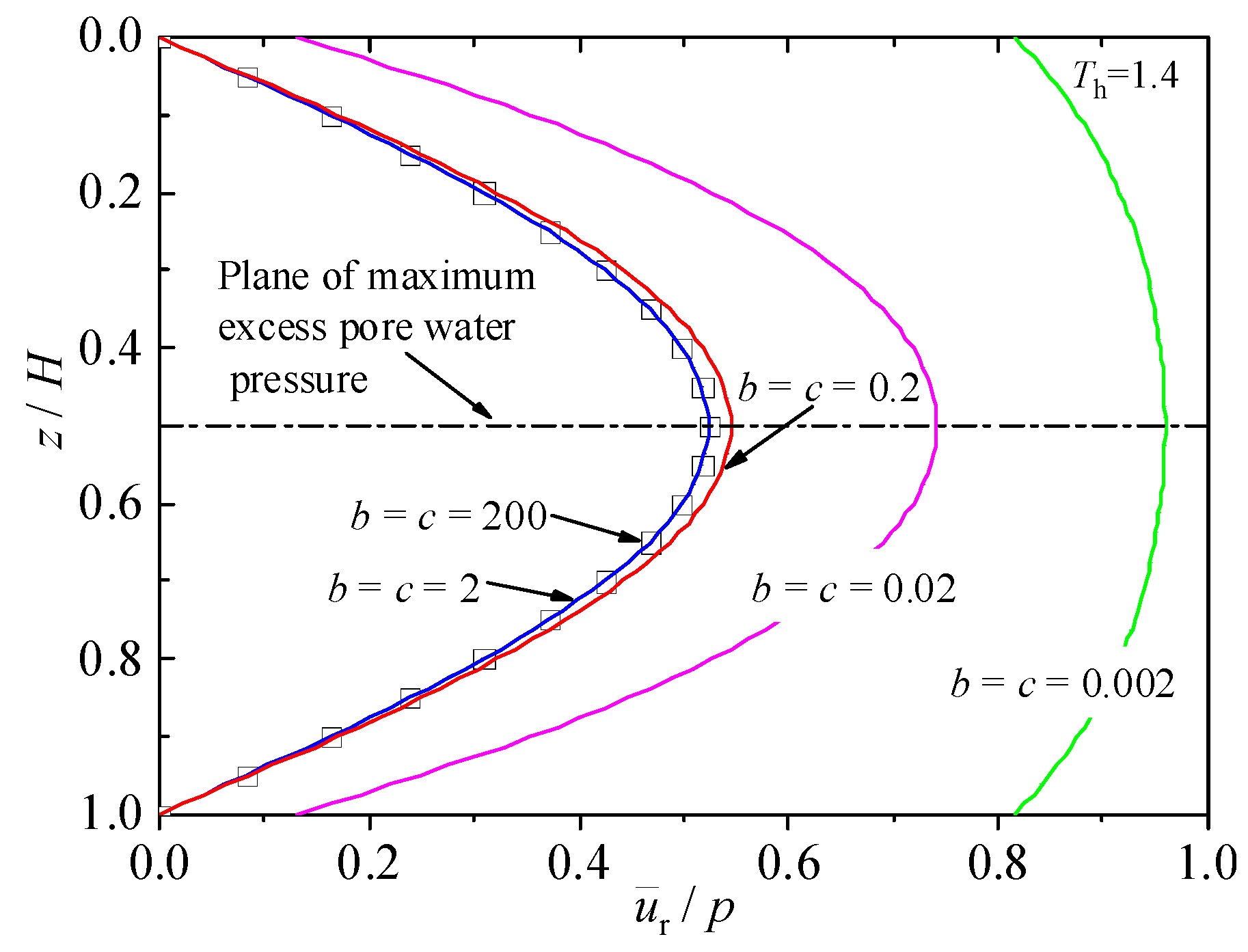
4.1. Average Excess Pore Water Pressure
4.2. Average Consolidation Degree
5. Conclusions
- (1)
- By varying the interface parameters b and c, continuous boundary conditions can simulate drainage capacity changes over time from fully permeable to completely impermeable, overcoming the limitations of traditional boundary conditions that can only model extreme drainage states.
- (2)
- Boundary drainage capacity significantly influences the consolidation process. As the interface parameters decrease, the drainage capacity of the continuous drainage boundary decreases, leading to a noticeable reduction in the consolidation rate of the foundation soil.
- (3)
- Under continuous drainage boundary conditions, when the drainage capacities of the upper and lower interfaces differ, the maximum excess pore water pressure plane is no longer located at the mid-high level of the foundation soil. This achievement is challenging for traditional consolidation theories.
- (4)
- The interaction between soil nonlinearity and foundation boundary permeability has a significant impact on consolidation characteristics. Soil nonlinearity parameter Cc/Ck with a value of 0 (without considering the nonlinearity) results in the shortest consolidation time, while on the contrary, larger values of Cc/Ck (Cc/Ck = 0.9) are less favorable for pore pressure dissipation or soil consolidation.
- (5)
- The consolidation rate under dual drainage conditions is significantly faster than under single drainage conditions. The drainage capacity of the bottom boundary should not be overlooked, and horizontal drainage trenches (such as sand cushions) can be installed before filling with dredged material to accelerate the consolidation process.
- (6)
- The well resistance effect and the smear effect have obvious adverse influences on the dissipation of average excess pore water pressure. Therefore, it is important to reduce the disturbance around vertical drains and increase the permeability of vertical drains as far as possible.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chan, C.-M. Geo-Parametric Study of Dredged Marine Clay with Solidification for Potential Reuse as Good Engineering Soil. Environ. Earth Sci. 2016, 75, 941. [Google Scholar] [CrossRef]
- Chai, J.; Anda, R. Cyclic Loads Induced Consolidation Deformation of PVD Unit Cells. Transp. Geotech. 2023, 38, 100911. [Google Scholar] [CrossRef]
- Xu, Z.; Cui, P.; Cao, W.; Zhang, X.; Zhang, J. Large-Strain Nonlinear Consolidation of Sand-Drained Foundations Considering Vacuum Preloading and the Variation in Radial Permeability Coefficient. Buildings 2023, 13, 2843. [Google Scholar] [CrossRef]
- Barron, R.A. Consolidation of Fine-Grained Soils by Drain Wells by Drain Wells. Trans. Am. Soc. Civ. Eng. 1948, 113, 718–742. [Google Scholar] [CrossRef]
- Hansbo, S.; Jamiolkowski, M.; Kok, L. Consolidation by Vertical Drains. Géotechnique 1981, 31, 45–66. [Google Scholar] [CrossRef]
- Wang, Z.-F.; Shen, S.-L.; Ho, C.-E.; Kim, Y.-H. Investigation of Field-Installation Effects of Horizontal Twin-Jet Grouting in Shanghai Soft Soil Deposits. Can. Geotech. J. 2013, 50, 288–297. [Google Scholar] [CrossRef]
- Yoshikuni, H.; Nakanodo, H. Consolidation of Soils by Vertical Drain Wells with Finite Permeability. Soils Found. 1974, 14, 35–46. [Google Scholar] [CrossRef] [PubMed]
- Basack, S.; Nimbalkar, S. Free strain analysis of the performance of vertical drains for soft soil improvement. Geomech. Eng. 2017, 13, 963–975. [Google Scholar]
- Geng, X.; Yu, H.-S. A Large-Strain Radial Consolidation Theory for Soft Clays Improved by Vertical Drains. Géotechnique 2017, 67, 1020–1028. [Google Scholar] [CrossRef]
- Chai, J.-C.; Miura, N. Investigation of Factors Affecting Vertical Drain Behavior. J. Geotech. Geoenviron. Eng. 1999, 125, 216–226. [Google Scholar] [CrossRef]
- Kim, R.; Hong, S.-J.; Lee, M.-J.; Lee, W. Time Dependent Well Resistance Factor of PVD. Mar. Georesour. Geotechnol. 2011, 29, 131–144. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, J.; Liu, Z. Large-Strain Elastic Viscoplastic Consolidation of Vertical Drains with Non-Darcian Flow Incorporating Well Resistance and Smear Zone. Int. J. Geomech. 2023, 23, 04022246. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Xie, K.H.; Wang, Z. Consolidation Analysis of Composite Ground Improved by Granular Columns Considering Variation of Permeability Coefficient of Soil. In Ground Modification and Seismic Mitigation, Proceedings of the GeoShanghai Conference, Shanghai, China, 6–8 June 2006; American Society of Civil Engineers: Reston, VA, USA, 2006; pp. 135–142. [Google Scholar] [CrossRef]
- Walker, R.; Indraratna, B. Vertical Drain Consolidation with Parabolic Distribution of Permeability in Smear Zone. J. Geotech. Geoenviron. Eng. 2006, 132, 937–941. [Google Scholar] [CrossRef]
- Nguyen, B.-P.; Kim, Y.-T. Radial Consolidation of PVD-Installed Normally Consolidated Soil with Discharge Capacity Reduction Using Large-Strain Theory. Geotext. Geomembr. 2019, 47, 243–254. [Google Scholar] [CrossRef]
- Azari, B.; Fatahi, B.; Khabbaz, H. Assessment of the Elastic-Viscoplastic Behavior of Soft Soils Improved with Vertical Drains Capturing Reduced Shear Strength of a Disturbed Zone. Int. J. Geomech. 2016, 16, B4014001. [Google Scholar] [CrossRef]
- Wu, X.-T.; Liu, J.-N.; Xie, Z.-M. Deformation and Strength Characteristics of Marine Soft Soil Treated by Prefabricated Vertical Drain-Assisted Staged Riprap under Seawall Construction. Buildings 2023, 13, 2322. [Google Scholar] [CrossRef]
- Gray, H. Simultaneous Consolidation of Contiguous Layers of Unlike Compressible Soils; American Society of Civil Engineers: Reston, VA, USA, 1944. [Google Scholar]
- Lei, G.H.; Fu, C.W.; Ng, C.W.W. Vertical-Drain Consolidation Using Stone Columns: An Analytical Solution with an Impeded Drainage Boundary under Multi-Ramp Loading. Geotext. Geomembr. 2016, 44, 122–131. [Google Scholar] [CrossRef]
- Wang, L.; Sun, D.; Li, L.; Li, P.; Xu, Y. Semi-Analytical Solutions to One-Dimensional Consolidation for Unsaturated Soils with Symmetric Semi-Permeable Drainage Boundary. Comput. Geotech. 2017, 89, 71–80. [Google Scholar] [CrossRef]
- Chen, H.-X.; Feng, S.-J.; Zhu, Z.-W.; Gao, L.; Chen, Z.-L.; Wang, S.-R. One-Dimensional Self-Weight Consolidation of Layered Soil under Variable Load and Semi-Permeable Boundary Condition. Comput. Geotech. 2023, 159, 105431. [Google Scholar] [CrossRef]
- Mei, G.; Chen, Q. Solution of Terzaghi One-Dimensional Consolidation Equation with General Boundary Conditions. J. Cent. South Univ. 2013, 20, 2239–2244. [Google Scholar] [CrossRef]
- Mei, G.-X.; Lok, T.; Xia, J.; Wu, S. One-Dimensional Consolidation with Asymmetrical Exponential Drainage Boundary. Geomech. Eng. 2014, 6, 47–63. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, W.; Mei, G.; Duan, L. Three-Dimensional Consolidation Theory of Vertical Drain Based on Continuous Drainage Boundary. J. Civ. Eng. Manag. 2019, 25, 145–155. [Google Scholar] [CrossRef]
- Mei, G.; Feng, J.; Xu, M.; Ni, P. Estimation of Interface Parameter for One-Dimensional Consolidation with Continuous Drainage Boundary Conditions. Int. J. Geomech. 2022, 22, 04021292. [Google Scholar] [CrossRef]
- Lu, M.-M.; Xie, K.-H.; Guo, B. Consolidation Theory for a Composite Foundation Considering Radial and Vertical Flows within the Column and the Variation of Soil Permeability within the Disturbed Soil Zone. Can. Geotech. J. 2010, 47, 207–217. [Google Scholar] [CrossRef]
- Terzaghi, K. Erdbaumechanik auf Bodenphysikalischer Grundlage; F. Deuticke: Vienna, Austria, 1925. [Google Scholar]
- Xie, K.; Zeng, G. Consolidation Theories for Drain Wells under Equal Strain Condition. Chin. J. Geotech. Eng. 1989, 11, 3–17. [Google Scholar]
- Feng, J.; Ni, P.; Mei, G. One-Dimensional Self-Weight Consolidation with Continuous Drainage Boundary Conditions: Solution and Application to Clay-Drain Reclamation. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 1634–1652. [Google Scholar] [CrossRef]
- Khan, R.M.; Shafighfard, T.; Ali, H.Q.; Mieloszyk, M.; Yildiz, M. Strength prediction and experimental damage investigations of plain woven CFRPs with interacting holes using multi-instrument measurements. Polym. Compos. 2023, 44, 3594–3609. [Google Scholar] [CrossRef]
- Khan, S.A.; Khan, H.A.; Khan, A.; Salamat, S.; Javaid, S.S.; Khan, R.M. Investigation of the mechanical behavior of FDM processed CFRP/Al hybrid joint at elevated temperatures. Thin-Walled Struct. 2023, 192, 111135. [Google Scholar] [CrossRef]
- Ma, K.; Gao, Z.; Wang, J.; Zhang, Y.; Zong, M.; Wu, W.; Mei, G. Nonlinear consolidation finite element analysis of a layered soft soil foundation under multistage loading based on the continuous drainage boundary. Comput. Geotech. 2024, 169, 106220. [Google Scholar] [CrossRef]

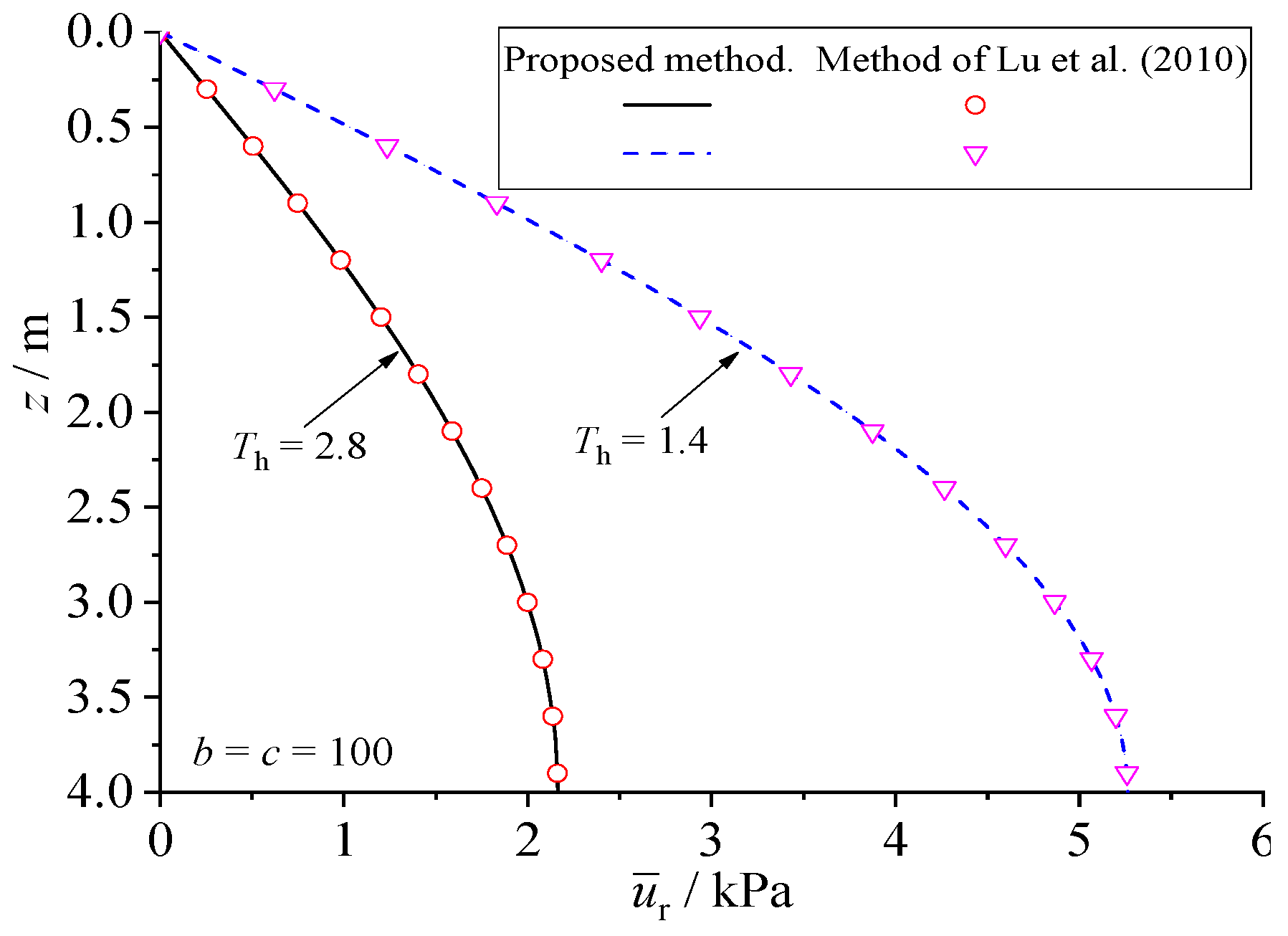






| Depth, H (m) | Permeability Coefficient, (m/d) | (kPa) | Radius, r (m) | |||||
|---|---|---|---|---|---|---|---|---|
| 8 | 4.3 × 10−4 | 2.16 × 10−4 | 4.31 × 10−5 | 1.08 | 2000 | 2.5 | 1 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Hou, B.; Ma, K.; Zhang, J.; Zong, M.; Kong, L. Double Drainage Consolidation Theory of Vertical Drains Based on Continuous Drainage Boundary Conditions. Buildings 2024, 14, 1137. https://doi.org/10.3390/buildings14041137
Zhang Y, Hou B, Ma K, Zhang J, Zong M, Kong L. Double Drainage Consolidation Theory of Vertical Drains Based on Continuous Drainage Boundary Conditions. Buildings. 2024; 14(4):1137. https://doi.org/10.3390/buildings14041137
Chicago/Turabian StyleZhang, Yi, Benchi Hou, Ke Ma, Jing Zhang, Mengfan Zong, and Lingzhou Kong. 2024. "Double Drainage Consolidation Theory of Vertical Drains Based on Continuous Drainage Boundary Conditions" Buildings 14, no. 4: 1137. https://doi.org/10.3390/buildings14041137
APA StyleZhang, Y., Hou, B., Ma, K., Zhang, J., Zong, M., & Kong, L. (2024). Double Drainage Consolidation Theory of Vertical Drains Based on Continuous Drainage Boundary Conditions. Buildings, 14(4), 1137. https://doi.org/10.3390/buildings14041137





