Numerical Investigation on the Seismic Behavior of Novel Precast Beam–Column Joints with Mechanical Connections
Abstract
:1. Introduction
2. Numerical Models of PBCJs-MCs
2.1. Overall Design of the Quasi-Static Test Program
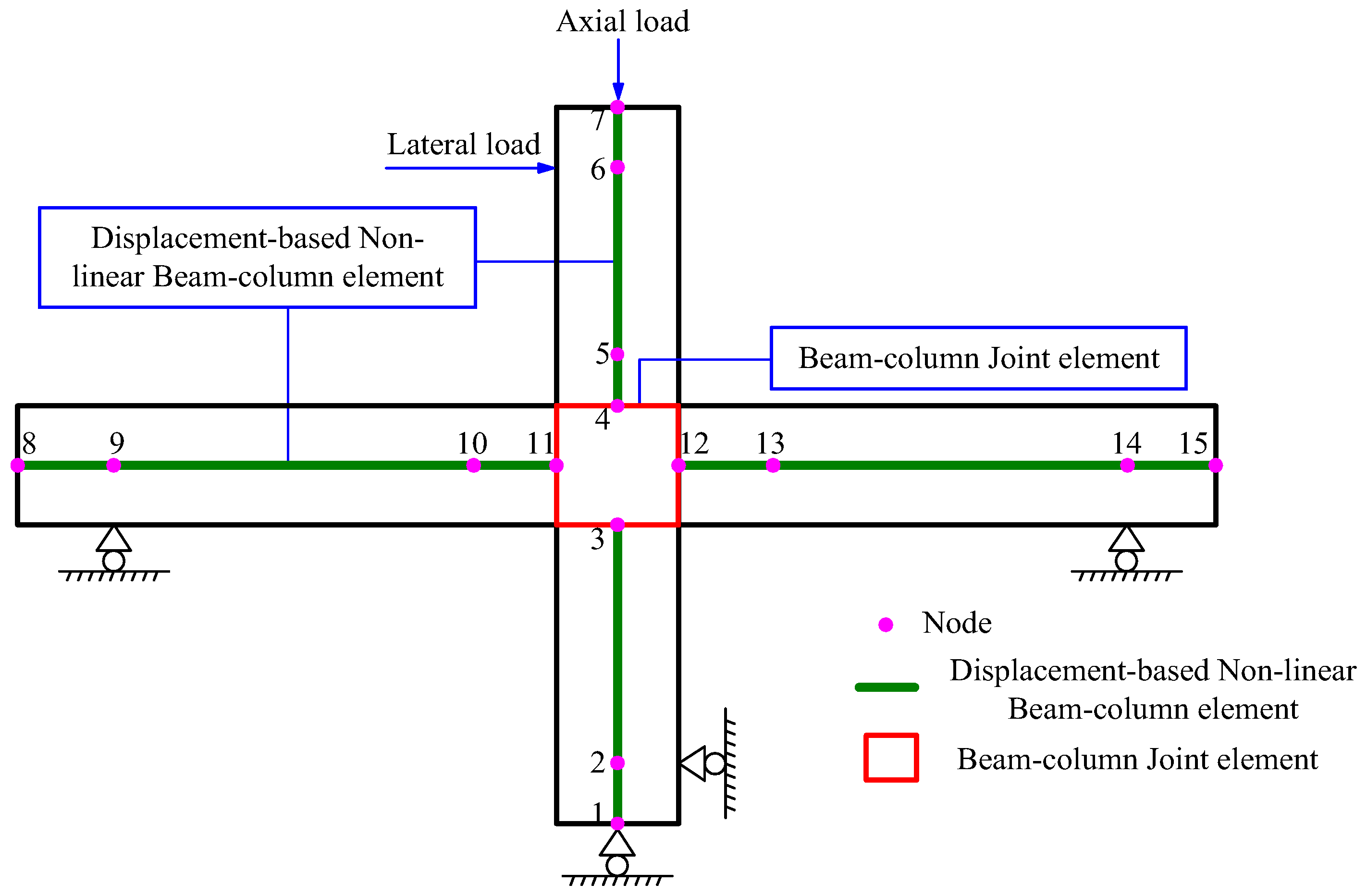
2.2. Establishment of FEMs
2.3. Element
2.4. Constitutive Models
2.4.1. Concrete
2.4.2. Reinforcement
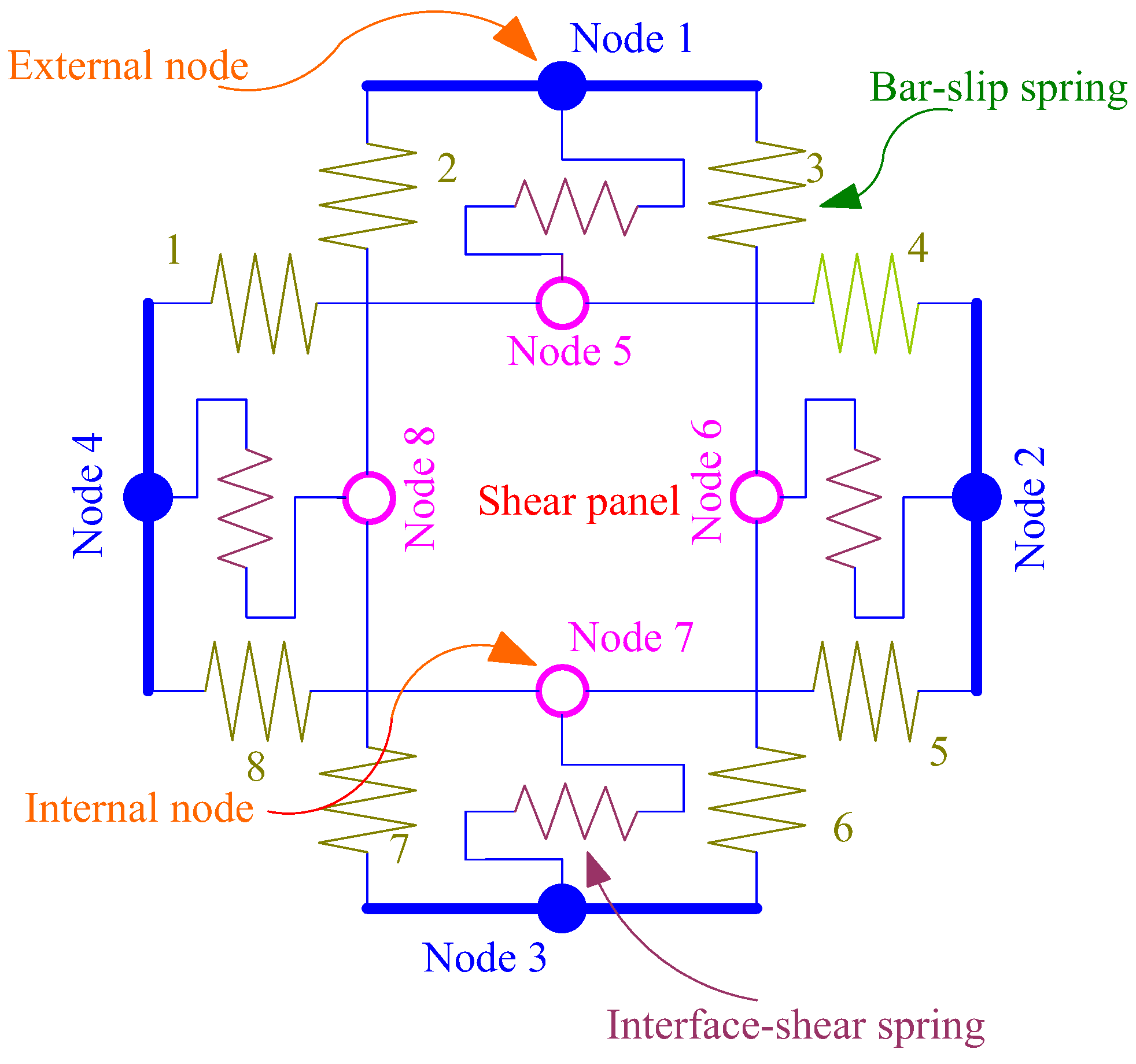
2.4.3. Shear Panel
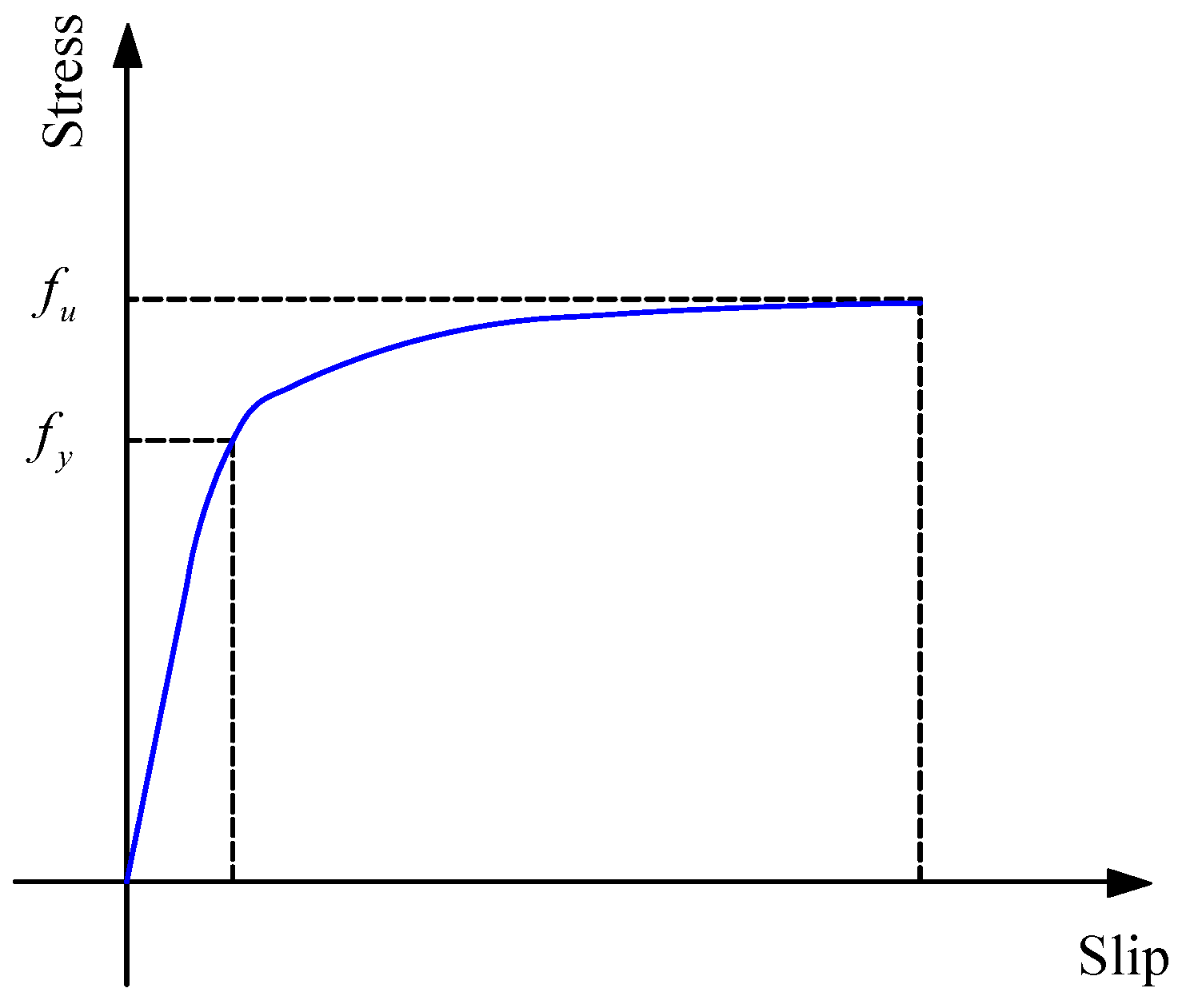
2.4.4. Constitutive Model of Bar–Slip Springs
2.4.5. Constitutive Model of Reinforcement Bond–Slip
3. Numerical Simulation Results and Discussion
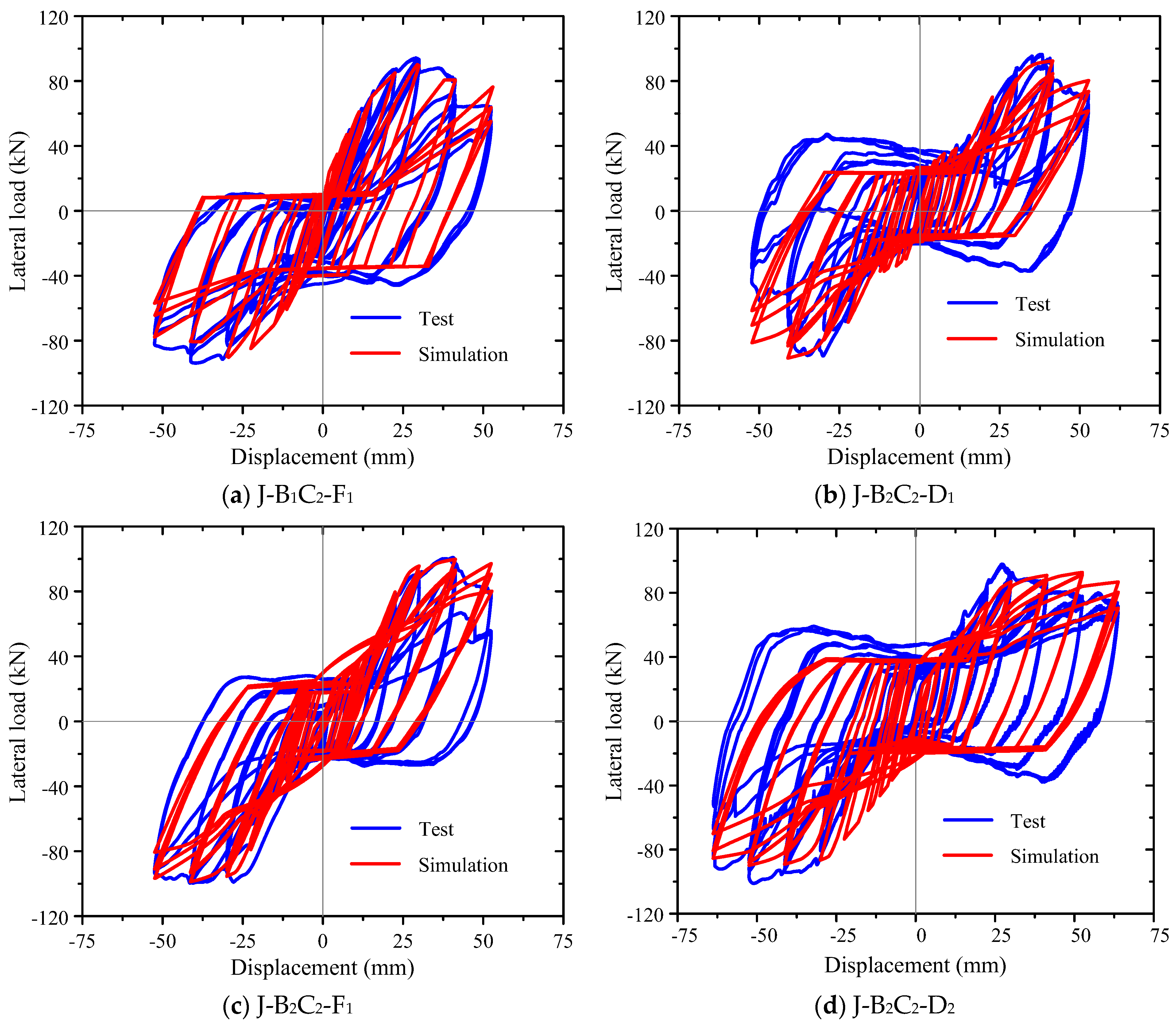
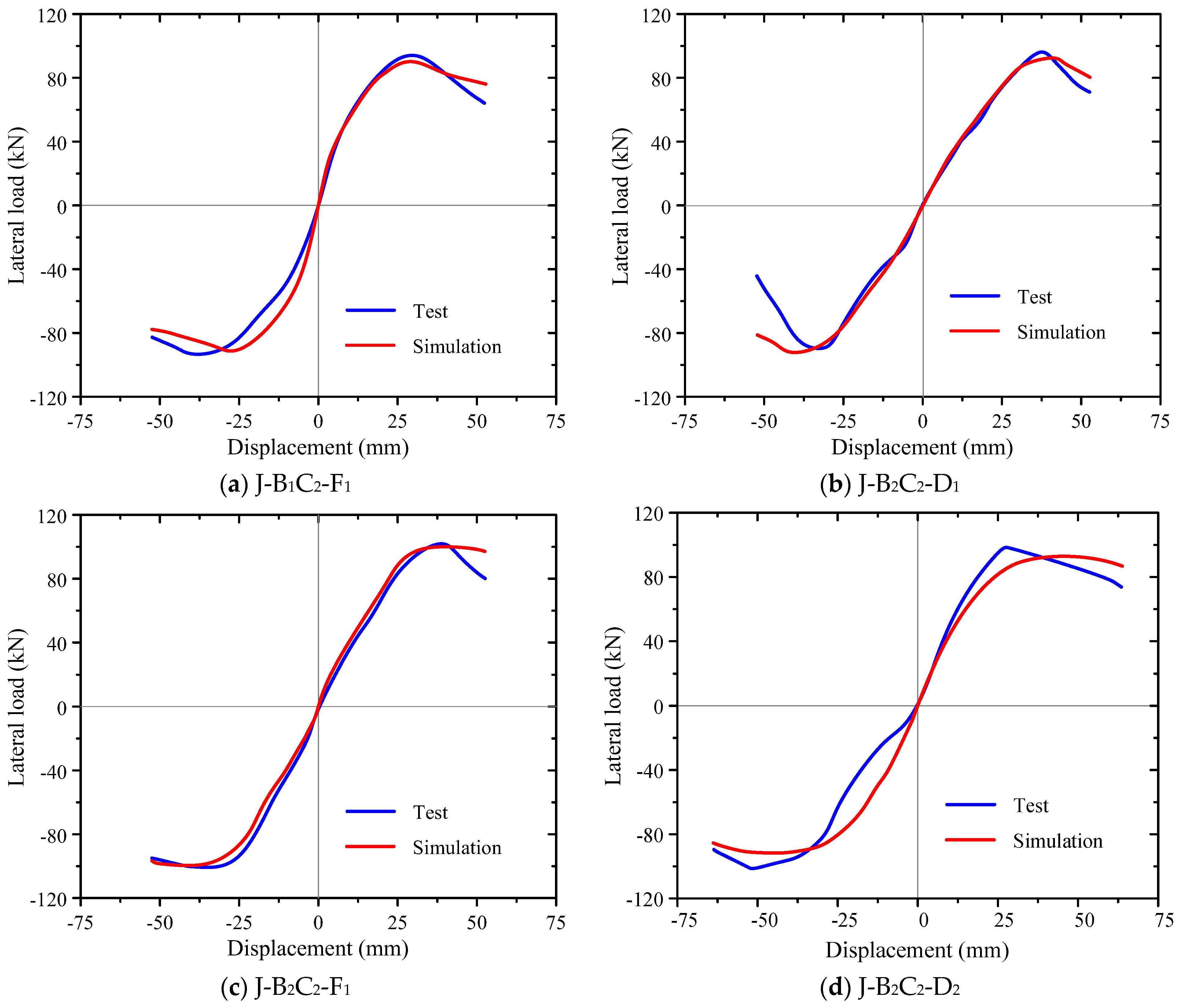
3.1. Hysteresis Curves
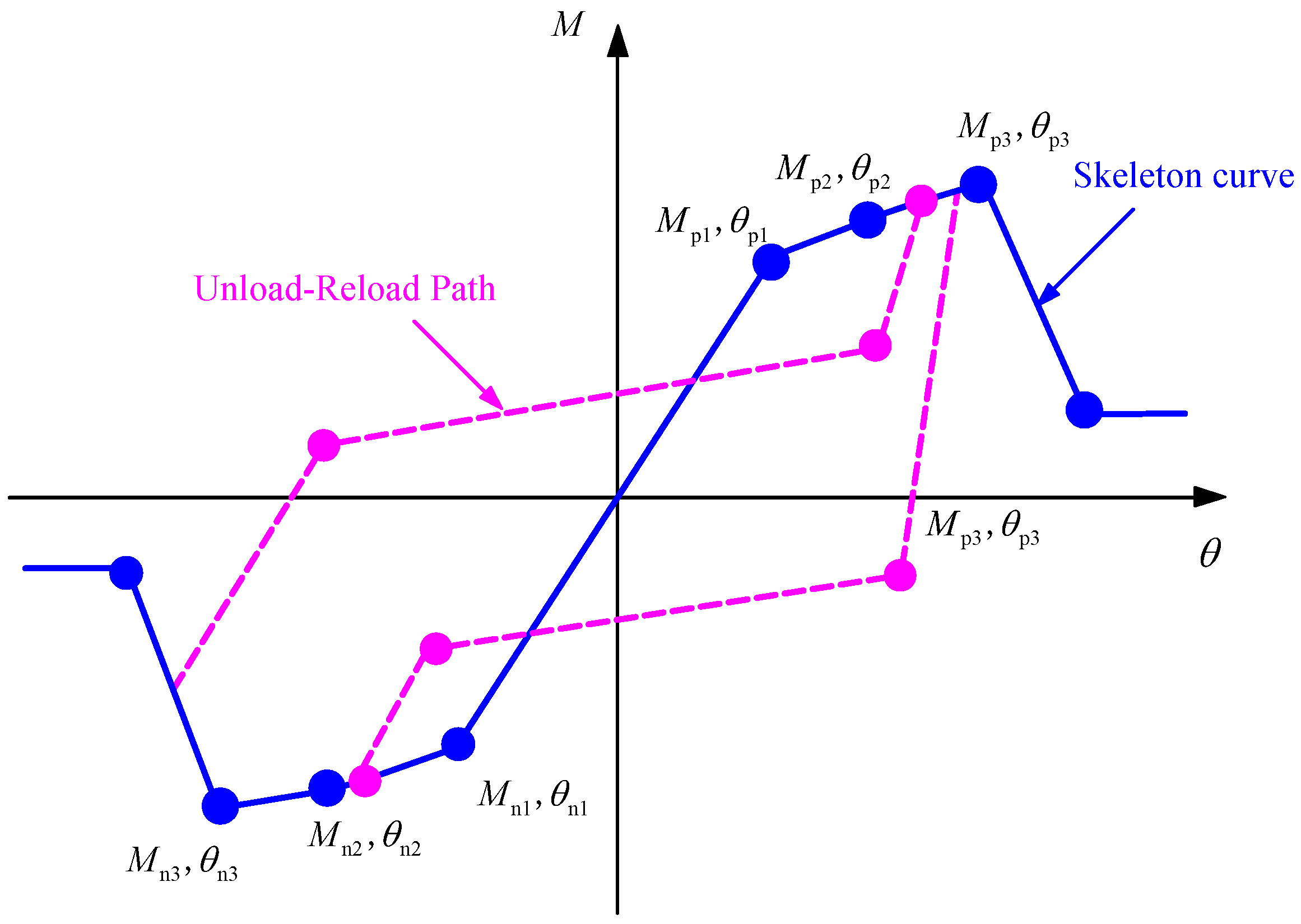
3.2. Skeleton Curves
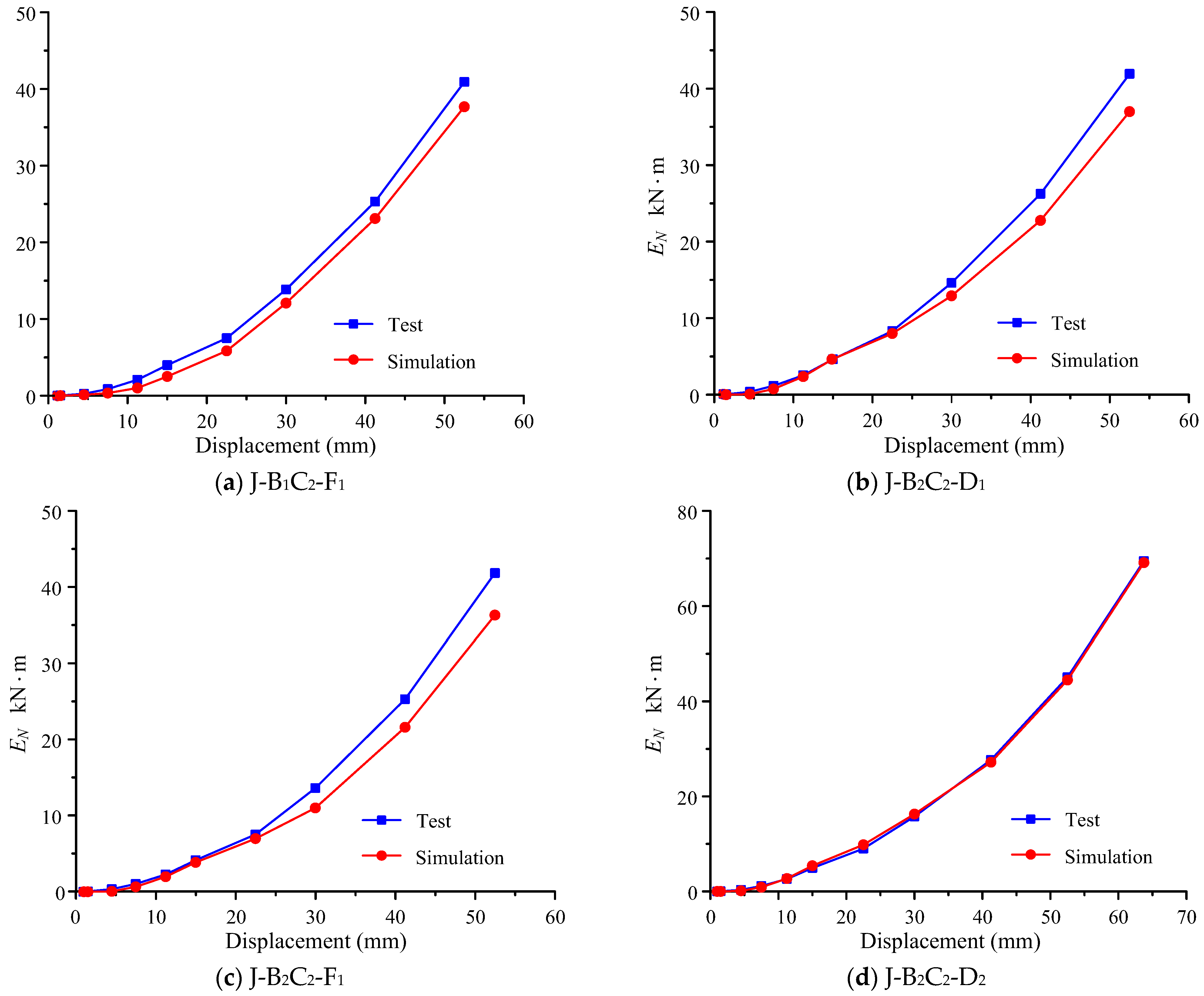
3.3. Energy Dissipation Capacity
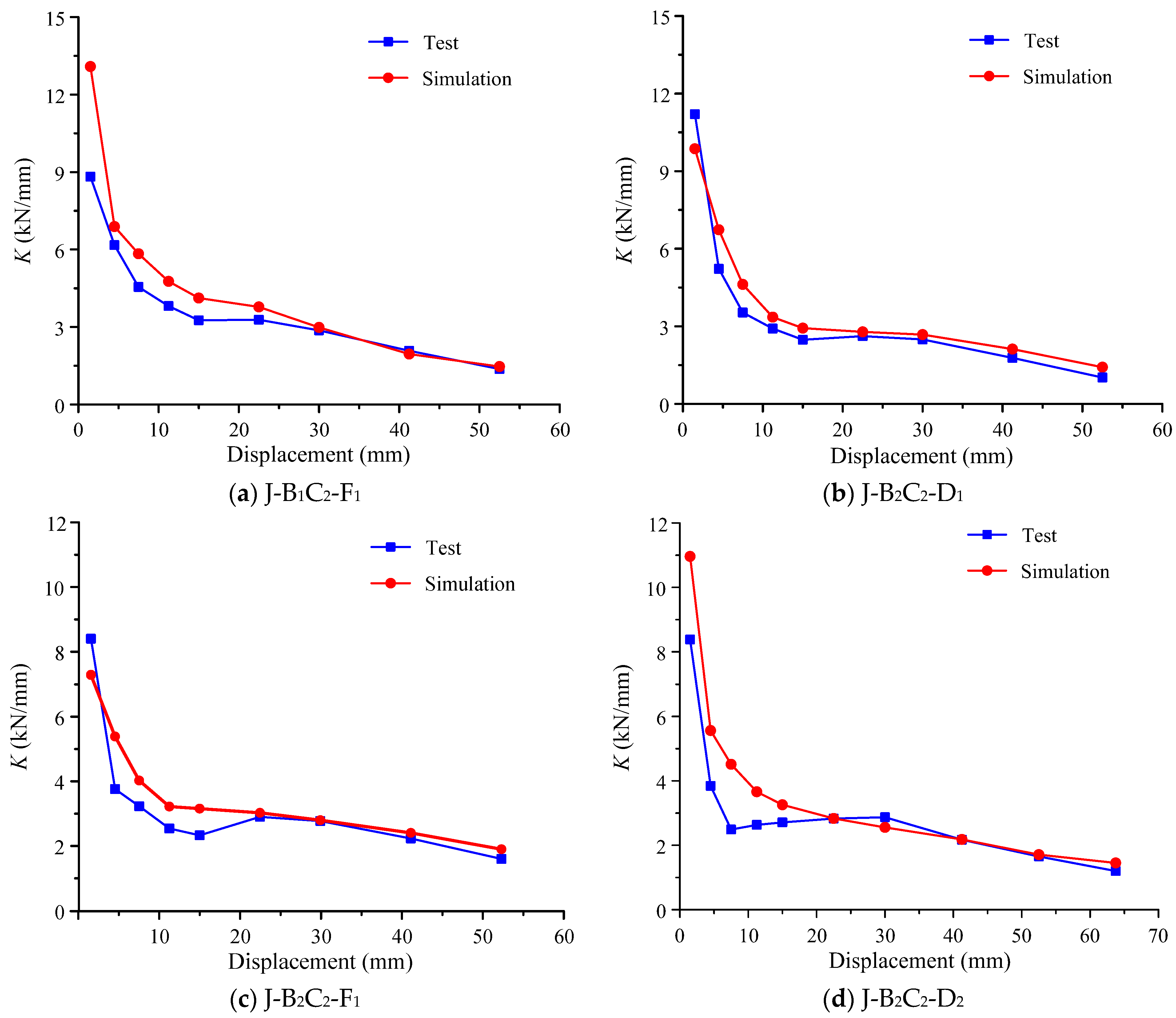
3.4. Stiffness Degradation
4. Parametric Analysis of Effect Factors
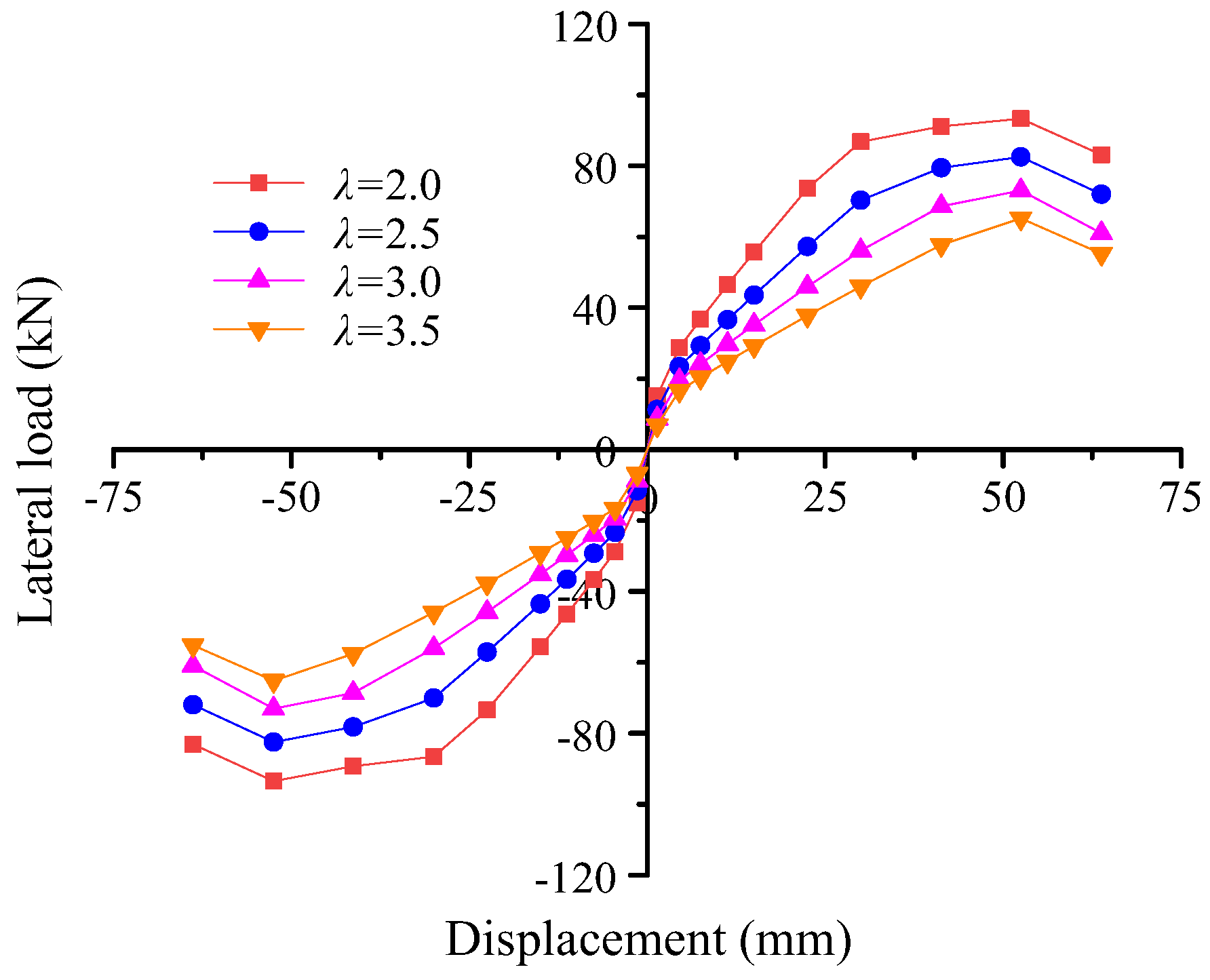
4.1. Effect of the Shear-to-Span Ratio
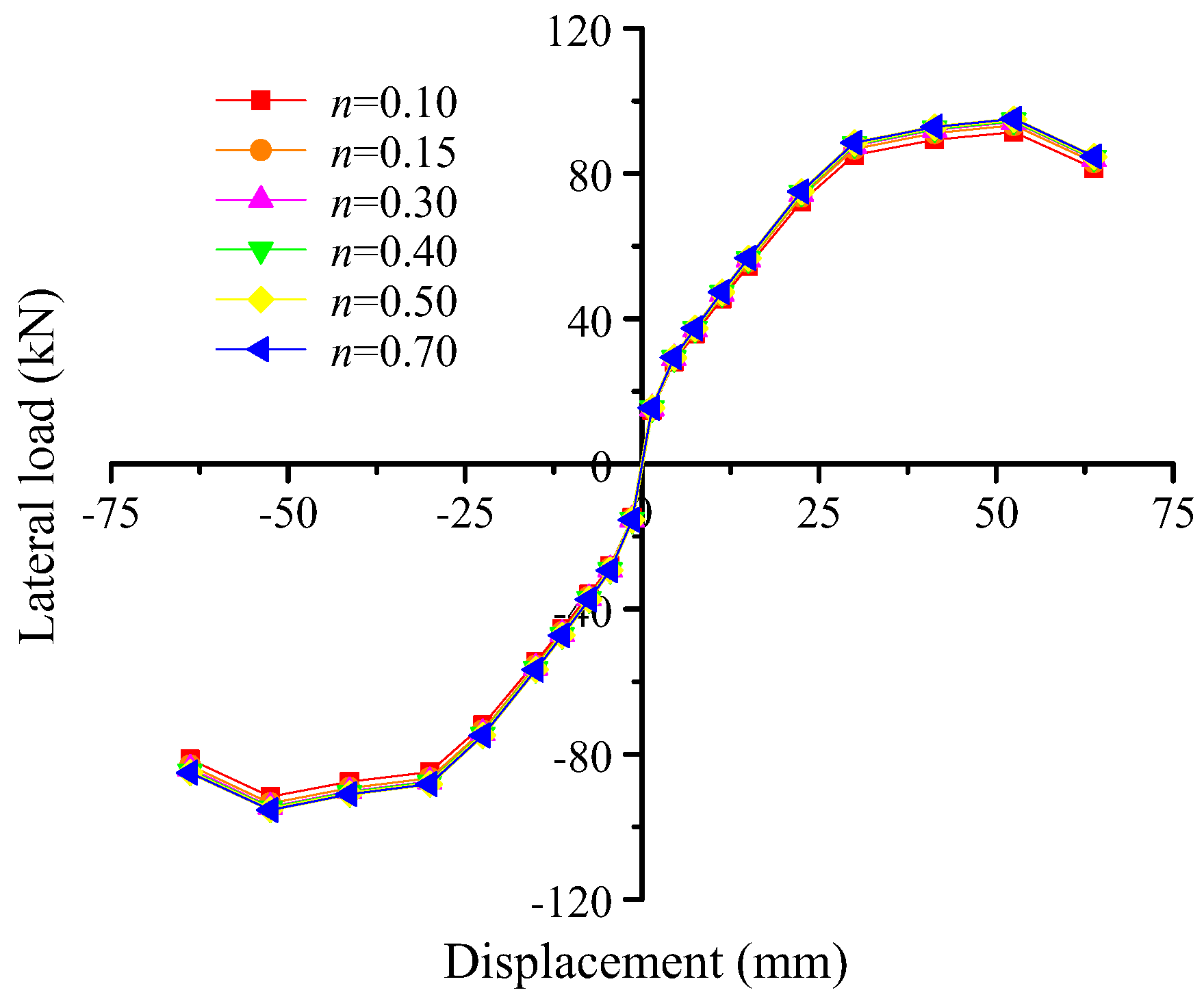
4.2. Effect of the Axial Load Ratio
5. Conclusions and Measurements
- (1)
- The Concrete02 model and Reinforcing Steel model can accurately simulate the constitutive relationship of concrete and reinforcement, respectively. The beam–column joint elements can accurately simulate the different damage behaviors of the joint zone. The Bond_SP01model can accurately simulate the bond–slip between the reinforcing steel, concrete, and mechanical connections.
- (2)
- The simulated hysteresis curves and skeleton curves of the PBCJs-MCs are similar to the experimental results. The simulated seismic behavior indexes, such as bearing capacity, energy dissipation capacity, and stiffness degradation, are not much different from the experimental results, with a relative error of about 15%.
- (3)
- The bearing capacity and displacement ductility coefficients of the PBCJs-MCs decrease rapidly as λ increases. It is recommended that the optimum λ range for PBCJs-MCs is 2.0–2.5. Regarding the high energy dissipation capacity and ductility requirements of the members in regions prone to both seismic and high wind events, it is prudent to use columns with λ > 3.
- (4)
- The axial load ratio has a very small influence on the seismic behavior of the PBCJs-MCs. The effect of the axial load ratio on the seismic behavior of the PBCJs-MCs can be negligible in the case of the PBCJs-MCs with a moderate value of shear-to-span ratio.
- (1)
- Researchers should be down-to-earth, strictly abide by academic ethics, rigorously conduct research to ensure the validity of research results and the reliability of research conclusions, and actively maintain cooperation with enterprises so that the benign development of the assembly building industry can be ensured.
- (2)
- For prefabricated assembly building construction technology, the government should take assembly building as a key research support area and provide multi-party support in terms of research funding and research conditions, strengthen the industry’s supervision and review mechanism to ensure the safety of the technology, and leave its beneficial attributes to the market to decide.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Li, X.P.; Zheng, X.H.; Song, Z. Experimental study on seismic response of precast bridge piers with double-grouted sleeve connections. Eng. Struct. 2020, 221, 111023. [Google Scholar] [CrossRef]
- Sun, C.Z.; Zhuang, M.L.; Bai, L.T. Experimental study on seismic behavior of novel precast concrete beam-column joints using mechanical connections. Bull. Earthq. Eng. 2023, 21, 4429–4448. [Google Scholar] [CrossRef]
- Qiao, D.H.; Xu, Y.Q.; Zhang, X.; Gao, L.; Yu, C.R.; Yang, J.; Zhu, H.B.; Qiao, Y.; Shao, Y.F.; Zhang, W.H. Seismic behaviour and size effect of column base joints with inverted exposed grouted sleeves. J. Build. Eng. 2022, 51, 104333. [Google Scholar] [CrossRef]
- Hadade, M.; Ferreira, M.; Carvalho, R.C.; Catoia, B. Moment-rotation response of beam-column connections in precast concrete structures. Solid State Phenom. 2017, 259, 269–274. [Google Scholar] [CrossRef]
- Sun, C.Z.; Zhuang, M.L.; Wang, Z.B.; Chen, B.D.; Gao, L.; Qiao, Y.; Zhu, H.B.; Zhang, W.H.; Yang, J.; Yu, C.R. Experimental investigation on the seismic behavior of prefabricated fiber reinforced concrete beam-column joints using grouted sleeve connections. Struc. Concr. 2023, 24, 4702–4718. [Google Scholar] [CrossRef]
- Chen, W.H.; Feng, K.; Wang, Y. Seismic Performance of a Novel Precast Beam-Column Joint Using Shape Memory Alloy Fibers-Reinforced Engineered Cementitious Composites. Buildings 2022, 12, 1404. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, D.C.; Wu, G. Experimental Study on Seismic Behavior of Precast Bolt-Connected Steel-Members End-Embedded Concrete (PBSEC) Beam-Column Connections. Buildings 2022, 12, 1652. [Google Scholar] [CrossRef]
- Zheng, J.H.; Pan, Z.Z.; Zhen, H.; Deng, X.H.; Zheng, C.M.; Xie, L.P.; Xiong, Z.; Li, L.J.; Liu, F. Experimental Investigation on the Seismic Behavior of Precast Concrete Beam-Column Joints with Five-Spiral Stirrups. Buildings 2023, 13, 2357. [Google Scholar] [CrossRef]
- Peng, W.; Lu, W.; Liu, S.; Liu, Y.; Xu, L.; Li, F. Experimental and Numerical Study on the Seismic Performances of Reinforcement-Embedded RC Column-to-Precast Cap Beams with Socket Connections. Buildings 2023, 13, 2367. [Google Scholar] [CrossRef]
- Bert, C.W.; Malik, M. Differential quadrature: A powerful new technique for analysis of composite structures. Compos. Struct. 1997, 39, 179–189. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Gu, Y.; Liu, J.L. A domain-decomposition generalized finite difference method for stress analysis in three-dimensional composite materials. Appl. Math. Lett. 2020, 104, 106226. [Google Scholar] [CrossRef]
- Kabir, H.; Aghdam, M.M. A generalized 2D Bézier-based solution for stress analysis of notched epoxy resin plates reinforced with graphene nanoplatelets. Thin Wall. Struct. 2021, 169, 108484. [Google Scholar] [CrossRef]
- Ni, X.Y.; Qiang, Z.; Li, Y.Z. Cyclic test and numerical analysis of the seismic behavior of concrete columns reinforced by HRB600 steel bars. J. Build. Eng. 2022, 50, 104211. [Google Scholar] [CrossRef]
- Kremmyda, G.D.; Fahjan, Y.M.; Tsoukantas, S.G. Nonlinear FE analysis of precast RC pinned beam-to-column connections under monotonic and cyclic shear loading. Bull. Earthq. Eng. 2014, 12, 1615–1638. [Google Scholar] [CrossRef]
- Zoubek, B.; Isakovic, T.; Fahjan, Y.; Fischinger, M. Cyclic failure analysis of the beam-to-column dowel connections in precast industrial buildings. Eng. Struct. 2013, 52, 179–191. [Google Scholar] [CrossRef]
- Cao, X.Y.; Feng, D.C.; Wang, Z.; Gang, W. Investigation on modelling approaches for prefabricated concrete beam-to-column connections using openSEEs. China Civil Eng. 2019, 52, 13–27. [Google Scholar]
- Zhuang, M.L.; Sun, C.Z.; Dong, B. Experimental and numerical investigations on seismic behavior of HTRB630 high-strength steel bars reinforced concrete columns. Case Stud. Constr. Mater. 2022, 17, e01185. [Google Scholar]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. Open System for Earthquake Engineering Simulation User Commandlanguage Manual; University of California: Berkeley, CA, USA, 2009. [Google Scholar]
- Paulay, T. Equilibrium criteria for reinforced concrete beam-column joints. ACI Struct. J. 1989, 86, 635–643. [Google Scholar]
- Pantazopoulou, S.J.; Bonacci, J.F. On earthquake-resistant reinforced concrete frame connections. Can. J. Civil Eng. 1994, 21, 307–328. [Google Scholar] [CrossRef]
- Lowes, L.N.; Altoontash, A. Modeling Reinforced Concrete Beam-Column Joints Subjected to Cyclic Loading. J. Struct. Eng. 2003, 129, 1686–1697. [Google Scholar] [CrossRef]
- Mitra, N. An Analytical Study of Reinforced Concrete Beam-Column Joint Behavior under Seismic Loading; University of Washington: Washington, DC, USA, 2007. [Google Scholar]
- Eligehausen, R.; Popov, E.P.; Bertero, V.V. Local Bond Stress-Slip Relationships of Deformed Bars under Generalized Excitations; EERC Report; University of California: Berkeley, CA, USA, 1982. [Google Scholar]
- Hawkins, N.M.; Lin, I.J.; Jeang, F.L. Local Bond Strength of Concrete for Cyclic Reversed Loadings; Bartos, P., Ed.; Bond in Concrete; Applied Science Publishers Ltd.: London, UK, 1982; pp. 151–161. [Google Scholar]
- Paudel, S.G.; Tanapornraweekit, G.; Tangtermsirikul, S. Numerical study on seismic behavior improvement of composite wide beam-column interior joints. J. Build. Eng. 2022, 46, 103637. [Google Scholar] [CrossRef]
- Yang, J.; Guo, T.; Chai, S. Experimental and numerical investigation on seismic behaviours of beam-column joints of precast prestressed concrete frame under given corrosion levels. Structures 2020, 27, 1209–1221. [Google Scholar] [CrossRef]
- Bohara, R.P.; Tanapornraweekit, G.; Tangtermsirikul, S. Experimental and numerical investigation on seismic behavior of a composite wide beam-column interior joint. Structures 2021, 30, 560–573. [Google Scholar] [CrossRef]
- Gharakhanloo, A. Distributed and Concentrated Inelasticity Beam-Column Elements Used in Earthquake Engineering; Norwegian University of Science and Technology: Tromsoe, Norway, 2014. [Google Scholar]
- Huang, Z.M. Finite Element Flexibility Method Based 3D Inelastic Seismic Response Analysis of Reinforced Concrete Frames; Chongqing University: Chongqing, China, 2013. [Google Scholar]
- Scott, B.D.; Park, R.; Priestley, M.J. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rate. J. Am. Conc. Inst. 1982, 79, 13–27. [Google Scholar]
- Bentz, E.C. Sectional Analysis of Reinforced Concrete Members. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2000. [Google Scholar]
- Zhao, J.; Sritharan, S. Modeling of Strain Penetration Effects in Fiber-Based Analysis of Reinforced Concrete Structures. ACI Struct. J. 2007, 104, 133–141. [Google Scholar]
- Cao, W.; Liu, X.; Qiao, Q.; Tian, Z.; Lin, D. Experimental study on bond slip behavior of ordinary and high strength recycled concrete and steel bars. J. Build. Struct. 2016, 37 (Suppl. S2), 127–134. [Google Scholar]

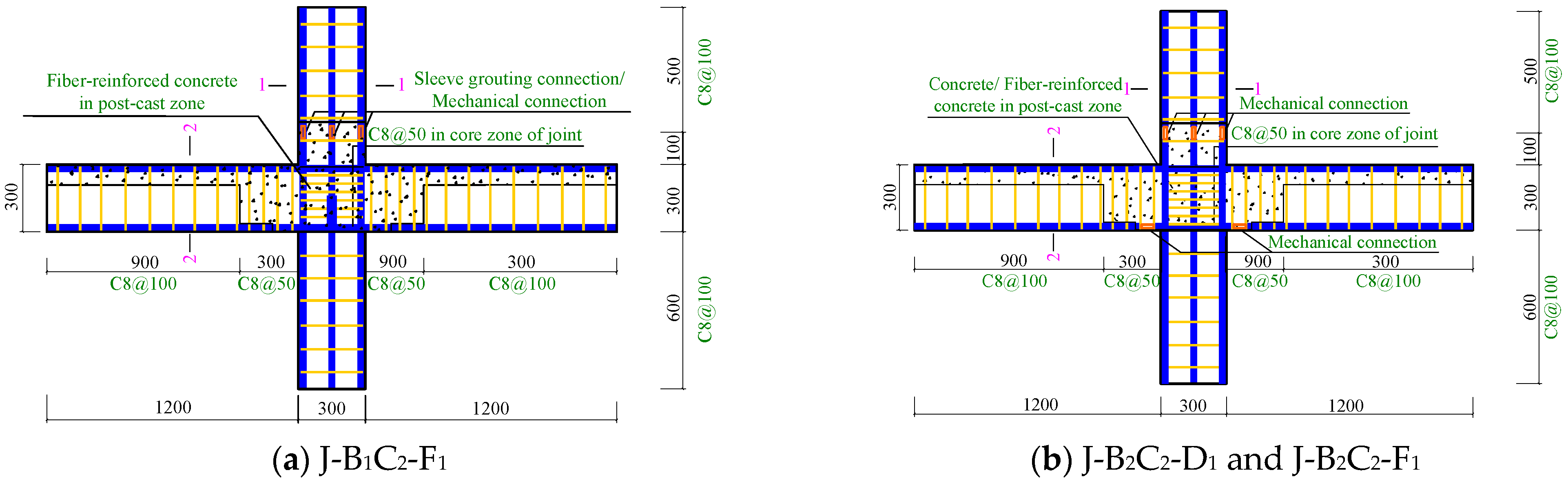
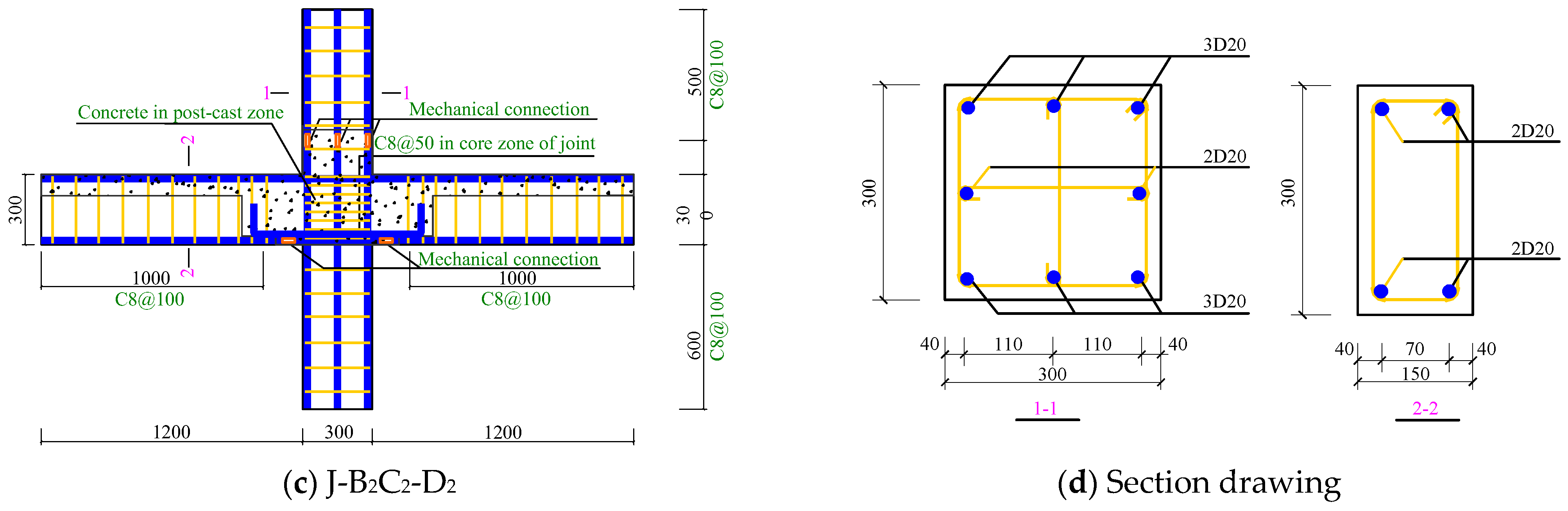
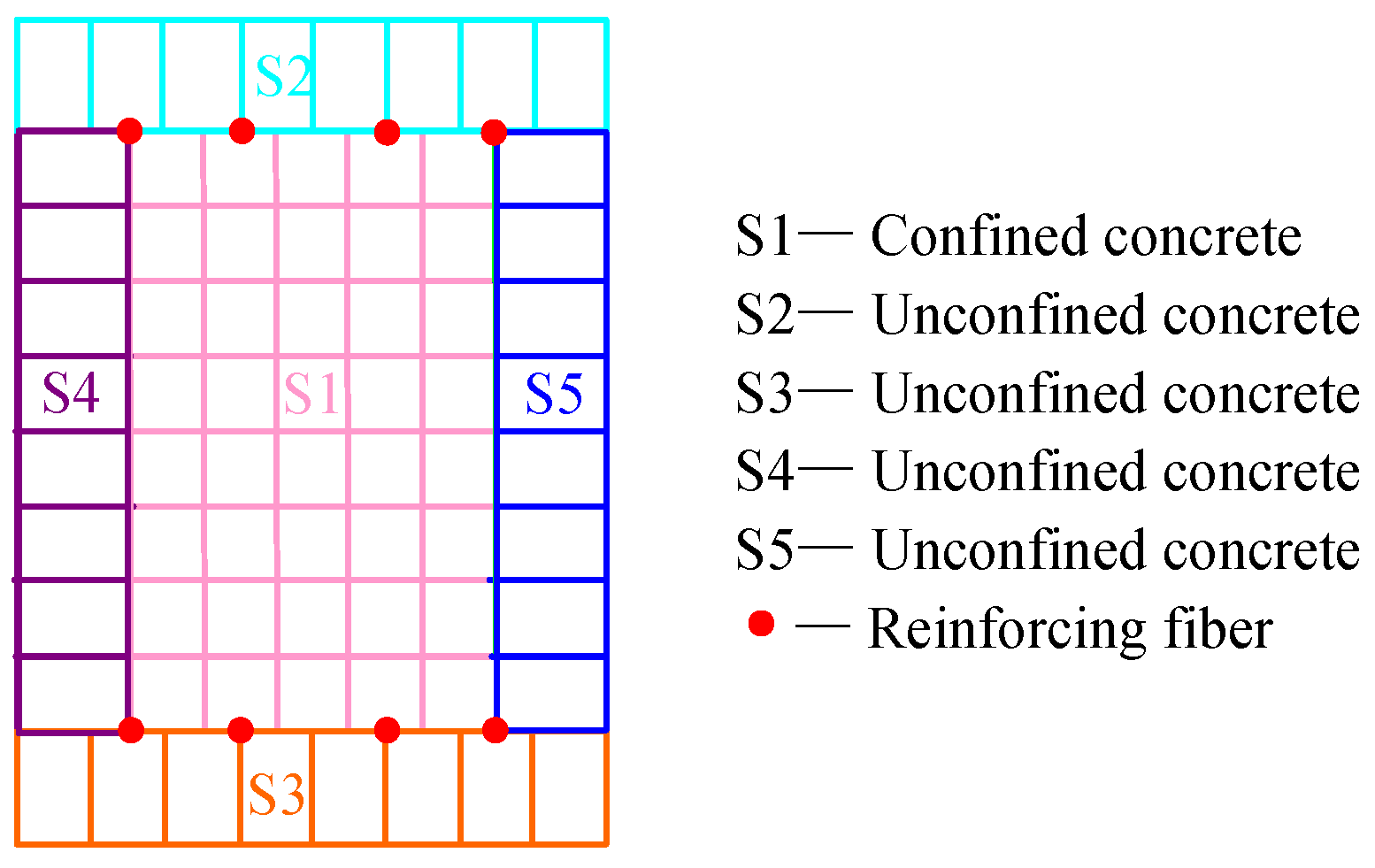



| Specimen | Precast Beam | Differences in the Joint Zone |
|---|---|---|
| J-B1C2-F1 | Anchor connection | PCFRC |
| J-B2C2-D1 | Mechanical connection | PCC |
| J-B2C2-F1 | Mechanical connection | PCFRC |
| J-B2C2-D2 | Mechanical connection | PCC |
| Loading Level | Drift Ratio (%) | Displacement (mm) | Number of Cycle |
|---|---|---|---|
| 1 | 0.10 | 1.50 | 3 |
| 2 | 0.30 | 4.50 | 3 |
| 3 | 0.50 | 7.50 | 3 |
| 4 | 0.75 | 11.25 | 3 |
| 5 | 1.00 | 15.00 | 3 |
| 6 | 1.50 | 22.50 | 3 |
| 7 | 2.00 | 30.00 | 3 |
| 8 | 2.75 | 41.25 | 3 |
| 9 | 3.50 | 52.50 | 3 |
| Constitutive Model | Stress–Strain Curve Shape | Bauschinger Effect Is Considered? | Compression Flexure Effect Is Considered? | Fatigue Damage Effect Is Considered? |
|---|---|---|---|---|
| Steel 01 | Bending Lines | No | No | No |
| Steel 02 | Smooth curves | Yes | No | No |
| Reinforcing Steel | Smooth curves | Yes | Yes | Yes |
| Specimen No. | Test Result T (kN) | Simulated Result S (kN) | Er (%) | |||
|---|---|---|---|---|---|---|
| + | − | + | − | + | − | |
| J-B1C2-F1 | 94.3 | −93.9 | 90.1 | −90.2 | −4.5 | −3.9 |
| J-B2C2-D1 | 96.7 | −89.2 | 91.8 | −91.3 | −5.1 | 2.4 |
| J-B2C2-F1 | 100.8 | −99.7 | 99.8 | −99.6 | −1.0 | −0.1 |
| J-B2C2-D2 | 97.9 | −101.2 | 94.4 | −94.3 | −3.6 | −6.8 |
| Specimen No. | ) | ) | Relative Error ((S-T)/T) |
|---|---|---|---|
| J-B1C2-F1 | 40.9 | 37.7 | −7.8% |
| J-B2C2-D1 | 41.9 | 37.0 | −11.7% |
| J-B2C2-F1 | 41.9 | 36.1 | −13.8% |
| J-B2C2-D2 | 69.5 | 69.1 | −0.6% |
| λ | Fyc (kN) | Δyc (mm) | Fmc (kN) | Δuc (mm) | |
|---|---|---|---|---|---|
| 2.0 | 68.7 | 19.6 | 93.4 | 63.8 | 3.3 |
| 2.5 | 59.2 | 21.1 | 82.5 | 63.8 | 3.0 |
| 3.0 | 52.8 | 25.9 | 73.1 | 63.8 | 2.5 |
| 3.5 | 45.9 | 29.9 | 65.2 | 63.8 | 2.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, M.-L.; Sun, C.; Yang, Z.; An, R.; Bai, L.; Han, Y.; Bao, G. Numerical Investigation on the Seismic Behavior of Novel Precast Beam–Column Joints with Mechanical Connections. Buildings 2024, 14, 1199. https://doi.org/10.3390/buildings14051199
Zhuang M-L, Sun C, Yang Z, An R, Bai L, Han Y, Bao G. Numerical Investigation on the Seismic Behavior of Novel Precast Beam–Column Joints with Mechanical Connections. Buildings. 2024; 14(5):1199. https://doi.org/10.3390/buildings14051199
Chicago/Turabian StyleZhuang, Mei-Ling, Chuanzhi Sun, Zhen Yang, Ran An, Liutao Bai, Yixiang Han, and Guangdong Bao. 2024. "Numerical Investigation on the Seismic Behavior of Novel Precast Beam–Column Joints with Mechanical Connections" Buildings 14, no. 5: 1199. https://doi.org/10.3390/buildings14051199
APA StyleZhuang, M. -L., Sun, C., Yang, Z., An, R., Bai, L., Han, Y., & Bao, G. (2024). Numerical Investigation on the Seismic Behavior of Novel Precast Beam–Column Joints with Mechanical Connections. Buildings, 14(5), 1199. https://doi.org/10.3390/buildings14051199





