Bearing Characteristics with Effect of Bond–Slip Behavior in Massive Ring-Type Reinforced Concrete Structures
Abstract
:1. Introduction
2. Theoretical Models
2.1. Modeling of Crack Model
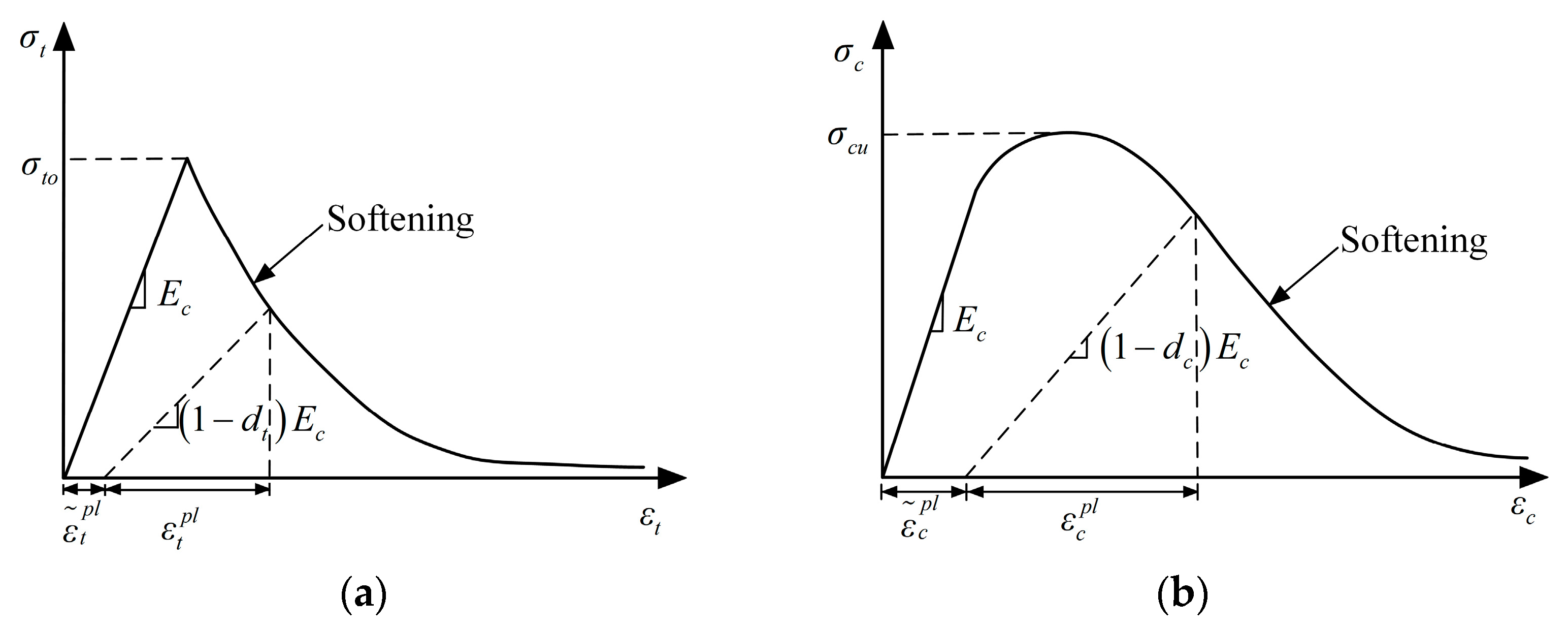
2.2. Modeling of Concrete
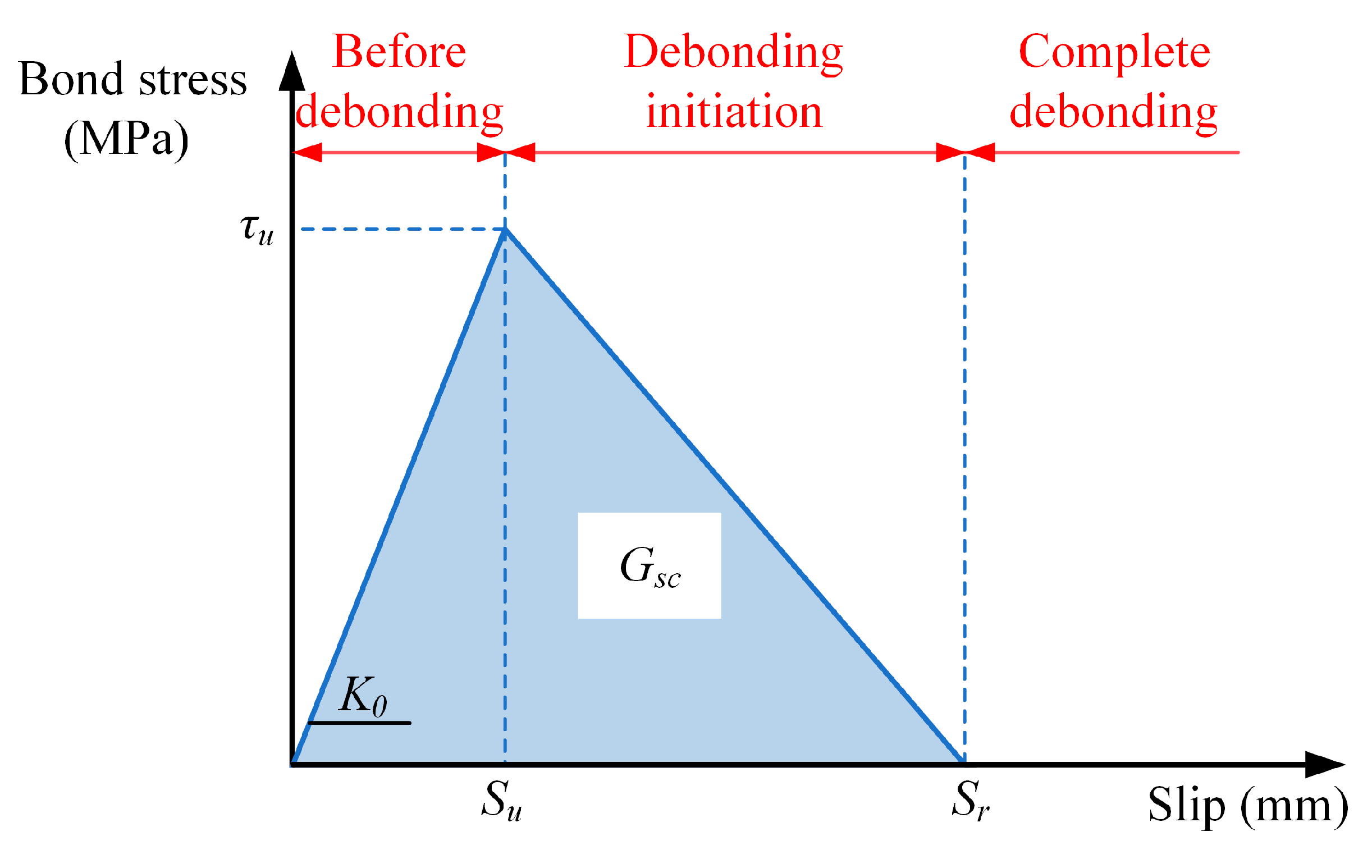
2.3. Modeling of Bond–Slip Behavior at the Concrete–Reinforcing Bar Interface
2.4. Modeling of Reinforcing Bars
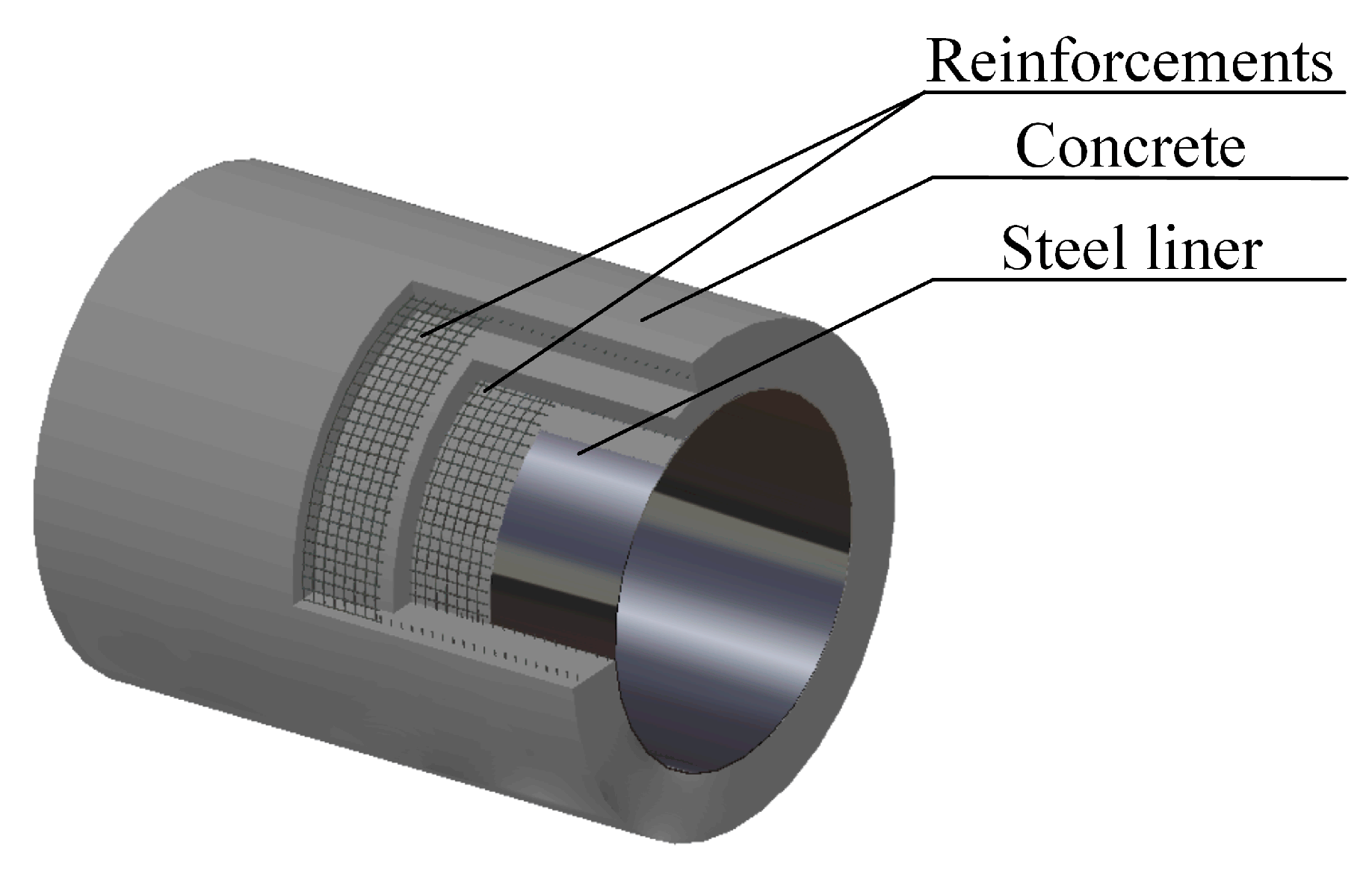
3. Finite Element Modeling of the SLRCP
3.1. Finite Element Model
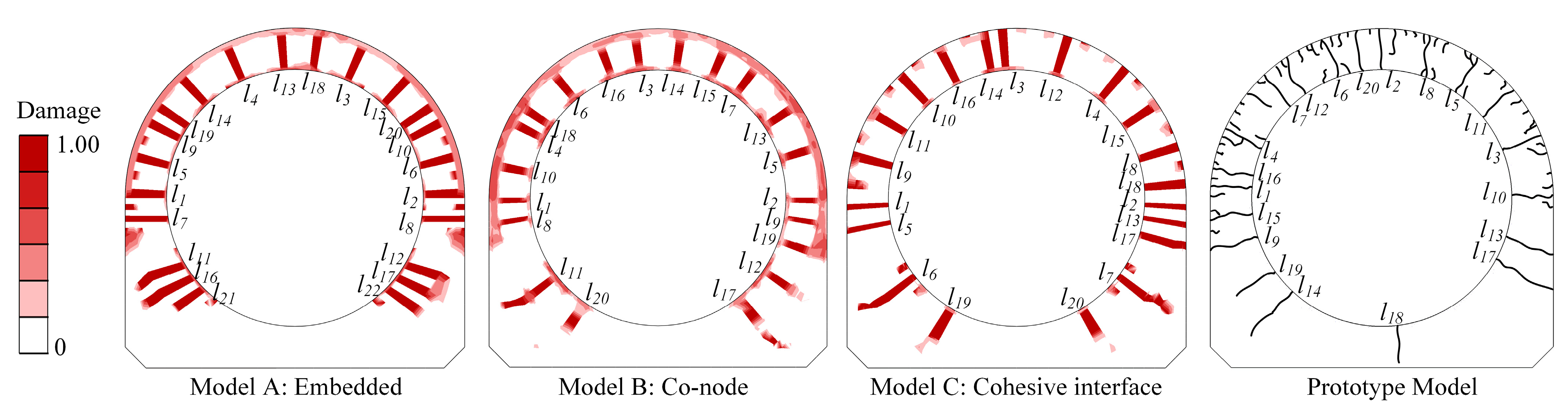
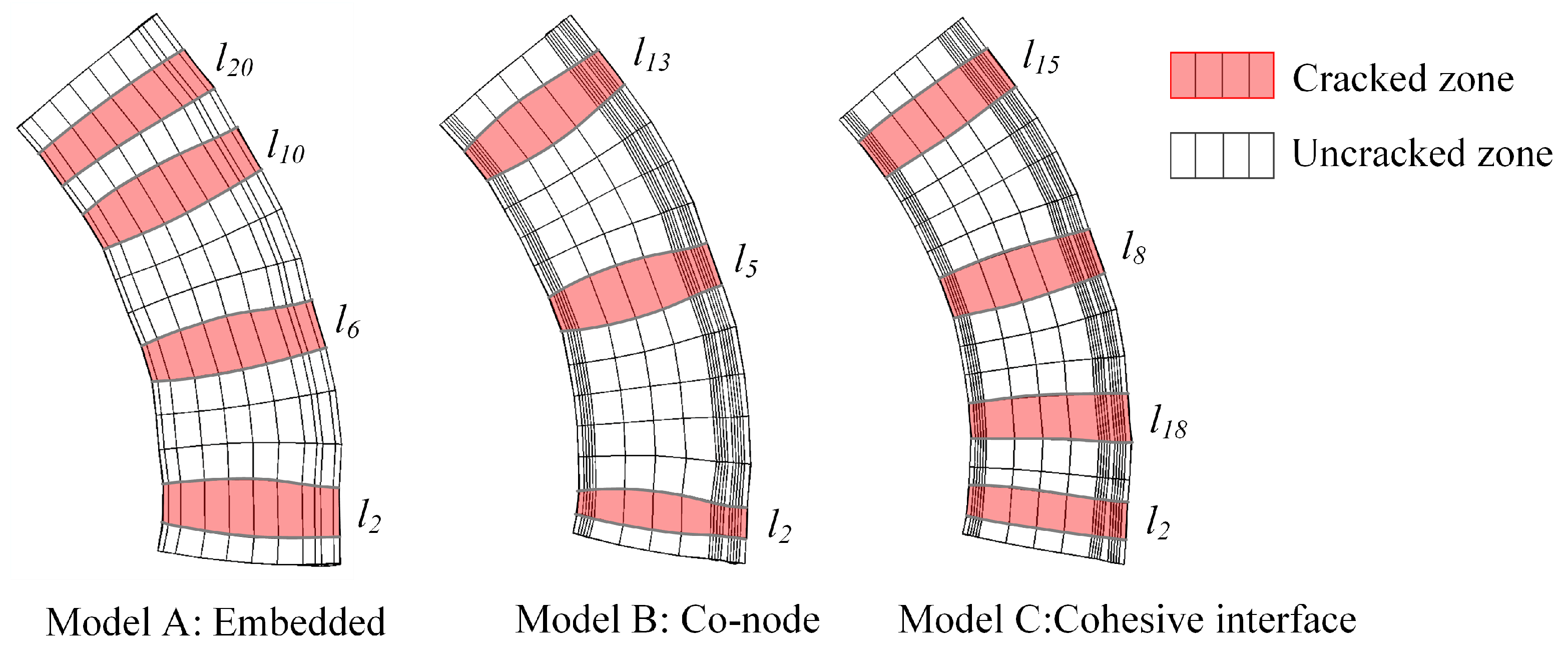
3.2. Crack Initiation and Propagation Analysis
3.3. Penstock Deformation Analysis
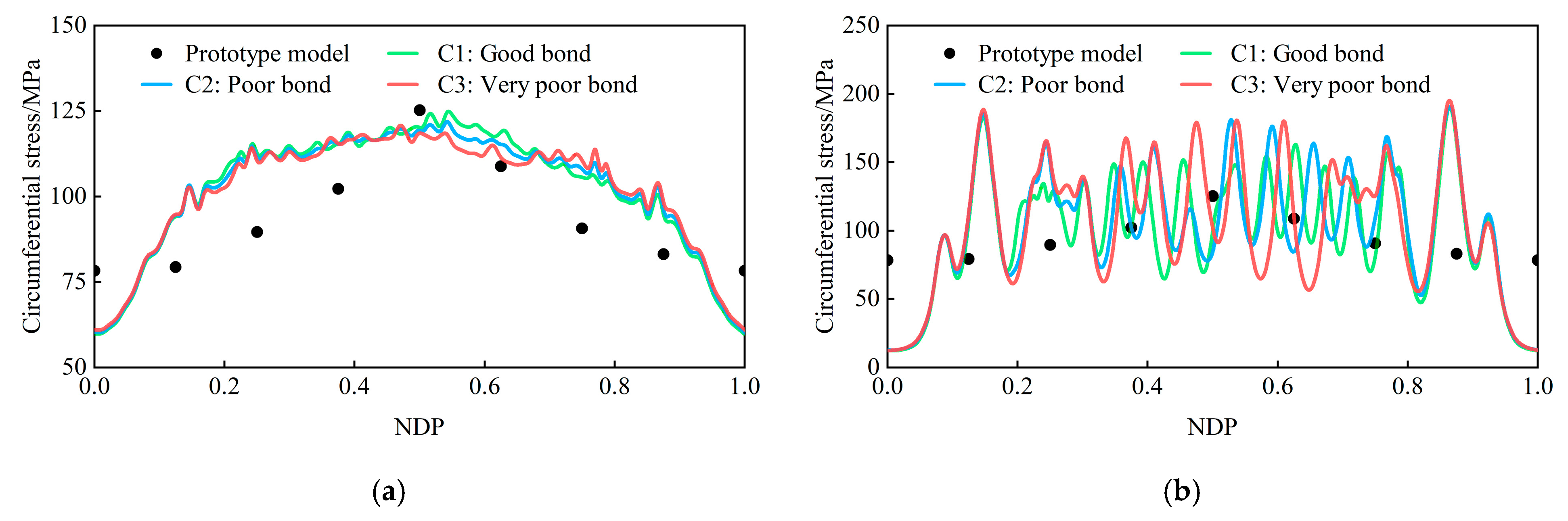
3.4. Reinforcements Stresses Analysis
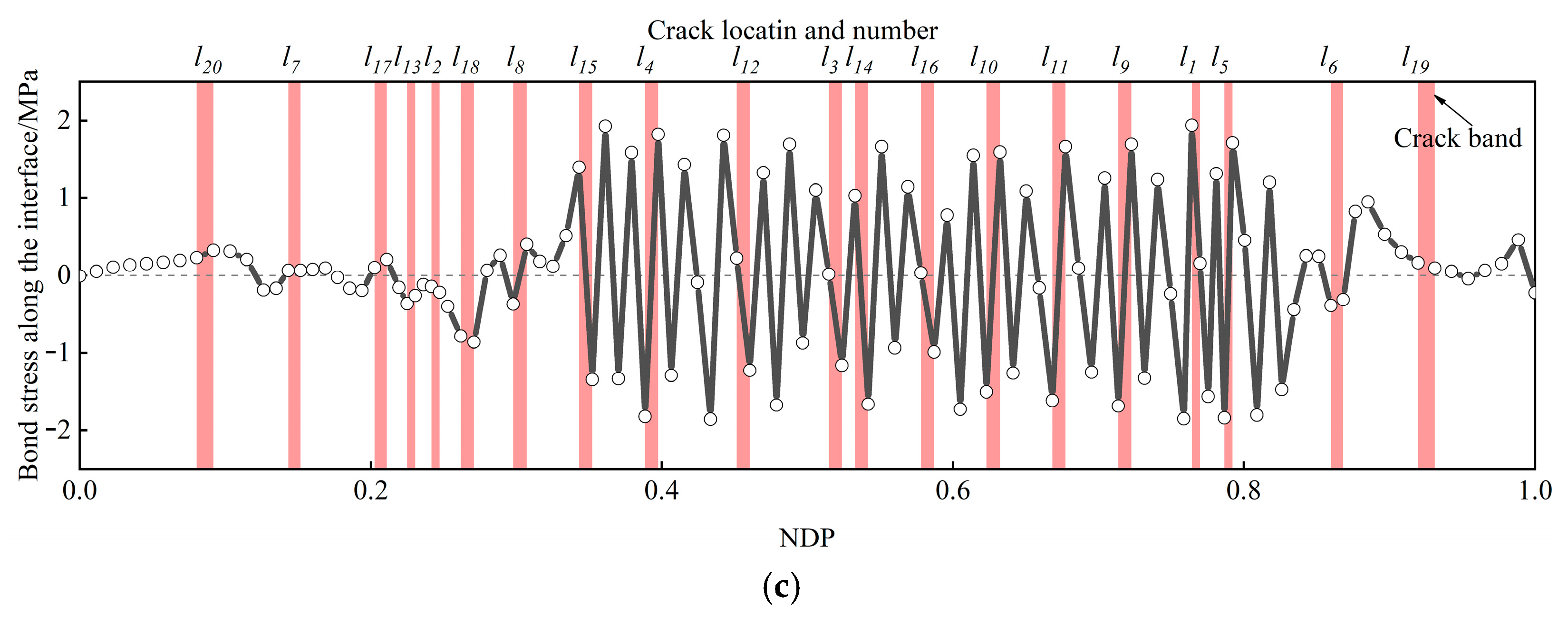
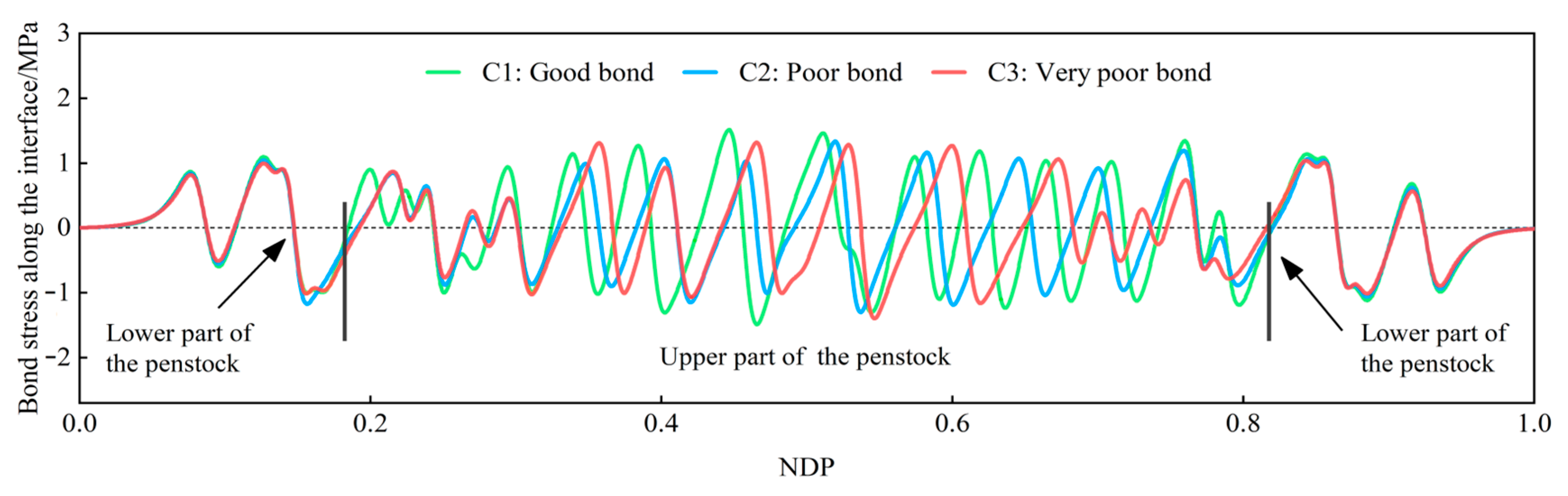
3.5. Bond Stress Analysis
4. Sensitivity Analysis of Bond Strength
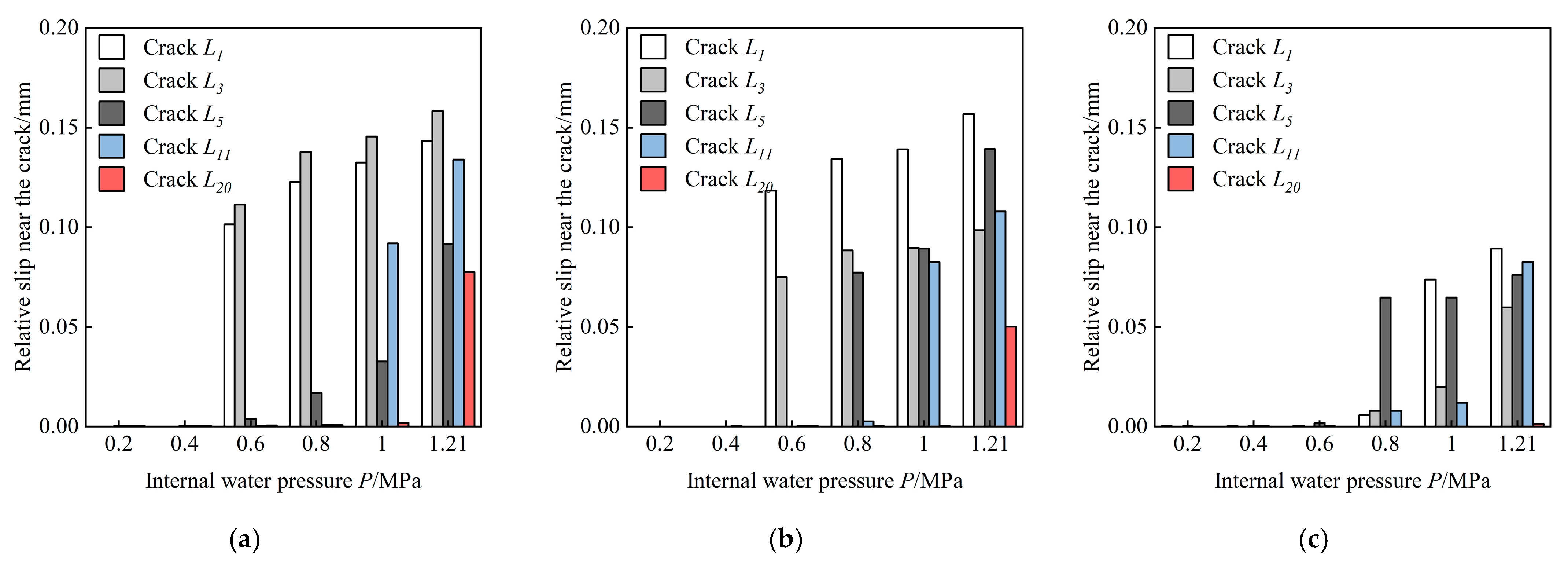
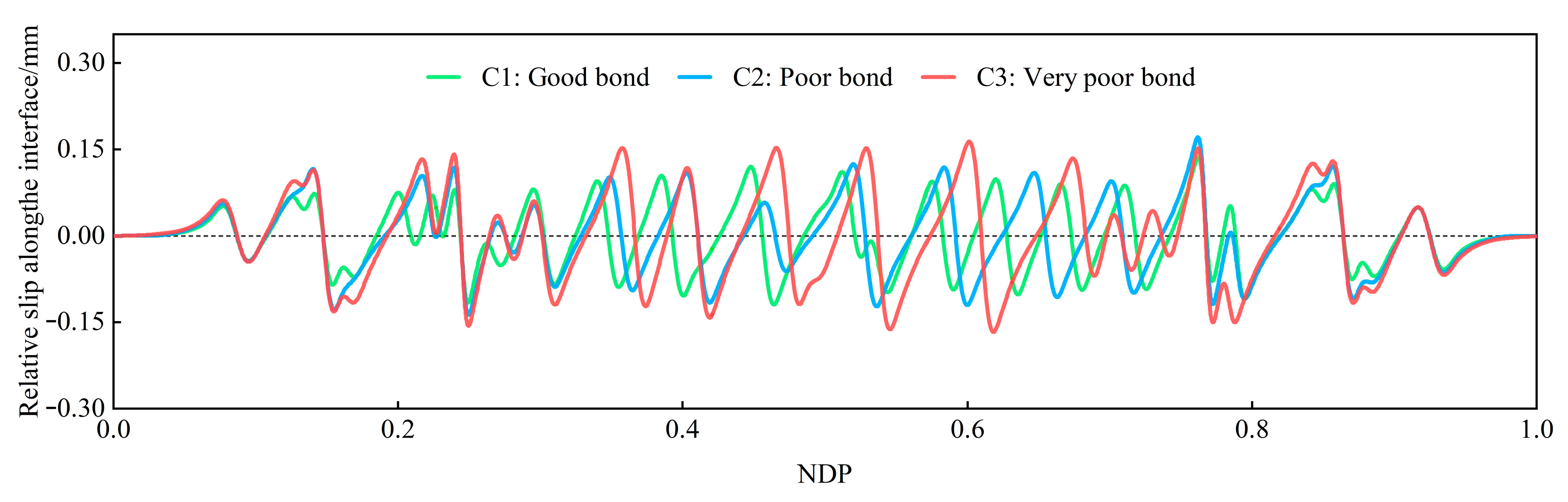
4.1. Relative Slip between Reinforcements and Concrete
4.2. Steel Stresses and Bond Stresses
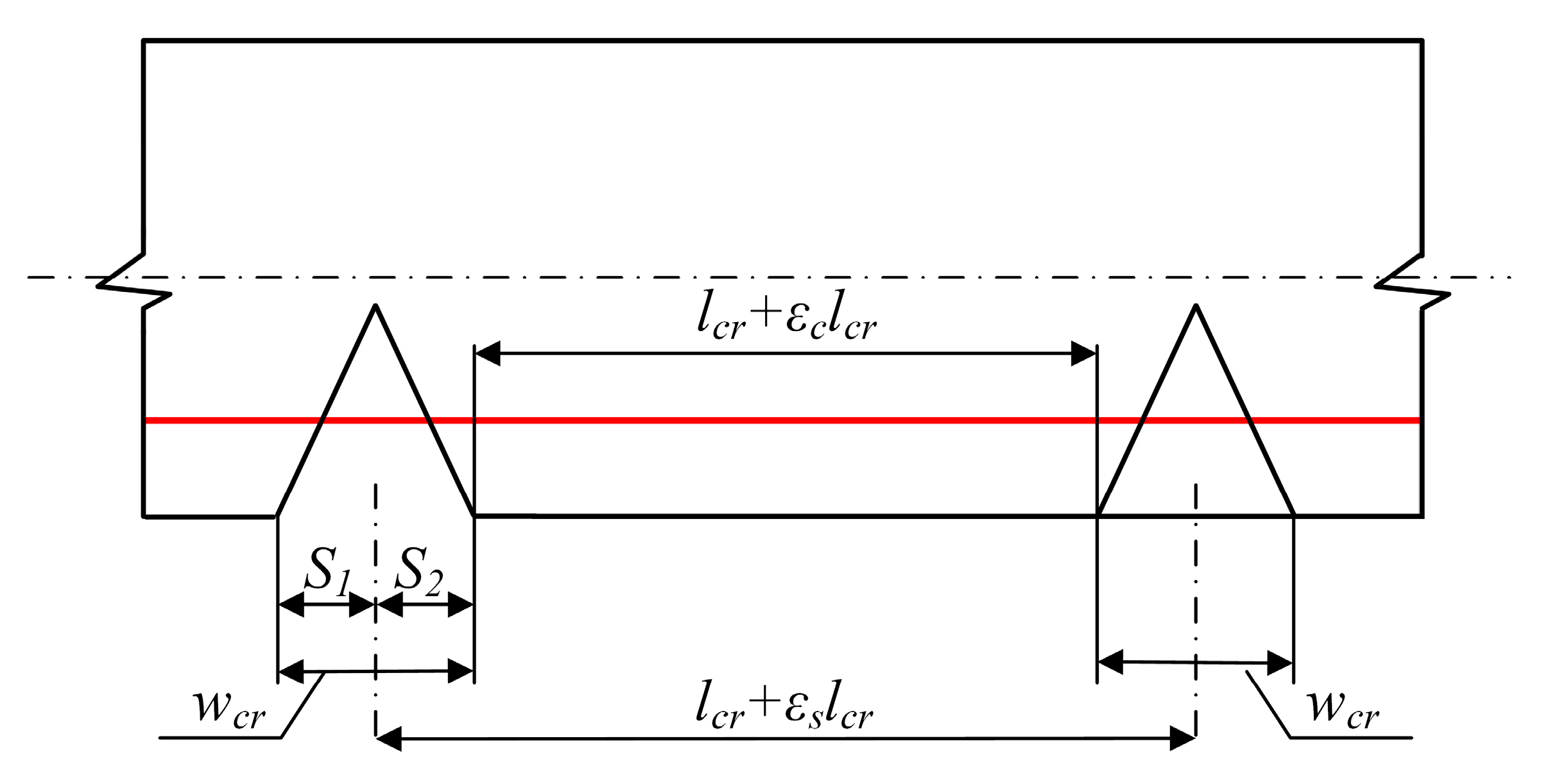
4.3. Concrete Crack Width and Distribution
5. Conclusions
- The interaction effects in the cohesive interface model between the reinforcing bars and concrete were weakened in contrast to the perfect relation models. It was observed that the stress distribution of the reinforcing bars and steel liner was more uniform and the peak stress was smaller than the other two models. This can be attributed to the bond performance, which caused the strain around the crack to be distributed along the interface rather than concentrated on the crack section.
- The numerical prediction results after considering the bond–slip behavior approximated the experimental results best. However, the differences in the steel stress and crack distribution were within 10%, which has a limited effect on the safety design of MRRC structures. The sensitivity analysis of the impact of the bond strength on the structural behavior and bond performance can also prove this. The relative slips under different bond conditions were smaller than 1.12 mm, within the allowable value in Code GB 50010-2011. Consequently, it can be assumed that there is a perfect bond between the reinforcing bars and concrete in MRRC structures. As a result, perfect relation models can be applied to simplify the calculation in the structural design analysis of MRRC structures.
- The bond–slip behavior in MRRC structures has a limited effect on the whole structural behavior, but has a great influence on the crack initiation and propagation. The crack numbers and mean spacing were in line with the experimental results with the consideration of bond–slip behavior. The crack widths based on the bond–slip calculation theory were closely related to the bond conditions, which can directly affect the durability of RC structures. In this situation, the bond–slip behavior should be paid more attention in structure durability design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Su, K.; Yang, Z.J.; Zhang, W.; Wu, H.L.; Zhang, Q.L.; Wu, H.G. Bearing mechanism of composite structure with reinforced concrete and steel liner: An application in penstock. Eng. Struct. 2017, 141, 344–355. [Google Scholar] [CrossRef]
- Shi, C.; Wu, H.; Su, K. Applications of FEM and elasticity centre method of structure mechanics in designing penstock laid on downstream surface of dam. J. Hydraul. Eng. 2010, 41, 856–862. [Google Scholar] [CrossRef]
- Wu, H.; Ma, Z.; Shi, C. Overview of research and engineering application of steel-lined reinforced concrete penstocks laid on downstream dam surfaces. Shuili Fadian Xuebao/J. Hydroelectr. Eng. 2020, 39, 1–12. [Google Scholar]
- Kai, S.; Wei, Z.; Hegao, W.; Changzheng, S. Bearing mechanism of reinforced concrete penstock with steel liner considering friction-contact behavior. J. Hydraul. Eng. 2016, 47, 1070–1078. [Google Scholar]
- Shi, C.; Wu, H. Damage and bearing characteristics of steel lined reinforced concrete penstock on downstream face of dam in hydropower station. Tianjin Daxue Xuebao (Ziran Kexue Yu Gongcheng Jishu Ban)/J. Tianjin Univ. Sci. Technol. 2014, 47, 1081–1087. [Google Scholar] [CrossRef]
- Su, K.; Yang, Z.; Wu, H.; Zhou, L.; Shi, C. Influence of Gap on Bearing Mechanism of Steel-Lined Reinforced Concrete Penstock. Tianjin Daxue Xuebao (Ziran Kexue Yu Gongcheng Jishu Ban)/J. Tianjin Univ. Sci. Technol. 2018, 51, 967–976. [Google Scholar] [CrossRef]
- Pang, Y.; Wu, G.; Wang, H.; Liu, Y. Interfacial bond-slip degradation relationship between CFRP plate and steel plate under freeze-thaw cycles. Constr. Build. Mater. 2019, 214, 242–253. [Google Scholar] [CrossRef]
- Coccia, S.; Di Maggio, E.; Rinaldi, Z. Bond slip model in cylindrical reinforced concrete elements confined with stirrups. Int. J. Adv. Struct. Eng. 2015, 7, 365–375. [Google Scholar] [CrossRef]
- Jin, L.; Li, X.; Zhang, R.; Du, X. Bond-slip behavior between concrete and deformed rebar at elevated temperature: Mesoscale simulation and formulation. Int. J. Mech. Sci. 2021, 205, 106622. [Google Scholar] [CrossRef]
- Lu, X.Z.; Teng, J.G.; Ye, L.P.; Jiang, J.J. Bond-slip models for FRP sheets/plates bonded to concrete. Eng. Struct. 2005, 27, 920–937. [Google Scholar] [CrossRef]
- Tang, C.W.; Cheng, C.K. Modeling local bond stress-slip relationships of reinforcing bars embedded in concrete with different strengths. Materials 2020, 13, 3701. [Google Scholar] [CrossRef] [PubMed]
- Casanova, A.; Jason, L.; Davenne, L. Bond slip model for the simulation of reinforced concrete structures. Eng. Struct. 2012, 39, 66–78. [Google Scholar] [CrossRef]
- Yazarlu, A.; Dehestani, M. Application of discrete element method (DEM) in characterization of bond-slip behavior in RC beams with confinement subjected to corrosion. Structures 2020, 28, 1965–1976. [Google Scholar] [CrossRef]
- Marin-Artieda, C.; Buitrago, D. Numerical predictions of observed failure modes on non-ductile reinforced concrete frames. Eng. Struct. 2021, 243, 112568. [Google Scholar] [CrossRef]
- Fawaz, G.; Murcia-Delso, J. Three-dimensional finite element modeling of RC columns subjected to cyclic lateral loading. Eng. Struct. 2021, 239, 112291. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, X.; Zheng, J.; Hu, Y.; Li, Q. Experimental study on the bond behavior of deformed bars embedded in concrete subjected to lateral tension. Mater. Struct. Constr. 2014, 47, 1647–1668. [Google Scholar] [CrossRef]
- Melo, J.; Rossetto, T.; Varum, H. Experimental study of bond-slip in RC structural elements with plain bars. Mater. Struct. Constr. 2015, 48, 2367–2381. [Google Scholar] [CrossRef]
- Murcia-Delso, J.; Benson Shing, P. Bond-Slip Model for Detailed Finite-Element Analysis of Reinforced Concrete Structures. J. Struct. Eng. 2015, 141, 04014125. [Google Scholar] [CrossRef]
- Ngo, D.; Scordelis, A.C. Finite element analysis of reinforced concrete beams. ACI J. 1967, 64, 152–163. [Google Scholar]
- Lowes, L.N. Concrete-steel bond model for use in finite element modeling of reinforced concrete structures. ACI Struct. J. 2004, 101, 501–511. [Google Scholar] [CrossRef]
- Richard, B.; Ragueneau, F.; Cremona, C.; Adélaide, L.; Tailhan, J.L. A three-dimensional steel/concrete interface model including corrosion effects. Eng. Fract. Mech. 2010, 77, 951–973. [Google Scholar] [CrossRef]
- Monti, G.; Filippou, F.C.; Spacone, E. Analysis of hysteretic behavior of anchored reinforcing bars. ACI Struct. J. 1997, 94, 248–261. [Google Scholar] [CrossRef] [PubMed]
- Hadjazi, K.; Sereir, Z.; Amziane, S. Cohesive zone model for the prediction of interfacial shear stresses in a composite-plate RC beam with an intermediate flexural crack. Compos. Struct. 2012, 94, 3574–3582. [Google Scholar] [CrossRef]
- Rabinovitch, O. An extended high order cohesive interface approach to the debonding analysis of FRP strengthened beams. Int. J. Mech. Sci. 2014, 81, 1–16. [Google Scholar] [CrossRef]
- Dias-da-Costa, D.; Cervenka, V.; Graça-e-Costa, R. Model uncertainty in discrete and smeared crack prediction in RC beams under flexural loads. Eng. Fract. Mech. 2018, 199, 532–543. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Ma, F.J.; Kwan, A.K.H. Crack width analysis of reinforced concrete members under flexure by finite element method and crack queuing algorithm. Eng. Struct. 2015, 105, 209–219. [Google Scholar] [CrossRef]
- Rimkus, A.; Cervenka, V.; Gribniak, V.; Cervenka, J. Uncertainty of the smeared crack model applied to RC beams. Eng. Fract. Mech. 2020, 233, 107088. [Google Scholar] [CrossRef]
- De Borst, R.; Remmers, J.J.C.; Needleman, A.; Abellan, M.A. Discrete vs smeared crack models for concrete fracture: Bridging the gap. Int. J. Numer. Anal. Methods Geomech. 2004, 28, 583–607. [Google Scholar] [CrossRef]
- Hany, N.F.; Hantouche, E.G.; Harajli, M.H. Finite element modeling of FRP-confined concrete using modified concrete damaged plasticity. Eng. Struct. 2016, 125, 1–14. [Google Scholar] [CrossRef]
- Mirmiran, A.; Zagers, K.; Yuan, W. Nonlinear finite element modeling of concrete confined by fiber composites. Finite Elem. Anal. Des. 2000, 35, 79–96. [Google Scholar] [CrossRef]
- Carrazedo, R.; Mirmiran, A.; de Hanai, J.B. Plasticity based stress-strain model for concrete confinement. Eng. Struct. 2013, 48, 645–657. [Google Scholar] [CrossRef]
- Samani, A.K.; Attard, M.M. A stress-strain model for uniaxial and confined concrete under compression. Eng. Struct. 2012, 41, 335–349. [Google Scholar] [CrossRef]
- Alfarah, B.; López-Almansa, F.; Oller, S. New methodology for calculating damage variables evolution in Plastic Damage Model for RC structures. Eng. Struct. 2017, 132, 70–86. [Google Scholar] [CrossRef]
- Yang, Q.; Cox, B. Cohesive models for damage evolution in laminated composites. Int. J. Fract. 2005, 133, 107–137. [Google Scholar] [CrossRef]
- Li, G.; Tan, K.H.; Fung, T.C.; Yu, Q.J.; May, M. A coupled dynamic cohesive zone model for FRP-concrete mixed-mode separation. Compos. Struct. 2021, 268, 113872. [Google Scholar] [CrossRef]
- De Morais, A.B. Mode I cohesive zone model for delamination in composite beams. Eng. Fract. Mech. 2013, 109, 236–245. [Google Scholar] [CrossRef]
- Alfano, G. On the influence of the shape of the interface law on the application of cohesive-zone models. Compos. Sci. Technol. 2006, 66, 723–730. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Ghasemi, A.R. Appropriate shape of cohesive zone model for delamination propagation in ENF specimens with R-curve effects. Theor. Appl. Fract. Mech. 2017, 90, 174–181. [Google Scholar] [CrossRef]
- Williams, J.G.; Hadavinia, H. Analytical solutions for cohesive zone models. J. Mech. Phys. Solids 2002, 50, 809–825. [Google Scholar] [CrossRef]
- GB 50010-2011; Code for Design of Concrete Structures. China Building Industry Press: Beijing, China, 2011.
- Wu, H.G.; Gosling, P.D. Structural Reseach on the Penstocks for Three Gorges. Hydropower Dams 2000, 1, 64–68. [Google Scholar]
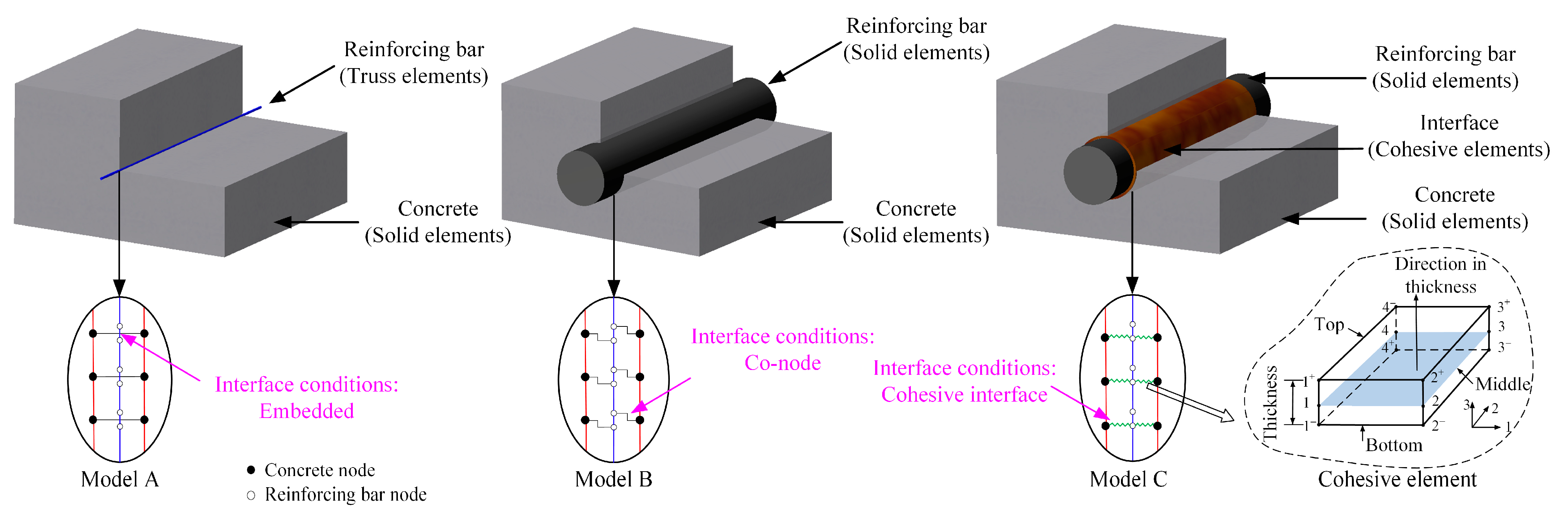
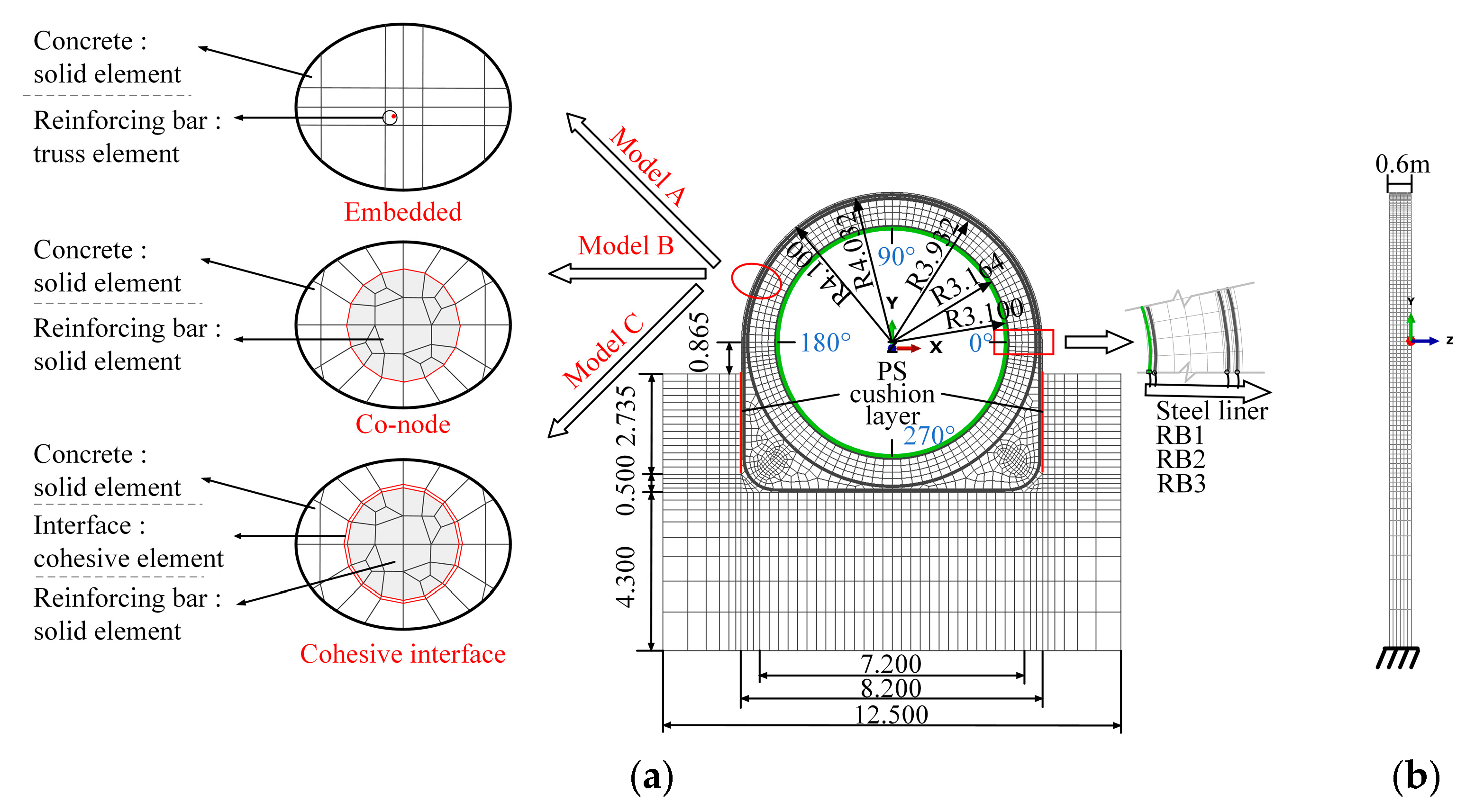








| Schemes | If the Bond–Slip Is Considered | Reinforcing Bars Element | Interface Conditions | Bond Strength |
|---|---|---|---|---|
| A | No | Truss | Embedded | / |
| B | No | Solid | Co-node | / |
| C1 | Yes | Solid | Cohesive interface | τu = 4.0ftk |
| C2 | Yes | Solid | Cohesive interface | τu = 2.0ftk |
| C3 | Yes | Solid | Cohesive interface | τu = ftk |
| Material | Elastic Modulus (MPa) | Poisson Ratio | Tensile Strength (MPa) | Compression Strength (MPa) |
|---|---|---|---|---|
| Concrete of penstock | 28,500 | 0.17 | 1.78 | 20.2 |
| Concrete of dam | 24,000 | 0.17 | 1.0 | 14.6 |
| Steel liner | 198,000 | 0.30 | 350 * 1 | 350 * |
| Steel bar | 205,000 | 0.30 | 375 * 1 | 375 * |
| PS cushion layer 2 | 0.4 | 0.30 | / | / |
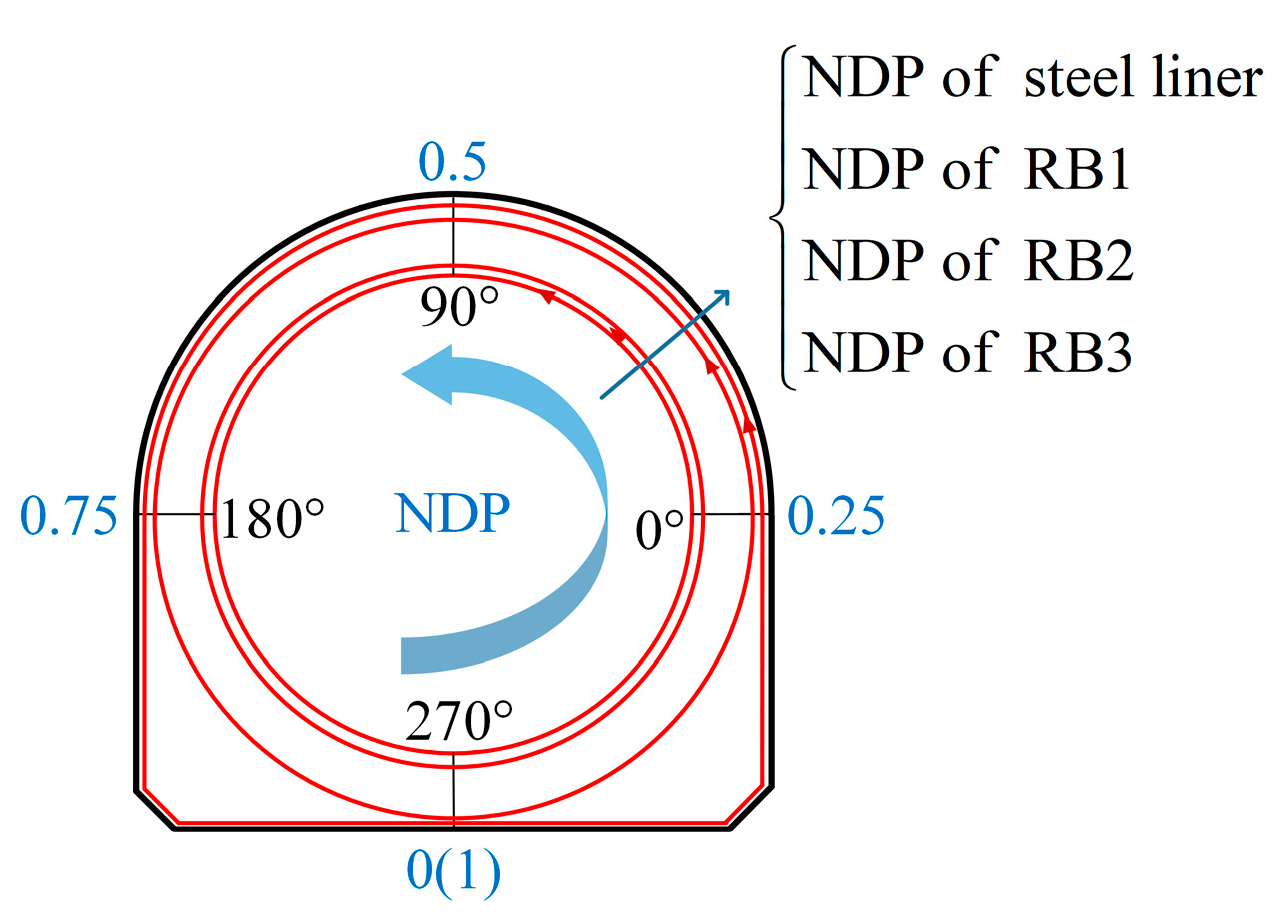
| Crack Location | Model Test | Schemes | |||
|---|---|---|---|---|---|
| C1 | C2 | C3 | |||
| Left waist | Inner | 0.078 | 0.083 | 0.109 | 0.124 |
| Middle | 0.300 | 0.235 | 0.329 | 0.356 | |
| Outer | 0.204 | 0.224 | 0.283 | 0.323 | |
| Right waist | Inner | 0.088 | 0.111 | 0.145 | 0.179 |
| Middle | 0.488 | 0.278 | 0.352 | 0.461 | |
| Outer | 0.157 | 0.221 | 0.328 | 0.316 | |
| Top | Inner | 0.100 | 0.102 | 0.118 | 0.158 |
| Middle | 0.423 | 0.220 | 0.294 | 0.331 | |
| Outer | 0.132 | 0.146 | 0.167 | 0.214 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.-T.; Ma, Z.; Wu, H.-G.; Shi, C.-Z. Bearing Characteristics with Effect of Bond–Slip Behavior in Massive Ring-Type Reinforced Concrete Structures. Buildings 2024, 14, 1332. https://doi.org/10.3390/buildings14051332
Xu W-T, Ma Z, Wu H-G, Shi C-Z. Bearing Characteristics with Effect of Bond–Slip Behavior in Massive Ring-Type Reinforced Concrete Structures. Buildings. 2024; 14(5):1332. https://doi.org/10.3390/buildings14051332
Chicago/Turabian StyleXu, Wen-Tao, Zhu Ma, He-Gao Wu, and Chang-Zheng Shi. 2024. "Bearing Characteristics with Effect of Bond–Slip Behavior in Massive Ring-Type Reinforced Concrete Structures" Buildings 14, no. 5: 1332. https://doi.org/10.3390/buildings14051332
APA StyleXu, W.-T., Ma, Z., Wu, H.-G., & Shi, C.-Z. (2024). Bearing Characteristics with Effect of Bond–Slip Behavior in Massive Ring-Type Reinforced Concrete Structures. Buildings, 14(5), 1332. https://doi.org/10.3390/buildings14051332







