Variable Pressure Difference Control Method for Chilled Water System Based on the Identification of the Most Unfavorable Thermodynamic Loop
Abstract
1. Introduction
2. Problem Descriptions
- Description of problem 1:
- Description of problem 2:
3. Methodology
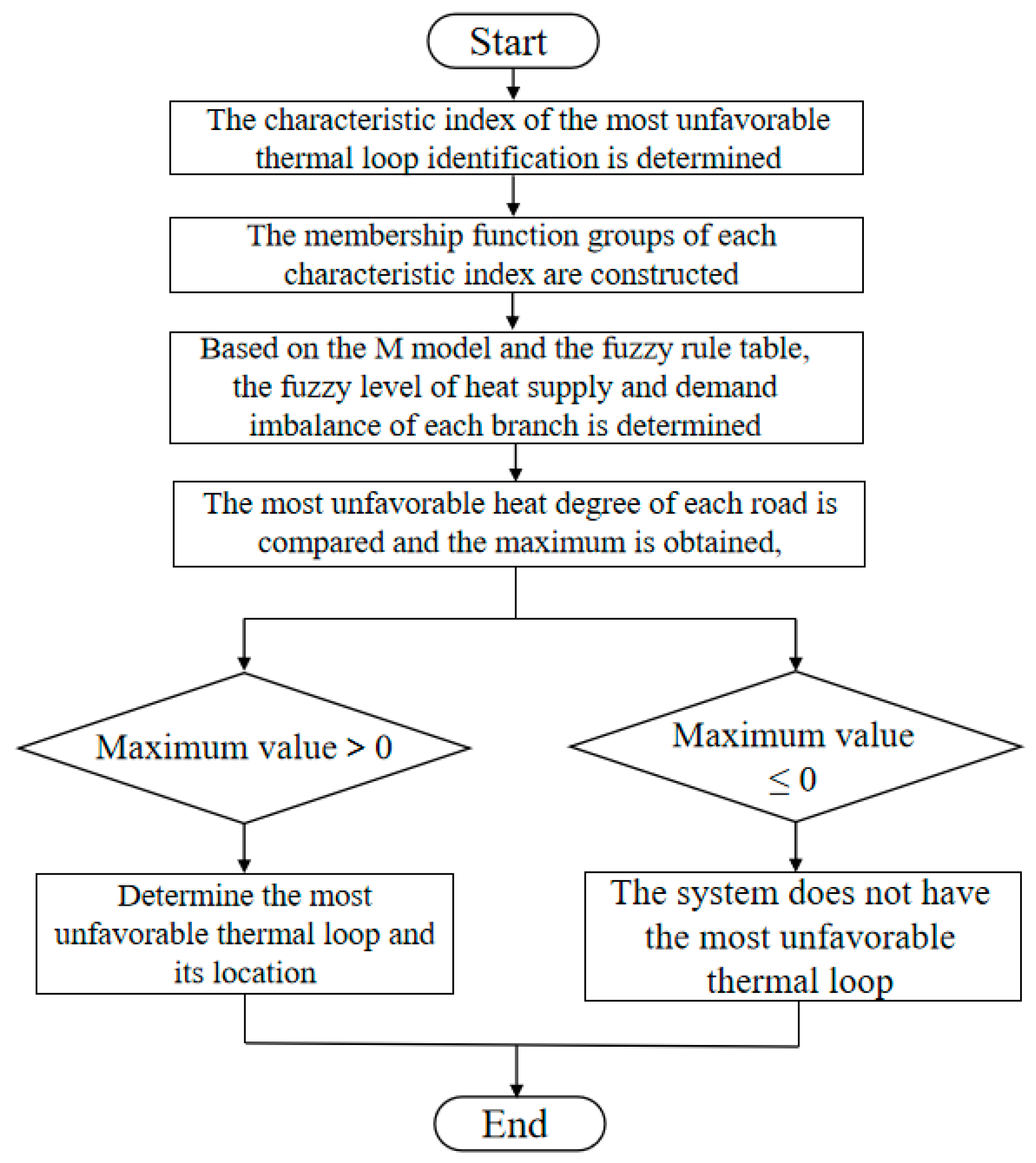
3.1. Characterization of the Response Trajectory of the Most Unfavorable Thermal Loop in the Phase Plane
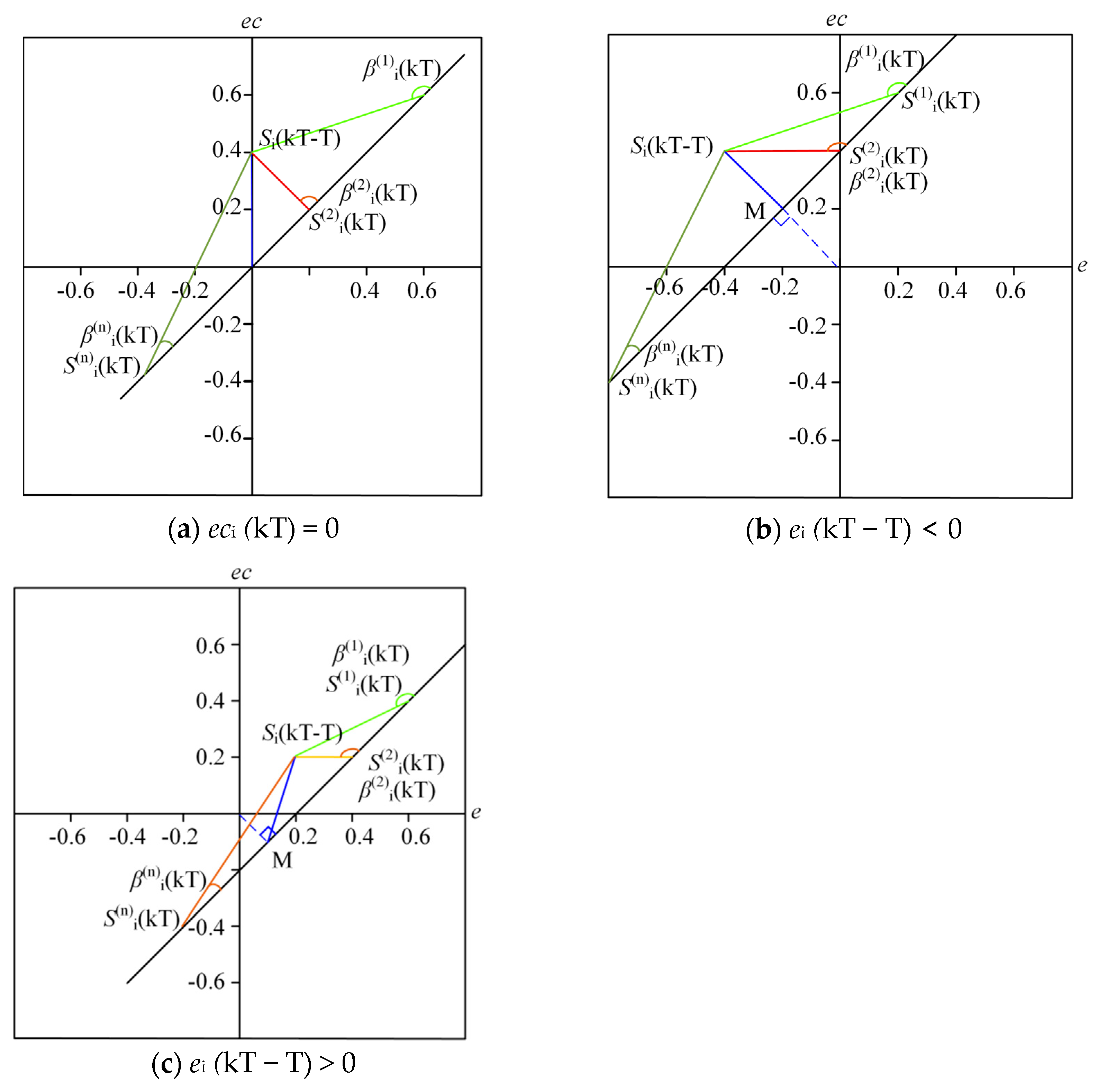
- If ei (kT) = 0 and eci (kT) = 0, the room temperature state point at the current moment is the thermal energy supply and demand balance state. But, if ei (kT) is not 0, point Si (kT) may be Si (1) (kT), Si(2) (kT), …, Si(n) (kT), at this time, the room thermal energy supply and demand imbalance, and the farther point Si (kT) is from the O point, the larger the room thermal energy supply and demand imbalance degree (i), as shown in Figure 3a.
- 2.
- When ei (kT − T) < 0 or ei (kT − T) > 0, the positions of line L and point Si (kT) are shown in Figure 3b,c, then end point O (0,0) can be used as the reference point to judge the most unfavorable thermal loop, and the coordinates of point Si (kT) in the phase plane and the relative position to point O reflect the size of the thermal energy supply and demand imbalance Φi(τ). The closer the distance from point O, the smaller the Φi(τ) will be. The farther the distance from point O, the larger the Φi(τ) will be, where the branch where Φi(τ) is the largest is the most unfavorable thermal loop.
- 3.
- When point Si (kT − T) is on the e axis, point Si (kT − T) coincides with point Si (kT) and there is no straight line L.
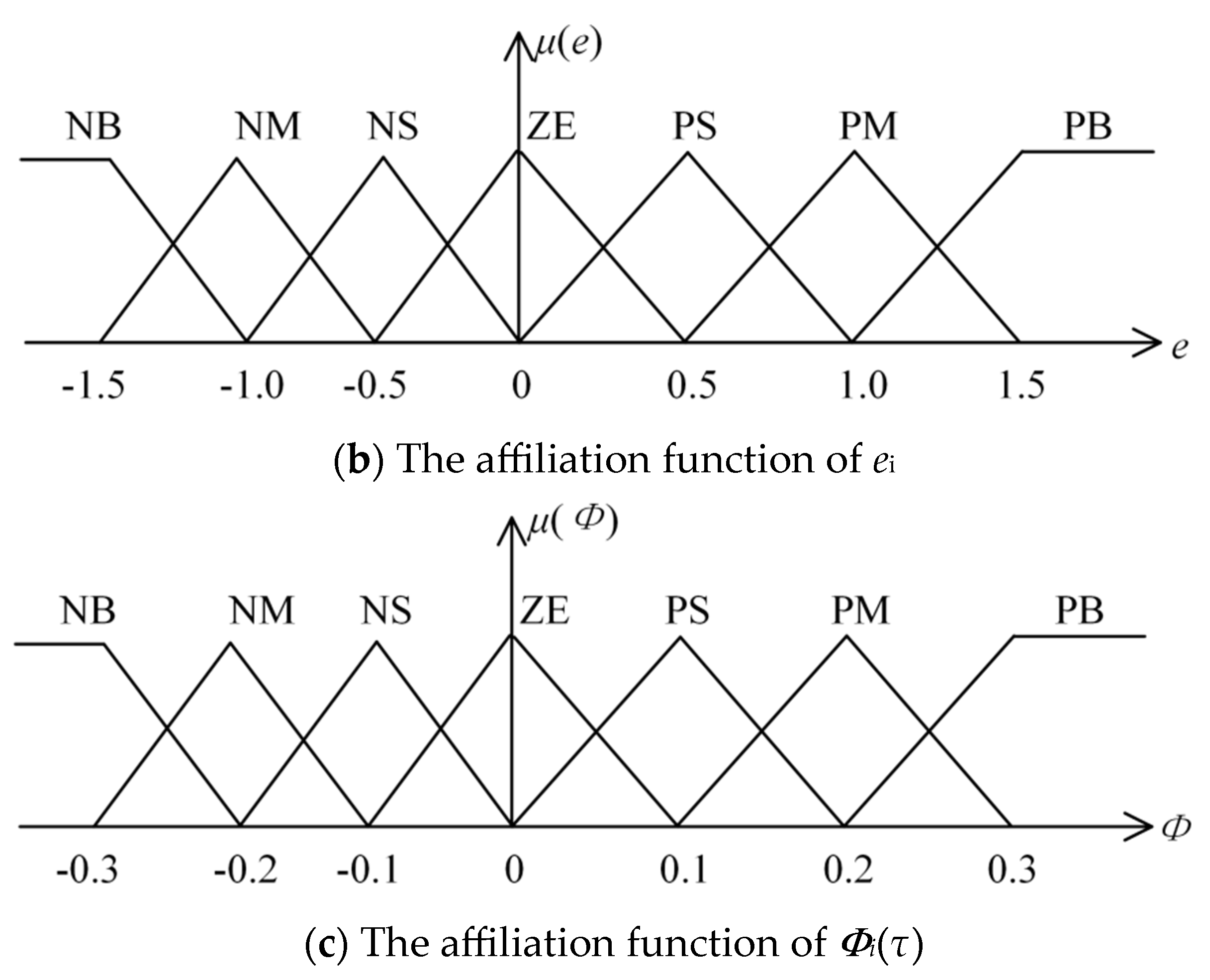
- Fuzzy recognition variables and their fuzzy levels
- 2.
- Affiliation function of fuzzy variables
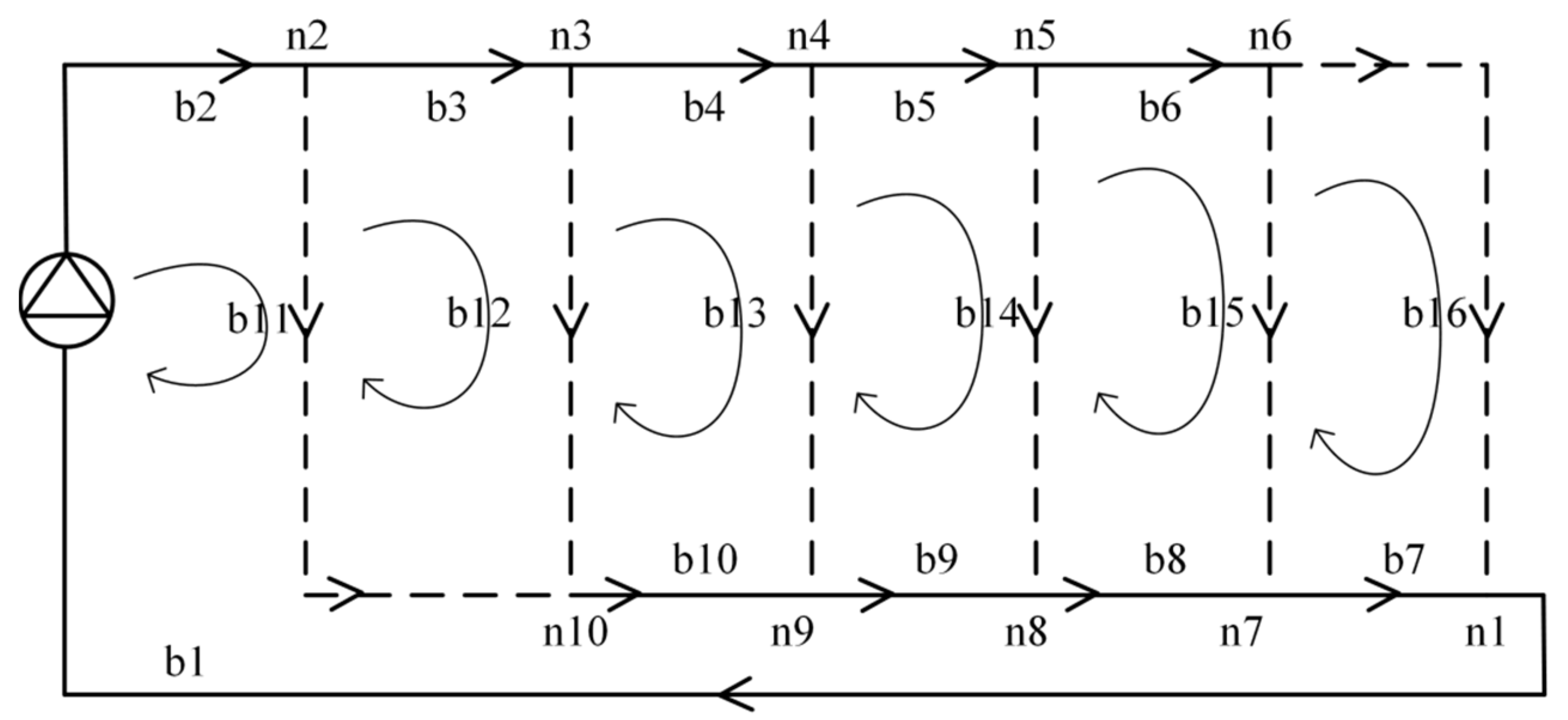
3.2. Role of Pipe Network Models in the Control Process
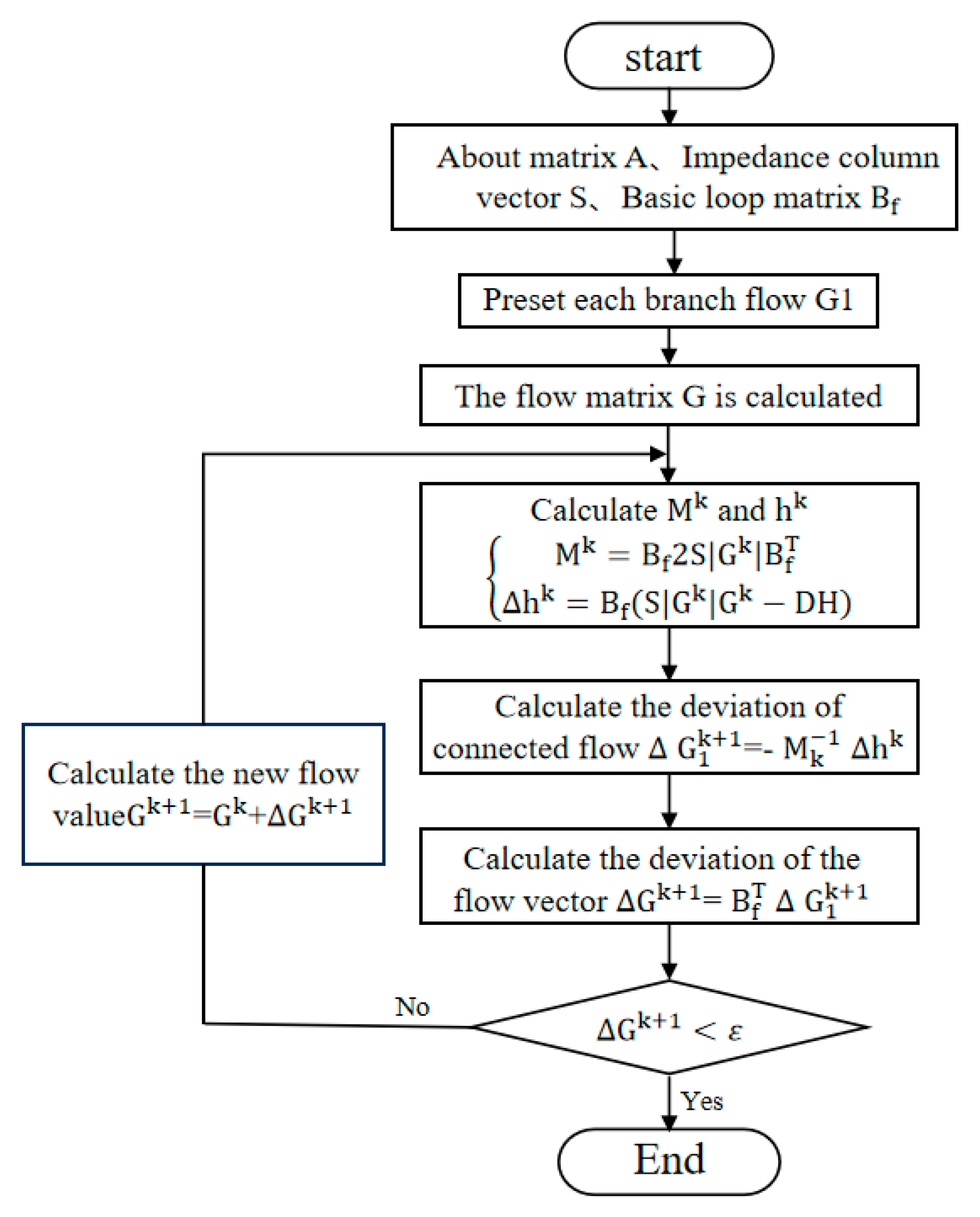
G = [Gt, Gl]
- For a given pipe network, the correlation matrix A and the basic loop matrix Bf, with impedance values S for each pipe segment, are created according to their structure;
- Given an initial value of Gl0 for even the tributary volume and a given iteration accuracy ε;
- The flow rate of the pipe network is obtained from the flow rate of the connected branch section, and the kth iteration of the connected branch flow column vector Glk is brought into the equation to obtain the flow rate vector Gk, which is brought into Equations (19) and (20) to obtain Mk and h k, and then ΔGlk;
- The ΔGlk+1 is brought into Equation (17) to obtain ΔGk+1;
- Discriminate ΔGk+1 ≤ ε. If the condition is satisfied, stop the calculation and output the result G* = Gk+1; otherwise, k = k+1 and repeat step (3).
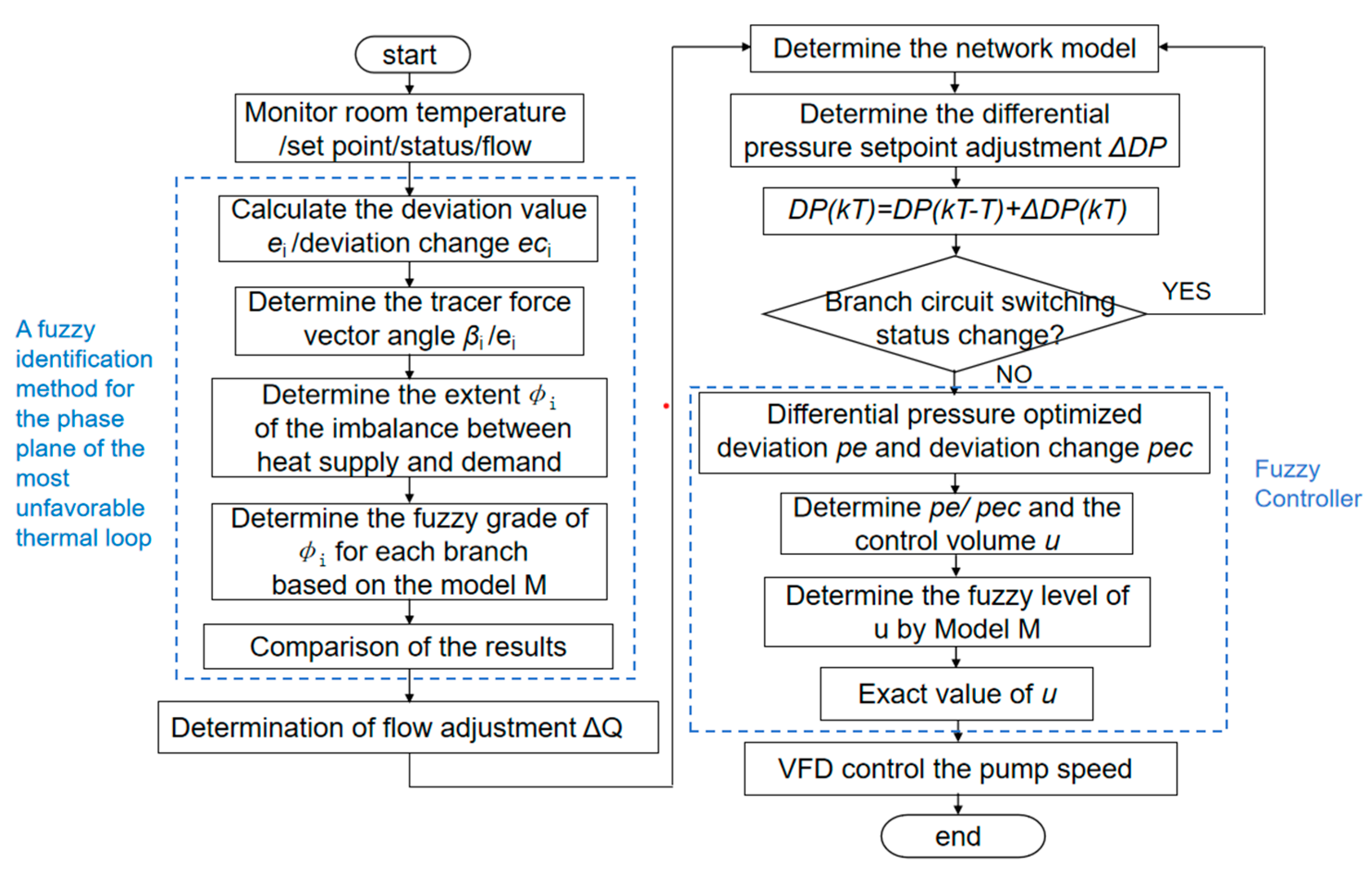
3.3. Variable Pressure Differential Fuzzy Control Method Based on Identifying the Most Unfavorable Thermal Loop
- Obtaining the flow adjustment Q of the branch based on the aforementioned identification results of the most unfavorable thermal loop;
- Calculating ΔDP(kT), the adjustment of the pump’s inlet and outlet pressure difference set value using matrices A and Bf, and variations in flow for the most unfavorable thermal loop through basic loop method;
- Obtaining re-normalized results of pressure difference set point using formula DP(kT) = DP(kT − T) + ΔDP(kT).
- Determining discourse domain and fuzzy level for deviation pe, deviation change value pec, and pump frequency u;
- Determining fuzzy level for u using M model and fuzzy control rule table;
- De-fuzzifying through gravity center method to obtain precise value for pump frequency regulation u, enabling control over pump speed via VFD to achieve energy-saving control.
4. Case Study and Results Analysis
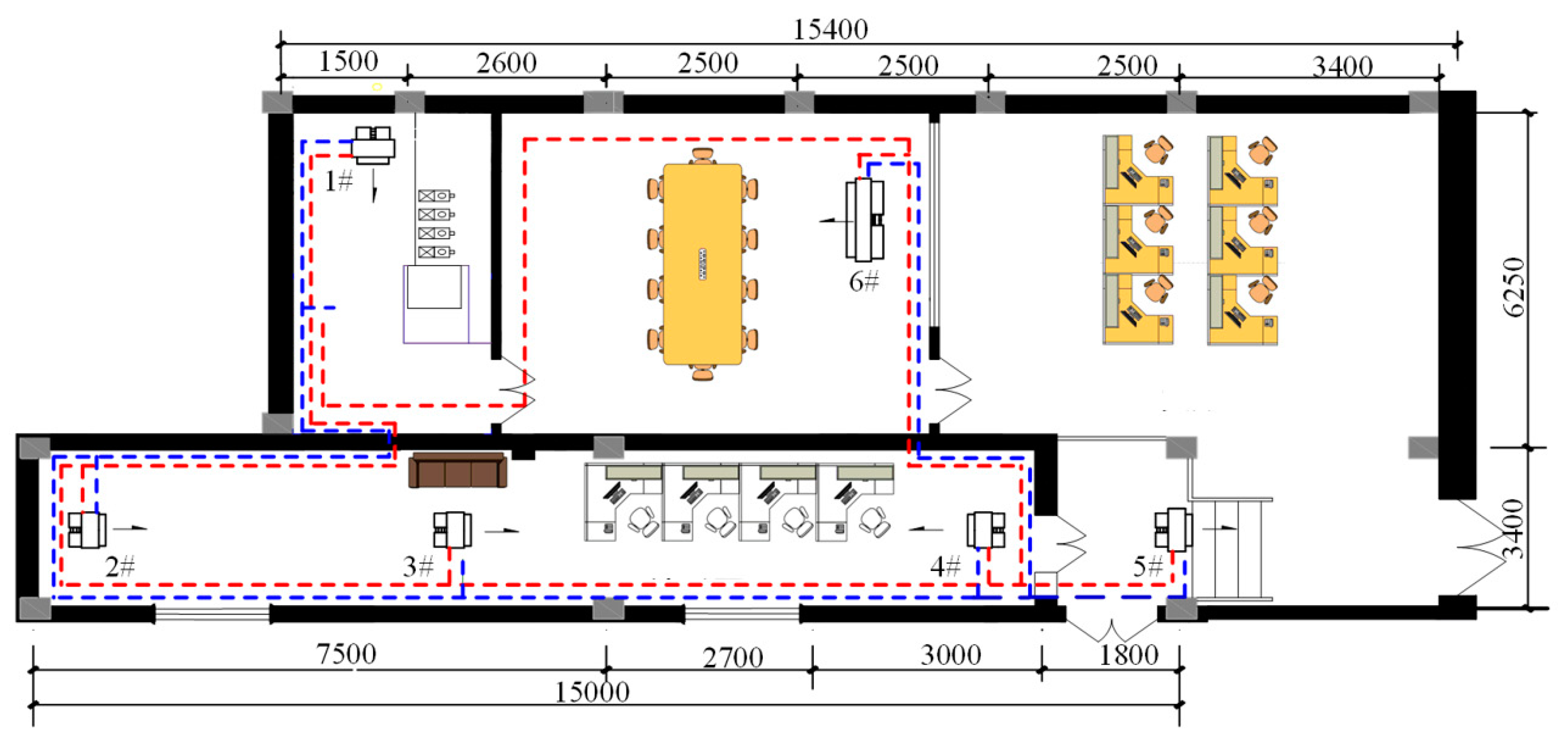
4.1. Variable Flow Air Conditioning System Test Bench
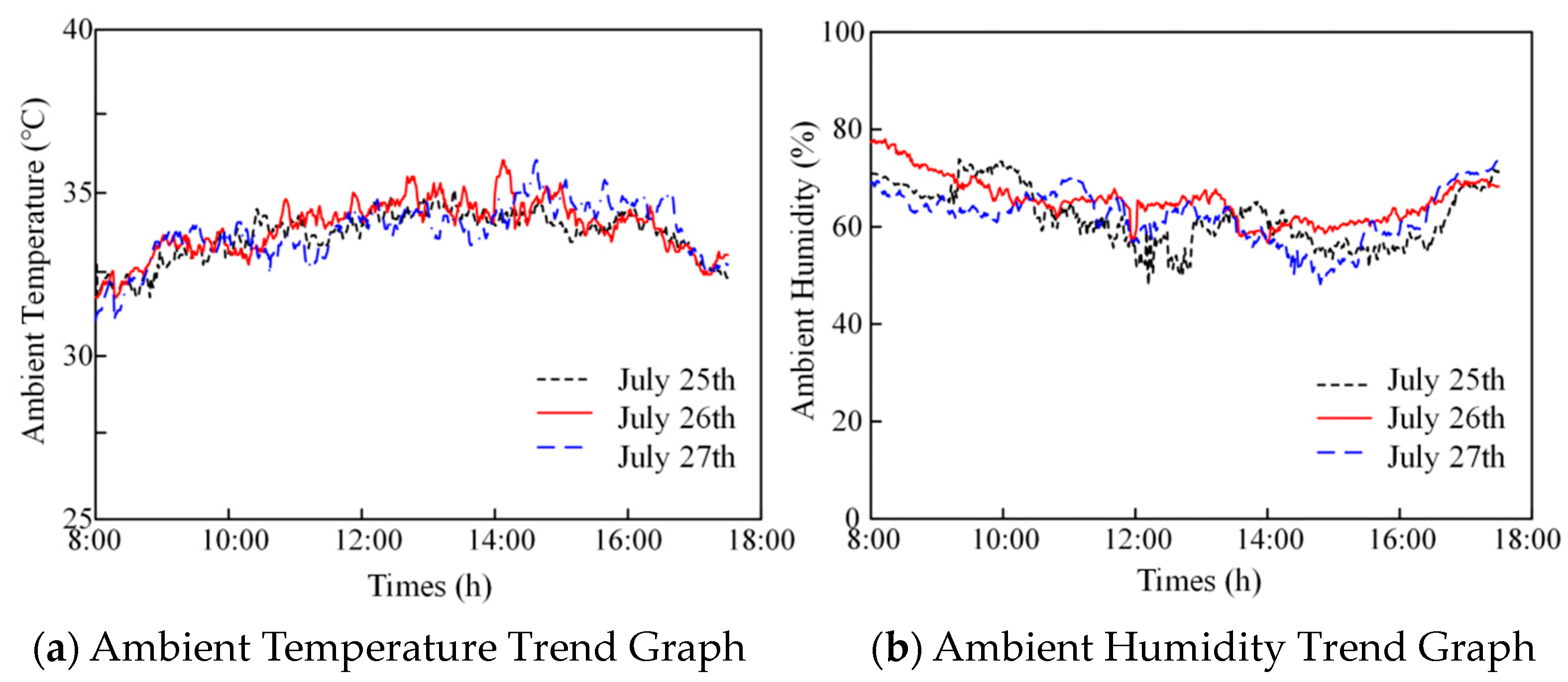
4.2. Test Conditions
4.3. Tests
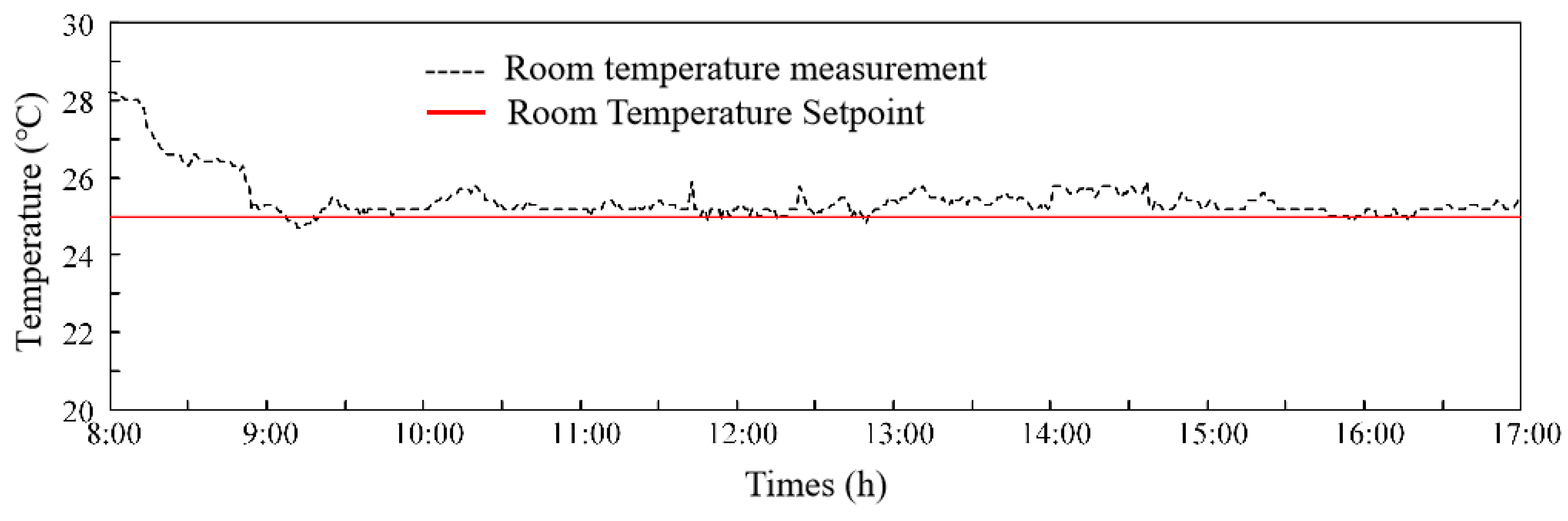
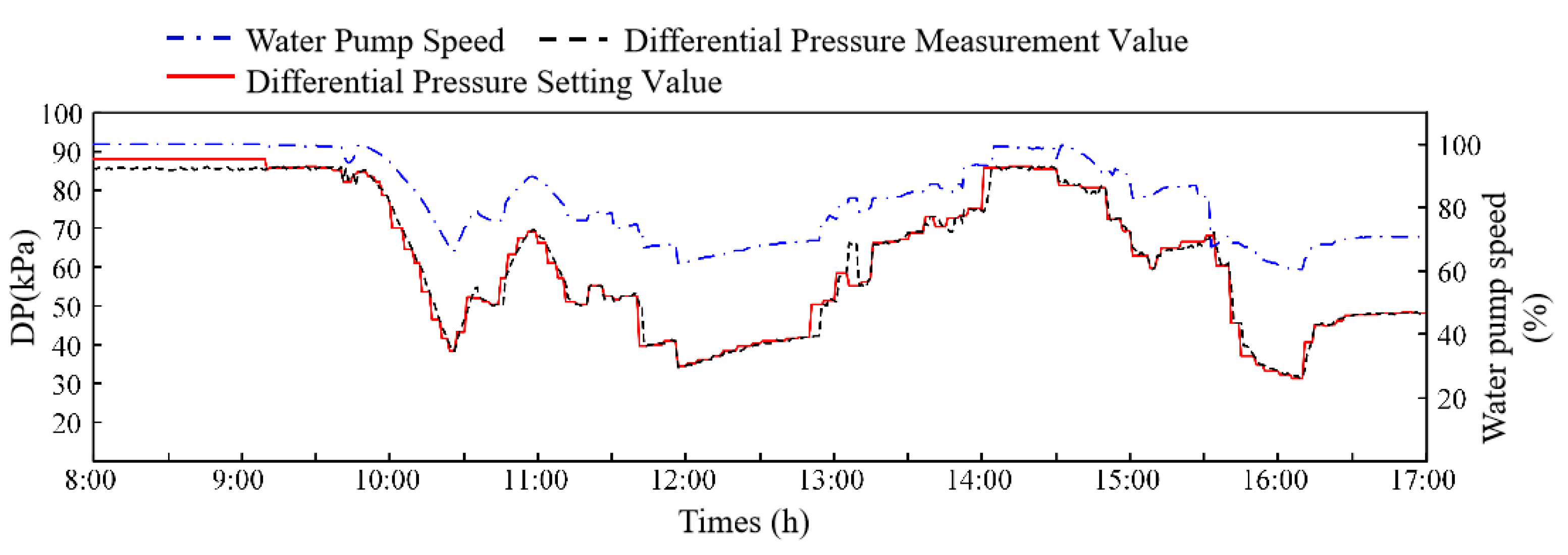
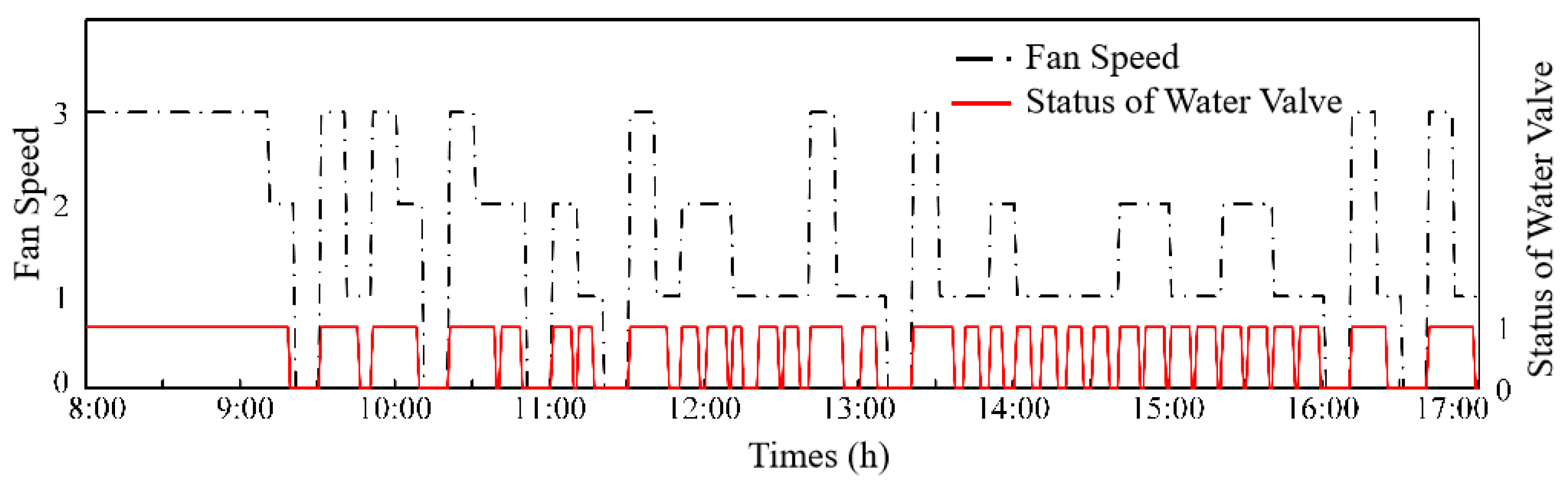
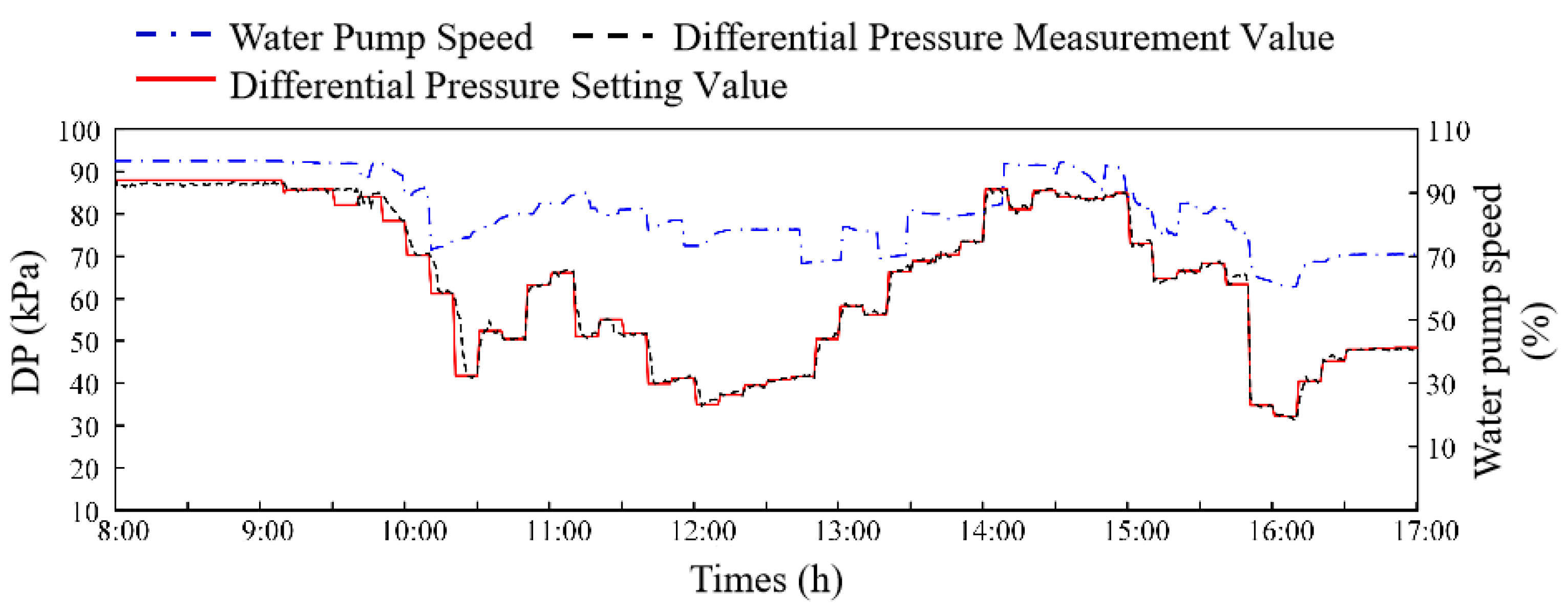
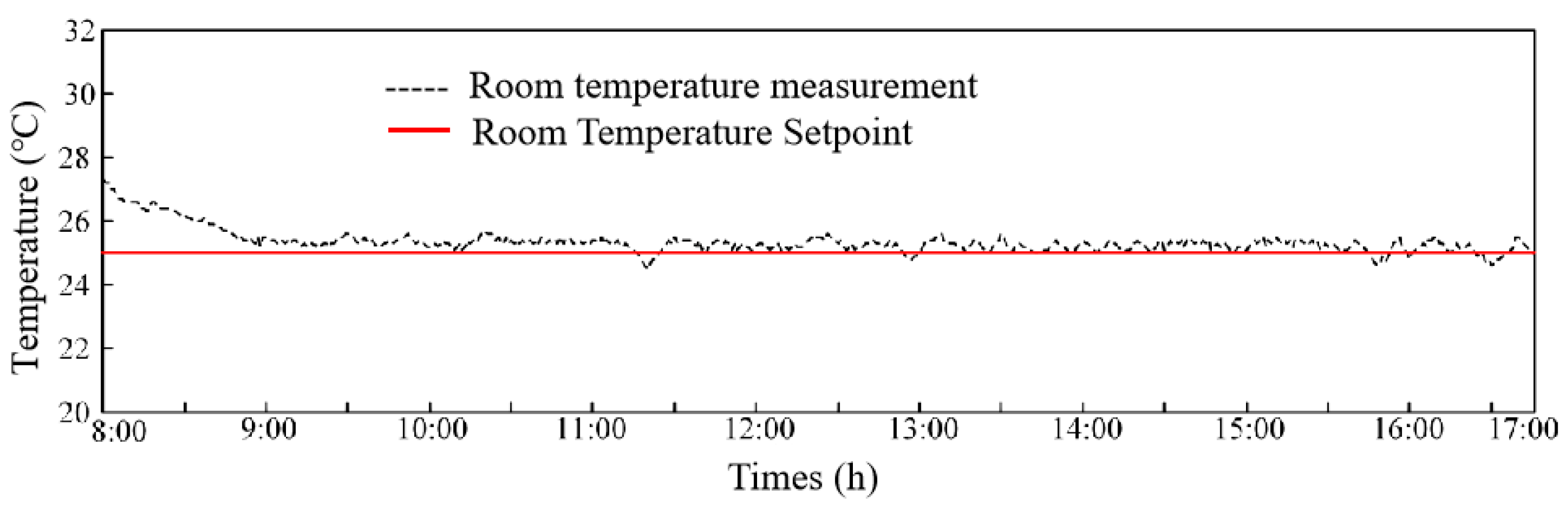
- Control performance test results of variable differential pressure fuzzy control method for water system
- 2.
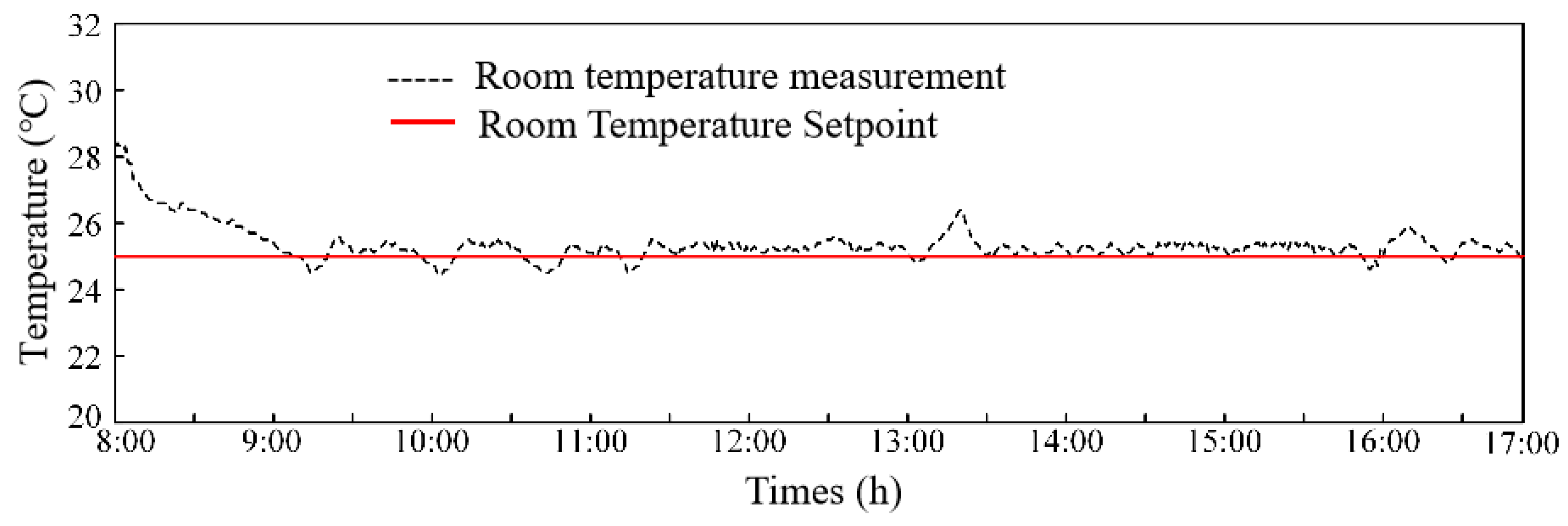
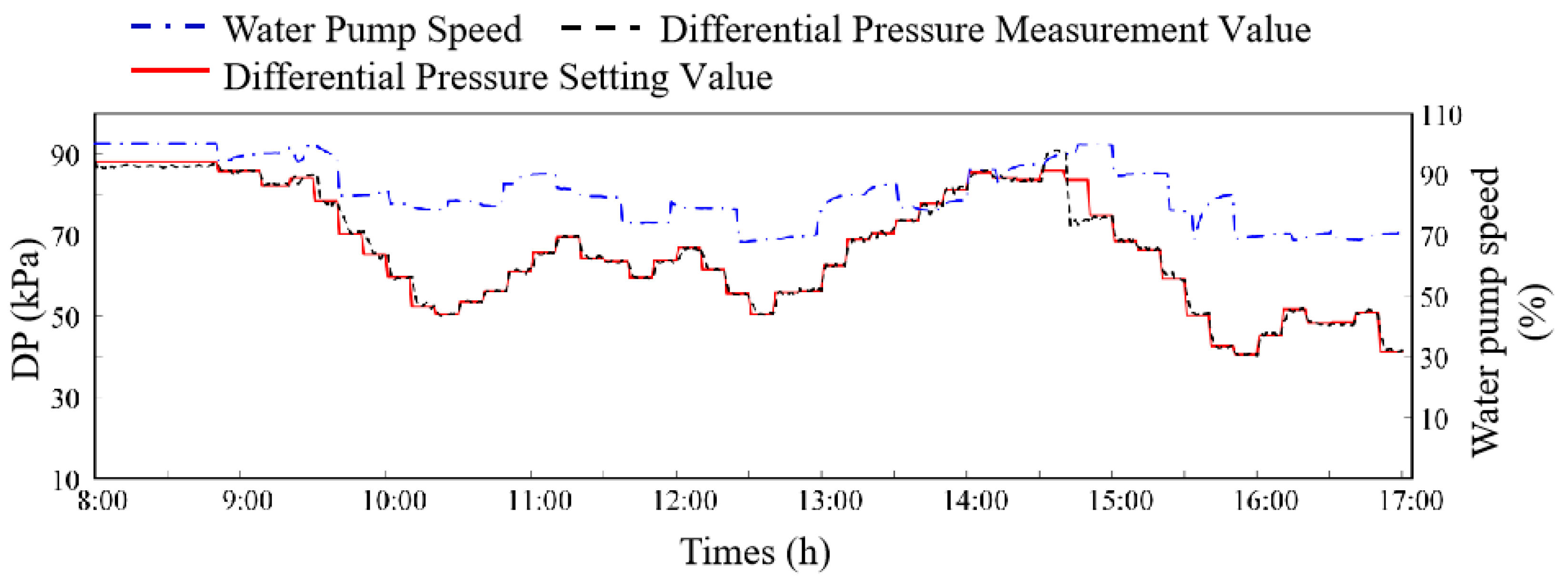
- Pump inlet and outlet pressure difference set value linear rectification method control performance test results
4.4. Results Analysis
5. Conclusions and Future Works
- This approach enables online identification of air conditioning water systems to serve as a suitable control reference loop for achieving energy-saving control of pump frequency conversion differential pressure set values.
- On the phase plane controlled by room temperature, any state point appearing at quadrant I of an end branch may represent the most unfavorable thermal loop. The likelihood of an end branch being identified as the most unfavorable thermal loop is closely associated with the angle of its real-time tracer vector on this phase plane. A larger angle at (0°, 180°) indicates a higher probability for that user branch to become identified as having a critical thermal loop.
- Compared with traditional linear variable differential pressure set point control algorithms, this method achieves remarkable energy saving ranging from 4.7% to 6.5%.
- The promotion and implementation of the concept, definition, determination, and online identification method of the most unfavorable thermal loop based on heat supply balance in HVAC air systems, heating systems, and central heating systems are crucial.
- The engineering application of a variable pressure differential fuzzy control method for water system based on the identification of the most unfavorable thermal loop in energy conservation regulation of different water systems still requires further research. The energy consumption in large public construction operation from variable flow air conditioning water systems is substantial with considerable potential for energy saving. Therefore, applying this method to practical projects can achieve significant energy saving. The focus should be on exploring how to promote and apply it in various forms of water systems.
- This algorithm utilizes the Siemens S7-1200 series PLC, which imposes higher demands on the controller compared to traditional linear algorithms. Additionally, the increased sensor component at the end results in significantly higher costs, a factor that should be considered during the promotion process.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fathollahzadeh, M.H.; Tabares-Velasco, P.C. Integrated framework for optimization of air- and water-side HVAC systems to minimize electric utility cost of existing commercial districts. Energy Build. 2022, 273, 112328. [Google Scholar] [CrossRef]
- Gidwani, B.N. Optimization of Chilled Water Systems. Energy Eng. J. Assoc. Energy Eng. 1984, 84. [Google Scholar]
- Wang, S.; Burnett, J. Online adaptive control for optimizing variable-speed pumps of indirect water-cooled chilling systems. Appl. Therm. Eng. Des. Process. Equip. Econ. 2001, 21, 1083–1103. [Google Scholar] [CrossRef]
- Mba, L.; Meukam, P.; Kemajou, A. Application of artificial neural network for predicting hourly indoor air temperature and relative humidity in modern building in humid region. Energy Build. 2016, 121, 32–42. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, J.; Xia, X. Energy consumption of air conditioners at different temperature set points. Energy Build. 2013, 65, 412–418. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, S. Energy efficient control of variable speed pumps in complex building central air-conditioning systems. Energy Build. 2009, 41, 197–205. [Google Scholar] [CrossRef]
- Gao, D.C.; Wang, S.; Sun, Y. A fault-tolerant and energy efficient control strategy for primary–secondary chilled water systems in buildings. Energy Build. 2011, 43, 3646–3656. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Fisher, B.J.M.D. Pump Differential Pressure Setpoint Reset Based on Chilled Water Valve Position. ASHRAE Trans. 2003, 2003, 371–377. [Google Scholar]
- Liu, X.; Liu, J.; Lu, Z.; Xing, K.; Mai, Y. Diversity of energy-saving control strategy for a parallel chilled water pump based on variable differential pressure control in an air-conditioning system. Energy 2015, 88, 718–733. [Google Scholar]
- Jiang, X.; Xu, Y.; Fang, Y. Energy-saving control strategy for chilled water systems of primary-secondary-tertiary pump. J. Fujian Univ. Technol. 2014. [Google Scholar]
- Zhao, T.; Ma, L.; Zhang, J. An optimal differential pressure reset strategy based on the most unfavorable thermodynamic loop on-line identification for a variable water flow air conditioning system. Energy Build. 2016, 110, 257–268. [Google Scholar]
- Suamir, I.N.; Ardita, I.N.; Santanu, G. Experimental and numerical optimization on chilled water configuration for improving temperature performance and economic viability of a centralized chiller plant. In Conference Series, Proceedings of the International Conference on Applied Science and Technology, Bali, Indonesia, 24–25 October 2019; IOP Publishing Ltd.: Bristol, UK, 2020. [Google Scholar]
- Cross, H. Analysis of flow in networks of conduits or conductors. Univ. Ill. Bull. 1936, 286, 42–47. [Google Scholar]
- Yu, J.; Liu, Q.; Zhao, A.; Chen, S.; Gao, Z.; Wang, F.; Zhang, R. A distributed optimization algorithm for the dynamic hydraulic balance of chilled water pipe network in air-conditioning system. Energy 2021, 223, 120059. [Google Scholar] [CrossRef]
- Morales, E.L.; Aguilar, J.; Garces-Jimenez, A.; Gutierrez De Mesa, J.A.; Gomez-Pulido, J.M. Advanced fuzzy-logic-based context-driven control for HVAC management systems in buildings. IEEE Access 2020, 8, 1. [Google Scholar] [CrossRef]
- Cai, X.; Jin, Z.; Li, H.; Kümpel, A.; Müller, D. Automated PLC Code Generation for the Implementation of Mode-Based Control Algorithms in Buildings. Buildings 2024, 14, 73. [Google Scholar] [CrossRef]






| Year | Authors | The Literature Review | Key Results Related to Work Outcomes |
|---|---|---|---|
| 1984 | Gidwani, B.N [2] | Investigated optimization methods for chilled water systems such as chilled water reset, condenser water reset, chiller sequencing, chilled water storage, and variable chilled water pumping. | Centrally chilled water systems offer potential energy and cost savings. |
| 2013 | Wang, N., J. Zhang, and X. Xia [5] | An adaptive online control method for chilled water systems was proposed. | It improved the robustness and reliability of the control system by adjusting the water supply temperature set point and number of operating pumps. |
| 2009 | Ma, Z. and S. Wang [6] | A variable flow rate air conditioning system for an ultra-high-rise building was established. | This was achieved by adjusting pump speed to achieve optimal control process for furthest end differential pressure set points using a pipe network pressure drop model. |
| 2003 | Moore and Fisher [9] | Utilized the opening of end valves as a reference to optimize the differential pressure setting value, aiming to ensure that at least one end valve is fully open in order to achieve the lowest pump power consumption. | The valve position value essentially reflects the system’s response to changes in water supply demand under a certain water supply temperature, while also indicating the operating conditions of the equipment system. |
| 2015 | Xuefeng, L. [10] | An analytical model for a parallel chilled water pump set was established, with particular emphasis on the crucial role of the adjustment characteristic of the bypass loop. | A hybrid control strategy proves most suitable for achieving variable flow in chilled water systems characterized by low flow ratios or high supply–return water differential pressures. |
| 2016 | Tianyi Zhao [12] | The most unfavorable thermal loop is used as a reference basis for control, and the Mamdani type variable differential pressure set point fuzzy control method for air conditioning system is proposed. | The effectiveness and energy-saving effect of the method are verified through experimental studies. |
| 2020 | Suamir, I.N. [13] | Chilled water circuit system of a central air conditioning plant was applied to a five-star hotel. Thermodynamic analyses and numerical simulations were established to evaluate chilled water flow rate. | Optimization on the chilled water flow rate between primary and secondary circuits by implementing variable speed pumping system incorporated with a balancing valve was estimated to potentially improve temperature performance and economic viability of the chiller plant operation. |
| 1936 | Hardy-Cross [14] | An iterative computation method for nonlinear systems of equations was proposed. | The results are more accurate, and the calculation accuracy meets the actual needs. |
| 2020 | L. Morales [16] | Demonstrates the utilization of LAMDA (multivariable data analysis learning algorithm) in the advanced control of building HVAC systems. | A new inference method integrated into LAMDA is employed to calculate control actions that drive the system to a zero-error state. |
| ei (kT) | NB | NM | NS | ZE | PS | PM | PB | ||
|---|---|---|---|---|---|---|---|---|---|
| (kT) | |||||||||
| (kT) | |||||||||
| NB | NB | NB | NB | NB | NM | NS | ZE | ||
| NM | NB | NB | NB | NM | NS | ZE | PS | ||
| NS | NB | NB | NM | NS | ZE | PS | PM | ||
| ZE | NB | N | NS | ZE | PS | PM | PB | ||
| PS | NM | NS | ZE | PS | PM | PB | PB | ||
| PM | NS | ZE | PS | PM | PB | PB | PB | ||
| PB | ZE | PS | PM | PB | PB | PB | PB | ||
| Test Methods | Energy Consumption Statistics (kWh) | Energy Saving (%) | |
|---|---|---|---|
| Fan Coil Electricity Consumption | Electricity Consumption of Water Pumps | ||
| System frequency operation (pump speed 50 Hz, fan in high gear) | 3.33 | 5.49 | - |
| VPDFC-IMUTL | 1.13 | 2.07 | 41.8 |
| Linear adjustment algorithm K = 0.5 | 1.20 | 2.21 | 38.0 |
| Linear adjustment algorithm K = 0.1 | 1.30 | 2.05 | 39.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Han, Y. Variable Pressure Difference Control Method for Chilled Water System Based on the Identification of the Most Unfavorable Thermodynamic Loop. Buildings 2024, 14, 1360. https://doi.org/10.3390/buildings14051360
Chen T, Han Y. Variable Pressure Difference Control Method for Chilled Water System Based on the Identification of the Most Unfavorable Thermodynamic Loop. Buildings. 2024; 14(5):1360. https://doi.org/10.3390/buildings14051360
Chicago/Turabian StyleChen, Tingting, and Yuhang Han. 2024. "Variable Pressure Difference Control Method for Chilled Water System Based on the Identification of the Most Unfavorable Thermodynamic Loop" Buildings 14, no. 5: 1360. https://doi.org/10.3390/buildings14051360
APA StyleChen, T., & Han, Y. (2024). Variable Pressure Difference Control Method for Chilled Water System Based on the Identification of the Most Unfavorable Thermodynamic Loop. Buildings, 14(5), 1360. https://doi.org/10.3390/buildings14051360





