Study on the Performance Evolution of Hydraulic Concrete under the Alternating Action of Freeze–Thaw and Abrasion
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Mixture Design
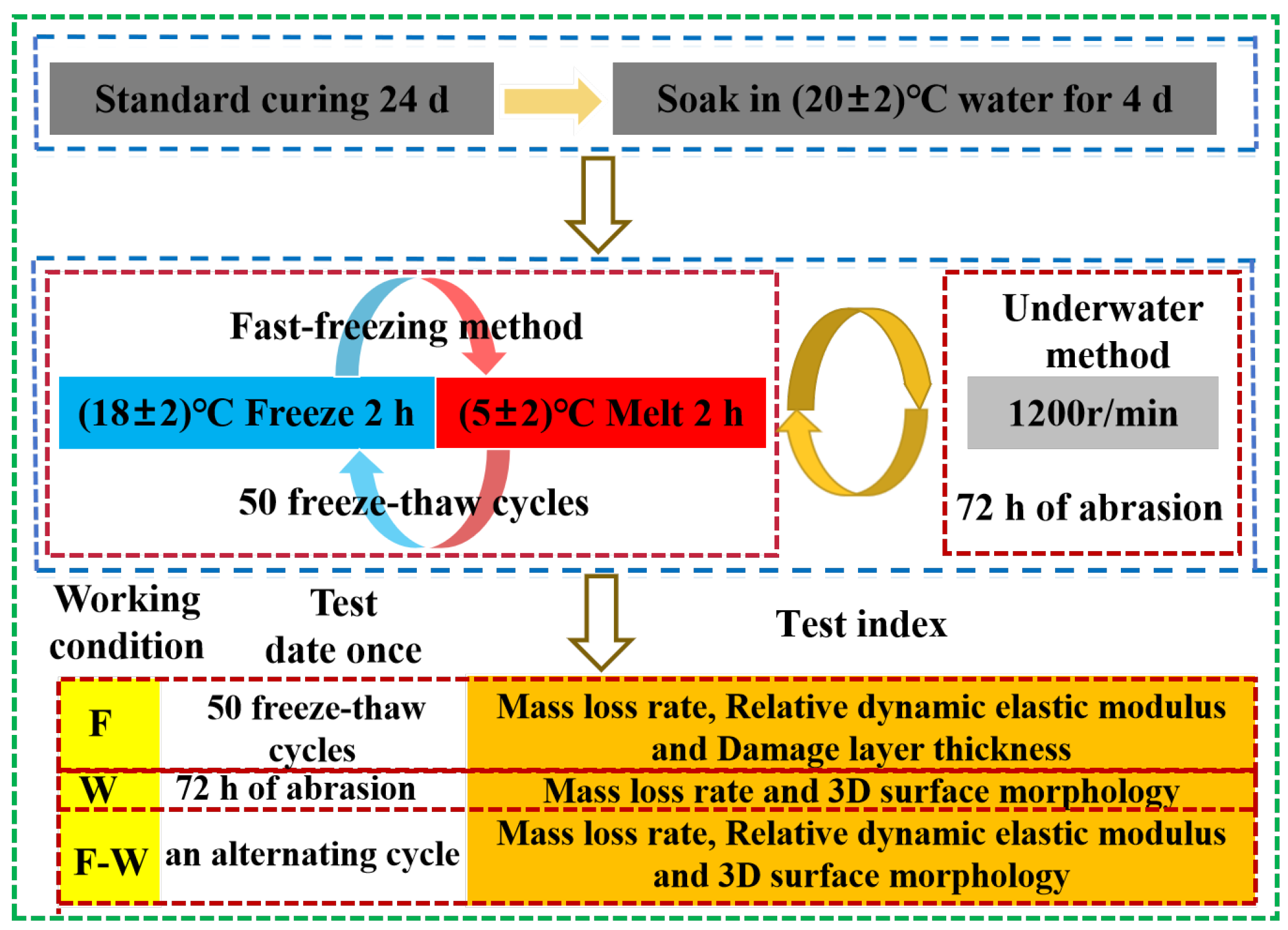
2.2. Test Scheme
2.3. Test Methods
2.3.1. Fast-Freezing Test
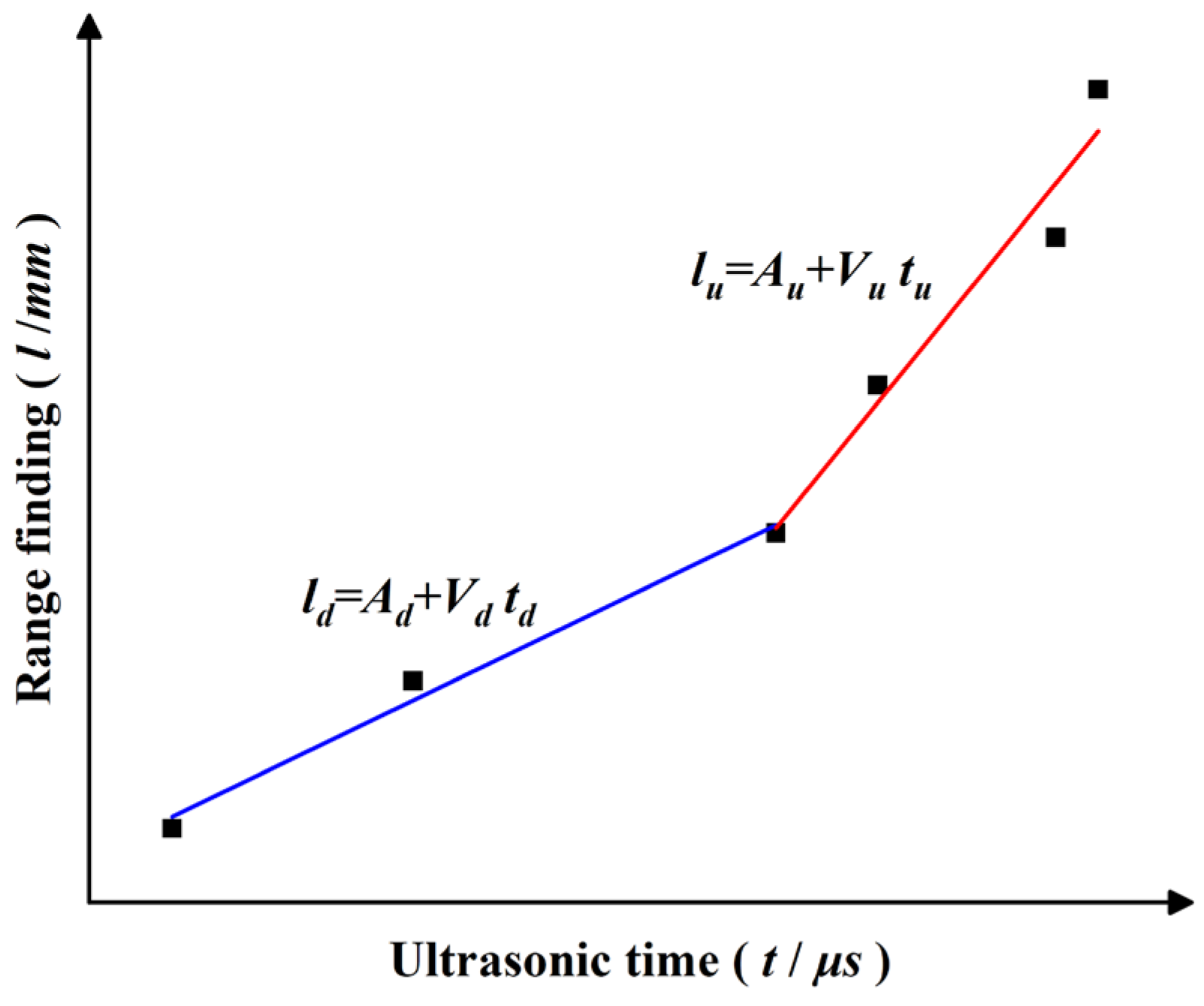
2.3.2. Damage Layer Thickness
2.3.3. Abrasion Test
2.3.4. The 3D Surface Morphology
3. Results and Discussion
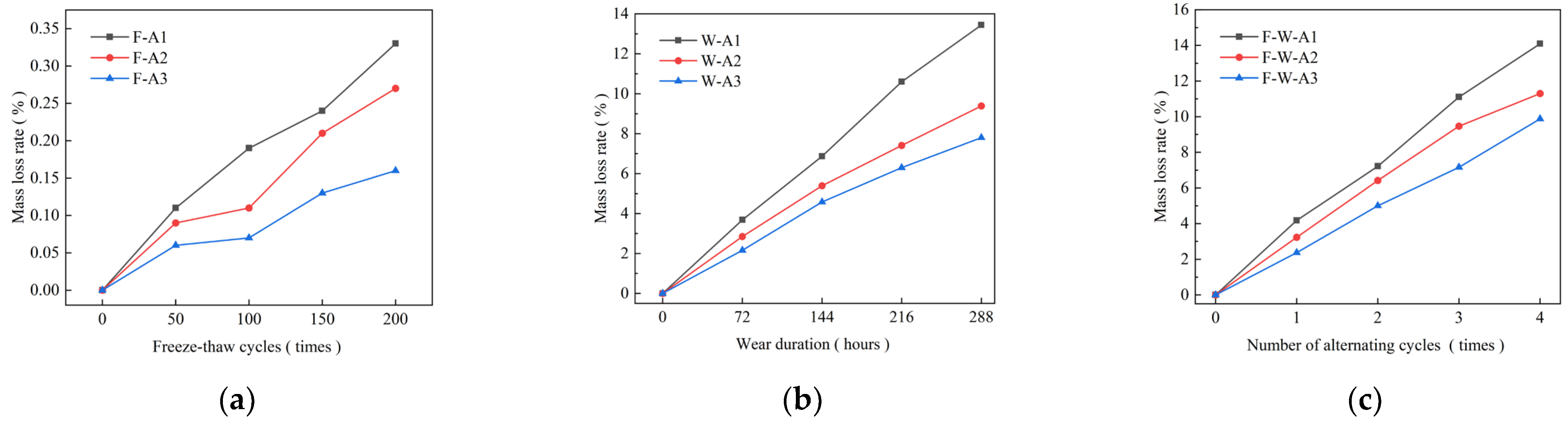
3.1. Mass Loss Rate
3.2. Relative Dynamic Elastic Modulus
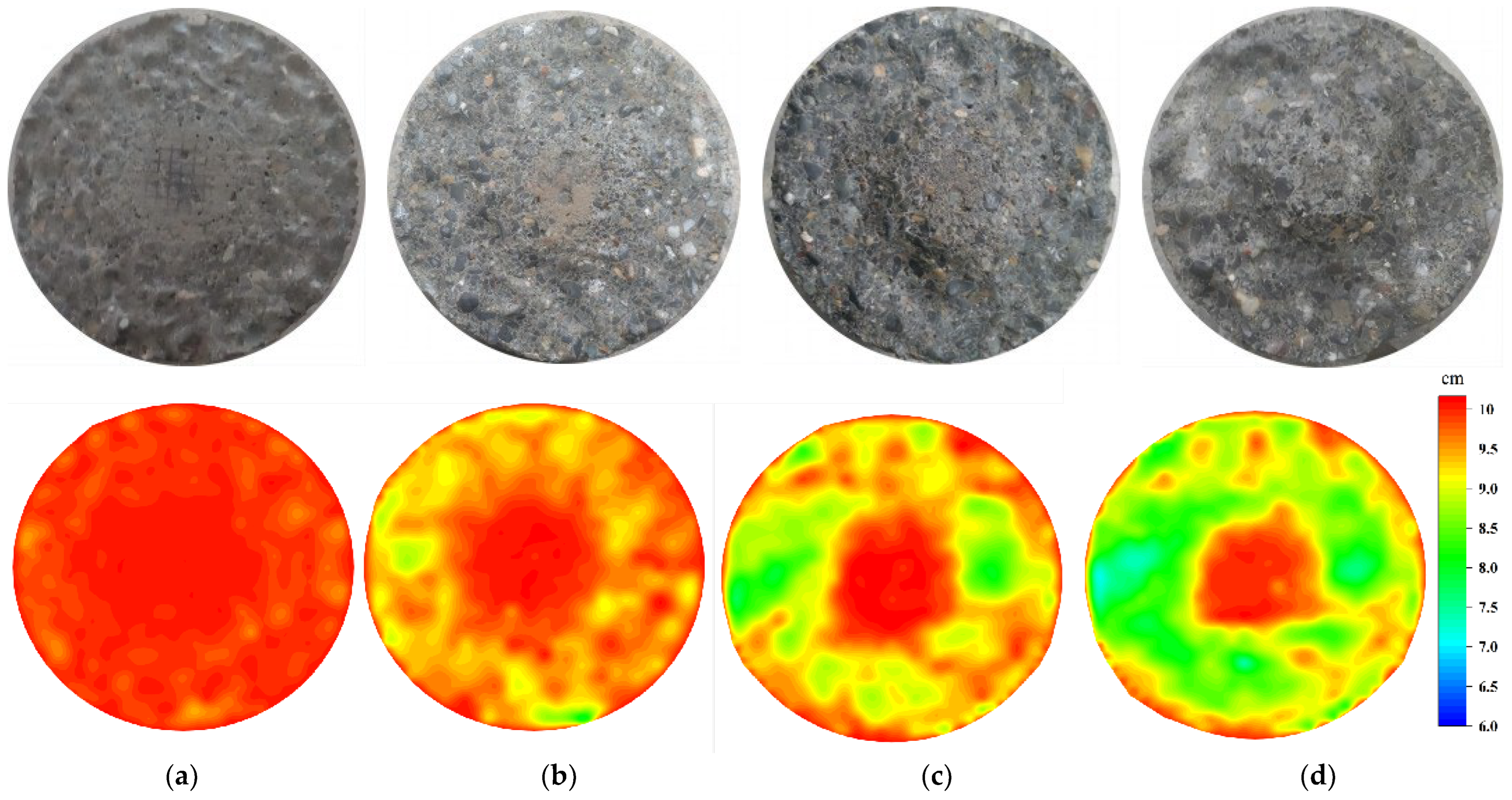
3.3. The 3D Surface Morphology and Fractal Dimension
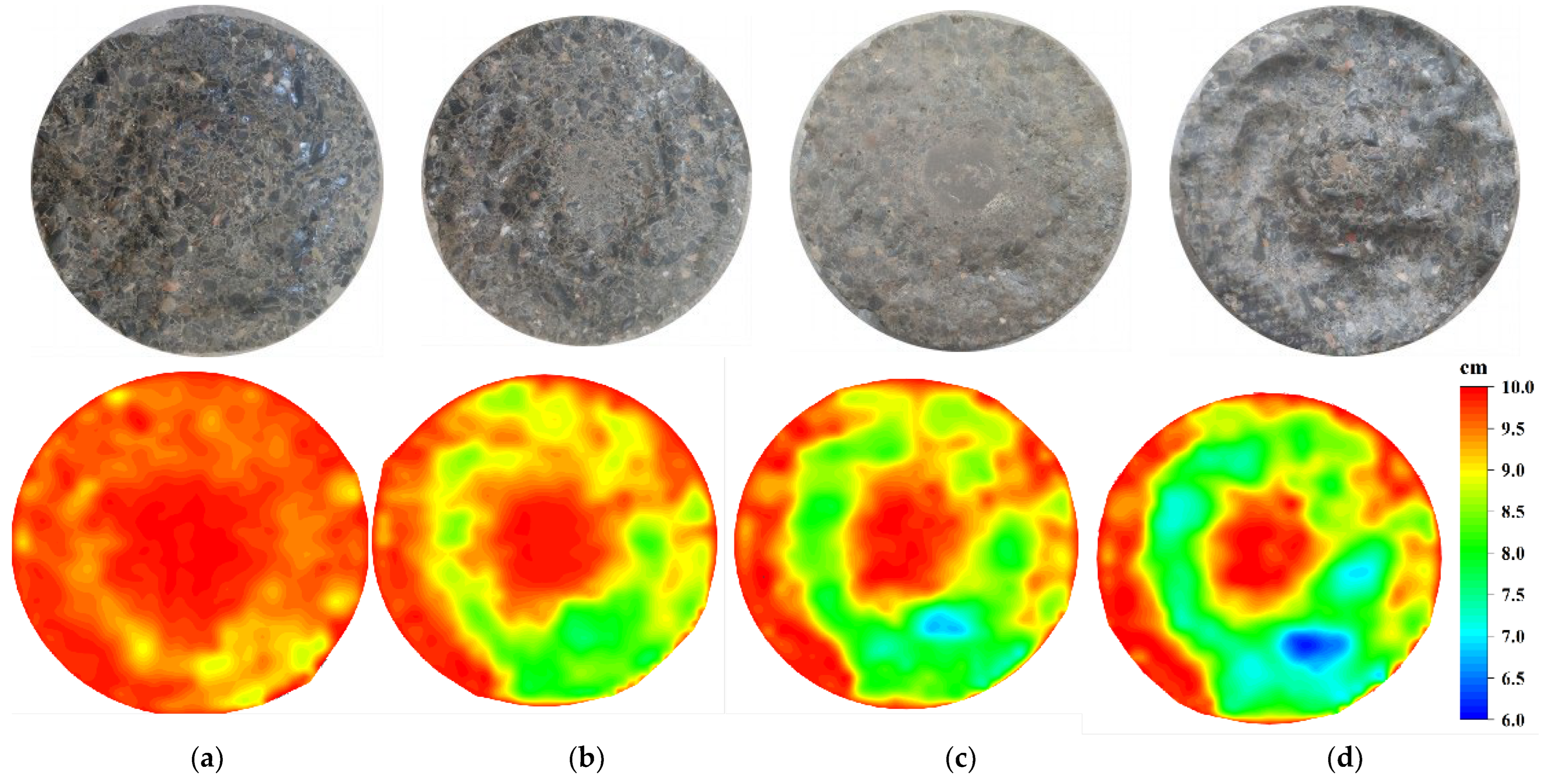
3.3.1. The 3D Surface Morphology
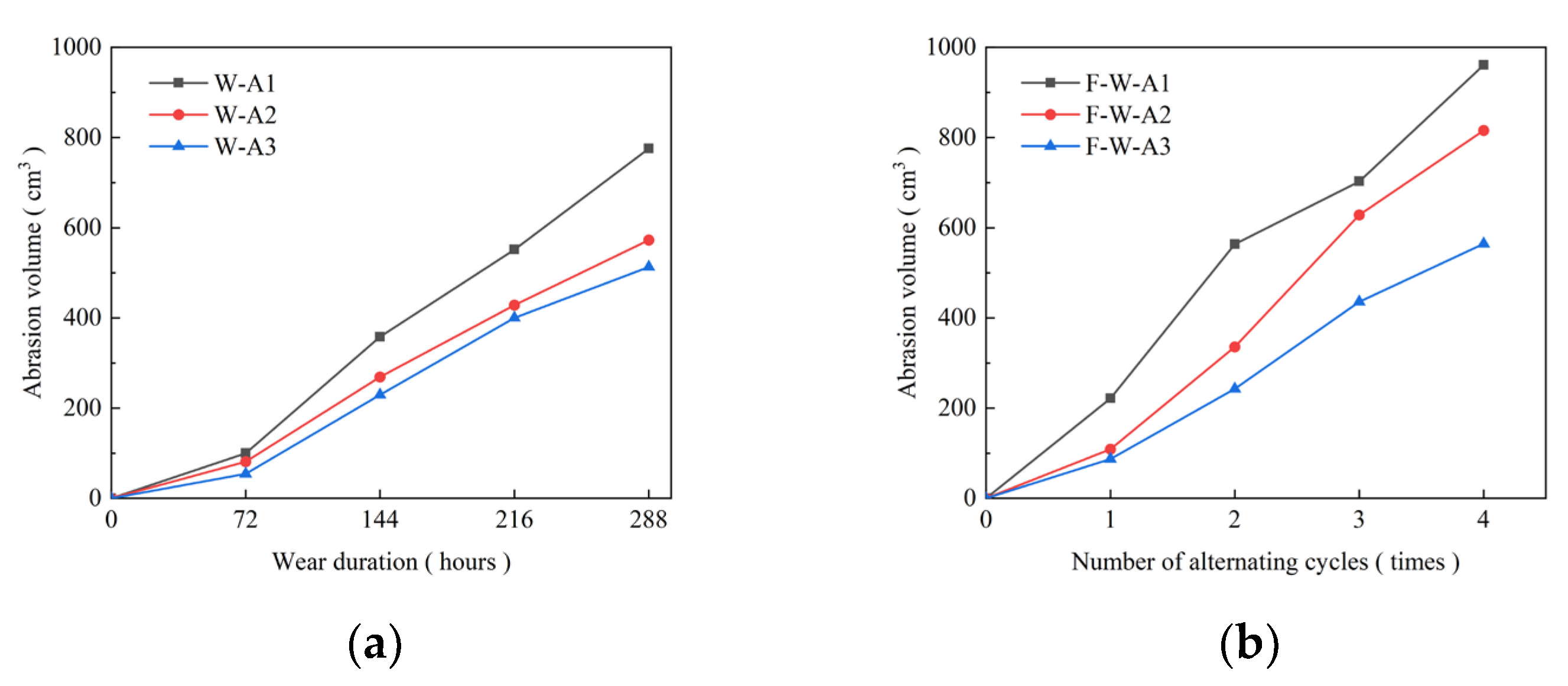
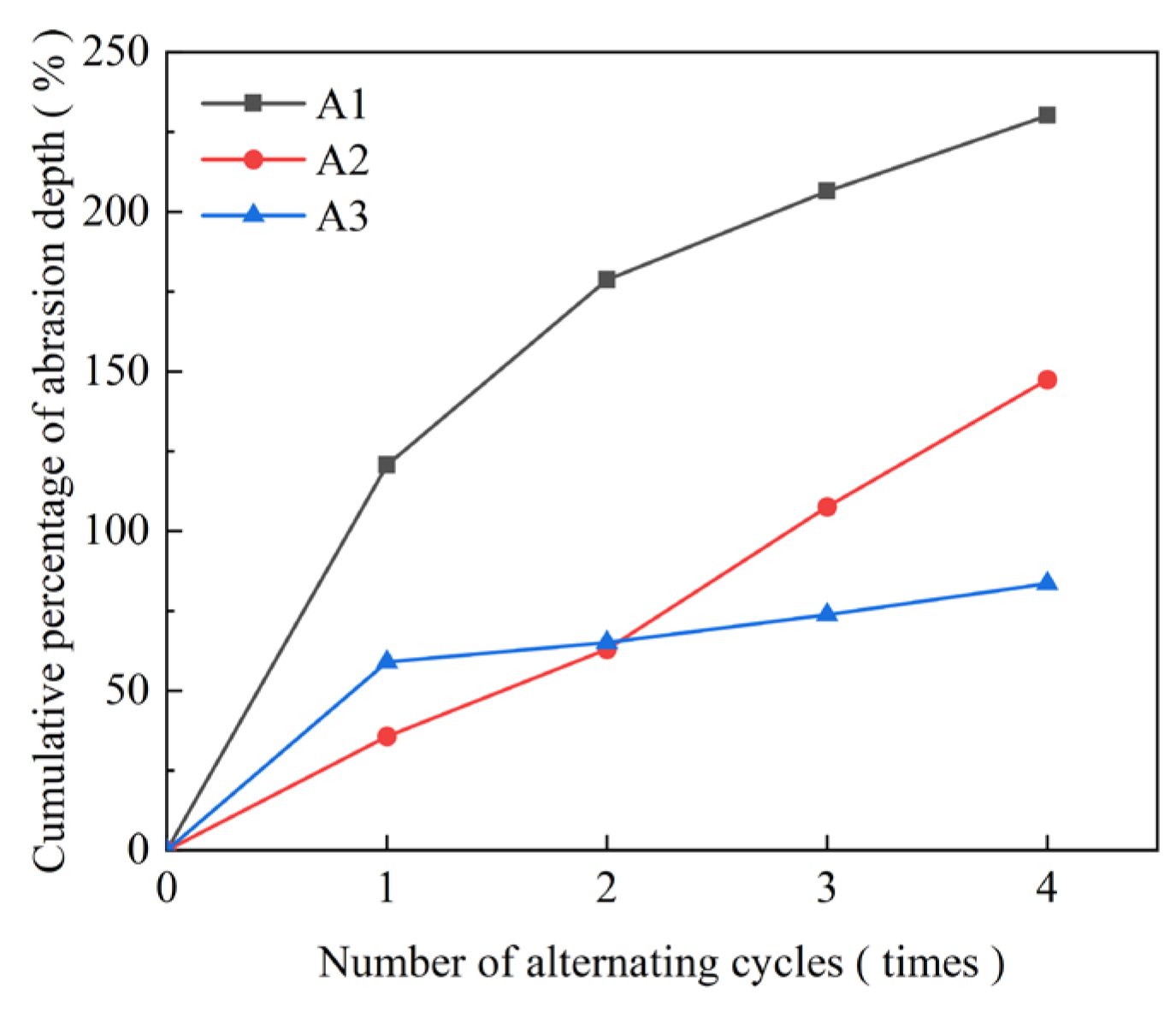
3.3.2. Abrasion Depth and Volume Loss
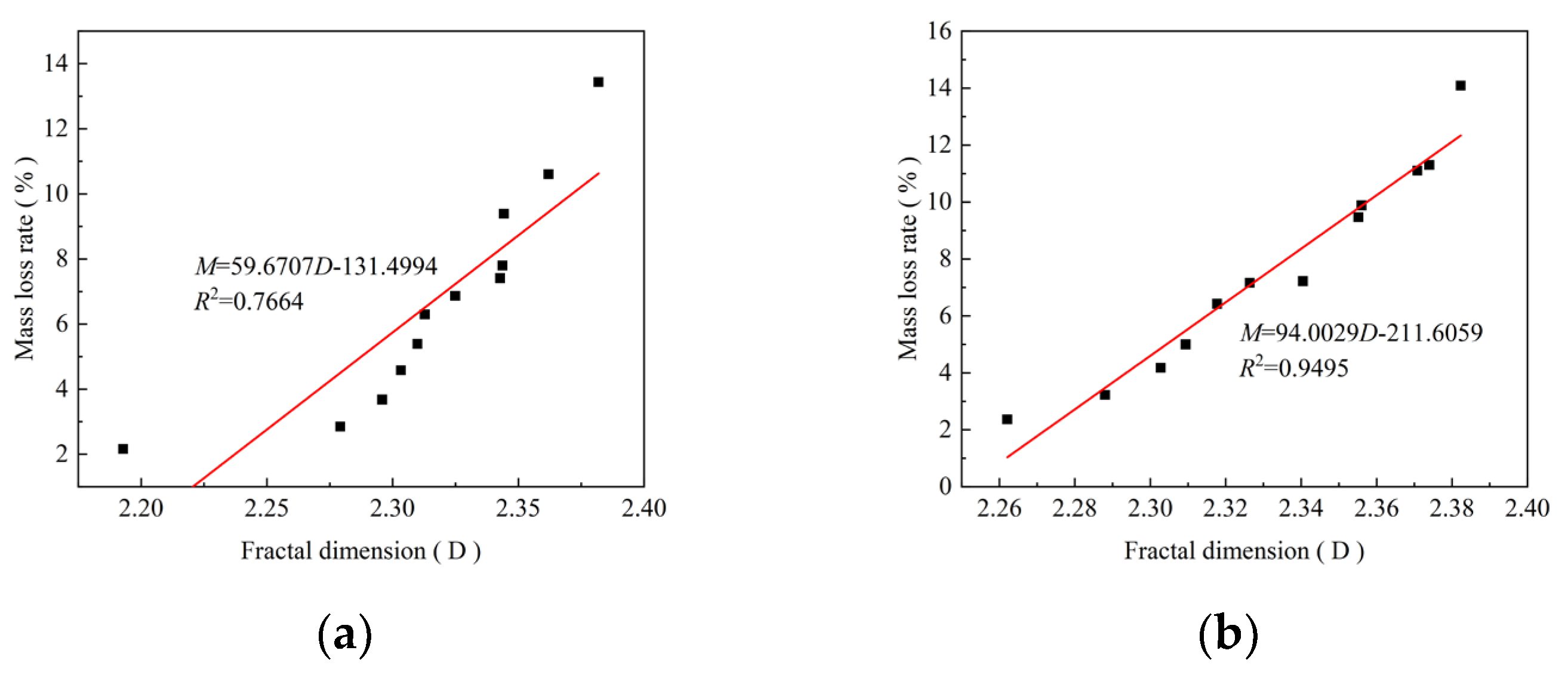
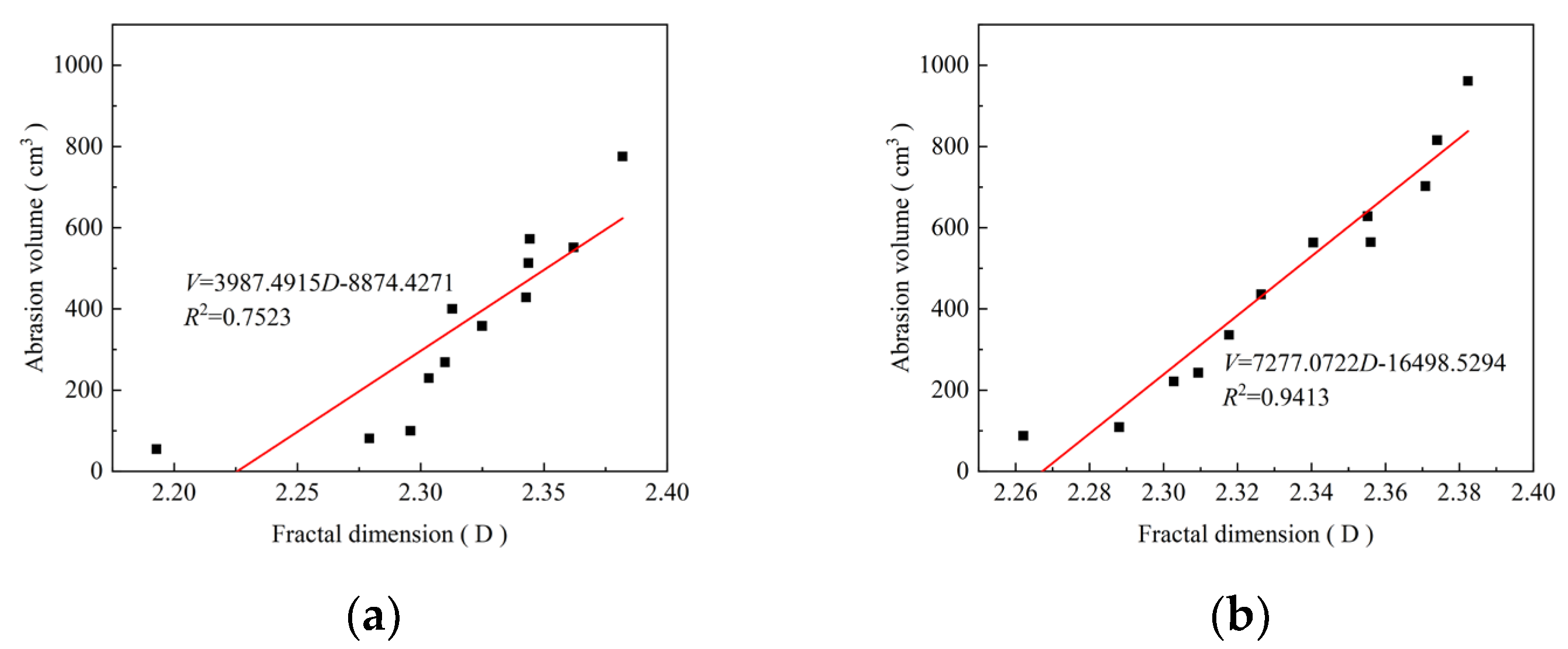
3.3.3. Fractal Dimension of Abrasion Surface
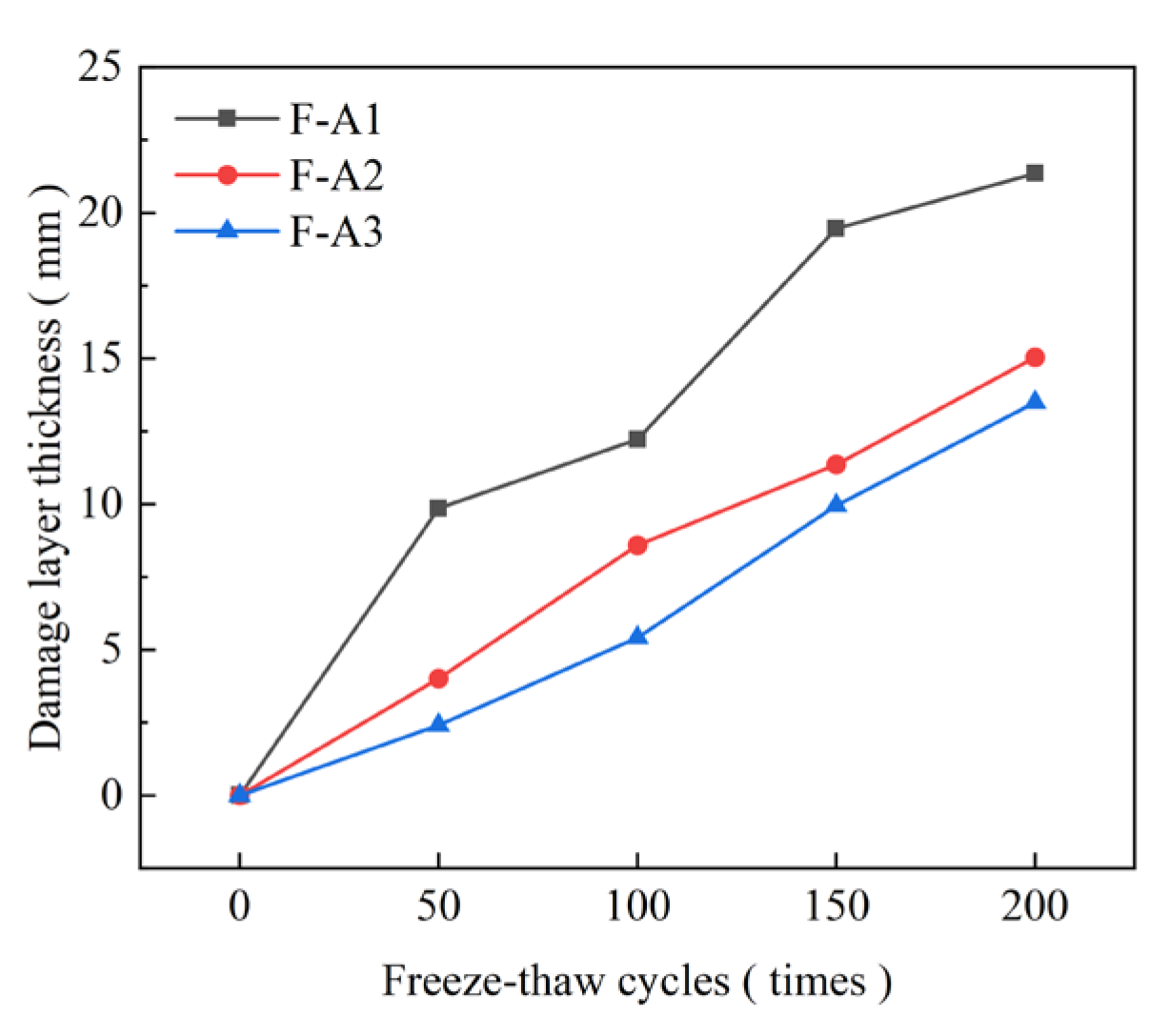
3.4. Damage Layer Thickness
4. Innovations and Deficiencies
4.1. Innovation
4.2. Deficiencies
5. Conclusions
- (1)
- During the initial stages of the alternating action of F and W, the surface layer of samples develops a crispy skin and pockmarked form due to F action. It becomes the area of plastic wear and stress concentration, which aggravates the damaging effect of wearing. This, in turn, provides an infiltration path for external water along the connecting pores and microcracks during freeze–thaw action. The internal structure of the concrete was damaged due to increased pore water crystallisation pressure, leading to a decrease in overall compactness. The alternating action accelerates the mass loss of concrete and reduces the RDEM. The maximum difference in mass loss rate and RDEM of concrete between the control and experimental groups was 1.92% and 20.11%, respectively.
- (2)
- With the increased alternating cycle period and wearing time, the change in apparent morphology characteristics of concrete shows a consistent development trend. The damage of the central part of the specimen increases gradually, while the proportion of the ring area between the undamaged part and the edge of the specimen increases. However, the F action accelerates the abrasion damage of the specimen, while the surface wear in the F-W group under operational conditions is more pronounced.
- (3)
- The fractal dimension of the sample increases with the increase of the test period. However, it did not exceed the limit of 2.4. It was found that the linear correlation between the fractal dimension, the mass loss rate, and the volume loss of the working condition F-W group was higher than that of the working condition W group, and it can be concluded that the alternating action exacerbated the damage to the concrete. The results showed that the experimental group had a good linear correlation; the correlation was close to 95%, and the control group was about 75%.
- (4)
- The tightness of low W/B concrete is stronger, so it has a stronger performance in inhibiting the development of pores and cracks. The freeze–thaw damage layer generated under freeze-thaw action still maintains high adhesive strength, reduces the wear depth of concrete under alternating action, and maintains the integrity of the whole concrete.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sharp, J.H. Surely we know all about cement—Don’t we? Adv. Appl. Ceram. 2006, 105, 162–174. [Google Scholar] [CrossRef]
- Ma, R.; Cui, C.; Ma, M.; Chen, A. Performance-based design of bridge structures under vehicle-induced fire accidents: Basic framework and a case study. Eng. Struct. 2019, 197, 109390. [Google Scholar] [CrossRef]
- Lu, P.; Shi, Q.; Ye, K.; Wu, Y.; Lu, L.; Zhou, Y. Prediction of mechanical behavior of reinforced concrete bridges following a fire based on the fire dynamics simulator–kriging model. Struct. Concr. 2023, 24, 5855–5871. [Google Scholar] [CrossRef]
- Alomari, Q.; Linzell, D. Reinforced Concrete Bridge Column Multihazard Performance: A Computational Tool to Assess Response to Vehicle Impact, Air Blast, and Fire. J. Perform. Constr. Fac. 2024, 38, 04023061. [Google Scholar] [CrossRef]
- Peng, X.; Zhou, M. Thermo-mechanical behavior of composite beams with corrugated steel webs exposed to localized fire. J. Constr. Steel Res. 2023, 211, 108180. [Google Scholar] [CrossRef]
- Zhu, X.; Bai, Y.; Chen, X.; Tian, Z.; Ning, Y. Evaluation and prediction on abrasion resistance of hydraulic concrete after exposure to different freeze-thaw cycles. Constr. Build. Mater. 2022, 316, 126055. [Google Scholar] [CrossRef]
- Yu, W.; Zhang, T.; Lu, Y.; Han, F.; Zhou, Y.; Hu, D. Engineering risk analysis in cold regions: State of the art and perspectives. Cold Reg. Sci. Technol. 2020, 171, 102963. [Google Scholar] [CrossRef]
- Doelhomid, S. Sediment control of the brantas river. Water Int. 1982, 7, 123–126. [Google Scholar] [CrossRef]
- Gong, J.; Qin, C.; Tang, X.; Zhang, T. Experimental study and field application of abrasion resistance for the repair of concrete water-conveying structures. Mater. Struct. 2022, 55, 167. [Google Scholar] [CrossRef]
- Su, X.; Wang, L.; Liu, W.; Wang, R.; Li, Y. Deterioration of interfacial bonding performance between metal mortar and concrete under the coupling effect of freeze-thaw cycle and abrasion. J. Build. Eng. 2024, 85, 108628. [Google Scholar] [CrossRef]
- Liu, M.; Han, B.; Ma, J. Research on the anti-abrasion capacity of concrete under freeze-thaw cycle. China Civ. Eng. J. 2019, 52, 100–109. (In Chinese) [Google Scholar]
- Tian, W.; Gao, F. Damage and degradation of concrete under coupling action of freeze-thaw cycle and sulfate attack. Adv. Mater. Sci. Eng. 2020, 2020, 8032849. [Google Scholar] [CrossRef]
- Lee, M.; Wang, Y.; Wang, W.; Hsieh, Y. Abrasion and Maintenance of High-Strength Fiber-Reinforced Pervious Concrete. Buildings 2024, 14, 127. [Google Scholar] [CrossRef]
- Lee, M.; Wang, Y.; Wang, W.; Chien, H.; Cheng, L. Experimental Study on the Mechanical Properties of Reinforced Pervious Concrete. Buildings 2023, 13, 2880. [Google Scholar] [CrossRef]
- Tan, K.; Zhang, T.; Zhu, W.; Yang, D.; Lin, D.; Wang, H.; Wei, J.; Yu, Q. Innovative High-Strength, High-Permeability Concrete for Large-Scale Applications in Permeable Subgrade of Highway Tunnel. Case Stud. Constr. Mater. 2024, 20, e02977. [Google Scholar] [CrossRef]
- Long, X.; Tan, Y.; Wan, X.; Zhou, L.; Wang, C. Effect of freeze-thaw cycles and chloride salt erosion coupling conditions on fatigue properties of PE-ECC. Case Stud. Constr. Mater. 2024, 20, e02726. [Google Scholar] [CrossRef]
- Xiao, Q.; Cao, Z.; Guan, X.; Li, Q.; Liu, X. Damage to recycled concrete with different aggregate substitution rates from the coupled action of freeze-thaw cycles and sulfate attack. Constr. Build. Mater. 2019, 221, 74–83. [Google Scholar] [CrossRef]
- Omran, H.Y.; El-Hacha, R. Effects of sustained load and freeze-thaw exposure on RC beams strengthened with prestressed NSM-CFRP strips. Adv. Struct. Eng. 2014, 17, 1801–1816. [Google Scholar] [CrossRef]
- Cao, D.; Qin, X.; Meng, S.; Tu, Y.; Elfgren, L.; Sabourova, N.; Grip, N.; Ohlsson, U.; Blanksvärd, T. Evaluation of prestress losses in prestressed concrete specimens subjected to freeze–thaw cycles. Struct. Infrastruct. Eng. 2016, 12, 159–170. [Google Scholar] [CrossRef]
- Wang, X.; Petrů, M. Mode I fracture evaluation of CFRP-to-concrete interfaces subject to aggressive environments agents: Freeze-thaw cycles, acid and alkaline solution. Compos. Part B Eng. 2019, 168, 581–588. [Google Scholar] [CrossRef]
- Fu, Q.; Bu, M.; Zhang, Z.; He, J.; Li, D.; Xu, W.; Niu, D. Chloride ion transport performance of lining concrete under coupling the action of flowing groundwater and loading. Cem. Concr. Compos. 2021, 123, 104166. [Google Scholar] [CrossRef]
- Huovinen, S. Abrasion of concrete by ice in arctic sea structures. Nord. Concr. Res. 1989, 8, 103–115. [Google Scholar]
- Huovinen, S. Abrasion of concrete structures by ice. Cem. Concr. Res. 1993, 23, 69–82. [Google Scholar] [CrossRef]
- Jacobsen, S.; Scherer, G.W.; Schulson, E.M. Concrete-ice abrasion mechanics. Cem. Concr. Res. 2015, 73, 79–95. [Google Scholar] [CrossRef]
- Guo, T.; Weng, X. Evaluation of the freeze-thaw durability of surface-treated airport pavement concrete under adverse conditions. Constr. Build. Mater. 2019, 206, 519–530. [Google Scholar] [CrossRef]
- Liu, Q.; Li, L.; Andersen, L.V.; Wu, M. Studying the abrasion damage of concrete for hydraulic structures under various flow conditions. Cem. Concr. Compos. 2023, 135, 104849. [Google Scholar] [CrossRef]
- Hasan, M.S.; Li, S.S.; Zsaki, A.M.; Nokken, M.R. Measurement of abrasion on concrete surfaces with 3D scanning technology. J. Mater. Civil. Eng. 2019, 31, 04019207. [Google Scholar] [CrossRef]
- Sarker, M.; Dias-da-Costa, D.; Hadigheh, S.A. Multi-scale 3D roughness quantification of concrete interfaces and pavement surfaces with a single-camera set-up. Constr. Build. Mater. 2019, 222, 511–521. [Google Scholar] [CrossRef]
- SL/T 352—2020; Text Code for Hydraulic Concrete. China Conservancy and Hydropower Press: Beijing, China, 2020. (In Chinese)
- Bai, Y.; Ye, X.; Liu, H.; Lu, L.; Ning, F.; Zhange, F. Concrete damage process under the coupling action of freeze-thaw cycle and water flow. Ewrhi 2019, 40, 64–69. (In Chinese) [Google Scholar]
- Jiang, C.; Jiang, L.; Chen, C.; Gong, J.; Li, S. Evaluation and prediction on the hydraulic abrasion performance of high belite cement-based concrete. KSCE J. Civ. Eng. 2021, 25, 2175–2185. [Google Scholar] [CrossRef]
- CECS 201-2000; Technical Specification for Ultrasonic Detection of Concrete Defects. Standards Press of China: Beijing, China, 2000. (In Chinese)
- Fu, Q.; Bu, M.; Li, D.; Xu, W.; He, J.; Niu, D. Resistance to sulfate attack and chemo-damage-transport model of sulfate ions for tunnel lining concrete under the action of loading and flowing groundwater. ACS Sustain. Chem. Eng. 2021, 9, 14307–14326. [Google Scholar] [CrossRef]
- ASTM C1138; Standard Test Method for Abrasion Resistance of Concrete (Underwater Method). ASTM International: West Conshohocken, PA, USA, 2012.
- Jiang, C.; Gong, J.; Jiang, L.; Chen, C.; Tang, X. Research on time-varying behavior and its influence factors of low heat concrete under abrasion. Mater. Rep. 2023, 37, 155–160. (In Chinese) [Google Scholar]
- Su, S.; Hou, P.; Gao, F.; Gao, Y.; Cai, C.; Zhang, Z.; Liang, X. A fractal perspective on structural damage and fracture characteristics of coal subjected to liquid nitrogen cooling at laboratory-scale. Fractals 2022, 30, 2250080. [Google Scholar] [CrossRef]
- Liu, W.; Lin, Y.; Zhong, H.; Su, H. Anti-abrasion test of erosion and denudation resistant concrete. Eng. Mech. 2011, 28, 157–160. [Google Scholar]
- Liu, J.; Lu, L.; Zhang, Z. Mechanism of concrete pavement subjected simultaneously to freeze-thaw and abrasion action. Concrete 2008, 9, 7–10. (In Chinese) [Google Scholar]
- Wu, F.; Chen, X.; Chen, J. Abrasion resistance of concrete under coupled debris flow and freeze-thaw cycles. Wear 2023, 524, 204805. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, J.; Yin, Z. Experimental study on mechanical properties and pore structure deterioration of concrete under freeze-thaw cycles. Materials 2021, 14, 6568. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.; Bolander, J. A topology measurement method examining hydraulic abrasion of high workability concrete. KSCE J. Civ. Eng. 2012, 16, 771–778. [Google Scholar] [CrossRef]
- Ismail, M.; Hassan, A. Abrasion and impact resistance of concrete before and after exposure to freezing and thawing cycles. Constr. Build. Mater. 2019, 215, 849–861. [Google Scholar] [CrossRef]
- Zhang, J.; Deng, H.; Taheri, A.; Ke, B.; Liu, C.; Yang, X. Degradation of physical and mechanical properties of sandstone subjected to freeze-thaw cycles and chemical erosion. Cold Reg. Sci. Technol. 2018, 155, 37–46. [Google Scholar] [CrossRef]
- Wu, F.; Chen, X.; Li, X. Abrasion performance of cement mortar by debris flow. Tribol. Int. 2022, 175, 107839. [Google Scholar] [CrossRef]





| Specimen Number | Water Cement Ratio | Cement/ kg·m−3 | Water/ kg·m−3 | Sand/ kg·m−3 | Stone/ kg·m−3 | Water Reducer/% |
|---|---|---|---|---|---|---|
| A1 | 0.43 | 387.5 | 168.4 | 801 | 1109.4 | 0.2 |
| A2 | 0.38 | 442.9 | 167.7 | 758.7 | 1050.7 | 0.2 |
| A3 | 0.32 | 516.7 | 167.3 | 732.0 | 1013.7 | 0.2 |
| Working Condition | Test Scheme | Test Specimen Number |
|---|---|---|
| F | 50, 100, 150, and 200 times of freeze–thaw cycles | F-A1, F-A2, F-A3 |
| W | 72, 144, 216, and 288 h of abrasion damage | W-A1, W-A2, W-A3 |
| F-W | 1, 2, 3, 4 alternating cycles | F-W-A1, F-W-A2, F-W-A3 |
| Working Condition | Test Specimen Number | Fractal Dimension/D | |||
|---|---|---|---|---|---|
| 72 h | 144 h | 216 h | 288 h | ||
| W | W-A1 | 2.2959 | 2.3249 | 2.3620 | 2.3819 |
| W-A2 | 2.2792 | 2.3099 | 2.3428 | 2.3443 | |
| W-A3 | 2.1929 | 2.3033 | 2.3128 | 2.3437 | |
| Working Condition | Test Specimen Number | Fractal Dimension/D | |||
|---|---|---|---|---|---|
| 1 Alternating Cycle | 2 Alternating Cycles | 3 Alternating Cycles | 4 Alternating Cycles | ||
| F-W | F-W-A1 | 2.3028 | 2.3405 | 2.3708 | 2.3823 |
| F-W-A2 | 2.2880 | 2.3177 | 2.3552 | 2.3740 | |
| F-W-A3 | 2.2621 | 2.3094 | 2.3264 | 2.3560 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, B.; Li, S.; Jiang, C. Study on the Performance Evolution of Hydraulic Concrete under the Alternating Action of Freeze–Thaw and Abrasion. Buildings 2024, 14, 1369. https://doi.org/10.3390/buildings14051369
Wu B, Li S, Jiang C. Study on the Performance Evolution of Hydraulic Concrete under the Alternating Action of Freeze–Thaw and Abrasion. Buildings. 2024; 14(5):1369. https://doi.org/10.3390/buildings14051369
Chicago/Turabian StyleWu, Baoguo, Shuangxi Li, and Chunmeng Jiang. 2024. "Study on the Performance Evolution of Hydraulic Concrete under the Alternating Action of Freeze–Thaw and Abrasion" Buildings 14, no. 5: 1369. https://doi.org/10.3390/buildings14051369
APA StyleWu, B., Li, S., & Jiang, C. (2024). Study on the Performance Evolution of Hydraulic Concrete under the Alternating Action of Freeze–Thaw and Abrasion. Buildings, 14(5), 1369. https://doi.org/10.3390/buildings14051369






