Triaxial Test and Discrete Element Numerical Simulation of Geogrid-Reinforced Clay Soil
Abstract
:1. Introduction
2. Indoor Triaxial Test
2.1. Test Methods
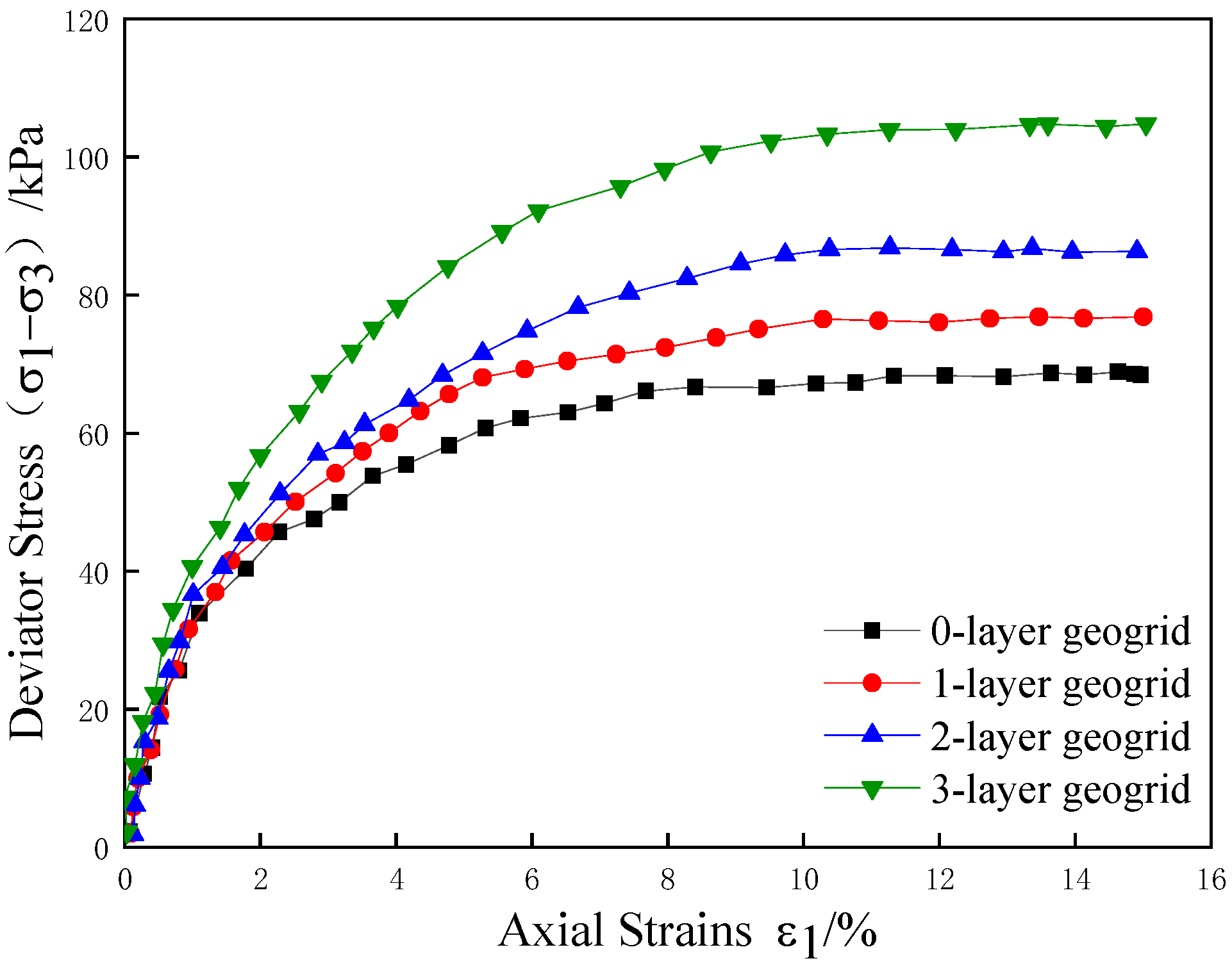
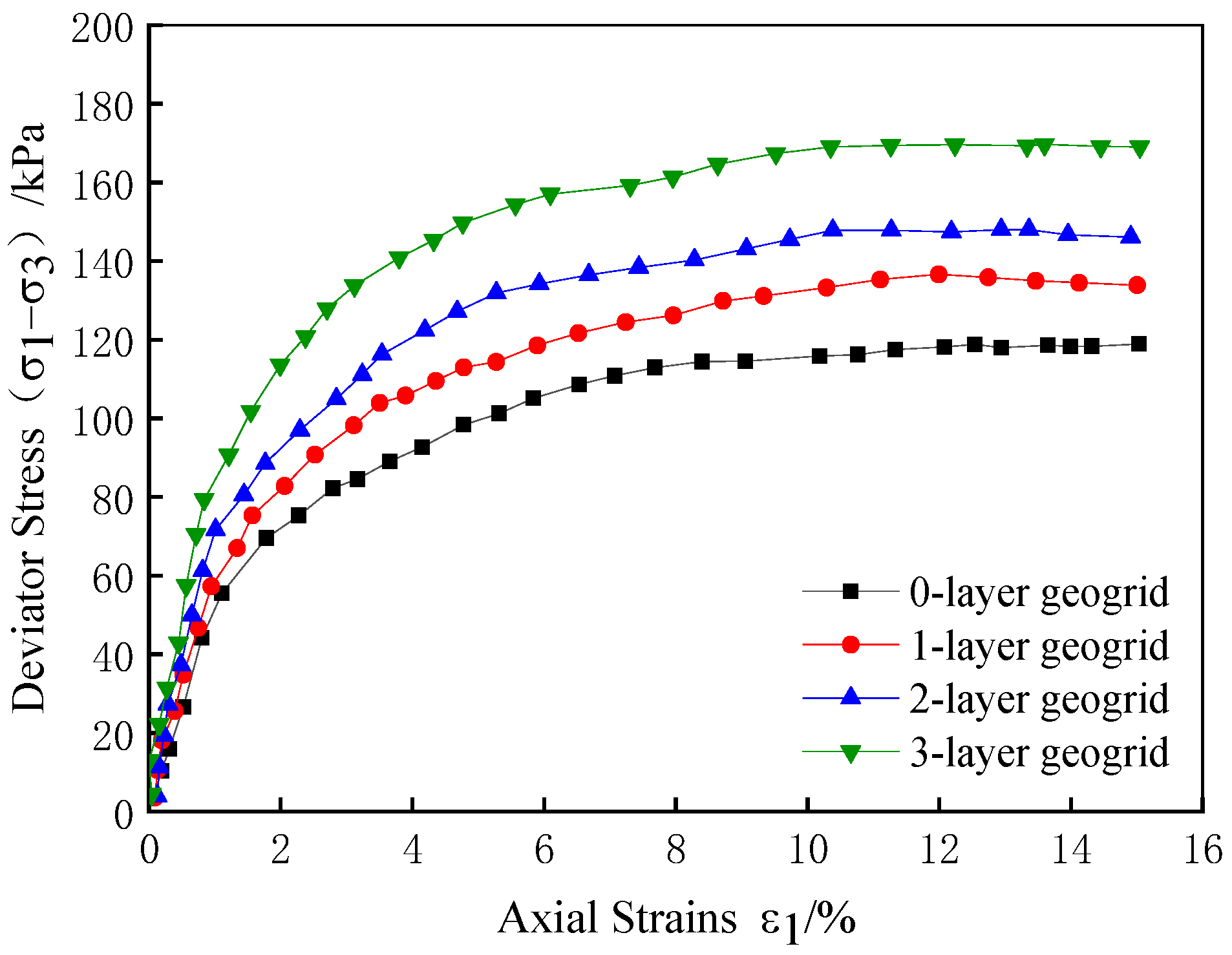
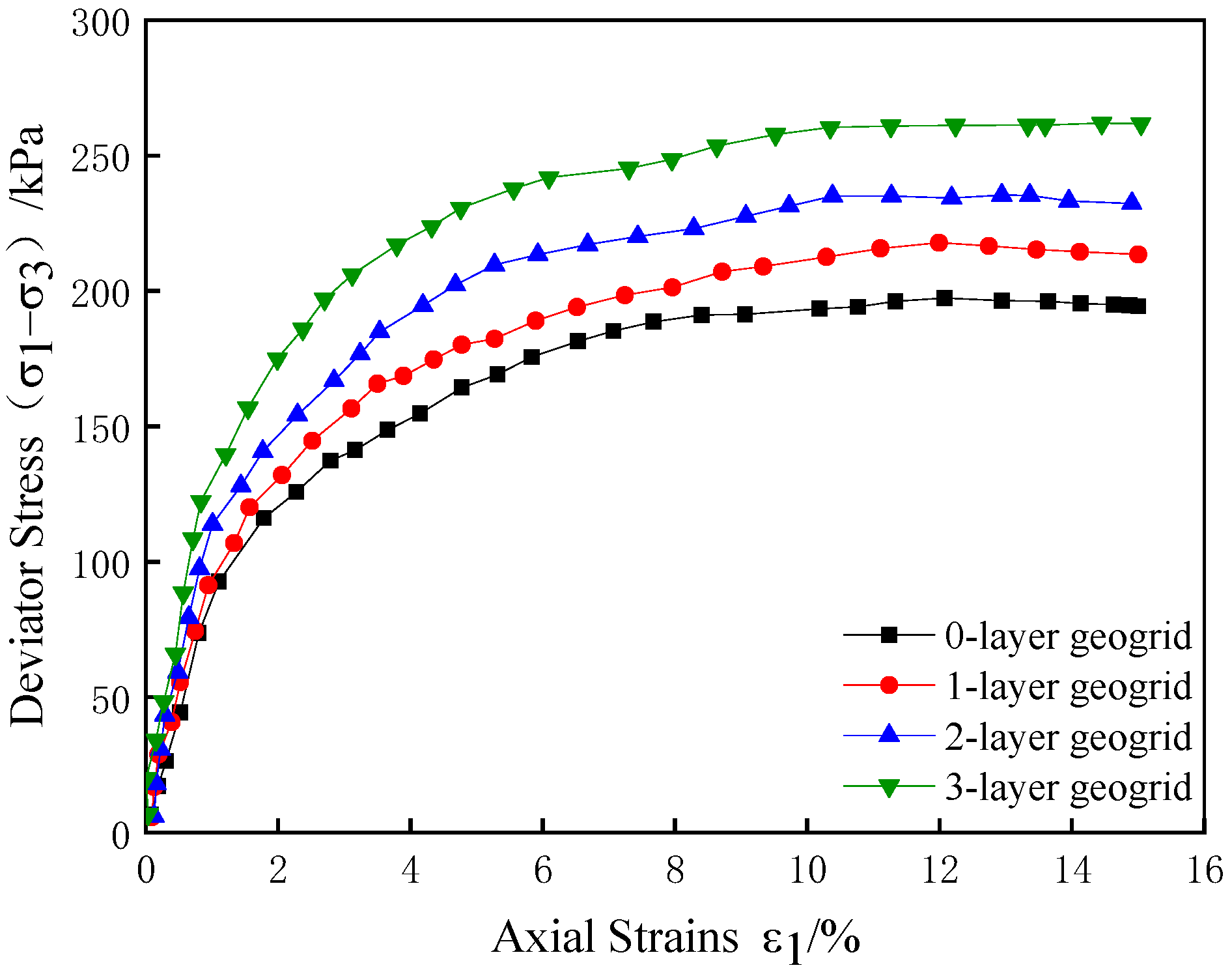
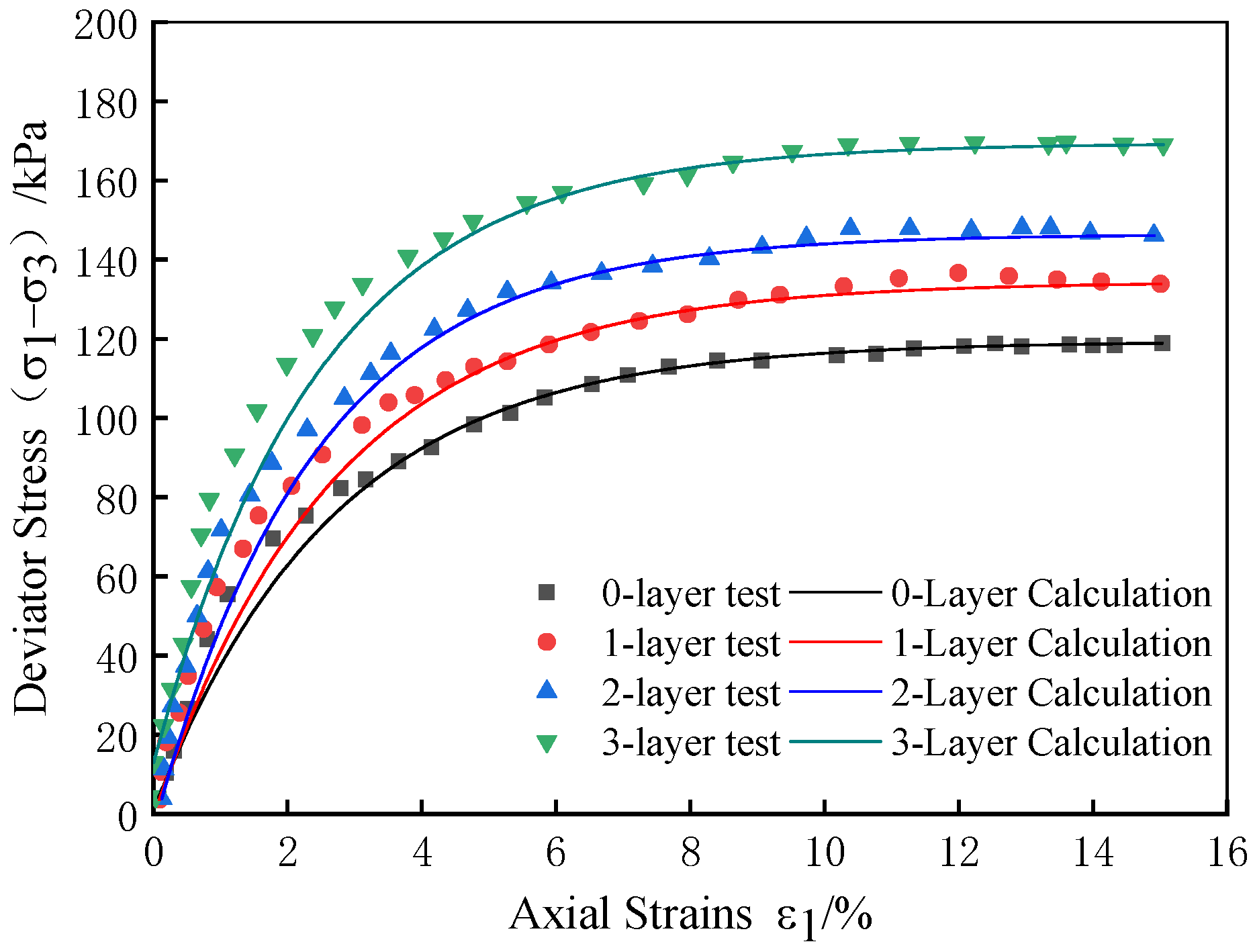
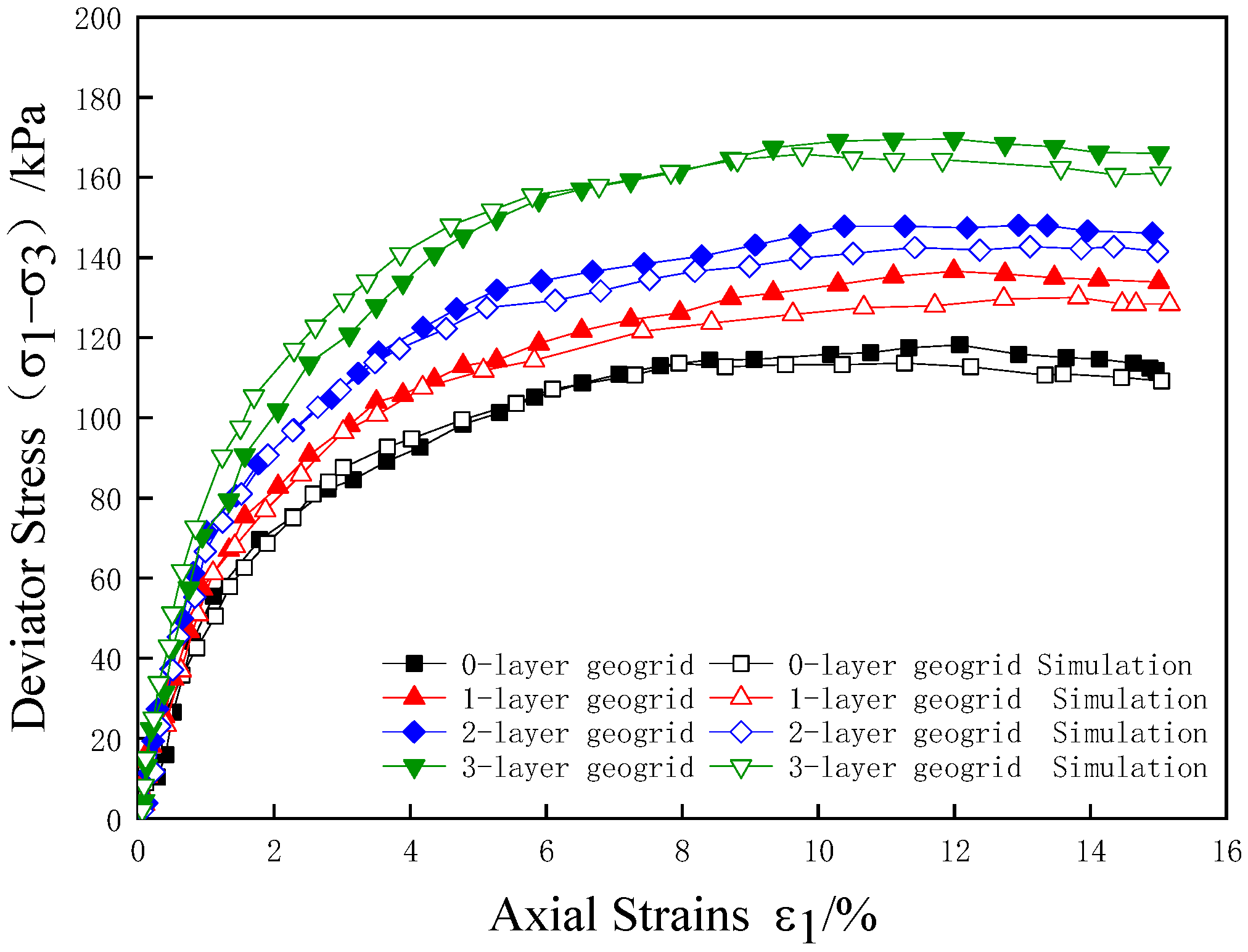
2.2. Stress–Strain Curve
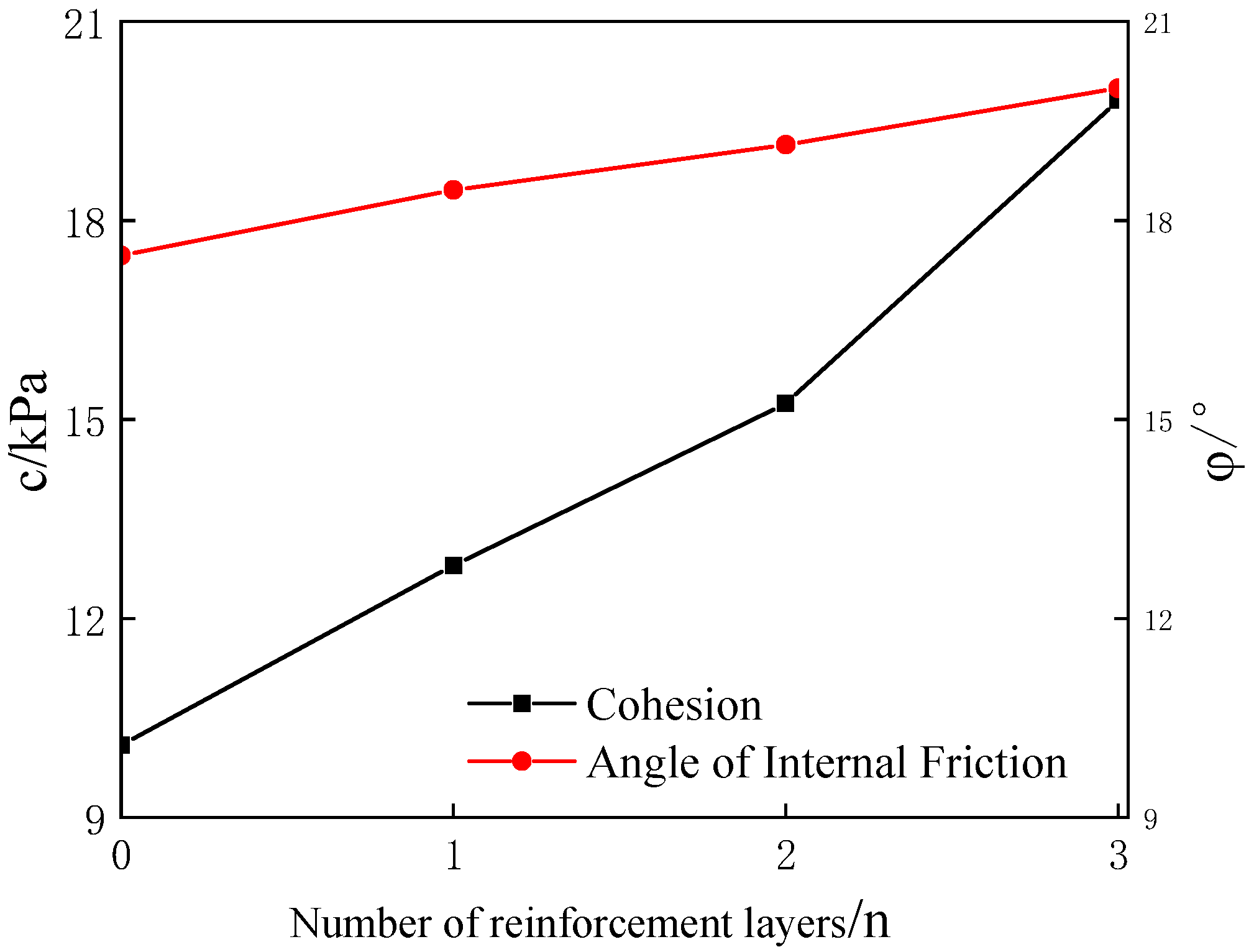
2.3. Reinforcement Effect and Shear Strength Index
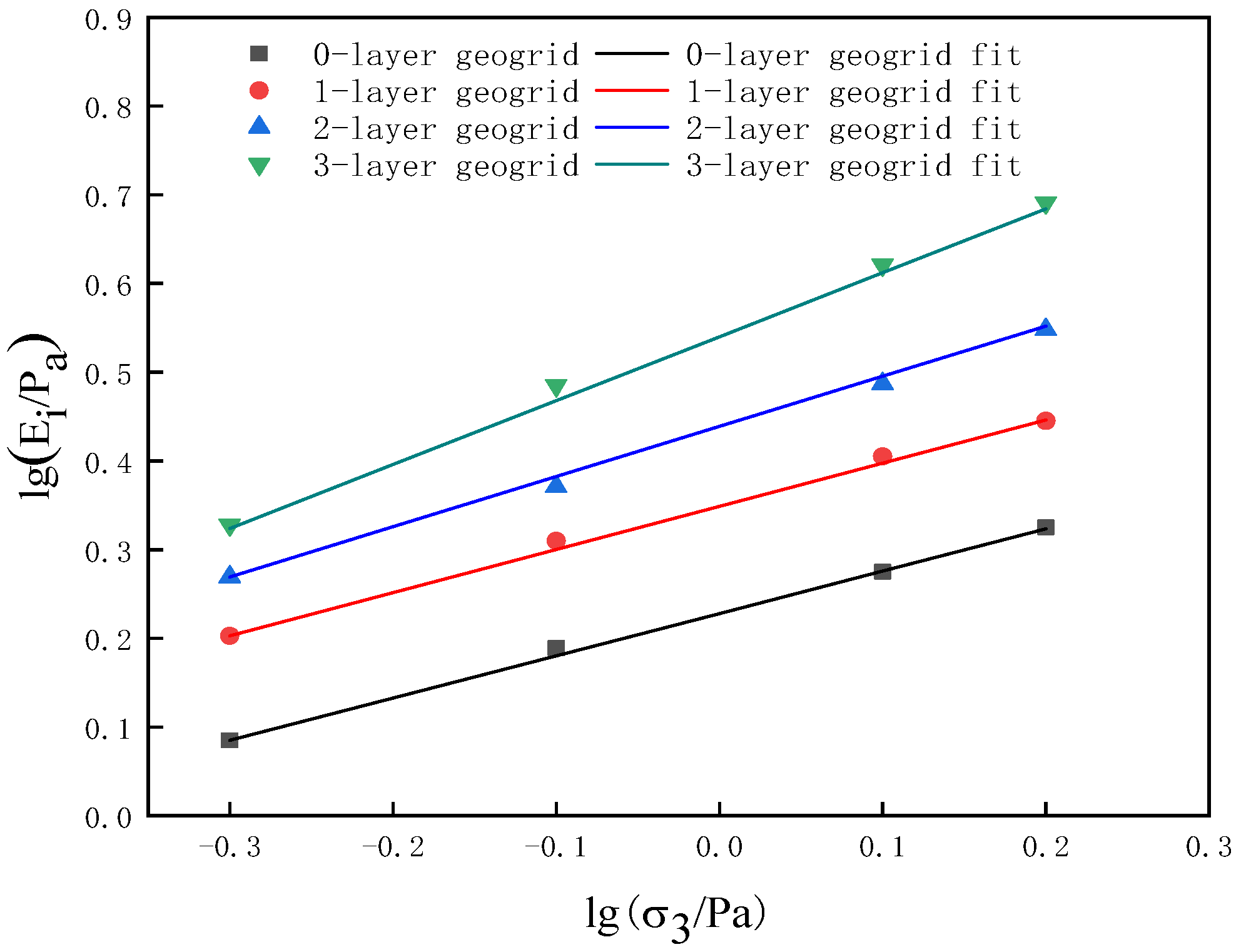
2.4. Reinforced Soil Principal Model
3. Discrete Element Numerical Simulation
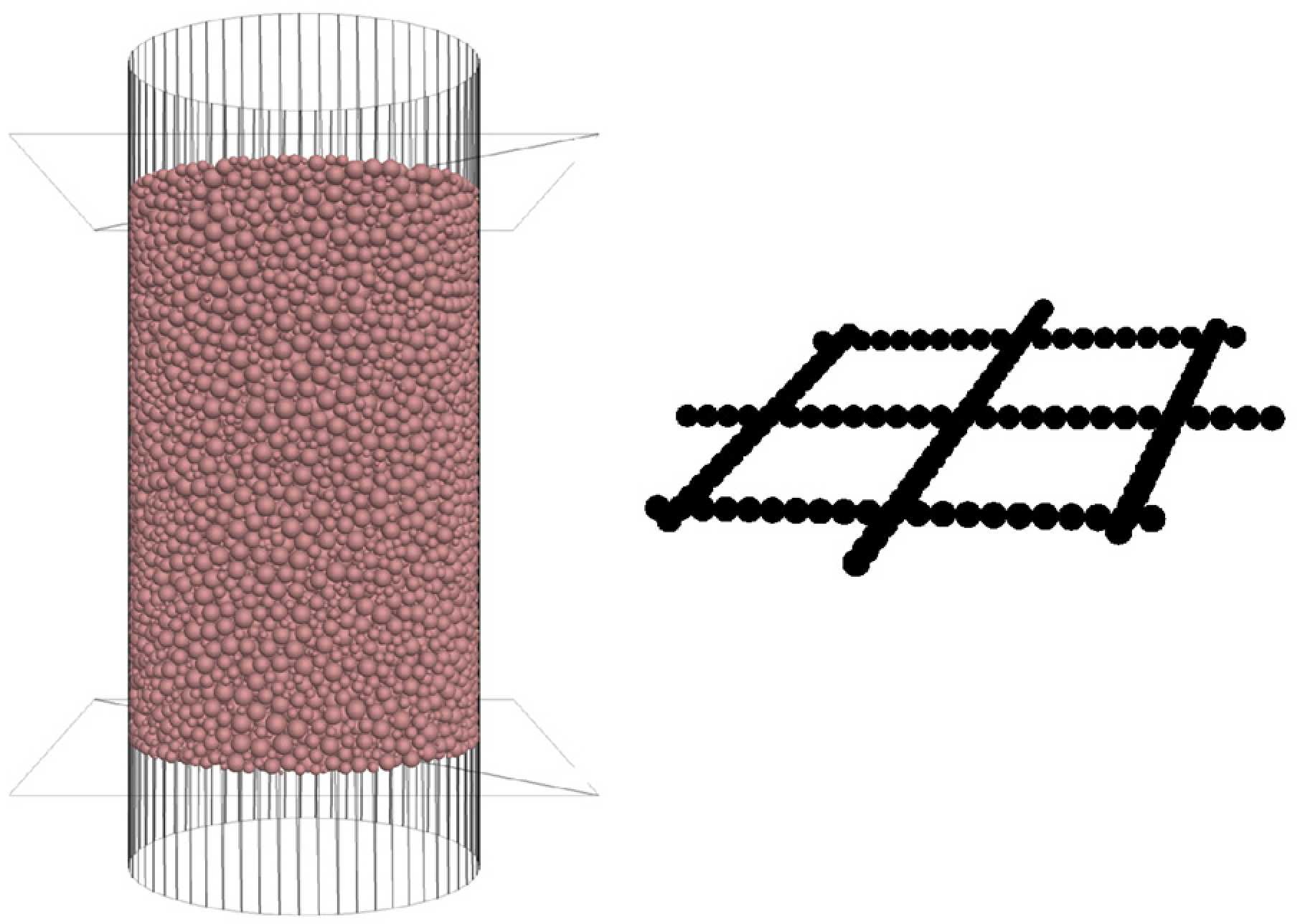
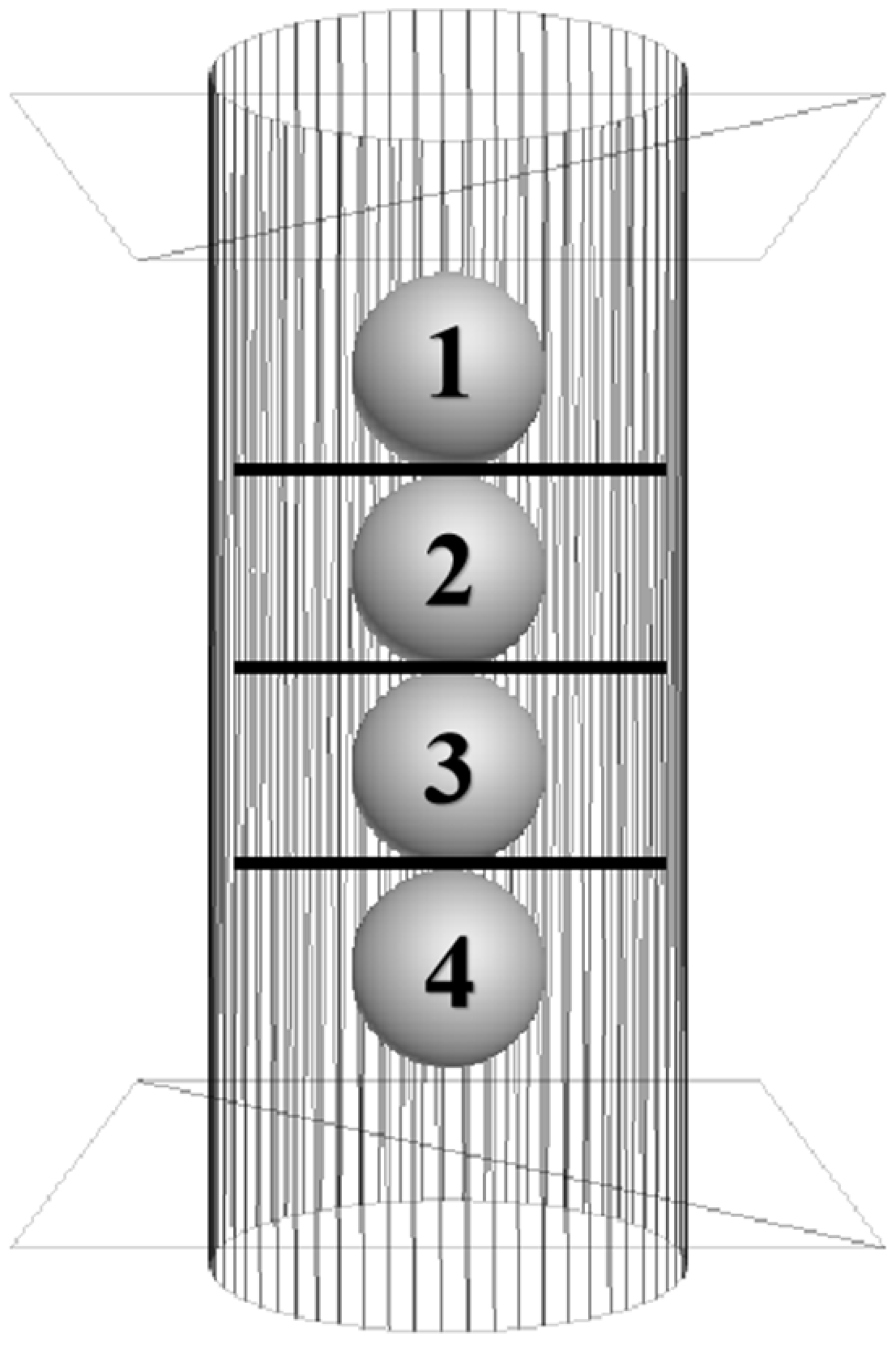
3.1. Model
3.2. Fine View Parameter Calibration
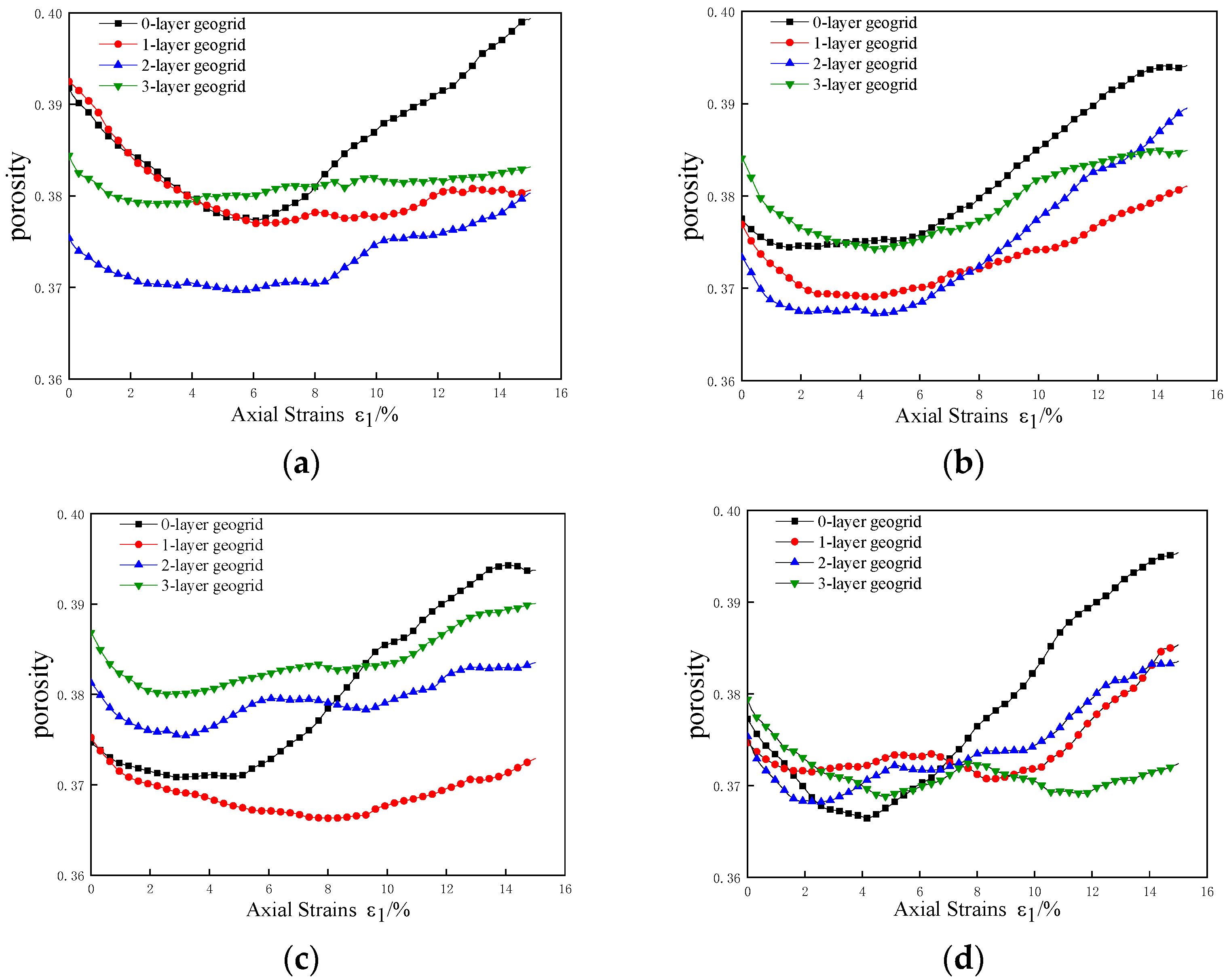
3.3. Effect of Reinforcement on Porosity and Contact Number
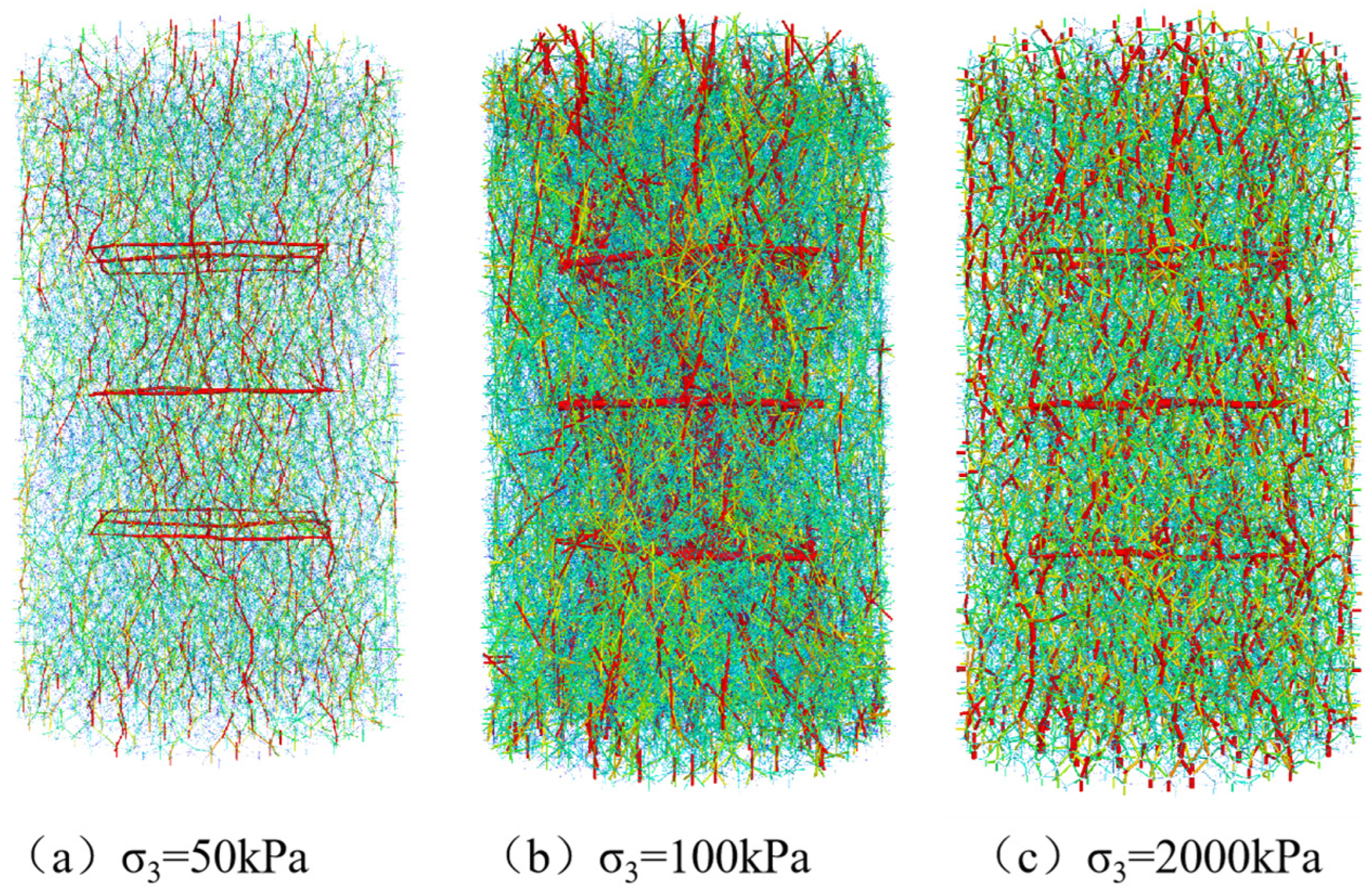
3.4. Change in Contact Force
4. Conclusions
- (1)
- The results of the indoor triaxial test show that the peak strength and cohesion c of the stress–strain curve of the specimen after reinforcement increase with the increase in the number of layers of reinforcement, and the enhancement of the angle of internal friction is not obvious. The three layers of reinforcement play a synergistic role between the grids, and the peak strength increases significantly. Analysis of the reinforcing effect coefficient found that, when the number of reinforced layers is the same, the effect of clay reinforcement at low perimeter pressure is better.
- (2)
- The analysis of triaxial test curves for reinforced soil revealed that the stress–strain relationship adheres to the Duncan–Chang model. Subsequent extraction of Duncan–Chang model parameters from the reinforced soil confirmed their validity. These parameters were then rigorously evaluated by comparing the model’s calculated values with experimental data, verifying the accuracy of the model parameters. This comparison underscores the reliability of the Duncan–Chang model in predicting the behavior of reinforced soils under stress conditions.
- (3)
- The results from discrete element numerical tests indicate that reinforcing a specimen significantly reduces soil porosity fluctuations. Notably, the porosity at both ends of the specimen is substantially influenced by the reinforcement. This suggests that the frictional resistance at the reinforcement-soil interface effectively inhibits soil particle displacement during shear processes. Furthermore, as the number of reinforcing layers increases, so does the inhibitory effect. In the central region of the specimen, there is a notable increase in soil particle count. The reinforcement constraints embedded within the material lead to increased inter-particle contact, thereby enhancing the compactness of the soil. This increase in particle contact directly contributes to improved soil structure and stability.
- (4)
- Analyzing the contact force distribution law of the reinforced soil particles demonstrated that the contact force at the reinforcement and the axial region of the specimen after reinforcement increased significantly, and the reinforcement played the role of restraining the soil particles and spreading the stress reinforcement, reflecting the characteristics of the stress transfer and distribution in the reinforced soil.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.-Q.; Xu, L.-J.; Huang, S.-B.; Liu, Z.-Q. Bearing capacity analysis of geogrid reinforced abutment retaining wall under dynamic load. Rock Soil Mech. 2019, 40, 4220–4228+4269. [Google Scholar]
- Jawad, Z.H.; Shakir, R.R. Behavior of foundation rested on geogrid-reinforced soil: A review. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1094, 012110. [Google Scholar] [CrossRef]
- Yang, G.-Q.; Zhou, Y.-T.; Zhou, Q.-Y.; Xue, X.-H. Experimental research on geogrid reinforced earth retaining wall. Rock Soil Mech. 2009, 30, 206–210. [Google Scholar]
- Luo, T.; Chen, P.; Qiu, H.; Fu, S.; Sun, C. A Review On The Interaction between Geogrid and backfill. Eng. J. Wuhan Univ. 2020, 53, 111–115. [Google Scholar]
- Xiao, C.-Z.; Liu, B.; Li, Y.-R.; Sun, J.-C. Test study of long-term performances of reinforced cohesion soil retaining wall. Rock. Soil. Mech. 2012, 33, 109–114. [Google Scholar]
- Wu, H.; Gao, J.; Liu, C.; Guo, Z.; Luo, X. Reusing waste clay brick powder for low-carbon cement concrete and alkali-activated concrete: A critical review. J. Clean. Prod. 2024, 449, 141755. [Google Scholar] [CrossRef]
- Cai, J.-T. Pull-out test on interface behavior between expansive soils and geogrids. Rock Soil Mech. 2015, 36, 204–208. [Google Scholar]
- Abdic, M.R.; Zandieh, A.R.; Mirzaeifar, H.; Arjomand, M.A. Influence of geogrid type and coarse grain size on pull out behaviour of clays reinforced with geogrids embedded in thin granular layers. Eur. J. Environ. Civ. Eng. 2021, 25, 2161–2180. [Google Scholar] [CrossRef]
- Sakleshpura, V.A.; Prezzia, M.; Salgadoa, R.; Siddikib, N.Z.; Choic, Y.S. Large-scale direct shear testing of geogrid-reinforced aggregate base over weak subgrade. Int. J. Pavement Eng. 2019, 20, 649–658. [Google Scholar] [CrossRef]
- Wang, J.-Q.; Zhou, Y.-F.; Tang, X.-Y.; Huang, S.-B. Development and application of large size direct shear test apparatus with visual and digital collection functions for reinforced soil. Rock Soil Mech. 2017, 38, 1533–1540. [Google Scholar]
- Akbarimehr, D.; Fakharian, K. Dynamic shear modulus and damping ratio of clay mixed with waste rubber using cyclic triaxial apparatus. Soil. Dyn. Earthq. Eng. 2021, 140, 106435. [Google Scholar] [CrossRef]
- Akbarimehr, D.; Hosseini, S.M.M.M. Elasto-plastic characteristics of the clay soil mixed with rubber waste using cyclic triaxial test results. Arab. J. Geosci. 2022, 15, 1280. [Google Scholar] [CrossRef]
- Yang, Z. Strength and Deformation Characteristics of Reinforced Sand; University of California: Los Angeles, CA, USA, 1972. [Google Scholar]
- Schlosser, F.; Long, N.T. Recent results of French research on reinforced earth. J. Constr. Div. 1974, 100, 223–237. [Google Scholar] [CrossRef]
- Zakarka, M.; Skuodis, Š.; Dirgėlienė, N. Triaxial Test of Coarse-Grained Soils Reinforced with One Layer of Geogrid. Appl. Sci. 2023, 13, 12480. [Google Scholar] [CrossRef]
- Skuodis, Š.; Dirgėlienė, N.; Medzvieckas, J. Using Triaxial Tests to Determine the Shearing Strength of Geogrid-Reinforced Sand. Stud. Geotech. Mech. 2020, 42, 341–354. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, J.; Li, Z. Shear behaviour of a geogrid-reinforced coarse-grained soil based on large-scale triaxial tests. Geotext. Geomembr. 2014, 42, 312–328. [Google Scholar] [CrossRef]
- Luo, Z.-G.; Ding, X.-M.; Ou, Q.; Jiang, C.-Y.; Fang, H.-Q. Experimental study on strength and deformation characteristics of coral sand reinforced by geogrid. Rock Soil Mech. 2023, 44, 1053–1064. [Google Scholar]
- Cai, Y.-M.; Wang, Z.-J.; Qi, Y.-F.; Yang, G.-Q.; Wang, H. Experimental study on dynamic properties of geogrid reinforced rubber gravel. Rock Soil Mech. 2024, 45, 87–96+107. [Google Scholar]
- Mittal, A.; Shrivastava, A.K. Stress-strain characteristics of landfill clay cover barriers under geogrid reinforcements. Innov. Infrastruct. Solut. 2020, 5, 19. [Google Scholar] [CrossRef]
- Wang, Z.; Qi, Y.; Yang, G.; Cai, Y.; Liu, W. Experimental Investigations of Large-scale Triaxial Tests on Geocell Reinforced Gravel Composites. J. China Railw. Soc. 2023, 45, 161–169. [Google Scholar]
- Song, F.; Shi, L.; Fan, M. Stress-strain response of geocell-reinforced normally consolidated silty clay. Bull. Geol. Sci. Technol. 2024, 43, 184–193. [Google Scholar]
- Zhao, X.; Lu, X.; Rong, S.; Zhu, J. Experimental Study on Deformation and Strength Behavior of Geotextile Reinforced Coarse-grained Soil. Adv. Eng. Sci. 2018, 50, 165–173. [Google Scholar]
- Liu, F.-C.; Wu, M.-T.; Yang, J. Experimental study of strength characteristics of geogrid reinforced rubber sand mixtures. Rock Soil Mech. 2019, 40, 580–591. [Google Scholar]
- Yi, F.; Du, C. Triaxial Testing of Geosynthetics Reinforced Tailings with Different Reinforced Layers. Materials 2020, 13, 1943. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.-Q.; Guo, M.; Hu, B. Triaxial testing study of expansive soil reinforced with geogrid. Rock Soil Mech. 2011, 3, 1649–1653. [Google Scholar]
- Xiaojun, L.; Xiaohong, B.; Xianzhi, H. Study on the constitutive relationship of geotechnical belt reinforced gravel soil by triaxial test. Rock Soil Mech. 2004, S2, 57–60. [Google Scholar]
- Hongwei, W.; Zehong, Y.; Huawei, Y. Study on Triaxial Test of Geosynthetics-reinforced Clay Soil. Eng. Mech. 2007, 5, 107–113. [Google Scholar]
- Xiong, S.; Jiasheng, Z.; Fei, M. Research on large-scale triaxial test of reinforced coarse-grained soi. Adv. Eng. Sci. 2014, 46, 52–58. [Google Scholar]
- He, Z.J.; Asiga; Zou, J.F. Analysis of large-scale triaxial test of reinforced sand with fine-grained soil. J. Railw. Sci. Eng. 2019, 16, 2451–2458. [Google Scholar]
- Zhao, Y.; Lin, X.; Gong, W.; Li, P.; Li, G.; Wang, L. Mechanical Properties of Fiber-Reinforced Soil under Triaxial Compression and Parameter Determination Based on the Duncan-Chang Model. Appl. Sci. 2020, 10, 9043. [Google Scholar] [CrossRef]
- Wu, M.; Wang, J.; Russell, A.; Cheng, Z. DEM modelling of mini-triaxial test based on one-to-one mapping of sand particles. Geotechnique 2021, 71, 714–727. [Google Scholar] [CrossRef]
- Wang, J.Q.; Zhang, L.L.; Chen, Y.J.; Shi, C.H. Mesoscopic analysis of reinforced sand triaxial test using PFC3D. J. Hydraul. Eng. 2017, 4, 426–434+445. [Google Scholar]
- Gonga, L.; Niea, L.; Liua, C.; Xua, Y. Modelling Triaxial Tests on Fibre-Reinforced Sands with Different Fibre Orientations Using the Discrete Element Method. Ksce J. Civ. Eng. 2020, 24, 2268–2280. [Google Scholar] [CrossRef]
- Stahl, M.; Konietzky, H.; Kamp, L.T.; Jas, H. Discrete element simulation of geogrid-stabilised soi. Acta Geotech. 2014, 9, 1073–1084. [Google Scholar] [CrossRef]
- Chen, C.; McDowell, G.R.; Thom, N.H. Discrete element modelling of cyclic loads of geogrid-reinforced ballast under confned and unconfned conditions. Geotext. Geomembr. 2012, 35, 76–86. [Google Scholar] [CrossRef]
- Cui, L.; Cao, W.; Sheng, Q.; Xie, M.; Yang, T.; Xiao, P. Analysis of Layered Geogrids-Sand-Clay Reinforced Structures under Triaxial Compression by Discrete Element Method. Appl. Sci. 2021, 11, 9952. [Google Scholar] [CrossRef]
- Wang, Z.; Jacobs, F.; Ziegler, M. Visualization of load transfer behaviour between geogrid and sand using PFC2D. Geotext. Geomembr. 2014, 42, 83–90. [Google Scholar] [CrossRef]
- Chen, C.; Duan, Y.-D.; Rui, R.; Wang, L. Study of single and two-layer geogrid reinforced ballasted trackbed using pull-out test and discrete element method. Rock Soil Mech. 2021, 42, 954–962+975. [Google Scholar]
- Tran, V.D.H.; Meguid, M.A.; Chouinard, L.E. A finiteediscrete element framework for the 3D modeling of geogride soil interaction under pullout loading conditions. Geotext. Geomembr. 2013, 37, 1–9. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, J.; Wu, H.; Xu, H. Discrete element mesoscopic simulation of the reinforced soil pullout test interface effect. J. Harbin Eng. Univ. 2014, 35, 839–845. [Google Scholar]
- Ngo, N.T.; Indraratna, B.; Rujikiatkamjorn, C. DEM simulation of the behaviour of geogrid stabilised ballast fouled with coal. Comput. Geotech. 2014, 55, 224–231. [Google Scholar] [CrossRef]
- Gaoa, G.; Meguidb, M.A. Effect of particle shape on the response of geogrid-reinforced systems: Insights from 3D discrete element analysis. Geotext. Geomembr. 2018, 46, 685–698. [Google Scholar] [CrossRef]
- Chen, W.-B.; Zhou, W.-H.; Jing, X.-Y. Modeling Geogrid Pullout Behavior in Sand Using Discrete-Element Method and Effect of Tensile Stiffness. Int. J. Geomech. 2019, 19, 04019039. [Google Scholar] [CrossRef]
- Adajar, J.B.; Ubay, I.O.; Alfaro, M.; Chen, Y. Discrete Element Modelling of Undrained Consolidated Triaxial Test on Cohesive Soils. In Geo-Congress 317; American Society of Civil Engineers: Reston, VA, USA, 2020. [Google Scholar]
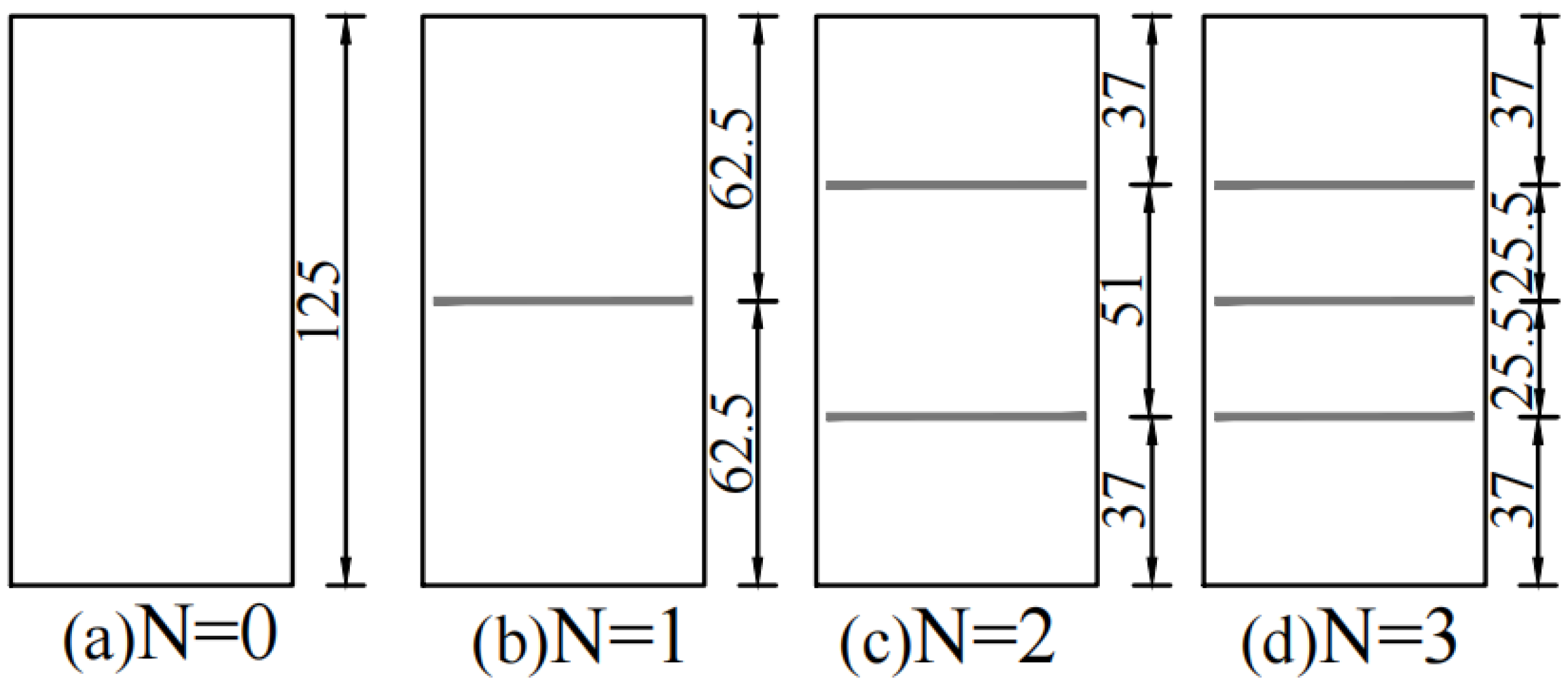





| Soil | Maximum Dry Density ρ/(g·cm−3) | Moisture Content ω/% | Liquid Limit ωL/% | Plastic Limit ωp/% | Plastic Limit Index Ip |
|---|---|---|---|---|---|
| clay | 1.68 | 17 | 33.6 | 19.2 | 14.4 |
| Reinforcing Material | Specification | Tensile Strength /(kN/m) | Elongation/(%) | Mesh Size/mm |
|---|---|---|---|---|
| Woven geogrid | PET50-50 | 50 | 13 | 20.0 × 20.0 |
| Number of Reinforcement Layers | σ3 = 50 kPa | σ3 = 100 kPa | σ3 = 2200 kPa |
|---|---|---|---|
| 1 | 1.13 | 1.16 | 1.06 |
| 2 | 1.29 | 1.25 | 1.19 |
| 3 | 1.53 | 1.42 | 1.32 |
| Number of Reinforcement Layers | a | b | K | n | |
|---|---|---|---|---|---|
| 0 | 0.0061 | 0.0072 | 0.942 | 1.691 | 0.477 |
| 1 | 0.0046 | 0.0062 | 0.954 | 2.232 | 0.486 |
| 2 | 0.0037 | 0.0055 | 0.959 | 2.748 | 0.566 |
| 3 | 0.0028 | 0.0045 | 0.965 | 3.467 | 0.721 |
| Parameter Items | Clay | Geogrid |
|---|---|---|
| Particle radius/×10−3 m | 0.4~1.8 | 1.0 |
| Particle density/Kg∙m−3 | 2650 | 800 |
| Coefficient of friction | 0.3 | 0.5 |
| Porosity | 0.45 | – |
| Bonding strength/kPa | 15 | 3.18 × 1011 |
| Cohesion/kPa | 15 | 3.18 × 1011 |
| Linear contact effective modulus/kPa | 4.4 × 103 | 6.0 × 1010 |
| Parallel bonded effective modulus/kPa | 33 | 2.42 × 105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Hu, Q.; Liu, Y.; Tao, G. Triaxial Test and Discrete Element Numerical Simulation of Geogrid-Reinforced Clay Soil. Buildings 2024, 14, 1422. https://doi.org/10.3390/buildings14051422
Wang X, Hu Q, Liu Y, Tao G. Triaxial Test and Discrete Element Numerical Simulation of Geogrid-Reinforced Clay Soil. Buildings. 2024; 14(5):1422. https://doi.org/10.3390/buildings14051422
Chicago/Turabian StyleWang, Xi, Qizhi Hu, Yiming Liu, and Gaoliang Tao. 2024. "Triaxial Test and Discrete Element Numerical Simulation of Geogrid-Reinforced Clay Soil" Buildings 14, no. 5: 1422. https://doi.org/10.3390/buildings14051422







