Theoretical and Experimental Investigations of Identifying Bridge Damage Using Instantaneous Amplitude Squared Extracted from Vibration Responses of a Two-Axle Passing Vehicle
Abstract
:1. Introduction
2. Theoretical Formulations of the Problem
2.1. Closed-Form Solutions of Residual CP Responses
2.2. Bridge Damage Detection Using Residual CP Acceleration
- Measure the vehicle accelerations 1 and 2 of the vehicle body at the front and rear axles of the two-axle test vehicle;
- Calculate the residual CP acceleration Δ of the front and rear vehicle axles using Equation (15);
- Analyze the frequency spectrum of Δ using FFT and isolate its first few orders of driving frequencies 2nπv/L using the multi-peak spectrum idealized filter;
- Obtain the time-domain results of the driving frequency components Rn(t) using the multi-point spectra idealized filter and inverse FFT and construct its instantaneous amplitude IAS index A(t) by Hilbert transform.
3. Numerical Investigations Using Finite Element Simulation
3.1. Finite Element Simulation of the VBI System with Damage
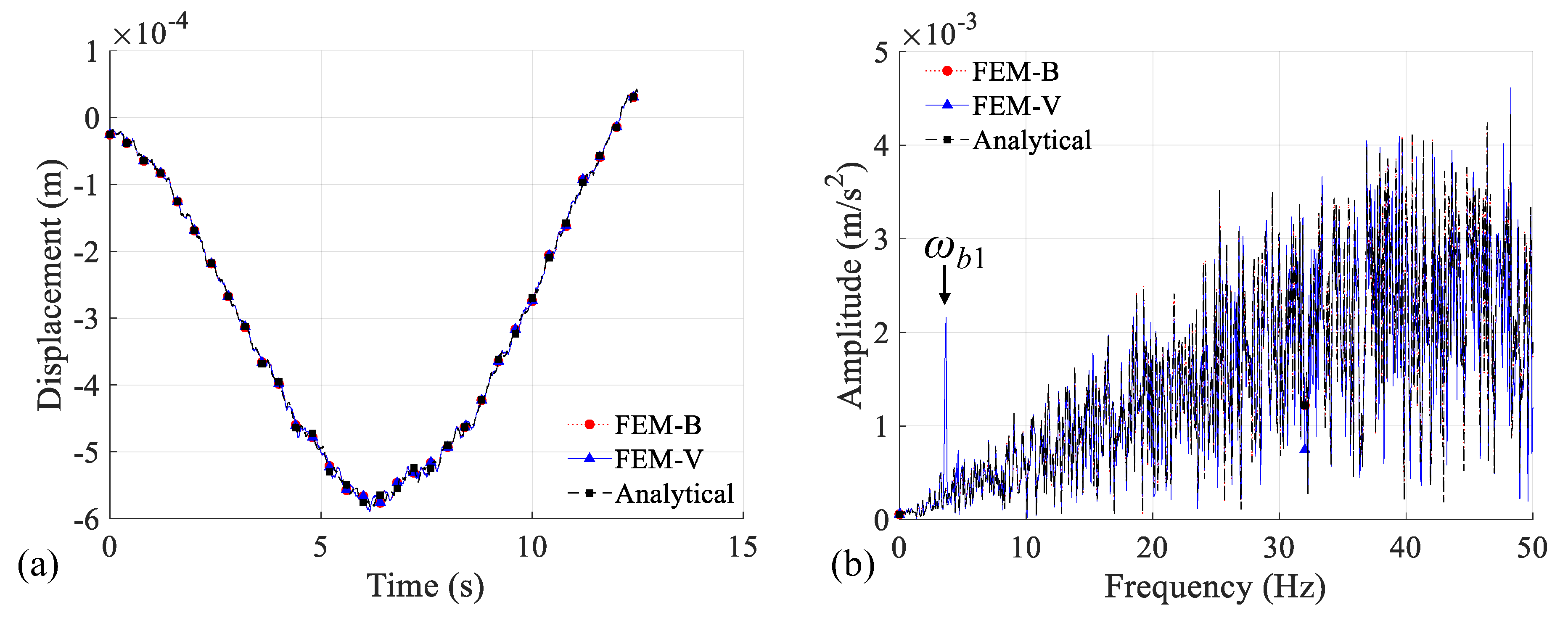
3.2. Numerical Validation of the Residual CP Response
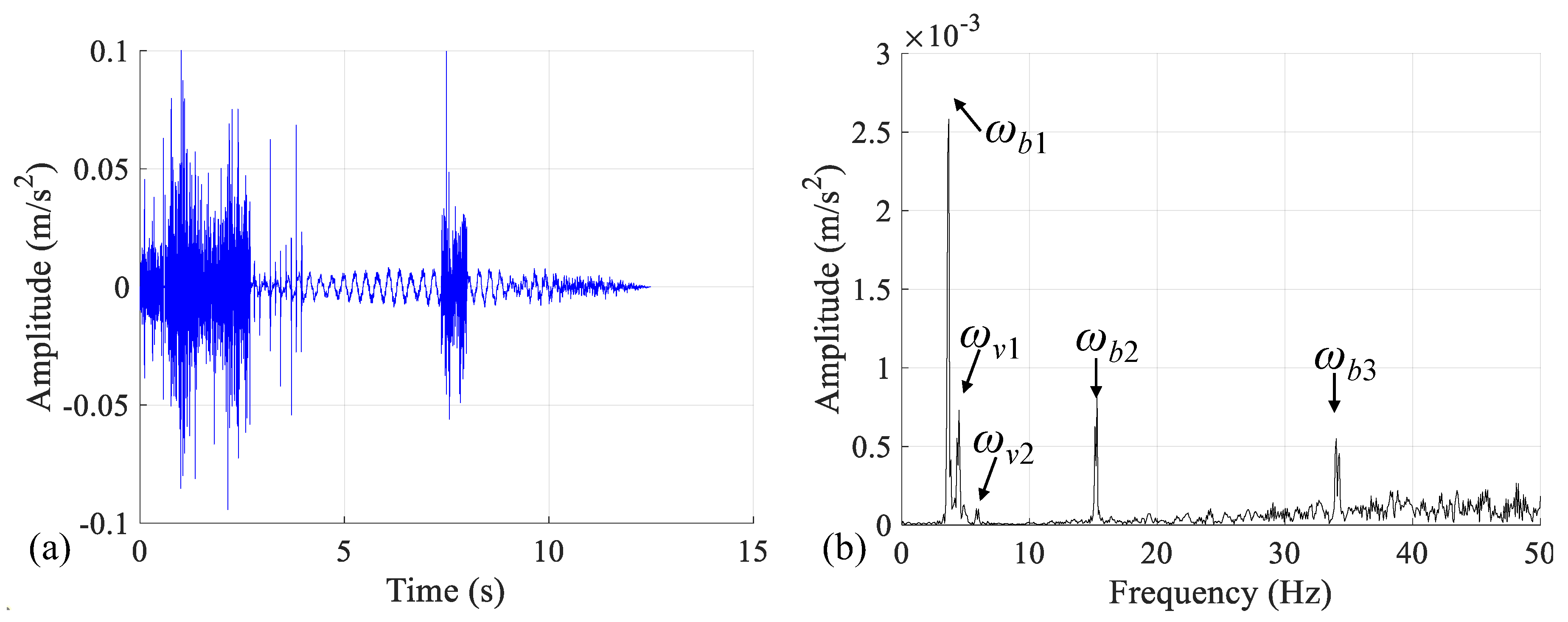
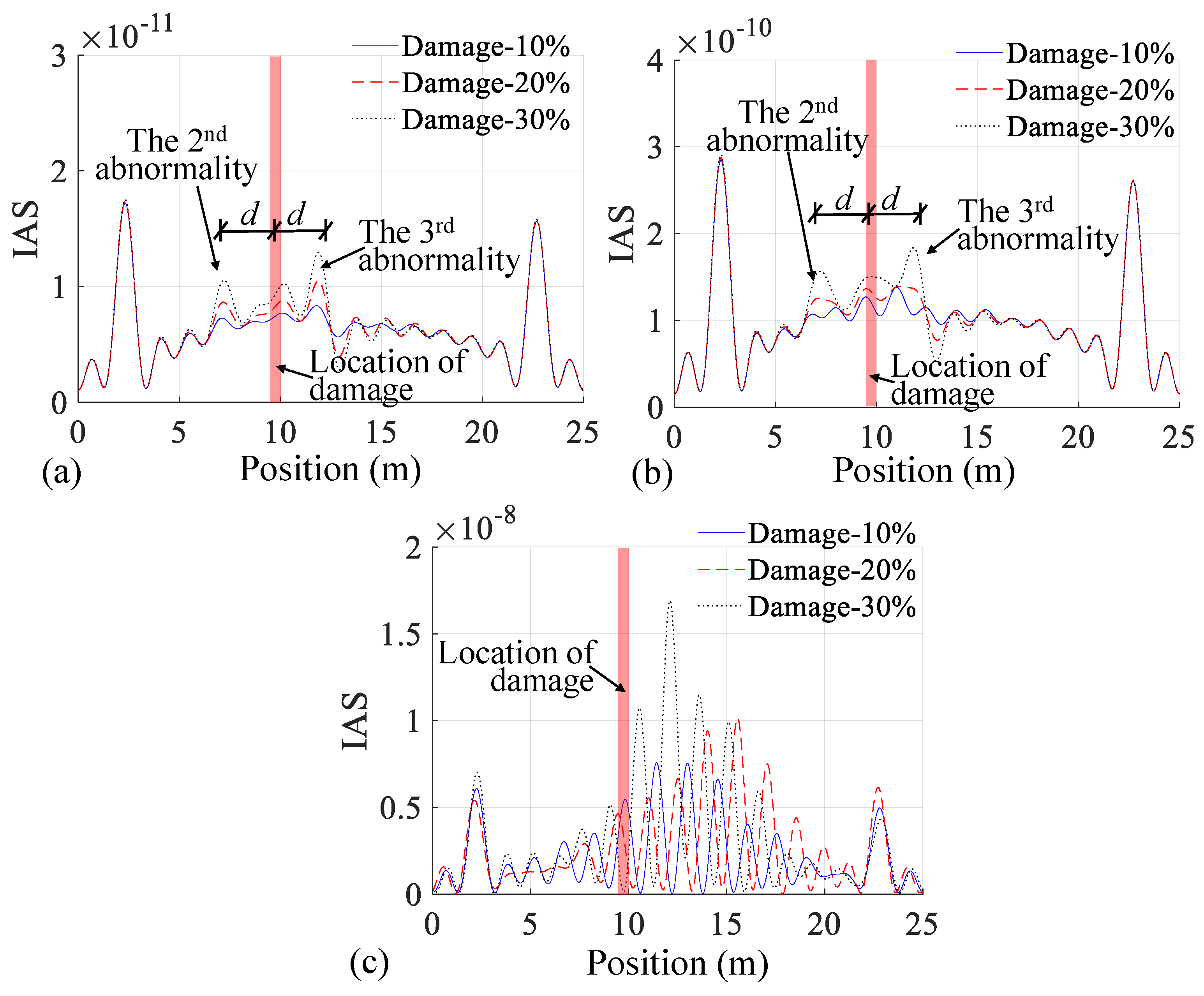
3.3. Numerical Validation of Damage Identification
3.4. Influence of Vehicle Speed on Damage Identification
3.5. Influence of Road Roughness on Damage Identification
4. Experimental Validations
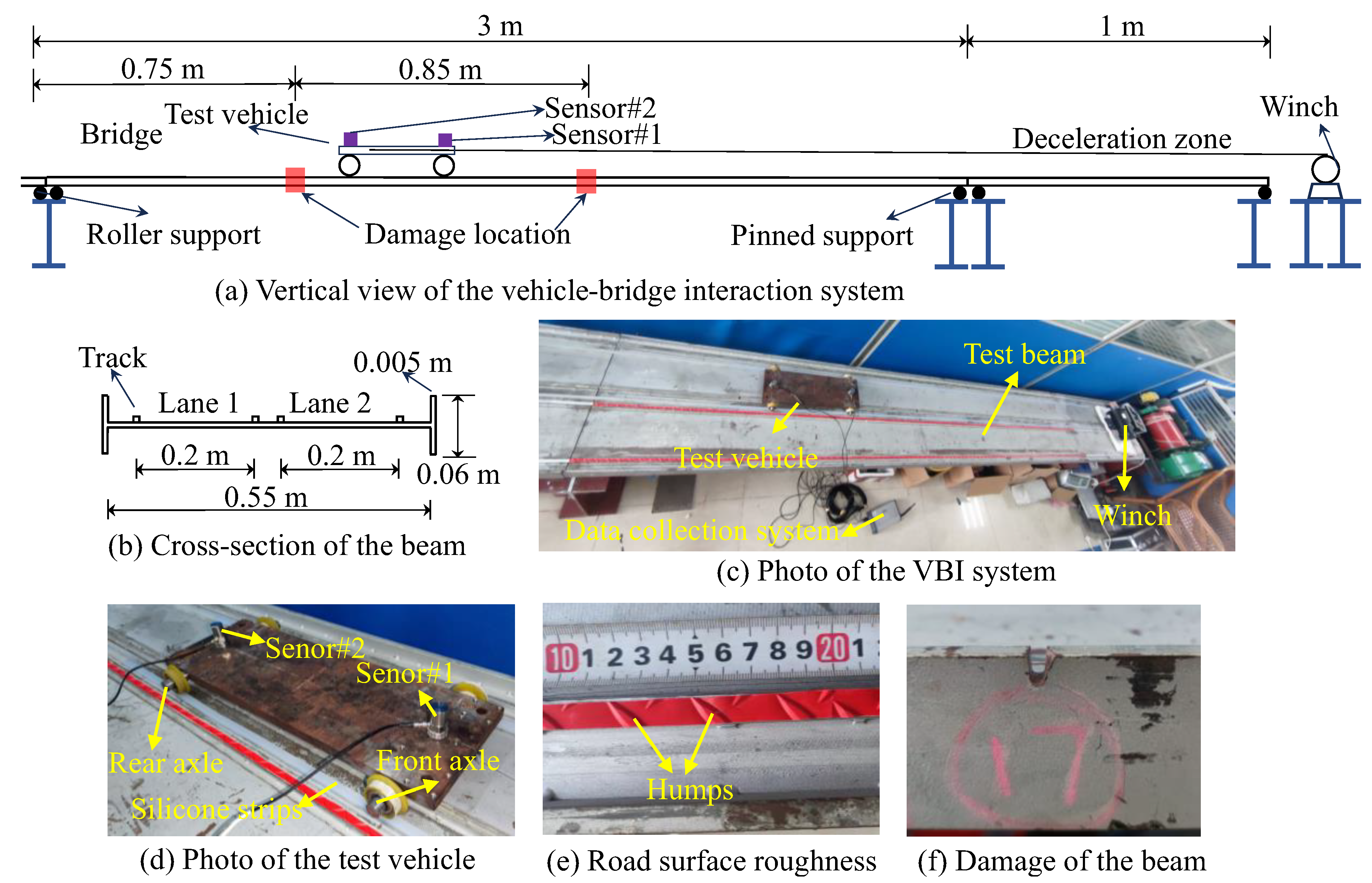
4.1. The Laboratory VBI System
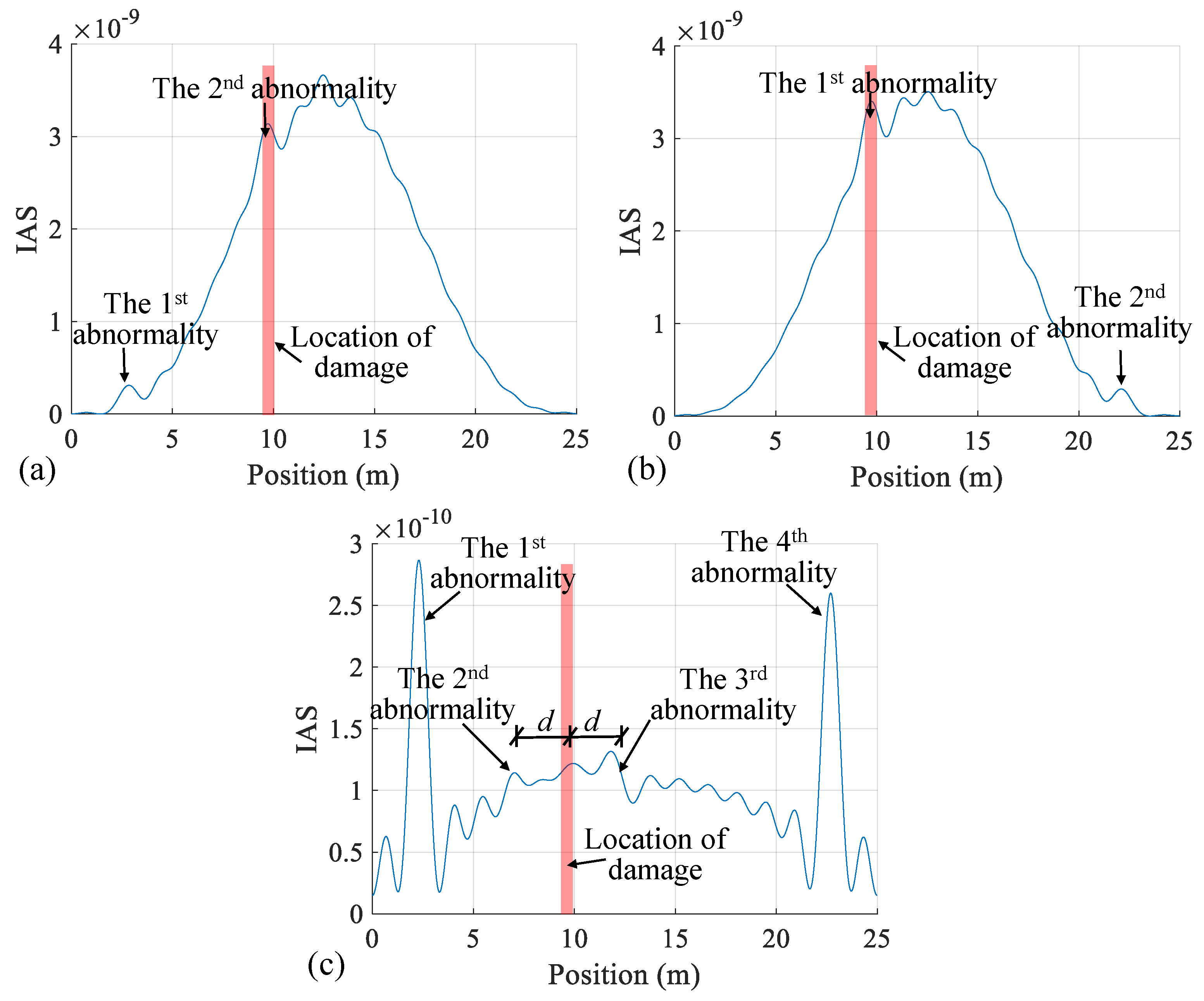
4.2. Damage Detection under the Perfect Road Surface
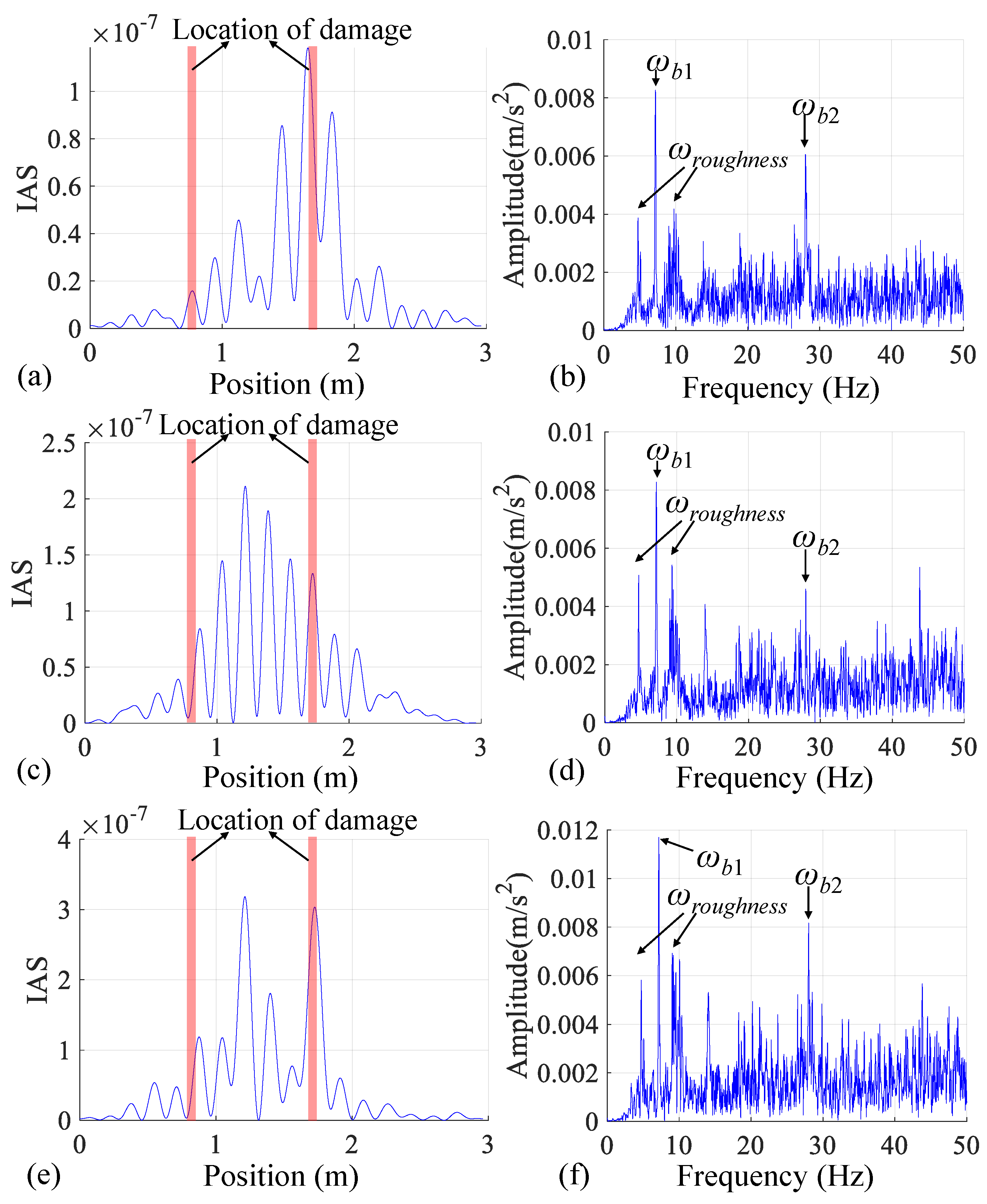
4.3. Damage Detection under Rough Road Surface
5. Conclusions
- (1)
- The IAS index of the residual CP acceleration can be constructed by applying a multi-peak idealized filter and the Hilbert transform to the driving frequency spectra. This index is theoretically sensitive to the bridge modal shape and can be used to identify bridge damage. Theoretically, it eliminates the influence of vehicle self-vibrations and road roughness when the vehicle–bridge coupling effect can be ignored;
- (2)
- Numerical investigations verify the accuracy of the theoretical derivations. The bridge damage can be determined by observing IAS abnormalities, which are baseline-free. The IAS of the residual CP acceleration can identify a 10% stiffness loss in a beam element under low road surface roughness and a 30% stiffness loss under high road surface roughness. A favorable vehicle speed of no greater than 2 m/s yields good damage identification results;
- (3)
- Laboratory tests show that it is possible to roughly identify bridge damage using the IAS extracted from residual CP acceleration under perfect road surfaces. The results of the IAS from residual CP acceleration show the same ability to locate damage as those of the IAS from CP accelerations at the front or rear axle. However, some irrelevant IAS abnormalities were observed, which have no relation to the bridge damage;
- (4)
- Regarding rough road surfaces in the experimental setup, while both IAS indicators derived from residual CP acceleration and axle CP acceleration successfully identify multiple bridge frequencies, it is likely that they both fall short in detecting damage. Hence, further experiments should be performed to fully examine the capacity of the IAS for bridge damage identification in practical applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, L.; Shang, Z.; Xia, Y.; Bhowmick, S.; Nagarajaiah, S. Review of bridge structural health monitoring aided by big data and artificial intelligence: From condition assessment to damage detection. J. Struct. Eng. 2020, 146, 04020073. [Google Scholar] [CrossRef]
- An, Y.; Chatzi, E.; Sim, S.H.; Laflamme, S.; Blachowski, B.; Ou, J. Recent progress and future trends on damage identification methods for bridge structures. Struct. Control Health Monit. 2019, 26, e2416. [Google Scholar] [CrossRef]
- Brownjohn, J.M.; De Stefano, A.; Xu, Y.L.; Wenzel, H.; Aktan, A.E. Vibration-based monitoring of civil infrastructure: Challenges and successes. J. Civ. Struct. Health Monit. 2011, 1, 79–95. [Google Scholar] [CrossRef]
- Hou, R.; Xia, Y. Review on the new development of vibration-based damage identification for civil engineering structures: 2010–2019. J. Sound Vib. 2021, 491, 115741. [Google Scholar] [CrossRef]
- Wang, Z.L.; Yang, J.P.; Shi, K.; Xu, H.; Qiu, F.Q.; Yang, Y.B. Recent advances in researches on vehicle scanning method for bridges. Int. J. Struct. Stab. Dyn. 2022, 22, 2230005. [Google Scholar] [CrossRef]
- Shokravi, H.; Shokravi, H.; Bakhary, N.; Heidarrezaei, M.; Rahimian Koloor, S.S.; Petrů, M. Vehicle-assisted techniques for health monitoring of bridges. Sensors 2020, 20, 3460. [Google Scholar] [CrossRef]
- Malekjafarian, A.; Corbally, R.; Gong, W. A review of mobile sensing of bridges using moving vehicles: Progress to date, challenges and future trends. Structures 2022, 44, 1466–1489. [Google Scholar] [CrossRef]
- Yang, Y.B.; Lin, C.W.; Yau, J.D. Extracting bridge frequencies from the dynamic response of a passing vehicle. J. Sound Vib. 2004, 272, 471–493. [Google Scholar] [CrossRef]
- Nagayama, T.; Reksowardojo, A.P.; Su, D.; Mizutani, T. Bridge natural frequency estimation by extracting the common vibration component from the responses of two vehicles. Eng. Struct. 2017, 150, 821–829. [Google Scholar] [CrossRef]
- Xu, H.; Huang, C.C.; Wang, Z.L.; Shi, K.; Wu, Y.T.; Yang, Y.B. Damped test vehicle for scanning bridge frequencies: Theory, simulation and experiment. J. Sound Vib. 2021, 506, 116155. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, H.; Tan, X.; Wang, R.; Zhang, Y. Mode shape identification and damage detection of bridge by movable sensory system. IEEE T. Intell. Transp. 2022, 24, 1299–1313. [Google Scholar] [CrossRef]
- Li, J.; Zhu, X.; Guo, J. Bridge modal identification based on successive variational mode decomposition using a moving test vehicle. Adv. Struct. Eng. 2022, 25, 2284–2300. [Google Scholar] [CrossRef]
- Yin, X.; Yang, Y.; Huang, Z. Bridge frequency extraction method based on contact point response of two-axle vehicle. Structures 2023, 57, 105176. [Google Scholar] [CrossRef]
- Hashlamon, I.; Nikbakht, E. Theoretical and numerical investigation of bridge frequency identification employing an instrumented vehicle in stationary and moving states. Structures 2023, 51, 1684–1693. [Google Scholar] [CrossRef]
- Zhan, Y.; Au, F.T.; Zhang, J. Bridge identification and damage detection using contact point response difference of moving vehicle. Struct. Control Health Monit. 2021, 28, e2837. [Google Scholar] [CrossRef]
- Yang, D.S.; Wang, C.M. Bridge damage detection using reconstructed mode shape by improved vehicle scanning method. Eng. Struct. 2022, 263, 114373. [Google Scholar] [CrossRef]
- He, Y.; Yang, J.P.; Yan, Z. Enhanced identification of bridge modal parameters using contact residuals from three-connected vehicles: Theoretical study. Structures 2023, 54, 1320–1335. [Google Scholar] [CrossRef]
- Liu, Y.; Zhan, J.; Wang, Y.; Wang, C.; Zhang, F. An effective procedure for extracting mode shapes of simply-supported bridges using virtual contact-point responses of two-axle vehicles. Structures 2023, 48, 2082–2097. [Google Scholar] [CrossRef]
- Hajializadeh, D. Deep learning-based indirect bridge damage identification system. Struct. Control Health Monit. 2023, 22, 897–912. [Google Scholar] [CrossRef]
- Hurtado, A.C.; Kaur, K.; Alamdari, M.M.; Atroshchenko, E.; Chang, K.C.; Kim, C.W. Unsupervised learning-based framework for indirect structural health monitoring using adversarial autoencoder. J. Sound Vib. 2023, 550, 117598. [Google Scholar] [CrossRef]
- Li, Z.; Lin, W.; Zhang, Y. Real-time drive-by bridge damage detection using deep auto-encoder. Structures 2023, 47, 1167–1181. [Google Scholar] [CrossRef]
- Zhou, J.; Lu, Z.; Zhou, Z.; Pan, C.; Cao, S.; Cheng, J.; Zhang, J. Extraction of bridge mode shapes from the response of a two-axle passing vehicle using a two-peak spectrum idealized filter approach. Mech. Syst. Signal Pr. 2023, 190, 110122. [Google Scholar] [CrossRef]
- Xu, H.; Yang, M.; Yang, J.P.; Wang, Z.L.; Shi, K.; Yang, Y.B. Vehicle scanning method for bridges enhanced by dual amplifiers. Struct. Control Health Monit. 2023, 2023, 6906855. [Google Scholar] [CrossRef]
- Yang, Y.B.; Li, Z.; Wang, Z.L.; Shi, K.; Xu, H.; Qiu, F.Q.; Zhu, J.F. A novel frequency-free movable test vehicle for retrieving modal parameters of bridges: Theory and experiment. Mech. Syst. Signal Pr. 2022, 170, 108854. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhou, J.; Deng, J.; Wang, X.; Liu, H. Identification of multiple bridge frequencies using a movable test vehicle by approximating axle responses to contact-point responses: Theory and experiment. J. Civ. Struct. Health Monit. 2024. under review. [Google Scholar]
- Zhang, B.; Qian, Y.; Wu, Y.; Yang, Y.B. An effective means for damage detection of bridges using the contact-point response of a moving test vehicle. J. Sound Vib. 2018, 419, 158–172. [Google Scholar] [CrossRef]
- Feng, K.; Casero, M.; González, A. Characterization of the road profile and the rotational stiffness of supports in a bridge based on axle accelerations of a crossing vehicle. Comput. Aided Civ. Inf. 2023, 38, 12974. [Google Scholar] [CrossRef]
- Yang, Y.B.; Xu, H.; Wang, Z.L.; Shi, K. Using vehicle–bridge contact spectra and residue to scan bridge’s modal properties with vehicle frequencies and road roughness eliminated. Struct. Control Health Monit. 2022, 29, e2968. [Google Scholar] [CrossRef]
- Hashlamon, I.; Nikbakht, E. The use of a movable vehicle in a stationary condition for indirect bridge damage detection using baseline-free methodology. Appl. Sci. 2022, 12, 11625. [Google Scholar] [CrossRef]
- Ma, X.; Roshan, M.; Kiani, K.; Nikkhoo, A. Dynamic response of an elastic tube-like nanostructure embedded in a vibrating medium and under the action of moving nano-objects. Symmetry 2023, 15, 1827. [Google Scholar] [CrossRef]
- Yu, G.; Kiani, K.; Roshan, M. Dynamic analysis of multiple-nanobeam-systems acted upon by multiple moving nanoparticles accounting for nonlocality, lag, and lateral inertia. Appl. Math. Model. 2022, 108, 326–354. [Google Scholar] [CrossRef]
- Dimitrovová, Z. Dynamic interaction and instability of two moving proximate masses on a beam on a Pasternak viscoelastic foundation. Appl. Math. Model. 2021, 100, 192–217. [Google Scholar] [CrossRef]
- Zhou, J.; Zhou, Z.; Jin, Z.; Liu, S.; Lu, Z. Comparative study of damage modeling techniques for beam-like structures and their application in vehicle-bridge-interaction-based structural health monitoring. J. Vib. Control 2023, 10775463231209357. [Google Scholar] [CrossRef]
- Xiao, J.; Huang, L.; He, Z.; Qu, W.; Li, L.; Jiang, H.; Zhong, Z.; Long, X. Probabilistic models applied to concrete corrosion depth prediction under sulfuric acid environment. Measurement 2024, 234, 114807. [Google Scholar] [CrossRef]
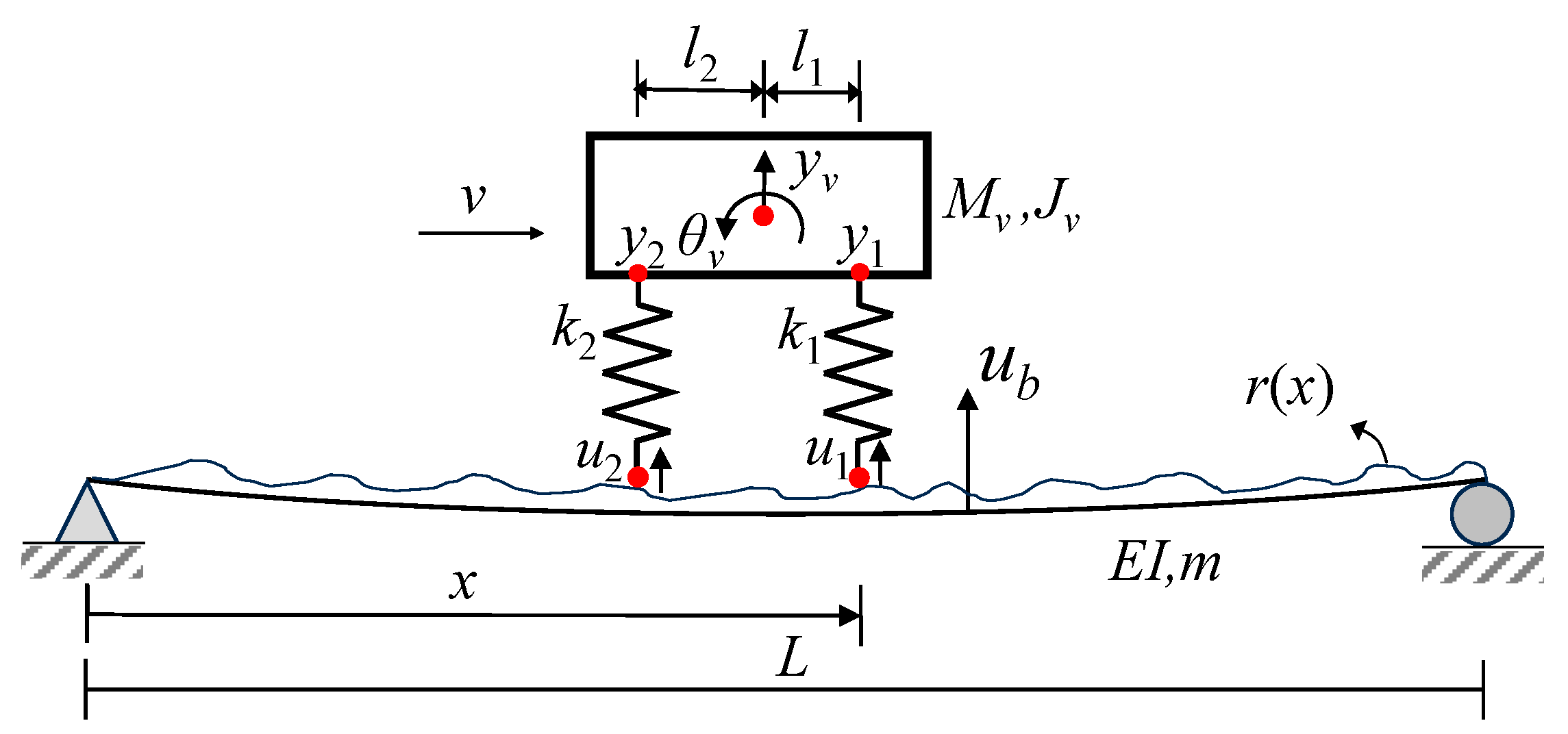




| Item | Parameters | Symbol | Unit | Value |
|---|---|---|---|---|
| Vehicle | Mass of vehicle | Mv | kg | 1000 |
| Mass moment of vehicle | Jv | kg·m2 | 900 | |
| Stiffness of front axle | k1 | N/m | 3.5 × 105 | |
| Stiffness of rear axle | k2 | N/m | 4 × 105 | |
| Distance from the front axle | l1 | m | 1.35 | |
| Distance from the rear axle | l2 | m | 1.25 | |
| Velocity | v | m/s | 2 | |
| Bridge | Length | L | m | 25 |
| Young’s modulus | E | MPa | 2.75 × 104 | |
| Moment of inertia | I | m4 | 0.20 | |
| Mass per unit length | m | kg/m | 2400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zhou, Z.; Zhang, Y.; Sun, Z.; Deng, J.; Zhou, J. Theoretical and Experimental Investigations of Identifying Bridge Damage Using Instantaneous Amplitude Squared Extracted from Vibration Responses of a Two-Axle Passing Vehicle. Buildings 2024, 14, 1428. https://doi.org/10.3390/buildings14051428
Liu S, Zhou Z, Zhang Y, Sun Z, Deng J, Zhou J. Theoretical and Experimental Investigations of Identifying Bridge Damage Using Instantaneous Amplitude Squared Extracted from Vibration Responses of a Two-Axle Passing Vehicle. Buildings. 2024; 14(5):1428. https://doi.org/10.3390/buildings14051428
Chicago/Turabian StyleLiu, Siying, Zunian Zhou, Yujie Zhang, Zhuo Sun, Jiangdong Deng, and Junyong Zhou. 2024. "Theoretical and Experimental Investigations of Identifying Bridge Damage Using Instantaneous Amplitude Squared Extracted from Vibration Responses of a Two-Axle Passing Vehicle" Buildings 14, no. 5: 1428. https://doi.org/10.3390/buildings14051428
APA StyleLiu, S., Zhou, Z., Zhang, Y., Sun, Z., Deng, J., & Zhou, J. (2024). Theoretical and Experimental Investigations of Identifying Bridge Damage Using Instantaneous Amplitude Squared Extracted from Vibration Responses of a Two-Axle Passing Vehicle. Buildings, 14(5), 1428. https://doi.org/10.3390/buildings14051428






