A Multiphysics Simulation Study of the Thermomechanical Coupling Response of Energy Piles
Abstract
1. Introduction
2. Energy Pile Simulation Study, Mechanism Analysis, and Modeling
2.1. Study and Analysis of Energy Pile Calculation Model and Mechanism
2.1.1. Analysis of the Heat Conduction Mechanism
- (1)
- Disregard impurities and non-uniformity within the soil around the pile, treating it as uniform with constant thermal conductivity and specific heat capacity.
- (2)
- The farther away from the pile, the smaller the temperature change in the soil mass, and the smaller the heat transfer effect. Therefore, only the influence of the soil mass within a certain range from the pile tip is considered, and it is considered that the soil mass outside the range will no longer have heat exchange.
- (3)
- There is contact heat transfer with contact thermal resistance between pile and soil.
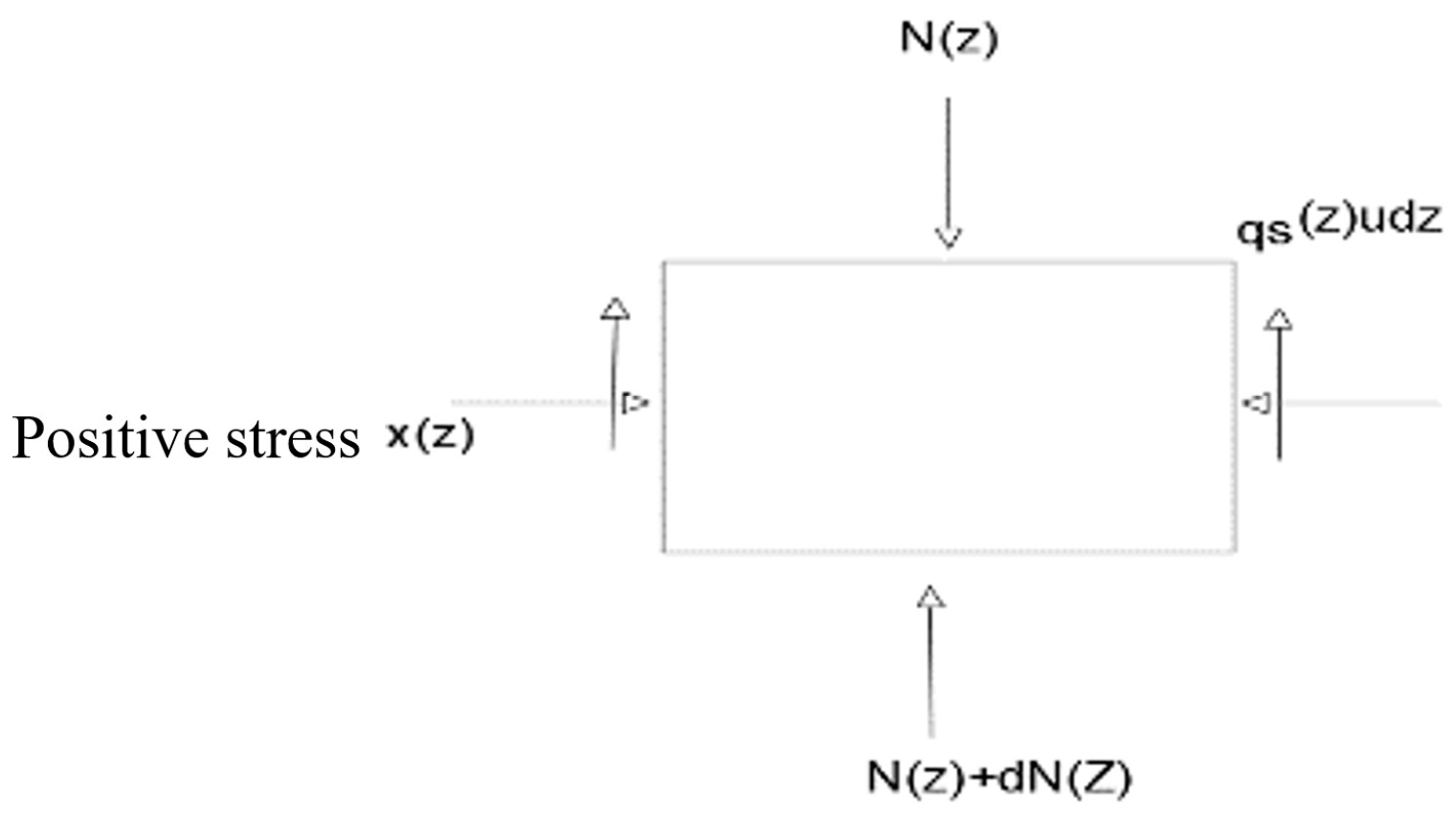
2.1.2. Mechanics Analysis
2.1.3. Analysis of Thermomechanical Coupling Mechanism
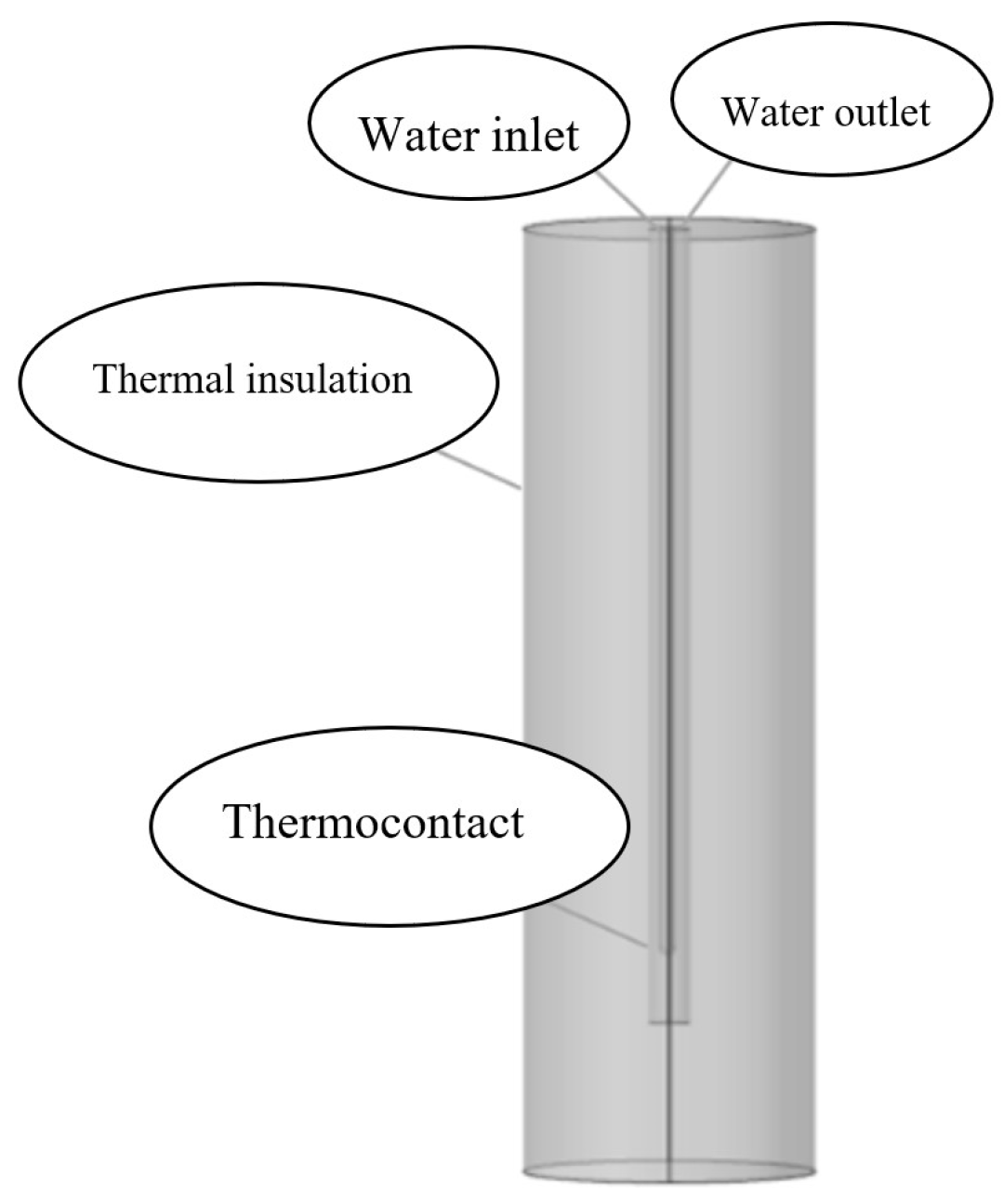
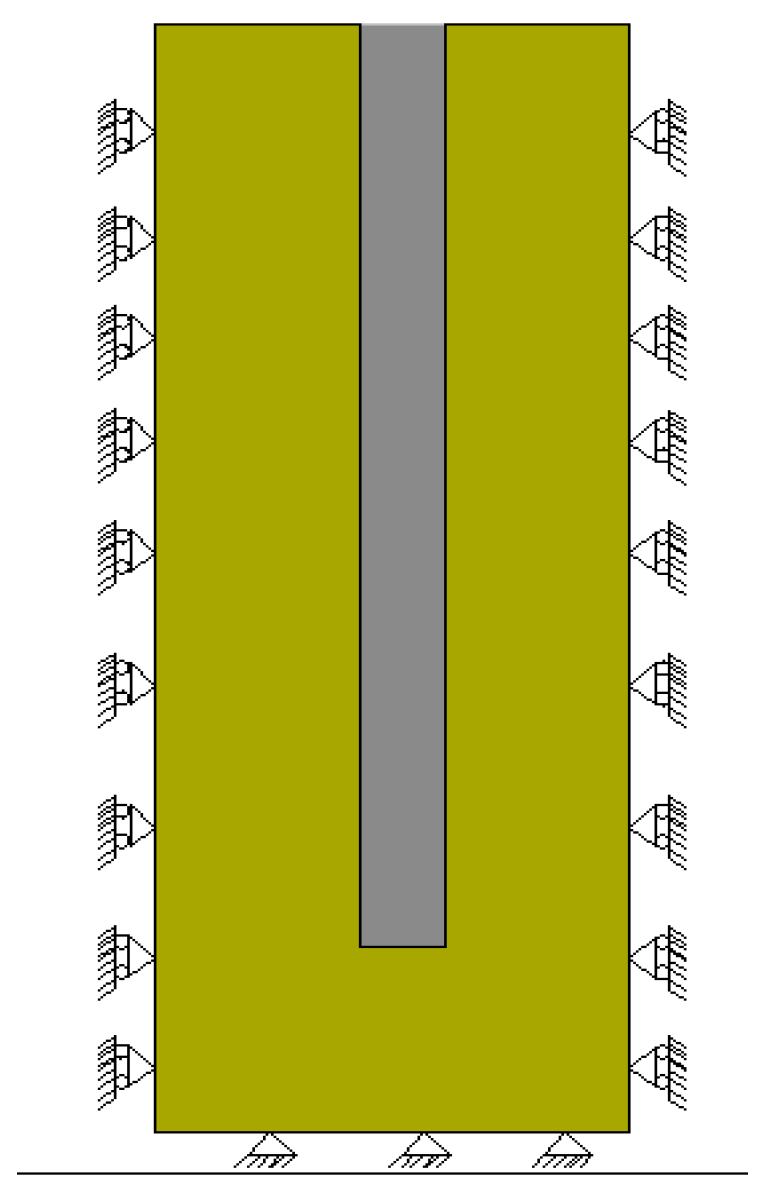
2.2. Design of Calculation Model
2.3. Grid Division and Grid Independence Verification for Calculation Model
3. Simulation Study and Analysis of Heat Transfer Performance of Energy Piles
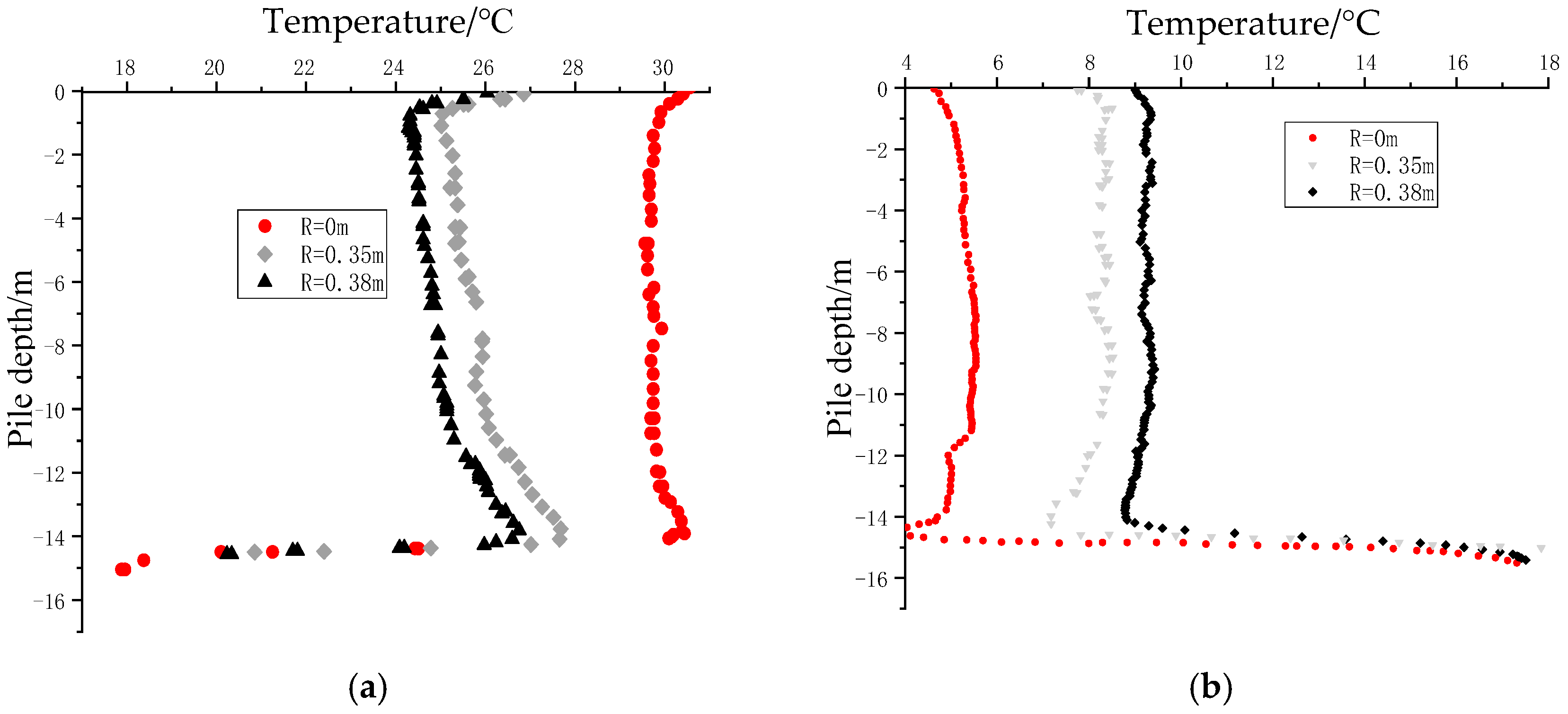
3.1. Model Reliability Verification
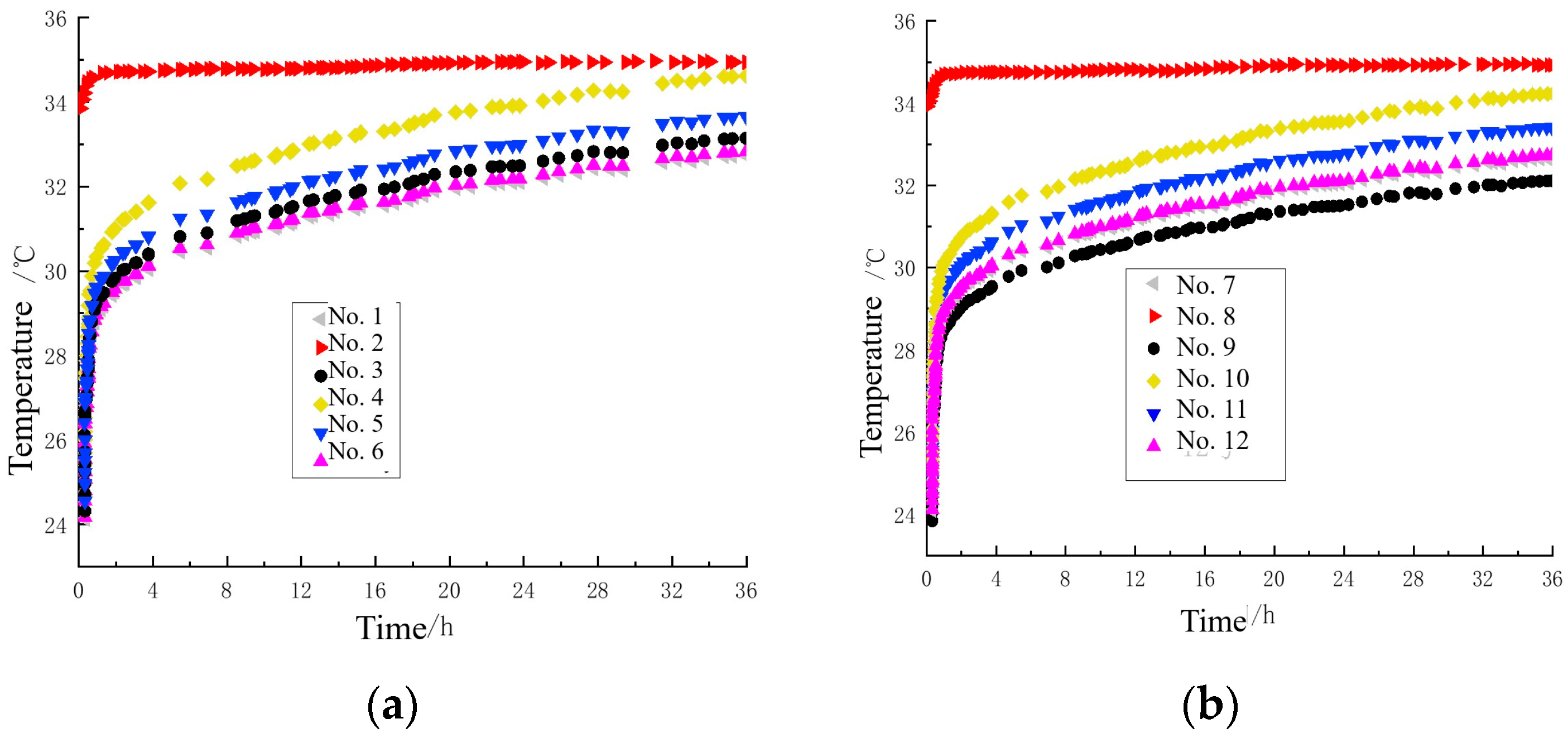
3.2. Study on Heat Transfer Performance of Energy Piles
3.2.1. Thermal Energy Analysis of Heat-Carrying Fluid Surface of Energy Piles
3.2.2. Analysis of Influencing Factors of Heat Exchange of Energy Piles
- The heat transfer efficiency of solid piles is better than that of piles filled with ordinary thermal physical materials;
- For energy pipe piles with U-shaped buried pipes, the materials filled inside have a great influence on the heat transfer efficiency of the piles. The heat transfer efficiency is water, urease mineralized carbon fiber soil, and undisturbed soil from high to low;
- When the soil around the energy pile is mineralized soil, the heat transfer performance is better than that of the undisturbed soil;
- When the pipe pile is filled with liquid material, the convection of liquid gives full play to the advantages of large heat exchange area of spiral buried pipe and improves the heat exchange efficiency of energy pile.
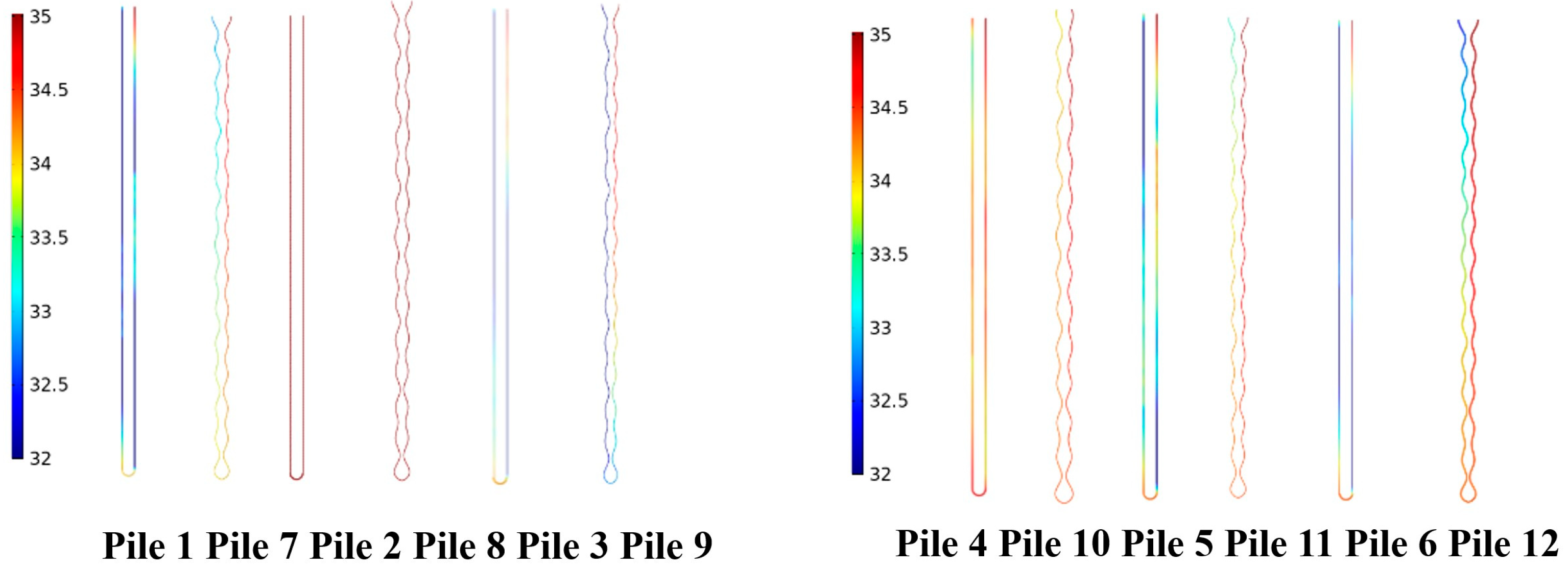
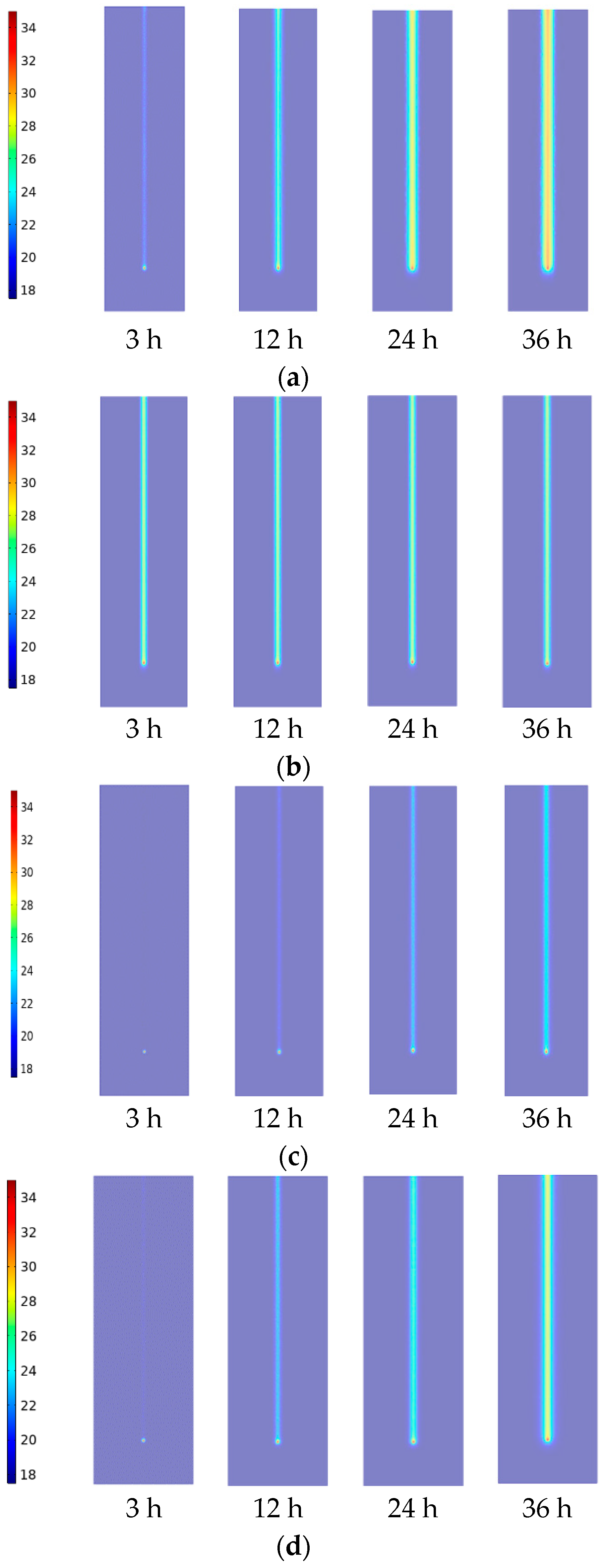
3.2.3. Study of the Temperature Distribution in the Longitudinal Section of an Energy Pile under Different Conditions
3.2.4. Study of Temperature Distribution in the Energy Pile Body under Different Conditions
3.2.5. Study on Heat Transfer Performance of Energy Piles with Different Types of Buried Pipes
4. Study and Analysis of the Thermomechanical Properties of Energy Piles
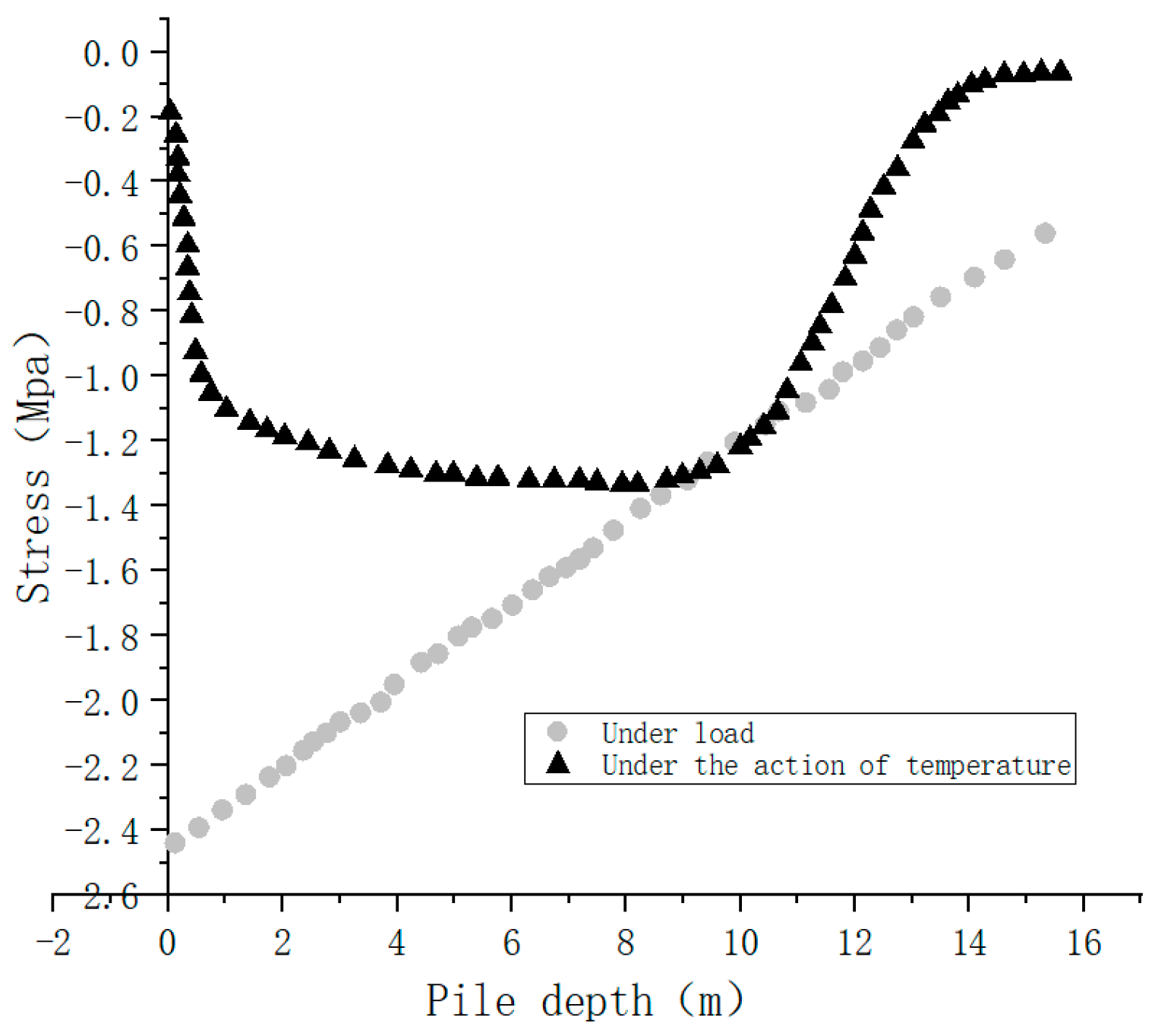
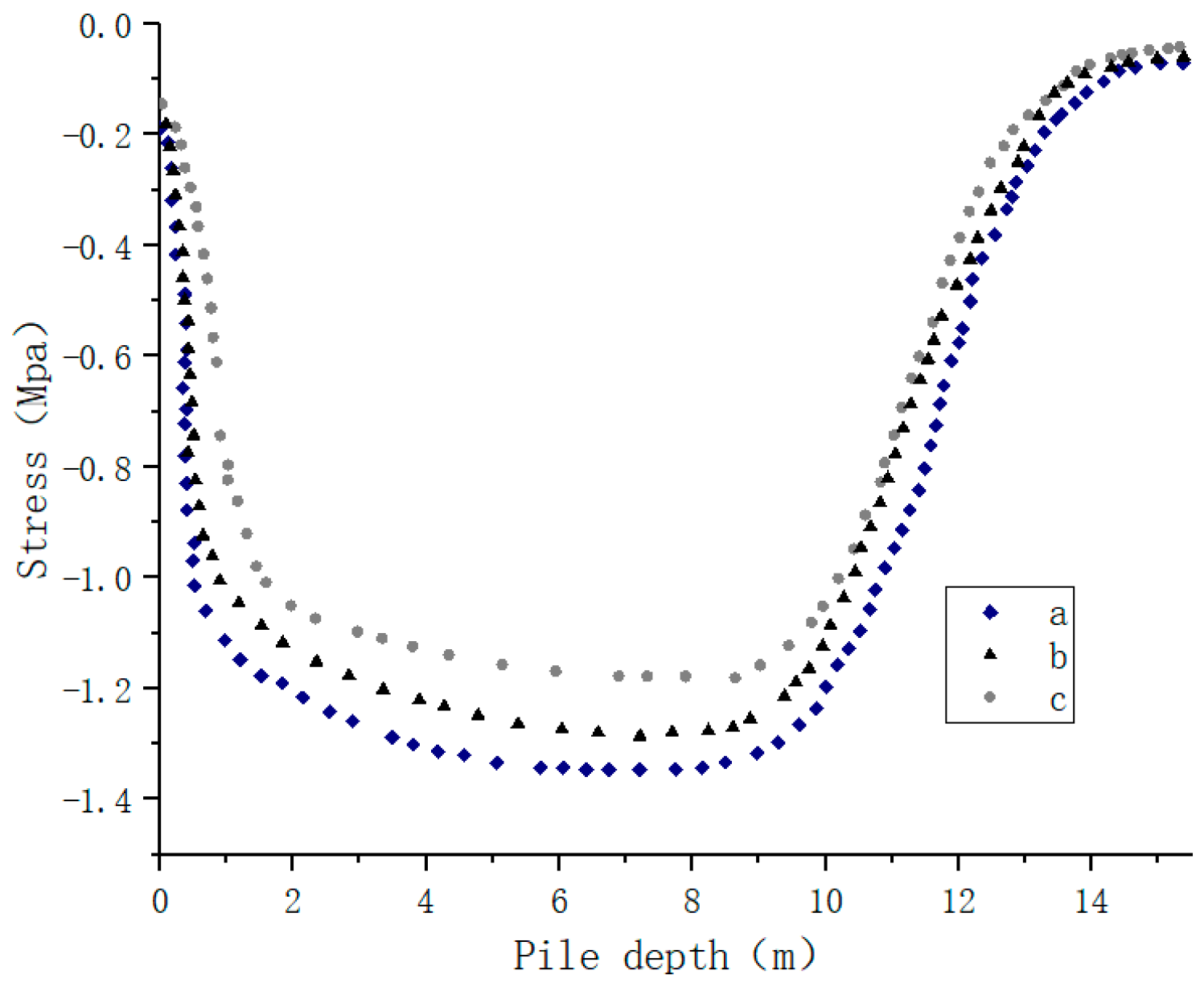
4.1. Study on the Law of Variation of Axial Stress under Load and Temperature
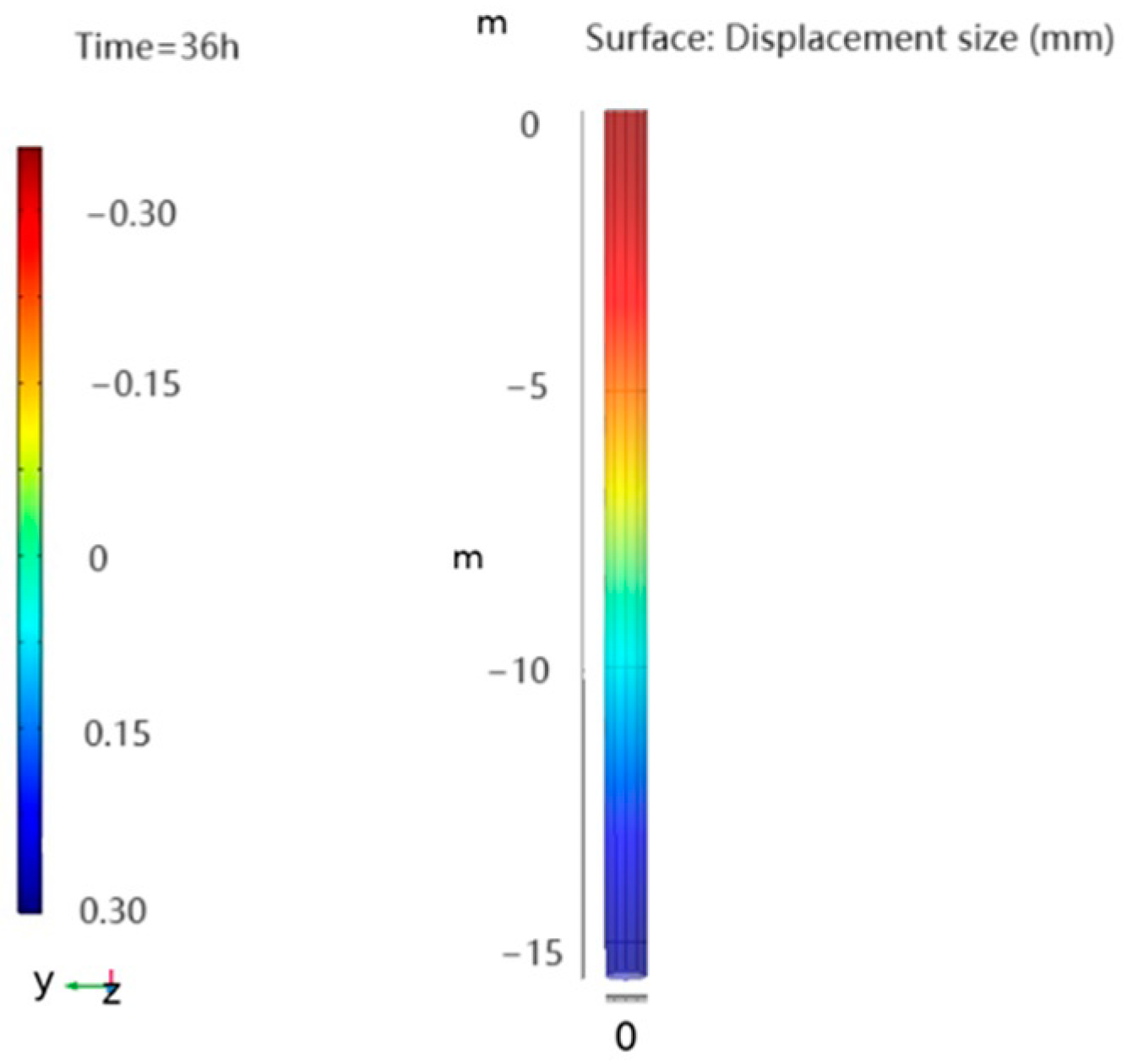
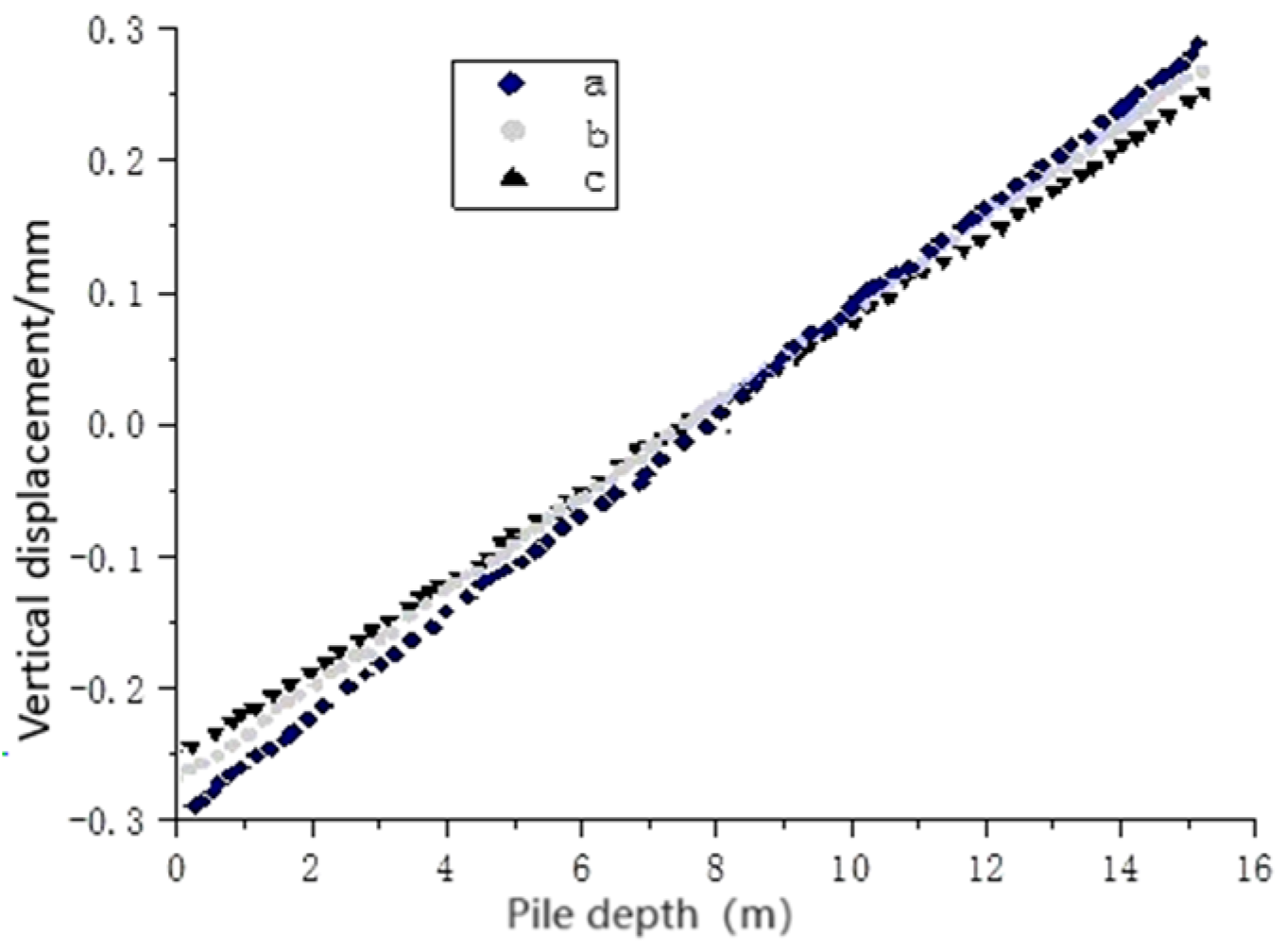
4.2. Study on the Law of Variation of Displacement under Load and Temperature
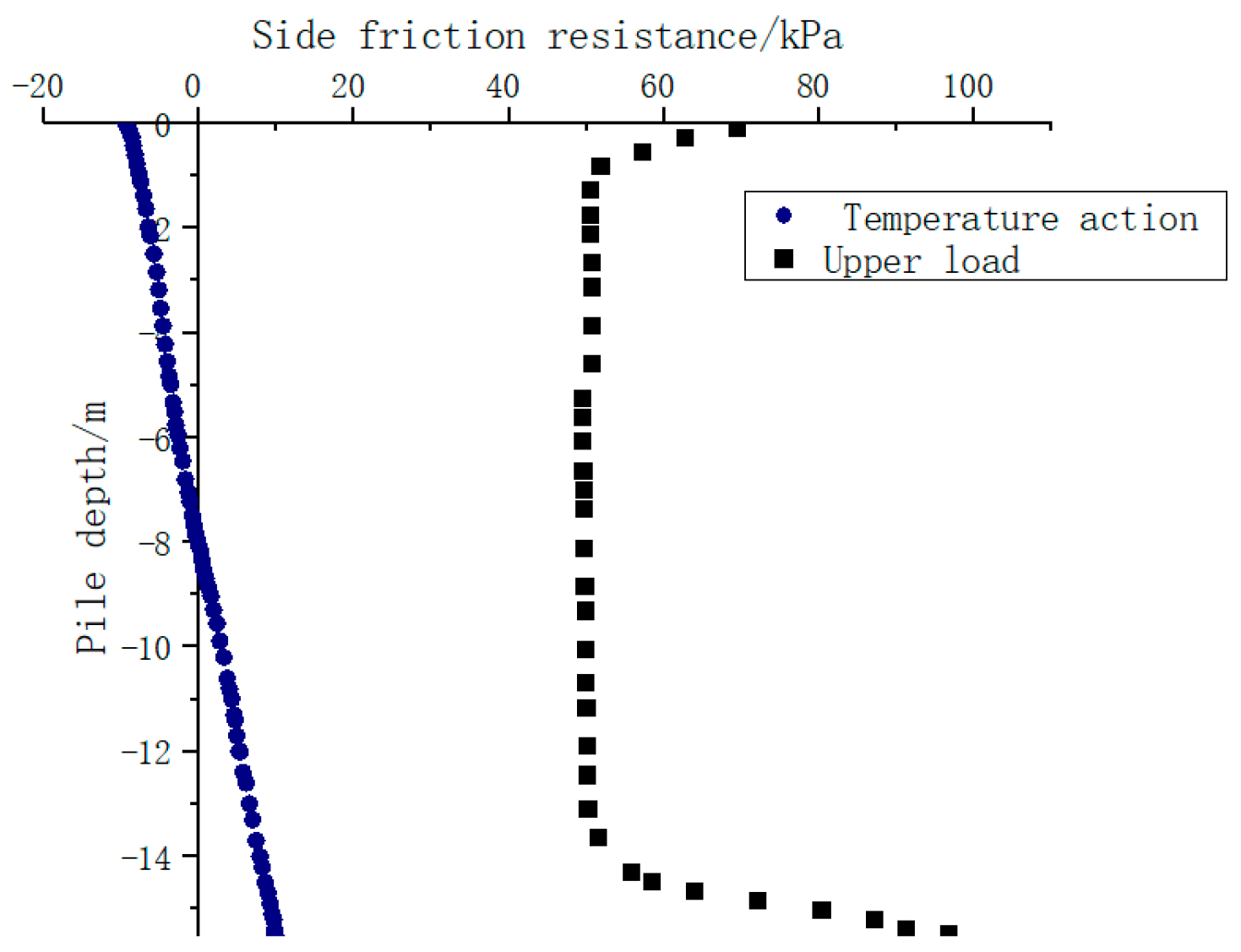
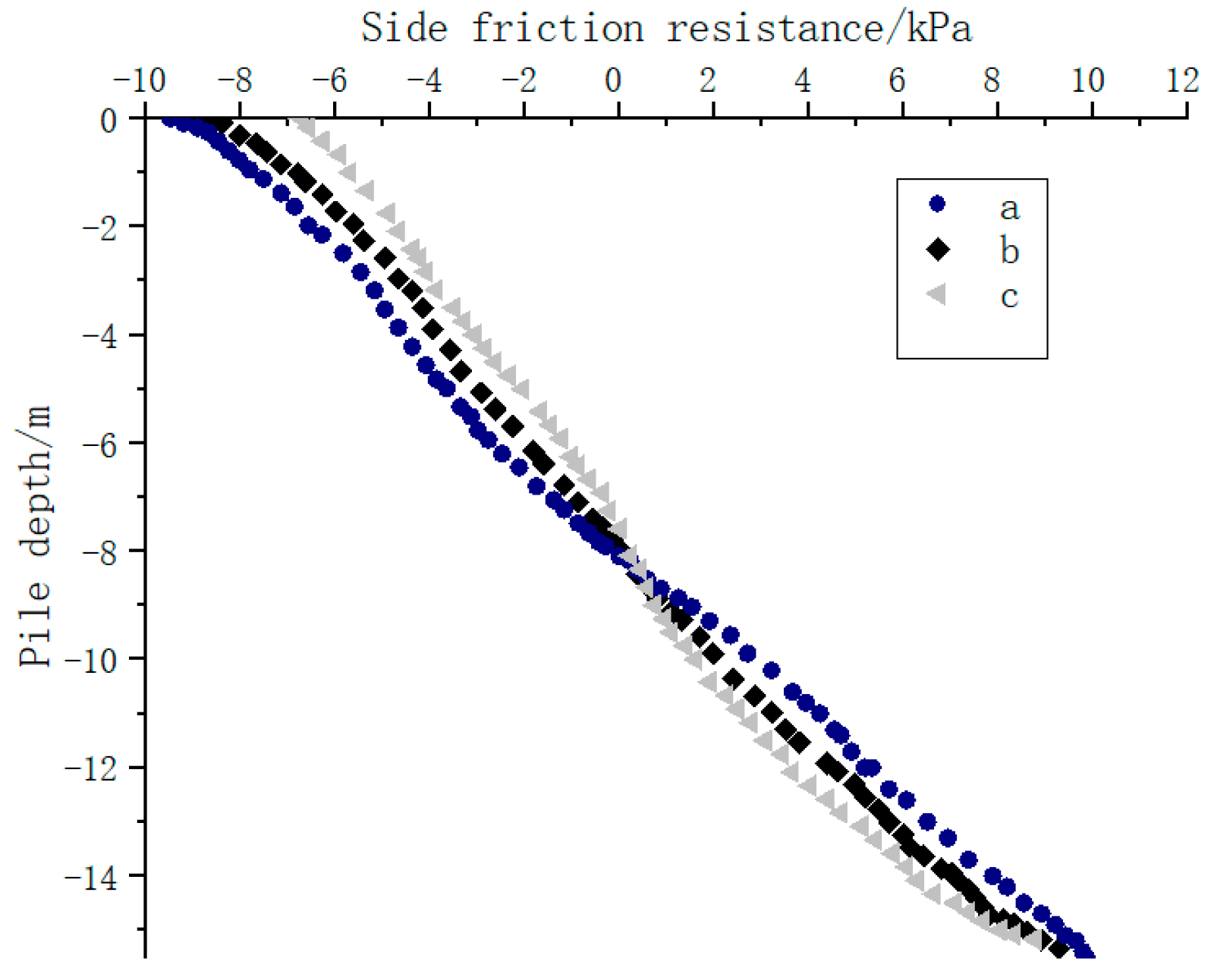
4.3. Study of the Law of Variation of Side Friction under Load and Temperature
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Q.; Chen, B.; Liu, F. Study on the thermal performance of several types of energy pile ground heat exchaners: U-shaped, W-shaped and spiral-shaped. Energy Build. 2016, 133, 335–344. [Google Scholar] [CrossRef]
- Li, X.-Y.; Guo, H.-X.; Cheng, X.-H. Experimental and numerical study on temperature distribution in energy piles. Civ. Eng. J. 2016, 49, 102–110. [Google Scholar]
- Hamzeh, F.A.; Behrad, A.; Mohsen, R. Thermal performance analysis of an energy pile with triple helix ground heat exchanger. Geothermics 2022, 104, 102459. [Google Scholar]
- Rui, Y. Thermo-hydro-mechanical coupling analysis of a thermal pile. Proc. Inst. Civ. Eng.-Geotech. Eng. 2018, 172, 155–173. [Google Scholar] [CrossRef]
- Francesco, C.; Diana, S. Energy performance assessment of thermo-active micro-piles via numerical modeling and statistical analysis. Geomech. Energy Environ. 2021, 29, 100268. [Google Scholar]
- Seokjae, L.; Sangwoo, P.; Dongwook, A.; Hangseok, C. Thermal performance of novel cast-in-place energy piles equipped with multipurpose steel pipe heat exchangers (SPHXs). Geothermics 2022, 102, 102389. [Google Scholar]
- Ding, X.-M.; Peng, C.; Wang, C.-L.; Kong, G.-Q. Heat transfer performance of energy piles in seasonally frozen soil areas. Renew. Energy 2022, 190, 903–918. [Google Scholar] [CrossRef]
- Mohammed, F.; Abdelmalek, B.; John, S.M. Thermal resistance analysis of an energy pile and adjacent soil using radial temperature gradients. Renew. Energy 2022, 190, 1066–1077. [Google Scholar]
- Sani, A.K.; Singh, R.M.; de Hollanda Cavalcanti Tsuha, C.; Cavarretta, I. Pipe–pipe thermal interaction in a geothermal energy pile. Geothermics 2019, 81, 209–223. [Google Scholar] [CrossRef]
- Gong, J.; Peng, W. Three-dimensional finite element analysis of deformation characteristics of energy piles under inclined load. J. Geotech. Eng. 2021, 43, 2105–2111. [Google Scholar]
- Han, C.; Yu, X. Analyses of the thermo-hydro-mechanical responses of energy pile subjected to non-isothermal heat exchange condition. Renew. Energy 2020, 157, 150–163. [Google Scholar] [CrossRef]
- Aria, M.; Mohammed, F.; Abdelmalek, B.; John, S.M. Cross-sectional thermo-mechanical responses of energy piles. Comput. Geotech. 2021, 138, 104320. [Google Scholar]
- Yu, L.; Deng, Y.-B.; Cao, G.-X.; Han, Y.-D.; Zhang, R.-H. The effect of thermal consolidation on bearing char-acteristics of static drilling rooted energy pile. In Proceedings of the ISRM Regional Symposium—11th Asian Rock Mechanics Symposium, Beijing, China, 21–25 October 2021; Volume 861. [Google Scholar]
- Lu, H.; Kong, G.; Liu, H.; Wu, D.; Chen, Y. Influence of thermo-mechanical properties of clay on me-chanical properties of energy piles. J. Geotech. Eng. 2022, 44, 53–61. [Google Scholar]
- Du, T.; Li, Y.; Bao, X.; Tang, W.; Cui, H. Thermo-Mechanical Performance of a Phase Change Energy Pile in Saturated Sand. Symmetry 2020, 12, 1781. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, L.J.; Zhang, H.; Wang, F.; Li, X. Numerical investigations of the effects of different factors on the displacement of energy pile under the thermo-mechanical loads. Case Stud. Therm. Eng. 2020, 21, 100711. [Google Scholar] [CrossRef]
- Huang, X.; Kong, G.-Q.; Liu, H.-L.; Wu, H.-W. Experimental research on thermomechanical characteristics of PCC energy pile under cyclic temperature. Rock Soil Mech. 2015, 36, 667–673. [Google Scholar]
- Fang, J.-C.; Kong, G.-Q.; Yang, Q. Group Performance of Energy Piles under Cyclic and Variable Thermal Loading. J. Geotech. Geoenvironmental Eng. 2022, 148, 04022060. [Google Scholar] [CrossRef]
- Wang, Z.-J. Analysis of an Energy Pile Enduring Cyclic Temperature Loads. Geotech. Res. 2019, 6, 227–233. [Google Scholar] [CrossRef]
- Chen, Z.; Yao, J.; Pan, P.; Xiao, H.; Ma, Q. Research on the heat exchange characteristics of the deeply buried pipe type of energy pile. Case Stud. Therm. Eng. 2021, 27, 101268. [Google Scholar] [CrossRef]
- Li, Q.; You, S.; Ji, H. Numerical Modelling of Structural Response Characteristics of Energy Piles under Long-term coupled Thermo-Mechanical Loads. In Proceedings of the ISRM Regional Symposium—11th Asian Rock Mechanics Symposium, Beijing, China, 21–25 October 2021; Volume 861. [Google Scholar]
- Casasso, A.; Sethi, R. Efficiency of closed loop geothermal heat pumps: A sensitivity analysis. Renew. Energy 2014, 62, 737–746. [Google Scholar] [CrossRef]
- Antelmi, M.; Turrin, F.; Zille, A.; Fedrizzi, R. A new type in TRNSYS 18 for simulation of Borehole Heat Exchangers affected by different groundwater flow velocities. Energies 2023, 16, 1288. [Google Scholar] [CrossRef]
- Vespasiano, G.; Cianflone, G.; Taussi, M.; De Rosa, R.; Dominici, R.; Apollaro, C. Shallow Geothermal Potential of the Sant’Eufemia Plain (South Italy) for Heating and Cooling Systems: An Effective Renewable Solution in a Climate-Changing Society. Geosciences 2023, 13, 110. [Google Scholar] [CrossRef]
- Alberti, L.; Angelotti, A.; Antelmi, M.; La Licata, I. Borehole Heat Exchangers in aquifers: Simulation of the grout material impact, Rendiconti Online Societa Geologica Italiana. Rend. Online Della Soc. Geol. Ital. 2016, 41, 268–271. [Google Scholar] [CrossRef]
- Di Dato, M.; D’angelo, C.; Casasso, A.; Zarlenga, A. The impact of porous medium heterogeneity on the thermal feedback of openloop shallow geothermal systems. J. Hydrol. 2021, 604, 127205. [Google Scholar] [CrossRef]
- Stewart, M.A.; McCartney, J.S. Centrifuge Modeling of Soil-Structure Interaction in Energy Foundations. J. Geotech. Geoenviron. Eng. 2013, 140, 04013044. [Google Scholar] [CrossRef]
- Bourne-Webb, P.J.; Amatya, B.; Soga, K.; Amis, T.; Davidson, C.; Payne, P. Energy pile test at Lambeth College, London: Ge-otechnical and thermodynamic aspects of pile response to heat cycles. Géotechnique 2009, 59, 237–248. [Google Scholar] [CrossRef]
- Gao, W. Study on Heat Transfer Performance of Double-Helix Energy Pile under the Mineralization of Carbon Fiber-Based Urease. Master’s Thesis, Qingdao University of Technology, Qingdao, China, 2021. [Google Scholar] [CrossRef]
- Gui, S.; Cheng, X. In-situ experimental study on structural response of energy piles during heat transfer. J. Geotech. Eng. 2014, 36, 1087–1094. [Google Scholar]
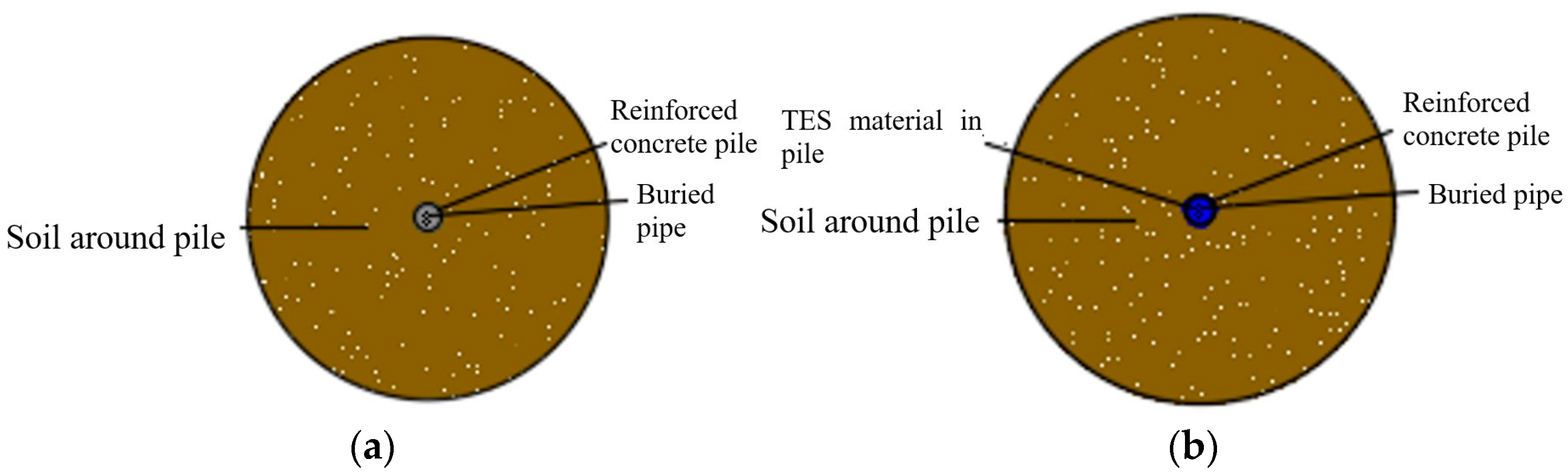
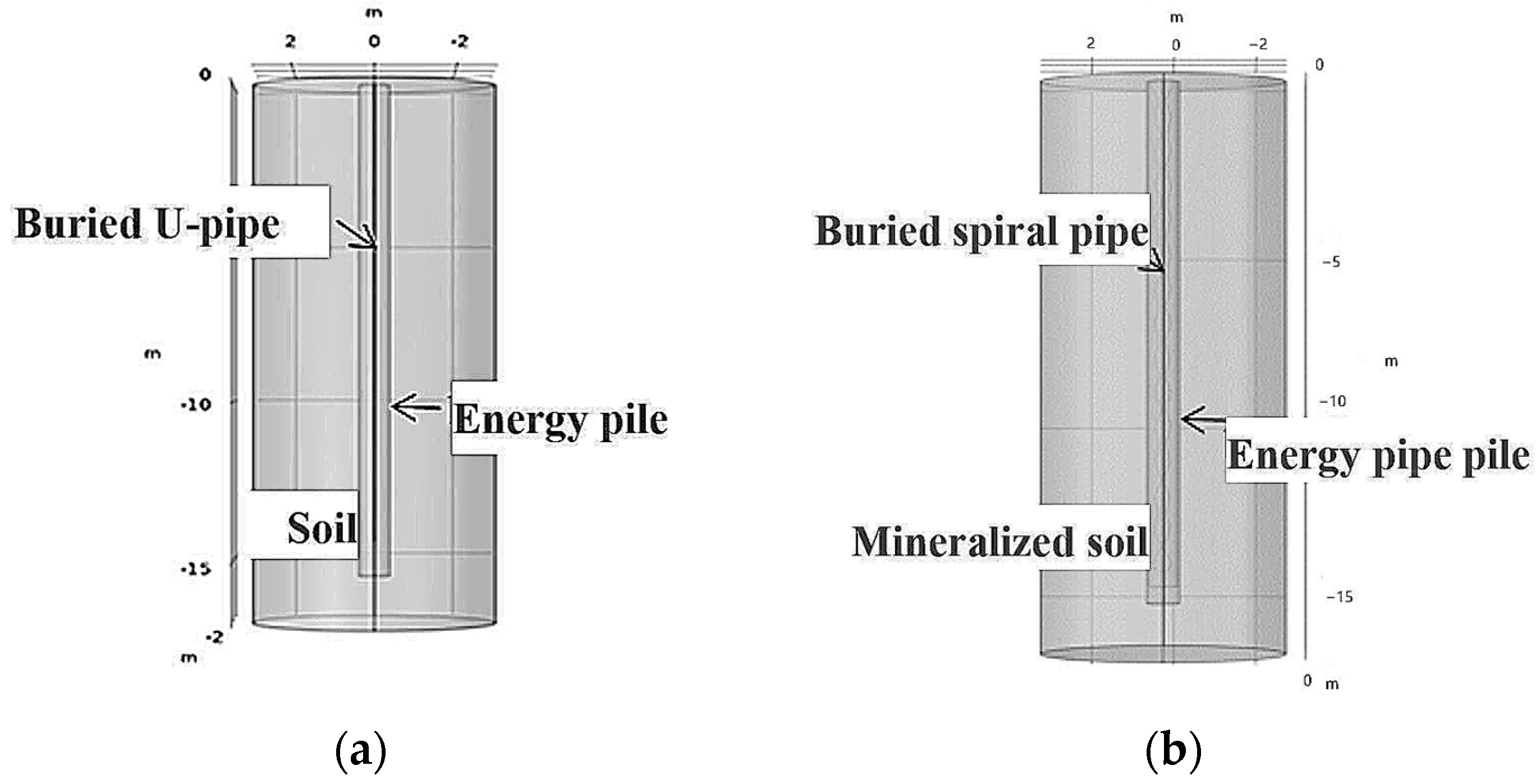

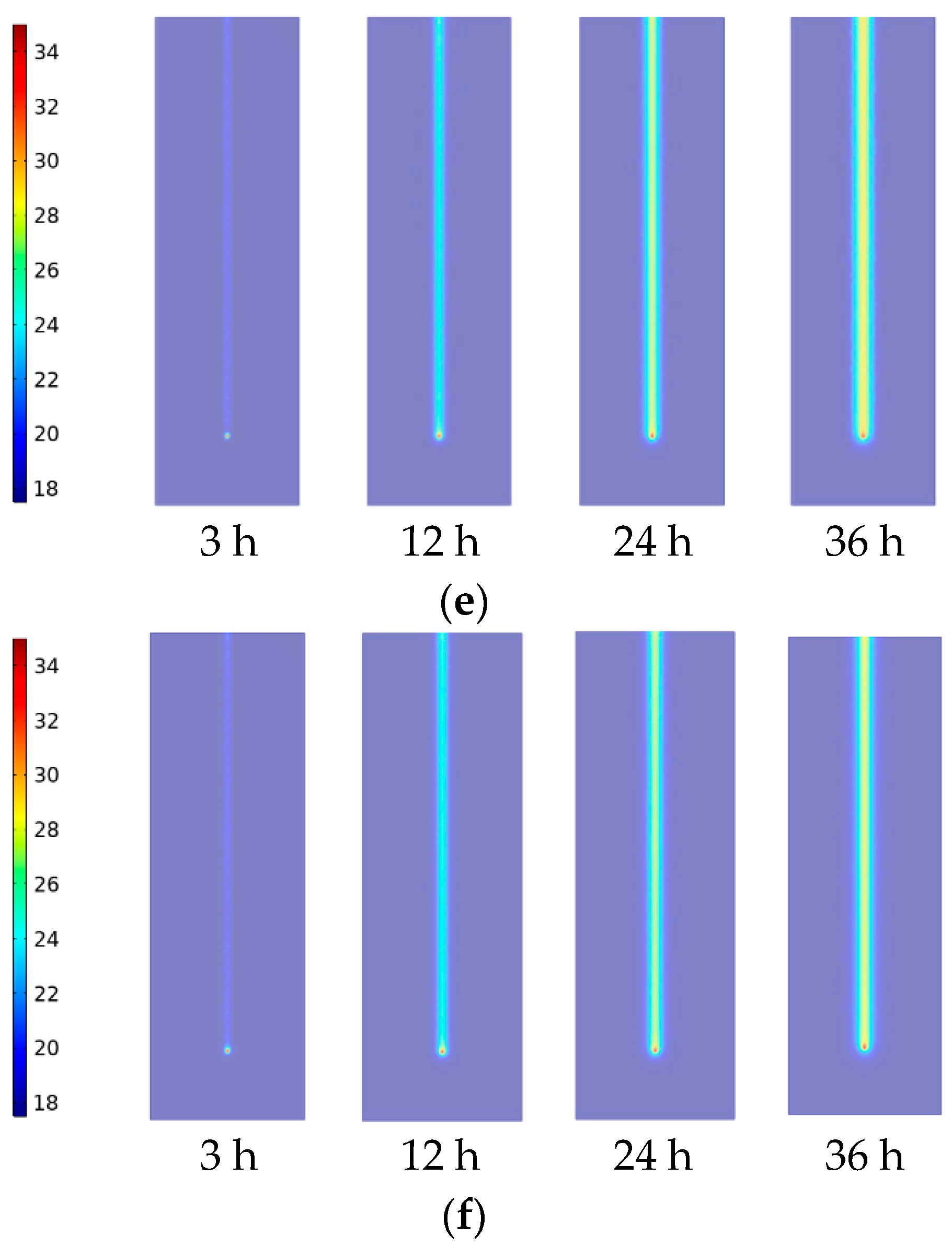
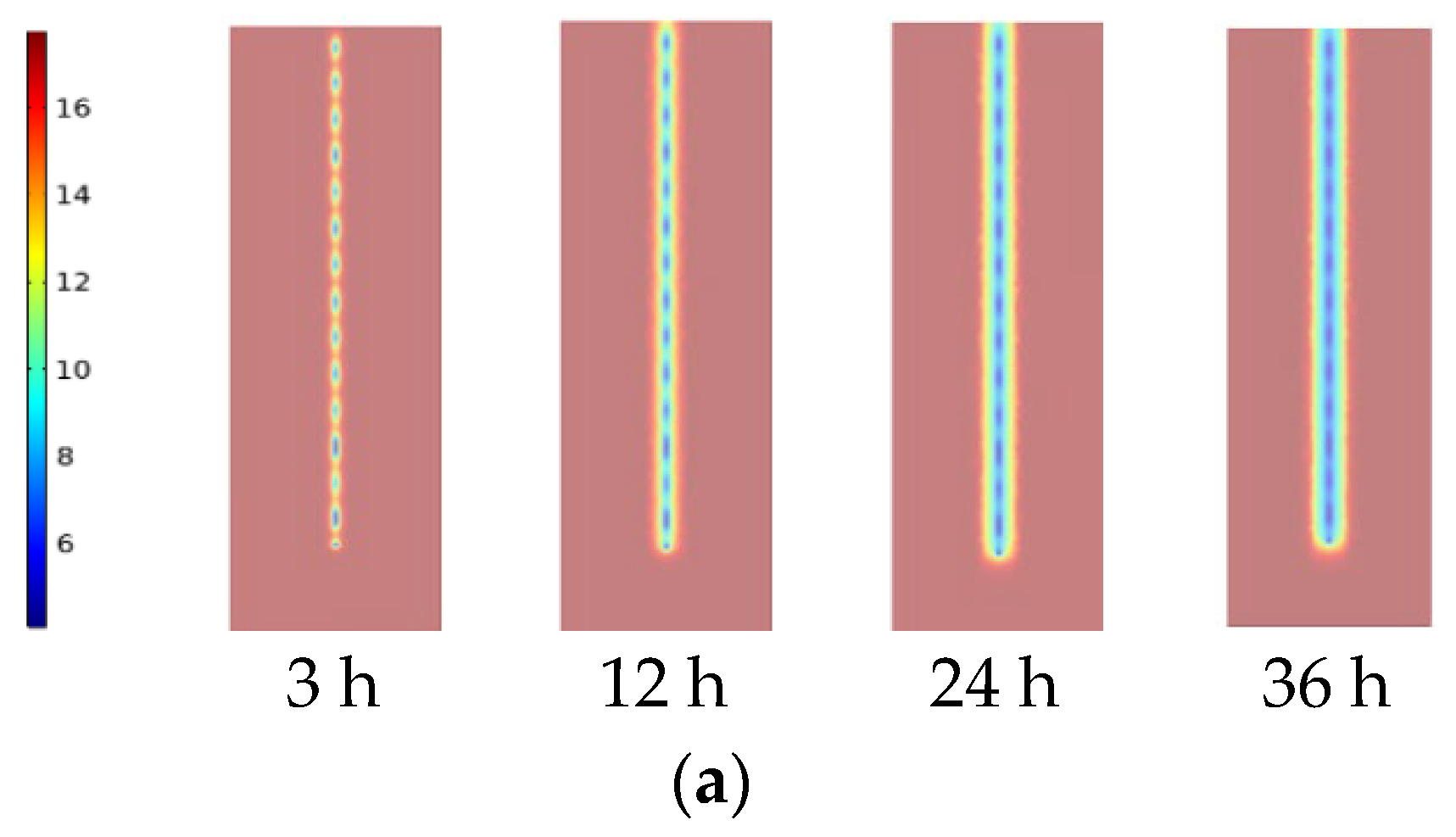
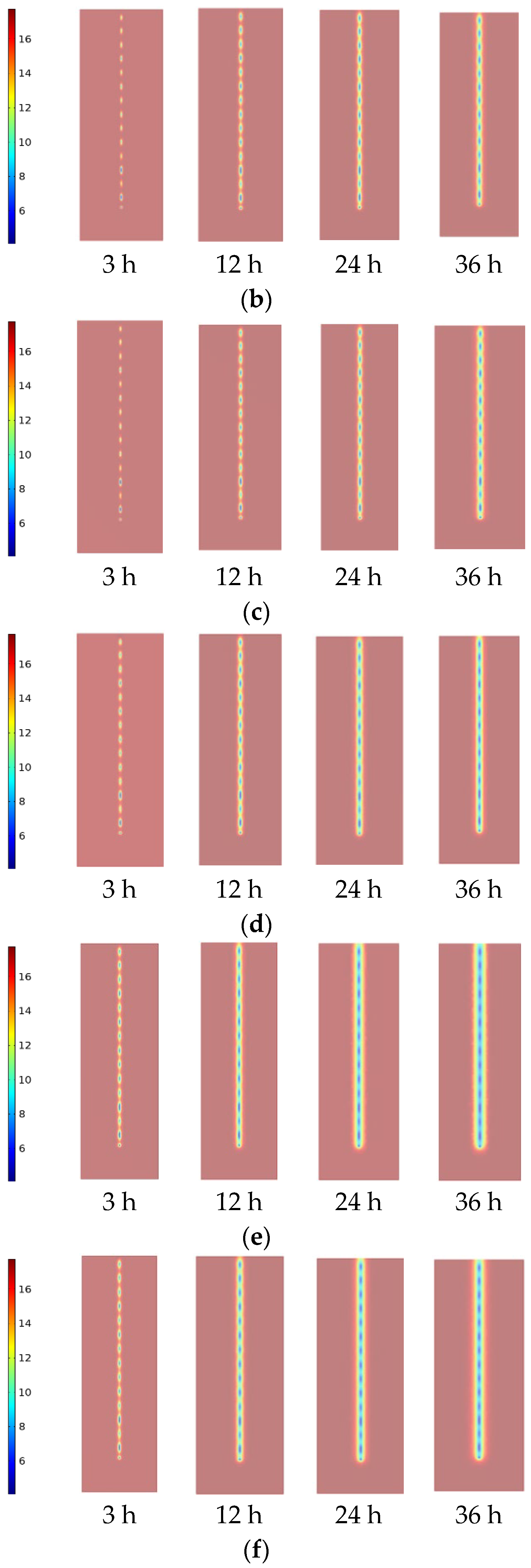


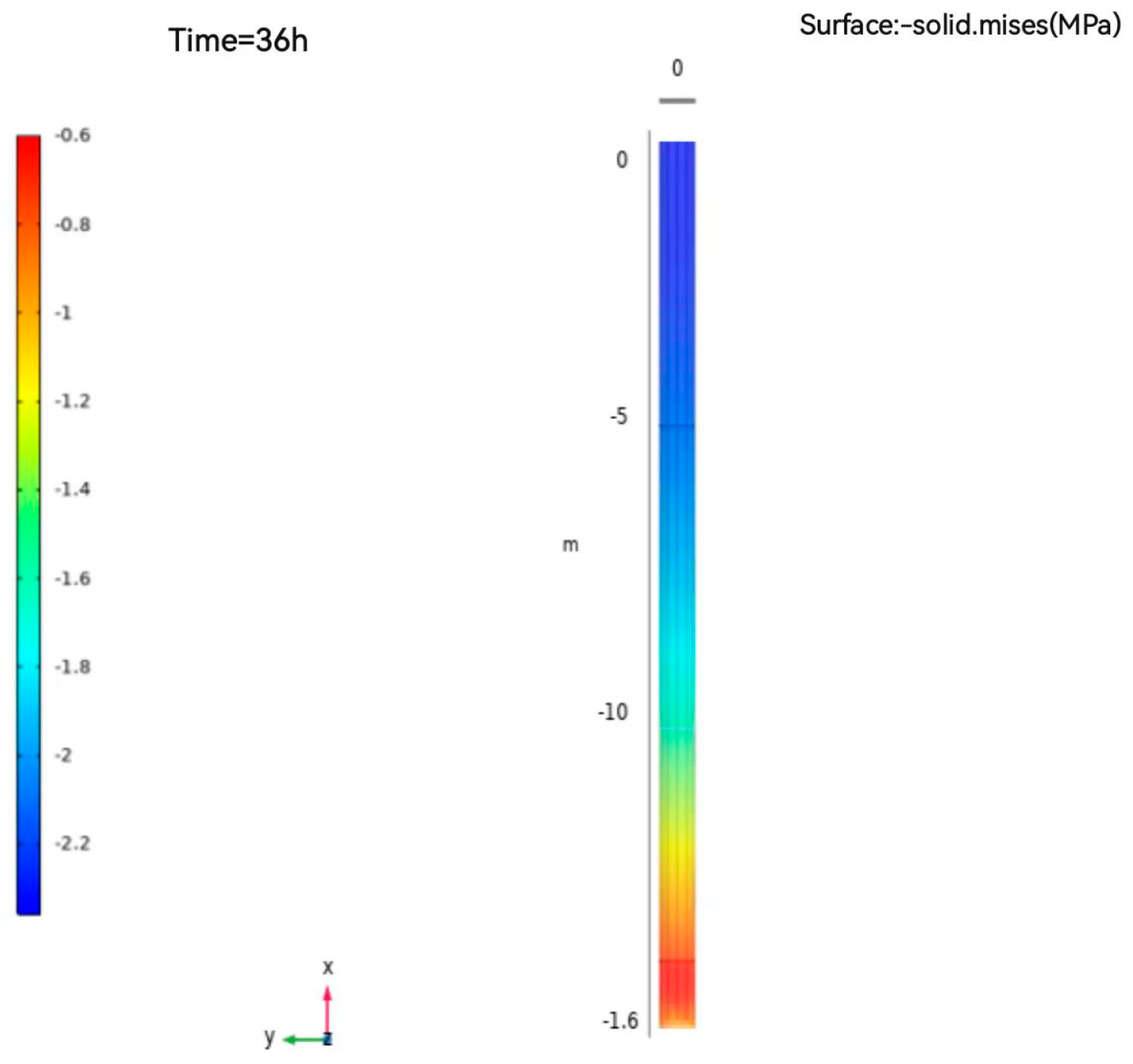
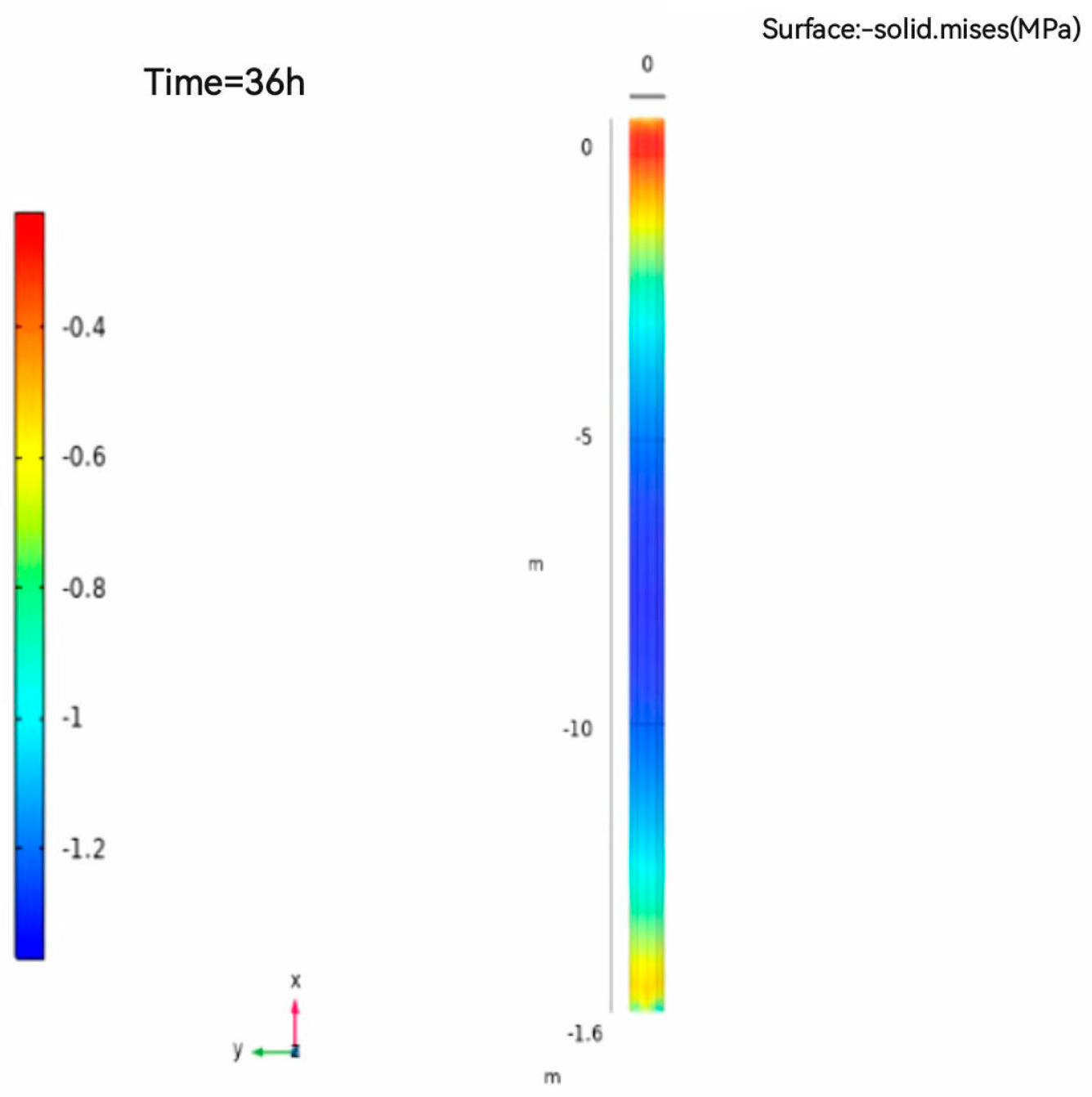

| # | Outer Radius of Pile Foundation/m | Pile Length/m | Inner Radius of Pile Foundation/m | Shape of Buried Pipe | TES Material in Pile | Soil around Pile |
|---|---|---|---|---|---|---|
| 1 | 0.38 | 15.5 | N/A (solid pile) | Buried U-pipe | N/A | In-situ sandy soil |
| 2 | 0.38 | 15.5 | 0.35 | Buried U-pipe | N/A | In-situ sandy soil |
| 3 | 0.38 | 15.5 | 0.35 | Buried U-pipe | Water | In-situ sandy soil |
| 4 | 0.38 | 15.5 | 0.35 | Buried U-pipe | Sandy soil | In-situ sandy soil |
| 5 | 0.38 | 15.5 | 0.35 | Buried U-pipe | Mineralized soil | In-situ sandy soil |
| 6 | 0.38 | 15.5 | 0.35 | Buried U-pipe | Mineralized soil | Mineralized soil |
| 7 | 0.38 | 15.5 | N/A (solid pile) | Buried spiral pipe | N/A | In-situ sandy soil |
| 8 | 0.38 | 15.5 | 0.35 | Buried spiral pipe | N/A | In-situ sandy soil |
| 9 | 0.38 | 15.5 | 0.35 | Buried spiral pipe | Water | In-situ sandy soil |
| 10 | 0.38 | 15.5 | 0.35 | Buried spiral pipe | Sandy soil | In-situ sandy soil |
| 11 | 0.38 | 15.5 | 0.35 | Buried spiral pipe | Mineralized soil | In-situ sandy soil |
| 12 | 0.38 | 15.5 | 0.35 | Buried spiral pipe | Mineralized soil | Mineralized soil |
| Number of Grid Cells | Outlet Water Temperature | Calculation Time |
|---|---|---|
| 19,797 | 29.3 °C | 0.5 h |
| 88,435 | 29.5 °C | 3 h |
| 105,930 | 29.9 °C | 5 h |
| 780,095 | 30.3 °C | 11 h |
| 2,329,287 | 30.7 °C | 23 h |
| Factor B | Buried U-Pipe | Buried Spiral Pipe | |||
|---|---|---|---|---|---|
| Factor A | |||||
| Solid pile | 31.925 | 32.733 | 31.848 | 32.662 | |
| Hollow pipe pile | 34.675 | 34.940 | 34.871 | 34.925 | |
| Pipe pile filled with water | 32.865 | 33.142 | 32.137 | 32.114 | |
| Pipe pile filled with sandy soil | 34.721 | 34.621 | 34.214 | 34.233 | |
| Pipe pile filled with mineralized soil | 33.326 | 33.656 | 33.184 | 33.414 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Wang, Y.; Meng, X.; Lv, Q.; Chen, H.; Wu, Q. A Multiphysics Simulation Study of the Thermomechanical Coupling Response of Energy Piles. Buildings 2024, 14, 1440. https://doi.org/10.3390/buildings14051440
Xu C, Wang Y, Meng X, Lv Q, Chen H, Wu Q. A Multiphysics Simulation Study of the Thermomechanical Coupling Response of Energy Piles. Buildings. 2024; 14(5):1440. https://doi.org/10.3390/buildings14051440
Chicago/Turabian StyleXu, Chang, Yawen Wang, Xiaolin Meng, Qihang Lv, Hui Chen, and Qingdong Wu. 2024. "A Multiphysics Simulation Study of the Thermomechanical Coupling Response of Energy Piles" Buildings 14, no. 5: 1440. https://doi.org/10.3390/buildings14051440
APA StyleXu, C., Wang, Y., Meng, X., Lv, Q., Chen, H., & Wu, Q. (2024). A Multiphysics Simulation Study of the Thermomechanical Coupling Response of Energy Piles. Buildings, 14(5), 1440. https://doi.org/10.3390/buildings14051440





