Calculation of Column Pile Heave in Deep Excavation Based on the Rebound–Recompression Method
Abstract
1. Introduction
2. Methods
2.1. Calculation of Soil Rebound Based on the RRM
2.1.1. Unloading Stress Caused by Excavation
2.1.2. Calculation of the In Situ Void Ratio and Field Recompression Index
2.1.3. Calculation of Soil Rebound Deformation
2.2. Calculation of Column Pile Heave
2.2.1. Analysis of Force and Rebound Deformation
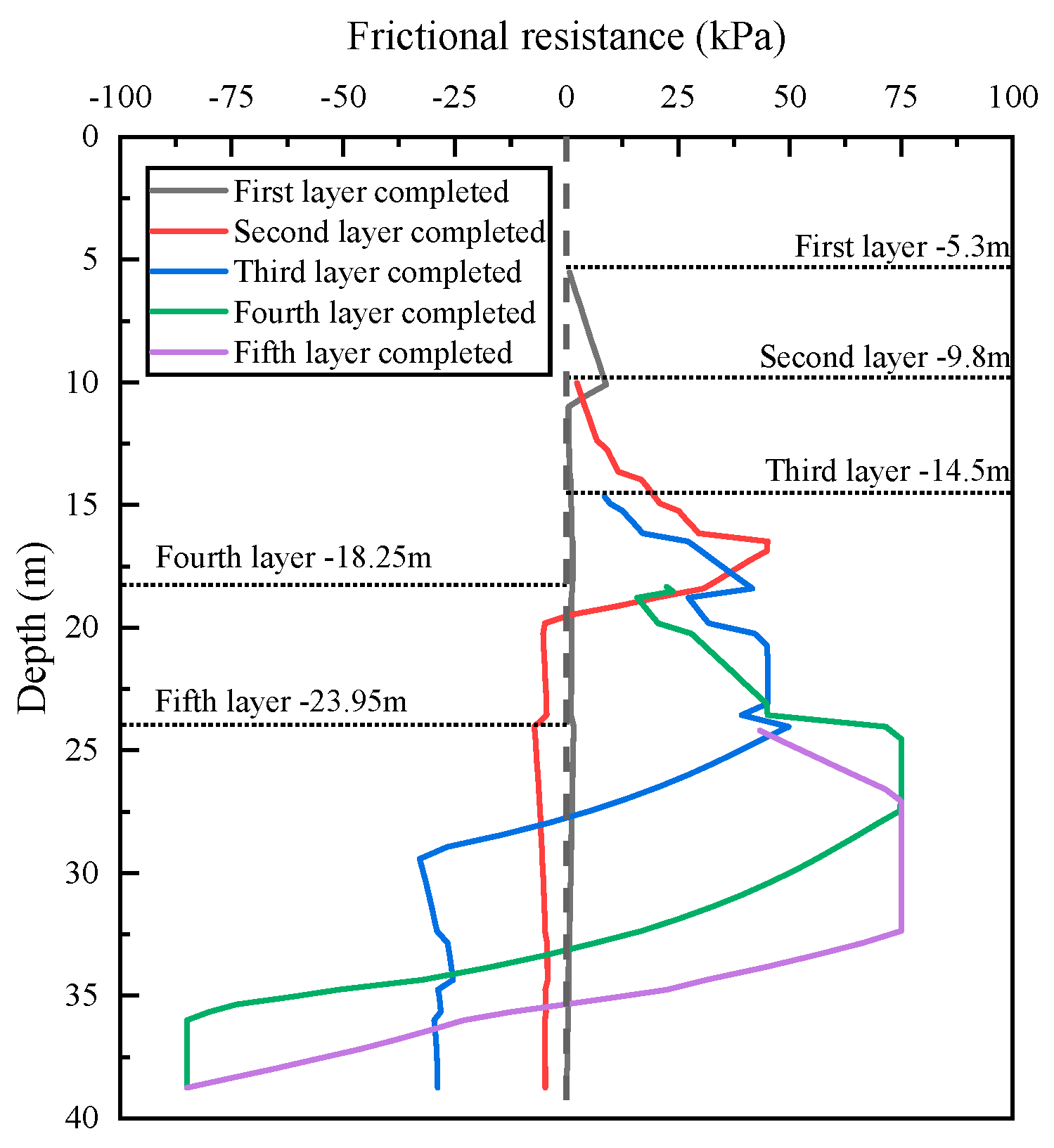
2.2.2. Pile-Side Friction and Force Balance
2.2.3. Calculation of Soil Rebound Considering the Action of Frictional Resistance
2.3. Calculation Steps and Iterative Solution
3. Results and Validation
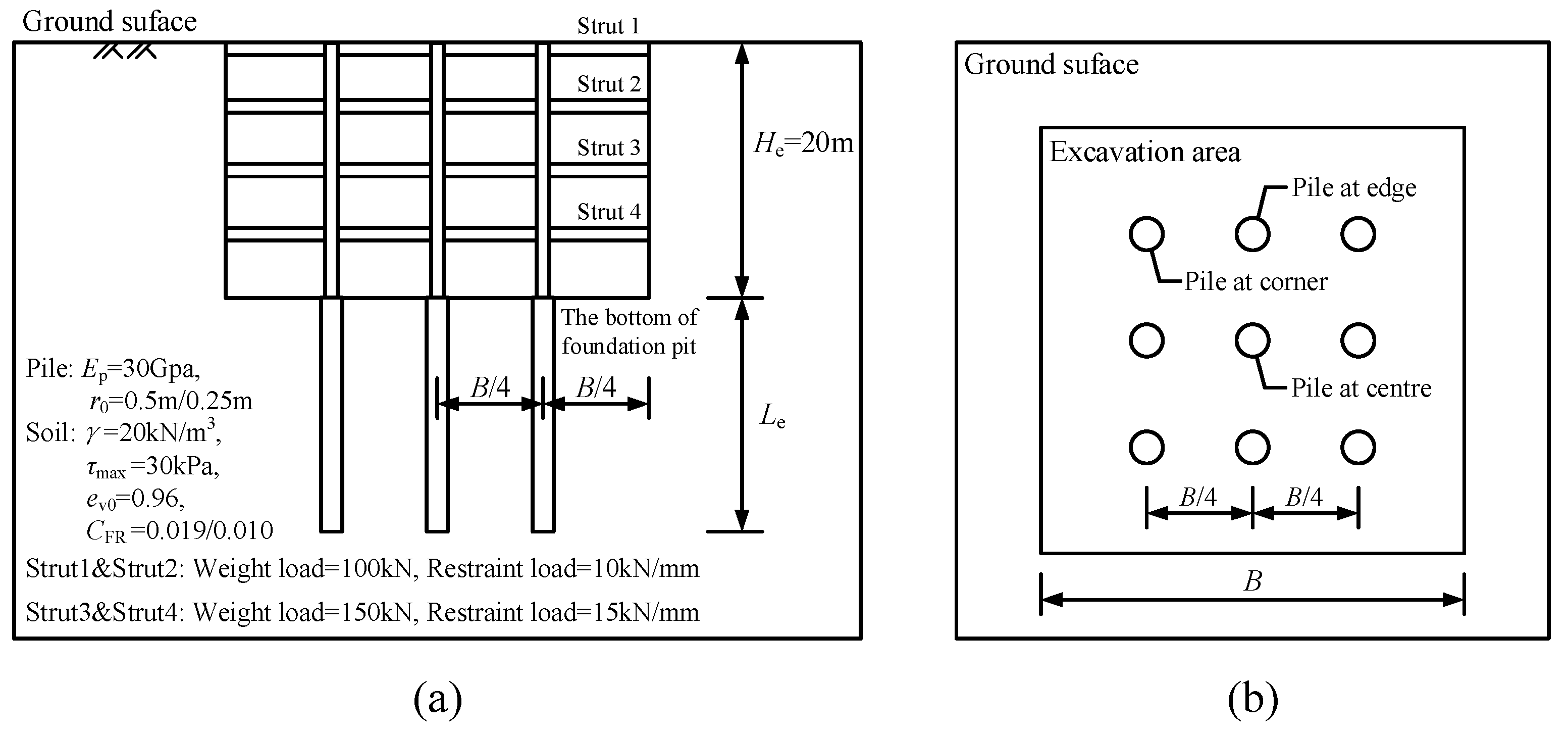
3.1. Project Overview
3.2. Site and Geology
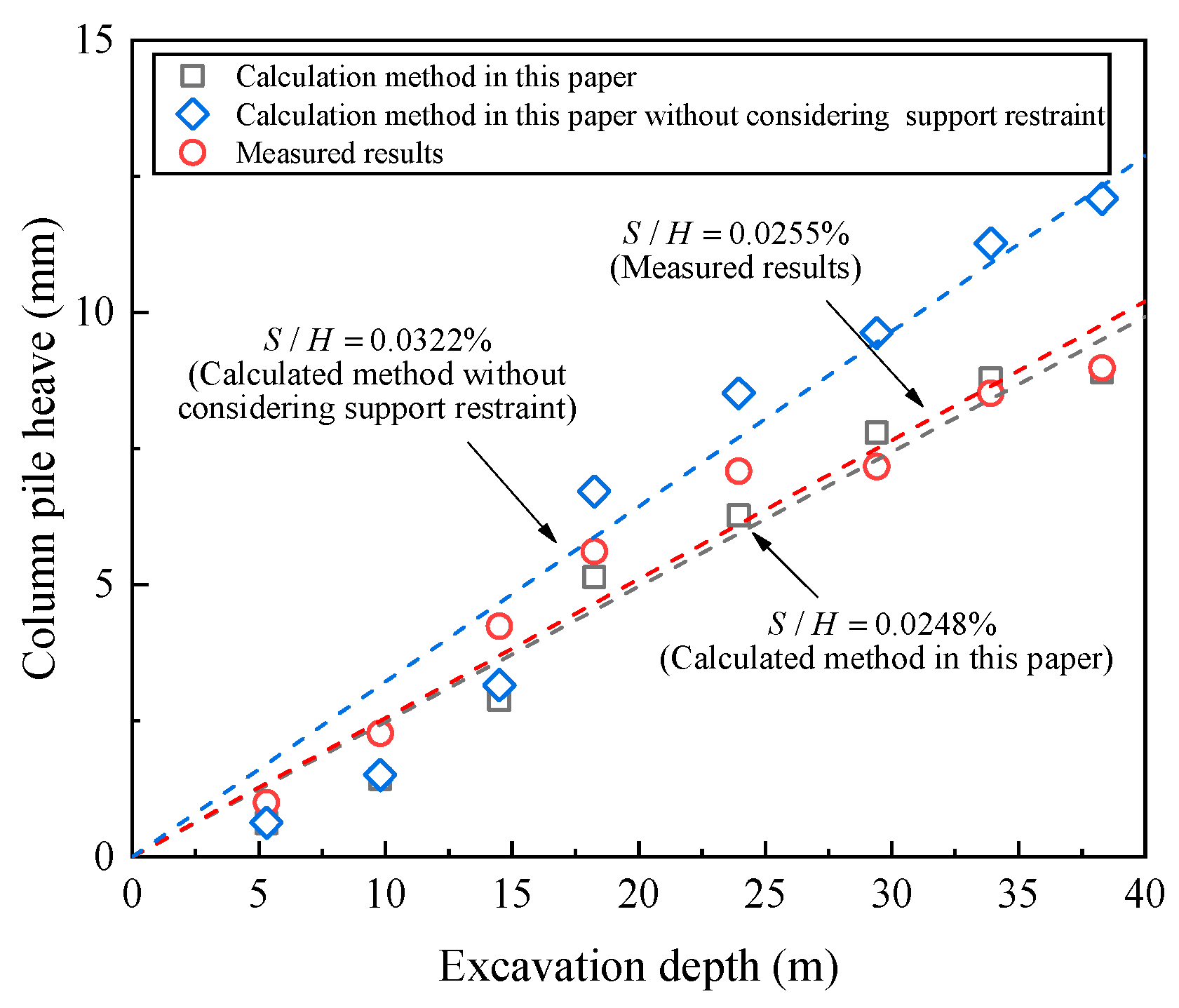
3.3. Measured and Calculated Results of Column Pile Heave
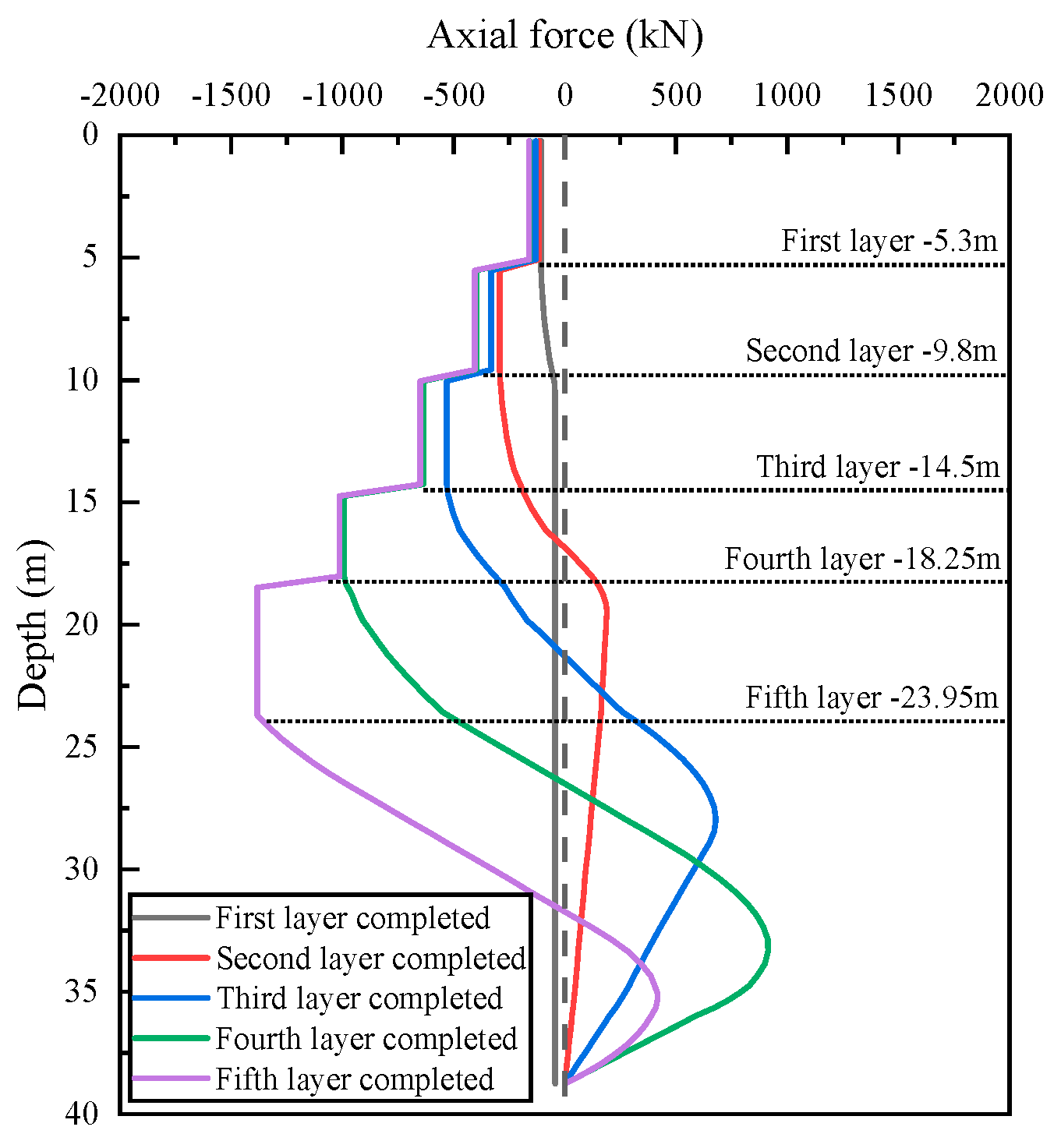
3.4. Analysis of the Results
4. Discussion
4.1. Effects of Effective Pile Length Le
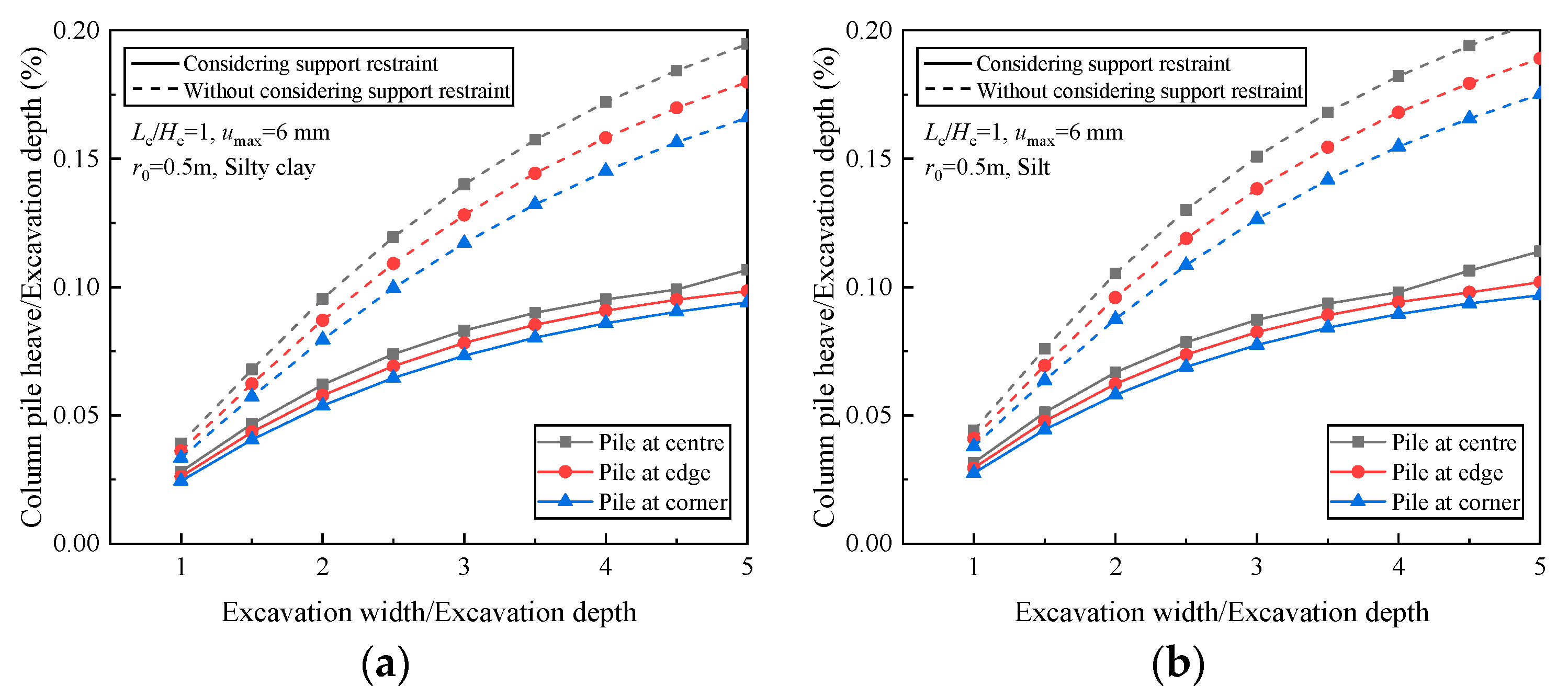
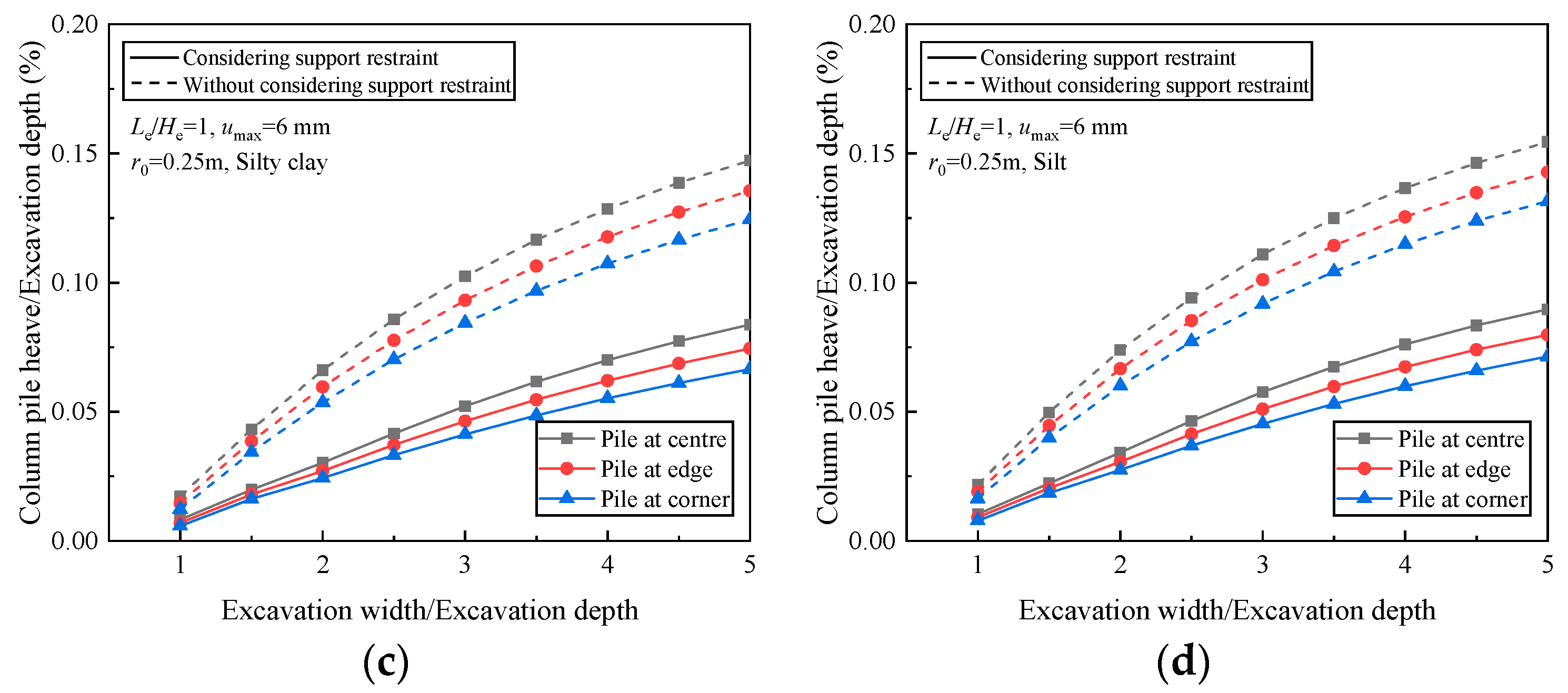
4.2. Effects of Excavation Width B
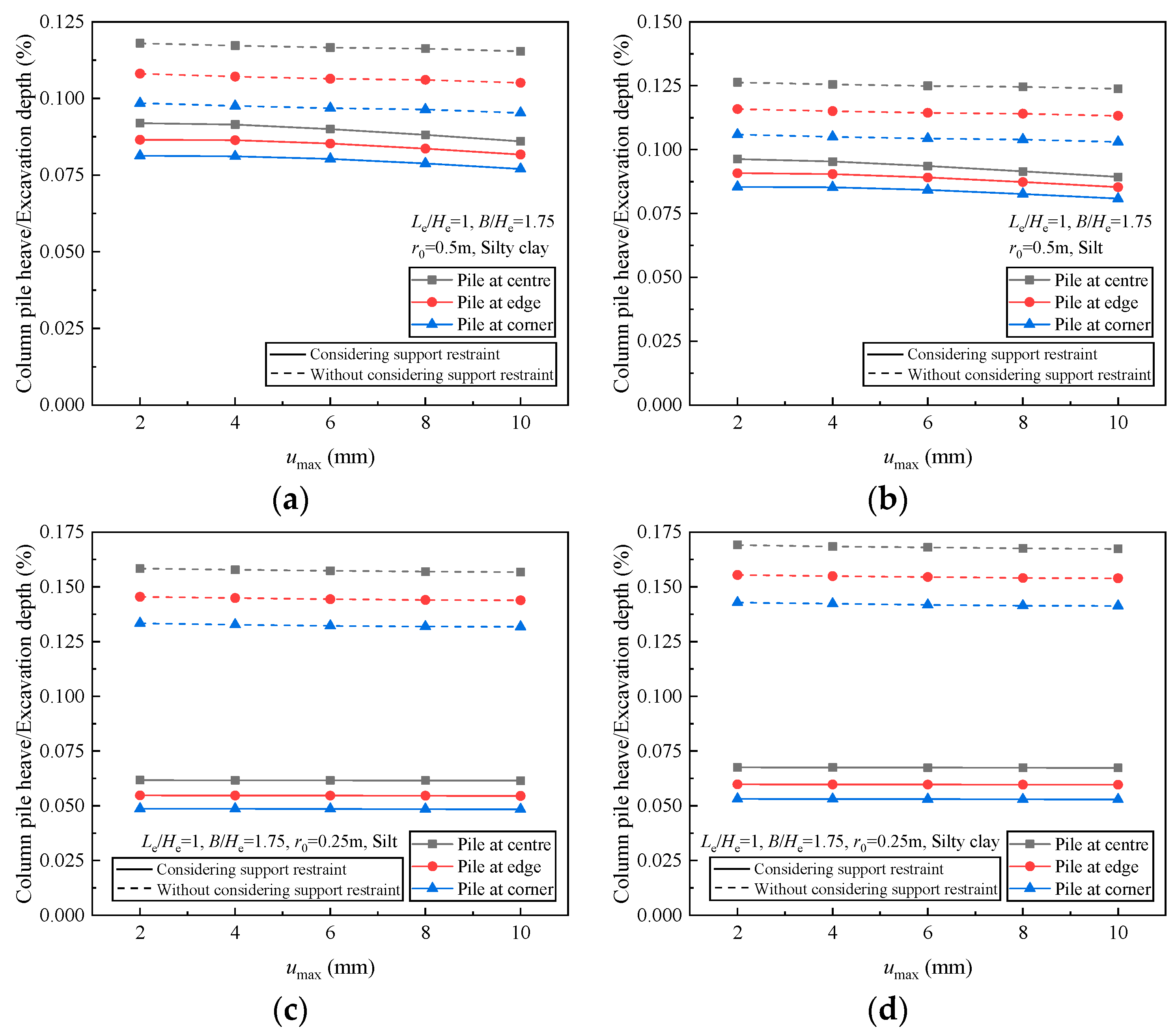
4.3. Effects of the Limit Relative Displacement umax
5. Conclusions
- The calculation method proposed in this paper reflects the development pattern of rebound deformation, and the results match measured values extremely well, validated by a field test. The method can also be used to calculate the development pattern of pile-side frictional resistance and pile axial force with excavation depth, providing theoretical basis and optimization guidance for the design of retaining structure and engineering piles below the bottom of the pit.
- With increasing excavation depth, pile-soil interaction and column pile heave increase, leading to the redistribution of internal forces in the retaining structure and increasing the structural safety hazard. Tension will also be generated in the column pile. When the tension is too large, the pile will crack or break. For the CHIEF case study, the maximum pile tension was found to be 1100 kN; the measured and calculated ratios of heave to excavation depth (S/H) were 0.0255% and 0.0248%, respectively. Therefore, enough attention should be paid to these problems in the engineering design and construction of deep excavation.
- The excavation width B, the effective pile length Le, and whether support restraints are considered will have a great impact on the results of column pile heave. The heave decreases more rapidly when the pile effective length is greater than the excavation depth. The support restraint causes a gentle stage in the heave versus the ratio of the pile effective length to the excavation depth curve in the range of 0.5–1.
- When the excavation area is large or the effective pile length is short, the factor of the position of the column pile in the foundation pit cannot be ignored. The column pile heave is hardly affected by the value of the limit relative displacement.
- The use of long piles with small diameter and the method of small block excavation are effective means to control the column pile heave.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notation
| Rebound index; | |
| Field recompression index; | |
| The field recompression index of the i-th layer of soil; | |
| The pile diameter; | |
| Initial void ratio; | |
| In situ initial void ratio; | |
| The in situ void ratio of the i-th layer of soil; | |
| The decrease in the void ratio; | |
| The unloading modulus of the i-th layer of soil; | |
| The ultimate frictional resistance of the soil; | |
| The weight of the i-th-layer horizontal support acting on the column; | |
| The thickness of the i-th layer; | |
| The thickness of the i-th layer of soil; | |
| Excavation depth; | |
| The restraint stiffness of the i-th-layer horizontal support to the column pile; | |
| The total number of layers after discretization of the column pile; | |
| The number of horizontal support layers; | |
| The residual effective stress; | |
| Force magnitude; | |
| The final rebound displacement at the top of the column pile; | |
| The pile top rebound displacement caused by the soil rebound deformation within the pile length; | |
| The final soil rebound deformation; | |
| The rebound deformation of the soil below the pile end; | |
| The soil rebound within the range of pile length; | |
| The rebound deformation at the i-th-layer horizontal support; | |
| The relative displacement between the soil and the pile; | |
| The limit of the relative displacement; | |
| The depth of calculation point; | |
| Bilinear distribution of concrete pressure; | |
| The vertical effective stress on the side of the pile; | |
| The vertical effective stress before the excavation; | |
| The vertical effective stress of the i-th layer of soil before the excavation; | |
| The additional vertical effective stress of the i-th layer of soil; | |
| The additional stress caused by the frictional resistance of the pile in the i-th layer of soil; | |
| Poisson’s ratio; | |
| The horizontal distance between the calculation point and force; | |
| The influence coefficient of a single vertically concentrated load in the i-th layer of soil; | |
| The pile-side frictional resistance; | |
| The frictional resistance around the column pile at the i-th-layer depth; | |
| The frictional resistance at the pile-soil interface of the j-th layer; | |
| The ultimate value of the pile-side frictional resistance; | |
| The pile-side frictional resistance coefficient. |
References
- Zhu, H.-G.; Sun, J.-P. Impact of subsoil rebound on engineering piles due to deep excavation in soft soil area. Geotech. Eng. World 2005, 8, 43–46. [Google Scholar]
- Xu, Q.-G.; Xu, X.-H.; Liang, C.-H.; Jin, Y.-G.; Chen, N.-L. Influence of the deep excavation on the bottom piles. Guangdong Archit. Civ. Eng. 2006, 1, 33–34. [Google Scholar] [CrossRef]
- Chen, X.-X. The discussion of pile risk for bottom soil resilience with deep foundation pit excavation. Fujian Constr. Sci. Technol. 2006, 3, 15–16. [Google Scholar] [CrossRef]
- Mao, J.; Xu, W.; Lu, P. Vertical displacement analysis of erect column in deep foundation pit. Archit. Technol. 2004, 35, 342. [Google Scholar] [CrossRef]
- Liu, T.; Liu, W.; Liu, G. Discussions on vertical displacement of stud piles in deep foundation pit. China Civ. Eng. J. 2007, 40, 387. [Google Scholar]
- Wang, L.; Zheng, G.; Ou, R.N. Differential uplift and settlement between inner column and diaphragm wall in top-down excavation. J. Cent. South Univ. 2015, 22, 3578–3590. [Google Scholar] [CrossRef]
- Feng, J.; Tan, Y.; Ma, K.; Zhang, J.; Pan, T.; Yao, S.; Song, J.; Li, Z. Stability classification and construction method analysis of subway stations in upper-soft and lower-hard strata. Eng. Fail. Anal. 2023, 153, 107550. [Google Scholar] [CrossRef]
- Yuan, B.; Sun, M.; Xiong, L.; Luo, Q.; Pradhan, S.P.; Li, H. Investigation of 3D deformation of transparent soil around a laterally loaded pile based on a hydraulic gradient model test. J. Build. Eng. 2020, 28, 101024. [Google Scholar] [CrossRef]
- Liu, G.B.; Jiang, R.J.; Ng, C.W.; Hong, Y. Deformation characteristics of a 38 m deep excavation in soft clay. Can. Geotech. J. 2011, 48, 1817–1828. [Google Scholar] [CrossRef]
- Tan, Y.; Li, M. Measured performance of a 26 m deep top-down excavation in downtown Shanghai. Can. Geotech. J. 2011, 48, 704–719. [Google Scholar] [CrossRef]
- Tan, Y.; Wang, D. Characteristics of a large-scale deep foundation pit excavated by the central-island technique in Shanghai soft clay. I: Bottom-up construction of the central cylindrical shaft. J. Geotech. Geoenviron. Eng. 2013, 139, 1875–1893. [Google Scholar] [CrossRef]
- Tan, Y.; Wang, D. Characteristics of a large-scale deep foundation pit excavated by the central-island technique in Shanghai soft clay. II: Top-down construction of the peripheral rectangular pit. J. Geotech. Geoenviron. Eng. 2013, 139, 1894–1910. [Google Scholar] [CrossRef]
- Goh, A.T.C. Assessment of basal stability for braced excavation systems using the finite element method. Comput. Geotech. 1990, 10, 325–338. [Google Scholar] [CrossRef]
- Goh, A.T.C. Estimating basal-Heave stability for braced excavations in soft clay. J. Geotech. Geoenviron. Eng. 1994, 120, 1430–1436. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Kulhawy, F.; Wong, K. Reliability assessment of basal-heave stability for braced excavations in clay. J. Geotech. Geoenviron. Eng. 2008, 134, 145–153. [Google Scholar] [CrossRef]
- Lu, P.-Y.; Yu, J.-X.; Xiao, J. Three-dimensional properties of foundation pit resilience under unloading. J. Tianjin Univ. 2006, 39, 301–305. [Google Scholar] [CrossRef]
- Yuan, B.; Li, Z.; Chen, W.; Luo, Q.; Yang, G.; Wang, Y. Experimental study on lateral cyclic loading model of pile-soil system based on PIV technique and fractal theory. Chin. J. Rock Mech. Eng. 2023, 42, 466–482. [Google Scholar] [CrossRef]
- Zheng, G.; Zhang, T.; Cheng, X.-S.; Diao, Y. Statistical analysis of measured data of center post upheaval in metro station excavations in Tianjin. Rock Soil Mech. 2017, 38, 387–394. [Google Scholar] [CrossRef]
- Yang, M.; Lu, J.-D. A calculation of behavior of underpinning pile subject to excavation of deep foundation pit. J. Tongji Univ. Nat. Sci. 2010, 38, 1730–1735. [Google Scholar] [CrossRef]
- He, C. Calculation of heave of soldier piles in deep foundation pits. Chin. J. Geotech. Eng. 2010, 32 (Suppl. S1), 74–78. [Google Scholar] [CrossRef]
- Lou, X.-M.; Yang, J.; Li, D.-N.; Liu, J.-H. Uplift displacement of soldier piles during stepped excavation of deep foundation pits. Chin. J. Geotech. Eng. 2013, 35, 193–198. [Google Scholar] [CrossRef]
- Zhai, L.; Ding, Z.; Wang, J. Simplified calculation of heaving of soldier piles during excavation of foundation pits. Chin. J. Geotech. Eng. 2014, 36 (Suppl. S2), 70–76. [Google Scholar] [CrossRef]
- Ng, C.W. Observed performance of multipropped excavation in stiff clay. J. Geotech. Geoenviron. Eng. 1998, 124, 889–905. [Google Scholar] [CrossRef]
- Lunne, T.; Berre, T.; Andersen, K.H.; Strandvik, S.; Sjursen, M. Effects of sample disturbance and consolidation procedures on measured shear strength of soft marine Norwegian clays. Can. Geotech. J. 2006, 43, 726–750. [Google Scholar] [CrossRef]
- Zapata-Medina, D.G.; Finno, R.J.; Vega-Posada, C.A. Stress history and sampling disturbance effects on monotonic and cyclic responses of overconsolidated Bootlegger Cove clays. Can. Geotech. J. 2014, 51, 599–609. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.; Zhou, Y.; Bian, X. Field Rebound and Recompression Curve of Soft Clay. Geotech. Test. J. 2021, 44, 67–86. [Google Scholar] [CrossRef]
- Mindlin, R.D. Force at a point in the interior of a semi-infinite solid. Australas. Inst. Min. Metall. Publ. Ser. 1936, 7, 195–202. [Google Scholar] [CrossRef]
- Xu, L. Study on the Longitudinal Settlement of Shield Tunnel in Soft Soil. Ph.D. Thesis, Tongji University, Shanghai, China, 2005. [Google Scholar]
- Tong, X.; Yuan, J.; Jiang, Y.-X.; Liu, X.-W.; Li, Y. Calculation of layered unloading additional stress of foundation pit based on Mindlin solution and the analysis of multiple factors influencing the rebound deformation. Rock Soil Mech. 2020, 41, 2432–2440. [Google Scholar] [CrossRef]
- Liu, G.-B.; Huang, Y.-X.; Hou, X.-Y. A practical method for calculating a heave of excavated foundation. China Civ. Eng. J. 2000, 33, 61–67. [Google Scholar] [CrossRef]
- Yu, J.-L.; Gong, X.-N. Research on deformation of foundation-pit engineering. China Civ. Eng. J. 2002, 35, 86–90. [Google Scholar] [CrossRef]
- Richard, J.; Finno, M.J.; Tanner Blackburn, A.M.; Roboski, J.F. Three-dimensional effects for supported excavations in clay. J. Geotech. Geoenviron. Eng. 2007, 133, 30–36. [Google Scholar] [CrossRef]
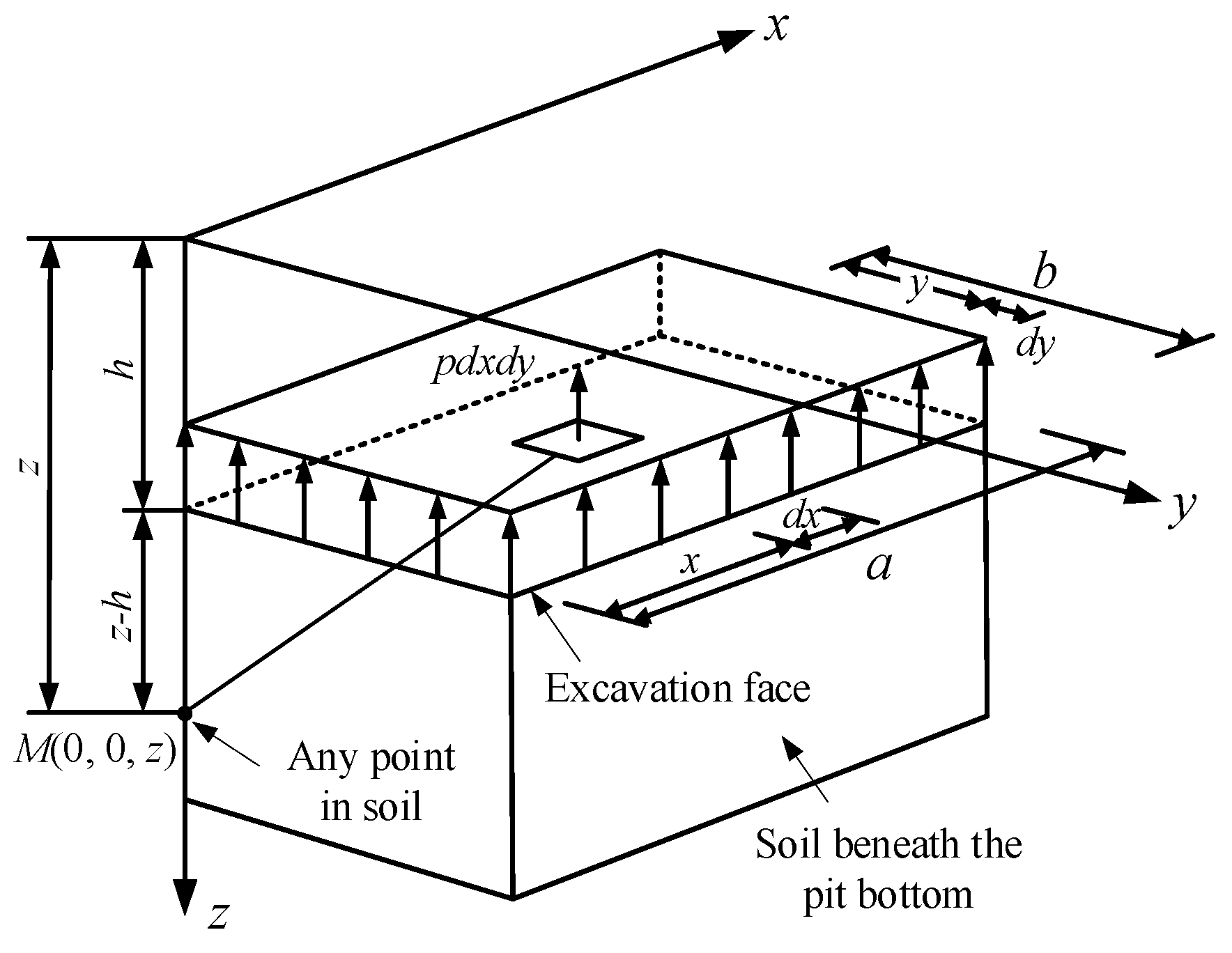

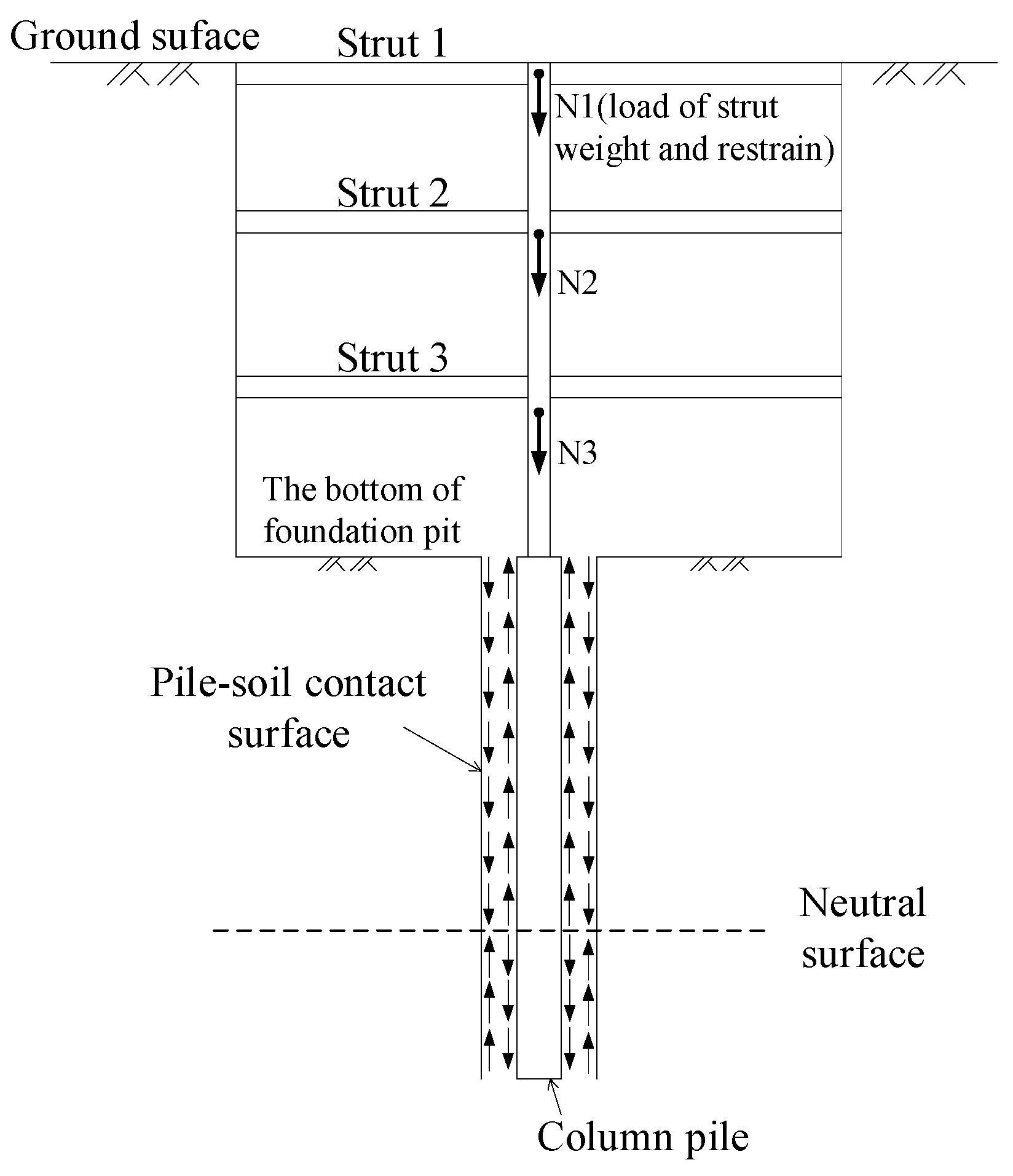
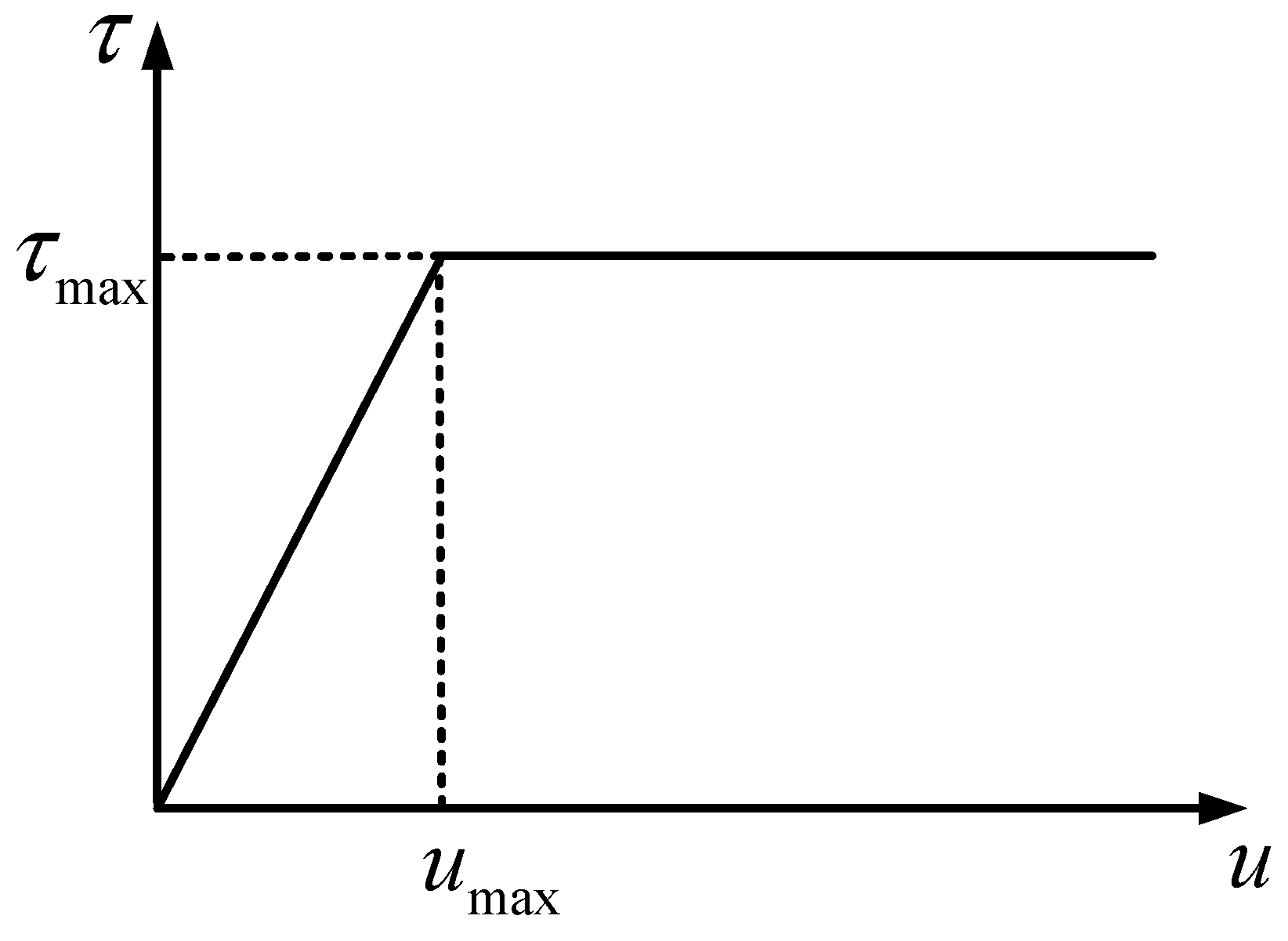
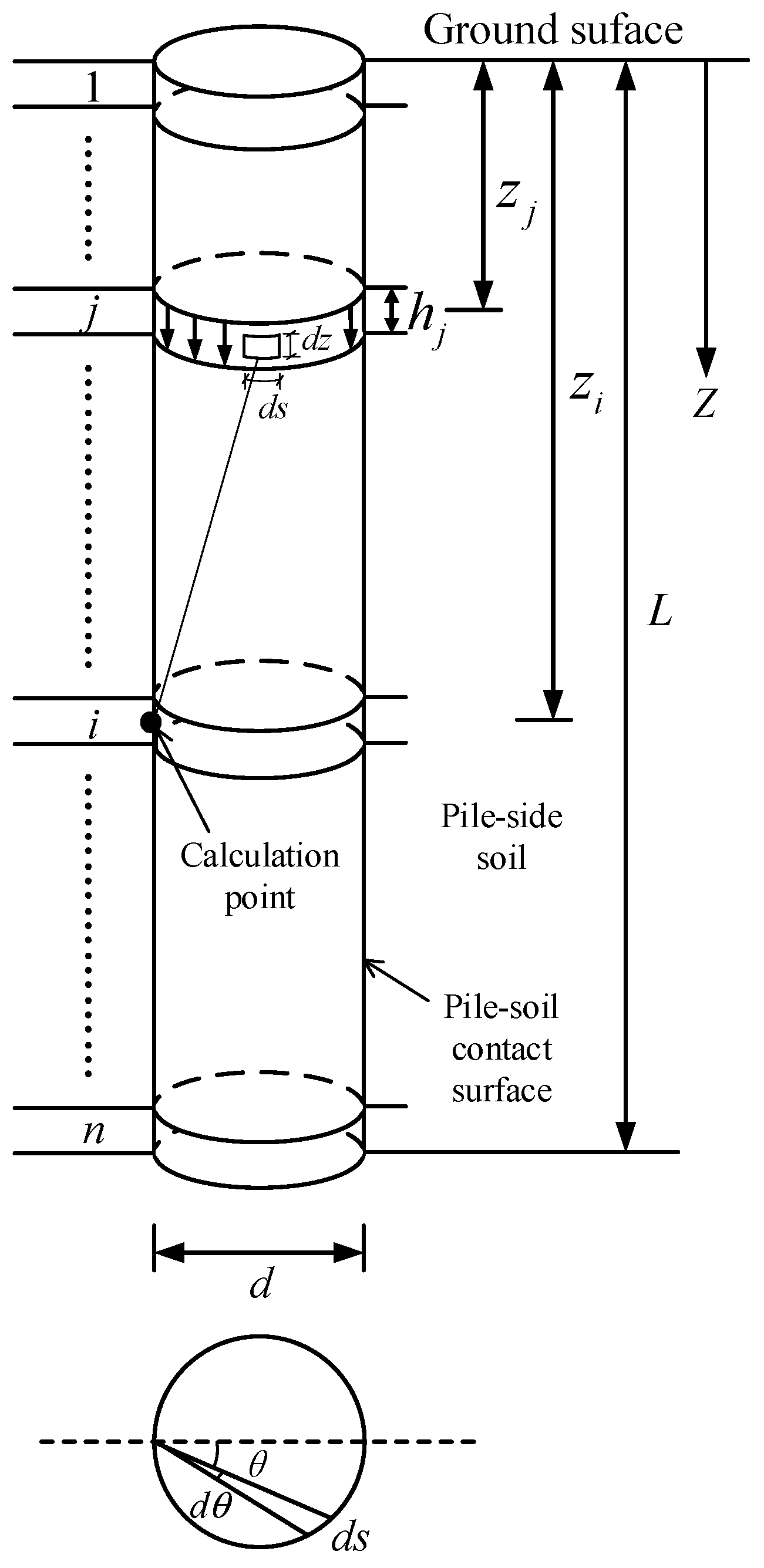


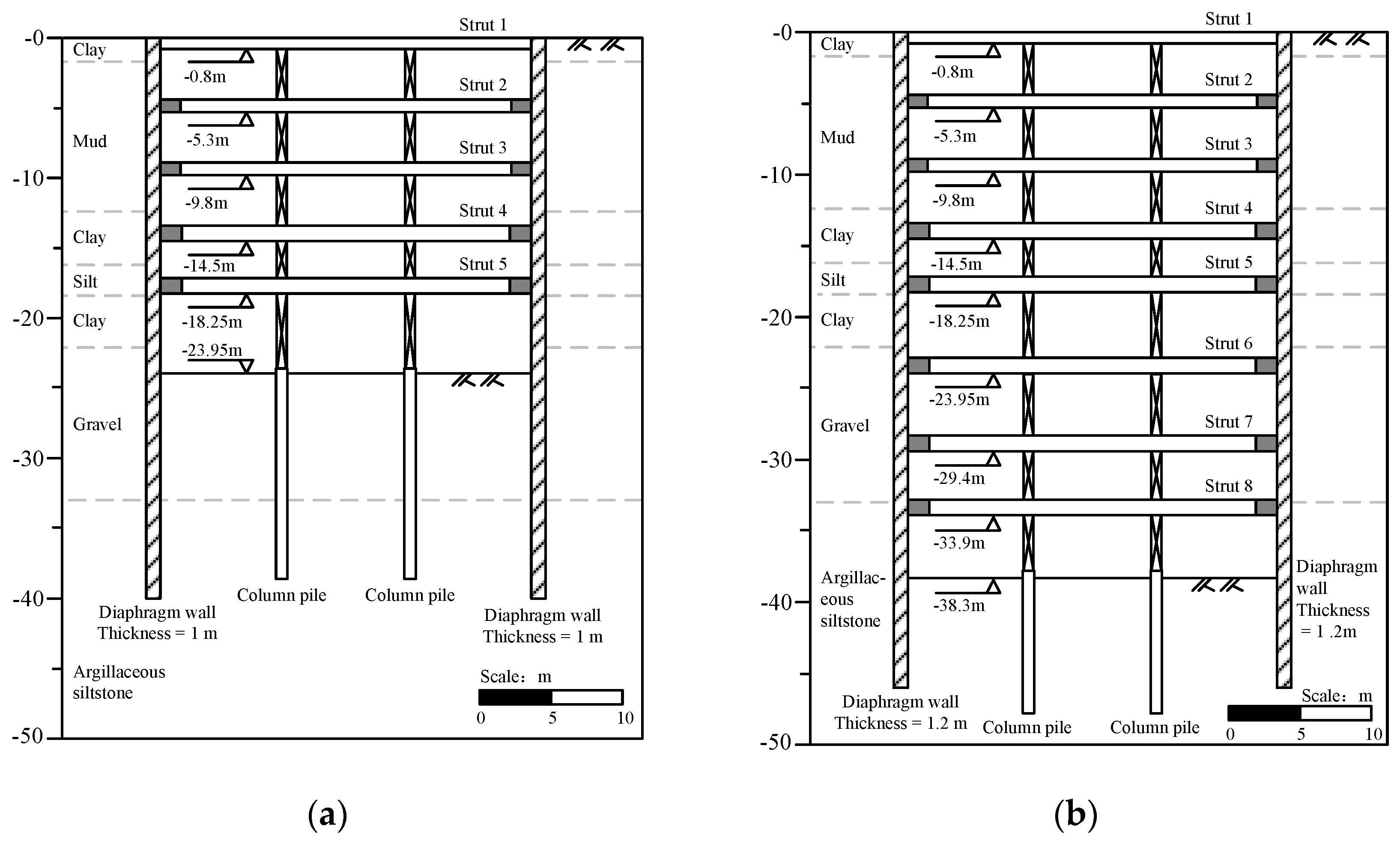

| Soil Layers | Bottom Elevation/m | Water Content/% | Total Bulk Weight of Soil/kN·m−3 | Unloading Modulus/MPa | Ultimate Frictional Resistance of the Soil/kPa |
|---|---|---|---|---|---|
| ① Silty clay | 1.9 | 32.9 | 18.5 | 16.1 | 20 * |
| ② Mud | 12.6 | 53.5 | 16.5 | 15.0 | 18 * |
| ③ Clay | 13.8 | 37.7 | 17.8 | 15.1 | 20 * |
| ④1 Silty clay | 15.1 | 25.7 | 19.5 | 23.5 | 30 * |
| ④2 Sandy silty clay | 16.3 | 23.3 | 19.6 | 22.0 | 35 * |
| ④3 Silt | 18.6 | 22.1 | 19.8 | 44.9 | 45 * |
| ⑤1 Clay | 20.0 | 29.0 | 19.0 | 23.2 | 40 * |
| ⑤2 Silty clay | 23.8 | 25.9 | 19.5 | 22.1 | 45 * |
| ⑥ Gravel | 32.6 | 24.0 * | 75 * | 75 * | |
| ⑩1 Fully weathered argillaceous siltstone | 34.6 | 20.0 * | 70 * | 70 * | |
| ⑩2 Strong-weathered argillaceous siltstone | 35.8 | 22.0 * | 80 * | 80 * | |
| ⑩3 Middle-weathered argillaceous siltstone | 25.0 * | 200 * | 85 * |
| Soil Layers | ||||
|---|---|---|---|---|
| ② Mud | 1.674 | 1.643 | 0.043 | 0.054 |
| ③ Clay | 1.105 | 1.083 | 0.021 | 0.027 |
| ④1 Silty clay | 0.973 | 0.960 | 0.011 | 0.019 |
| ⑤1 Clay | 0.785 | 0.767 | 0.012 | 0.031 |
| ⑤2 Silty clay | 0.644 | 0.627 | 0.012 | 0.034 |
| Layer Number of Struts | Strut Size (Width × Height)/mm | Weight Load/kN | Restraint Load/kN·mm−1 |
|---|---|---|---|
| Strut 1 | 800 × 900 | 100 | 10 |
| Strut 2 | 1100 × 900 | 150 | 15 |
| Strut 3 | 1100 × 900 | 150 | 15 |
| Strut 4 | 1200 × 1100 | 200 | 25 |
| Strut 5 | 1200 × 1100 | 200 | 25 |
| Strut 6 | 1200 × 1100 | 200 | 25 |
| Strut 7 | 1200 × 1100 | 200 | 25 |
| Strut 8 | 1200 × 1100 | 200 | 25 |
| Excavation Depth | Measuring Point Number | |||||||
|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | ||
| 5.3 m | Measured result | 1.62 | 1.13 | 1.52 | 0.91 | 0.60 | 0.47 | 0.73 |
| Considering support restraint | 0.52 | 0.68 | 0.77 | 0.73 | 0.75 | 0.44 | 0.44 | |
| Without considering support restraint | 0.53 | 0.70 | 0.79 | 0.75 | 0.77 | 0.44 | 0.45 | |
| 9.8 m | Measured result | 1.81 | 1.79 | 2.90 | 1.99 | 2.62 | 2.05 | 2.73 |
| Considering support restraint | 1.21 | 1.54 | 1.70 | 1.62 | 1.66 | 1.14 | 1.16 | |
| Without considering support restraint | 1.25 | 1.63 | 1.80 | 1.71 | 1.76 | 1.18 | 1.20 | |
| 14.5 m | Measured result | 3.18 | 3.12 | 4.42 | 4.83 | 4.24 | 4.90 | 4.97 |
| Considering support restraint | 2.59 | 3.03 | 3.25 | 3.12 | 3.20 | 2.50 | 2.52 | |
| Without considering support restraint | 2.74 | 3.37 | 3.62 | 3.47 | 3.56 | 2.65 | 2.67 | |
| 18.25 m | Measured result | 5.69 | 5.29 | 5.74 | 5.98 | 5.61 | 5.53 | 5.45 |
| Considering support restraint | 5.08 | 5.58 | 5.88 | 5.66 | 5.84 | 3.96 | 3.98 | |
| Without considering support restraint | 6.08 | 7.82 | 8.28 | 7.93 | 8.21 | 4.34 | 4.37 | |
| 23.95 m | Measured result | 6.71 | 6.67 | 7.29 | 7.51 | 7.65 | 6.97 | 6.80 |
| Considering support restraint | 5.60 | 5.91 | 6.18 | 5.95 | 6.15 | 7.04 | 7.10 | |
| Without considering support restraint | 6.92 | 8.75 | 9.17 | 8.78 | 9.14 | 8.41 | 8.48 | |
| 29.4 m | Measured result | 7.22 | 7.12 | |||||
| Considering support restraint | 7.74 | 7.84 | ||||||
| Without considering support restraint | 9.56 | 9.69 | ||||||
| 33.9 m | Measured result | 8.50 | 8.53 | |||||
| Considering support restraint | 8.73 | 8.85 | ||||||
| Without considering support restraint | 11.19 | 11.35 | ||||||
| 38.3 m | Measured result | 8.94 | 9.03 | |||||
| Considering support restraint | 8.84 | 8.97 | ||||||
| Without considering support restraint | 12.00 | 12.19 | ||||||
| Le/He | 0.5, 0.7, 0.8, 0.9, 1, 1.1, 1.2, 1.3, 1.4, 1.5 |
| B/He | 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5 |
| umax | 2, 4, 6, 8, 10 |
| Position of pile | Center, edge, corner |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Chen, Y.; Li, Z. Calculation of Column Pile Heave in Deep Excavation Based on the Rebound–Recompression Method. Buildings 2024, 14, 1477. https://doi.org/10.3390/buildings14051477
Yang K, Chen Y, Li Z. Calculation of Column Pile Heave in Deep Excavation Based on the Rebound–Recompression Method. Buildings. 2024; 14(5):1477. https://doi.org/10.3390/buildings14051477
Chicago/Turabian StyleYang, Kaiwen, Yun Chen, and Zhuofeng Li. 2024. "Calculation of Column Pile Heave in Deep Excavation Based on the Rebound–Recompression Method" Buildings 14, no. 5: 1477. https://doi.org/10.3390/buildings14051477
APA StyleYang, K., Chen, Y., & Li, Z. (2024). Calculation of Column Pile Heave in Deep Excavation Based on the Rebound–Recompression Method. Buildings, 14(5), 1477. https://doi.org/10.3390/buildings14051477







