U-Values for Building Envelopes of Different Materials: A Review
Abstract
1. Introduction
1.1. Theoretical U-Values of Building Envelopes
1.2. Measured U-Values of Building Envelopes
2. Theoretical and Measured U-Values of Inorganic and Bio-Based Envelopes
2.1. Concrete Envelopes
2.2. Brick Envelopes
| Year | Envelope Type | Measurement Type | Measurement Method | Theoretical U-Value (W/m2·K) | Measured U-Value (W/m2·K) | Reference |
|---|---|---|---|---|---|---|
| 2003 | A clay brick envelope | Laboratory measurement | CHB | 0.302 | 0.304 | [63] |
| 2010 | Brick envelopes | In situ measurement | QIRT | 0.225 | 0.285 | [60] |
| 2011 | 2 types of limestone brick envelopes | Laboratory measurement | The Hot Disk technique | NA | 3.03 | [64] |
| 5.26 | ||||||
| 2011 | 3 perforated brick envelopes | In situ measurement | QIRT | 1.39 | 1.51 | [65] |
| 1.31 | ||||||
| 1.63 | ||||||
| 2012 | A ceramic brick | In situ measurement | HFM | NA | 0.97–2.56 | [66] |
| 2014 | 3 types of lightweight clay bricks | NA | NA | 0.62 | NA | [67] |
| 0.54 | ||||||
| 0.55 | ||||||
| 2015 | 3 types of brick envelopes | In situ measurement | QIRT | 0.30 | 0.37 (in winter) | [68] |
| 0.57 | 0.62 (in winter) | |||||
| 0.44 | 0.51 (in winter) | |||||
| 2015 | A fired-clay brick envelope | In situ measurement | HFM | NA | 1.32 | [69] |
| 2015 | 2 types of hollow brick envelopes | Laboratory measurement | CHB | NA | 1.24 | [70] |
| 1.20 | ||||||
| 2015 | 5 types of hollow bricks | Laboratory measurement | HBT | NA | 0.25 | [71] |
| 0.17 | ||||||
| 0.15 | ||||||
| 0.15 | ||||||
| 0.16 | ||||||
| 2015 | A solid brick envelope | In situ measurement | HFM | NA | 0.428–1.933 (in summer) | [72] |
| 2015 | A tuff brick envelope; 2 types of hollow brick envelopes | In situ measurement | HFM | 1.897 | 0.750 | [62] |
| 0.734 | 1.072 | |||||
| 0.945 | 0.810 | |||||
| 2016 | 3 types of hollow brick envelopes | In situ measurement | HFM | 0.72 | 0.75 (in winter) | [73] |
| 2.35 | 2.40 (in winter) | |||||
| 0.49 | 0.59 (in spring) | |||||
| 2016 | 3 types of solid brick envelopes | In situ measurement | HFM | 0.683 | 0.926 | [74] |
| 0.947 | 0.687 | |||||
| 0.678 | 0.797 | |||||
| 2016 | A brick envelope | Laboratory measurement | HBT | 0.56 | 0.62 | [17] |
| 2017 | 2 types of historic red brick envelopes | In situ measurement | HFM | 1.05 | 1.23 | [75] |
| 0.24 | 0.21 | |||||
| 2017 | Solid brick envelopes | In situ measurement | HFM | 1.00–1.25 | 0.80–0.85 | [76] |
| 2018 | 8 types of hollow brick envelopes | In situ measurement | THM | 1.18 | 1.03 | [27] |
| 0.57 | 0.59 | |||||
| 1.50 | 1.39 | |||||
| 0.56 | 0.45 | |||||
| 1.10 | 0.98 | |||||
| 0.76 | 0.38 | |||||
| 0.45 | 0.48 | |||||
| 0.48 | 0.88 | |||||
| 2018 | A solid brick envelope with gypsum plaster | In situ measurement | QIRT | 2.09 | 1.57 | [61] |
| 2018 | Solid brick envelopes | In situ measurement | HFM | NA | 1.740 (in spring) | [77] |
| 1.27 (in spring) | ||||||
| 1.98 (in spring) | ||||||
| 1.815 (in spring) | ||||||
| 2018 | 2 types of ceramic brick envelopes | In situ measurement | HFM | 0.151; | 0.161 (in winter) | [52] |
| 0.159 | 0.320 (in winter) | |||||
| 2019 | 2 types of hollow brick envelopes; a perforated brick envelope | In situ measurement | QIRT | 0.657 | 0.654 | [53] |
| 0.362 | 0.404 | |||||
| 0.586 | 0.559 | |||||
| 2020 | A silica brick envelope | In situ measurement | HFM; | 0.244 | 0.221 (in winter) | [54] |
| QIRT | 0.229 (in winter) | |||||
| 2024 | A pumice block envelope, two clay block envelopes | Laboratory measurement | HBT | NA | 0.887–1.65 | [59] |
| 1.16–2.07 | ||||||
| 0.718–0.83 |
2.3. Timber Envelopes
| Year | Envelope Type | Measurement Type | Measurement Method | Theoretical U-Value (W/m2·K) | Measured U-Value (W/m2·K) | Reference |
|---|---|---|---|---|---|---|
| 2010 | A light timber external envelope; a CLT envelope | In situ measurement | QIRT | 0.29 | 0.38 | [60] |
| 0.148 | 0.194 | |||||
| 2014 | 2 types of vapour open timber frame envelopes | In situ measurement | HFM | NA | 0.17–0.46 (in summer) | [86] |
| 2014 | Block and wood envelopes | In situ measurement | THM | 1.1 | 0.67–0.98 (before retrofit) | [87] |
| 0.26 (after retrofit) | ||||||
| 2015 | 2 types of light timber envelopes | In situ measurement | QIRT | 0.17 | 0.14 (in winter) | [68] |
| 0.18 | 0.16 (in winter) | |||||
| 2015 | Timber frame envelopes with wood-hemp insulation | In situ measurement | HFM | NA | 0.20–0.31 (in winter) | [83] |
| 2016 | 2 types of OSB envelopes | In situ measurement | HFM | 0.10 | 0.11 (in winter) | [85] |
| 0.23 | 0.38 (in winter) | |||||
| 2018 | A timber frame envelope with wheat chaff insulation | Laboratory measurement | HBT | NA | 0.307 | [84] |
| 2018 | A wood panel envelope; a modular plywood panel envelope | In situ measurement | HFM | 0.150 | 0.174 (in winter) | [52] |
| 0.154 | 0.201 (in winter) | |||||
| 2020 | CLT envelopes | Laboratory measurement | HBT | 0.16 | 0.148 | [81] |
| 0.15 | 0.199 | |||||
| 2020 | Timber envelopes | In situ measurement | HFM | 0.50 | 0.60–0.65 | [88] |
| 2021 | A four-layered spruce wood envelope | Laboratory measurement | HBT | NA | 0.375 | [89] |
| 2021 | 3 types of wood-framed envelopes with different structures | In situ measurement | QIRT | 0.23 | 0.09–0.25 | [90] |
| 0.16 | 0.04–0.21 | |||||
| 0.16 | 0.20–0.26 | |||||
| 2022 | 4 types of wood-framed envelopes with different structures | In situ measurement | QIRT | NA | 0.43 | [32] |
| 0.31 | ||||||
| 0.26 | ||||||
| 0.24 |
2.4. Straw Bale Envelopes
3. Environmental Factors Influencing U-Values
| Factors | Year | Building Material | Influence | Reference |
|---|---|---|---|---|
| Temperature | 2016 | Hemp concrete, flax concrete and rape straw concrete | The thermal conductivity increases by approximately 10% for hemp and flax and 18% for rape straw from 10 to 40 °C. | [107] |
| 2019 | AIC with different aerogel volume admixtures | The thermal conductivity increases by 15.5% from 20 to 90 °C. | [102] | |
| 2022 | Common insulation materials | The thermal conductivity increases by 12.6% from 20 to 60 °C. | [105] | |
| 2022 | CLT panels; woodchip insulation panels; wood–fibre insulation panels | The thermal conductivity increases by 10.2% for CLT, 26% for woodchips and 21% for wood–fibre from 10 to 50 °C. | [103] | |
| Relative humidity | 2012 | Mineral wools | The thermal conductivity increases from 0.10–0.14 W/m K to 0.7–0.9 W/m K (from low moisture contents of 5–20% to saturation). | [104] |
| 2014 | Stone wool panels; hemp panels | U-values of both stone wool panels and hemp panels increase in 56–90% RH. | [86] | |
| 2016 | Hemp concrete, flax concrete and rape straw concrete | The thermal conductivity is proportional to the water content. | [107] | |
| 2016 | Solid brick envelopes | The transient U-values achieve higher values within the moist stage. | [108] | |
| 2017 | Insulating building materials made from DPF mesh | Thermal conductivity increases with water content. | [105] | |
| 2019 | AIC with aerogel volume admixtures | The thermal conductivity increases by 76.33% from 0% to 100% RH. | [102] | |
| 2022 | Common insulation materials | The thermal conductivity increases by 171.9% from 0% to 100% RH. | [105] | |
| 2022 | CLT panels; woodchip insulation panels; wood–fibre insulation panels | The thermal conductivity increases by 12% for CLT, 18% for woodchips and 8% for wood–fibre from low to high moisture content. | [103] | |
| Solar radiation | 2014 | Hollow-reinforced precast concrete envelopes | The U-value of the north envelope was 37.3% lower than that of the east envelope, because the north envelope was exposed to solar radiation for a shorter time than the east envelope. | [45] |
| 2020 | RC envelopes | The obtained U-value can be heightened by solar radiation. | [23] |
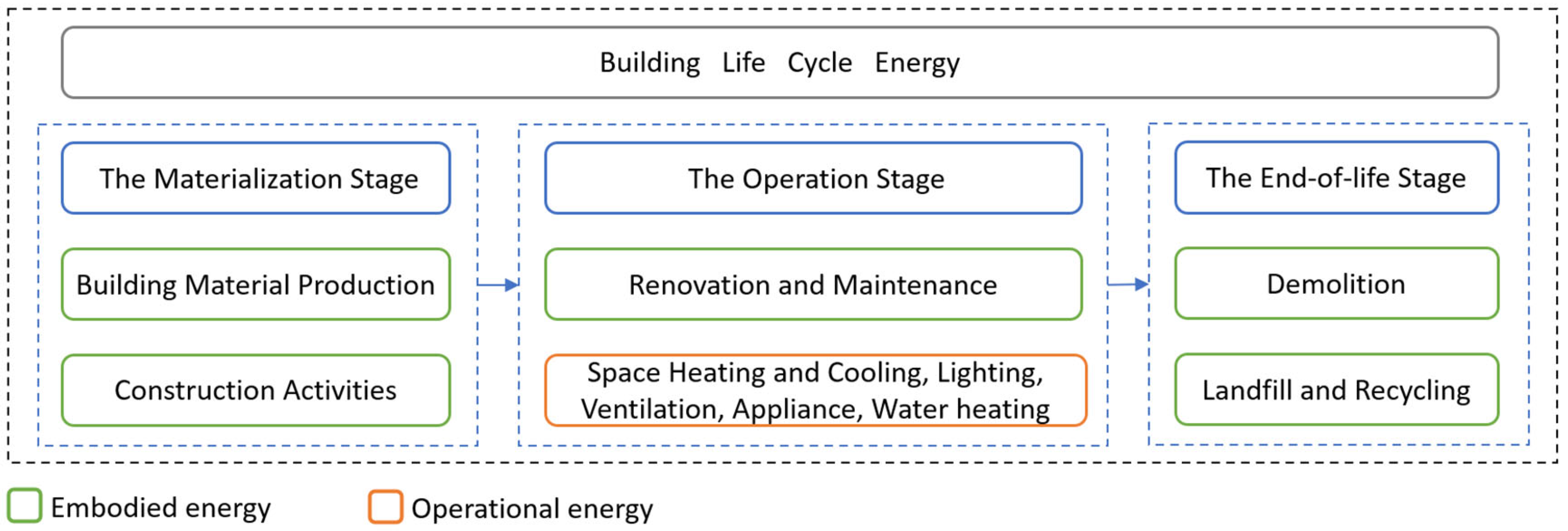
4. Impacts of U-Values on Building Energy Consumption
| Year | Building Use | Envelope Type | Influence on Energy Consumption | Reference |
|---|---|---|---|---|
| 2006 | All use | The breathing envelope | This envelope achieves ultra-low U-values. It is responsible for a 10% reduction in space heating and cooling energy. | [111] |
| 2011 | All use | Concrete-backed stone masonry envelope | When U-values of external envelopes are 3.03 W/(m2·K) and 5.26 W/(m2·K), the corresponding estimated annual energy consumption are 40.26 kWh/m2 and 69.93 kWh/m2 in North Africa. | [64] |
| 2012 | All use | Timber envelopes | There is a linear relationship between the average U-value of the envelope and the cooling and heating energy consumption. | [112] |
| 2015 | Office | RC envelopes | The energy use decreased due to the reduction in the U-values of windows. The energy use increased due to the reduction in the U-value of the non-transparent envelopes in high-rise buildings. | [110] |
| 2015 | Residential | RC envelopes | In cold areas, the yearly heating energy use of buildings modelled with the 3D dynamic method is 8–13% higher than that modelled with the average method. In warm areas, the yearly cooling energy use is underestimated by 17% with the average method. | [113] |
| 2016 | Residential | RC envelopes | The equivalent U-value method underestimates heating energy use by up to 15%. | [114] |
| 2016 | Residential | Straw bale envelopes | Straw bale envelopes have a lower U-value than traditional building materials and are more energy efficient in Estonia. | [96] |
| 2016 | Residential | NA | The variability of U-values can underestimate the energy performance of approximately 90% of residences. | [115] |
| 2017 | Residential | Concrete block envelopes | The average U-value method underestimates yearly heating energy consumption by 13%. | [116] |
| 2018 | All use | RC, brick, CLT, and timber-frame envelopes | The U-values of building components impact the energy performance of building components significantly. | [117] |
| 2018 | Office | NA | In the hot–arid climate zone, U-values of the envelopes do not impact energy performance significantly. | [118] |
| 2018 | Residential | NA | Low U-values can increase building energy demand in temperate regions. | [119] |
| 2019 | All use | NA | In cold areas, building energy consumption decreased due to the reduction in U-values. In warmer climates, low U-values building increased energy consumption. | [109] |
| 2021 | All use | Straw bale envelopes | The theoretical U-value of the straw bale envelope is 0.13 W/(m2·K). The heat load loss is from 18% to 25%, while heat load gain is from 3% to 10% in the whole building. | [91] |
| 2022 | Residential | Straw bale envelopes | The U-value of straw bale envelope is 0.1 W/(m2·K), the U-value of the conventional envelope is 2.6 W/(m2·K). Straw bale reduced energy consumption in all climates except for the warm–humid one in Iran. | [40] |
| 2022 | Residential | Brick and concrete envelopes | Due to the variation in U-value, the yearly total heating load increased by 26%, and the yearly total cooling load increased by 13% in Beijing. | [120] |
| 2022 | All use | Brick and concrete envelopes | In the Mediterranean climate, the change in U-value each month is significant, providing deviances as much as 9.2% in quarterly energy consumption. | [12] |
5. Comparison of Theoretical and Measured U-Values
6. Conclusions
- (1)
- The relationship between environmental factors and U-values needs to be studied in detail. Some studies have focused on the relationship between the environmental factors and thermal conductivities of building materials. However, there is limited research examining the quantitative relationship between important factors (such as temperature, relative humidity and solar radiation) and the U-values of various envelopes.
- (2)
- The gaps between theoretical and measured U-values are significant, especially for concrete and brick envelopes. The theoretical U-values of concrete envelopes range from 0.12 to 1.61 W/m2K. Meanwhile, the measured U-values of concrete envelopes range from 0.14 to 5.45 W/m2K. The theoretical U-values of brick envelopes range from 0.22 to 2.09 W/m2K. Meanwhile, the measured U-values of brick envelopes range from 0.15 to 5.26 W/m2K.
- (3)
- The accuracy of both theoretical and the measured U-values needs to be verified. In building energy simulation, it is also necessary to verify which type of U-value to input can make the simulation results more accurate.
Funding
Conflicts of Interest
Abbreviations
| Nomenclature | |
| Φ | Heat tranfer |
| A | Area |
| λ | |
| HBT | Hot Box Test |
| GHB | Guarded hot box |
| CHB | Calibrated hot box |
| HFM | Heat flow meter |
| SHB-HFM | Simple hot box-heat flow meter |
| THM | Thermometric |
| QIRT | Quantitative infrared thermography |
| h | Heat transfer coefficient |
| LCA | Life cycle assessment |
| RC | Reinforced concrete |
| CLT | Cross-laminated timber |
| OSB | Oriented strand board |
| AIC | Aerogel-incorporated concrete |
| Subscripts | |
| sum | Sum of all layers within the envelope |
| se | External surface of the envelope |
| si | Internal surface of the envelope |
| ij | Indoor environment at time j |
| ej | Outdoor environment at time j |
| n | The number of recorded samples during the measurement period |
| sij | Internal surface of the envelope at time j |
| i | Internal surface of the envelope |
References
- Lee, J.; Kim, J.; Song, D.; Kim, J.; Jang, C. Impact of external insulation and internal thermal density upon energy consumption of buildings in a temperate climate with four distinct seasons. Renew. Sustain. Energy Rev. 2017, 75, 1081–1088. [Google Scholar] [CrossRef]
- Almasri, R.A.; Alshitawi, M.S. Electricity consumption indicators and energy efficiency in residential buildings in GCC countries: Extensive review. Energy Build. 2022, 255, 111664. [Google Scholar] [CrossRef]
- Zhu, S.; Causone, F.; Gao, N.; Ye, Y.; Jin, X.; Zhou, X.; Shi, X. Numerical simulation to assess the impact of urban green infrastructure on building energy use: A review. Build. Environ. 2023, 228, 109832. [Google Scholar] [CrossRef]
- Nematchoua, M.K.; Sendrahasina, R.M.; Malmedy, C.; Orosa, J.A.; Simo, E.; Reiter, S. Analysis of environmental impacts and costs of a residential building over its entire life cycle to achieve nearly zero energy and low emission objectives. J. Clean. Prod. 2022, 373, 133834. [Google Scholar] [CrossRef]
- Wang, P.; Yang, Y.; Ji, C.; Huang, L. Positivity and difference of influence of built environment around urban park on building energy consumption. Sustain. Cities Soc. 2023, 89, 104321. [Google Scholar] [CrossRef]
- Ni, S.; Zhu, N.; Hou, Y.; Zhang, Z. Research on indoor thermal comfort and energy consumption of zero energy wooden structure buildings in severe cold zone. J. Build. Eng. 2023, 67, 105965. [Google Scholar] [CrossRef]
- Dougherty, T.R.; Jain, R.K. Invisible walls: Exploration of microclimate effects on building energy consumption in New York City. Sustain. Cities Soc. 2023, 90, 104364. [Google Scholar] [CrossRef]
- Moradi, A.; Kavgic, M.; Costanzo, V.; Evola, G. Impact of typical and actual weather years on the energy simulation of buildings with different construction features and under different climates. Energy 2023, 270, 126875. [Google Scholar] [CrossRef]
- Catto Lucchino, E.; Gennaro, G.; Favoino, F.; Goia, F. Modelling and validation of a single-storey flexible double-skin façade system with a building energy simulation tool. Build. Environ. 2022, 226, 109704. [Google Scholar] [CrossRef]
- Guarino, F.; Tumminia, G.; Longo, S.; Cellura, M.; Cusenza, M.A. An integrated building energy simulation early—Design tool for future heating and cooling demand assessment. Energy Rep. 2022, 8, 10881–10894. [Google Scholar] [CrossRef]
- Klemp, S.; Abida, A.; Richter, P. A method and analysis of predicting building material U-value ranges through geometrical pattern clustering. J. Build. Eng. 2021, 44, 103243. [Google Scholar] [CrossRef]
- Bruno, R.; Bevilacqua, P. Heat and mass transfer for the U-value assessment of opaque walls in the Mediterranean climate: Energy implications. Energy 2022, 261, 124894. [Google Scholar] [CrossRef]
- ISO 6946:2007; Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Method. International Standard ISO: Geneva, Switzerland, 2007.
- ASTM C1363-05; Standard Test Method for Thermal Performance of Building Materials and Envelope Assemblies by Means of a Hot Box Apparatus. American Society for Testing and Materials: West Conshohocken, PA, USA, 2005.
- EN ISO 8990; Thermal Insulation—Determination of Steady-State Thermal Transmission Properties—Calibrated and Guarded Hot Box. European Standard: Lausanne, Switzerland, 1996.
- Yang, L.; Yang, J.; Liu, Y.; An, Y.; Chen, J. Hot box method to investigate U-values for straw bale walls with various structures. Energy Build. 2021, 234, 110706. [Google Scholar] [CrossRef]
- Nardi, I.; Paoletti, D.; Ambrosini, D.; de Rubeis, T.; Sfarra, S. U-value assessment by infrared thermography: A comparison of different calculation methods in a Guarded Hot Box. Energy Build. 2016, 122, 211–221. [Google Scholar] [CrossRef]
- Asdrubali, F.; Baldinelli, G. Thermal transmittance measurements with the hot box method: Calibration, experimental procedures, and uncertainty analyses of three different approaches. Energy Build. 2011, 43, 1618–1626. [Google Scholar] [CrossRef]
- Chen, F.; Wittkopf, S.K. Summer condition thermal transmittance measurement of fenestration systems using calorimetric hot box. Energy Build. 2012, 53, 47–56. [Google Scholar] [CrossRef]
- ISO 9869-1; Thermal Insulation, Building Elements, In-Situ Measurement of Thermal Resistance and Thermal Transmittance—Part 1: Heat Flow Meter Method. International Standard ISO: Geneva, Switzerland, 2014.
- ASTM C1155-95; Standard, Standard Practice for Determining Thermal Resistance of Building Envelope Components from the In-situ Data. American Society for Testing and Materials: West Conshohocken, PA, USA, 2007.
- Gumbarević, S.; Milovanović, B.; Bašić, B.D.; Gaši, M. Combining Deep Learning and the Heat Flux Method for In-Situ Thermal-Transmittance Measurement Improvement. Energies 2022, 15, 5029. [Google Scholar] [CrossRef]
- Evangelisti, L.; Guattari, C.; Vollaro, R.D.L.; Asdrubali, F. A methodological approach for heat-flow meter data post-processing under different climatic conditions and wall orientations. Energy Build. 2020, 223, 110216. [Google Scholar] [CrossRef]
- Gaspar, K.; Casals, M.; Gangolells, M. In situ measurement of façades with a low U-value: Avoiding deviations. Energy Build. 2018, 170, 61–73. [Google Scholar] [CrossRef]
- Ficco, G.; Guattari, C.; Vollaro, R.D.L.; Asdrubali, F. U-value in situ measurement for energy diagnosis of existing buildings. Energy Build. 2015, 104, 108–121. [Google Scholar] [CrossRef]
- Meng, X.; Gao, Y.; Wang, Y.; Yan, B.; Zhang, W.; Long, E. Feasibility experiment on the simple hot box-heat flow meter method and the optimization based on simulation reproduction. Appl. Therm. Eng. 2015, 83, 48–56. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Rodríguez-Álvaro, R.; Moyano, J.J.; Rico, F.; Marín, D. Determining the U-Value of Façades Using the Thermometric Method: Potentials and Limitations. Energies 2018, 11, 360. [Google Scholar] [CrossRef]
- ISO 9869-2; Thermal Insulation—Building Elements—In-Situ Measurement of Thermal Resistance and Thermal Transmittance—Part 2: Infrared Method for Frame Structure Dwelling. International Standard ISO: Geneva, Switzerland, 2018.
- ASTM C1060; Standard Practice for Thermographic Inspection of Insulation Installations in Envelope Cavities of Frame Buildings. American Society for Testing and Materials: West Conshohocken, PA, USA, 2011.
- Teni, M.; Krstić, H.; Kosiński, P. Review and comparison of current experimental approaches for in-situ measurements of building walls thermal transmittance. Energy Build. 2019, 203, 109417. [Google Scholar] [CrossRef]
- Tardy, F. A review of the use of infrared thermography in building envelope thermal property characterization studies. J. Build. Eng. 2023, 75, 106918. [Google Scholar] [CrossRef]
- Mahmoodzadeh, M.; Gretka, V.; Lee, I.; Mukhopadhyaya, P. Infrared thermography for quantitative thermal performance assessment of wood-framed building envelopes in Canada. Energy Build. 2022, 258, 111807. [Google Scholar] [CrossRef]
- O’Hegarty, R.; Kinnane, O.; Lennon, D.; Colclough, S. In-situ U-value monitoring of highly insulated building envelopes: Review and experimental investigation. Energy Build. 2021, 252, 111447. [Google Scholar] [CrossRef]
- Papadakos, G.; Marinakis, V.; Konstas, C.; Doukas, H.; Papadopoulos, A. Managing the uncertainty of the U-value measurement using an auxiliary set along with a thermal camera. Energy Build. 2021, 242, 110984. [Google Scholar] [CrossRef]
- Krstić, H.; Miličević, I.; Markulak, D.; Domazetović, M. Thermal Performance Assessment of a Wall Made of Lightweight Concrete Blocks with Recycled Brick and Ground Polystyrene. Buildings 2021, 11, 584. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Wang, Z.; Shao, S.; Deng, G.; Xue, H.; Xu, Z.; Yang, Y. Integrated building envelope performance evaluation method towards nearly zero energy buildings based on operation data. Energy Build. 2022, 268, 112219. [Google Scholar] [CrossRef]
- Guo, Y.-Y. Revisiting the building energy consumption in China: Insights from a large-scale national survey. Energy Sustain. Dev. 2022, 68, 76–93. [Google Scholar] [CrossRef]
- Ninikas, K.; Tallaros, P.; Mitani, A.; Koutsianitis, D.; Ntalos, G.; Taghiyari, H.R.; Papadopoulos, A.N. Thermal Behavior of a Light Timber-Frame Wall vs. a Theoretical Simulation with Various Insulation Materials. J. Compos. Sci. 2022, 6, 22. [Google Scholar]
- Evola, G.; Costanzo, V.; Urso, A.; Tardo, C.; Margani, G. Energy performance of a prefabricated timber-based retrofit solution applied to a pilot building in Southern Europe. Build. Environ. 2022, 222, 109442. [Google Scholar] [CrossRef]
- Mehravar, M.; Veshkini, A.; Veiseh, S.; Fayaz, R. Physical properties of straw bale and its effect on building energy conservation and carbon emissions in different climatic regions of Iran. Energy Build. 2022, 254, 111559. [Google Scholar] [CrossRef]
- Zhou, Y.; Trabelsi, A.; El Mankibi, M. A review on the properties of straw insulation for buildings. Constr. Build. Mater. 2022, 330, 127215. [Google Scholar] [CrossRef]
- Andersen, J.H.; Rasmussen, N.L.; Ryberg, M.W. Comparative life cycle assessment of cross laminated timber building and concrete building with special focus on biogenic carbon. Energy Build. 2022, 254, 111604. [Google Scholar] [CrossRef]
- Hawkins, W.; Cooper, S.; Allen, S.; Roynon, J.; Ibell, T. Embodied carbon assessment using a dynamic climate model: Case-study comparison of a concrete, steel and timber building structure. Structures 2021, 33, 90–98. [Google Scholar] [CrossRef]
- Li, H.; Luo, Z.; Xu, X.; Cang, Y.; Yang, L. Assessing the embodied carbon reduction potential of straw bale rural houses by hybrid life cycle assessment: A four-case study. J. Clean. Prod. 2021, 303, 127002. [Google Scholar] [CrossRef]
- Ahmad, A.; Maslehuddin, M.; Al-Hadhrami, L.M. In situ measurement of thermal transmittance and thermal resistance of hollow reinforced precast concrete walls. Energy Build. 2014, 84, 132–141. [Google Scholar] [CrossRef]
- Nussbaumer, T.; Wakili, K.G.; Tanner, C. Experimental and numerical investigation of the thermal performance of a protected vacuum-insulation system applied to a concrete wall. Appl. Energy 2006, 83, 841–855. [Google Scholar] [CrossRef]
- Asdrubali, F.; D’alessandro, F.; Baldinelli, G.; Bianchi, F. Evaluating in situ thermal transmittance of green buildings masonries—A case study. Case Stud. Constr. Mater. 2014, 1, 53–59. [Google Scholar] [CrossRef]
- Mandilaras, I.; Atsonios, I.; Zannis, G.; Founti, M. Thermal performance of a building envelope incorporating ETICS with vacuum insulation panels and EPS. Energy Build. 2014, 85, 654–665. [Google Scholar] [CrossRef]
- Samardzioska, T.; Apostolska, R. Measurement of Heat-Flux of New Type Façade Walls. Sustainability 2016, 8, 1031. [Google Scholar] [CrossRef]
- Caruana, C.; Yousif, C.; Bacher, P.; Buhagiar, S.; Grima, C. Determination of thermal characteristics of standard and improved hollow concrete blocks using different measurement techniques. J. Build. Eng. 2017, 13, 336–346. [Google Scholar] [CrossRef]
- Choi, D.S.; Ko, M.J. Comparison of Various Analysis Methods Based on Heat Flowmeters and Infrared Thermography Measurements for the Evaluation of the In Situ Thermal Transmittance of Opaque Exterior Walls. Energies 2017, 10, 1019. [Google Scholar] [CrossRef]
- Ratnieks, J.; Jakovics, A.; Gendelis, S. Wall assemblies U-value calculation in test buildings using constant power heating. Energy Procedia 2018, 147, 207–213. [Google Scholar] [CrossRef]
- Tejedor, B.; Casals, M.; Macarulla, M.; Giretti, A. U-value time series analyses: Evaluating the feasibility of in-situ short-lasting IRT tests for heavy multi-leaf walls. Build. Environ. 2019, 159, 106123. [Google Scholar] [CrossRef]
- Tejedor, B.; Barreira, E.; de Freitas, V.P.; Kisilewicz, T.; Nowak-Dzieszko, K.; Berardi, U. Impact of Stationary and Dynamic Conditions on the U-Value Measurements of Heavy-Multi Leaf Walls by Quantitative IRT. Energies 2020, 13, 6611. [Google Scholar] [CrossRef]
- O’Hegarty, R.; Reilly, A.; West, R.; Kinnane, O. Thermal investigation of thin precast concrete sandwich panels. J. Build. Eng. 2020, 27, 100937. [Google Scholar] [CrossRef]
- Huang, B.; Lu, W. Experimental Investigation of the Multi-Physical Properties of an Energy Efficient Translucent Concrete Panel for a Building Envelope. Appl. Sci. 2020, 10, 6863. [Google Scholar] [CrossRef]
- Sun, J.; Xiao, J.; Li, Z.; Feng, X. Experimental study on the thermal performance of a 3D printed concrete prototype building. Energy Build. 2021, 241, 110965. [Google Scholar] [CrossRef]
- Lee, Y.-J.; Moon, J.-H.; Choi, D.-S.; Ko, M.-J. Application of the Heat Flow Meter Method and Extended Average Method to Improve the Accuracy of In Situ U-Value Estimations of Highly Insulated Building Walls. Sustainability 2024, 16, 5687. [Google Scholar] [CrossRef]
- Calis, M. Change of U-value with extreme temperatures on different types of block walls. J. Build. Eng. 2024, 85, 108653. [Google Scholar] [CrossRef]
- Albatici, R.; Tonelli, A.M. Infrared thermovision technique for the assessment of thermal transmittance value of opaque building elements on site. Energy Build. 2010, 42, 2177–2183. [Google Scholar] [CrossRef]
- Marshall, A.; Francou, J.; Fitton, R.; Swan, W.; Owen, J.; Benjaber, M. Variations in the U-Value Measurement of a Whole Dwelling Using Infrared Thermography under Controlled Conditions. Buildings 2018, 8, 46. [Google Scholar] [CrossRef]
- Evangelisti, L.; Guattari, C.; Gori, P.; Vollaro, R.D.L. In Situ Thermal Transmittance Measurements for Investigating Differences between Wall Models and Actual Building Performance. Sustainability 2015, 7, 10388–10398. [Google Scholar] [CrossRef]
- Ghazi Wakili, K.; Tanner, C. U-value of a dried wall made of perforated porous clay bricks: Hot box measurement versus numerical analysis. Energy Build. 2003, 35, 675–680. [Google Scholar] [CrossRef]
- Suleiman, B.M. Estimation of U-value of traditional North African houses. Appl. Therm. Eng. 2011, 31, 1923–1928. [Google Scholar] [CrossRef]
- Fokaides, P.A.; Kalogirou, S.A. Application of infrared thermography for the determination of the overall heat transfer coefficient (U-Value) in building envelopes. Appl. Energy 2011, 88, 4358–4365. [Google Scholar] [CrossRef]
- Naveros, I.; Jiménez, M.J.; Heras, M.R. Analysis of capabilities and limitations of the regression method based in averages, applied to the estimation of the U value of building component tested in Mediterranean weather. Energy Build. 2012, 55, 854–872. [Google Scholar] [CrossRef]
- Morales, M.P.; Juárez, M.; Muñoz, P.; Mendívil, M.; Ruiz, J. Possibilities for improving the equivalent thermal transmittance of single-leaf walls for buildings. Energy Build. 2014, 69, 473–480. [Google Scholar] [CrossRef]
- Albatici, R.; Tonelli, A.M.; Chiogna, M. A comprehensive experimental approach for the validation of quantitative infrared thermography in the evaluation of building thermal transmittance. Appl. Energy 2015, 141, 218–228. [Google Scholar] [CrossRef]
- Walker, R.; Pavía, S. Thermal performance of a selection of insulation materials suitable for historic buildings. Build. Environ. 2015, 94, 155–165. [Google Scholar] [CrossRef]
- Santos, P.; Martins, C.; Júlio, E. Enhancement of the thermal performance of perforated clay brick walls through the addition of industrial nano-crystalline aluminium sludge. Constr. Build. Mater. 2015, 101, 227–238. [Google Scholar] [CrossRef]
- Pavlík, Z.; Jerman, M.; Fořt, J.; Černý, R. Monitoring Thermal Performance of Hollow Bricks with Different Cavity Fillers in Difference Climate Conditions. Int. J. Thermophys. 2015, 36, 557–568. [Google Scholar] [CrossRef]
- Litti, G.; Khoshdel, S.; Audenaert, A.; Braet, J. Hygrothermal performance evaluation of traditional brick masonry in historic buildings. Energy Build. 2015, 105, 393–411. [Google Scholar] [CrossRef]
- Gaspar, K.; Casals, M.; Gangolells, M. A comparison of standardized calculation methods for in situ measurements of façades U-value. Energy Build. 2016, 130, 592–599. [Google Scholar] [CrossRef]
- Evangelisti, L.; Guattari, C.; Gori, P.; Vollaro, R.d.L.; Asdrubali, F. Experimental investigation of the influence of convective and radiative heat transfers on thermal transmittance measurements. Int. Commun. Heat Mass Transf. 2016, 78, 214–223. [Google Scholar] [CrossRef]
- Campbell, N.; McGrath, T.; Nanukuttan, S.; Brown, S. Monitoring the hygrothermal and ventilation performance of retrofitted clay brick solid wall houses with internal insulation: Two UK case studies. Case Stud. Constr. Mater. 2017, 7, 163–179. [Google Scholar] [CrossRef]
- Lucchi, E. Thermal transmittance of historical brick masonries: A comparison among standard data, analytical calculation procedures, and in situ heat flow meter measurements. Energy Build. 2017, 134, 171–184. [Google Scholar] [CrossRef]
- Rotilio, M.; Cucchiella, F.; De Berardinis, P.; Stornelli, V. Thermal Transmittance Measurements of the Historical Masonries: Some Case Studies. Energies 2018, 11, 2987. [Google Scholar] [CrossRef]
- Mouton, L.; Allacker, K.; Röck, M. Bio-based building material solutions for environmental benefits over conventional construction products—Life cycle assessment of regenerative design strategies (1/2). Energy Build. 2023, 282, 112767. [Google Scholar] [CrossRef]
- Mouton, L.; Cucchiella, F.; De Berardinis, P.; Stornelli, V. Low-tech passive solar design concepts and bio-based material solutions for reducing life cycle GHG emissions of buildings—Life cycle assessment of regenerative design strategies (2/2). Energy Build. 2023, 282, 112678. [Google Scholar] [CrossRef]
- Benzaama, M.-H.; Rajaoarisoa, L.; Boukhelf, F.; El Mendili, Y. Hygrothermal transfer modelling through a bio-based building material: Validation of a switching-linear model. J. Build. Eng. 2022, 55, 104691. [Google Scholar] [CrossRef]
- Švajlenka, J.; Kozlovská, M.; Vranay, F.; Pošiváková, T.; Jámborová, M. Comparison of Laboratory and Computational Models of Selected Thermal-Technical Properties of Constructions Systems Based on Wood. Energies 2020, 13, 3127. [Google Scholar] [CrossRef]
- Caniato, M.; Marzi, A.; Bettarello, F.; Gasparella, A. Designers’ expectations of buildings physics performances related to green timber buildings. Energy Build. 2022, 276, 112525. [Google Scholar] [CrossRef]
- Latif, E.; Ciupala, M.A.; Tucker, S.; Wijeyesekera, D.C.; Newport, D.J. Hygrothermal performance of wood-hemp insulation in timber frame wall panels with and without a vapour barrier. Build. Environ. 2015, 92, 122–134. [Google Scholar] [CrossRef]
- Pavelek, M.; Prajer, M.; Trgala, K. Static and dynamic thermal characterization of timber frame/wheat (Triticum Aestivum) chaff thermal insulation panel for sustainable building construction. Sustainability 2018, 10, 2363. [Google Scholar] [CrossRef]
- Bros-Williamson, J.; Garnier, C.; Currie, J.I. A longitudinal building fabric and energy performance analysis of two homes built to different energy principles. Energy Build. 2016, 130, 578–591. [Google Scholar] [CrossRef]
- Latif, E.; Ciupala, M.A.; Wijeyesekera, D.C. The comparative in situ hygrothermal performance of Hemp and Stone Wool insulations in vapour open timber frame wall panels. Constr. Build. Mater. 2014, 73, 205–213. [Google Scholar] [CrossRef]
- Johansson, P.; Hagentoft, C.-E.; Kalagasidis, A.S. Retrofitting of a listed brick and wood building using vacuum insulation panels on the exterior of the facade: Measurements and simulations. Energy Build. 2014, 73, 92–104. [Google Scholar] [CrossRef]
- Fedorczak-Cisak, M.; Radziszewska-Zielina, E.; Orlik-Kożdoń, B.; Steidl, T.; Tatara, T. Analysis of the Thermal Retrofitting Potential of the External Walls of Podhale’s Historical Timber Buildings in the Aspect of the Non-Deterioration of Their Technical Condition. Energies 2020, 13, 4610. [Google Scholar] [CrossRef]
- Bishara, N.; Pernigotto, G.; Prada, A.; Baratieri, M.; Gasparella, A. Experimental determination of the building envelope’s dynamic thermal characteristics in consideration of hygrothermal modelling—Assessment of methods and sources of uncertainty. Energy Build. 2021, 236, 110798. [Google Scholar] [CrossRef]
- Mahmoodzadeh, M.; Gretka, V.; Hay, K.; Steele, C.; Mukhopadhyaya, P. Determining overall heat transfer coefficient (U-Value) of wood-framed wall assemblies in Canada using external infrared thermography. Build. Environ. 2021, 199, 107897. [Google Scholar] [CrossRef]
- Koh, C.H.; Kraniotis, D. Hygrothermal performance, energy use and embodied emissions in straw bale buildings. Energy Build. 2021, 245, 111091. [Google Scholar] [CrossRef]
- Tlaiji, G.; Ouldboukhitine, S.; Pennec, F.; Biwole, P. Thermal and mechanical behavior of straw-based construction: A review. Constr. Build. Mater. 2022, 316, 125915. [Google Scholar] [CrossRef]
- Koh, C.H.; Kraniotis, D. A review of material properties and performance of straw bale as building material. Constr. Build. Mater. 2020, 259, 120385. [Google Scholar] [CrossRef]
- Sun, K.; Zheng, C.; Wang, X. Thermal performance and thermal transmittance prediction of novel light-gauge steel-framed straw walls. J. Build. Eng. 2023, 67, 105973. [Google Scholar] [CrossRef]
- Miljan, M.; Miljan, J. Thermal Transmittance and the Embodied Energy of Timber Frame Lightweight Walls Insulated with Straw and Reed. IOP Conf. Ser. Mater. Sci. Eng. 2015, 96, 012076. [Google Scholar] [CrossRef]
- Douzane, O.; Promis, G.; Roucoult, J.-M.; Le, A.-D.T.; Langlet, T. Hygrothermal performance of a straw bale building: In situ and laboratory investigations. J. Build. Eng. 2016, 8, 91–98. [Google Scholar] [CrossRef]
- D’Alessandro, F.; Bianchi, F.; Baldinelli, G.; Rotili, A.; Schiavoni, S. Straw bale constructions: Laboratory, in field and numerical assessment of energy and environmental performance. J. Build. Eng. 2017, 11, 56–68. [Google Scholar] [CrossRef]
- Cascone, S.; Catania, F.; Gagliano, A.; Sciuto, G. Energy performance and environmental and economic assessment of the platform frame system with compressed straw. Energy Build. 2018, 166, 83–92. [Google Scholar] [CrossRef]
- Cascone, S.; Evola, G.; Gagliano, A.; Sciuto, G.; Parisi, C.B. Laboratory and in-situ measurements for thermal and acoustic performance of straw bales. Sustainability 2019, 11, 5592. [Google Scholar] [CrossRef]
- Cornaro, C.; Zanella, V.; Robazza, P.; Belloni, E.; Buratti, C. An innovative straw bale wall package for sustainable buildings: Experimental characterization, energy and environmental performance assessment. Energy Build. 2020, 208, 109636. [Google Scholar] [CrossRef]
- Sabapathy, K.A.; Gedupudi, S. In situ thermal characterization of rice straw envelope of an outdoor test room. J. Build. Eng. 2021, 33, 101416. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, J.; Wang, D.; Liu, Y.; Zhao, Z.; Liu, J. Experimental investigation on thermal conductivity of aerogel-incorporated concrete under various hygrothermal environment. Energy 2019, 188, 115999. [Google Scholar] [CrossRef]
- Danovska, M.; Huang, J.; Wang, D.; Liu, Y.; Zhao, Z.; Liu, J. Simulation uncertainty in heat transfer across timber building components in the Italian climates: The role of thermal conductivity. Energy Build. 2022, 268, 112190. [Google Scholar] [CrossRef]
- Jerman, M.; Černý, R. Effect of moisture content on heat and moisture transport and storage properties of thermal insulation materials. Energy Build. 2012, 53, 39–46. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, K.; Liu, Y.; Wang, D.; Liu, J. The impact of temperature and relative humidity dependent thermal conductivity of insulation materials on heat transfer through the building envelope. J. Build. Eng. 2022, 46, 103700. [Google Scholar] [CrossRef]
- Boukhattem, L.; Boumhaout, M.; Hamdi, H.; Benhamou, B.; Nouh, F.A. Moisture content influence on the thermal conductivity of insulating building materials made from date palm fibers mesh. Constr. Build. Mater. 2017, 148, 811–823. [Google Scholar] [CrossRef]
- Rahim, M.; Douzane, O.; Le, A.T.; Langlet, T. Effect of moisture and temperature on thermal properties of three bio-based materials. Constr. Build. Mater. 2016, 111, 119–127. [Google Scholar] [CrossRef]
- Coelho, G.B.A.; Henriques, F.M.A. Influence of driving rain on the hygrothermal behavior of solid brick walls. J. Build. Eng. 2016, 7, 121–132. [Google Scholar] [CrossRef]
- Fernandes, M.S.; Rodrigues, E.; Gaspar, A.R.; Costa, J.J.; Gomes, Á. The impact of thermal transmittance variation on building design in the Mediterranean region. Appl. Energy 2019, 239, 581–597. [Google Scholar] [CrossRef]
- Ihara, T.; Gustavsen, A.; Jelle, B.P. Effect of facade components on energy efficiency in office buildings. Appl. Energy 2015, 158, 422–432. [Google Scholar] [CrossRef]
- Imbabi, M.S.-E. Modular breathing panels for energy efficient, healthy building construction. Renew. Energy 2006, 31, 729–738. [Google Scholar] [CrossRef]
- Leskovar, V.Ž.; Premrov, M. Design Approach for the Optimal Model of an Energy-Efficient Timber Building with Enlarged Glazing Surface on the South Façade. J. Asian Archit. Build. Eng. 2012, 11, 71–78. [Google Scholar] [CrossRef][Green Version]
- Ge, H.; Baba, F. Dynamic effect of thermal bridges on the energy performance of a low-rise residential building. Energy Build. 2015, 105, 106–118. [Google Scholar] [CrossRef]
- Baba, F.; Ge, H. Dynamic effect of balcony thermal bridges on the energy performance of a high-rise residential building in Canada. Energy Build. 2016, 116, 78–88. [Google Scholar] [CrossRef]
- Ahern, C.; Norton, B.; Enright, B. The statistical relevance and effect of assuming pessimistic default overall thermal transmittance coefficients on dwelling energy performance certification quality in Ireland. Energy Build. 2016, 127, 268–278. [Google Scholar] [CrossRef]
- Ge, H.; Baba, F. Effect of dynamic modeling of thermal bridges on the energy performance of residential buildings with high thermal mass for cold climates. Sustain. Cities Soc. 2017, 34, 250–263. [Google Scholar] [CrossRef]
- Žigart, M.; Kovačič Lukman, R.; Premrov, M.; Žegarac Leskovar, V. Environmental impact assessment of building envelope components for low-rise buildings. Energy 2018, 163, 501–512. [Google Scholar] [CrossRef]
- Košir, M.; Pajek, L.; Iglič, N.; Kunič, R. A theoretical study on a coupled effect of building envelope solar properties and thermal transmittance on the thermal response of an office cell. Sol. Energy 2018, 174, 669–682. [Google Scholar] [CrossRef]
- Fernandes, M.S.; Soares, N.; Gomes, A.; Gaspar, A.R.; Costa, J.J. The potential impact of low thermal transmittance construction on the European design guidelines of residential buildings. Energy Build. 2018, 178, 379–390. [Google Scholar]
- Liu, Z.; Zhou, X.; Tian, W.; Liu, X.; Yan, D. Impacts of uncertainty in building envelope thermal transmittance on heating/cooling demand in the urban context. Energy Build. 2022, 273, 112363. [Google Scholar] [CrossRef]
- GB 50176-2016; Code for Thermal Design of Civil Building. China Architecture & Building Press: Beijing, China, 2016.
- Williamson, A.; Finnegan, S. Sustainability in Heritage Buildings: Can We Improve the Sustainable Development of Existing Buildings under Approved Document L? Sustainability 2021, 13, 3620. [Google Scholar] [CrossRef]
- Papadopoulos, A.M. Forty years of regulations on the thermal performance of the building envelope in Europe: Achievements, perspectives and challenges. Energy Build. 2016, 127, 942–952. [Google Scholar] [CrossRef]
- Yang, X.E.; Liu, S.; Zou, Y.; Ji, W.; Zhang, Q.; Ahmed, A.; Han, X.; Shen, Y.; Zhang, S. Energy-saving potential prediction models for large-scale building: A state-of-the-art review. Renew. Sustain. Energy Rev. 2022, 156, 111992. [Google Scholar] [CrossRef]
- Franceschini, P.B.; Neves, L.O. A critical review on occupant behaviour modelling for building performance simulation of naturally ventilated school buildings and potential changes due to the COVID-19 pandemic. Energy Build. 2022, 258, 111831. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, M.; Chen, Z.; Chen, Z.; Ji, Y. Physical energy and data-driven models in building energy prediction: A review. Energy Rep. 2022, 8, 2656–2671. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Guo, M.; Chen, Z.; Chen, Z.; Ji, Y. Review of in situ methods for assessing the thermal transmittance of walls. Renew. Sustain. Energy Rev. 2019, 102, 356–371. [Google Scholar] [CrossRef]
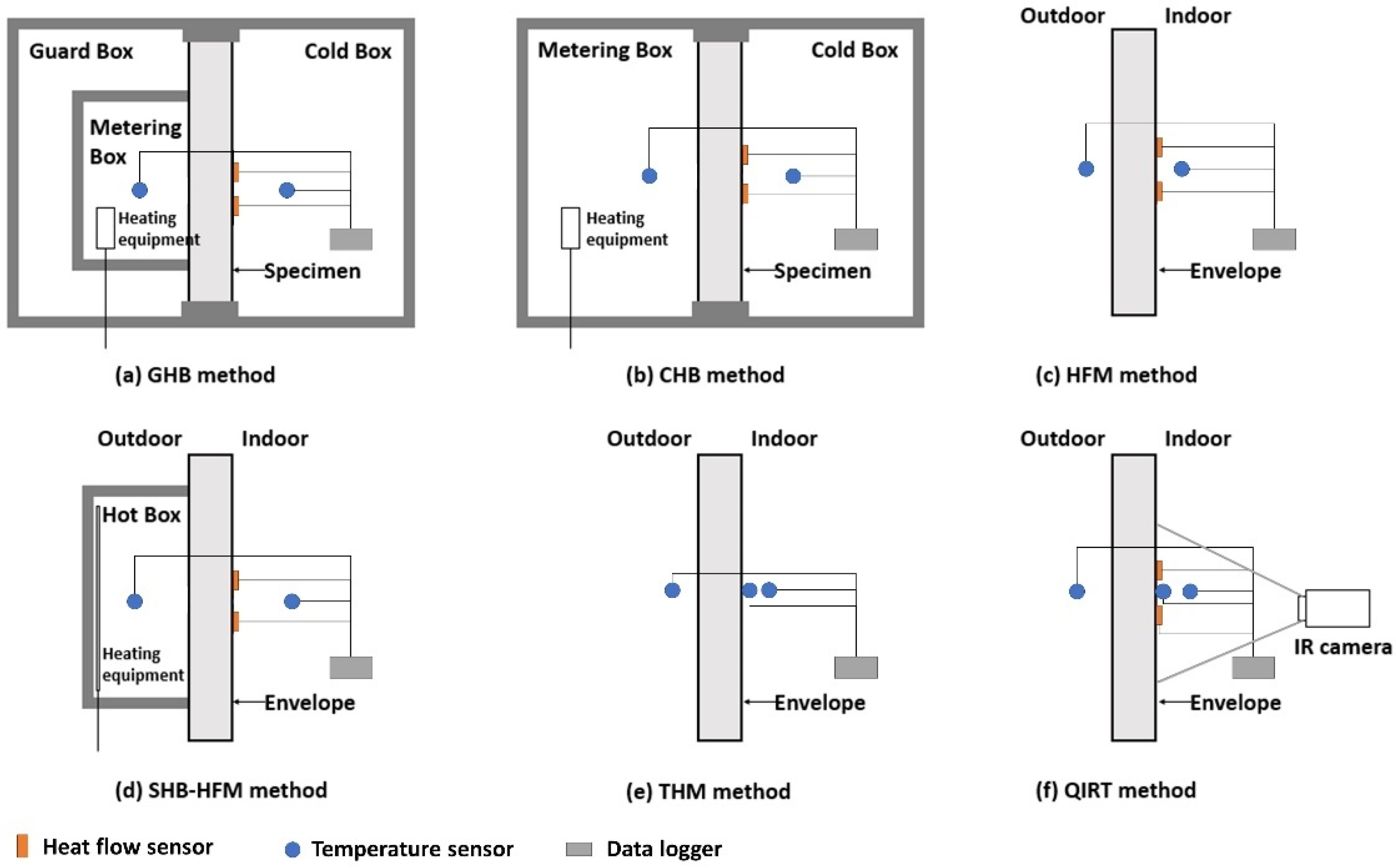

| Year | Envelope Type | Measurement Type | Measurement Method | Theoretical U-Value (W/m2·K) | Measured U-Value (W/m2·K) | Reference |
|---|---|---|---|---|---|---|
| 2006 | Concrete envelopes with vacuum-insulation | Laboratory measurement | GHB | NA | 3.74 | [46] |
| 0.16 | ||||||
| 0.17 | ||||||
| 0.19 | ||||||
| 0.21 | ||||||
| 0.25 | ||||||
| 0.29 | ||||||
| 2014 | 6 types of concrete block envelopes with different structures | In situ measurement | HFM | 0.23 | 0.22 | [47] |
| 0.25 | 0.34 | |||||
| 0.27 | 0.34 | |||||
| 0.30 | 0.37 | |||||
| 0.32 | 0.56 | |||||
| 0.33 | 0.39 | |||||
| 2014 | Hollow reinforced precast concrete envelopes | In situ measurement | HFM | NA | 1.459 (north envelope in summer) | [45] |
| 1.803 (east envelope in summer) | ||||||
| 2014 | A cavity envelope | In situ measurement | HFM | 0.20 | 0.26 | [48] |
| 2015 | A concrete block envelope | In situ measurement | SHB-HFM | 1.315 | 1.22–1.26 | [26] |
| 2016 | An RC envelope | In situ measurement | HFM | 0.22 | 0.23–0.35 | [49] |
| 2017 | Hollow concrete blocks | In situ measurement | HFM | NA | 2.1–2.7 | [50] |
| 2017 | 7 types of RC envelopes | In situ measurement | HFM | 0.431 | 0.475 (in winter) | [51] |
| 0.429 | 0.479 (in winter) | |||||
| 0.418 | 0.434 (in winter) | |||||
| 0.312 | 0.316 (in winter) | |||||
| 0.280 | 0.273 (in winter) | |||||
| 0.269 | 0.269 (in winter) | |||||
| 2018 | An RC envelope | In situ measurement | HFM | 0.270 | 0.250–0.265 | [24] |
| 2018 | A concrete block envelope | In situ measurement | HFM | 0.153 | 0.176 (in winter) | [52] |
| 2019 | RC envelopes; lightweight concrete envelopes | In situ measurement | QIRT | 0.480; | 0.480 | [53] |
| 0.252 | 0.261 | |||||
| 2020 | RC envelopes | In situ measurement | HFM | 0.333 | 0.400 (north envelope in summer); 0.522 (south envelope in summer); 0.393 (north envelope in winter); 0.536 (south envelope in winter) | [23] |
| 2020 | A lightweight concrete envelope | Laboratory measurement | HBT | 0.313 | 0.314–0.323 | [54] |
| 2020 | Thin precast concrete envelopes | Laboratory measurement | HBT | NA | 0.144–0.555 | [55] |
| 2020 | Translucent concrete envelopes | Laboratory measurement | CHB | NA | 4.25 | [56] |
| 5.45 | ||||||
| 2021 | 7 types of concrete envelopes with different structures | In situ measurement | HFM | 0.144 | 0.46 (in summer) | [33] |
| 0.165 | 0.18 (in spring) | |||||
| 0.14 | 0.56 (in spring) | |||||
| 0.118 | 0.21 (in autumn) | |||||
| 0.191 | 0.64 (in winter) | |||||
| 0.381 | 1.02 (in winter) | |||||
| 1.612 | 1.46 (in winter) | |||||
| 2021 | A lightweight concrete block envelope | In situ measurement | HFM | 2.01 | 1.363–1.782 | [35] |
| 2021 | A 3D-printed concrete envelope | In situ measurement | QIRT | NA | 0.54–1.00 | [57] |
| 2022 | A concrete envelope | In situ measurement | HFM | 0.21 | 0.17–0.41 | [22] |
| 2024 | A concrete envelope with internal insulation | In situ measure-ment | HFM | 0.145 | 0.136–0.148 | [58] |
| 2024 | An autoclaved concrete block envelope | Laboratory measurement | HBT | NA | 0.795–1.23 | [59] |
| Year | Envelope Type | Measurement Type | Measurement Method | Theoretical U-Value (W/m2·K) | Measured U-Value (W/m2·K) | Reference |
|---|---|---|---|---|---|---|
| 2015 | A straw bale envelope with a timer frame | In situ measurement | HFM | 0.092 | 0.125 | [95] |
| 2016 | A straw bale envelope with a timer frame | Laboratory measurement | CHB | NA | 0.20 ± 0.016 | [96] |
| 2017 | Two straw bale envelopes with timber frames | In situ measurement | HFM | NA | 0.119 ± 0.041 (in winter) | [97] |
| 0.253 ± 0.085 (in winter) | ||||||
| 2018 | Straw envelopes with timber frames | NA | NA | 0.72 | NA | [98] |
| 2019 | A straw bale envelope with a timber frame | Laboratory measurement | HBT | NA | 0.281 | [99] |
| 2020 | A multi-sheet straw bale envelope with a timber frame | Laboratory measurement | HBT | NA | 0.154 | [100] |
| 2021 | Straw bale envelopes with plywood frames | In situ measurement | THM | NA | 0.3–1.3 | [101] |
| 2021 | Straw bale envelopes with different structures | Laboratory measurement | GHB | NA | 0.48–0.53 | [16] |
| 2023 | Light-gauge steel-framed straw envelopes | Laboratory measurement | CHB | NA | 0.661–0.912 | [94] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Dong, Y.; Wang, T.-H.; Chang, W.-S.; Park, J. U-Values for Building Envelopes of Different Materials: A Review. Buildings 2024, 14, 2434. https://doi.org/10.3390/buildings14082434
Yu J, Dong Y, Wang T-H, Chang W-S, Park J. U-Values for Building Envelopes of Different Materials: A Review. Buildings. 2024; 14(8):2434. https://doi.org/10.3390/buildings14082434
Chicago/Turabian StyleYu, Jiaqi, Yu Dong, Tsung-Hsien Wang, Wen-Shao Chang, and Jihyun Park. 2024. "U-Values for Building Envelopes of Different Materials: A Review" Buildings 14, no. 8: 2434. https://doi.org/10.3390/buildings14082434
APA StyleYu, J., Dong, Y., Wang, T.-H., Chang, W.-S., & Park, J. (2024). U-Values for Building Envelopes of Different Materials: A Review. Buildings, 14(8), 2434. https://doi.org/10.3390/buildings14082434








