Abstract
Taiwan’s encouragement of installing solar photovoltaic power plants (SPPPs) on warehouse rooftops is a step towards sustainability and profitable investment. This study, analyzing the installations of STY Company, found that rooftop SPPPs significantly boost revenue, with rates increasing from 2.0088% to 6.8681% over 20 years. The break-even point is in the 7th year, with a return rate ranging from 2.0088 to 2.1748%. This shows that SPPP investments are a benefit for investors, shortening construction times and allowing warehouses to sell solar energy at an earlier date. This research utilized a fuzzy nonlinear multi-objective programming model to examine trade-offs between construction time, cost, quality, and revenue (TCQR) to optimize SPPP construction. The findings suggest that reducing construction time is an effective strategy to lower carbon emissions despite potential cost increases. However, time and quality costs are inversely proportional, highlighting the importance of efficient project management in minimizing the impacts of this trade-off. Adjusting funding can maintain quality while speeding up construction. Completing projects early also heightens revenue from green energy sales, offsetting higher initial investments. The TCQR focuses on investment revenue, managing time efficiently, and making data-driven decisions to expedite SPPP development. This model improves project profitability and promotes sustainable growth by reducing construction time and optimizing financial strategies. This study’s contribution includes: 1. Optimizing the installation process of warehouse rooftop SPPPs, which provide significant long-term revenue and environmental benefits. 2. Combining the different research methods of scholars into fuzzy methods that can solve complex systems with high uncertainty. The nonlinear model put forth by this study is closer to the actual situation and can handle balancing complex problems in multi-objective programming. 3. Improving the efficiency of time management to make it feasible to reduce construction time to lower carbon emissions. 4. Concocting a comprehensive approach integrating financial, environmental, and operational factors for successful SPPP development. This study addresses an academic gap. Previously, scholars conducted research independently, focusing solely on financial investment or time, cost, and quality (TCQ) issues without considering the two together. By combining financial investment with TCQ, this study fills a significant gap in academic research. According to this study, better investment returns could improve the promotion of solar energy. Unlike previous research, this study integrates the analysis of TCQ with that of revenue by assessing costs and revenues together. This approach allows decision-makers to derive judgments from the TCQR model quickly.
1. Introduction
Global energy demands and environmental awareness rise. Kumar, Gupta, and Dagar [1] highlight that solar energy is a clean and sustainable option, even relative to other renewable sources, which can help in achieving energy independence and reducing pollution. Therefore, investing in solar photovoltaic power plants (SPPPs) aligns with the global shift towards clean energy solutions and offers profitable opportunities for investors looking to minimize their environmental impact. Installing SPPPs on the rooftops of warehouse buildings is a significant low-carbon development for urban areas in Taiwan and can simultaneously boost companies’ revenue.
Through sensitivity analysis, Ronyastra, Saw, and Low [2] showed that internal systemic risks cannot control the level of solar irradiance and inflation rates, but even so, there are significant incentives. Direct benefits for investors include low loan interest, tax exemptions, higher on-grid electricity prices, reduced operating costs, and a low capital cost structure. In addition, SPPPs provide additional socio-economic and environmental benefits, such as job creation, biodiversity protection, and pollution reduction.
Alzarrad et al. [3] point out that construction project management includes modulating between time, cost, and risk (TCR). Reducing project duration to decrease total cost results in a decreased probability of completing a given project on time and an increased risk of schedule delays. Regarding finances, Ghadir, Shayannia, and Miandargh [4] propose that while minimizing construction time and costs incurred is an important objective, the ultimate goal should be to maximize quality. Projects that disregard resource restrictions and rely on an expectation of unlimited resources result in financial shortfalls. Egwunatum and Oboreh [5] explain that project management needs more flexibility, especially in the capabilities of the technology used to manage, when the external environment limits the satisfactory fulfillment time, cost, quality, and safety constraints. Thus, improving organizational productivity and competitiveness is critical for survival. By reducing construction time, construction companies can increase capital efficiency and operational speed and heighten returns on building SPPPs.
Aminbakhsh and Abdulsattar [6] emphasize the importance of achieving a reasonable sale price, the shortest possible completion time, and the best quality in construction projects. Decision-makers must balance the conflicting aspects of project time, cost, and quality (TCQ). Tarigan’s [7] study, based on the 2018 policies of Indonesia’s Ministry of Energy and Mineral Resources (MEMR), suggests that investing in rooftop photovoltaic systems has a payback period of approximately 9–10 years.
In alignment with the Taiwanese government’s policies, the Taiwan Power Company has committed to a 20-year clean energy purchase agreement with companies equipped with the SPPP. This contractual commitment fosters a stable purchasing environment by guaranteeing the reliability of demand, enabling SPPPs to achieve a long-term sustainable objective. Companies can then sell the generated energy for profit and reduce carbon emissions. By 2025, Taiwan aims to accomplish the maturation of solar energy. The most practical approach is to construct SPPPs on the roofs of the company’s warehouses, thereby avoiding disruption to the terrestrial environment.
In past research, this author found that previous scholars only studied independent issues or focused on risks that come with linking issues. The scholars Aminbakhsh and Abdul-sattar [6] focused on the impact of TQC. Tarigan [7] focused on the payback period of investment. Scholars Alzarad et al. [3] focused on the relationship between TQC and risk. This study differs from the others mainly in that it connects the issues of TQC and financial investment and promotes the construction of SPPPs to accelerate the development of clean energy generation. Potential revenue is a key factor in encouraging enterprises to complete the construction and installation of SPPPs. Therefore, this study seeks to provide a management decision-making model that can help to reduce the construction time and time needed to obtain adequate funding while maintaining quality, accelerate capital utilization, and adjust the financing structure to optimize the trade-off results of time, cost, quality, and revenue (TCQR) elements. This is in line with the belief of Komurlu, Kalkan Ceceloglu, and Arditi [8] that buildings should consume less water, electricity, and other resources. They posited that construction strategies should focus on reducing waste, improving efficiency, and speeding up the construction process to help reduce carbon emissions and promote sustainable development.
In addition, this study focuses on time, cost, quality, and revenue (TCQR) and emphasizes the importance of time management in project strategy. Solving the uncertainties and constraints that hinder the acceleration of SPPP construction and reducing carbon emissions in the production process will help achieve sustainable development and green earth.
2. Literature Review
Policymakers often refrain from investing in constructing SPPPs and rely on traditional energy because of risk considerations and aversion to the unknown. However, it is known that designing green buildings, which reduces the demand for conventional energy and thereby reduces carbon emissions, helps to improve a city’s air quality and slow down climate change. In addition, increasing the independent energy generation capabilities of warehouse buildings can provide the city with more clean energy and reduce dependence on external energy grids. However, incorporating financial investment into the design process is indispensable. This article provides financial decision-making investment models to solve SPPPs construction issues, including the trade-off issues of TCQR for accelerating the installation of SPPPs on warehouse buildings and achieving the carbon reduction goal. Therefore, installing SPPPs and converting them into building assets from which the company can obtain stable revenue from solar power is a powerful motivation to create a low-carbon city.
Regarding trade-offs, financial investment revenue is the most significant factor affecting accelerated SPPP construction time and cost. Briera and Lefèvre [9] evaluate the role of the expectations of international financiers as a group in reducing variable renewable energy (VRE) investment costs in developing countries. Their IMACLIM-R multi-regional integrated assessment model (IAM) simulates different finance scenarios. IAM is a dedicated model for the average cost of capital (CoC) that analyzes the interaction between public and private capital. By 2030, VRE energy generation can increase by 43%. Reducing the financing cost of VRE investment can effectively accelerate the transition to green energy as it makes financiers more favorable to VREs. Muñoz et al. [10] focus on the technical aspects of the implementation costs of integrating unconventional renewable energy sources into Colombia’s electricity system and arrive at precise cost estimates; from their results, it can be concluded that financial feasibility indicators, net present value (NPV), internal rate of return (IRR), and payback period (PP), show that lowering kilowatt-hour prices adversely impacts the project’s economic feasibility for low-revenue groups.
Low capital costs mean the opportunity to generate revenue; financial investment costs are subtracted from total investment revenue when calculating net profit. Therefore, this study uses weighted average capital cost (WACC) to analyze investment revenue regarding the acceleration of the construction of SPPPs.
Brest et al. [11] promoted a photovoltaic-based energy structure that includes social benefits and financial profit. The authors used NPV, IRR, and PP in their research and suggested that an investor’s primary goal is to maximize returns. Stala-Szlugaj et al. [12] noted that governments and enterprises in various countries must thoroughly consider potential economic benefits when given the opportunity to make large investments in optoelectronics. Their analysis methods involved dynamic payback period (DPP), NPV, and IRR, and their results showed that the ability to transfer electric energy to the energy grid smoothly is the primary factor determining the success or failure of the investment. Leewiraphan, Ketjoy, and Thanarak [13] highlight the phenomenon that the growth of the solar photovoltaic business and industry and the reduction in photovoltaic energy costs have driven investment in solar photovoltaic energy generation in Thailand; their analysis using the solar photovoltaic roof-as-a-service (RaaS) business model. Their research results show that, in line with the trend of the costs of photovoltaic cost energy becoming ever lower, it is economically feasible for medium and large photovoltaic energy sources to independently sell electricity without being connected to the grid. Imasiku [14] used the system advisor model (SAM) simulation method to conduct a performance and financial analysis of solar photovoltaic systems on grid-connected households in Zambia. The study found that such systems achieved an internal rate of return of 28.52% within three years. The debt-service ratio (DSCR) was 5.12%, demonstrating the potential of such systems to end energy poverty in Zambia and progress toward UN Sustainable Development Goal 7 (ensure access to affordable, reliable, sustainable, and modern energy for all). The study also showed that financial gains were the driving force behind the construction of SPPPs. Balducci et al. [15] discussed the financial advantages of distributed energy resources (DER), using a linear programming approach to model various service and DER operational constraints. Their goal was to find the optimal DER schedule to maximize financial gains. Their analysis indicated that the PV solar array they studied could yield $2.5 million in present value benefits over a 20-year economic lifespan, resulting in a return on investment of 1.16%.
Based on the above research, the development of the solar energy industry is inseparable from its economic benefits. Investors wish to maximize returns, and governments and enterprises also value economic growth. However, traditional metrics such as NPV and IRR may be limited when evaluating complex investment projects. To more accurately assess the investment value and risk of solar energy projects, this study adopts MIRR as an alternative to NPV and IRR specifically to address the issue of having multiple IRRs. By recalculating cash flows based on borrowing rates, MIRR provides a precise rate of return that more accurately reflects the time value of money and the true profitability of the project. Having accurate knowledge of the rates of return helps enhance investment confidence and accelerate industrial development. In addition to economic returns, this can help accelerate the construction of SPPPs in warehouses to make them more environmentally sustainable and promote the development of clean electricity by allowing money to be reinvested into solar energy development.
Developing construction methods that conserve energy and reduce carbon emissions is crucial for warehouses. Despite having all the necessary information, decision-makers often feel the need to have more certainty about the impact of various factors on the environment, particularly in the context of the trade-off problem of TCQR. Mashhadizadeh, Dastgir, and Salahshour [16] have acknowledged that investments in solar energy face numerous uncertainties and are prone to impacting the environment, making investments in this sector largely irreversible as the situation post-investment and before are not the same. The researcher employed a fuzzy accurate options method to evaluate photovoltaic power stations, revealing that when realistic options for expansion and abandonment are considered, the investment value of these stations increases. Nuriyev [17] has noted that uncertainties, incomplete information, and vagueness characterize perceived problems in most cases where difficulties are encountered. To counter this, multi-criteria decision-making (MCDM) models have been used for energy selection, ranking options, and aiding decision-makers in choosing the best solutions. Thomasi et al. [18] utilized the fuzzy Delphi technique to scrutinize incentive elements in clean energy technologies, such as photovoltaics. They conducted a hierarchical analysis of each component in centralized photovoltaic energy production projects. The model increased the performance index by 41.91%, enhancing the competitiveness of photovoltaic power station projects in energy auctions.
The above scholars’ research found that TCQR situations often have multiple conflicting goals, and decision-makers, limited by their perspective, make subjective judgments, which are suboptimal. To navigate these complexities and uncertainties, it is imperative to adopt a fuzzy multi-objective programming approach. According to Mohammadi and Sheikholeslam’s [19] study, multi-objective optimization (MOO) is a dynamic and preeminent research area, often recognized as in need of multi-criteria optimization or vector optimization. This methodology can provide a more comprehensive and realistic evaluation of alternative solutions. It can assist decision-makers in balancing TCQR, reliably leading to more sustainable outcomes.
The decision-making model in fuzzy environments, initially developed by Bellman and Zadeh [20], has been the basis for proposing models that include flexibility as a constraint and fuzziness in the objective function in conventional linear and nonlinear programming, integer and fractional programming and dynamic programming.
In the energy field, where uncertainties and challenges in the investment and application of clean energy technologies such as solar energy are prevalent, the potential of fuzzy decision-making models to improve the investment value is clear. Leandry et al. [21] pointed out that the frequency at which fuzzy problems, which deal with uncertain or vague information, arise is increasing. The researchers employed the α-cut technique, explaining their choice by claiming that using the α-cut method makes the calculations of all the essential functions more straightforward to understand than other methods. Yang et al. [22] proposed using renewable energy to increase the adaptability of energy systems. The researchers utilized a hybrid efficient-integer linear programming model for efficient problem-solving. Application in a real-life energy system confirmed the model’s economic feasibility and adaptability. Middelhauve et al. [23] explored the growing trend of integrating photovoltaic (PV) panels to decrease the carbon emissions of building energy systems (BES). Their study used a mixed integer linear optimization problem, focusing on the cost of PV installation as the primary decision factor and on a residential area of 40 buildings in western Switzerland as the object of their research. Their study revealed that installing PV panels could result in up to 20% more efficiency. In 2023, Grisales-Noreña et al. [24] studied the optimal output of photovoltaic (PV) energy sources within a single-phase AC distribution network, considering various objective functions. Their research utilized a nonlinear programming (NLP) model with a nonconvex framework. Each objective function was optimized using a singular accurate function methodology. Zimmermann’s [25] research explored scenarios with multiple conflicting goals and utilized fuzzy mathematics programming to solve optimization issues. This method is particularly suitable for practical problem-solving models, as many decision-making situations involve uncertainty, ambiguity, and multiple objectives.
Therefore, this study integrates the perspectives of Mohammadi and Sheikholeslam [19] and Zimmermann [25] to address the TCQR problem in real-world conditions. It expects that a multi-objective programming model, developed under fuzzy and nonlinear conditions, can solve the TCQR problem for warehouse SPPPs.
Unlike the study conducted by Mohammadjafari et al. [26], this study minimized the net present value of project costs and completion time while seeking to improve the project’s productivity through multi-objective genetic algorithms for optimization of a wide range of situations and on a large scale. To this end, this study sought to develop multi-objective genetic algorithms capable of solving examples involving a large number of objectives and variables. The effectiveness of the multi-objective genetic algorithm is evaluated by comparing its performance with that of the nontranscendent sequencing genetic algorithm (NSGA-II) using well-established efficiency metrics. The results prove that the multi-objective genetic algorithm with perfect efficiency index is superior.
Fuzzy nonlinear multi-objective programming and NSGA-II are both practical tools for solving multi-objective optimization problems. Fuzzy nonlinear multi-objective programming is specially designed to deal with complex systems full of uncertainties. It can handle fuzzy goals and constraints and is especially suitable for analyzing the installation situation of warehouse solar photovoltaic systems. NSGA-II is good at handling large-scale, deterministic multi-objective optimization problems and can quickly generate a set of non-dominated solutions. In terms of practical application, this study chose a fuzzy nonlinear multi-objective programming model where the issue involves more uncertainty and the decision-maker’s preference for the goal is fuzzy. If the objective function and constraints of the decision-maker’s problem are clear, NSGA-II will be a more appropriate tool. Different models should be used in research to solve different issues.
A comprehensive literature review revealed the potential for warehouse rooftops to return a profit for investors, which drives the motivation to invest in SPPPs for carbon reduction. Therefore, as it is the trend supported by investors, the clean energy generated by SPPPs can contribute to carbon emissions mitigation. TCQR can achieve sustainability goals by using clean energy.
3. Methodology
3.1. Research Structure
The research structure of this study falls under the TCQR framework of the SPPP program. Using financial evaluation correctly accelerates the construction of SPPPs on the rooftops of warehouse buildings to generate satisfactory revenue by performing multi-objective programming in a fuzzy nonlinear environment to obtain clean energy for warehouse buildings and reduce carbon emissions. The framework is shown in Figure 1 below to express the significant impact of shortening the construction time of SPPPs. This study uses the mathematical method of fuzzy nonlinear multi-objective programming to deal with TCQR situations where multiple objectives exist simultaneously and conflict with each other. However, shortening the construction period is not without cost, as it may lead to higher construction costs and lower construction quality. To accelerate the construction of SPPPs and generate clean electricity to reduce carbon emissions, an accurate assessment of TCQR factors and the situation at hand is necessary.
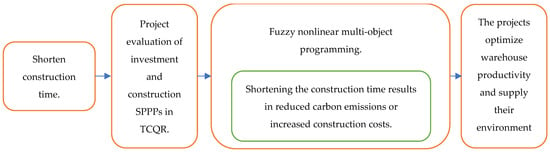
Figure 1.
The TCQR framework of the SPPPs project.
3.2. Case Assumptions
With considerations for the intricate interplay of time, cost, quality, and revenue (TCQR) in construction projects, this research takes a unique approach and proposes a series of hypotheses that seek to shed new light on the subject:
Hypothesis 1.
Building SPPPs on warehouse roofs is a niche with great potential revenue on investment and contributes to the trend of reducing carbon emissions.
Hypothesis 2.
A contraction in the duration of construction escalates the costs.
Hypothesis 3.
In terms of trade-off issues, quality requirements will affect cost increases.
Hypothesis 4.
The policy of guaranteed price acquisition catalyzes the process of establishment of SPPPs.
At the core of these hypotheses lies the central idea of the significant potential of shortening construction time to reduce carbon emissions effectively, a key consideration in the current environmental crisis.
3.3. Case Methodology
This study focuses on developing a unified model that seamlessly integrates fuzzy, nonlinear, and multi-objective programming models.
Step 1: Use the critical path method (CPM) to make projections more accurate in a construction project. This method helps decision-makers grasp the implications of shortening the construction period.
Step 2: Using the fuzzy set theory of Bellman and Zadeh [20], the fuzzy computation method of Dong and Shah [27], and the α-cut defuzzification method of Leandry et al. [21] to calculate the capital cost, complete the financial structure, and accelerate the construction’s payback period.
Step 3: Combine Yager’s [28] multi-objective approach and Zimmermann’s [25] mathematical programming into one model.
The following is the progression of the CPM, fuzzy set theory, fuzzy financial, and fuzzy nonlinear multi-objective model:
(This represents the minimization of the scheduling time of the crash status of items).
(This represents the minimization of the scheduling cost of the crash status of items).
(This represents the maximization of the scheduling quality of the crash status of items).
The restrictions are:
(This is the start-to-finish relationship between fuzzy item i and fuzzy item j).
(These are the non-negative bounds at the start time of each fuzzy item).
(The start time of each fuzzy item is a positive integer).
The definitions for the above symbols are as follows:
is the number of each fuzzy item in the project, i = A, B, …, m;
is the start time of each fuzzy item in the project;
is the duration of each fuzzy item in the project;
is the necessary time interval between two fuzzy items, i and j;
represents the quality ratio of each fuzzy item in the project;
represents the cost amount of each fuzzy item in the project.
The fuzzy set theory of Bellman and Zadeh [20] identified the time-cost slope of the membership function, which is , the fuzzy set of defined as . This interval is the set of all valued with possibility .
The α-cut method is a technique for ranking fuzzy numbers. A fuzzy number is a set of real numbers with associated membership degrees. The membership function defines the membership degrees of each number in the fuzzy set.
Let be I a fuzzy number with two membership functions, and the left and right membership functions be and ; suppose that and are the inverse functions of and ; and define the left integral value and right integral value of (Equations (11) and (12)) are by Liou and Wang [29] and Leandry et al. [21]. The mathematical manipulations of the two positive fuzzy numbers A and B can be represented by the fuzzy addition: (AB)α = [Alα + Blα, Auα + Buα]; by fuzzy subtraction: (AB)α = [Alα − Buα, Auα − Blα]; by fuzzy multiplication: (AB)α = [AlαBlα, AuαBuα]; and by fuzzy division: (AB)α = [Alα/Buα, Auα/Blα]:
To obtain a more accurate measure of relative profitability for SPPPs, this study uses the MIRR. COF represents cash outflows (negative numbers) or the project’s cost, and CIF represents cash inflows (all positive numbers). On the left side of the equation, the present value (PV) of the investment outlays is reduced by the cost of capital. The correct term’s numerator represents the future value of the inflows, assuming that the cash reinvested flows in again to reduce the expense of capital. This future value coming from cash inflows is also known as the terminal value (TV). The MIRR is the reduction rate required to equate the PV of the terminal value with the PV of cost. This study uses the fuzzy set theory to set a fuzzy modified internal rate of return (FMIRR), which is shown below as Equations (14) and (15). According to Tarigan’s [7] study, the yield has a payback period of approximately 9 or 10 years. The calculation equations are as follows:
The definitions for the above symbols are as follows:
is the debt ratio;
is the common equity ratio;
is cash outflow;
is cash inflow;
is the fuzzy cost of debt;
is the fuzzy cost of common equity;
is the fuzzy margin tax;
is the fuzzy present value;
is the fuzzy terminal value;
FCIF is the fuzzy cash inflow;
is the weighted average cost of capital;
is the fuzzy weighted average cost of capital;
is the fuzzy modified internal rate of return;
The meanings of the equations employed in this analysis are subsequently elaborated upon below. Initially, the calculation is composed of the fuzzy time cost (), direct fuzzy cost (), fuzzy quality cost () and fuzzy direct revenue (). This arrangement aligns with the suggestions laid out by the pioneering work that identified the inherent trade-off between time and quality considerations. Eventually, the originally linear relationship between time and cost transforms into a nonlinear function. Revenue is the subtractive phase of the trade-off equation. Building upon this foundation, Zimmermann’s [25] proposed mathematical model defines as a constant value, enabling the quantification of the time cost ).
The definitions for the above symbols are as follows:
is the duration time of each fuzzy item in the normal state of the project;
is the duration of each fuzzy item in the crash status of the project;
is the direct cost of the normal working status of each fuzzy item in the project;
is the direct cost of the crash work status of each fuzzy item in the project;
is the quality ratio of each fuzzy item in the normal state of the project;
is the quality ratio of the crash status of each fuzzy item in the project;
is fuzzy interest expense value;
calculates the cost of quality ratio for each fuzzy item in the project;
calculates the quality of time ratio for each fuzzy item in the project;
represents the unit cost of the quality ratio variation in each fuzzy item in the normal state;
represents the unit cost of the quality ratio variation in each fuzzy item in the crash state.
This study presents a novel model for comprehensive variable analysis that explicitly focuses on optimizing project deadlines. The model incorporates a detailed analysis of the phases of execution to maintain the equilibrium between each element’s TCQR parameters. It aims to achieve the ideal schedule while ensuring the project does not overrun its expected overall cost. This model’s primary objectives are minimizing completion time, reducing cost, enhancing quality ratio, and maximizing revenue. Excel 2016 and the Python 3.11 Fuzzy Program are used to simulate construction and calculate items. First, data were typed into Excel and then fed into the Python Fuzzy Program for execution. After obtaining the results, they were listed systematically as tables to ensure a comprehensive and accurate project analysis.
4. Sample Problem and Results
This article proposes a method for decision-based project management, offering an integrated method that lets the decision-maker transform fuzzy values into precise values. The proposed method uses fuzzy set theory, α-cut defuzzification, nonlinear, multi-objective, and mathematical programming to solve TCQR.
4.1. Case Introduction
A real-life case can be seen on the rooftops of the warehouses of Taiwan’s SHIN TUNG YANG Co., Ltd. (STY Co.), where SPSS systems were installed in 2018. The total rooftop warehouse area spans 2800 m2 and contains 1018 solar panels. The total amount of money invested into this project amounted to TWD 15,418,618, and the energy generation capacity stands at 283.2 kWh. Taiwan Power Company purchases the generated energy at TWD 4.4861/kWh, resulting in a yearly revenue of TWD 1,270,464 from selling solar energy to Taiwan Power Company for STY Co. (Taoyuan City, Taiwan).
The construction process is detailed in Table 1 as follows:

Table 1.
Case data.
Item A: In a 3-day on-site survey, engineers assessed roof orientation, building structure, roof area, the process of construction via simulation, potential energy generation capacity, construction method planning, and calculated equipment costs.
Item B: A 4-day on-site survey was carried out.
Item C: The application to Taiwan Power Company to construct an SPPP took 60 days to be approved.
Item D: The filing and approval process with the Energy Bureau also spanned 60 days.
Item E: The erection of solar steel frames and the structure’s construction (the system itself, safety fences, and the solar panels) took 83 days.
Items F and G: The installation of electrical equipment and pipeline configuration took 51 days.
Items H and I: It took 30 days for the Taiwan Power Company to approve its quality officially.
The quality had to be higher than 90%. STY Co. used a method of constructing SPPP that does not aim to shorten construction times. Their project procedures were A, C, D, E, G, and I (Project STY-1), and the interest cost rate was 1.908% (Taiwan Cathay Pacific Bank loan interest rate in 2018). The saving rate of interest tax was 30%.
The following model integrates fuzzy set theory, nonlinearity, and multi-objective mathematical programming to establish a model. The solution steps are as follows:
Step 1: Refer to Figure 2 to find the main path (Project STY-2) on the network map.
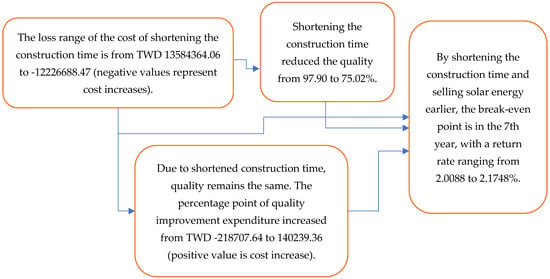
Figure 2.
The project’s critical path.
Step 2: Establish a fuzzy weighted cost of capital.
Step 3: Assess the shortened duration of each item; time reduced = normal time ( − crash time (). Determine each task’s normal cost () and crash cost (), and calculate the slope ().
Step 4: Next, α-cuts were applied to fuzzy numbers to obtain definite numbers for different degrees of uncertainty.
Using the principle of CPM, find out the start point in time and operation time of each operation from Table 1, compare items A and B, and, with the understanding that the construction time of item B is longer, select item B for optimization to shorten the construction path. At the same time, it must also be considered that items B and C have finish-start relationships. According to the principle planning of CPM, the construction path sequence is B, C, D, E, F, and H in that order, respectively, as shown in Figure 2.
Next, calculate each item’s crash time, unit cost slope, and unit quality slope, the resulting data are shown in Table 2. The critical path items are B, C, D, E, F, and H. This critical path is called Project STY-2.

Table 2.
Calculate each item’s crash time, unit cost slope, and unit quality slope.
4.2. Fuzzy Nonlinear Multi-Objective Method for TCQR
First, the average cost of capital for Project STY-2 must be known, as capital is the source of investment funds. This investment fund could be the company’s own money or be borrowed from the bank, so it is necessary to know the composition model of the average capital of cost. The following table shows the weighted average of fuzzified average capital, called the fuzzy weight average capital of cost (FWACC). The numbers range from 0% to 70% in increments of 10%. In Table 3, the fuzzy cost of common equity (FKs) is 1.710546, calculated as the cube root of 1.3 × 1.75 × 2.2, , (Table 3, presented as *).

Table 3.
The fuzzy weighted average cost of capital (FWACC).
This research utilizes previously mentioned data to calculate the fuzzy-weighted debt and common equity cost. Then, it constructs the FWACC with α-cuts defuzzification while considering different debt ratios. For α-cuts ranging from 0 to 1 in intervals of 0.2, the process involves evaluating the and bounds of the and summing up these data to obtain the values. The minimum arrangement value = 2.139709777 in Table 4 indicates the fuzzy weighted average cost of capital for a debt ratio of 50%. It corresponds to a minimal interest rate range of = [0.80875, 1.054772, 1.361125] (Table 4, presented as *).

Table 4.
FWACC under α-cuts defuzzification.
Within this model, the fuzzy unit time cost slope for each operation item is modeled as a triangular fuzzy number. Project STY-2’s fuzzy number serves as an illustration. ( is the cube root of , accurate within a range of variability of 10% in either direction.
However, it must be noted that items C, D, and H are for quasi-governmental agencies that cannot shorten construction times. The results are shown in Table 5.

Table 5.
Fuzzy numbers of nonlinear variation in crashing unit of Project STY-2.
As illustrated in Table 6, the defuzzification values for items B, E, and F are 4.65, 133.79, and 98.98, respectively. However, it is crucial to note that these numerical values do not directly translate into the number of days the period of construction was shortened; the numbers are indicators of relative magnitudes. Significantly, item E = 133.79 (presented as *) boasts the highest defuzzification value, implying that even during a crash, it would still shorten the construction period by the greatest number of days.

Table 6.
Defuzzification in shortened time = normal time ( crash time ().
The cost ranking values in the defuzzification ranking (Table 7) are B = 2,134,940.249, E = 20,380,254.57, and F = 10,033,890.33. This means that the cost of item E (presented as *) is the highest and needs attention and control because E’s construction period is longer, and the total cost is higher than other items.

Table 7.
Defuzzification in cost ranking values.
As shown in Table 8, item E has the highest-ranking value, denoted by an asterisk (*). The ranking value measures the quality–cost trade-off for each item, and a higher ranking value indicates comparatively higher quality provided that costs are equal, indicating that item E is of the highest quality and relatively low cost. This suggests that item E is the most cost-effective option. This finding is significant for decision-makers looking to optimize projects’ quality–cost ratio.

Table 8.
Defuzzification in quality ranking values.
An analysis of unit time costs reveals negative values for items B, E, and F, signifying an inverse relationship between time and cost. This inverse proportionality underscores the fundamental trade-off between the time and cost of these items. Their sorting value directly corresponds to the magnitude of the cumulative value, which is calculated by multiplying cost and time. Item B cannot be considered for this analysis as it is still in the planning and on-site survey stages. Therefore, out of all the items, item E exhibits the smallest sorting value (as shown in Table 9, as indicated by *), signifying that its construction is the shortest. However, this efficiency comes at the expense of having the highest cumulative cost, again highlighting the inherent trade-off between time and cost within items B, E, and F. While item E demonstrates the potential for time reduction, it simultaneously incurs the most costs, necessitating careful consideration by decision-makers before deciding to shorten construction times in a bid to reduce the value of carbon emissions.

Table 9.
Defuzzification in unit time cost.
The provided values represent each item’s “slopes” of their unit-time quality curves. These slopes represent the rate of change in quality per unit of time at different points. A positive slope value indicates an increase in quality, and a negative value indicates a decrease. Notably, item B is excluded from the slope analysis due to its quality remaining constant at 100%: there is no variation in quality over time for this item.
Comparatively, item E exhibits a positive slope, indicating a slight increase in quality over time, showing that the critical issues associated with Project STY-2 may have been addressed through significant cost investment during the implementation of item E. This investment, likely associated with the rapid quality improvement observed, resolved the project’s core challenges (as shown in Table 10, as indicated by the number marked by the asterisk *).

Table 10.
Defuzzification in unit time quality.
Item E exemplifies the time-cost nonlinearity within the fuzzy mutation curvature, which shows that alteration in time and cost is nonlinear. Specifically, the cost per unit of time exhibits a range of changes when pressed by outside factors. With meticulous management, the cost can decrease to TWD 40,467.07. Conversely, without careful management, the cost may escalate to TWD 91,050.88.
The slope interval of the fuzzy nonlinear time cost is represented as [299.76, −186.73, −674.46]. After accounting for the nonlinearity of the time cost and other related factors, the variation range of the total cost of item E ranges from TWD 13,584,364.06 to −12,226,688.47 (negative values represent cost increases; refer to Appendix A).
Item E demonstrates that the cost of compressing time can transition from a decrease to an increase. For such scenarios, the original budget intended to last 31 days must consider expenses that may arise post-time compression. If the costs are effectively controlled, a range exists for decreasing costs. A shortened construction timeframe can also contribute to reducing carbon emissions due to the mechanical processes involved in running for less time. This method resolves the ambiguity and uncertainty inherent to the trade-off and facilitates decision-making by providing a structured approach to thinking.
In calculations based on fuzzy variance, each value may vary by 10% in either direction after the value has been cube rooted, leading to fuzzy numbers being represented by ranges as shown here: [67.50, 74.75, 82.50], [14,400, 15,946.49, 17,600], and [63,540, 70,363.88, 77,660]. Item E, while within the α-cut (interval of possible values based on membership function), exhibits the lowest unit time cost, and maintaining that minimum cost from item E requires achieving a quality threshold of 90%. The quality ranges from [75.02, 85.98, 97.90], implying further cost increases to reach the desired threshold. Depending on the achieved quality within the [75.02, 85.98, 97.90] range, additional costs may be incurred in an attempt at quality improvement, ranging from TWD −218,707.64 to −65,233.89, and exceeding 90% quality will increase to TWD 140,239.36. Additional spending on quality improvement depends on the actual level attained. Project STY-2 can efficiently achieve cost analysis through item E if a 90% quality threshold is met (refer to Appendix A).
Based on the above results, this study will concentrate on item E due to its multifaceted cost structure for the following reasons: 1. The base cost decreases as the number of days decreases; 2. Costs increase because of the expedited work; 3. Increased crash costs are necessary to achieve a 90% quality standard. Time influences costs, but estimating time can be challenging and is not easily quantifiable. Regarding cost, the key to enhancing control over SPPPs in a fuzzy environment lies in managing capital costs and returns on investment. It involves a careful balance between investing in quality improvements and managing the associated costs.
This study requires financial support to achieve the long-term goal of sustainably managing warehouse buildings. The optimal fuzzy weighted average cost of capital values is [0.8087%, 1.0547%, 1.3611%], while the initial investment cost is TDW 7,709,309. From the perspective of reinvestment profit and after undergoing cost–benefit analysis for green photovoltaic energy policy, this analysis evaluates the financial aspect of implementing an energy policy focused on warehouse rooftop SPPPs. Table 11 shows the following financial results: Reinvestment profit: 1.908%, FMIRR twentieth-year yield: 6.8073% to 6.8681%, Interest cost interval: 0.0080% to 0.0136%, Break-even point: seventh-year, with a yield of 2.0088% to 2.1748%. The FMIRR indicates that the margin remains positive from the seventh to the twentieth year, suggesting a predictable cost–benefit analysis favoring a green energy policy centered around photovoltaics. Installing SPPPs is a worthy investment because of its stable profit performance. A higher capacity attracts lower contract prices from Taiwan Power Company and thus generates higher total revenue for its producers. This analysis demonstrates the financial viability of an energy policy that drives SPPP installation. In the long term, the revenue of FMIRR supports the implementation of the SPPP initiative. Project remuneration allows for faster profit recovery through reduced construction time, and the high profitability of the project also supports efforts to shorten construction time and reduce carbon emissions.

Table 11.
FMIRR.
Reducing construction time can yield a higher financial FMIRR. Given that the policy of the Taiwan Power Company is to procure solar energy at elevated prices to incentivize production, a substantial rate of revenue can be realized even when confronted with high costs. This rate of revenue embodies the core principle that drives carbon emission reduction: incentive. This study uses a fuzzy nonlinear multi-objective model by the mathematical programming that profited SPPPs on the roof of a warehouse building. Concurrently, the fuzzy financial benefit has established a decision-making framework for environmental sustainability. This framework introduces significant additional value to Taiwan’s energy landscape and the warehouse rooftops of numerous manufacturing plants. It underscores the potential of sustainable practices in enhancing environmentally reduced carbon emissions and increasing financial revenue.
To more clearly illustrate the sensitivity and situation of the numerical value of Project E, the study graphic below was made; it represents the sensitivity and situation of each event so that readers can better understand the exploration of the significance of the trade-off made in shortening the construction time by this study, the framework of which is shown below in Figure 3.
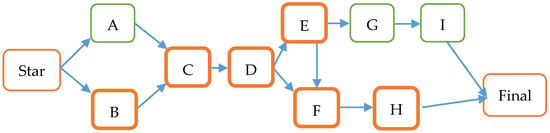
Figure 3.
Sensitivity analyses illustrate the framework.
The sensitivity refers to the impact of changes in shortening construction time on cost and quality. Shortening the construction time inevitably leads to increased direct costs, a range that can vary from TWD 13,584,364.06 to −12,226,688.47 (negative values represent cost increases). This means that to speed up the construction, more resources may need to be invested, such as additional manpower, overtime pay, etc., thus pushing the overall cost. However, this acceleration often comes at the expense of construction quality, which can drop from 97.90% to 75.02%. If the quality is to be improved, the cost will increase from TWD −218,707.64 to 140,239.36 (positive value is cost increase). If construction focuses on quality from the beginning, you can avoid high-quality improvement costs later on. Furthermore, although shortening the construction time will increase short-term costs, it can also accelerate the early generation of revenue. By shortening the construction time and selling electricity early, the MIRR can reach 2.0088% and 2.1748% in the seventh year of the investment payback period.
Ultimately, the decision to shorten the construction time is a delicate balance. On one hand, it can expedite investment recovery, but on the other, it can lead to increased costs and compromised quality. This underscores the necessity of making a trade-off between cost, quality, and time when determining the construction schedule. It can help identify the optimal balance between these factors, using fuzzy numerical values to guide decisions on acceptable cost increases and methods for shortening the construction time while maintaining quality.
5. Discussion
Reducing carbon emissions requires significant financial investments. Therefore, balancing TCQR and deploying SPPPs in warehouse buildings face multiple obstacles. Initial construction costs are high, including solar panels and related infrastructure costs. Additionally, large-scale solar power plants require much land, which is particularly difficult in areas with limited land resources in Taiwan. Therefore, warehouse rooftops are suited for developing and installing SPPPs. Alwulayi and Debbage [30] emphasized that the construction of SPPPs will be affected by various socioeconomic factors, changes in the built environment, social information networks, and institutional and pricing environments. Survey data show that the economic incentive to adopt rooftop solar panels is related to the fact that the benefits of solar panels far outweigh the costs. However, Taiwan Power Company purchases high prices from SPPPs to solve financial investment issues, which is the right ambition road for installing SPPPs.
Sama and Some [31] explained the relatively complex process of deriving problem solutions through fuzzy algebraic operations and converting deterministic solutions into fuzzy solutions. Then, it is decomposed into the single-objective solution of the fuzzy objective function and constraint function to solve real-world problems. According to the literature mentioned above research results, this study uses fuzzy nonlinear methods that align with the actual situation and provide broader information. Even if the numerical value changes significantly, it can help decision-makers judge in an uncertain environment.
Pham et al. [32] emphasize that the management of construction projects has long emphasized the trade-off between time and cost. This study’s framework provides a realistic option for clearing up the fuzzy environment to make corporate decision-making more efficient. It ensures more value for decision-makers regarding warehouse buildings’ carbon reduction. Although the decrease from shortening the construction time may involve higher costs, this remains a sustainable development strategy for the future and the global economy.
Reducing carbon emissions presents numerous challenges, particularly in warehousing buildings. Balancing economic benefits with environmental responsibility is a complex task. Accelerating the construction of SPPPs can help reduce carbon emissions and save on electricity bills. The use of fuzzy mathematical methods aids decision-making in uncertain environments. Although shortening construction time may increase costs, it also has the potential to speed up carbon reduction. In summary, promoting the green transformation of warehouse buildings requires the government’s policy to offer good revenue for companies to achieve sustainable development and clean energy goals.
6. Conclusions
6.1. Research Conclusions
Taiwan’s policies incentivize companies to build SPPPs on warehouse roofs. Based on data presented in a case study of STY Company, it is evident that investing in building SPPPs on the warehouse roof can increase the revenue rate from a low of 2.0088% in the seventh year to a high of 6.8681% in the twentieth year. After the twelfth year, the revenue rate consistently remains above 6%. These revenue data align with Hypotheses 1 and 4, suggesting that having an appropriate financial acquisition policy is the best way to guide investment in building SPPPs.
This study employs a fuzzy nonlinear multi-objective model to analyze the trade-off problem under compressed construction time conditions. In fuzzy numerical expression, the cost range resulting from the shortening of the construction period will fall within TWD 13,584,390.83 to −12,226,723.05. The sign of this positive and negative value indicates that the cost may either increase or decrease. It shows that shortening the construction time is an effective method. However, it should be noted that s costs have increased as a result of circumstances external to the aforementioned conditions since the shortening time construction started. The results indicate that shortening the construction time will indeed affect the cost, which is consistent with Hypothesis 2. Therefore, shortening construction time is the best way to reduce carbon emissions.
In the trade-off issues discussed in Hypothesis 3, heightened quality requirements will increase costs. This study finds that both time-quality and quality–cost intervals fall within 75.02 to 97.90% and from TWD −218,707.64 to 140,239.36, indicating that time is the most significant factor leading to an increase in quality costs.
Item E emphasizes using input amount costs to shorten time to ensure quality remains at 90% or above. Simultaneously, using shortened construction time to start operations earlier can boost revenue from selling green energy and compensate for installation costs.
The crash model has made significant research contributions by emphasizing the following factors as drivers of reducing carbon emissions:
- (1)
- Investment Revenue: Investment revenue is crucial for reducing carbon emissions, but development cannot be achieved if investors find a given venture unprofitable. In the long term, SPPPs generate clean energy without emitting carbon dioxide or other harmful gases. Additionally, SPPPs provide a source of revenue by selling green energy.
- (2)
- Emissions Management: Adopting a crash mode methodology expedites the construction of SPPPs, showcasing a critical mode of time management [33]. The primary achievement of this approach is the reduction in carbon emissions during construction via the minimization of construction time.
- (3)
- Methodology Choice: Fuzzy nonlinear multi-objective programming suits complex systems with high uncertainty and fuzzy objectives. Compared with NSGA-II, it is better at dealing with large-scale deterministic multi-objective problems; depending on the characteristics of the problem, researchers should select the more suitable model for their particular problem.
In summary, the TCQR framework emphasizes maximizing investment returns, optimizing time, and utilizing data-driven strategies to speed up SPPP deployment. Project profitability is enhanced by streamlining construction processes and refining financial methods, thereby promoting sustainable growth. This research highlights the significant long-term financial and environmental benefits of warehouse rooftop SPPPs. It employs fuzzy methods to tackle complex and uncertain systems through nonlinear multi-objective modeling, optimizing project timelines to expedite carbon emission reduction. Additionally, it provides a comprehensive framework that integrates financial, environmental, and operational considerations for the successful development of SPPPs. This approach not only reduces carbon emissions but also generates revenue, thereby incentivizing investors and construction companies to promote sustainability.
6.2. Research Recommendations
Policy Enhancement for Renewable Energy: This proposal champions a new and robust policy model to further the advancement of solar energy in Taiwan, and it is necessary that the government obtain a resilient energy procurement policy to increase generated economic value and facilitate industrial transformation. Taiwan’s renewable energy mainly comes from solar, wind, and hydropower, which require effective purchasing policies to align with consumer needs, drive economic growth, stimulate industrial development, and contribute to environmental conservation. Therefore, it can be known that strengthening policy development is essential for promoting green energy.
Carbon Reduction: This study employs time management decision analysis to implement fuzzy nonlinear multi-objective sustainable development technologies. This approach addresses the undeniably significant contribution of construction to carbon emissions. However, numerous challenges related to carbon emissions persist. This study serves as an initial step towards a green future by emphasizing the sustainable goal of reducing carbon emissions.
Funding
This research received no external funding.
Data Availability Statement
The datasets analyzed during the current study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A
Fuzzy nonlinear time costs in curvature.
Crash unit time cost in the fuzzy equation.
Item E compresses the time cost fuzzy nonlinear in variation.
Variation in time quality of fuzzy item E.
Variation in quality cost of fuzzy item E.
References
- Kumar, P.; Gupta, S.; Dagar, V. Sustainable energy development through non-residential rooftop solar photovoltaic adoption: Empirical evidence from India. Sustain. Dev. 2024, 32, 795–814. [Google Scholar] [CrossRef]
- Ronyastra, I.M.; Saw, L.H.; Low, F.S. Techno-economic analysis with financial risk identification for solar power plant as post-mining land use in Indonesia. Energy Sustain. Dev. 2024, 80, 101462. [Google Scholar] [CrossRef]
- Alzarrad, M.A.; Moynihan, G.P.; Hatamleh, M.T.; Song, S. Fuzzy multicriteria decision-making model for time-cost-risk trade-off optimization in construction projects. Adv. Civ. Eng. 2019, 2019, 7852301. [Google Scholar] [CrossRef]
- Ghadir, H.; Shayannia, S.A.; Miandargh, M.A. Solving the problem of time, cost, and quality trade-off in project scheduling under fuzzy conditions using meta-heuristic algorithms. Discret. Dyn. Nat. Soc. 2022, 2022, 6401061. [Google Scholar] [CrossRef]
- Egwunatum, S.I.; Oboreh, J.C. Factors limiting knowledge management among construction small and medium enterprises. J. Eng. Proj. Prod. Manag. 2022, 12, 25–38. [Google Scholar] [CrossRef]
- Aminbakhsh, S.; Abdulsattar, A.M. Optimizing Three-Dimensional Trade-Off Problem of Time–Cost–Quality over Multi-Mode Projects with Generalized Logic. Buildings 2024, 14, 1676. [Google Scholar] [CrossRef]
- Tarigan, E. Rooftop PV system policy and implementation study for a household in Indonesia. Int. J. Energy Econ. Policy 2020, 10, 110–115. [Google Scholar] [CrossRef]
- Komurlu, R.; Kalkan Ceceloglu, D.; Arditi, D. Exploring the Barriers to Managing Green Building Construction Projects and Proposed Solutions. Sustainability 2024, 16, 5374. [Google Scholar] [CrossRef]
- Briera, T.; Lefèvre, J. Reducing the cost of capital through international climate finance to accelerate the renewable energy transition in developing countries. Energy Policy 2024, 188, 114104. [Google Scholar] [CrossRef]
- Muñoz, Y.; Suárez, C.A.; Castro, A.O.; López, O.J. Technical and financial analysis for the implementation of small-scale self-generation projects, based on grid-tied photovoltaic solar energy, for residential users under Colombian regulations. Int. J. Energy Econ. Policy 2024, 14, 197–205. [Google Scholar] [CrossRef]
- Brest, P.; Gilson, R.J.; Wolfson, M.A. Essay: How investors can (and can’t) create social value. J. Corp. L. 2018, 44, 205. [Google Scholar]
- Stala-Szlugaj, K.; Olczak, P.; Kulpa, J.; Soltysik, M. Methodology for Selecting a Location for a Photovoltaic Farm on the Example of Poland. Energies 2024, 17, 2394. [Google Scholar] [CrossRef]
- Leewiraphan, C.; Ketjoy, N.; Thanarak, P. An assessment of the economic viability of delivering solar PV rooftop as a service to strengthen business investment in the residential and commercial sectors. Int. J. Energy Econ. Policy 2024, 14, 226–233. [Google Scholar] [CrossRef]
- Imasiku, K. A solar photovoltaic performance and financial modeling solution for grid-connected homes in Zambia. Int. J. Photoenergy 2021, 2021, 8870109. [Google Scholar] [CrossRef]
- Balducci, P.; Mongird, K.; Wu, D.; Wang, D.; Fotedar, V.; Dahowski, R. An evaluation of the economic and resilience benefits of a microgrid in Northampton Massachusetts. Energies 2020, 13, 4802. [Google Scholar] [CrossRef]
- Mashhadizadeh, M.; Dastgir, M.; Salahshour, S. Economic appraisal of investment projects in solar energy under uncertainty via fuzzy real option approach (case study: A 2-MW photovoltaic plant in South of Isfahan, Iran). Adv. Math. Financ. Appl. 2019, 3, 29–51. [Google Scholar] [CrossRef]
- Nuriyev, M. Z-numbers based hybrid MCDM approach for energy resources ranking and selection. Int. J. Energy Econ. Policy 2020, 10, 9950. [Google Scholar] [CrossRef]
- Thomasi, V.; Siluk, J.C.M.; Rigo, P.D.; Rosa, C.B.; Garcia, E.D.; Cassel, R.A.; Ramos, C.F.D.S. A model for measuring the photovoltaic project performance in energy auctions. Int. J. Energy Econ. Policy 2022, 12, 501–511. [Google Scholar] [CrossRef]
- Mohammadi, A.; Sheikholeslam, F. Intelligent optimization: Literature review and state-of-the-art algorithms (1965–2022). Eng. Appl. Artif. Intell. 2023, 126, 106959. [Google Scholar] [CrossRef]
- Bellman, R.E.; Zadeh, L.A. Decision-making in a fuzzy environment. Manag. Sci. 1970, 17, B-141–B-273. [Google Scholar] [CrossRef]
- Leandry, L.; Sosoma, I.; Koloseni, D. Basic fuzzy arithmetic operations using α-cut for the Gaussian membership function. J. Fuzzy Ext. Appl. 2022, 3, 337–348. [Google Scholar]
- Yang, J.; Liu, C.; Mi, Y.; Zhang, H.; Terzija, V. Optimization operation model of electricity market considering renewable energy accommodation and flexibility requirement. Glob. Energy Interconnect. 2021, 4, 227–238. [Google Scholar] [CrossRef]
- Middelhauve, L.; Baldi, F.; Stadler, P.; Maréchal, F. Grid-aware layout of photovoltaic panels in sustainable building energy systems. Front. Energy Res. 2021, 8, 573290. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Montoya, O.D.; Cortés-Caicedo, B.; Zishan, F.; Rosero-García, J. Optimal power dispatch of PV generators in AC distribution networks by considering solar, environmental, and power demand conditions from Colombia. Mathematics 2023, 11, 484. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Applications of fuzzy set theory to mathematical programming. Read. Fuzzy Sets Intell. Syst. 1993, 795–809. [Google Scholar] [CrossRef]
- Mohammadjafari, A.; Ghannadpour, S.F.; Bagherpour, M.; Zandieh, F. Multi-Objective Multi-mode Time-Cost Tradeoff modeling in Construction Projects Considering Productivity Improvement. arXiv 2024, arXiv:2401.12388. [Google Scholar] [CrossRef]
- Dong, W.; Shah, H.C. Vertex methods for computing functions of fuzzy variable. Fuzzy Sets Syst. 1987, 24, 65–78. [Google Scholar] [CrossRef]
- Yager, R.R. Concepts, theory, and techniques a new methodology for ordinal multi-objective decisions based on fuzzy sets. Decis. Sci. 1981, 12, 589–600. [Google Scholar] [CrossRef]
- Liou, T.S.; Wang, M.J.J. Ranking fuzzy numbers with integral value. Fuzzy Sets Syst. 1992, 50, 247–255. [Google Scholar] [CrossRef]
- Alwulayi, S.; Debbage, K. Factors Affecting the Willingness to Adopt Residential Rooftop Solar Panels: Evidence from Saudi Arabia. Arab. World Geogr. 2024, 27, 141–149. [Google Scholar] [CrossRef]
- Sama, J.D.L.C.; Some, K. Solving fuzzy nonlinear optimization problems using null set concept. Int. J. Fuzzy Syst. 2024, 26, 674–685. [Google Scholar] [CrossRef]
- Pham, V.H.S.; Nguyen Dang, N.T.; Nguyen, V.N. Achieving improved performance in construction projects: Advanced time and cost optimization framework. Evol. Intell. 2024, 17, 2885–2897. [Google Scholar] [CrossRef]
- Chiang, K.L. Delivering Goods Sustainably: A Fuzzy Nonlinear Multi-Objective Programming Approach for E-Commerce Logistics in Taiwan. Sustainability 2024, 16, 5720. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).