Bearing Capacity of Hybrid (Steel and GFRP) Reinforced Columns under Eccentric Loading: Theory and Experiment
Abstract
:1. Introduction
2. Experimental Program
2.1. Test Specimens
2.2. Materials
2.3. Test Setup and Loading
2.4. Test Results
2.5. Verification of Plane Section Assumption
3. Calculation of Bearing Capacity
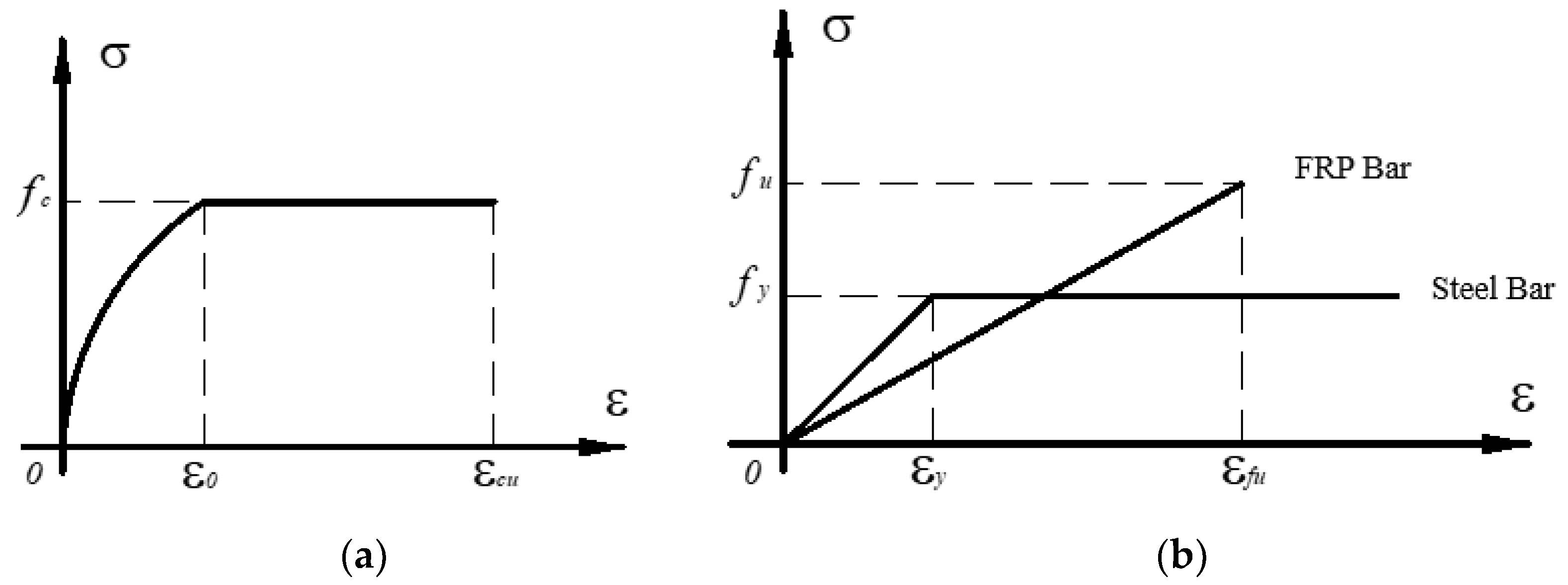
3.1. Basic Assumptions for Calculations
- Plane section assumption.
- The tensile action of concrete is ignored.
- The compressive stress of concrete is treated using the equivalent rectangle method, which is convenient for stress analyses.
- The ultimate strain of concrete during crushing εcu = 0.0033.
- The constitutive relationship of longitudinal reinforcement and concrete is simplified as shown in Figure 8.
3.2. Boundary State
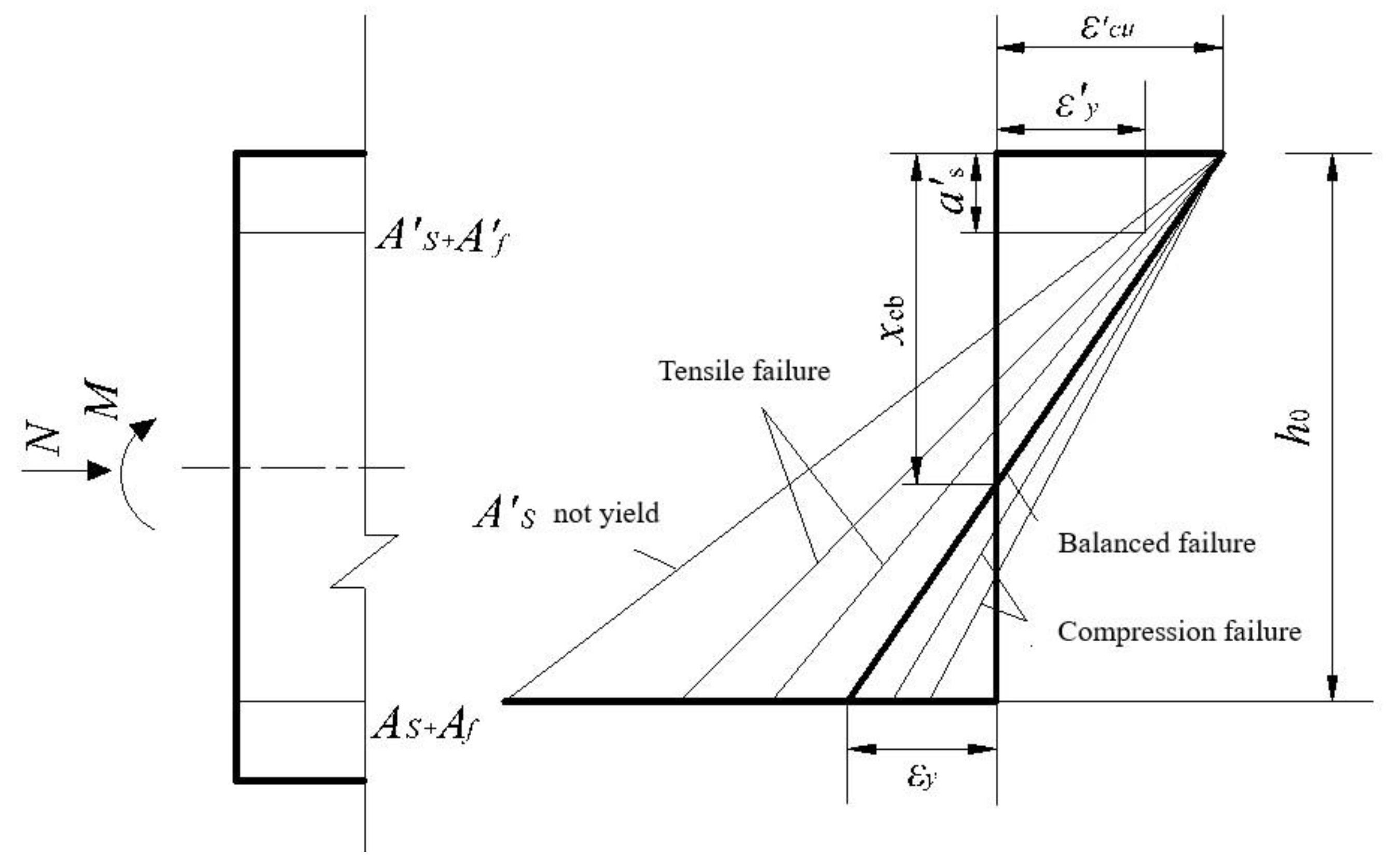
3.2.1. Failure Mode
- (1)
- If , ; then failure mode controlled by compression (small eccentricity compression failure)
- (2)
- If , ; then failure mode controlled by tension (large eccentricity compression failure)
- (3)
- If , ; it is boundary failure I
- (4)
- If , ; it is boundary failure II
3.2.2. Discrimination of Large and Small Eccentric Compression Limits for Eccentrically Loaded Columns
- (1)
- Boundary state I: The compressive failure of concrete and the tensile yielding of the reinforcement occur simultaneously: when the reinforcement far away from the loading point yields in tension, the compressive concrete is just crushed. At this time, the height of the neutral axis in the section is , the height of the relative compression zone is , and the calculation formulae are shown as follows in Equations (5)–(7).where is the equivalent rectangular stress figure coefficient.
- (2)
- Boundary state II: When the tensile FRP bars are broken, the concrete in the compression zone just reaches the ultimate compressive strain. The height of the relative compression zone is , and the calculation is shown in Equation (8).Generally, , therefore .
4. Calculation Formula of Bearing Capacity
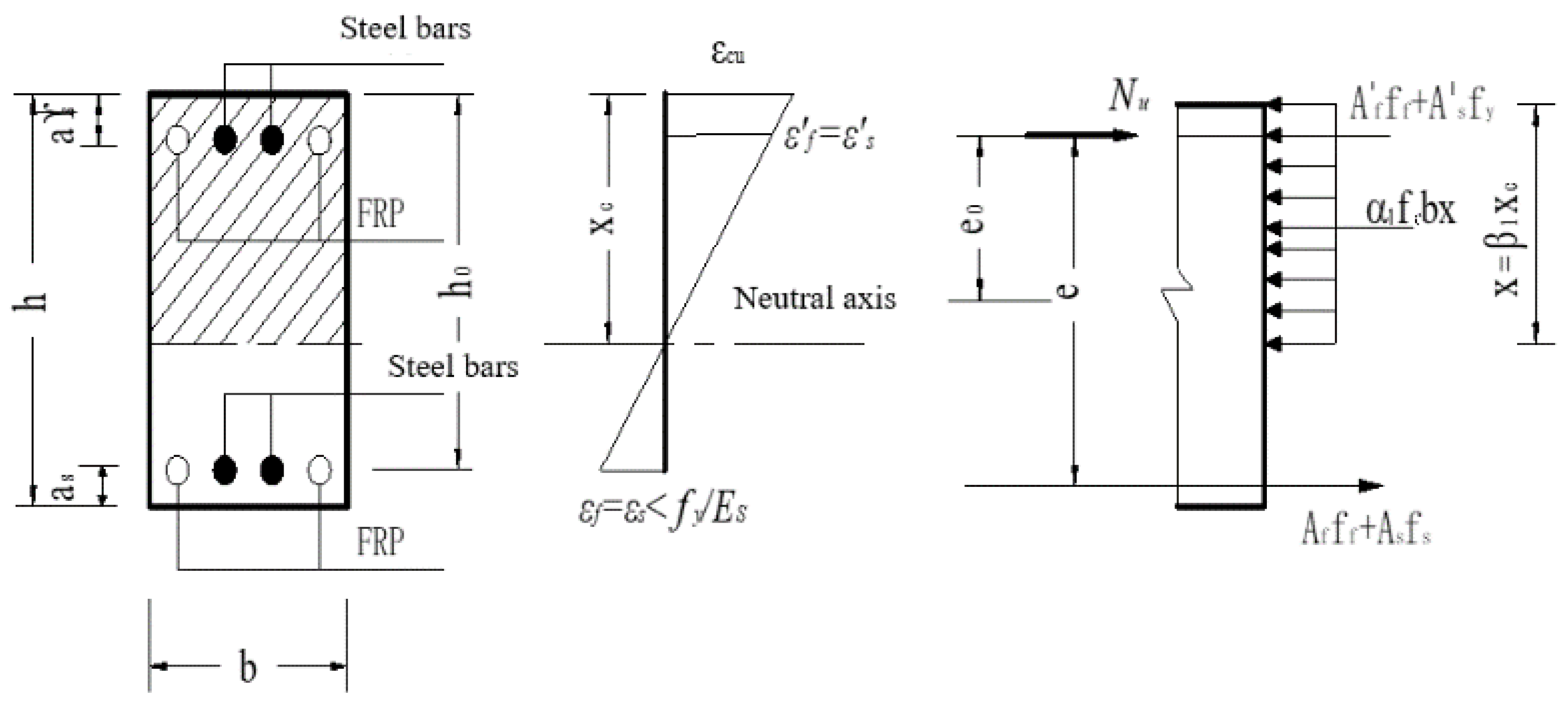
4.1. Large Eccentricity Compression
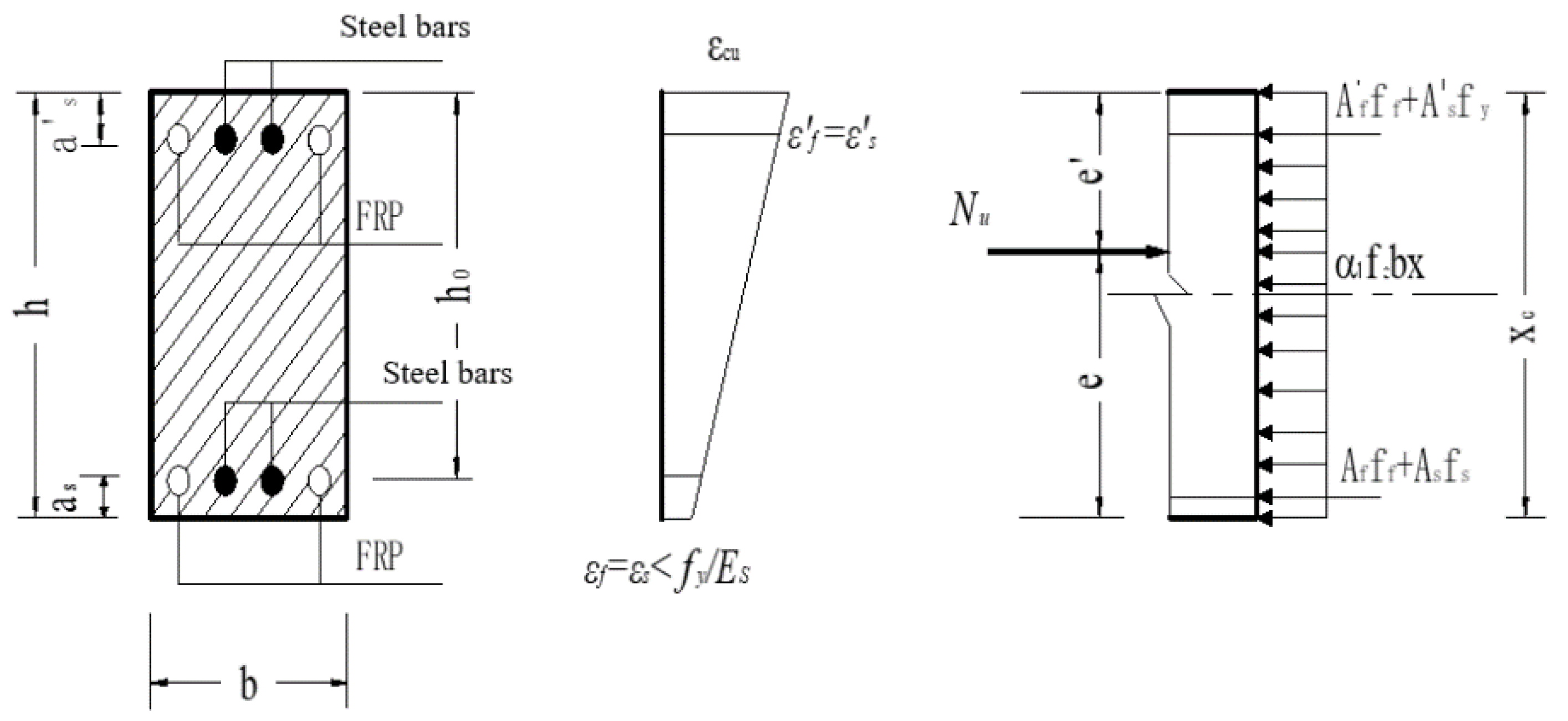
4.2. Small Eccentricity Compression
- (1)
- At the time of failure, the reinforcement farther from the loading point is in tension, as shown in Figure 11.
- (2)
- At the time of failure, the reinforcement farther from the loading point is under pressure, as shown in Figure 12.
4.3. Boundary Failure State
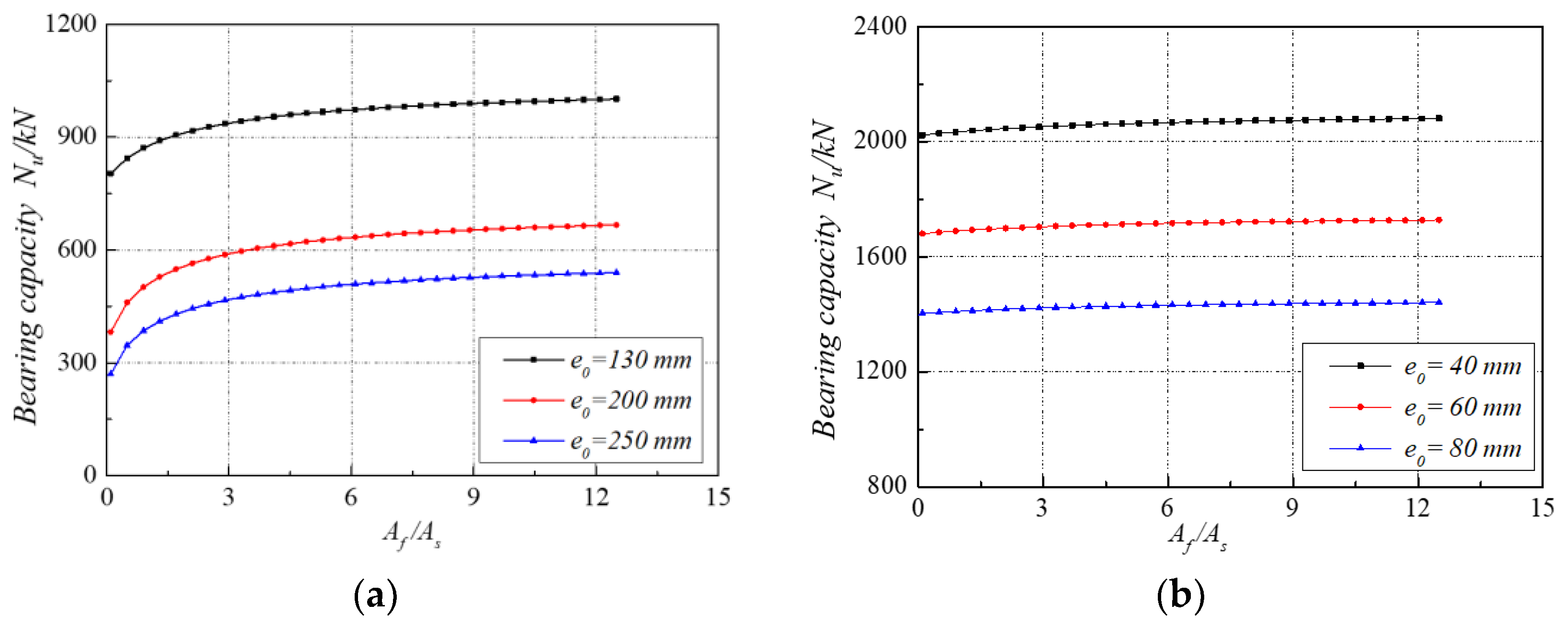
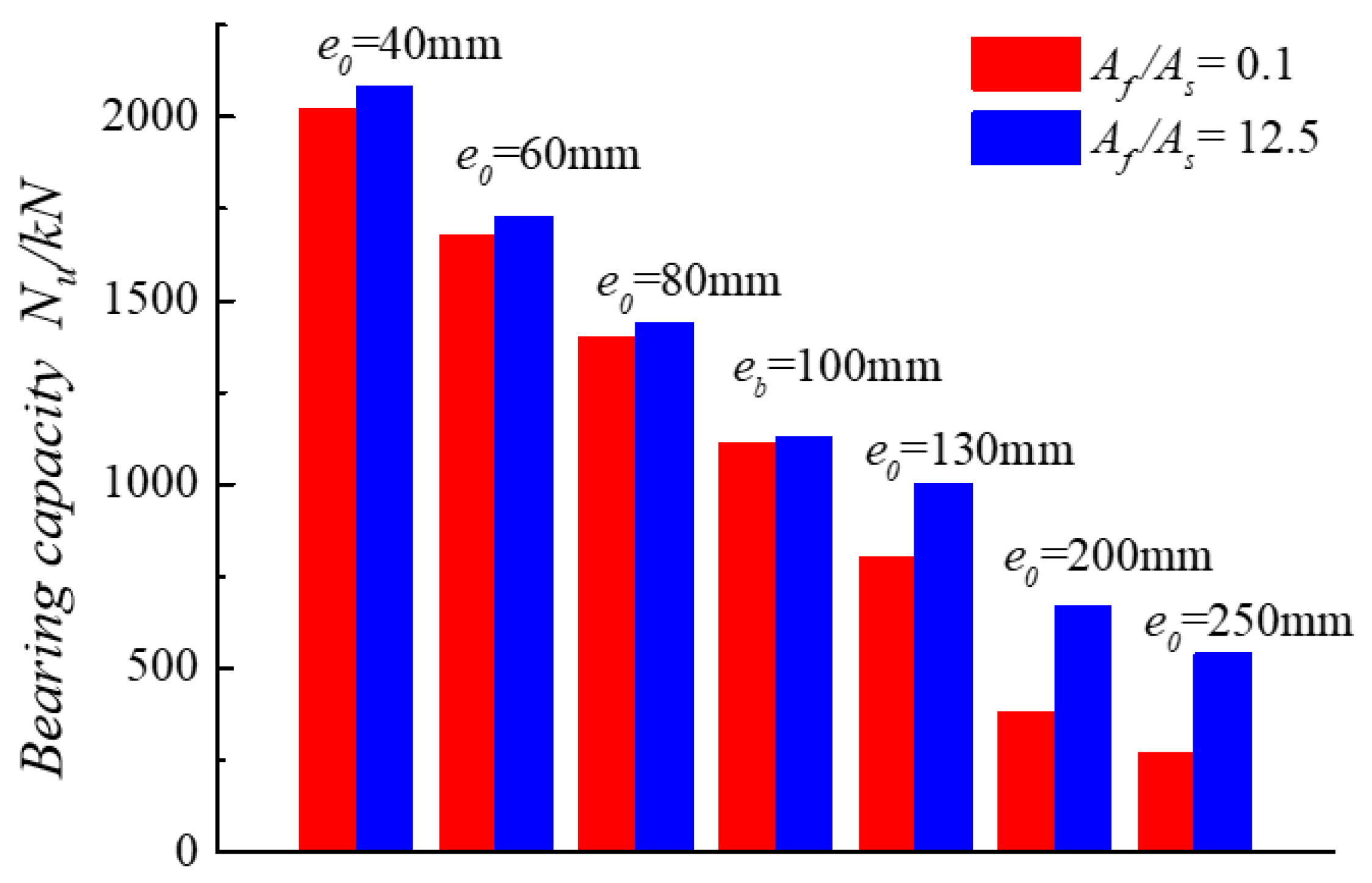
4.4. Effect of Cross-Section Reinforcement Ratio
4.5. Comparison between Experimental and Theoretical Results
5. Conclusions
- (1)
- Based on the equal stiffness principle, ten hybrid RC columns under large eccentric loading are designed. The failure processes of all specimens are similar to that of RC columns subjected to large eccentric compression load. The failure mode was ductile, namely, the steel rebars in the tensile zone firstly yielded, while the FRP bars in the tensile zone remained in a tensile state, and at last the concrete on the compression side was crushed.
- (2)
- The test results showed that the ultimate bearing capacity of the columns decreases with the increase in eccentricity. However, the impact of the varying axial stiffness ratio between GFRP and steel bars on the bearing capacity can be considered negligible.
- (3)
- Theoretical analysis showed that the failure mode of hybrid RC columns also could be divided into large eccentricity compression failure and small eccentricity compression failure based on whether the reinforcement on the relatively tensile side (the side far away from the axial force) yields or not, but there were two boundary failure states.
- (4)
- The tests have verified the assumption of the plane section and, based on it, two relative heights of the compression zone ( and could be calculated, corresponding two different boundary failure states. was used as a criterion to judge the failure mode, and was used as a limiting condition to prevent FRP bars from breaking suddenly.
- (5)
- Theoretical analysis showed that the enhancement effect of FRP bars in a hybrid RC section is more significant in the case of large eccentric compression than the case of small eccentric compression.
- (6)
- Calculation formulae for the bearing capacity of eccentrically compressed hybrid RC columns were proposed. The calculated values were in good agreement with the experimental values.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| area of the FRP bars in the tension zone of the section | |
| area of the steel bars in the tension zone of the section | |
| area of the steel bars in the compression zone of the section | |
| area of the FRP bars in the compression zone of the section | |
| D | average crack spacing |
| e | eccentric distance |
| tensile elastic modulus of the FRP bars | |
| modulus of elasticity of steel reinforcement | |
| compressive elastic modulus of the FRP bars | |
| ultimate compressive stress of the FRP bars | |
| ultimate tensile stress of the FRP bars | |
| compressive stress of the FRP bars | |
| effective height of the section | |
| bending moment of control cross-section | |
| bending moment of control cross-section | |
| axial load | |
| ultimate load | |
| balance the axial force in the event of failure | |
| Nu,e | experimental data |
| Nu,t1 | theoretical data |
| column lateral deflection | |
| column lateral deflection | |
| x | height of the compression zone |
| xcb1 | the height of the neutral axis in the section |
| equivalent rectangular stress figure coefficient | |
| equivalent rectangular stress figure coefficient | |
| yielding strain of steel reinforcement | |
| ultimate strain of FRP bars | |
| maximum tensile strain of steel bar | |
| maximum tensile strain of GFRP bar | |
| maximum compressive strain of steel bar | |
| maximum compressive strain GFRP bar | |
| maximum compressive strain of concrete | |
| strain corresponding to the peak stress | |
| compressive strain of the FRP bars | |
| tensile strain of the FRP bars | |
| strain of steel reinforcement | |
| the height of the relative compression zone under boundary state 1 | |
| the height of the relative compression zone under boundary state 2 | |
| effective reinforcement ratio |
References
- Deng, B.Y.; Li, L.Z.; Tan, D.; Uddin, M.N.; Cai, Z.W.; Yu, K.Q. Sustainable and cost-effective ultra-lightweight engineered cementitious composite: Design and material characterization. Cem. Concr. Compos. 2023, 136, 104895. [Google Scholar] [CrossRef]
- Xiao, J.; Huang, L.; He, Z.; Qu, W.; Li, L.; Jiang, H.; Zhong, Z.; Long, X. Probabilistic models applied to concrete corrosion depth prediction under sulfuric acid environment. Measurement 2024, 234, 114807. [Google Scholar] [CrossRef]
- Xiao, J.; Zeng, H.; Huang, H.; Liu, L.; Li, L.; Yuan, B.; Zhong, Z. Experimental Investigation on the Influence of Strength Grade on the Surface Fractal Dimension of Concrete under Sulfuric Acid Attack. Buildings 2024, 14, 713. [Google Scholar] [CrossRef]
- Zhou, B.; Wu, R.; Feng, J.; Yin, S. Modeling of tensile behavior of hybrid GFRP-steel reinforced concrete chords. Compos. Struct. 2020, 236, 111853. [Google Scholar] [CrossRef]
- Scattarreggia, N.; Malomo, D.; DeJong, M.J. A new Distinct Element meso-model for simulating the rocking-dominated seismic response of RC columns. Earthq. Eng. Struct. Dyn. 2023, 52, 828–838. [Google Scholar] [CrossRef]
- Scattarreggia, N.; Qiao, T.Y.; Malomo, D. Earthquake Response Modeling of Corroded Reinforced Concrete Hollow-Section Piers via Simplified Fiber-Based FE Analysis. Sustainability 2021, 13, 9342. [Google Scholar] [CrossRef]
- Wu, G.; Dong, Z.; Wang, X.; Zhu, Y.; Wu, Z. Prediction of Long-Term Performance and Durability of BFRP Bars under the Combined Effect of Sustained Load and Corrosive Solutions. J. Compos. Constr. 2015, 19, 4014058. [Google Scholar] [CrossRef]
- Ibrahim, M.; Asadian, A.; Galal, K. A simplified approach for design of steel-GFRP hybrid reinforced concrete sections. Eng. Struct. 2023, 278, 115352. [Google Scholar] [CrossRef]
- Xu, J.; Zhu, P.; Ma, Z.J.; Qu, W. Fatigue flexural analysis of concrete beams reinforced with hybrid GFRP and steel bars. Eng. Struct. 2019, 199, 109635. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, M. Behaviour of inorganic polymer concrete columns reinforced with basalt FRP bars under eccentric compression: An experimental study. Compos. Part B Eng. 2016, 104, 44–56. [Google Scholar] [CrossRef]
- Sim, J.; Park, C.; Moon, D.Y. Characteristics of basalt fiber as a strengthening material for concrete structures. Compos. Part B Eng. 2005, 36, 504–512. [Google Scholar] [CrossRef]
- Lu, C.; Qi, Z.; Zheng, Y.; Xuan, G.; Yan, Y. Long-term tensile performance of GFRP bars in loaded concrete and aggressive solutions. J. Build. Eng. 2023, 64, 105587. [Google Scholar] [CrossRef]
- Kara, I.F.; Ashour, A.F.; Köroğlu, M.A. Flexural behavior of hybrid FRP/steel reinforced concrete beams. Compos. Struct. 2015, 129, 111–121. [Google Scholar] [CrossRef]
- Zhu, P.; Xu, J.; Qu, W.; Hao, H. Experimental Study of Fatigue Flexural Performance of Concrete Beams Reinforced with Hybrid GFRP and Steel Bars. J. Compos. Constr. 2017, 21, 4017036. [Google Scholar] [CrossRef]
- Qu, W.; Zhang, X.; Huang, H. Flexural Behavior of Concrete Beams Reinforced with Hybrid (GFRP and Steel) Bars. J. Compos. Constr. 2009, 13, 350–359. [Google Scholar] [CrossRef]
- Pang, L.; Qu, W.; Zhu, P.; Xu, J. Design Propositions for Hybrid FRP-Steel Reinforced Concrete Beams. J. Compos. Constr. 2016, 20, 4015086. [Google Scholar] [CrossRef]
- Gu, X.; Dai, Y.; Jiang, J. Flexural behavior investigation of steel-GFRP hybrid-reinforced concrete beams based on experimental and numerical methods. Eng. Struct. 2020, 206, 110117. [Google Scholar]
- Lu, C.; Cai, Q.; Xu, K.; Sha, X.; Yan, Y. Comparison of flexural behaviors between plain and steel-fiber-reinforced concrete beams with hybrid GFRP and steel bars. Structures 2022, 43, 1–11. [Google Scholar] [CrossRef]
- Moolaei, S.; Sharbatdar, M.K.; Kheyroddin, A. Experimental evaluation of flexural behavior of HPFRCC beams reinforced with hybrid steel and GFRP bars. Compos. Struct. 2021, 275, 114503. [Google Scholar] [CrossRef]
- Aiello, M.A.; Ombres, L. Structural Performances of Concrete Beams with Hybrid (Fiber-Reinforced Polymer-Steel) Reinforcements. J. Compos. Constr. 2002, 6, 133–140. [Google Scholar] [CrossRef]
- Lau, D.; Pam, H.J. Experimental study of hybrid FRP reinforced concrete beams. Eng. Struct. 2010, 32, 3857–3865. [Google Scholar] [CrossRef]
- De Luca, A.; Matta, F.; Nanni, A. Behavior of Full-Scale Glass Fiber-Reinforced Polymer Reinforced Concrete Columns under Axial Load. ACI Struct. J. 2010, 107, 589–596. [Google Scholar]
- Tobbi, H.; Farghaly, A.S.; Benmokrane, B. Concrete Columns Reinforced Longitudinally and Transversally with Glass Fiber-Reinforced Polymer Bars. ACI Struct. J. 2012, 109, 551–558. [Google Scholar]
- Tobbi, H.; Farghaly, A.S.; Benmokrane, B. Strength Model for Concrete Columns Reinforced with Fiber-Reinforced Polymer Bars and Ties. ACI Struct. J. 2014, 111, 789–798. [Google Scholar] [CrossRef]
- Mohamed, H.M.; Afifi, M.Z.; Benmokrane, B. Performance Evaluation of Concrete Columns Reinforced Longitudinally with FRP Bars and Confined with FRP Hoops and Spirals under Axial Load. J. Bridge Eng. 2014, 19, 4014020. [Google Scholar] [CrossRef]
- Hamed, R.Z.; Hassan, H.F. Structural behavior of GFRP-RC slender columns under various eccentricity loading conditions. Civ. Environ. Eng. 2023, 19, 1–16. [Google Scholar] [CrossRef]
- Xue, W.C.; Peng, F.; Fang, Z.Q. Behavior and Design of Slender Rectangular Concrete Columns Longitudinally Reinforced with Fiber-Reinforced Polymer Bars. ACI Struct. J. 2018, 115, 311–322. [Google Scholar] [CrossRef]
- Choo, C.C.; Harik, I.E.; Gesund, H. Strength of rectangular concrete columns reinforced with fiber-reinforced polymer bars. ACI Struct. J. 2006, 103, 452–459. [Google Scholar]
- Choo, C.C.; Harik, I.E.; Gesund, H. Minimum reinforcement ratio for fiber-reinforced polymer reinforced concrete rectangular columns. ACI Struct. J. 2006, 103, 460–466. [Google Scholar]
- Zadeh, H.J.; Nanni, A. Flexural stiffness and second-order effects in fiber-reinforced polymer-reinforced concrete frames. ACI Mater. J. 2017, 114, 533–544. [Google Scholar]
- Peng, F.; Xue, W. Calculation approach of ultimate capacity of FRP reinforced concrete columns under eccentric compression. Jianzhu Jiegou Xuebao/J. Build. Struct. 2018, 39, 147–155. [Google Scholar]
- Roudsari, S.S.; Ungureanu, L.M.; Soroushnia, S.; Abu-Lebdeh, T.; Petrescu, F.I.T. Optimization of fiber-reinforced polymer bars for reinforced concrete column using nonlinear finite element algorithms. Algorithms, 2022; 15, 12. [Google Scholar] [CrossRef]
- Ibrahim, A.M.A.; Wu, Z.; Fahmy, M.F.M.; Kamal, D. Experimental Study on Cyclic Response of Concrete Bridge Columns Reinforced by Steel and Basalt FRP Reinforcements. J. Compos. Constr. 2016, 20, 4015062. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design Concrete Structures. Ministry of Construction of the People’s Republic of China, China Building Industry Press: Beijing, China, 2015.
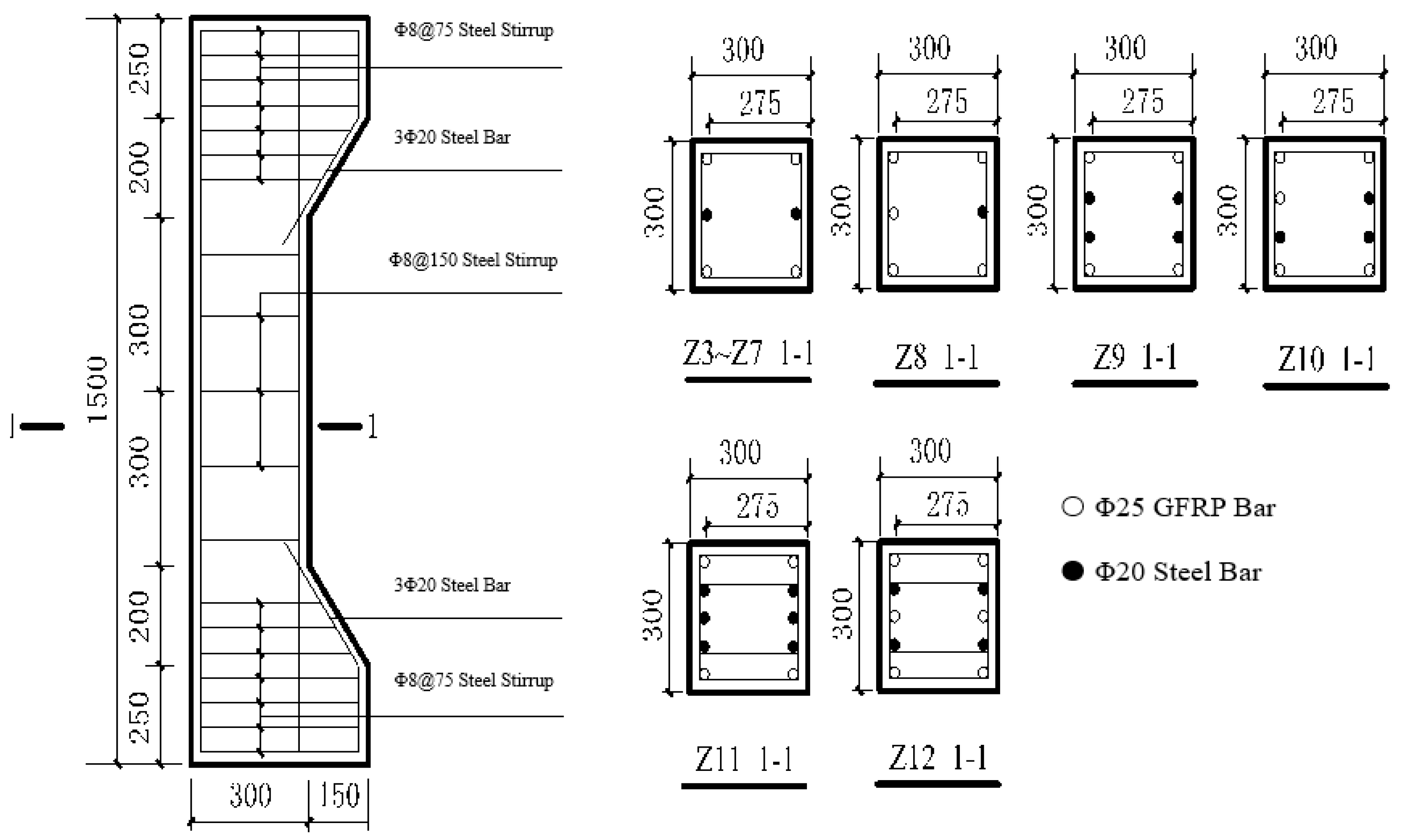
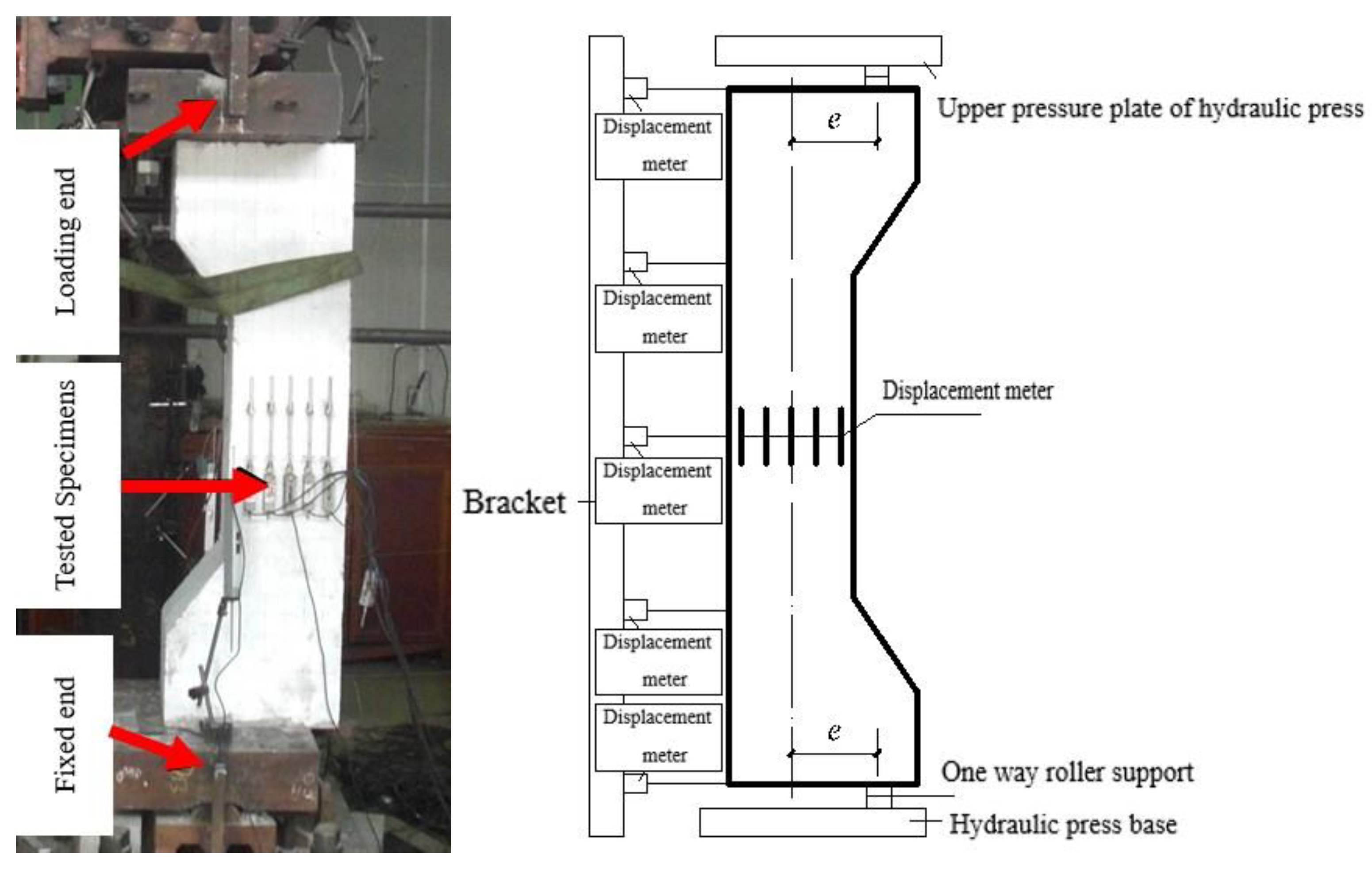
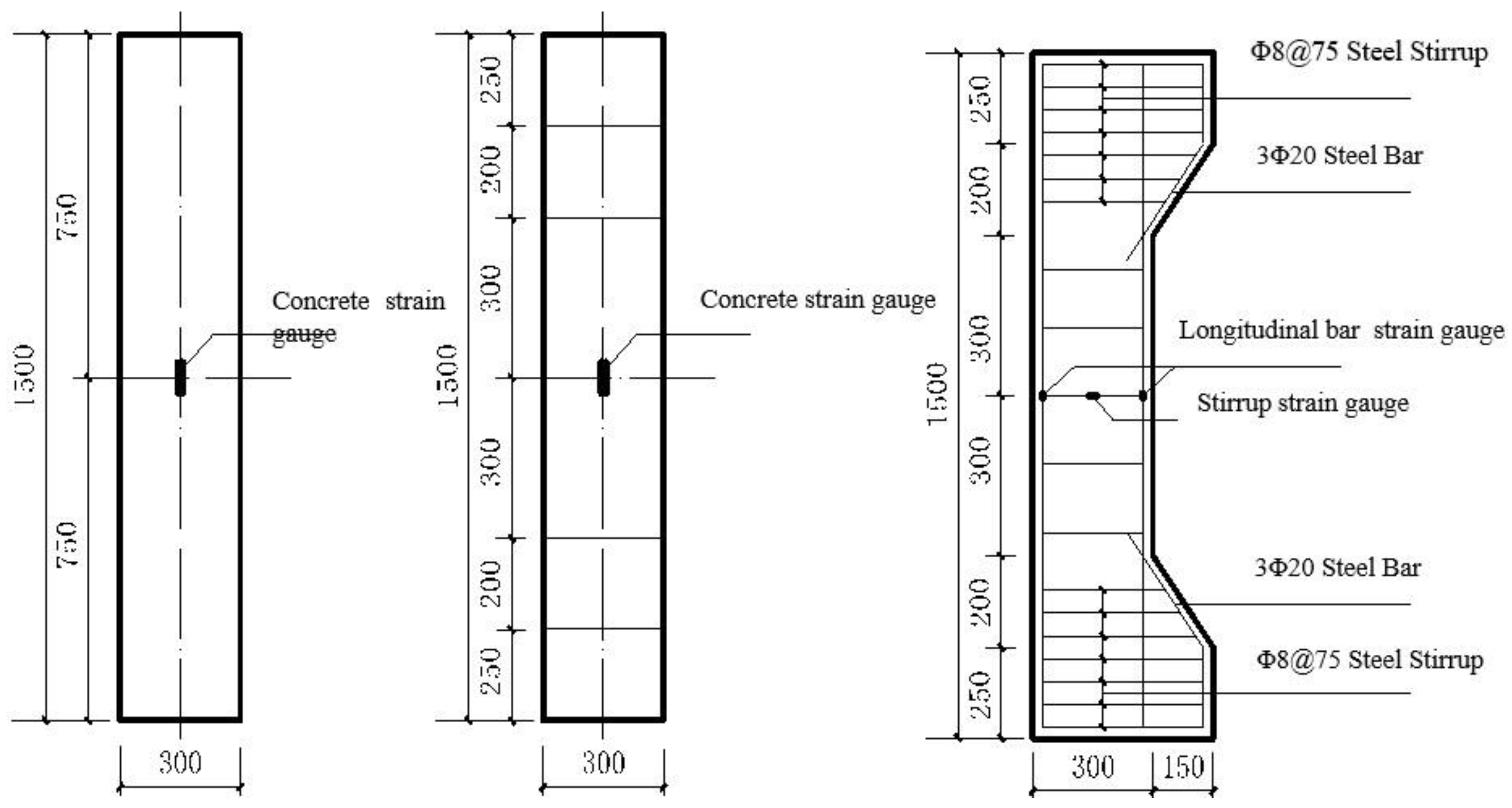



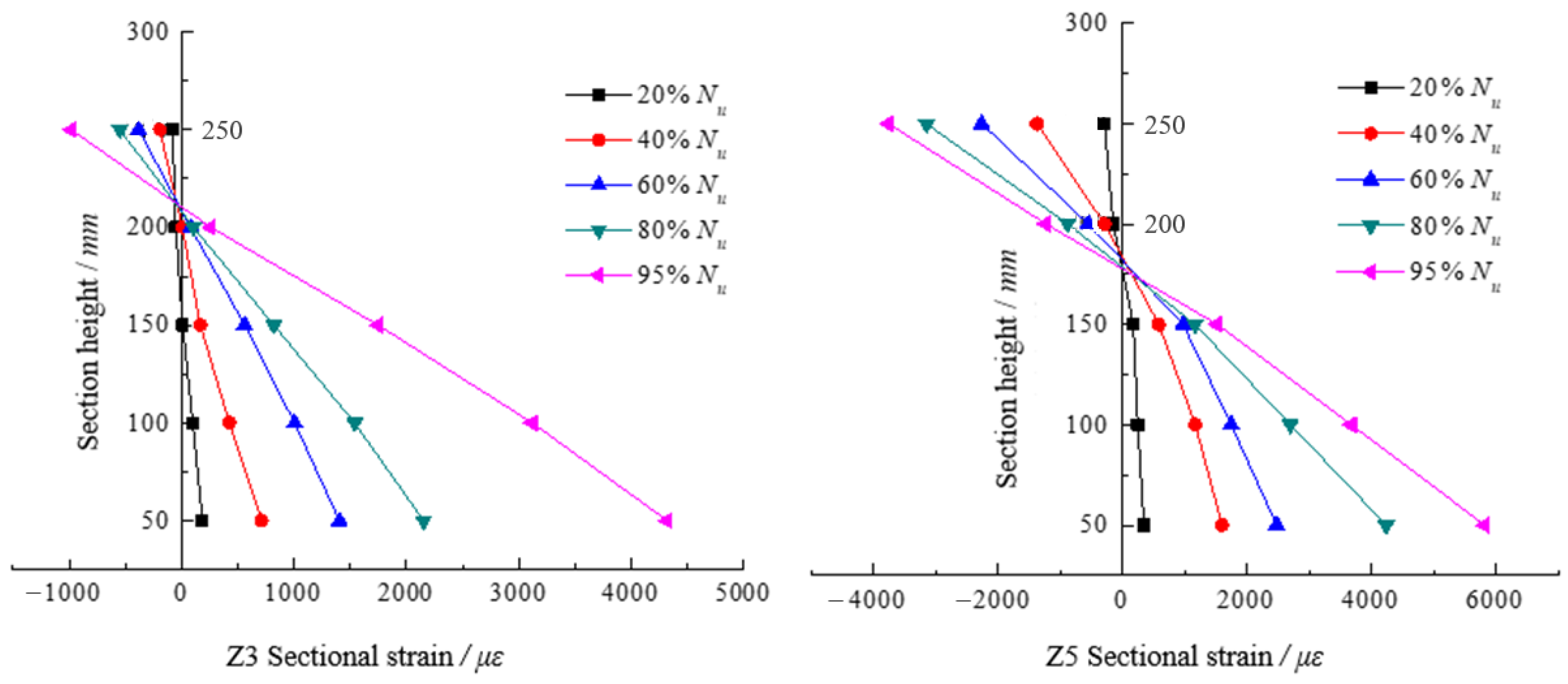


| Specimen Number | [15] | ||||
|---|---|---|---|---|---|
| Z3 | 200 | 226.2 | 1964 | 0.67 | 46.2 |
| Z4 | 110 | 226.2 | 1964 | 0.67 | 46.2 |
| Z5 | 130 | 226.2 | 1964 | 0.67 | 46.2 |
| Z6 | 200 | 226.2 | 1964 | 0.67 | 27.3 |
| Z7 | 130 | 226.2 | 1964 | 0.67 | 27.3 |
| Z8 | 200 | 113.1 | 2455 | 0.66 | 46.2 |
| Z9 | 200 | 452.4 | 1964 | 0.92 | 46.2 |
| Z10 | 200 | 339.3 | 2455 | 0.91 | 46.2 |
| Z11 | 200 | 678.6 | 1964 | 1.18 | 46.2 |
| Z12 | 200 | 452.4 | 2946 | 1.14 | 46.2 |
| Model | ||||||
|---|---|---|---|---|---|---|
| HRB335 | 12 | 375 | 555 | 200 | 0.1875 | >10 |
| HPB235 | 8 | 300 | 465 | 205 | 0.1463 | >10 |
| 25 | 837 | 40.4 | 2.09 |
| Model | Loading Method | |||||
|---|---|---|---|---|---|---|
| GFRP Bars | 25 | End-strengthening method | 194 | 535 | —— | —— |
| 138 | 394 | 37 | 1.06 |
| Specimen Number | Horizontal Cracking Load Ncr/kN | Vertical Cracking Load Ncr/kN | Nu/kN | Crack Width d/mm | Average Crack Spacing D/cm | Remarks |
|---|---|---|---|---|---|---|
| Z3 | 85 | 340 | 678 | 0.12 | 13.9 | —— |
| Z4 | 220 | 1000 | 1245 | 0.08 | 14.9 | Longitudinal cracking of compressed GFRP bars |
| Z5 | 180 | 960 | 1064 | 0.10 | 16.3 | Same as Z4 |
| Z6 | 100 | 340 | 564 | 0.06 | 14.3 | —— |
| Z7 | 250 | 630 | 728 | 0.05 | 14.0 | Same as Z4 |
| Z8 | 120 | 450 | 786 | 0.10 | 14.3 | —— |
| Z9 | 175 | 500 | 776 | 0.05 | 12.3 | —— |
| Z10 | 125 | 610 | 790 | 0.10 | 13.8 | —— |
| Z11 | 175 | 830 | 854 | 0.10 | 13.9 | Same as Z4 |
| Z12 | 90 | 650 | 843 | 0.10 | 13.3 | —— |
| Specimen Number | Tensile Reinforcement Yield εs = 1875 με | Maximum Bearing Capacity | Failure Mode | ||||
|---|---|---|---|---|---|---|---|
| Axial Load Ny/kN | Column Lateral Deflection Vy/mm | Bending Moment of Control Cross-Section My/kN·m | Ultimate Load Nu/kN | Column Lateral Deflection Vu/mm | Bending Moment of Control Cross-Section Mu/kN·m | ||
| Z3 | 343.0 | 1.7 | 69.2 | 678 | 6.5 | 140.0 | A |
| Z4 | 1180.5 | 2.3 | 132.6 | 1245 | 2.7 | 140.3 | A |
| Z5 | 721.5 | 1.5 | 94.9 | 1064 | 3.9 | 142.5 | A |
| Z6 | 299.0 | 1.7 | 60.3 | 564 | 17.8 | 122.8 | B |
| Z7 | 539.5 | 2.2 | 71.3 | 728 | 6.2 | 99.2 | B |
| Z8 | 388.0 | 1.8 | 78.3 | 786 | 5.9 | 161.8 | C |
| Z9 | 382.5 | 1.5 | 77.1 | 776 | 5.1 | 159.2 | B |
| Z10 | 342.5 | 1.4 | 69.0 | 790 | 5.3 | 162.2 | A |
| Z11 | 398.5 | 1.7 | 80.4 | 854 | 6.1 | 176.0 | A |
| Z12 | 447.5 | 1.0 | 89.9 | 843 | 4.3 | 172.2 | A |
| Specimen Number | Maximum Tensile Strain of Longitudinal Bar | Maximum Compressive Strain of Longitudinal Bar | Maximum Compressive Strain of Concrete εcu/με | ||
|---|---|---|---|---|---|
| Steel Bar εsu/με | GFRP Bar εfu/με | Steel Bar /με | GFRP Bar /με | ||
| Z3 | 5030 | 4829 | −1881 | −2505 | −3631 |
| Z4 | 1921 | 1473 | −1847 | −1355 | −3424 |
| Z5 | 6403 | 2648 | −1993 | −2836 | −2750 |
| Z6 | 4351 | 7557 | −6977 | −4139 | −2253 |
| Z7 | 2390 | 2650 | −3312 | −2919 | −3010 |
| Z8 | —— | 2836 | −2435 | −1343 | −3657 |
| Z9 | 2800 | 2943 | −3396 | −2027 | −3525 |
| Z10 | 3857 | 2460 | −1932 | −2442 | −2634 |
| Z11 | 4670 | 4577 | −1966 | −2406 | −3420 |
| Z12 | 5817 | 3086 | −1862 | −1605 | −3234 |
| Specimen Number | Longitudinal Reinforcement Stiffness Ratio (Rf) | Experimental Data Nu,e/kN | Theoretical Data Nu,t1/kN | Nu,t1/Nu,e | |
|---|---|---|---|---|---|
| Z3 | 8.7 | 1.8 | 678 | 647.1 | 0.96 |
| Z4 | 8.7 | 1.8 | 1245 | 1150.3 | 0.92 |
| Z5 | 8.7 | 1.8 | 1064 | 982.7 | 0.92 |
| Z6 | 8.7 | 1.8 | 564 | 475.2 | 0.84 |
| Z7 | 8.7 | 1.8 | 728 | 693.3 | 0.95 |
| Z8 | 21.7 | 4.4 | 786 | 691.0 | 0.88 |
| Z9 | 4.3 | 0.9 | 776 | 698.6 | 0.90 |
| Z10 | 7.2 | 1.5 | 790 | 738.9 | 0.94 |
| Z11 | 2.9 | 0.6 | 854 | 750.2 | 0.88 |
| Z12 | 6.5 | 1.3 | 843 | 789.3 | 0.94 |
| Average | 0.91 | ||||
| Standard deviation | 0.04 | ||||
| Coefficient of variation | 0.044 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, L.; Han, Z.; Xiao, J.; Liu, Z.; Qu, W.; Dong, S. Bearing Capacity of Hybrid (Steel and GFRP) Reinforced Columns under Eccentric Loading: Theory and Experiment. Buildings 2024, 14, 2472. https://doi.org/10.3390/buildings14082472
Pang L, Han Z, Xiao J, Liu Z, Qu W, Dong S. Bearing Capacity of Hybrid (Steel and GFRP) Reinforced Columns under Eccentric Loading: Theory and Experiment. Buildings. 2024; 14(8):2472. https://doi.org/10.3390/buildings14082472
Chicago/Turabian StylePang, Lei, Zebin Han, Jie Xiao, Zexuan Liu, Wenjun Qu, and Sansheng Dong. 2024. "Bearing Capacity of Hybrid (Steel and GFRP) Reinforced Columns under Eccentric Loading: Theory and Experiment" Buildings 14, no. 8: 2472. https://doi.org/10.3390/buildings14082472
APA StylePang, L., Han, Z., Xiao, J., Liu, Z., Qu, W., & Dong, S. (2024). Bearing Capacity of Hybrid (Steel and GFRP) Reinforced Columns under Eccentric Loading: Theory and Experiment. Buildings, 14(8), 2472. https://doi.org/10.3390/buildings14082472






