Analytical Formulation and Optimization of the Initial Morphology of Double-Layer Cable Truss Flexible Photovoltaic Supports
Abstract
:1. Introduction
2. The Relationship between the Force and the Geometric Morphology of the Single-Cable Structure
2.1. Basic Assumption
- (1)
- The cable is ideally flexible, and can only be tensioned, not compressed or bent.
- (2)
- The material properties of cables conform to Hooke’s law without considering plastic deformation.
- (3)
- The strain of cables under the upper load is small.
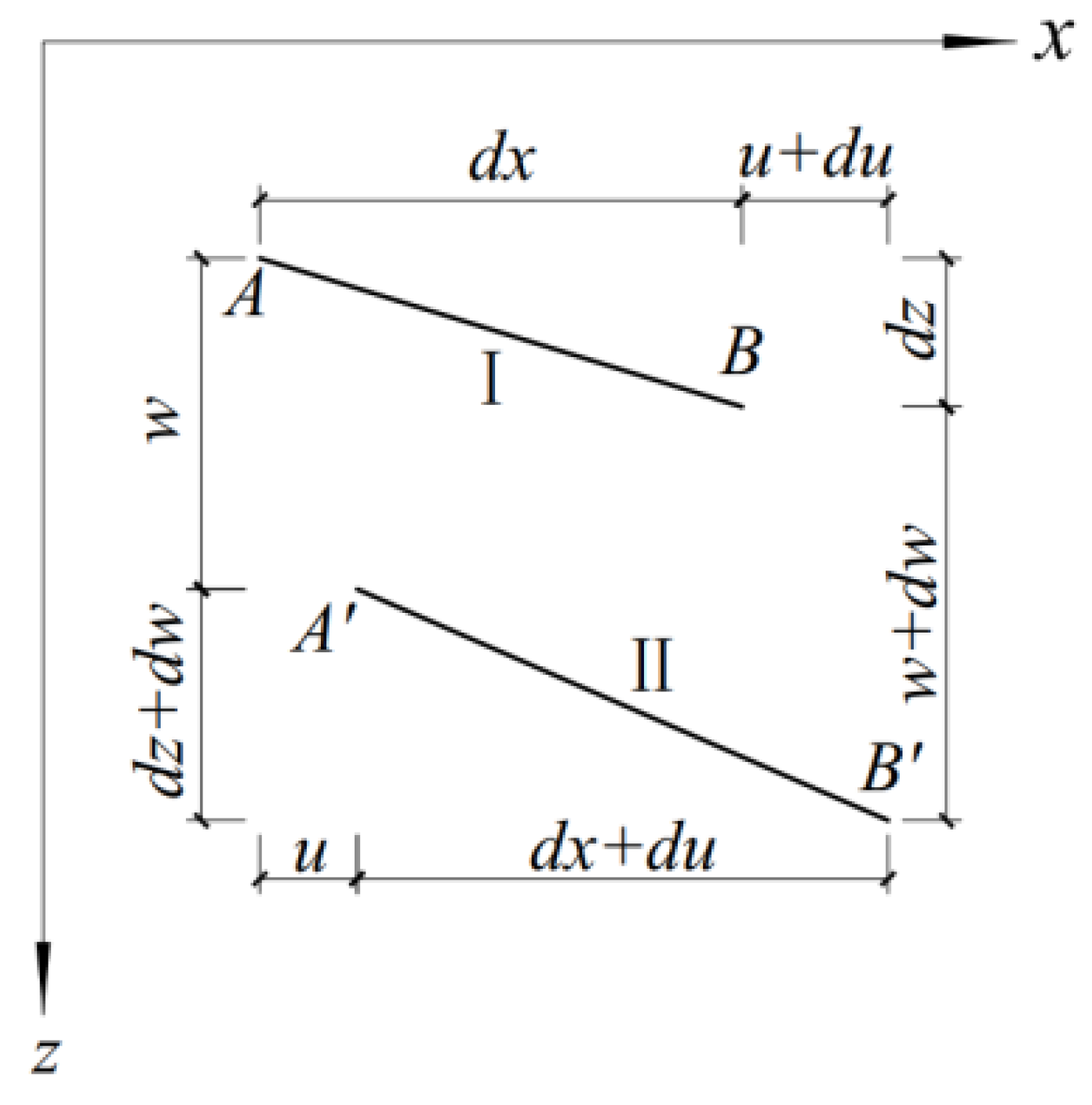
2.2. Deformation Coordination Equation
2.3. Analytical Formulations of Displacement and Cable Force
3. Analytical Formulation of Double-Layer Cable Flexible Photovoltaic Supports
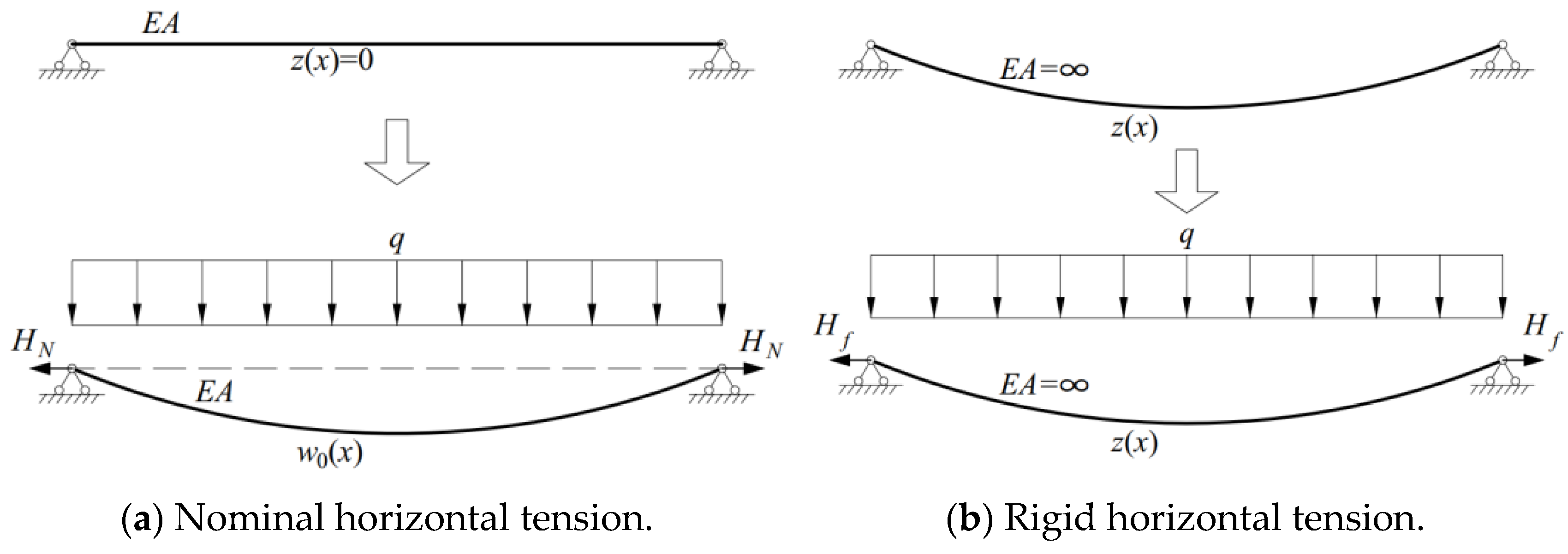
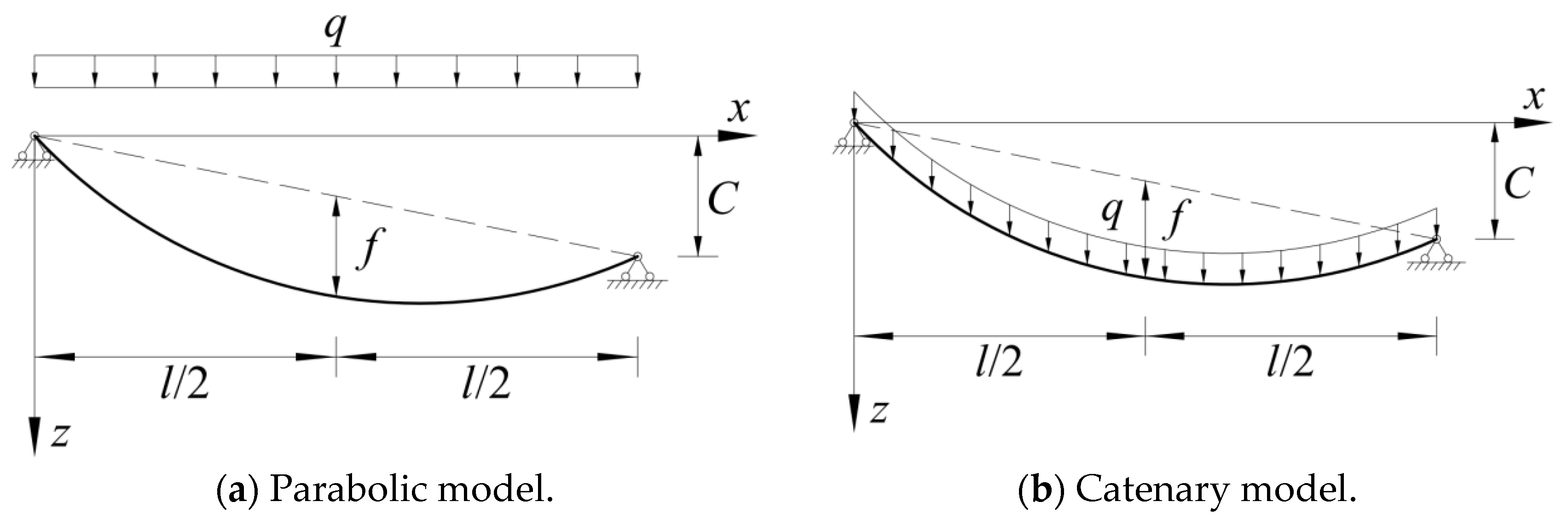
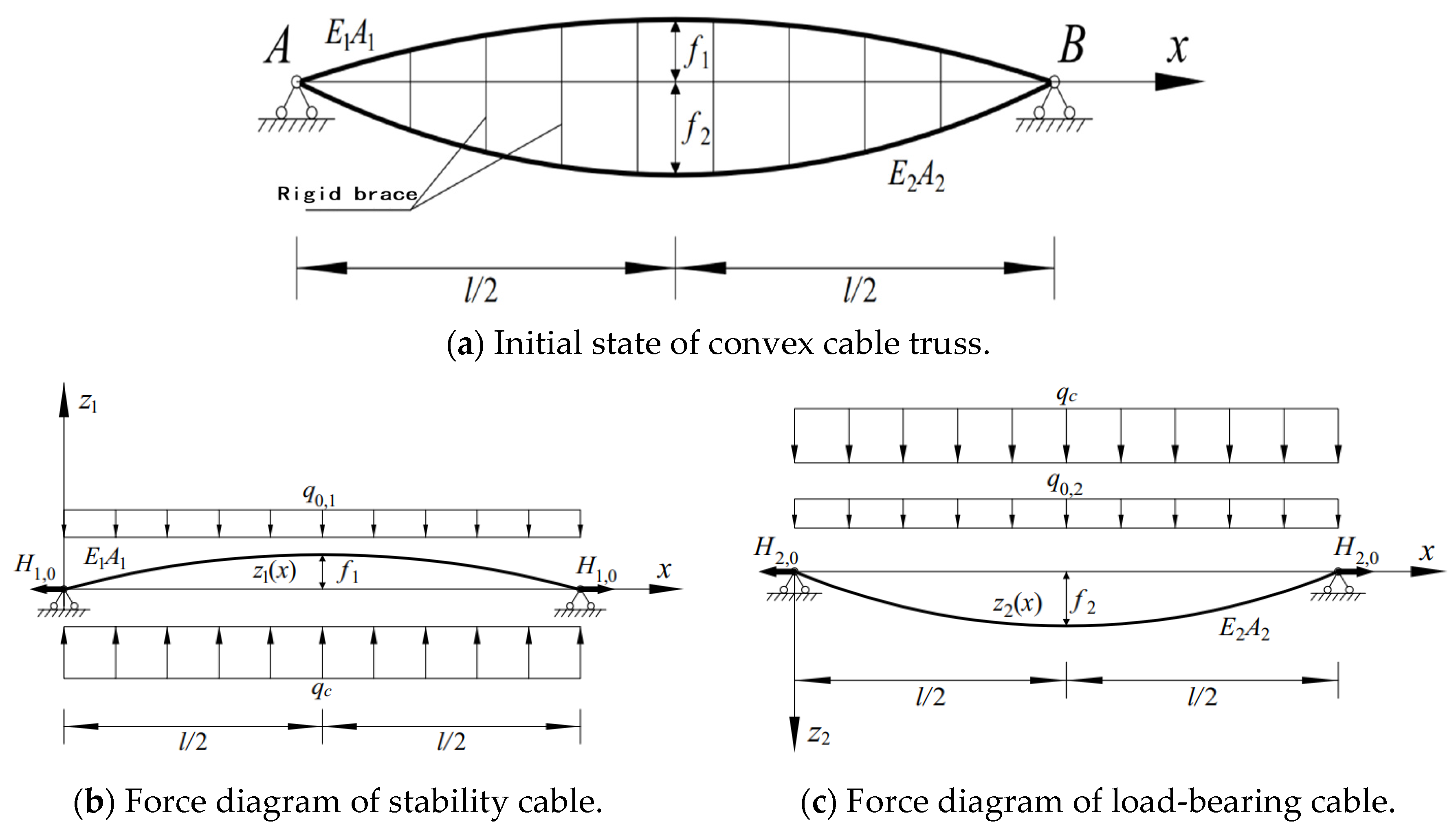
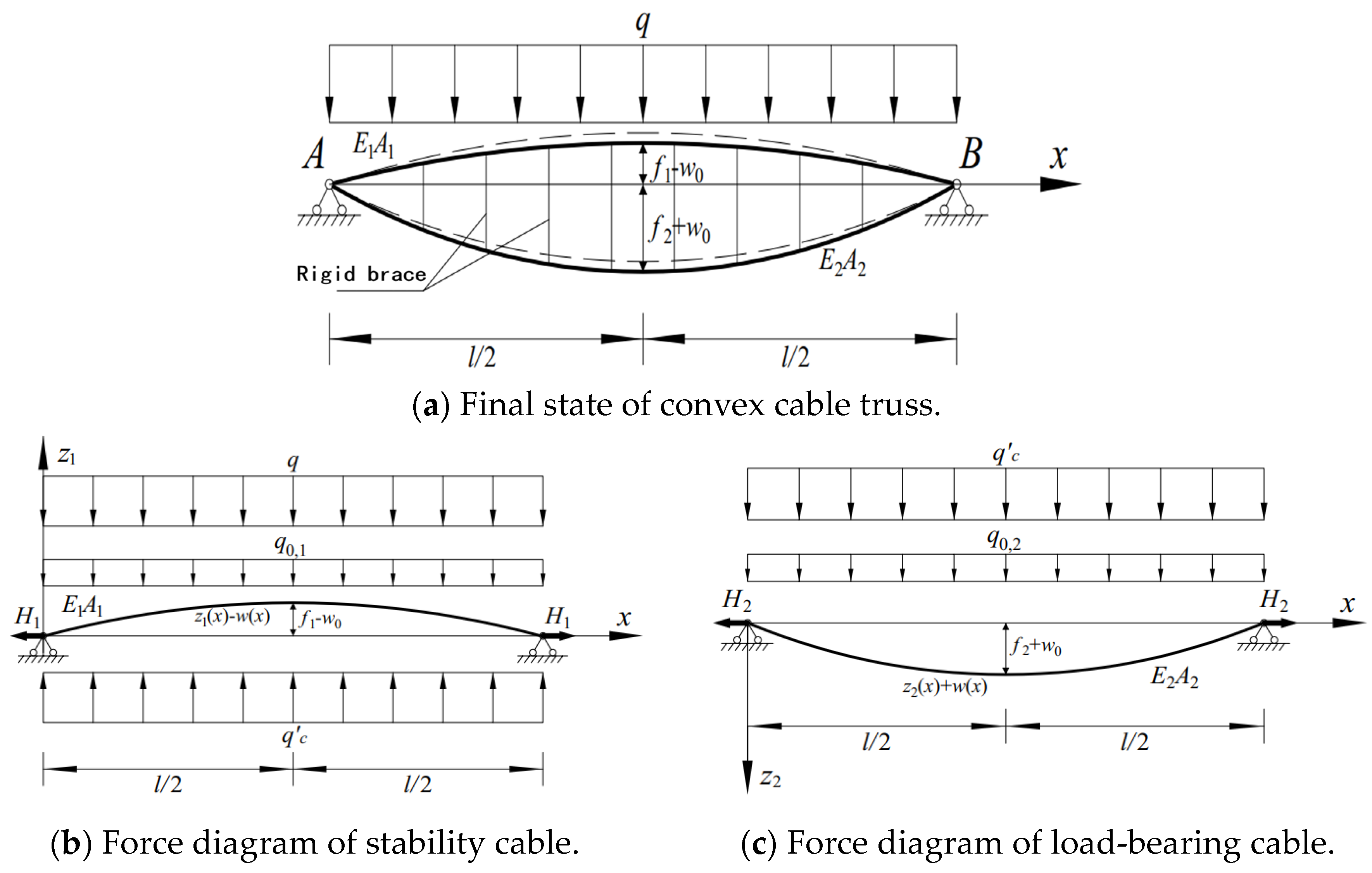
3.1. Structural Morphology and Load Assumption
- (1)
- Zero state: In this state, the cable only bears the initial prestress, without considering the effect of elastic elongation of the cable-on-cable force. It is assumed that cable force in this state is P.
- (2)
- Initial equilibrium state: The initial state refers to the self-equilibrium state of structure under prestress and dead weight. Assuming that the change in the cable length of the initial state from the zero state is Δs, and the cable force in this state is H0, through Hooke’s law, it can be deduced that .
- (3)
- The load equilibrium state, i.e., the final state, refers to the equilibrium state of structure under the external loads, assuming that the cable force in this state is H.
3.2. Analytical Formulation of Displacement
3.3. Analytical Formulation of Cable Force
4. The Finite Element Verification of Analytical Formulation
4.1. Finite Element Model
4.2. Comparison of Finite Element Calculation Results
4.2.1. Displacement
4.2.2. Cable Force
5. Mathematical Model of Optimization of the Initial Morphology
5.1. Optimization Objective
5.2. Optimization Variable
5.3. Constraint Condition
- (1)
- The maximum deformation of the structure meets the deflection control requirements.
- (2)
- In the serviceability limit state, the lower cables of cable truss structure are allowed to relax, while the upper cables are not allowed to relax.
- (3)
- In the ultimate limit state, the cables meet the strength limit requirements.
5.4. Load Case
5.5. The Mathematical Model of Structural Optimization
- (1)
- Firstly, the minimum prestress H1,0 and H2,0, satisfying the constraint conditions, are determined according to the fact that the cable cannot relax under any standard load combination. When the structure is subjected to a downward load q1, it is assumed that the structural deformation reaches the maximum limit [Δ]; at the same time, the upper stability cables still need to have a certain amount of cable stress, i.e., the minimum allowable stress, σ1,min. Equation (51) can be obtained by substituting them into Equation (41). If the vector height f1 in the initial state of the stability cable is known, then H1,0,min are deterministic quantities. In the same way, the minimum prestress H2,0,min of the lower load-bearing cable can be calculated when the structure is subjected to the upward load q2.
- (2)
- According to the equilibrium conditions of the initial state, the following equation can be established:
- (3)
- Following the previous two steps, the initial morphology of the cable truss can be obtained under the condition that the maximum deflection control index is met. If the lower load-bearing cable is not allowed to relax in the serviceability limit state, it is necessary to check whether the load-bearing cable force H2 meets the allowable minimum stress requirements under the upward variable load q2. If it does not meet the requirements, it is necessary to increase H2,0 and H1,0, correspondingly. Finally, the bearing capacity of the stability cable and the load-bearing cable is checked. According to Equation (43), the deformation of the structure under the basic combination and is calculated, and the maximum cable force of the load-bearing cable under the load and the maximum cable force of the stability cable under the load are calculated according to the deformation. If both and do not exceed the design bearing capacity corresponding to the selected cable size, the iteration is terminated. Otherwise, the cable area is increased and the iterative solution is continued.
6. Example of Optimization of the Initial Morphology
6.1. No Slack in Lower Load-Bearing Cable
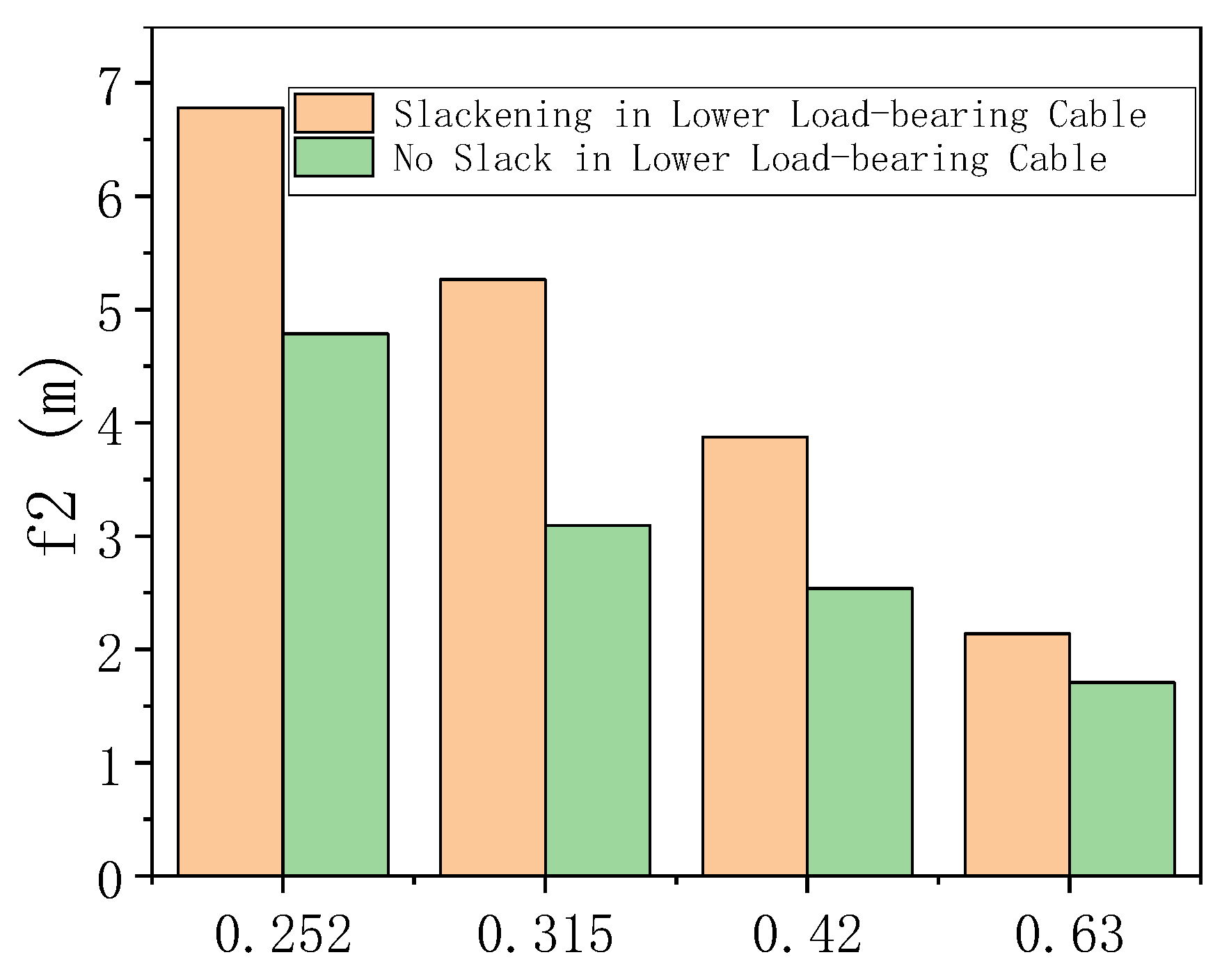
6.2. Slackening in Lower Load-Bearing Cable
6.3. Economic Discussion
7. Conclusions
- (1)
- Based on the theory of cable structure design, the relationship between morphology and internal force of single-cable structure is deduced, and the analytical method for solving the internal force and displacement of CTFPS structure under uniform load is provided. By comparing to the results of finite element analysis, the error of displacement is less than 3%, and the error of the cable force is less than 4%, which verifies the accuracy of the analytical formulations.
- (2)
- So far, there is no relevant specification to stipulate a reasonable value range of deflection deformation of flexible photovoltaic support, this paper establishes a finite element analysis model of the flexible photovoltaic support structure and analyzes the cable force and displacement under the static action. It is suggested that the deflection deformation of the double-layer cable truss structure should be taken as 1/100 of the single span.
- (3)
- According to the analytical formulations, a mathematical model for optimizing the initial morphology is proposed with the objective of reducing the construction cost of flexible photovoltaic supports, which achieves the optimization objective of minimizing the cable force, i.e., minimizing the cable specification.
- (4)
- For CTFPS structure, compared with ensuring that the lower load-bearing cable is always in the tension state under serviceability limit state, allowing it to relax under wind suction load can effectively reduce the cable specification. Therefore, it is recommended that the lower load-bearing cable is allowed to relax during the structural design.
- (5)
- For CTFPS structures, the stability cables can be pre-arched to bring their mid-span vector height up to the deflection deformation limits. With the increase in the prestress of the load-bearing cable, the brace height required to maintain the structural deformation limit decreases gradually, but the specification of the load-bearing cable increases accordingly. Therefore, when choosing the most economical morphology, it is necessary to comprehensively consider the cost of both steel structure and cables, and it is recommended that the total height of the mid-span should be between 1/20 and 1/15 of the single span of the structure.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, F.; Shang, R.; Sun, Y. Tension and Deformation Analysis of Suspension Cable of Flexible Photovoltaic Support under Concentrated Load with Small Rise-span Ratio. J. Phys. Conf. Ser. 2022, 2381, 12069. [Google Scholar] [CrossRef]
- Ding, H.; He, X.; Jing, H.; Wu, X.; Weng, X. Design Method of Primary Structures of a Cost-Effective Cable-Supported Photovoltaic System. Appl. Sci. 2023, 13, 2968. [Google Scholar] [CrossRef]
- Desai, Y.M.; Popplewell, N.; Shah, A.H.; Buragohain, D.N. Geometric nonlinear static analysis of cable supported structures. Comput. Struct. 1988, 29, 1001–1009. [Google Scholar] [CrossRef]
- Bartholet, F.P.; Büchel, A. Solar Wings a new Lightweight PV Tracking System. In Proceedings of the 23rd European Photovoltaic Solar Energy Conference and Exhibition, Valencia, Spain, 1–5 September 2008. [Google Scholar]
- Li, Z.; Zhai, J.; Wu, C.; Wang, Y.; Zhang, P.; Jiang, S.; Guo, Z. Parametric Analysis of Structural Design of Flexible Photovoltaic Supports with Single-Layer Cable System. J. Taiyuan Univ. Technol. 2024. [Google Scholar]
- Zhang, L.; Zhao, J.K. Analysis of the Effects of Initial Tension and Upper Arch of Cords on Internal Forces and Structural Displacements of Cords in Flexible Photovoltaic Supports with Cord Trusses. In Proceedings of the 2024 Conference on Seismic Technology for Engineering Structures, Kunming, China, 2–4 August 2024. [Google Scholar]
- Du, Z.; Meimeti Aili, A.; Ma, X.; Zhao, Y.; Du, Y.; Zhi, C. Research on Structural Selection and Static Performance Analysis of Flexible Photovoltaic Supports. Build. Technol. 2024, 55, 1777–1782. [Google Scholar] [CrossRef]
- Yuan, H.-X.; Song, J.-M.; Du, X.-X.; Wang, R.-L.; Ma, W.-Y. Study on the Structural Stress Performance of Flexible Photovoltaic Supports with Double-Layer Cable System. J. Shenyang Univ. Archit. (Nat. Sci. Ed.) 2024, 40, 395–403. [Google Scholar]
- He, X.; Ding, H.; Jing, H.; Wu, X.; Weng, X. Mechanical characteristics of a new type of cable-supported photovoltaic module system. Sol. Energy 2021, 226, 408–420. [Google Scholar] [CrossRef]
- Shen, W.; Zeng, Y.; Zhang, W.; Tang, Z.; Xie, H. Structural design and simulation analysis of fixed adjustable photovoltaic support. J. Comput. Methods Sci. Eng. 2023, 23, 1409–1423. [Google Scholar] [CrossRef]
- Kilikevicius, A.; Cereska, A.; Kilikevicien, K. Analysis of external dynamic loads influence to photovoltaic module structural performance. Eng. Fail. Anal. 2016, 66, 445–454. [Google Scholar] [CrossRef]
- Bao, T.; Li, Z.; Pu, O.; Chan, R.W.K.; Zhao, Z.; Pan, Y.; Yang, Y.; Huang, B.; Wu, H. Modal analysis of tracking photovoltaic support system. Sol. Energy 2023, 265, 112088. [Google Scholar] [CrossRef]
- Tang, J.F.; Lin, J.P.; Huo, J.S. Structural Characterisation of Flexible Photovoltaic Supports and Their Optimal Design. J. Huaqiao Univ. (Nat. Sci. Ed.) 2019, 40, 331–337. [Google Scholar]
- Chen, F.; Zhu, Y.; Wang, W.; Shu, Z.; Li, Y. A Review on Aerodynamic Characteristics and Wind-Induced Response of Flexible Support Photovoltaic System. Atmosphere 2023, 14, 731. [Google Scholar] [CrossRef]
- Xu, H.; Ding, K.; Shen, G.; Du, H.; Chen, Y. Experimental investigation on wind-induced vibration of photovoltaic modules supported by suspension cables. Eng. Struct. 2024, 299, 117125. [Google Scholar] [CrossRef]
- Liu, J.; Li, S.; Luo, J.; Chen, Z. Experimental study on critical wind velocity of a 33-meter-span flexible photovoltaic support structure and its mitigation. J. Wind. Eng. Ind. Aerodyn. 2023, 236, 105355. [Google Scholar] [CrossRef]
- Li, J.; Hong, G.; Xu, H. Wind Load Effects and Gust Loading Factor for Cable-Suspended Photovoltaic Structures. Energies 2024, 17, 38. [Google Scholar] [CrossRef]
- Abiola-Ogedengbe, A.; Hangan, H.; Siddiqui, K. Experimental investigation of wind effects on a standalone photovoltaic (PV) module. Renew. Energy 2015, 78, 657–665. [Google Scholar] [CrossRef]
- Jubayer, C.M.; Hangan, H. Numerical simulation of wind effects on a stand-alone ground mounted photovoltaic (PV) system. J. Wind. Eng. Ind. Aerodyn. 2014, 134, 56–64. [Google Scholar] [CrossRef]
- Alan, G.; Davenport, A.A. Gust Loading Factors. J. Struct. Div. 1967, 93. [Google Scholar] [CrossRef]
- Tamura, Y.; Kim, Y.C.; Yoshida, A.; Itoh, T.; Feltrin, G. Wind-induced vibration experiment on solar wing. MATEC Web Conf. 2015, 24, 4006. [Google Scholar] [CrossRef]
- Kim, Y.C.; Tamura, Y.; Yoshida, A.; Ito, T.; Shan, W.; Yang, Q. Experimental investigation of aerodynamic vibrations of solar wing system. Adv. Struct. Eng. 2018, 21, 2217–2226. [Google Scholar] [CrossRef]
- Tan, Y.J.; Zheng, X.X.; Zhao, C.X.; Jin, S.H.; Ma, W.Y. Wind vibration response of a single-layer prestressed suspension photovoltaic support. Wind vibration response analysis of single-layer prestressed suspension photovoltaic supports. J. Wuhan Univ. (Eng. Ed.) 2022, 55, 68–71. [Google Scholar]
- Finotto, V.C.; Da Silva, W.R.L.; Valášek, M.; Atemberk, P. Hybrid fuzzy-genetic system for optimising cabled-truss structures. Adv. Eng. Softw. 2013, 62–63, 85–96. [Google Scholar] [CrossRef]
- Ma, S.; Yuan, X.; Deng, M.; Yang, L. Minimal mass design of a new cable truss in two states. Mech. Res. Commun. 2022, 125, 103995. [Google Scholar] [CrossRef]
- Barbón, A.; Bayón-Cueli, C.; Bayón, L.; Carreira-Fontao, V. A methodology for an optimal design ofground-mounted photovoltaic power plants. Appl. Energy 2022, 314, 118881. [Google Scholar] [CrossRef]
- Li, X.; Zhu, J.; Wang, J.; Zhang, W. Topology optimization for prestressed cable-truss structure considering geometric nonlinearity. Struct. Multidiscip. Optim. 2023, 66, 201. [Google Scholar] [CrossRef]
- Lou, Y.; Zhang, J.; Pan, Y. Static and Dynamic Response Analysis of Flexible Photovoltaic Mounts. Buildings 2024, 14, 2037. [Google Scholar] [CrossRef]
- Wang, X.; Ji, G.; Gu, H.; Lv, S.; Ni, H.; Wang, P.; Chen, K.; Meng, Y. Research and Design of Fixed Photovoltaic Support Structure Based on SAP2000. MATEC Web Conf. 2018, 166, 3002. [Google Scholar] [CrossRef]
- Li, X.; Xue, S.; Li, X. Prestress design and geometric correction method of cable-truss structures based on equivalent equilibrium force model. Thin-Walled Struct. 2023, 191, 111058. [Google Scholar] [CrossRef]
- Barbón, A.; Carreira-Fontao, V.; Bayón, L.; Silva, C.A. Optimal design and cost analysis of single-axis tracking photovoltaic power plants. Renew. Energy 2023, 211, 626–646. [Google Scholar] [CrossRef]
- Chen, Z.; Cao, H.; Zhu, H.; Hu, J.; Li, S. A simplified structural mechanics model for cable-truss footbridges and its implications for preliminary design. Eng. Struct. 2014, 68, 121–133. [Google Scholar] [CrossRef]
- JGJ257-2012; Technical Specification for Cable Structures. China Construction Industry Press: Beijing, China, 2012; Volume 42, p. 136.
- Huang, Z.Y. Conceptual Design Study on Performance and Morphology of Suspension Structures; China Academy of Building Research Ltd.: Shenzhen, China, 2022. [Google Scholar]



| Case Number | Load Combination |
| 1 | Downward load q1 |
| 2 | Downward load q1 and temperature effect (−30 °C) |
| 3 | Downward load q1 and temperature effect (+30 °C) |
| 4 | Upward load q2 |
| 5 | Upward load q2 and temperature effect (−30 °C) |
| 6 | Upward load q2 and temperature effect (+30 °C) |
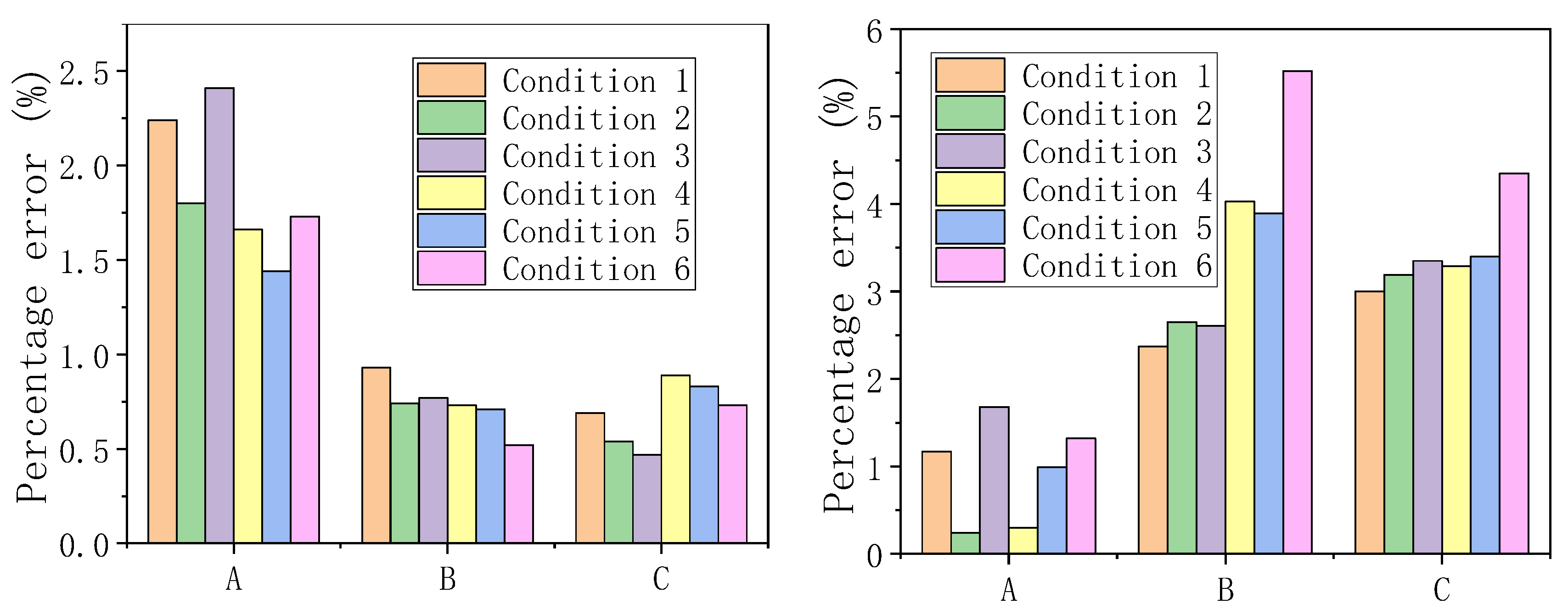
| Structural Response | Case Number | Analytical Result | Finite Element Result | Percentage Difference | |
|---|---|---|---|---|---|
| Mid-span Displacement w0/m | 1 | A | −0.4934 | −0.4508 | 9.45% |
| B | −0.4570 | 1.36% | |||
| C | −0.4504 | −0.09% | |||
| 2 | A | −0.4448 | −0.4092 | 8.72% | |
| B | −0.4130 | 0.93% | |||
| C | −0.4070 | −0.53% | |||
| 3 | A | −0.5404 | −0.4949 | 9.19% | |
| B | −0.4990 | 0.83% | |||
| C | −0.4918 | −0.62% | |||
| 4 | A | 0.3084 | 0.3218 | −4.17% | |
| B | 0.3270 | 1.63% | |||
| C | 0.3239 | 0.64% | |||
| 5 | A | 0.3302 | 0.3395 | −2.75% | |
| B | 0.3460 | 1.92% | |||
| C | 0.3434 | 1.13% | |||
| 6 | A | 0.2886 | 0.3024 | −4.56% | |
| B | 0.3104 | 2.67% | |||
| C | 0.3067 | 1.42% | |||
| Structural Response | Case Number | Analytical Result | Finite Element Result | Percentage Difference | |
|---|---|---|---|---|---|
| H1/kN | 1 | A | 259.7 | 265.7 | −2.24% |
| B | 263.2 | −0.93% | |||
| C | 263.9 | −0.69% | |||
| 2 | A | 298.5 | 304.0 | −1.80% | |
| B | 301.8 | −0.74% | |||
| C | 302.4 | −0.54% | |||
| 3 | A | 221.3 | 226.8 | −2.41% | |
| B | 225.1 | −0.77% | |||
| C | 225.7 | −0.47% | |||
| 4 | A | 373.4 | 379.8 | −1.66% | |
| B | 377.0 | −0.73% | |||
| C | 376.4 | −0.89% | |||
| 5 | A | 411.4 | 417.4 | −1.44% | |
| B | 414.5 | −0.71% | |||
| C | 414.0 | −0.83% | |||
| 6 | A | 335.9 | 341.8 | −1.73% | |
| B | 340.0 | −0.52% | |||
| C | 339.3 | −0.73% | |||
| H2/kN | 1 | A | 398.1 | 393.5 | 1.17% |
| B | 384.2 | −2.37% | |||
| C | 381.7 | −3.00% | |||
| 2 | A | 415.3 | 414.3 | 0.24% | |
| B | 403.3 | −2.65% | |||
| C | 401.1 | −3.19% | |||
| 3 | A | 380.7 | 374.4 | 1.68% | |
| B | 364.6 | −2.61% | |||
| C | 361.8 | −3.35% | |||
| 4 | A | 126.0 | 125.6 | 0.30% | |
| B | 120.5 | −4.03% | |||
| C | 121.4 | −3.29% | |||
| 5 | A | 156.1 | 157.6 | −0.99% | |
| B | 151.5 | −3.89% | |||
| C | 152.3 | −3.40% | |||
| 6 | A | 95.3 | 94.1 | 1.32% | |
| B | 88.9 | −5.52% | |||
| C | 90.0 | −4.35% | |||
| Load Case | Load Combination | Control Index |
|---|---|---|
| SC-1 | Down-warping deformation | |
| SC-2 | Up-warping deformation | |
| DC-1 | Cable stress (load-bearing cable) | |
| DC-2 | Cable stress (stability cable) |
| Deflection Limit | Stability Cable | Lower-Bearing Cable | Structural Thickness H/m | ||
|---|---|---|---|---|---|
| Vector Height f1/m | Specification | Sag f2/m | Specification | ||
| l/250 | 1.260 | 2 × D19.3 | 4.786 | D21.8 | 6.046 |
| l/200 | 2 × D19.3 | 3.095 | D28.6 | 4.355 | |
| l/150 | 2 × D18.9 | 2.537 | D28.6 | 3.797 | |
| l/100 | 2 × D17.8 | 1.710 | 2 × D21.8 | 2.970 | |
| Deflection Limit | Stability Cable | Lower-Bearing Cable | Structural Thickness H/m | ||
|---|---|---|---|---|---|
| Vector Height f1/m | Specification | Sag f2/m | Specification | ||
| l/250 | 1.260 | 2 × D17.8 | 6.782 | D17.8 | 8.042 |
| l/200 | 2 × D17.8 | 5.265 | D19.3 | 6.525 | |
| l/150 | 2 × D17.8 | 3.874 | D21.8 | 5.134 | |
| l/100 | 2 × D17.8 | 2.137 | D28.6 | 3.397 | |
| Deflection Limit | Stability Cable | Lower-Bearing Cable | Cable Mass M/kg | ||
|---|---|---|---|---|---|
| Vector Height f1/m | Specification | Sag f2/m | Specification | ||
| l/250 | 0 | 2 × D17.8 | 7.076 | D17.8 | 286.86 |
| 0.315 | 7.048 | 286.67 | |||
| 0.630 | 6.990 | 286.65 | |||
| 0.945 | 6.902 | 286.64 | |||
| 1.260 | 6.782 | 286.62 | |||
| l/200 | 0 | 2 × D17.8 | 5.877 | D18.9 | 300.33 |
| 0.315 | 5.844 | 300.31 | |||
| 0.630 | 5.779 | 300.29 | |||
| 0.945 | 5.682 | 300.27 | |||
| 1.260 | 5.265 | D19.3 | 313.12 | ||
| l/150 | 0 | 2 × D17.8 | 4.237 | D21.8 | 347.35 |
| 0.315 | 4.198 | 347.23 | |||
| 0.630 | 4.127 | 347.21 | |||
| 0.945 | 4.020 | 347.18 | |||
| 1.260 | 3.874 | 347.14 | |||
| l/100 | 0 | 2 × D17.8 | 2.603 | D28.6 | 456.64 |
| 0.315 | 2.554 | 456.61 | |||
| 0.630 | 2.466 | 456.57 | |||
| 0.945 | 2.332 | 456.51 | |||
| 1.260 | 2.137 | 456.45 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di, Z.; Wang, F.; Yu, H.; Dai, X.; Luo, B.; Liu, X. Analytical Formulation and Optimization of the Initial Morphology of Double-Layer Cable Truss Flexible Photovoltaic Supports. Buildings 2024, 14, 2549. https://doi.org/10.3390/buildings14082549
Di Z, Wang F, Yu H, Dai X, Luo B, Liu X. Analytical Formulation and Optimization of the Initial Morphology of Double-Layer Cable Truss Flexible Photovoltaic Supports. Buildings. 2024; 14(8):2549. https://doi.org/10.3390/buildings14082549
Chicago/Turabian StyleDi, Zenghui, Fei Wang, Hualong Yu, Xiang Dai, Bin Luo, and Xin Liu. 2024. "Analytical Formulation and Optimization of the Initial Morphology of Double-Layer Cable Truss Flexible Photovoltaic Supports" Buildings 14, no. 8: 2549. https://doi.org/10.3390/buildings14082549






