Structural Design and Mechanical Characteristics of a New Prefabricated Combined-Accident Oil Tank
Abstract
1. Introduction
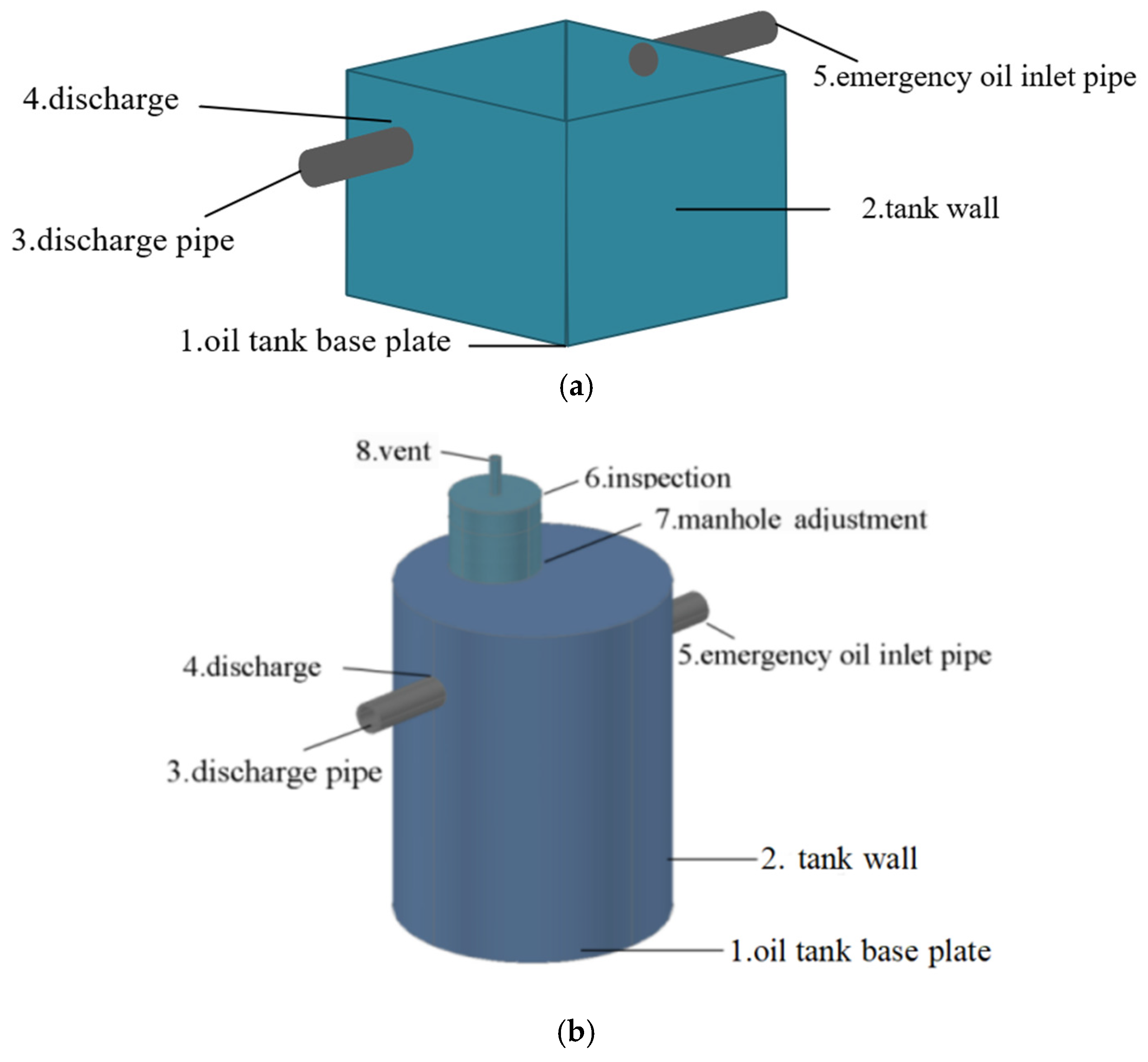
2. Design of the Novel Integrally Prefabricated Accident Oil Tank Structure
2.1. Design Concept
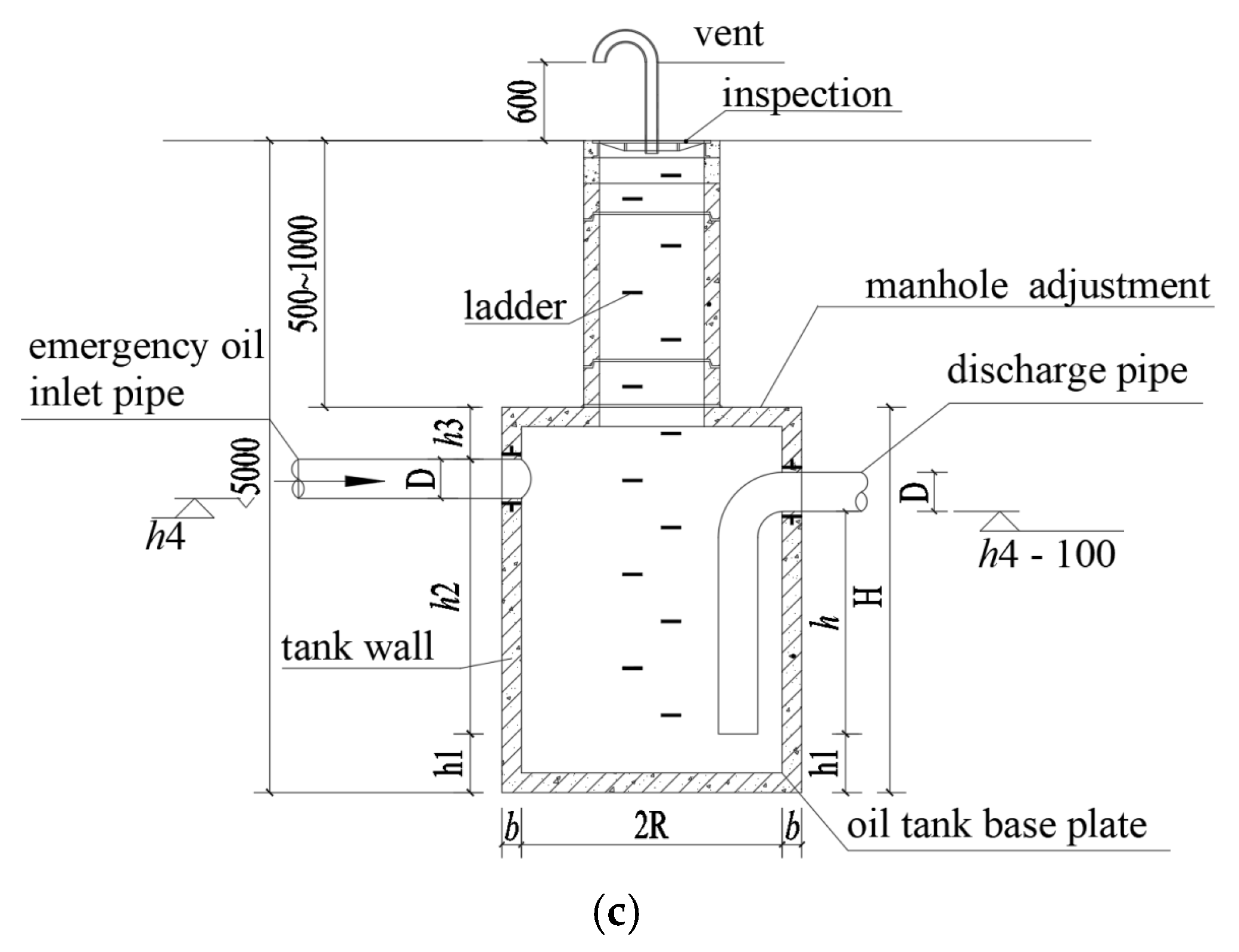
2.2. Design Parameters
- (1)
- The accidental oil discharge capacity Q(t) can be determined by selecting the maximum oil discharge rate from a single main transformer. This ensures the design accounts for the worst-case scenario during failure events.
- (2)
- The oil discharge volume V can be calculated using the oil density = 0.89 t/m3, resulting in V = Q/0.89 m3. This conversion standardizes the mass-to-volume relationship for containment planning.
- (3)
- The post-discharge base water depth h1 (m) must be larger than 0.6 m to accommodate oil recovery pipes and partition wall openings. However, h1 may be reduced if a top-mounted pump is used for oil extraction, depending on operational requirements.
- (4)
- The oil pool wall thickness b should be designed within the range of 150 mm to 200 mm. This specification balances structural stability with construction feasibility.
- (5)
- The maximum oil level after discharge must remain below the lowest elevation of the main transformer pit or the bottom elevation of the discharge inlet. This prevents oil backflow and ensures safe containment.
- (6)
- Fully enclosed oil pools require ventilation holes with an area more than the cross-section of the discharge pipe, positioned more than 0.3 m above the maximum oil level. These holes are unnecessary if manholes or open ports exist at the upper section of the pool.
- (7)
- For covered oil pools, manholes with a radius no smaller than 300 mm must be installed on the top or upper walls. These manholes should extend at least 0.4 m above the siphon crown to prevent oil overflow before siphon activation, while avoiding excessive height, which complicates the process.
- (8)
- The pool radius R must not be smaller than 0.6 m, to prevent oil surface icing and debris accumulation. A radius of 1.0 m is recommended, in practice, to simplify dredging and construction activities.
- (9)
- The height of the oil layer h2 can be determined by the geometric relationship of the pool. Specifically, the pool area is A = πR2 and the pool volume is V = Ah2 = 1.12 Q, so h2 is calculated as 1.12 Q/(πR2).
- (10)
- The total pool height H can be calculated by the formula H = h1 + h2 + h3, where h3 (the vertical distance from the maximum oil level to the pool crown) is determined by the largest value derived from manhole or ventilation requirements. For open-top pools, h3 may be minimized to below the discharge pipe invert or increased if site conditions allow, potentially eliminating the need for ventilation holes or manholes.
- (11)
- Drainpipe height h is the siphon outlet-to-water level height (see Figure 1c). In detail, the drainage pipe height h can be governed by the hydrostatic equilibrium equation, which is related to the oil layer height h2 (h = 0.89h2).
- (12)
- The initial water level must be positioned below the bottom elevation of the drainage pipe, to ensure proper siphon functionality during emergency operations.
- (13)
- A water replenishment valve is installed above the initial water level to offset leakage or evaporation losses. This valve is kept slightly open for continuous drip-feed water supply, though indoor pools serving outdoor transformers may omit it after initial filling.
- (14)
- The oil inlet height h4 must exceed ground level by at least 0.5 m and be positioned at least 100 mm above outlets to prevent spills. Anti-clogging devices such as screens are required at inlets.
- (15)
- The inlet- and outlet-pipe diameters D are determined by oil flow rate and velocity requirements. The minimum inlet diameter must not be smaller than 150 mm to ensure adequate discharge capacity.
3. Mechanical Characteristics Analysis of the Novel Integrally Prefabricated Accident Oil Tank Structure
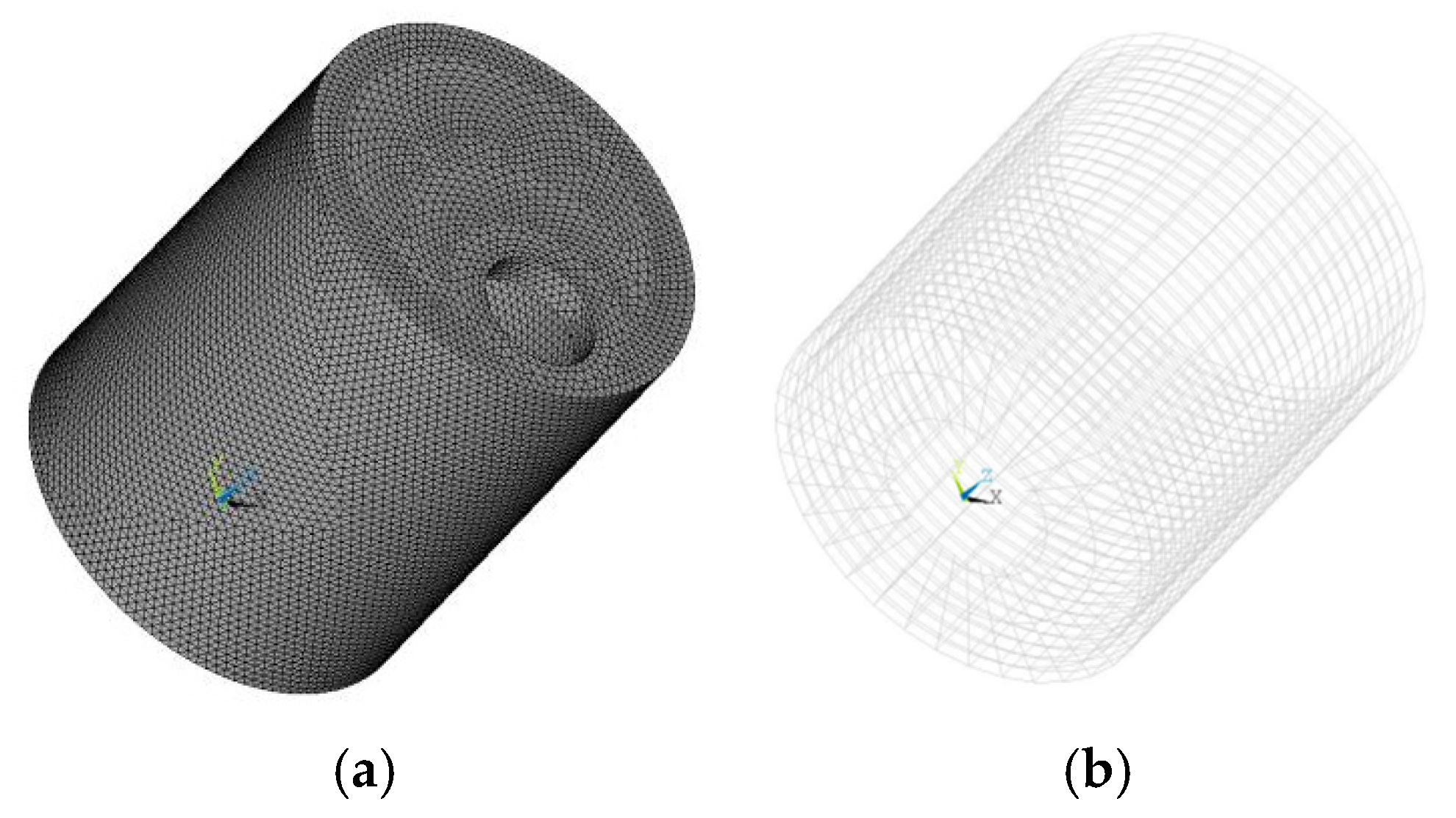
3.1. Finite Element Model
3.1.1. Model Parameters and Meshing
3.1.2. Material Properties
3.1.3. Load and Boundary Conditions
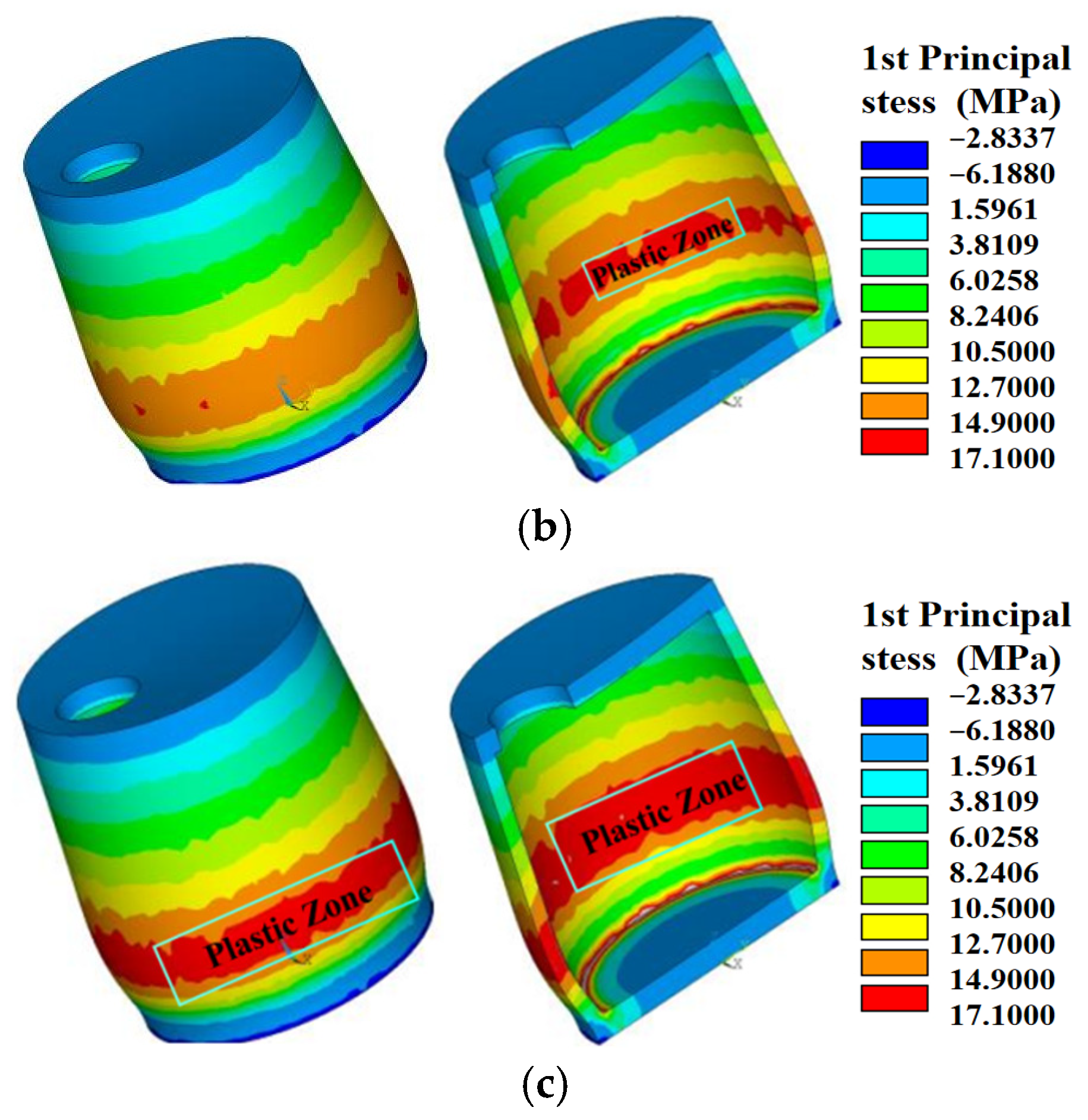
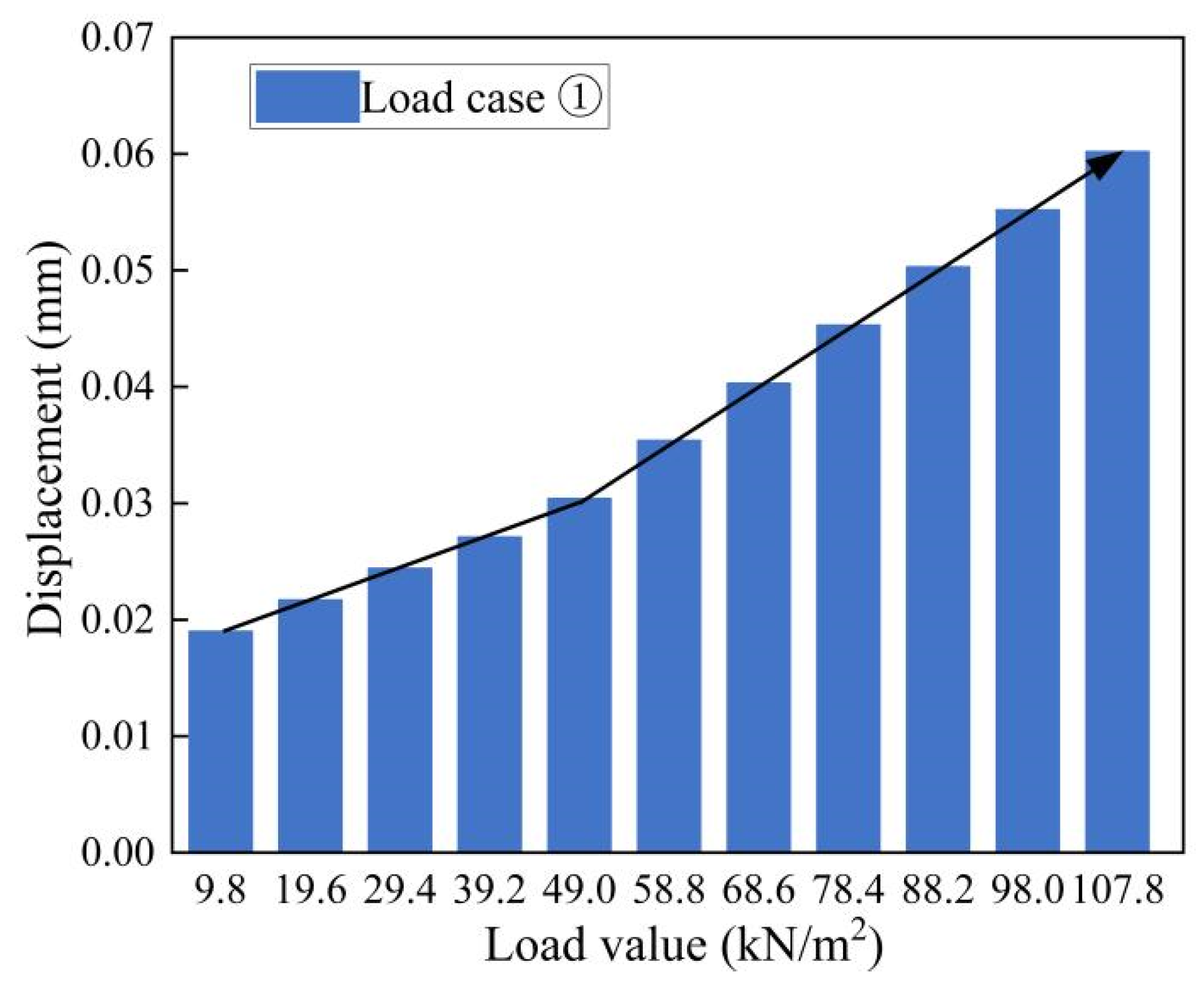
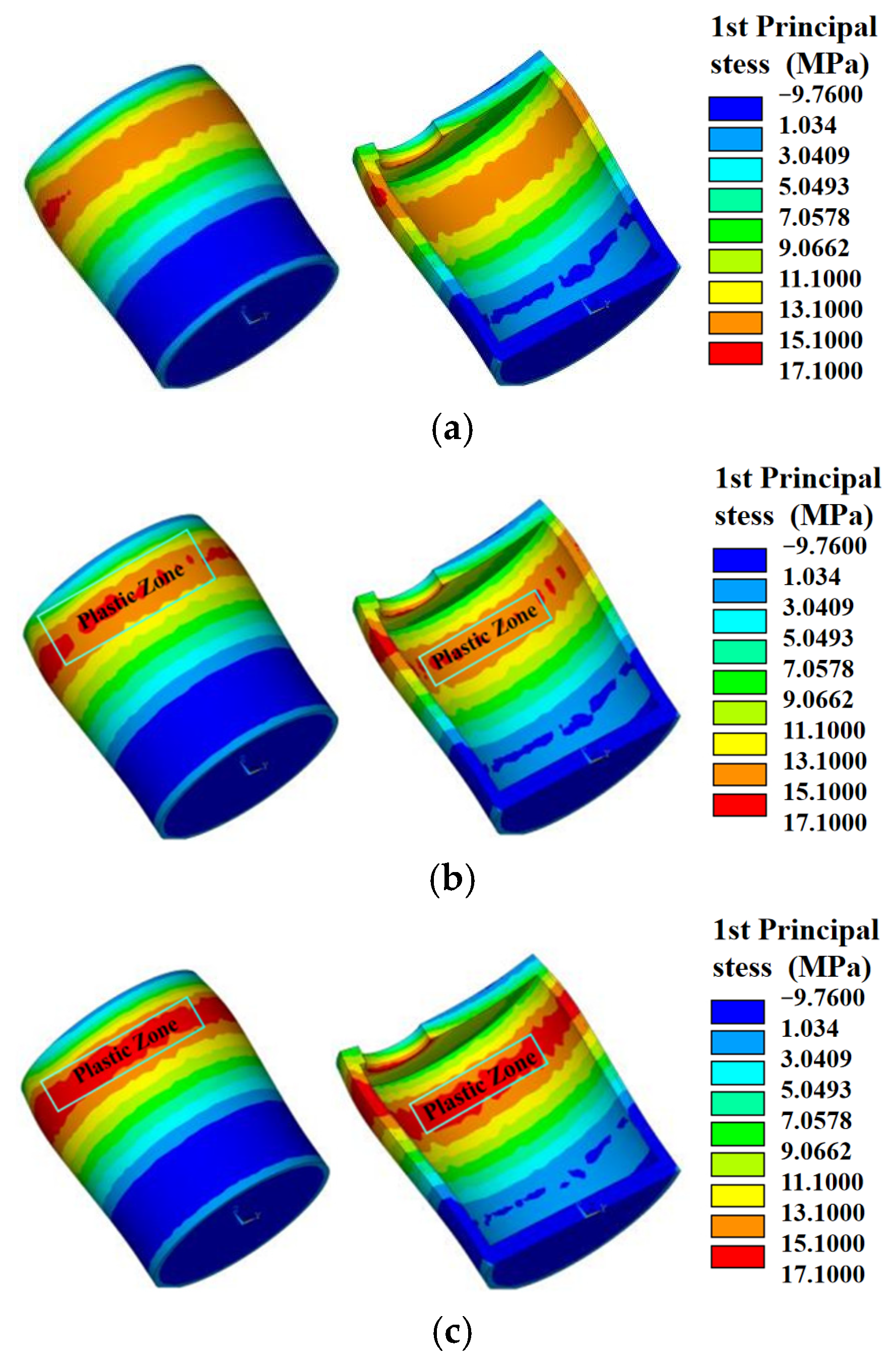
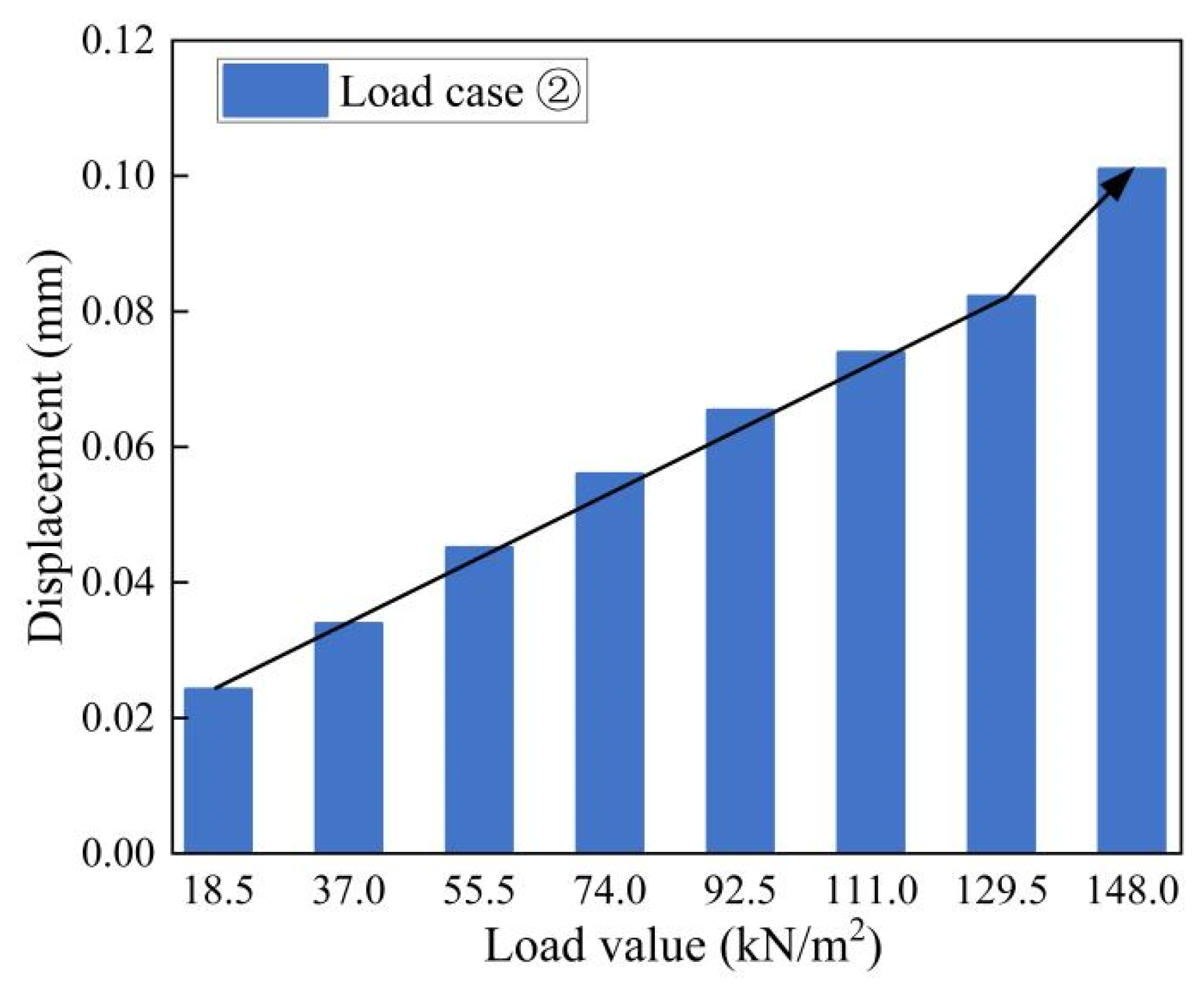
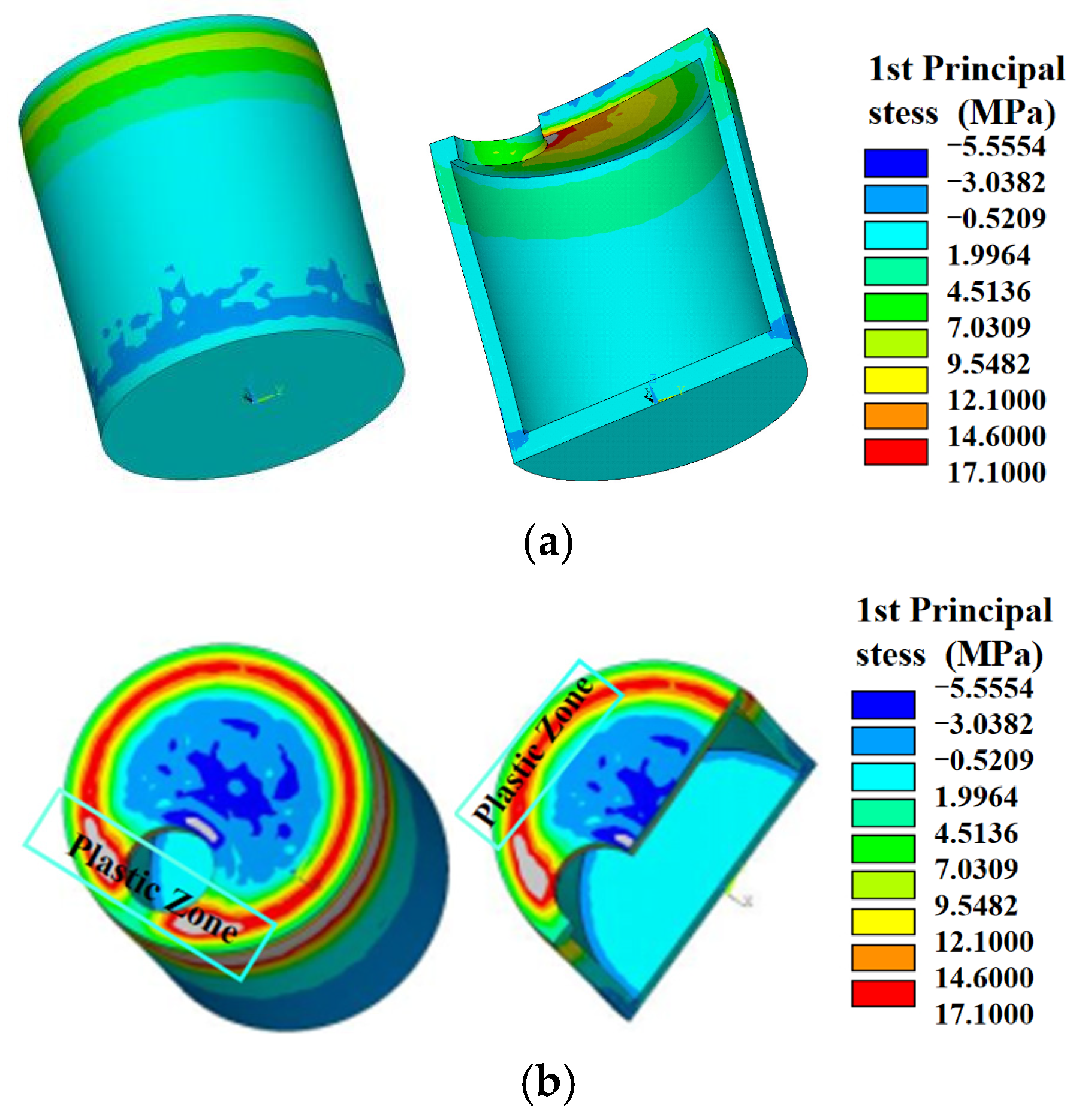
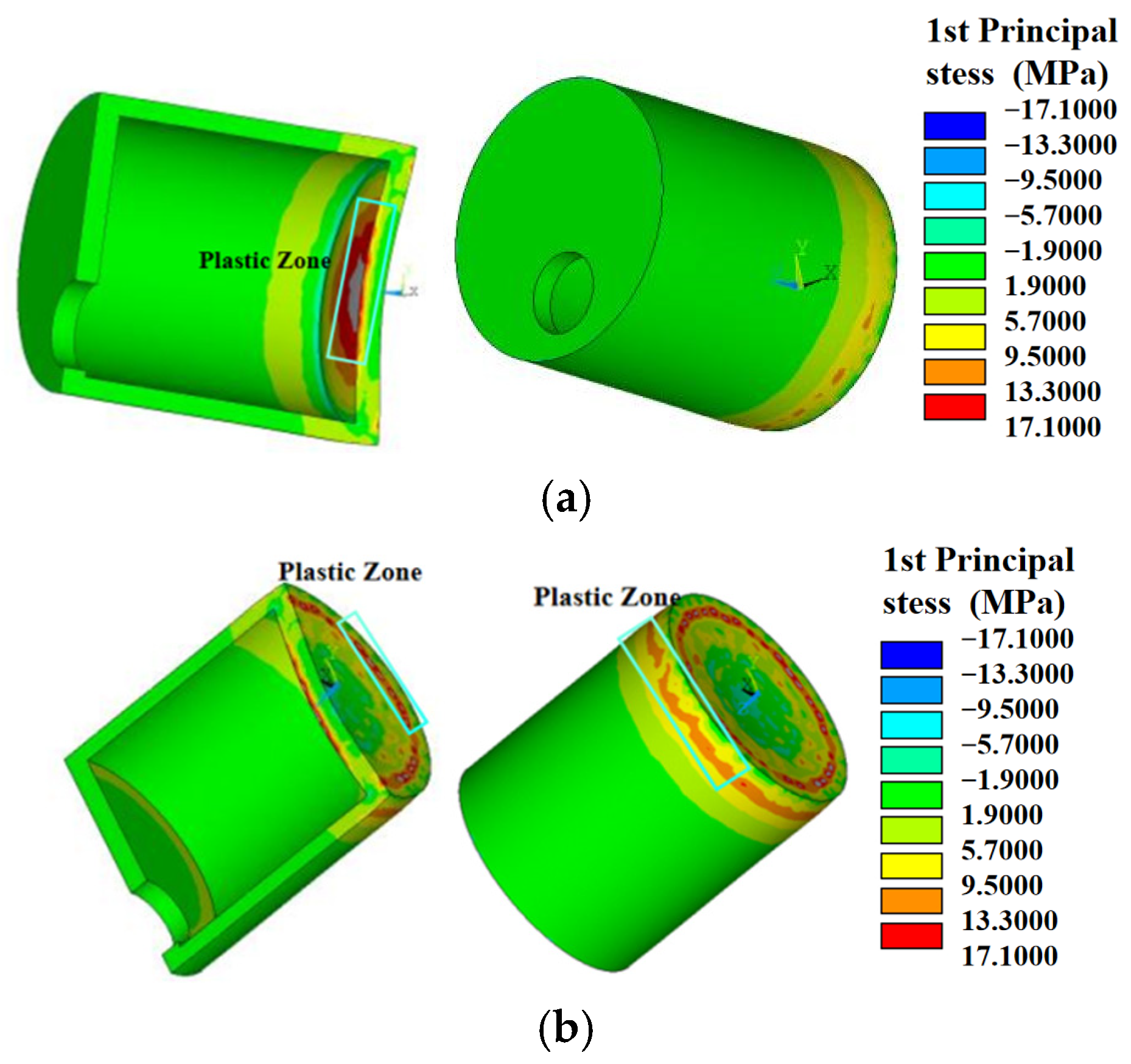
3.2. Analysis Results of Mechanical Characteristics
4. Structural Optimization of Prefabricated Composite Monolithic Accident Oil Tanks
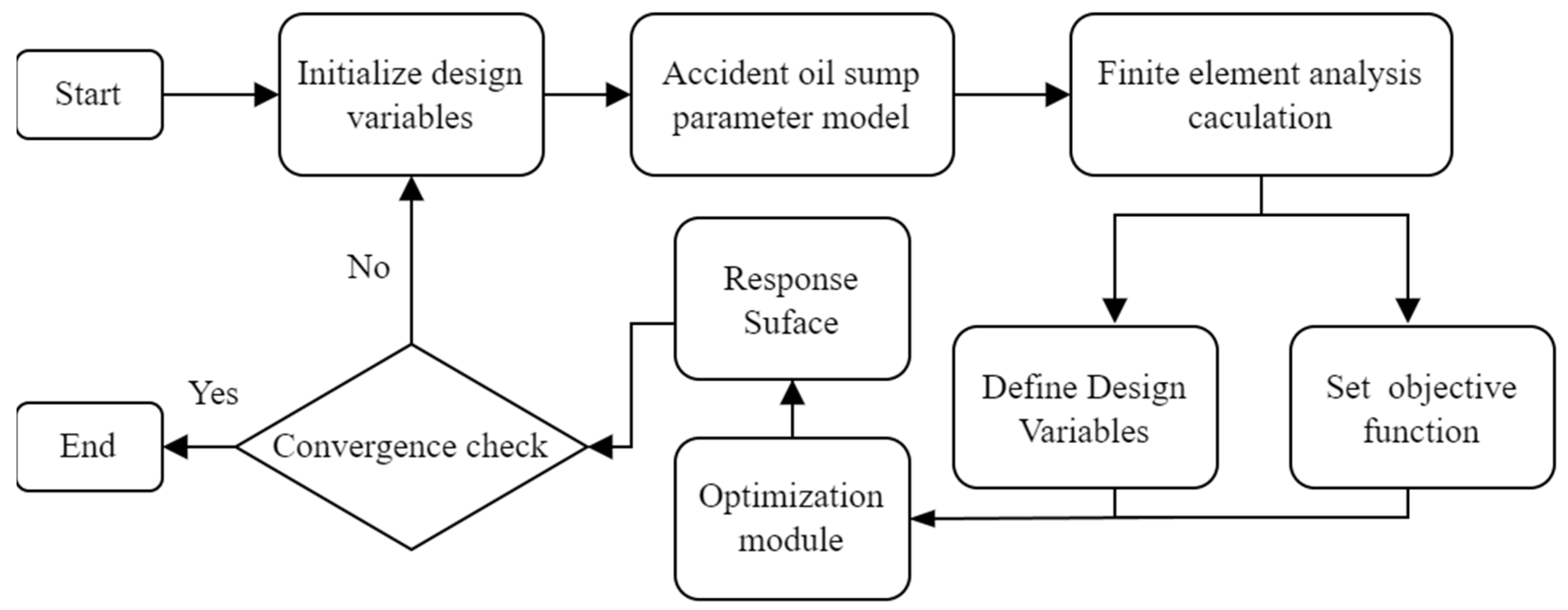
4.1. Optimized Design Process
4.2. Optimization Variables and Methodology
- ①
- Reinforcement diameter: from 10 mm to 20 mm.
- ②
- Thickness-to-diameter ratio: from 140/2100 to 220/2100.
- ③
- Height-to-diameter ratio: from 2600/2100 to 3400/2100.
- ④
- Concrete grade: form C20 to C70.
4.3. Parametric Investigation of Structural Systems Under Multifaceted Operational Cases
4.3.1. Load Case ①: Dead Load + Internal Hydrostatic Pressure
4.3.2. Load Case ②: Dead Load+ External Soil Pressure
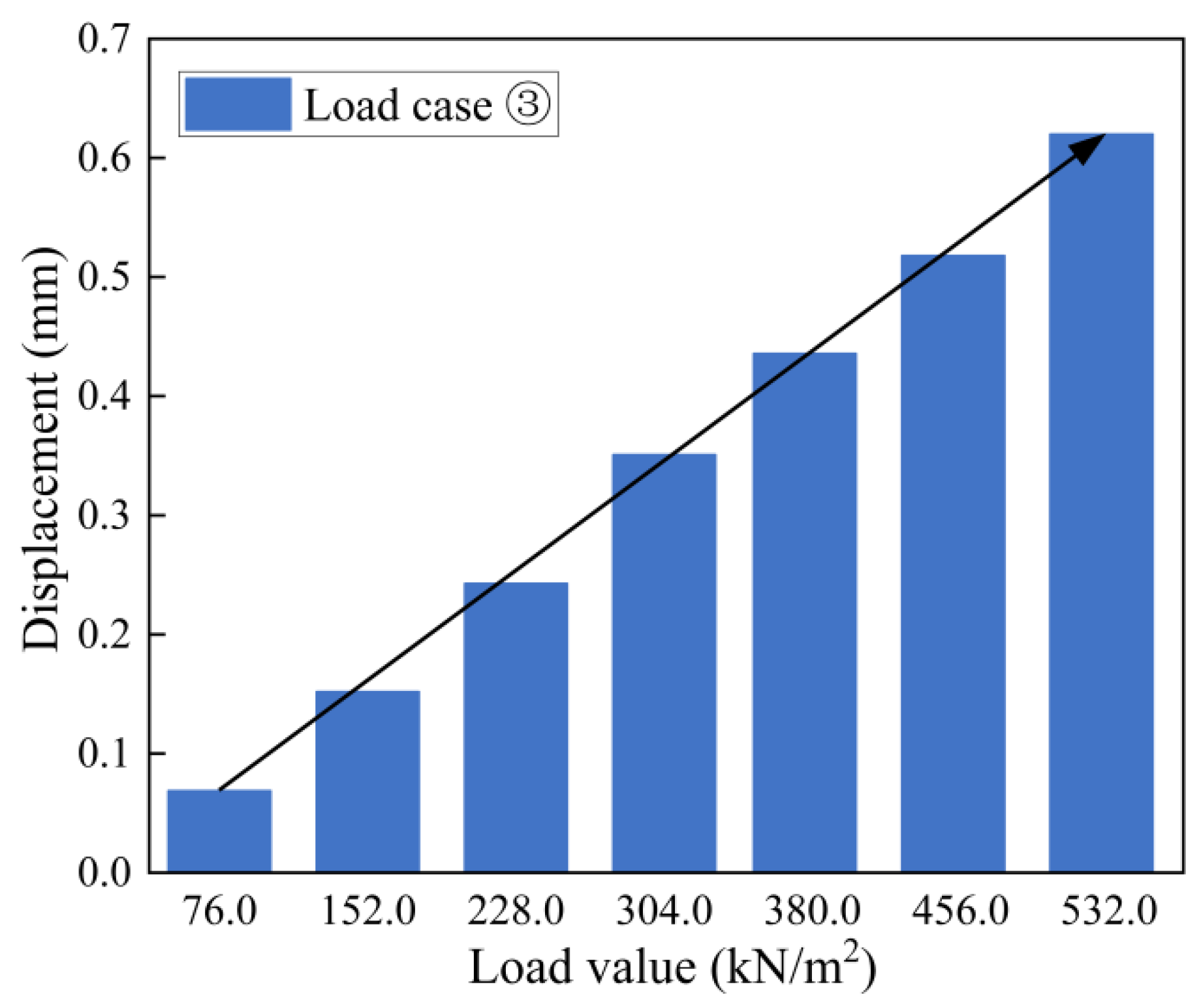
4.3.3. Load Case ③: Dead Load + External Soil Pressure + Top Load
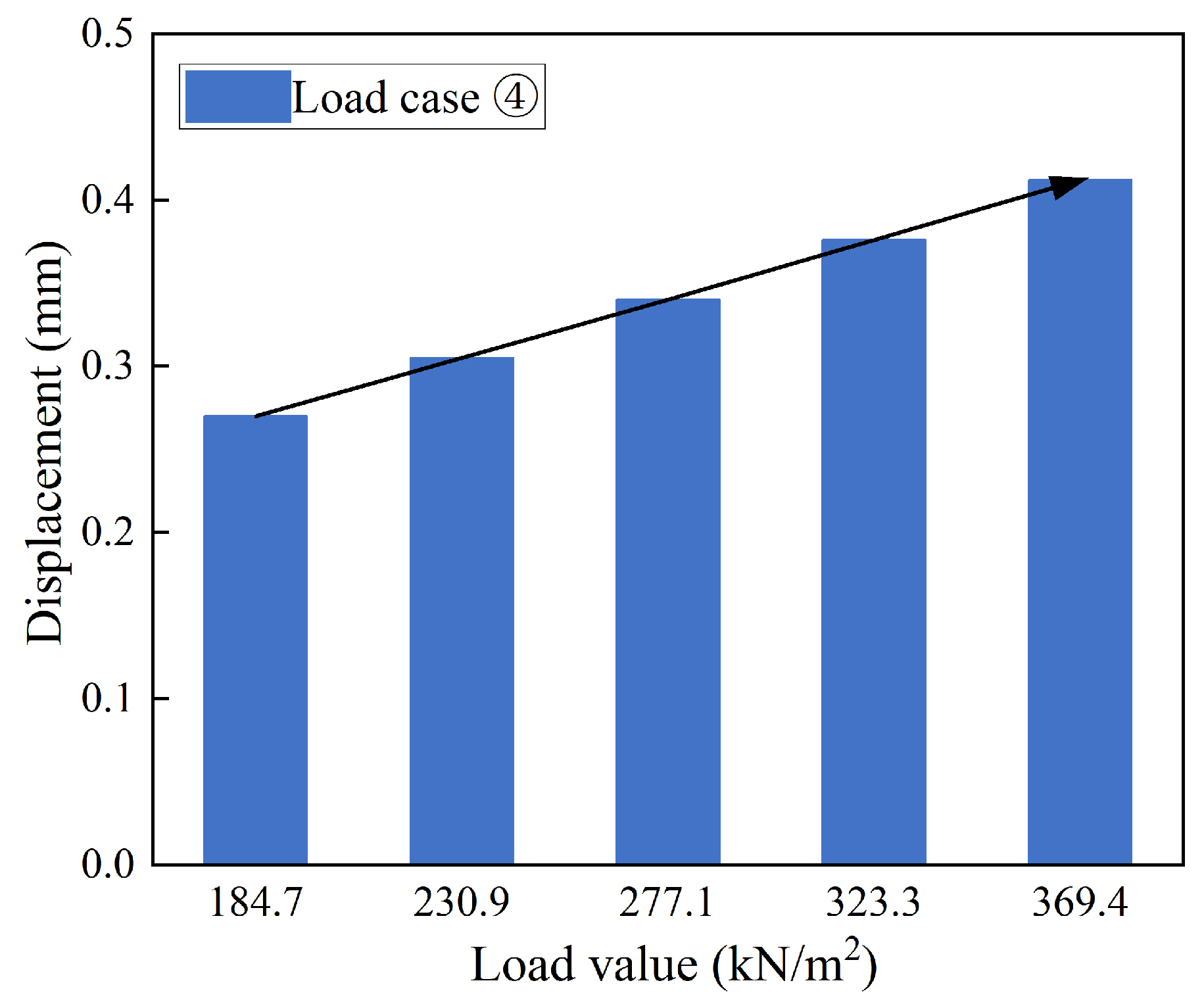
4.3.4. Load Case ④: Dead Load + External Soil Pressure + Buoyancy
4.4. Multi-Parameter Response Surface Optimization Results Under Different Load Cases
4.4.1. Case ①: Self-Weight + Internal Water Pressure
| Pre-Optimization Maximum Value | Post-Optimization Maximum Value | Pre-Optimization Minimum Value | Post-Optimization Minimum Value | |
|---|---|---|---|---|
| First principal stress on inner wall (MPa) | 0.14 | 0.11 | −0.089 | −0.054 |
| Total displacement on inner wall (mm) | 0.0059 | 0.0042 | 6.27 × 10−5 | 4.67 × 10−5 |
4.4.2. Case ②: Self-Weight + External Soil Pressure
4.4.3. Case ③: Self-Weight + External Soil Pressure + Top Load
4.4.4. Case ④: Self-Weight + External Soil Pressure + Buoyancy
5. Conclusions
- (1)
- The systematic quantification of failure thresholds across four load combinations reveals fundamental vulnerability mechanisms, particularly under the different load combinations. The failure modes of the oil pool differ significantly: failure occurs when internal water pressure reaches 11 times the initial value in load case ①, 8.8 times the initial external soil pressure in load case ②, 7 times the initial external load in load case ③, and 1.5 times the initial external load in load case ④, highlighting buoyancy’s critical role in accelerating structural degradation.
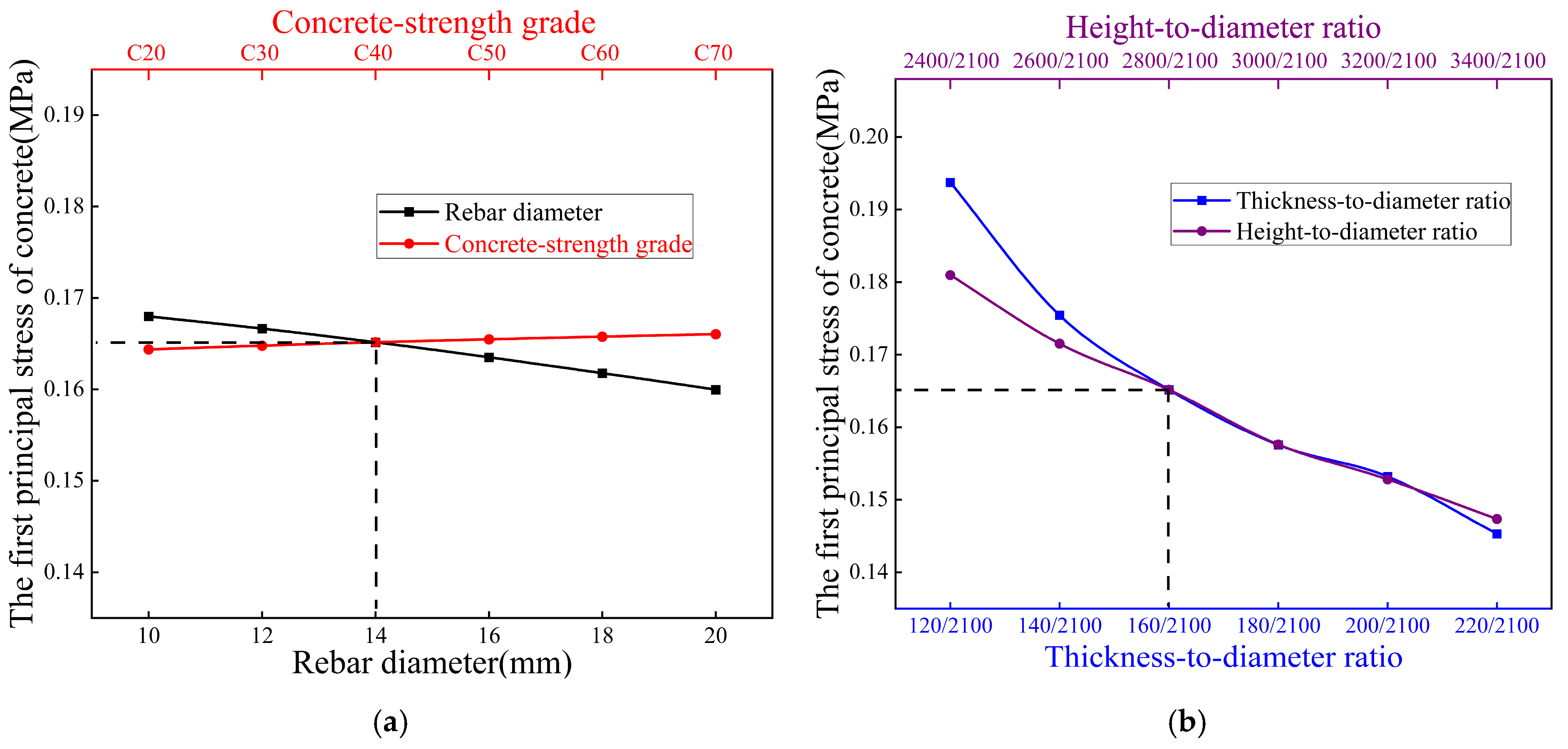
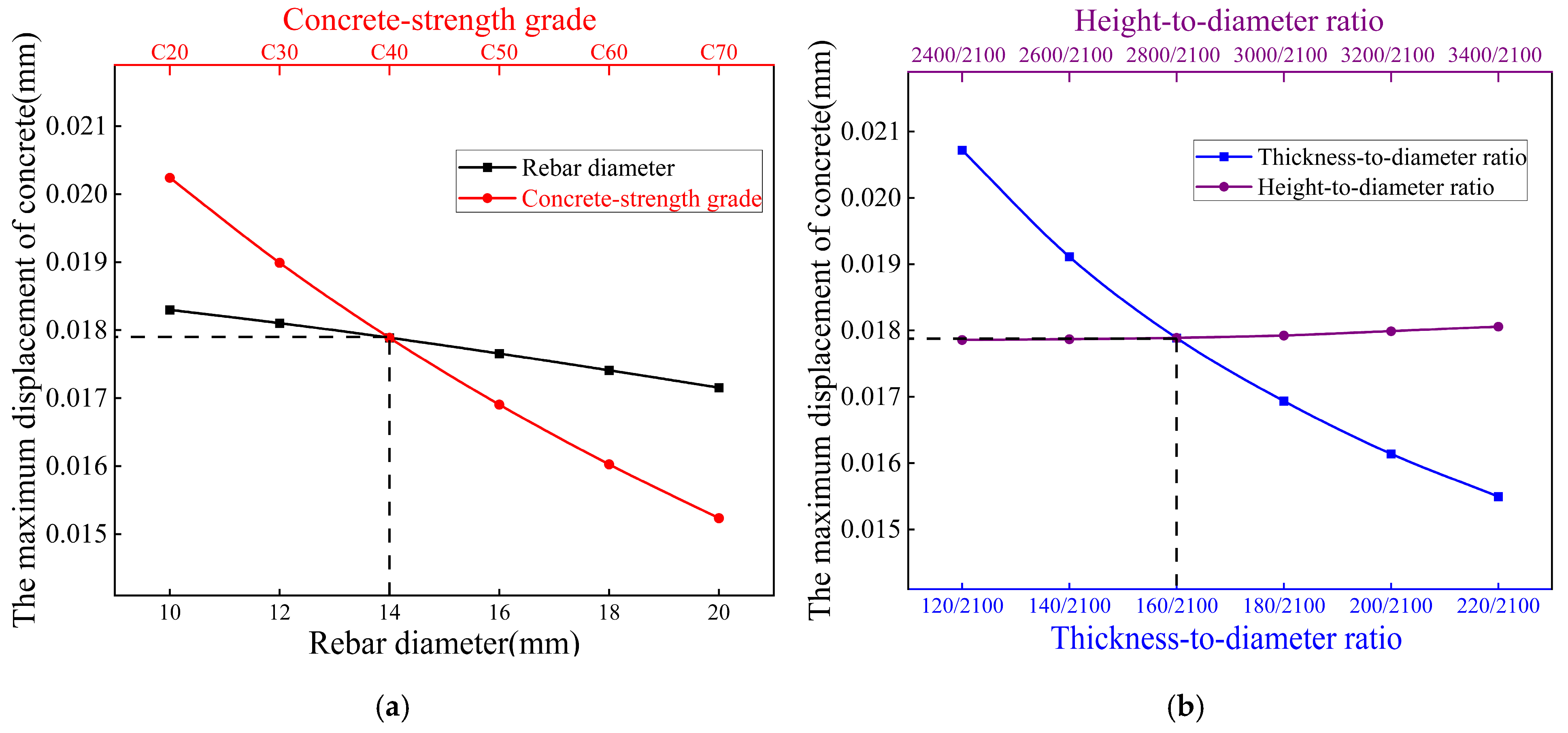
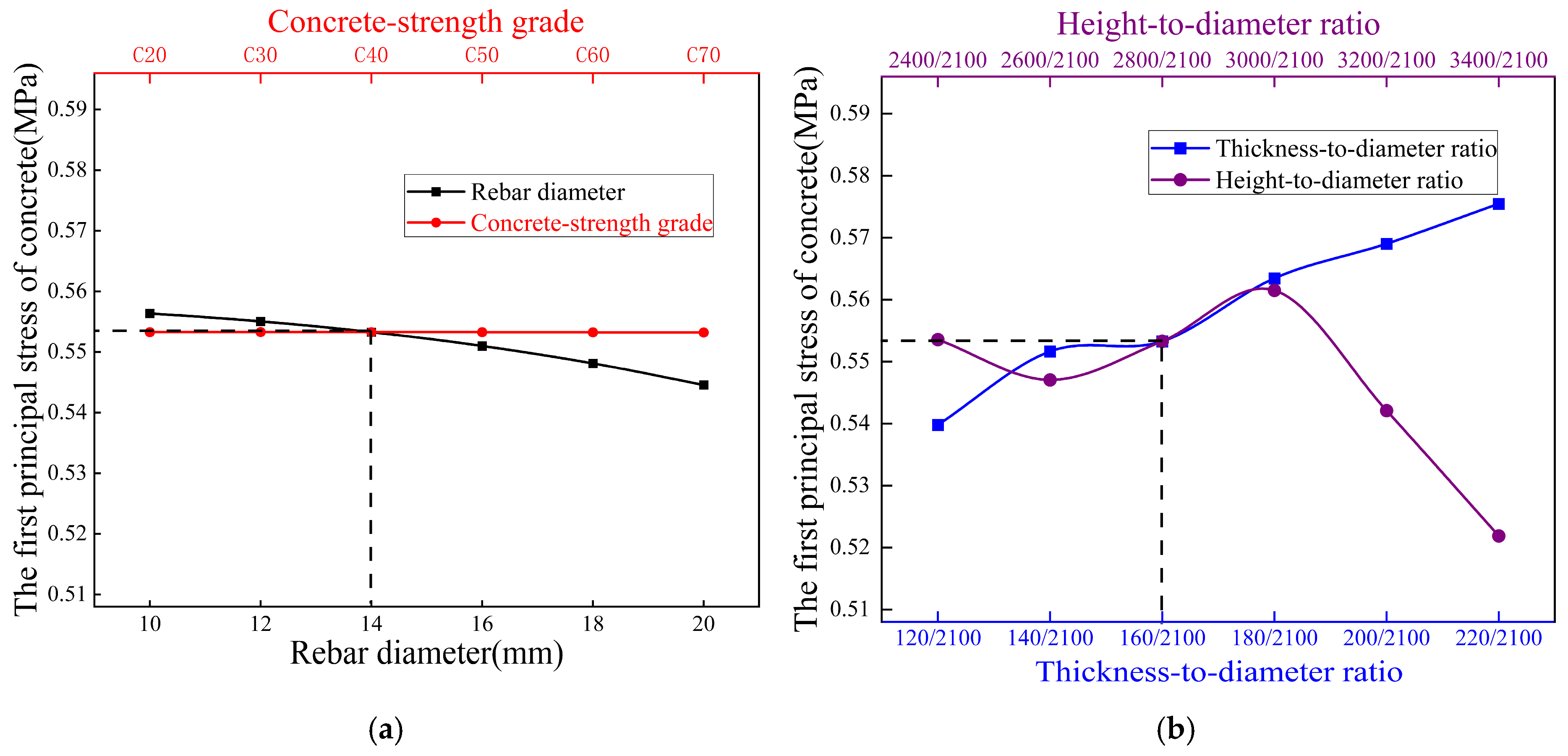
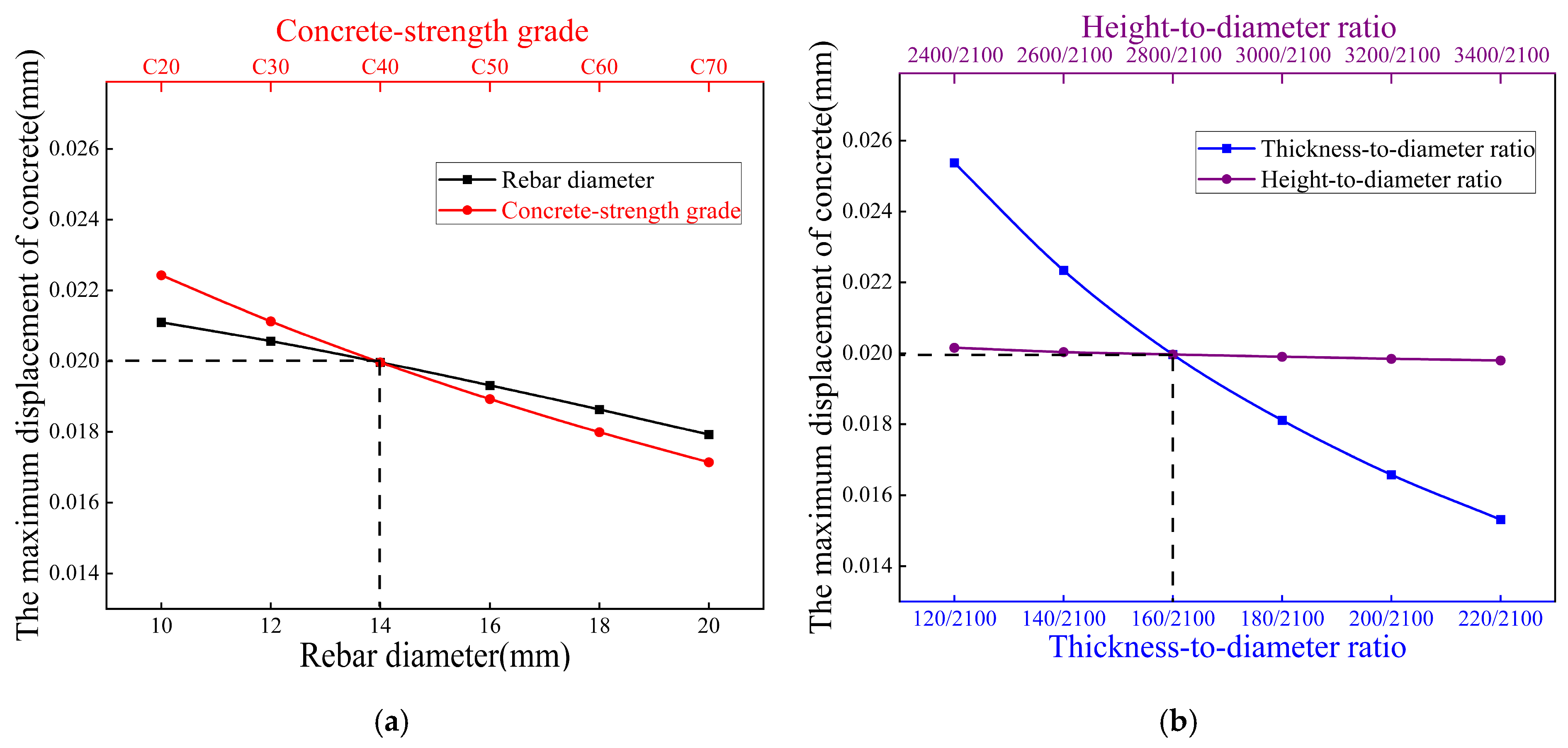
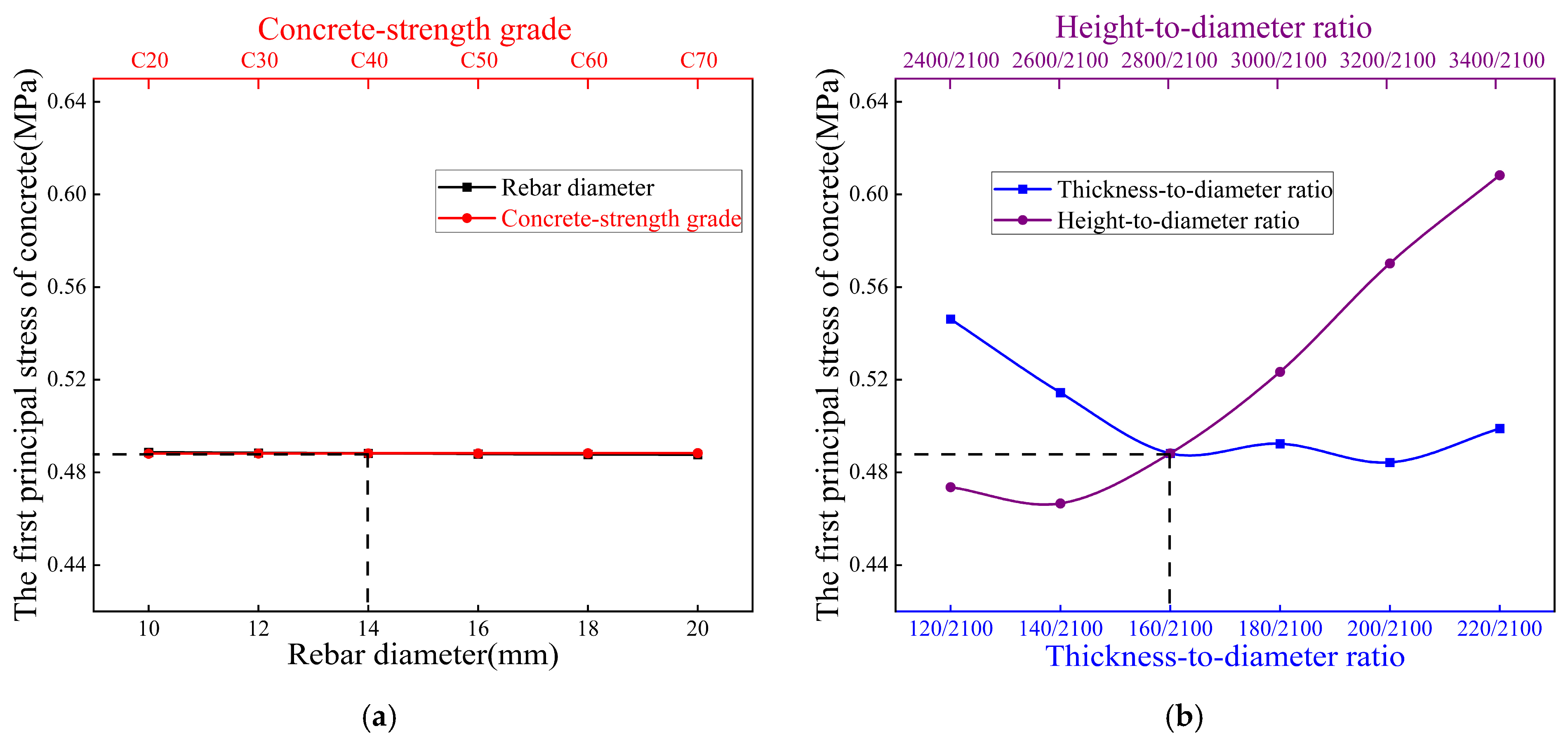
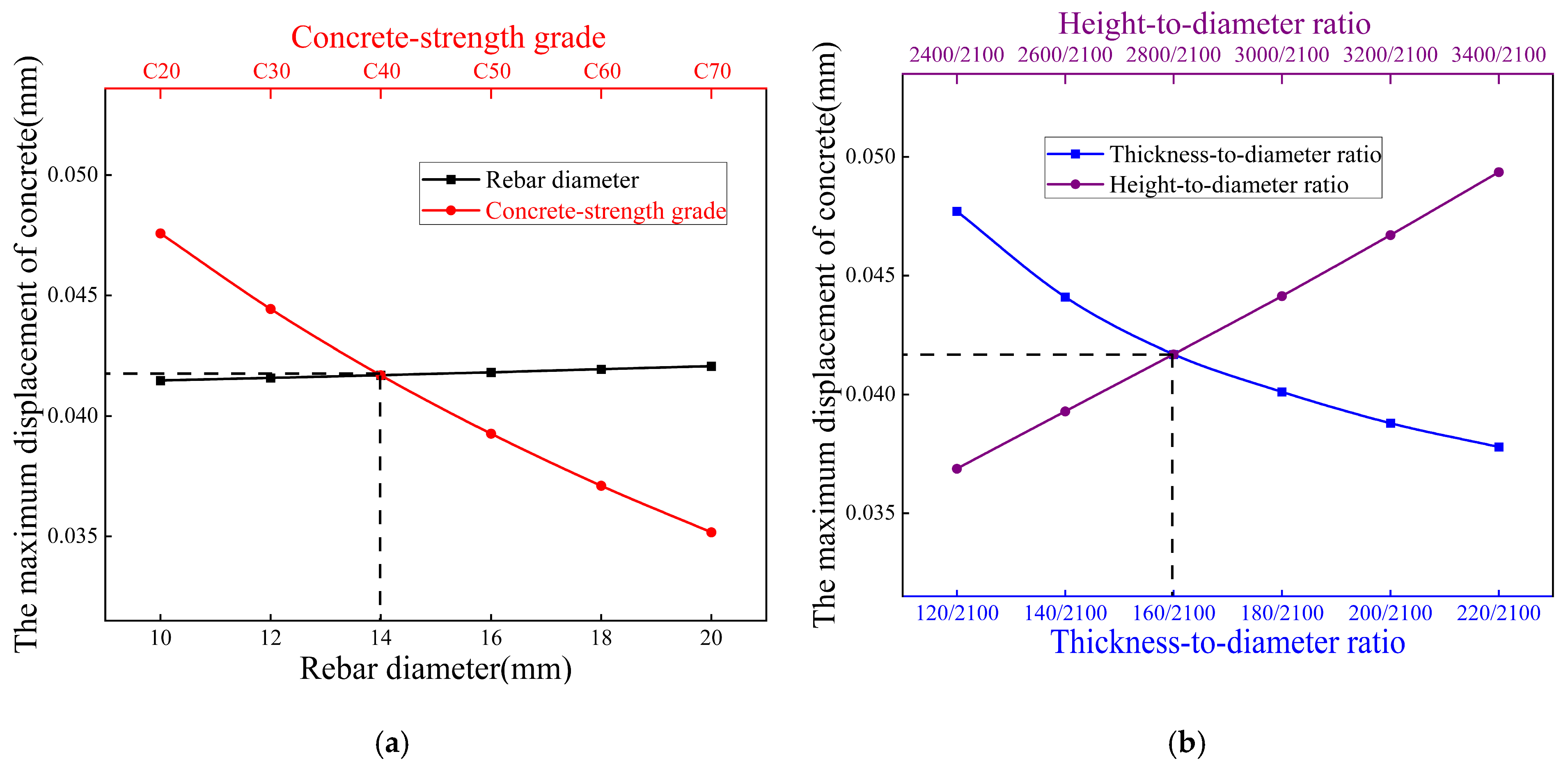
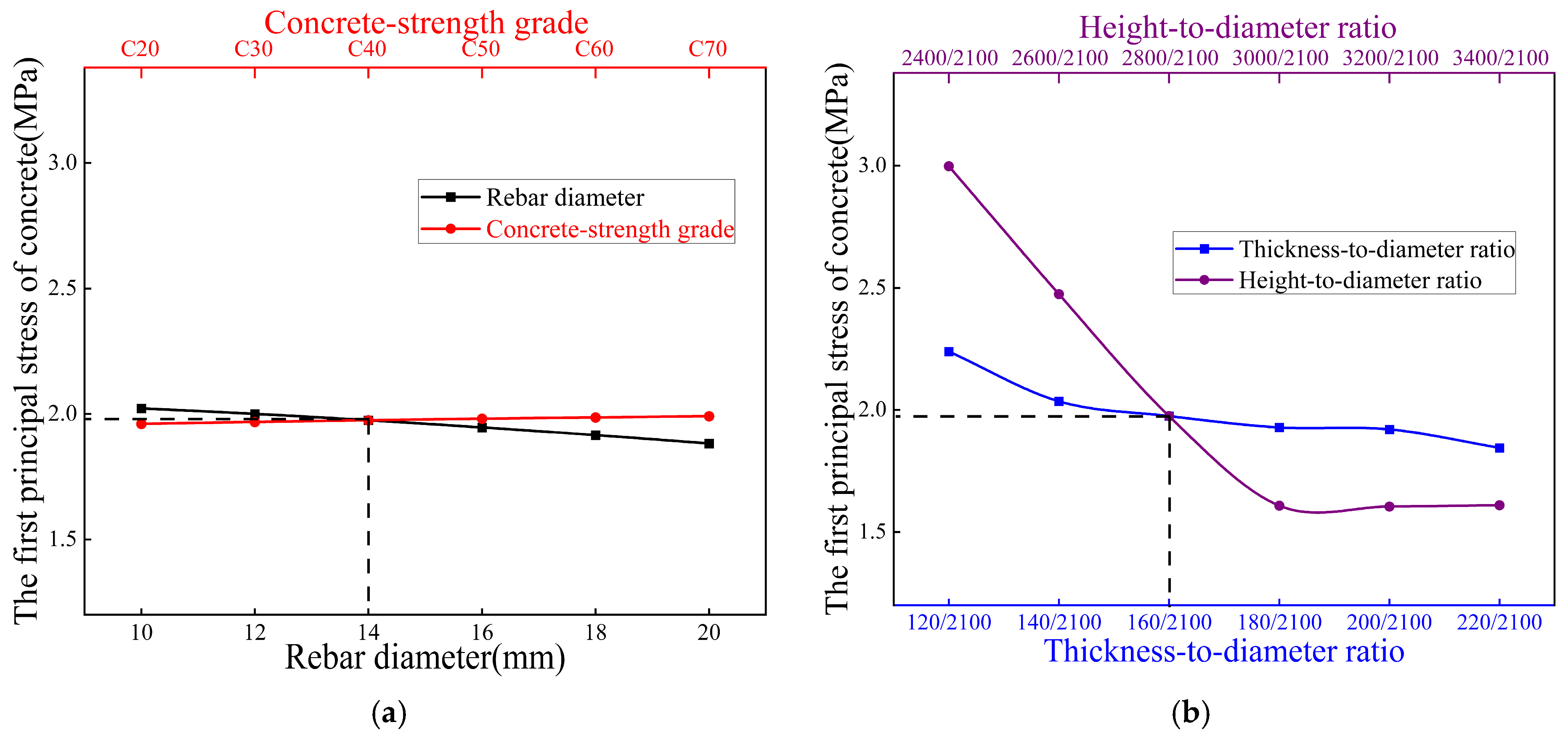
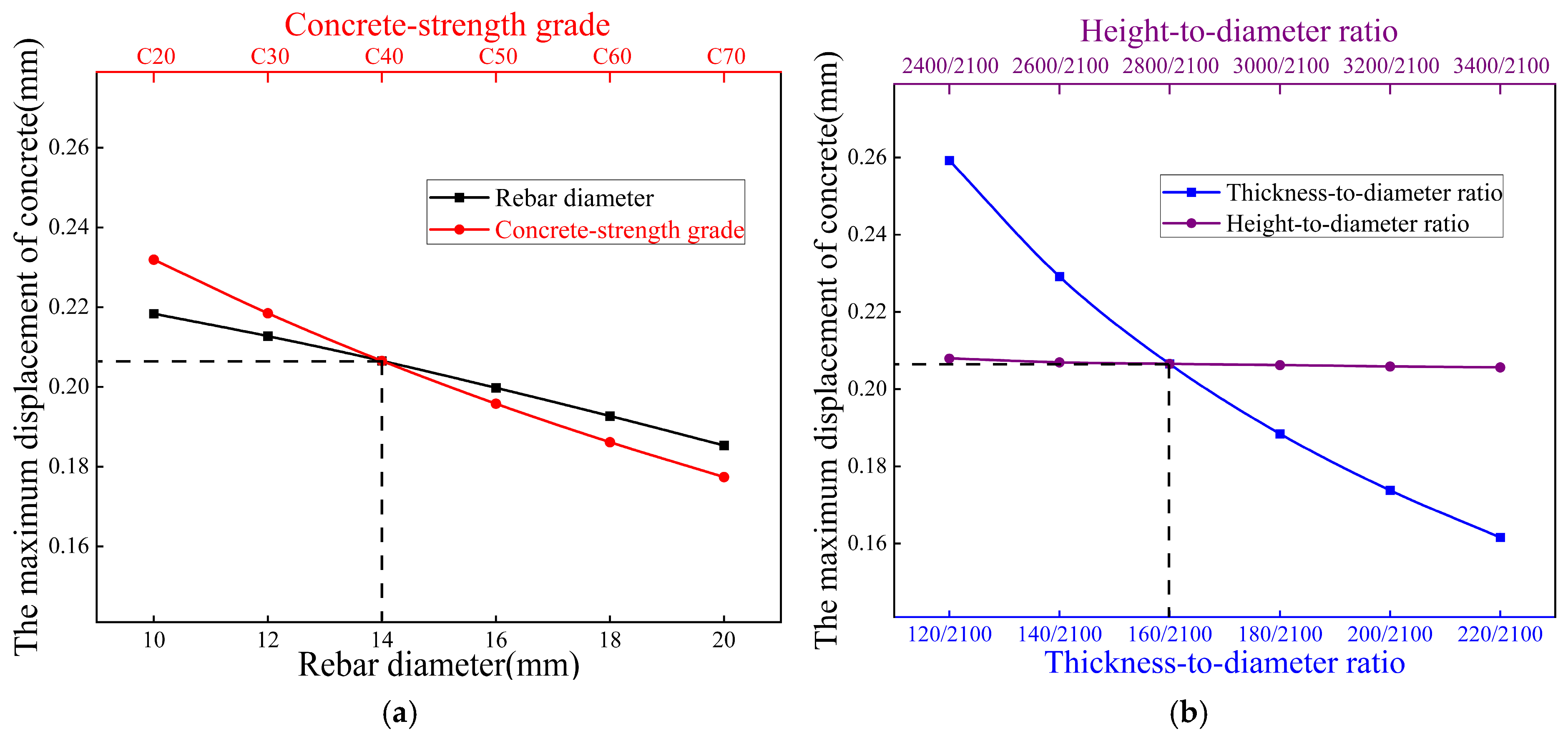
- (2)
- Longitudinal rebar diameter exhibits negligible influence on structural responses, demonstrating minimal impact on concrete maximum principal stress and displacement across all investigated conditions (including internal water pressure, external earth pressure, top loads, and buoyancy effects).
- (3)
- Thickness-to-diameter ratio governs displacement mitigation (14–23% reduction) but exerts dual stress effects, decreasing stress under internal pressure (e.g., 12% at 220 mm) while increasing it under external pressure (e.g., 4% at 220 mm), establishing its role as a displacement-control dominant parameter.
- (4)
- Concrete-strength grades (C30–C50) primarily serve displacement control under top loading, with limited stress influence under external pressure/buoyancy, but significant displacement reduction (e.g., 18% at C50). This contrasts with the adverse stress increase under internal pressure.
- (5)
- Height-to-diameter ratio induces condition-dependent stress trade-offs: reducing stress more than 18% beyond 3000 mm height under external pressure while amplifying stress more than 20% under top loads, reveals its context-sensitive optimization requirements.
- (6)
- Geometric parameter (thickness-to-diameter ratio, height-to-diameter ratio) optimization delivers superior efficacy over material adjustments, achieving 33–115% stress reduction at critical zones (e.g., 115% at walls, 830% at barrel tops) and 34–50% displacement mitigation. This demonstrates geometric tuning as the pivotal strategy for holistic structural enhancement. Structurally, the geometric optimization achieves measurable weight reduction, directly lowering material consumption. Logistically, standardized prefabrication offers inherent advantages in reducing on-site labor inputs and transportation volumes, due to component modularity. Combined with controlled stress levels below failure thresholds, these attributes contribute to improved technical feasibility and the life-cycle economy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, W.C.; Liu, Y.D.; Gao, Y.Y.; Hu, J.Z.; Liao, Z.H.; Zhao, J. Intelligent Substation Noise Monitoring System: Design, Implementation and Evaluation. Energies 2024, 17, 3083. [Google Scholar] [CrossRef]
- Gong, W.; Wang, N. Study and Improvement of The Volume Availability of Transformer Accident Oil Pool. Rural Electrif. 2023, 2, 44–47. [Google Scholar]
- Wang, P.Y.; Ren, J.W.; Yu, M.D.; Zheng, X.Y.; Hu, H.F.; Hu, P.F. Structural Design of Fully Prefabricated Accident Oil Pool in Transformer Substation. Build. Struct. 2021, 51, 1049–1054. [Google Scholar]
- Uwe, Z.; Markus, H.; Claudio, D.D.; Dirk, S. Fracture and Damage Mechanics Modelling of Thin-Walled Structures—An Overview. Eng. Fract. Mech. 2009, 76, 5–43. [Google Scholar]
- Ma, H.; Jiao, P.; Li, H.F.; Cheng, Z.; Chen, Z.P. Buckling Analyses of Thin-Walled Cylindrical Shells Subjected to Multi-Region Localized Axial Compression: Experimental and Numerical Study. Thin-Walled Struct. 2023, 183, 110330. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.X.; Zhang, H.Y.; Li, Y.B.; Pan, Q.; Han, X.L. Investigation of A Renovating Process for Failure Clinched Joint to Join Thin-Walled Structures. Thin-Walled Struct. 2020, 151, 106686. [Google Scholar] [CrossRef]
- Liu, M.; Wang, W.X.; Wang, Y.X.; Long, Y. Study on Mechanical Properties of Pre-stressed Thin-Walled Cylinder. Mach. J. 2019, 57, 23–26. [Google Scholar]
- Chang, J.I.; Lin, C.-C. A Study of Storage Tank Accidents. J. Loss Prev. Process 2006, 19, 51–59. [Google Scholar] [CrossRef]
- Beshr, A.A.E.-W. Structural Data Analysis for Monitoring the Deformation of Oil Storage Tanks Using Geodetic Techniques. J. Surv. Eng. 2014, 140, 44–51. [Google Scholar] [CrossRef]
- Qu, Z.H.; Zhang, Y.; Cai, X.; Guan, J.M. Study on the Dimension Design of Rectangular Transformer Oil Containment Basins. J. Green Sci. Technol. 2022, 24, 256–258. [Google Scholar]
- Godoy, L.A. Buckling of Vertical Oil Storage Steel Tanks: Review of Static Buckling Studies. Thin-Walled Struct. 2016, 103, 1–21. [Google Scholar] [CrossRef]
- Maués, F.P.; Ferreira, M.P.; Díaz, R.A.S.; Liberati, E.A.P.; Trautwein, L.M.; Santos, J.P.B. Numerical Modelling of Flat Slabs with Different Amounts of Double-Headed Studs as Punching Shear Reinforcement. Buildings 2025, 15, 960. [Google Scholar] [CrossRef]
- Yang, F.; Zhao, H.; Ma, T.; Bao, Y.; Cao, K.; Li, X. Three-Dimensional Numerical Analysis of Seismic Response of Steel Frame–Core Wall Structure with Basement Considering Soil–Structure Interaction Effects. Buildings 2024, 14, 3522. [Google Scholar] [CrossRef]
- Hamoda, A.; Abadel, A.A.; Sennah, K.; Ahmed, M.; Zhang, X.; Emara, M. Shear Strengthening of RC Beams Incorporating Post-Tensioned Bars and Engineered Cementitious Composite Reinforced with Palm Fronds. Buildings 2024, 14, 3277. [Google Scholar] [CrossRef]
- Luo, S.Q.; Liu, X.H.; Fu, L.M. Experimental Study on Joint Waterproofing of U-type Stirrup Assembly Pipe Gallery. Chin. J. Undergr. Space Eng. 2021, 17, 728–732. [Google Scholar]
- Cheng, H. Optimal Design of Oil-Immersed Transformer Accident Oil Pool. Constr. Des. Eng. 2022, 3, 72–74. [Google Scholar]
- Cai, S.T.; Ren, B.T.; Wang, S.Q.; Xiao, S.; Liao, S.K. New Thoughts on the Design and Construction of The Main Transformer Accident Oil Pool in the Transformer Substation. Commun. Power Technol. 2018, 35, 234–236. [Google Scholar]
- Tao, C.D. Design of Emergency Oil Containment Basins for Main Transformers in Hydropower Stations. Hunan Water Conserv. Hydropower 2010, 6, 12–13. [Google Scholar]
- Wu, Z.; Hou, L.; Wu, S.Z.; Wu, X.G.; Liu, F.Y. The Time-to-Failure Assessment of Large Crude Oil Storage Tank Exposed to Pool Fire. Fire Saf. J. 2020, 117, 103192. [Google Scholar] [CrossRef]
- 22S521; Prefabricated Inspection Chambers Standard Drawings. Standards Press of China: Beijing, China, 2022.
- GB50229-2019; Standard for Design of Fire Protection for Fossil Fuel Power Plants and Substations. China Planning Press: Beijing, China, 2019.
- GB50059-2011; Code for Design of 35kV~110kV Substation. China Planning Press: Beijing, China, 2011.
- GB50160-2008; Fire Prevention Code of Petrochemical Enterprise Design. China Planning Press: Beijing, China, 2008.
- Zhao, S.H. Design of Tubular Transformer Emergency Oil Pool. Water Conserv. Hydropower News 2021, 42, 44–47. [Google Scholar]
- Zhang, T.; Hou, Z.M.; Chen, Q.J.; Li, X.Q.; Fang, Y.L.; Zhang, S.Y.; Sun, W. A Novel Damage Model Integrated into the Elastoplastic Constitutive Model and Numerical Simulations of Reinforced Concrete Structures Under Cyclic Loading. J. Build. Eng. 2024, 84, 108670. [Google Scholar] [CrossRef]
- Naser, M.Z.; Hawileh, R.A.; Abdalla, J. Modeling Strategies of Finite Element Simulation of Reinforced Concrete Beams Strengthened With FRP: A Review. J. Compos. Sci. 2021, 5, 19. [Google Scholar] [CrossRef]
- Meguro, K.; Tagel-Din, H. Applied Element Simulation of RC Structures Under Cyclic Loading. J. Struct. Eng. 2001, 127, 1295–1305. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, G.S.; Qi, C.Y.; Zhang, P.; Cui, T.; Song, R. Experimental and Numerical Research on The Mechanical Properties of a Novel Prefabricated Diaphragm Wall–Beam Joint. Buildings 2025, 15, 1158. [Google Scholar] [CrossRef]
- Chahar, A.S.; Pal, P. Study on Various Properties of Reinforced Concrete—A Review. Mater. Today Proc. 2022, 65, 597–602. [Google Scholar] [CrossRef]
- Wang, Z.; Du, K.; Xie, Y.; Su, X.; Shi, Y.; Li, X.; Liu, T. Buckling Analysis of An Innovative Type of Steel-Concrete Composite Support in Tunnels. J. Constr. Steel Res. 2021, 179, 106503. [Google Scholar] [CrossRef]
- Fazeli, H.; Izadi Zaman Abadi, E.; Hosseini, S.J. Development of William-Warnke Failure Criteria Based on Experimental Studies of Scaled Masonry Materials. J. Struct. Constr. Eng. 2023, 9, 215–231. [Google Scholar]
- Xu, Z.; Li, J.; Wu, P.; Wu, C. Experimental Investigation of Triaxial Strength of Ultra-High Performance Concrete After Exposure to Elevated Temperature. Constr. Build. Mater. 2021, 295, 123689. [Google Scholar] [CrossRef]
- Zhou, Q.S. Parameters Analysis and Optimal Design for the Suspension Footbridge; Zhejiang University: Hangzhou, China, 2007; pp. 40–45. (In Chinese) [Google Scholar]
- Peng, Z.; Jia, L.; Xu, J.; Luo, K.; Pei, H. Parameter Study and Optimization of Static Performance for a Hybrid Cable-Stayed Suspension Bridge. Buildings 2024, 14, 3514. [Google Scholar] [CrossRef]
- Shir Ofer, M.; Emmerich, M. Multi-Objective Mixed-Integer Quadratic Models: A Study on Mathematical Programming and Evolutionary Computation. IEEE Trans. Evol. Comput. 2024, 3, 661–675. [Google Scholar]
- Li, Z.; Lu, D.; Gao, X. Optimization of mixture proportions by statistical experimental design using response surface method—A review. J. Build. Eng. 2021, 36, 102101. [Google Scholar] [CrossRef]




| Tensile Strength/(MPa) | Compressive Strength/(MPa) | Elasticity Modulus/(MPa) | Mass Density/(kg·m−3) | Poisson’s Ratio | |
|---|---|---|---|---|---|
| C40 grade for concrete | 1.71 | 19.1 | 3.25 × 104 | 2500 | 0.2 |
| HPB400 grade reinforced bar | 360 | 360 | 2.0 × 105 | 7850 | 0.3 |
| Notation | Meaning | Value (MPa) |
|---|---|---|
| Uniaxial ultimate tensile strength | 1.71 | |
| Uniaxial ultimate compressive strength | 17.1 | |
| Isobaric biaxial compressive strength | 20.52 | |
| Hydrostatic pressure | 0 | |
| Biaxial axial compressive strength under hydrostatic pressure | 24.8 | |
| Uniaxial axial compressive strength under hydrostatic pressure | 29.5 |
| Design Variable | Name | Unit | Lower Bound | Upper Bound |
|---|---|---|---|---|
| Diameter of longitudinal reinforcement bars | Dia | mm | 10 | 20 |
| Model wall thickness | Thin | mm | 140 | 220 |
| Height | Hight | mm | 2600 | 3400 |
| Concrete elastic modulus | EX | MPa | 3.05 × 105 | 3.65 × 105 |
| Pre-Optimization Maximum Value | Post-Optimization Maximum Value | Pre-Optimization Minimum Value | Post-Optimization Minimum Value | |
|---|---|---|---|---|
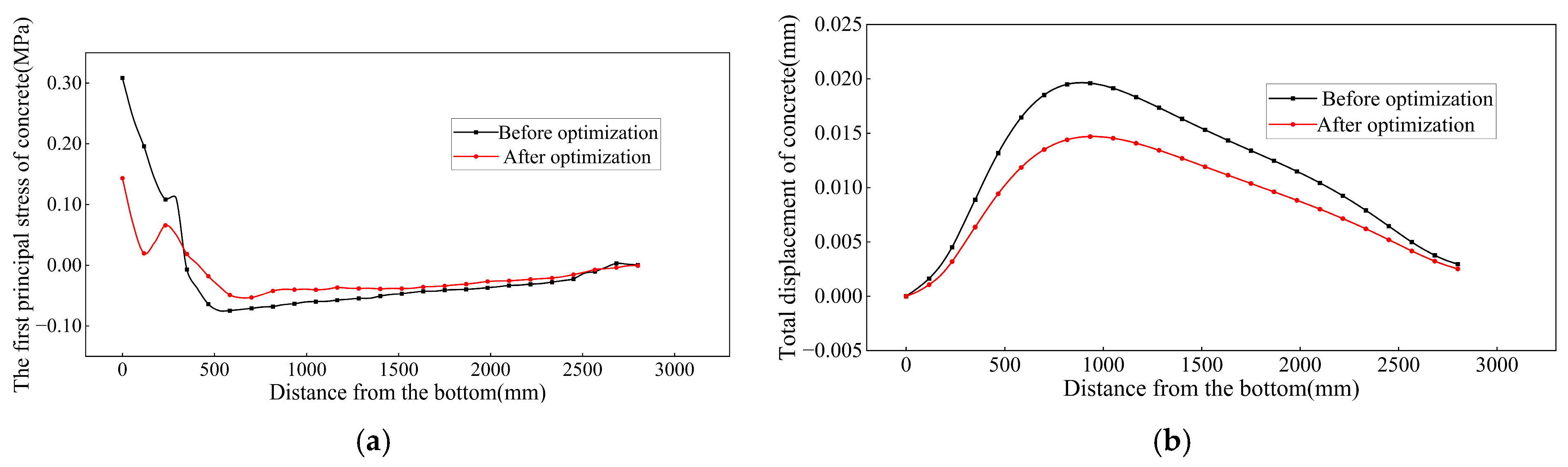
| First principal stress on outer wall (MPa) | 0.31 | 0.14 | −0.075 | −0.053 |
| Total displacement on outer wall (mm) | 0.020 | 0.015 | 7.5 × 10−4 | 4.3 × 10−4 |
| Pre-Optimization Maximum Value | Post-Optimization Maximum Value | Pre-Optimization Minimum Value | Post-Optimization Minimum Value | |
|---|---|---|---|---|
| First principal stress on outer wall (MPa) | 0.25 | 0.14 | −0.075 | −0.058 |
| Total displacement on outer wall (mm) | 0.019 | 0.014 | 6.5 × 10−4 | 3.8 × 10−4 |
| Pre-Optimization Maximum Value | Post-Optimization Maximum Value | Pre-Optimization Minimum Value | Post-Optimization Minimum Value | |
|---|---|---|---|---|
| First principal stress on outer wall (MPa) | 1.27 | 0.20 | −0.76 | −0.63 |
| Total displacement on outer wall (mm) | 0.20 | 0.14 | 3.01 × 10−3 | 1.12 × 10−3 |
| Influencing Factors | Rebar Diameter | Thickness-to-Diameter Ratio | Height-to-Diameter Ratio | Concrete-Strength Grade | |
|---|---|---|---|---|---|
| Load case ① | Principal stress | −13.09 | −43.72 | −36.62 | 2.70 |
| Displacement | −12.39 | −37.65 | 2.60 | −47.06 | |
| Load case ② | Principal stress | −12.51 | −18.99 | −20.09 | 2.23 |
| Displacement | −22.87 | −46.53 | −1.80 | −28.66 | |
| Load case ③ | Principal stress | −5.82 | −49.88 | 56.96 | −2.14 |
| Displacement | 1.50 | −24.70 | 24.67 | −49.98 | |
| Load case ④ | Principal stress | −8.45 | −6.75 | −64.63 | 2.17 |
| Displacement | −20.06 | −36.93 | −0.70 | −39.54 | |
| Weighted average | Principal stress | −9.97 | −29.83 | −16.10 | 1.24 |
| Displacement | −13.46 | −36.45 | 6.19 | −41.31 | |
| Load Case | Rebar Diameter (mm) | Thickness-to-Diameter Ratio | Height-to-Diameter Ratio | Concrete-Strength Grade |
|---|---|---|---|---|
| ① | 20 | 200/2100 | 3200/2100 | C60 |
| ② | 14 | 160/2100 | 2800/2100 | C50 |
| ③ | 20 | 160/2100 | 3200/2100 | C70 |
| ④ | 18 | 160/2100 | 2800/2100 | C60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Zhao, C.; Xu, H.; Zhu, J.; Feng, Y.; Shi, X.; Wang, P. Structural Design and Mechanical Characteristics of a New Prefabricated Combined-Accident Oil Tank. Buildings 2025, 15, 2477. https://doi.org/10.3390/buildings15142477
Lu X, Zhao C, Xu H, Zhu J, Feng Y, Shi X, Wang P. Structural Design and Mechanical Characteristics of a New Prefabricated Combined-Accident Oil Tank. Buildings. 2025; 15(14):2477. https://doi.org/10.3390/buildings15142477
Chicago/Turabian StyleLu, Xuan, Cheng Zhao, Hui Xu, Jie Zhu, Yan Feng, Xinyang Shi, and Pengyan Wang. 2025. "Structural Design and Mechanical Characteristics of a New Prefabricated Combined-Accident Oil Tank" Buildings 15, no. 14: 2477. https://doi.org/10.3390/buildings15142477
APA StyleLu, X., Zhao, C., Xu, H., Zhu, J., Feng, Y., Shi, X., & Wang, P. (2025). Structural Design and Mechanical Characteristics of a New Prefabricated Combined-Accident Oil Tank. Buildings, 15(14), 2477. https://doi.org/10.3390/buildings15142477




