Human–Structure System Coupled Vibration Test and Human Body Model
Abstract
:1. Introduction
2. Human–Structure Interaction Test
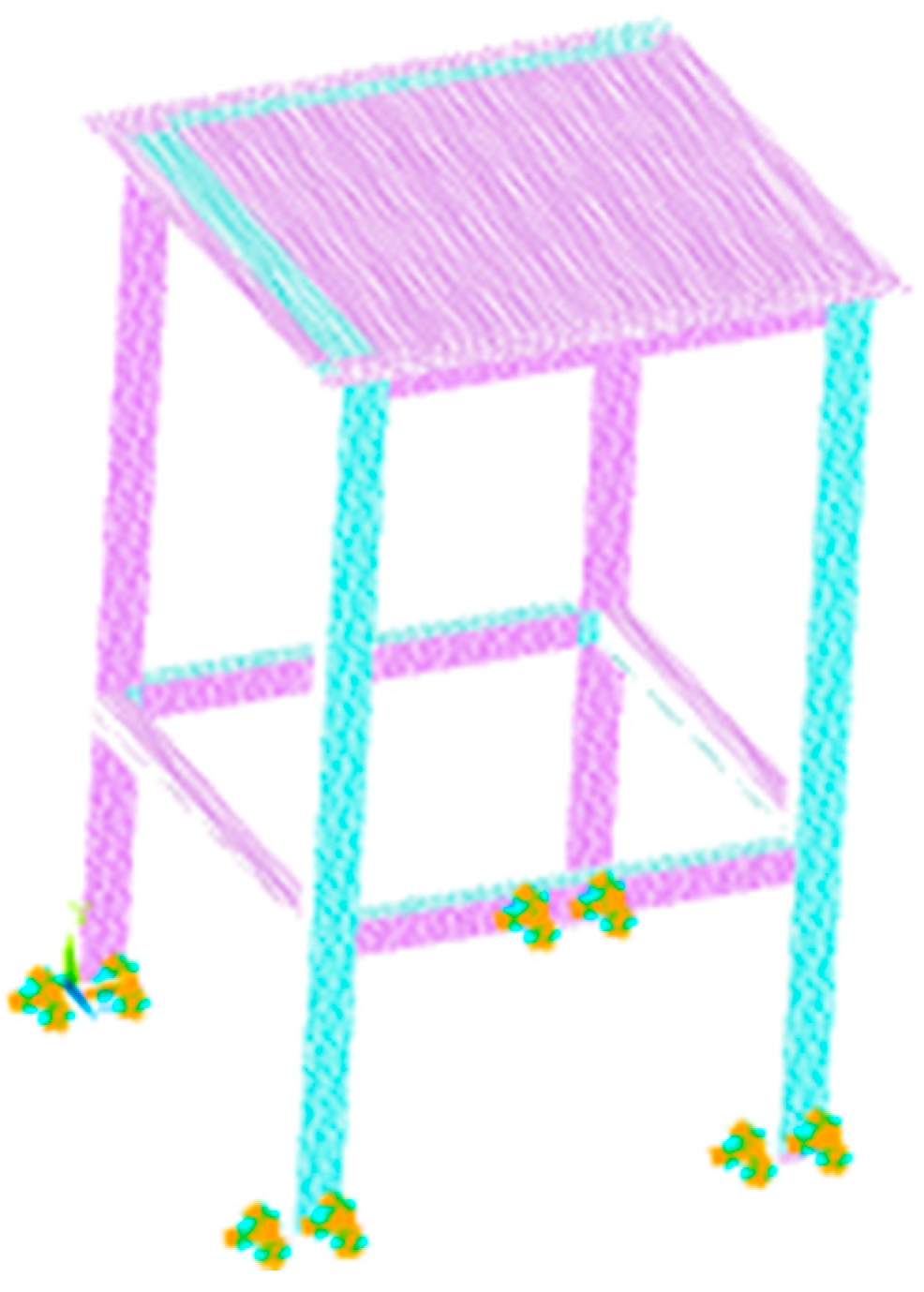
2.1. Test Rig
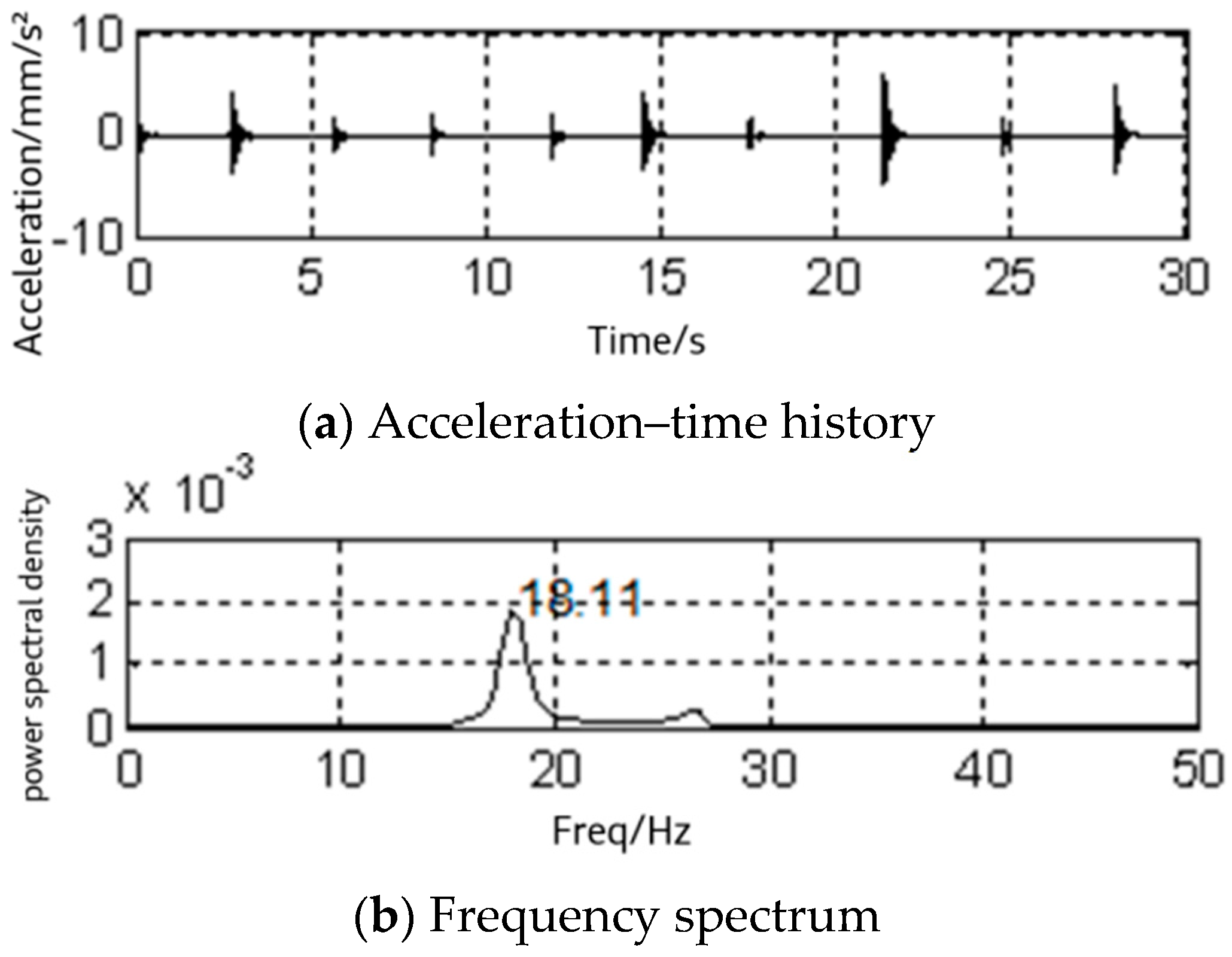
2.2. Modal Test of the Empty Steel Frame
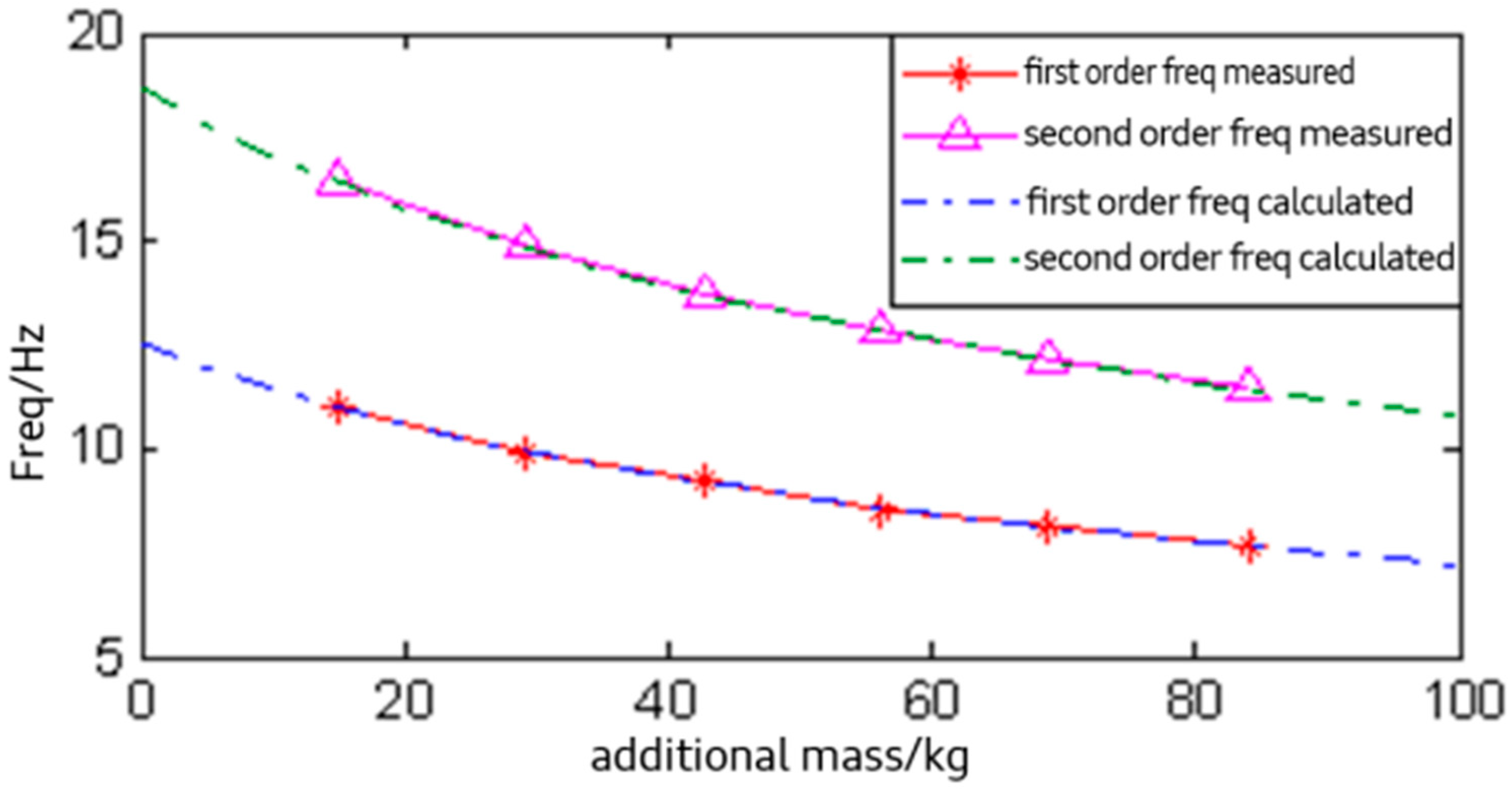
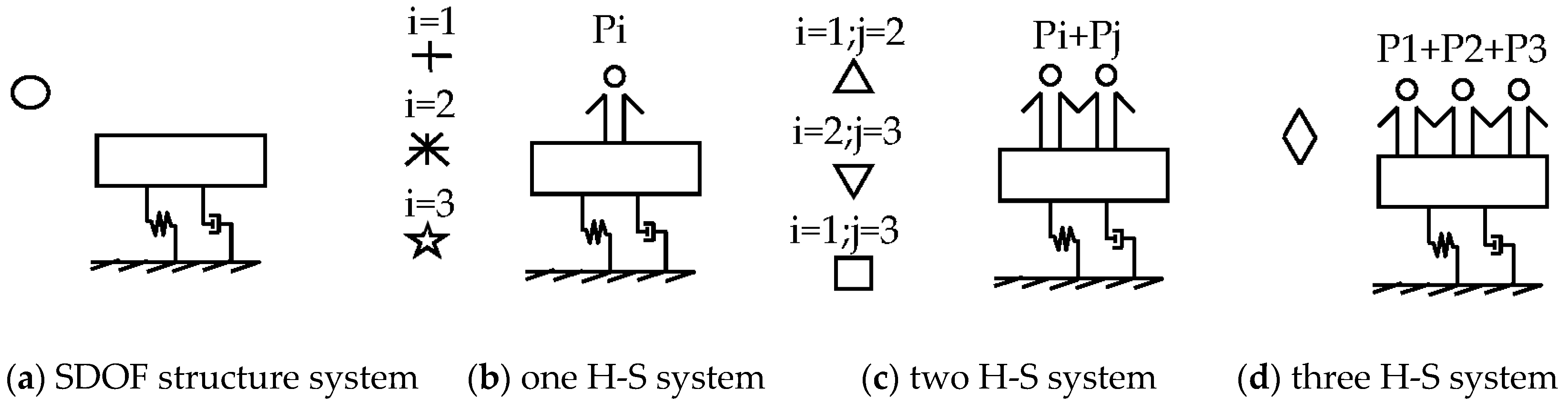
2.3. Research on Mass–Structure Systems
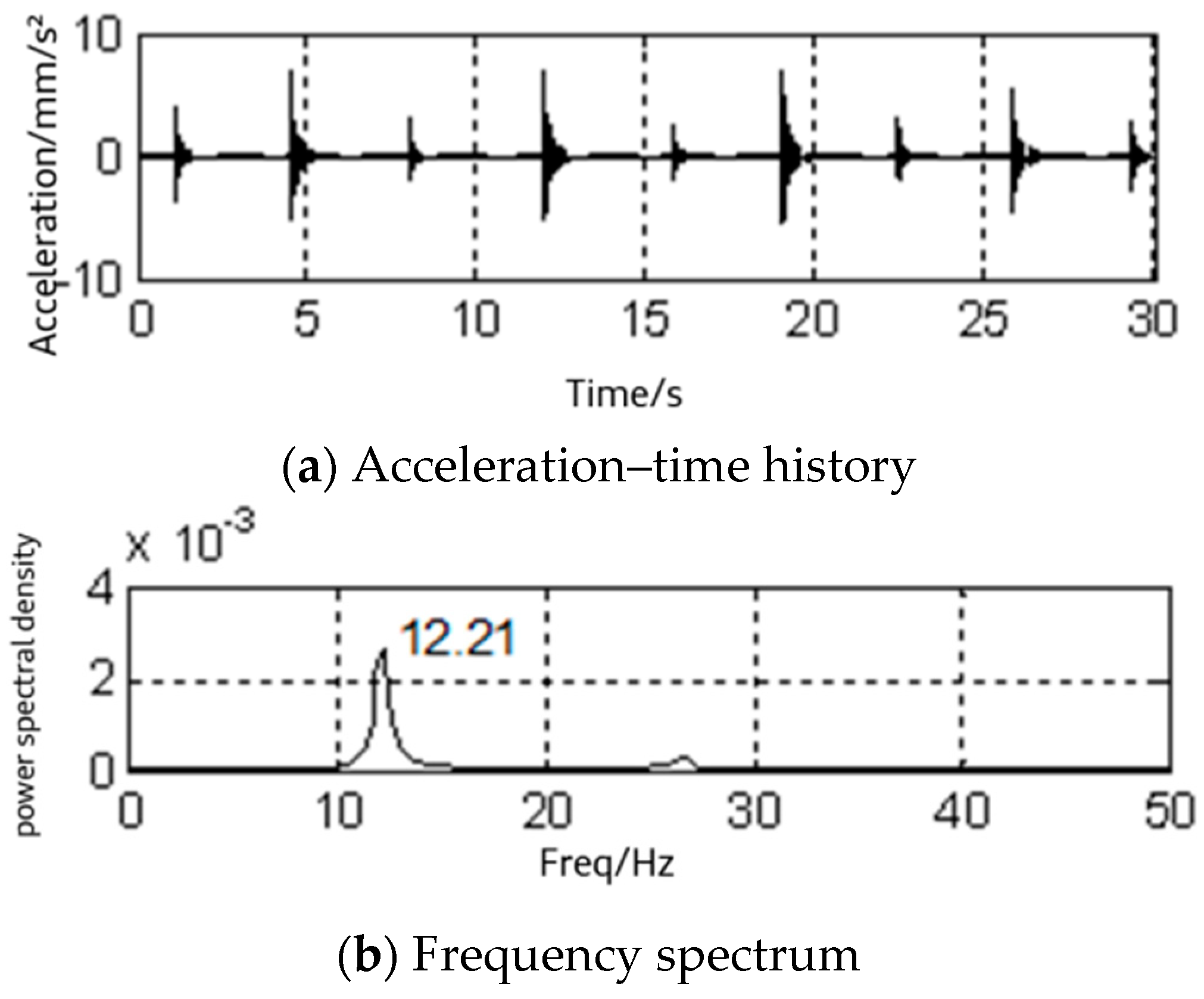
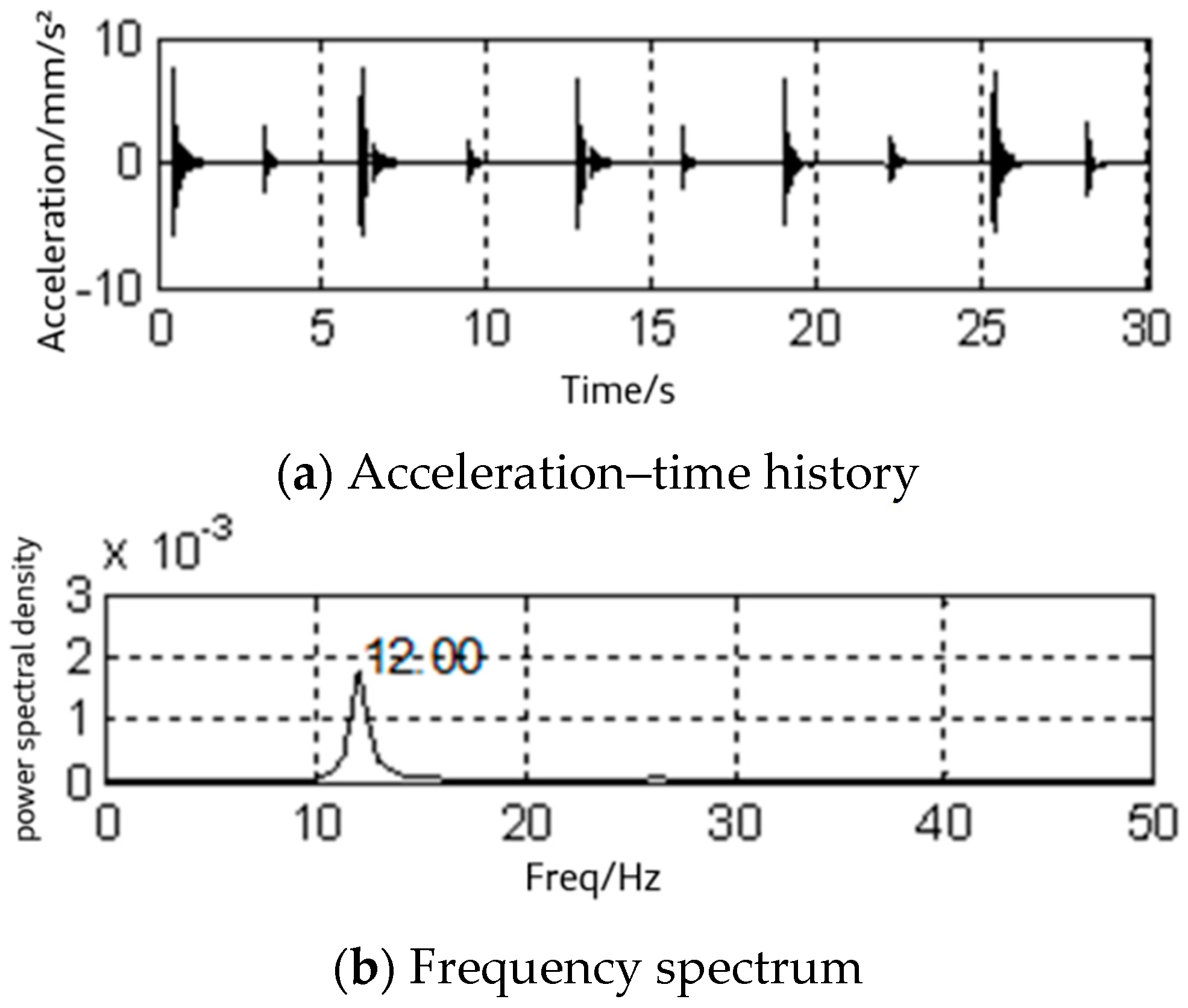
2.4. Dynamic Test of a Human–Steel Frame Platform in the Horizontal Direction
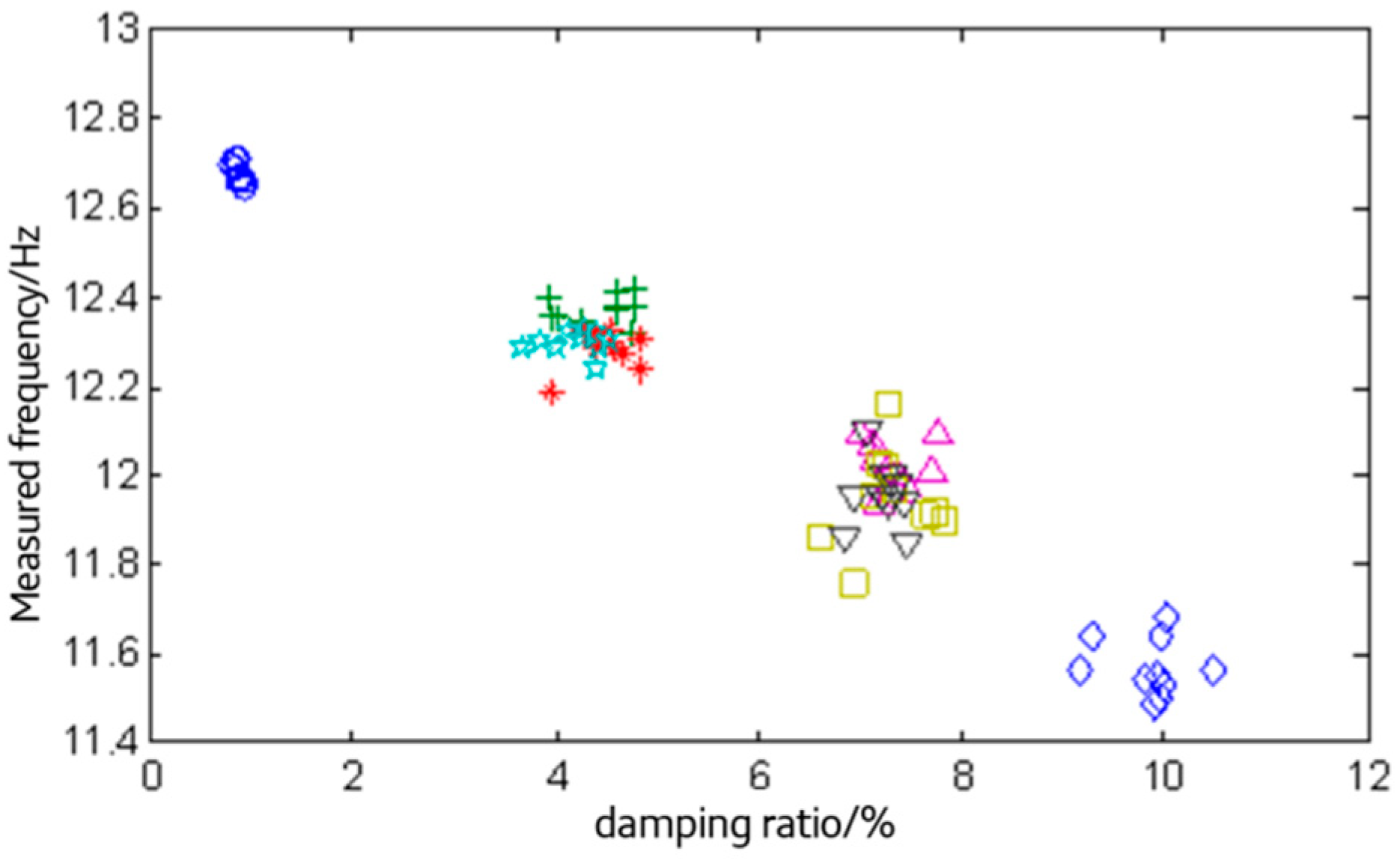
2.5. Experimental Studies on Multi-Person-Structure Systems
3. Effect of the Human Body on Structural Damping
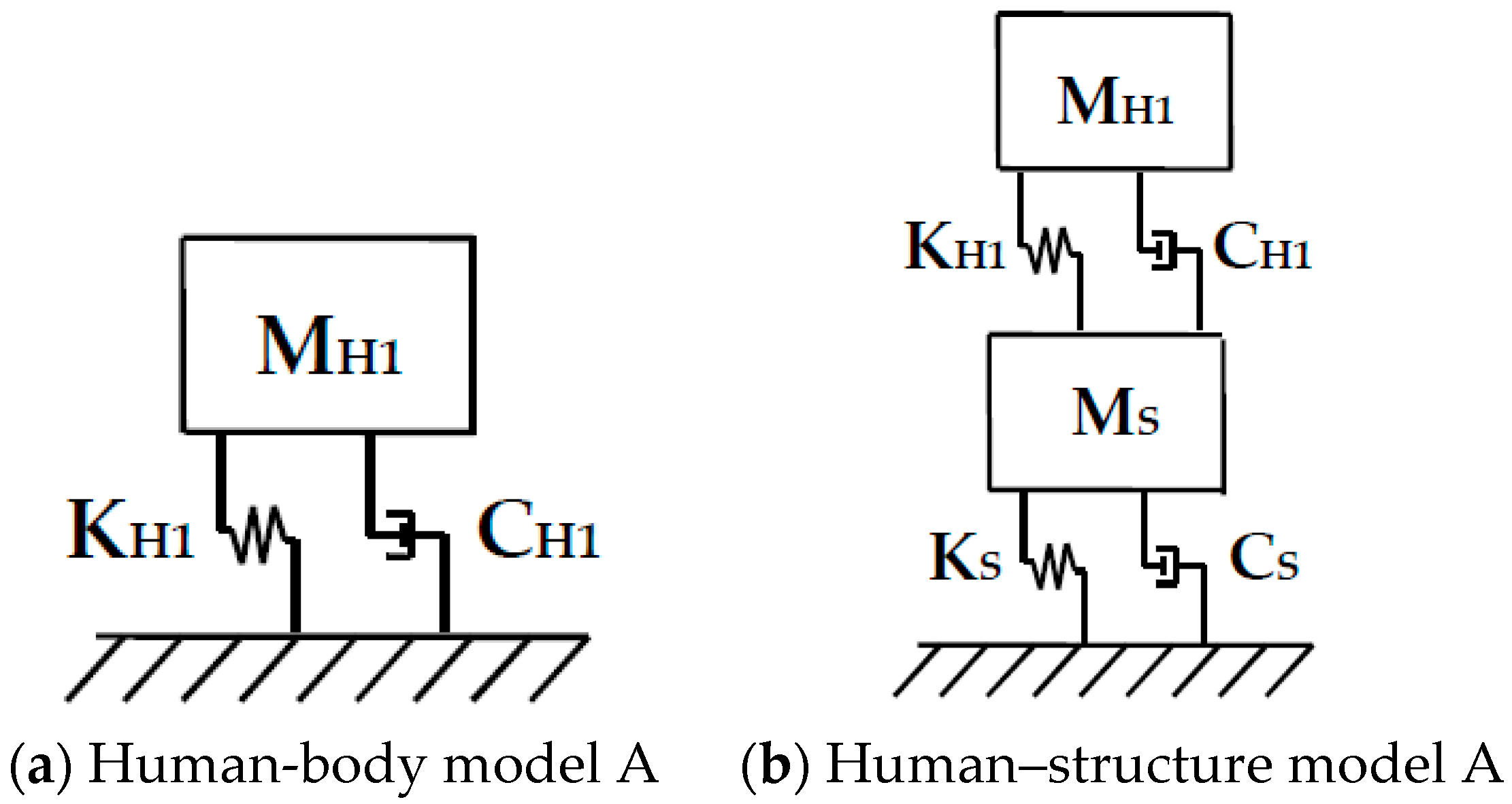
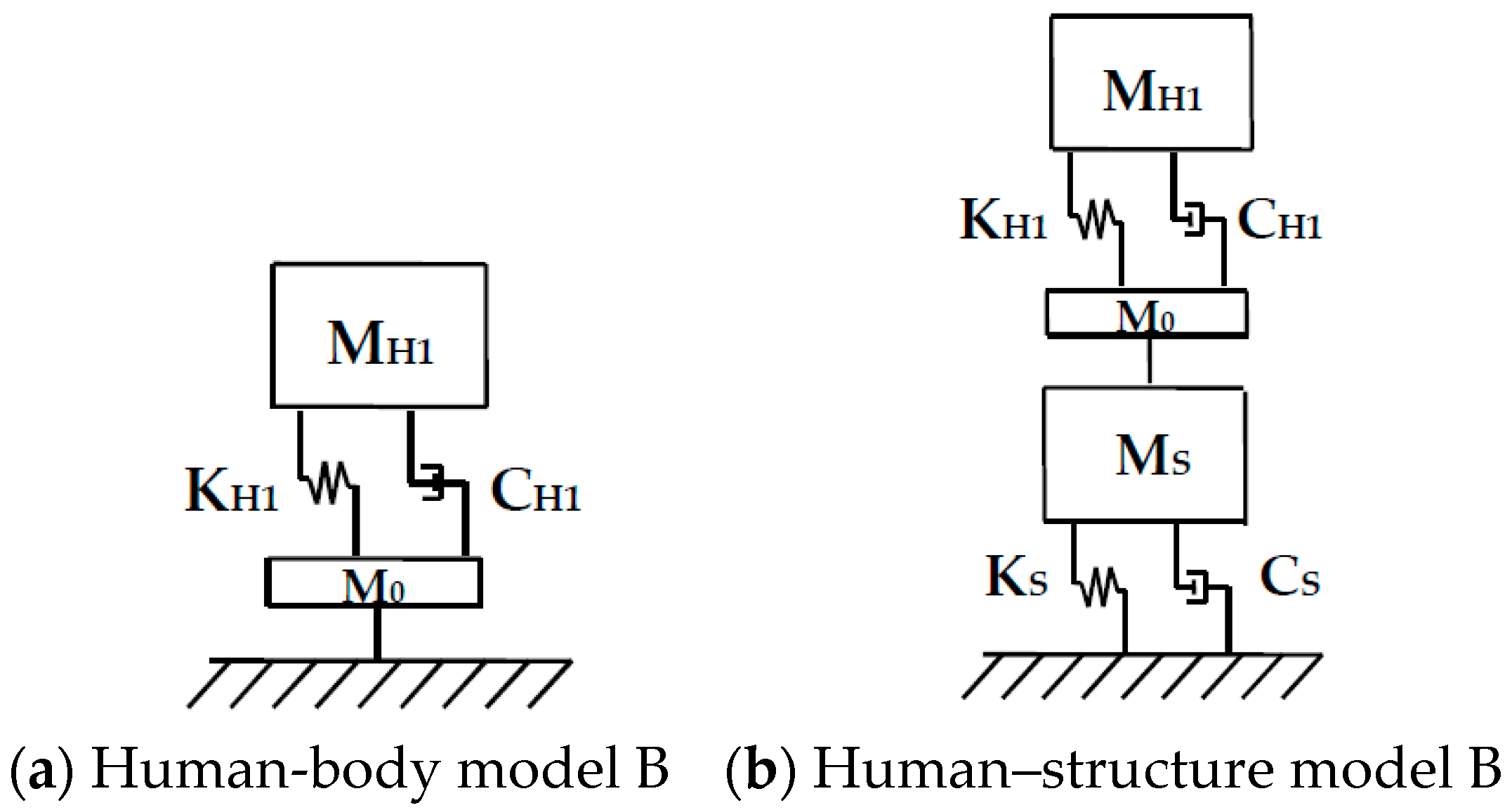
4. Human–Structure System Model
4.1. Static Horizontal Couple Motion Equations of Human-Structure System
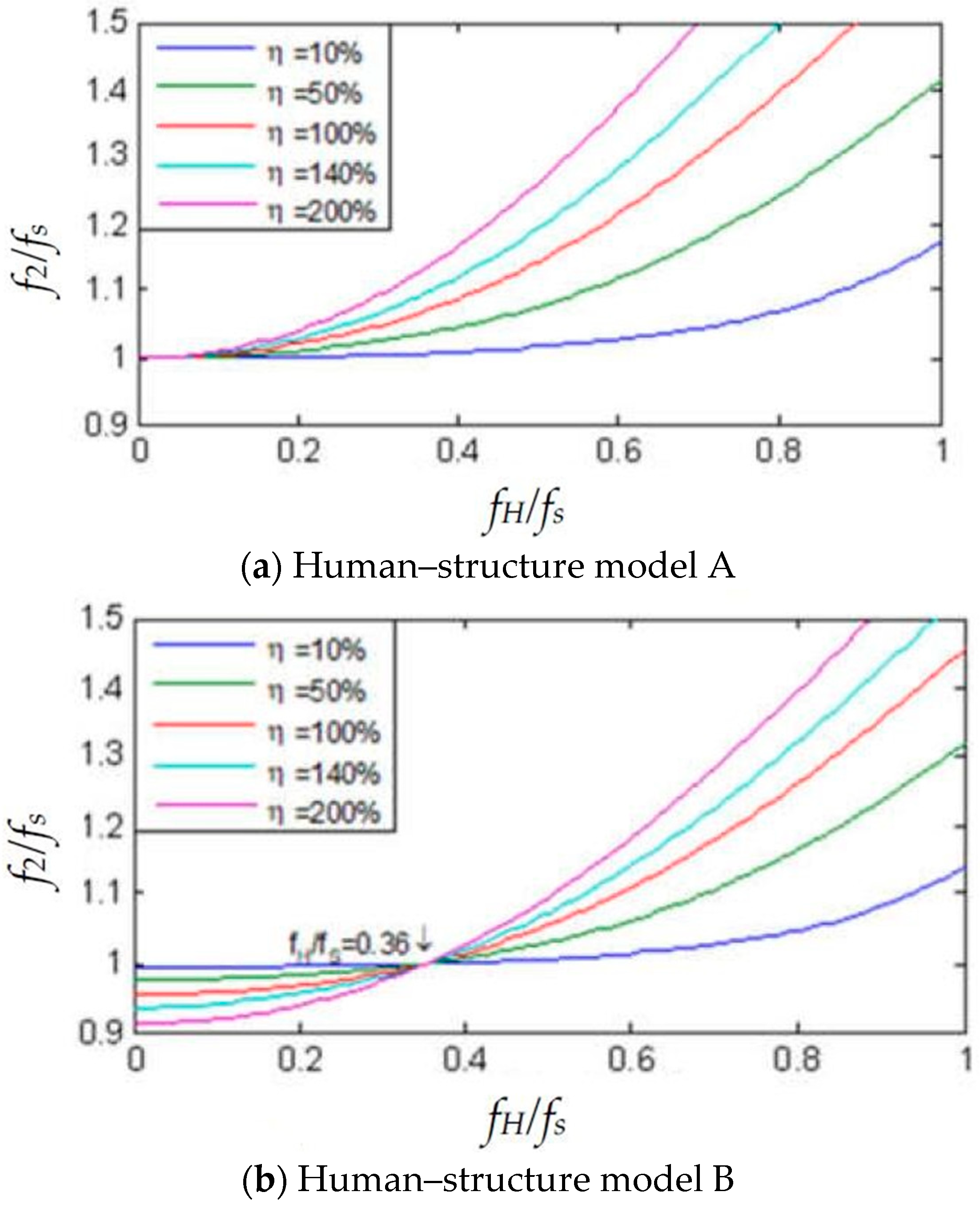
4.2. Research on Human–Structure System Model
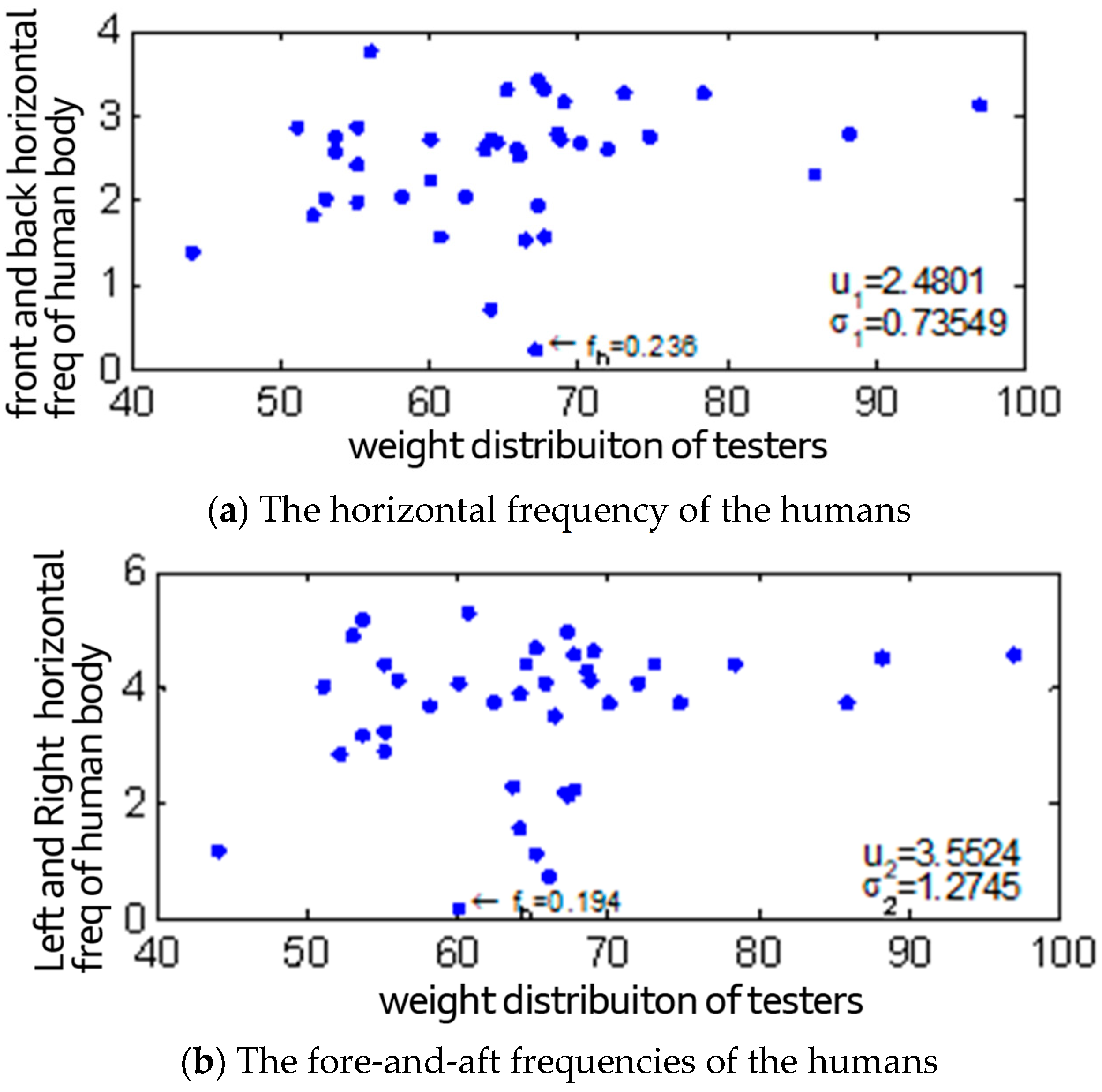
4.3. Horizontal Frequency Range of Human Bod
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IFENG. The Auditorium Collapsed at Faye Wong Concert, 17 February 2012. IFENG. Available online: http://yue.ifeng.com/news/detail_2012_03/03/12942865_0.shtml (accessed on 3 March 2012).
- Griffin, M.J. Handbook of Human Vibration; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Ji, T.; Bell, A. Seeing and Touching Structural Concepts; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Ji, T.; Ellis, B.R. A continuous model for the vertical vibration of the human body in a standing position. In Proceedings of the UK Informal Group Meeting on Human Response to Vibration, Silsoe, UK, 18–20 September 1995; pp. 18–20. [Google Scholar]
- Ji, T.; Zhou, D.; Zhang, Q. Models of a standing human body in vertical vibration. Proc. Inst. Civ. Eng.-Struct. Build. 2013, 166, 367–378. [Google Scholar] [CrossRef]
- Zhang, Q.Z. Models of a Standing Human Body in Structural Vibration. Ph.D. Thesis, The University of Manchester, Manchester, UK, 2013. [Google Scholar]
- Zhang, Q.; Ji, T. Representation of a standing body in the vertical vibration. In Proceedings of the 45th UK Conference on Human Response to Vibration, Gosport, UK, 6–8 September 2010. [Google Scholar]
- Zhou, D.; Ji, T. Free vibration of rectangular plates with attached discrete sprung masses. J. Vib. Shock 2012, 19, 101–118. [Google Scholar] [CrossRef]
- Hai, W.; Ding, Z. Modeling of the dynamic interaction of human occpupants and beam. Eng. Mech. 2010, 27, 14-020. [Google Scholar]
- Li, Y. Multi-Rigid Human Body Model in Human–Structure Interaction System. Ph.D. Dissertation, Wuhan University of Technology, Wuhan, China, 2021. [Google Scholar]
- Li, S.; Ren, M.; Zhang, Z.; Xu, M. Vertical-structure interaction system theoretical model study. J. Vib. Shock 2019, 38, 174–179+220. (In Chinese) [Google Scholar]
- Wang, Z. Comparisons of vertical dynamic characteristics of single standing occupant-simply supported beam interaction systems with three kinds of models. J. Vib. Shock 2020, 33, 952–960. [Google Scholar]
- Chen, J.-Y.; Fang, Z.-C. Study on modeling of human occupants-structure dynamic interaction. J. Vib. Shock 2007, 26, 10–13. [Google Scholar]
- He, H.; Yan, W.; Zhang, A.; Zhuo, W. Human–structure dynamic interaction and comfort evaluation in vertical ambient vibration. J. Vib. Eng. 2008, 21, 446–451. [Google Scholar]
- Van Nimmen, K.; Lombaert, G.; De Roeck, G.; Van den Broeck, P. The impact of vertical human–structure interaction on the response of footbridges to pedestrian excitation. J. Sound Vib. 2017, 402, 104–121. [Google Scholar] [CrossRef]
- Piccardo, G.; Tubino, F. Equivalent spectral model and maximum dynamic response for the serviceability analysis of footbridges. Eng. Struct. 2012, 40, 445–456. [Google Scholar] [CrossRef]
- Van Nimmen, K.; Verbeke, P.; Lombaert, G.; De Roeck, G.; Van den Broeck, P. Numerical and Experimental Evaluation of the Dynamic Performance of a Footbridge with Tuned Mass Dampers. J. Bridge Eng. 2016, 21, C4016001. [Google Scholar] [CrossRef]
- Bassoli, E.; Van Nimmen, K.; Vincenzi, L.; Van den Broeck, P. A spectral load model for pedestrian excitation including vertical human–structure interaction. Eng. Struct. 2018, 156, 537–547. [Google Scholar] [CrossRef]
- Shahabpoor, E.; Pavic, A.; Racic, V. Structural vibration serviceability: New design framework featuring human–structure interaction. Eng. Struct. 2017, 136, 295–311. [Google Scholar] [CrossRef]
- Ahmadi, E.; Caprani, C.C.; Heidarpour, A. An equivalent moving force model for consideration of human–structure interaction. Appl. Math. Model. 2017, 51, 526–545. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Griffin, M.J. The horizontal apparent mass of the standing human body. J. Sound Vib. 2011, 330, 3284–3297. [Google Scholar] [CrossRef]








| First Modal Frequency (X-Direction) | Second Modal Frequency (Y-Direction) | ||
|---|---|---|---|
| Measured (Hz) | Simulated (Hz) | Measured (Hz) | Simulated (Hz) |
| 12.51 | 12.05 | 18.80 | 18.28 |
| Condition | Frequency (Hz) | Damping Ratio (%) | ||
|---|---|---|---|---|
| First (X) | Second (Y) | First | Second | |
| Platform system | 12.54 | 18.72 | 1.242 | 1.099 |
| M1-Platform system | 10.52 | 15.68 | 1.225 | 1.081 |
| M2-Platform system | 9.33 | 13.89 | 1.186 | 1.029 |
| M3-Platform system | 8.498 | 12.62 | 1.119 | 1.029 |
| M4-Platform system | 7.842 | 11.64 | 1.103 | 1.034 |
| M5-Platform system | 7.359 | 10.92 | 1.091 | 1.059 |
| M5-Platform system | 6.856 | 10.18 | 1.192 | 1.051 |
| Condition | First Frequency (Hz) | Second Frequency (Hz) | ||||
|---|---|---|---|---|---|---|
| Measured | Calculated | Error (%) | Measured | Calculated | Error (%) | |
| Platform structure | 12.54 | - | - | 18.72 | - | - |
| M3–platform structure (42.8 kg) | 8.498 | 8.479 | 0.23 | 12.62 | 12.603 | 0.13 |
| Single-human–structure (44 kg) | 11.96 | 8.415 | 29.64 | 18.04 | 12.507 | 30.67 |
| Tester Number | Tester Mass (Kg) | X-Direction (Hz) | Y-Direction (Hz) |
|---|---|---|---|
| A | 52.4 | 12.25 | 18.34 |
| B | 67.3 | 12.22 | 18.30 |
| C | 65.1 | 12.21 | 18.27 |
| D | 53.5 | 12.18 | 18.35 |
| E | 61.7 | 12.16 | 18.22 |
| F | 79.2 | 12.00 | 18.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Lin, Y.; Ye, M.; Wu, L. Human–Structure System Coupled Vibration Test and Human Body Model. Buildings 2025, 15, 168. https://doi.org/10.3390/buildings15020168
Chen X, Lin Y, Ye M, Wu L. Human–Structure System Coupled Vibration Test and Human Body Model. Buildings. 2025; 15(2):168. https://doi.org/10.3390/buildings15020168
Chicago/Turabian StyleChen, Xiaotong, Yaofa Lin, Mao Ye, and Liqin Wu. 2025. "Human–Structure System Coupled Vibration Test and Human Body Model" Buildings 15, no. 2: 168. https://doi.org/10.3390/buildings15020168
APA StyleChen, X., Lin, Y., Ye, M., & Wu, L. (2025). Human–Structure System Coupled Vibration Test and Human Body Model. Buildings, 15(2), 168. https://doi.org/10.3390/buildings15020168




