Experimental and Finite Element Analysis on the Structural Performance of Lightweight Hollow Slab Prefabricated Staircases
Abstract
1. Introduction
2. Overview of Specimens
2.1. Design of Components
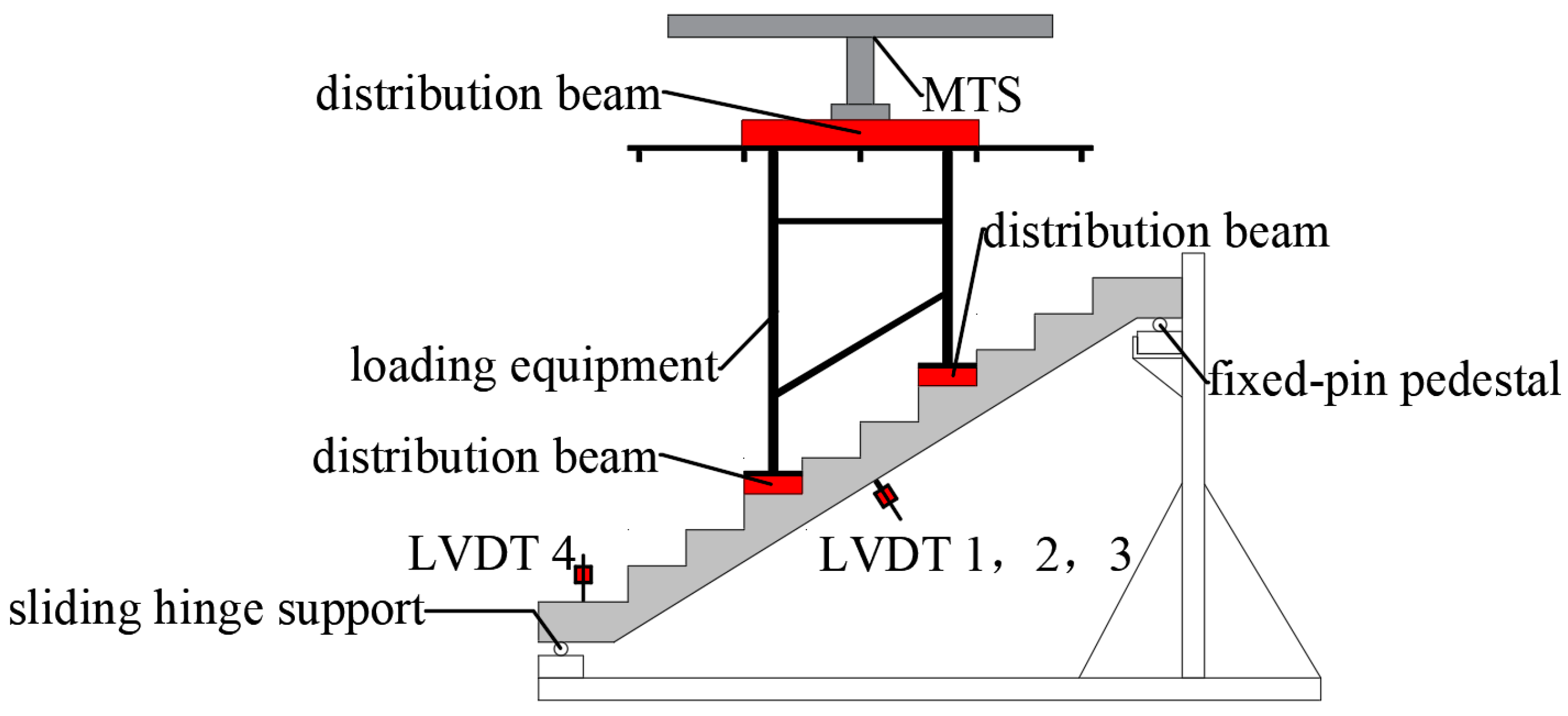
2.2. Experimental Setup and Loading Scheme
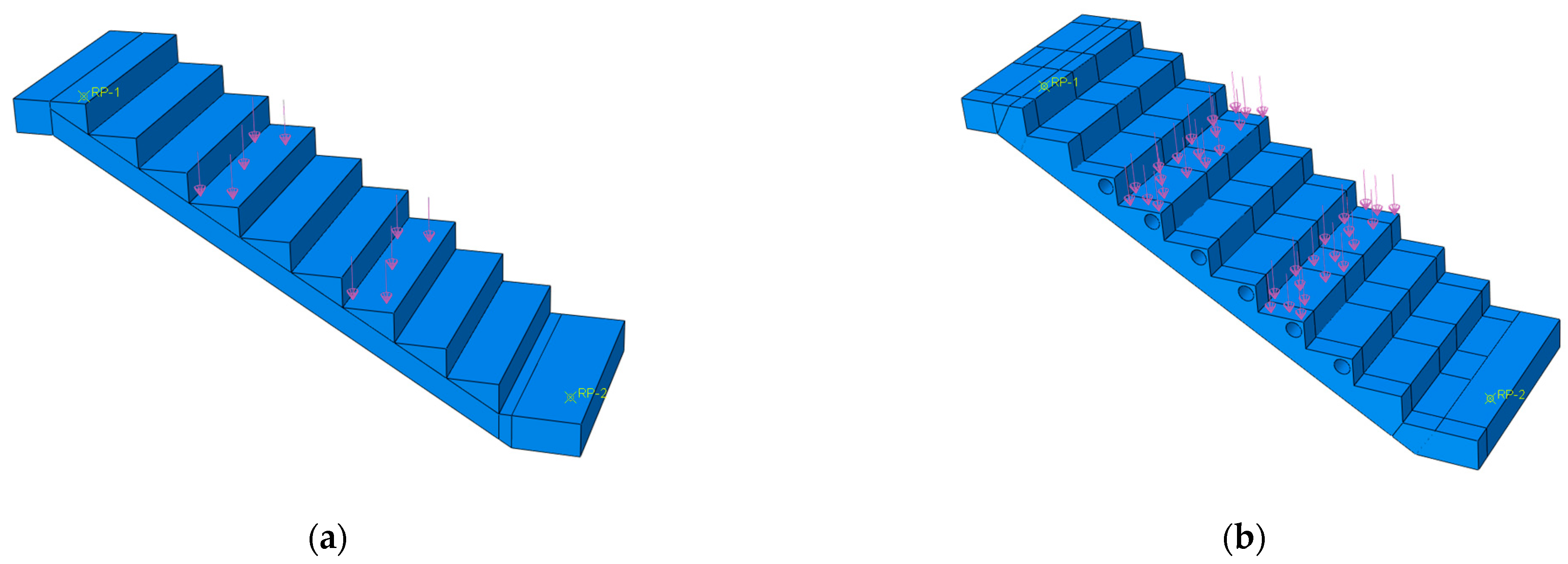
2.3. Measurement Point Arrangement
3. Experimental Results and Analysis
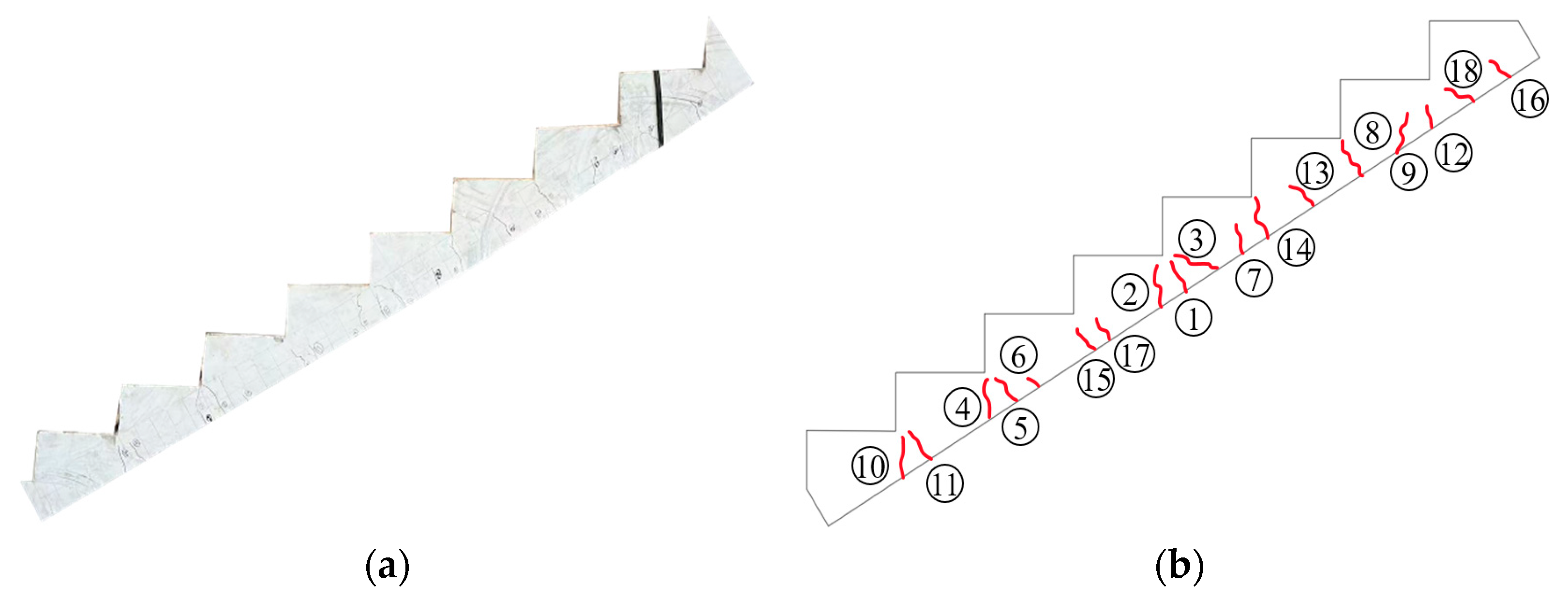
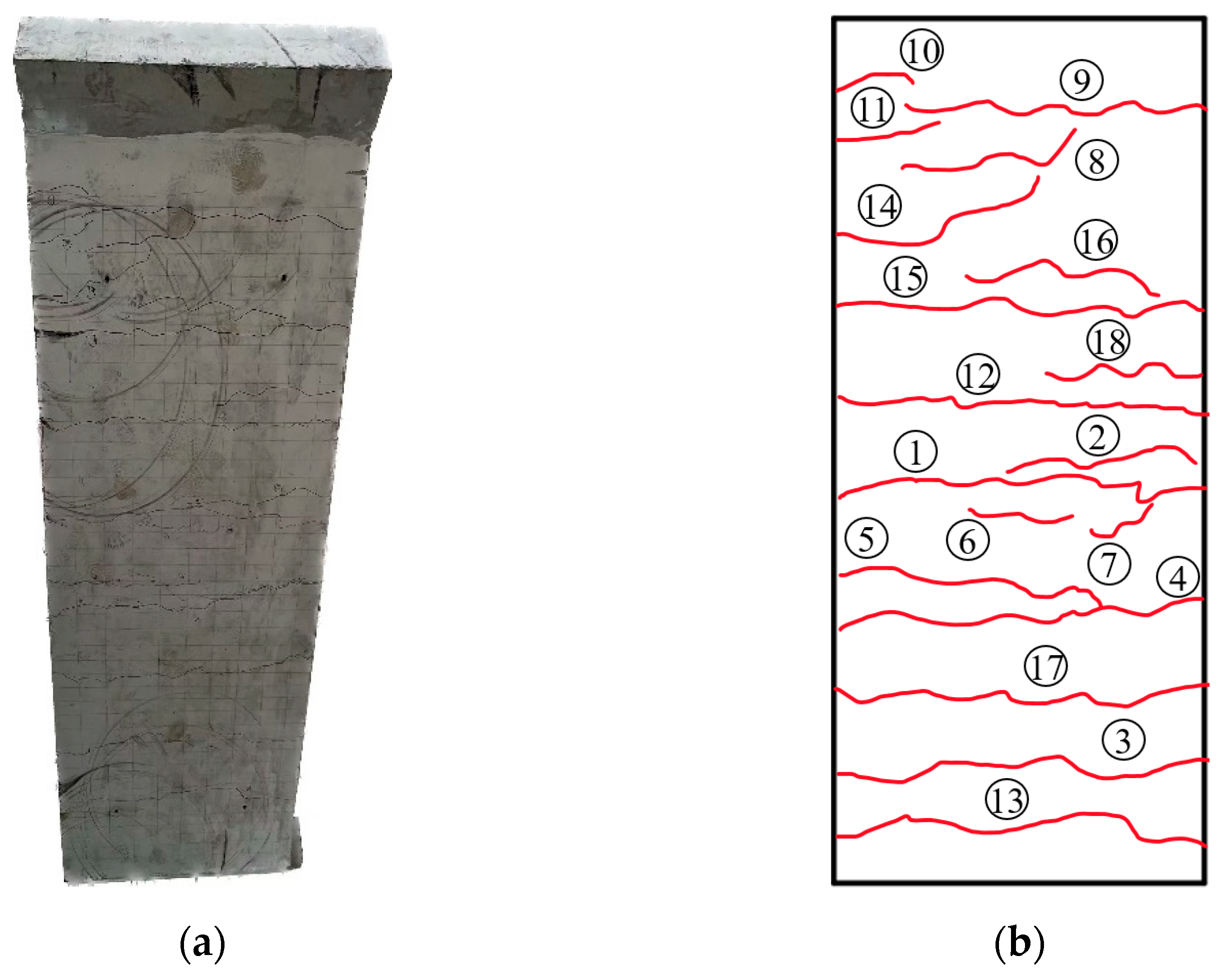
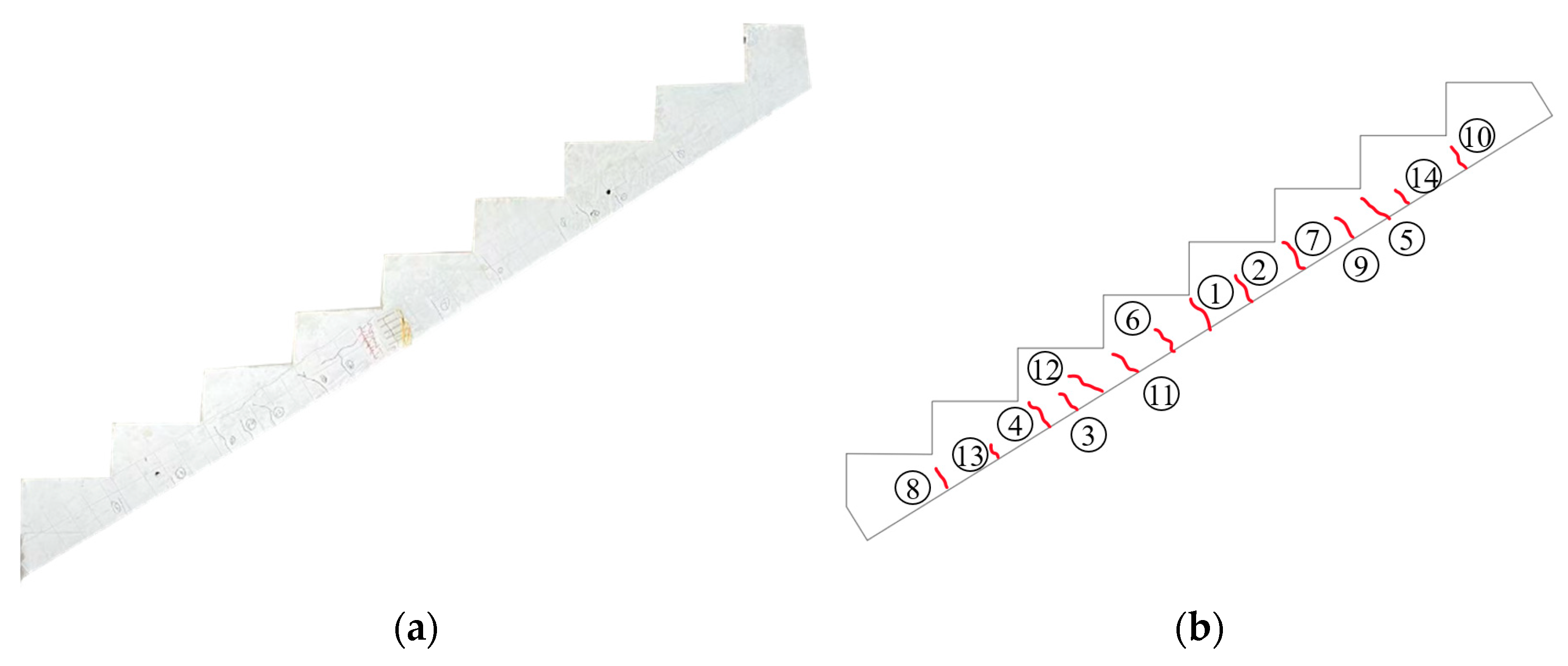
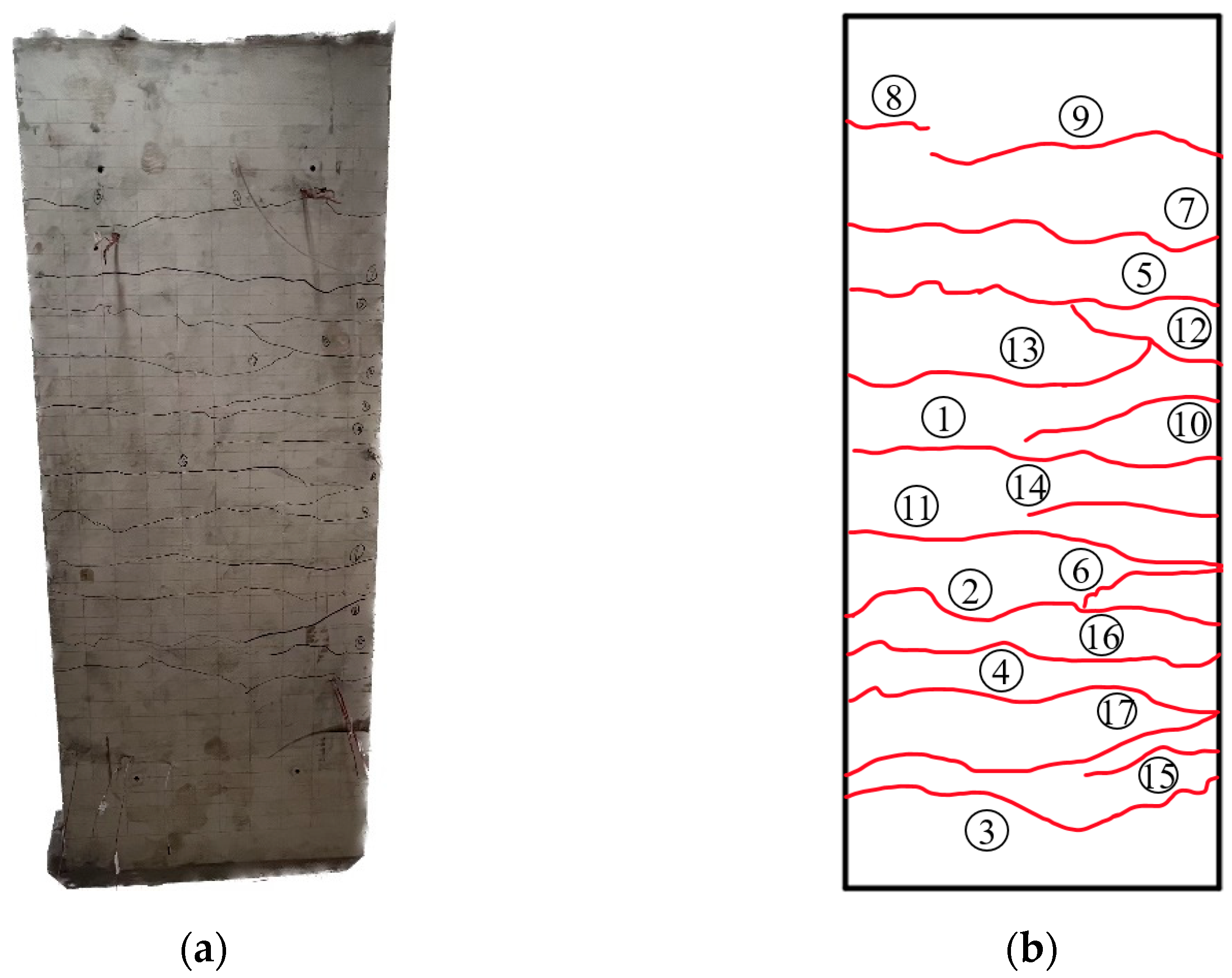
3.1. Experimental Phenomena
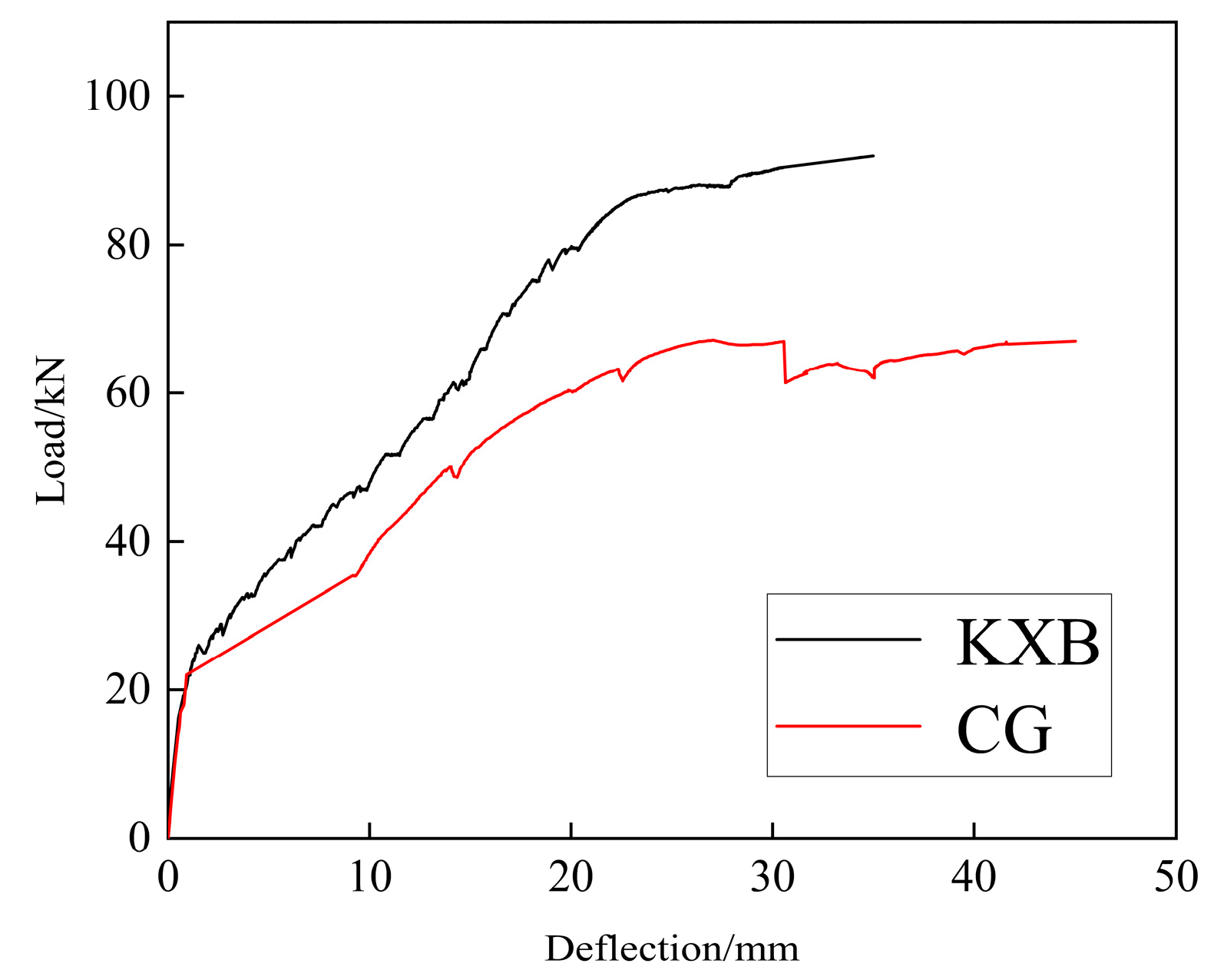
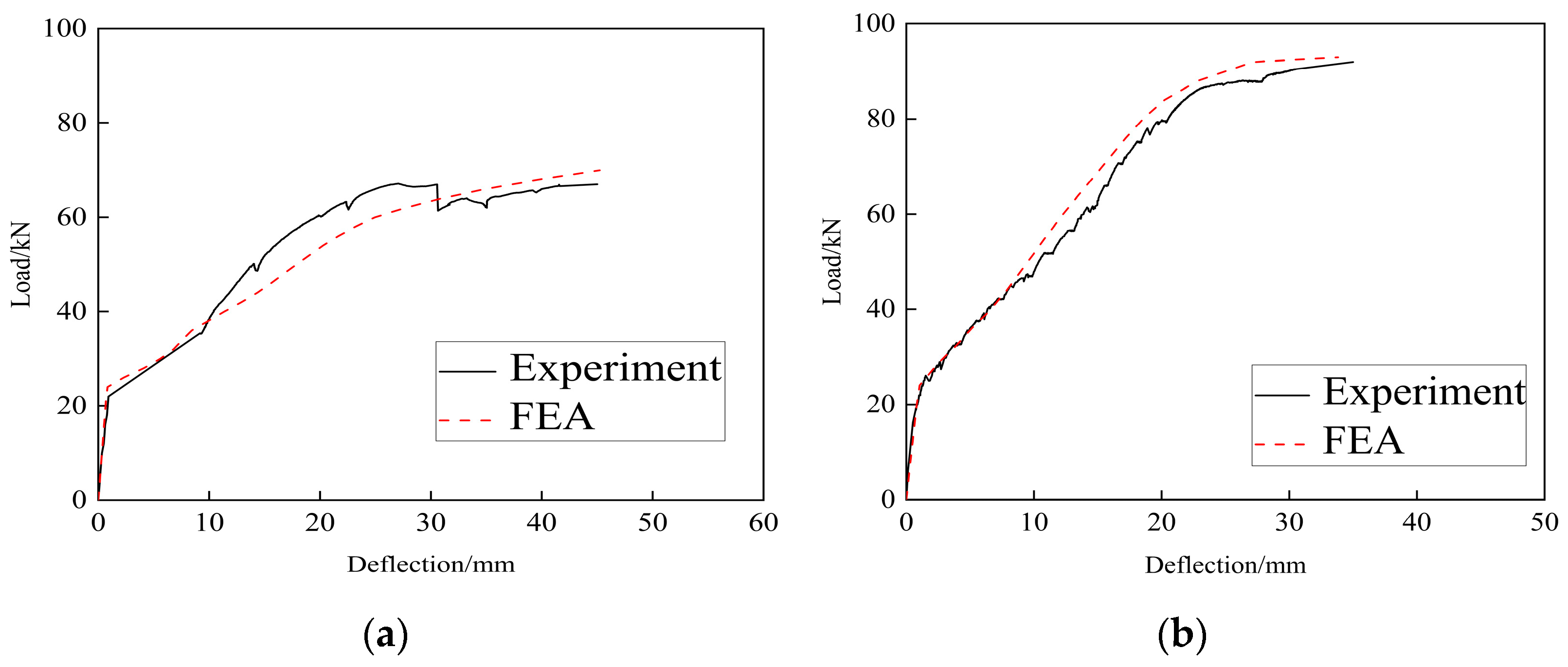
3.2. Load-Deflection Curves
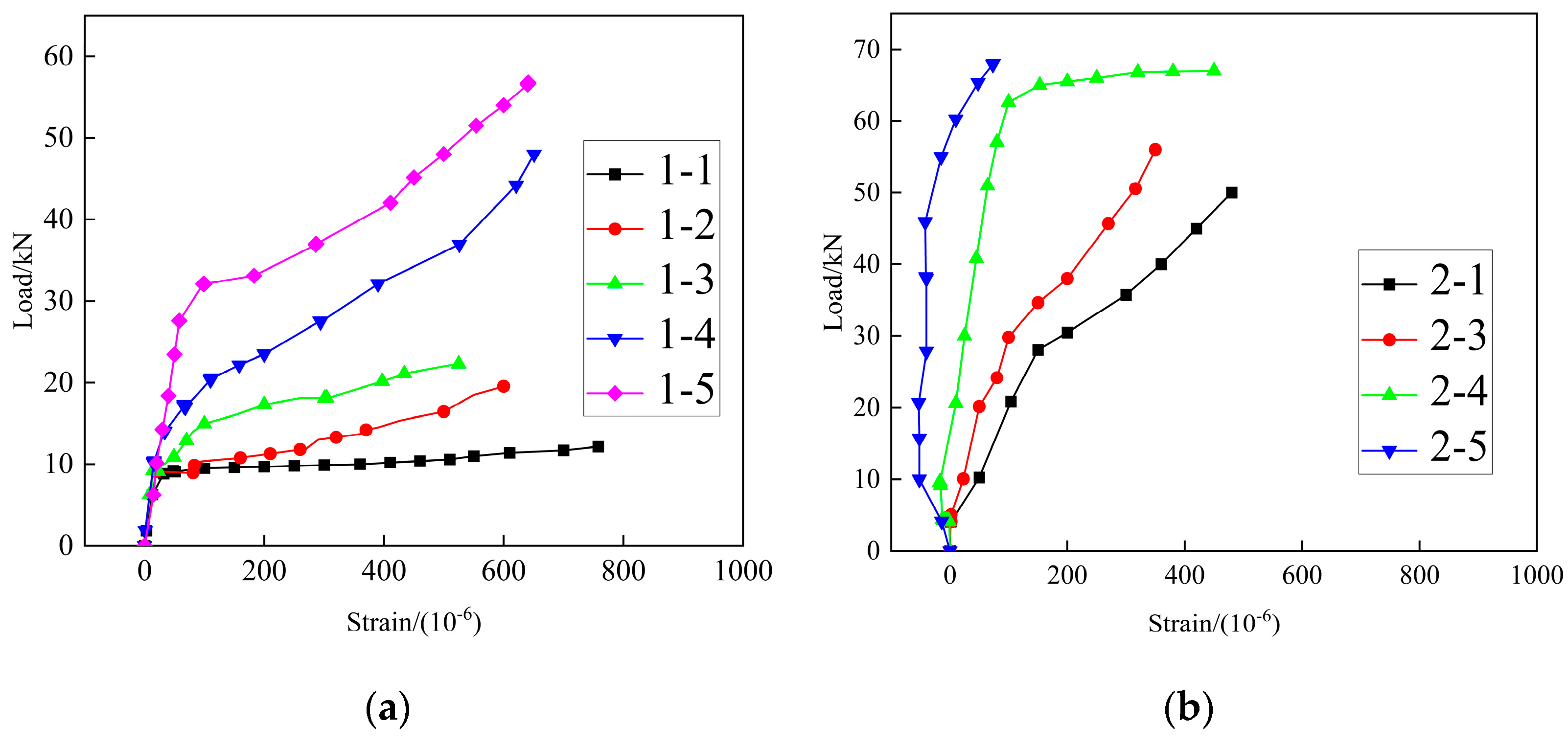
3.3. Load-Strain Curves
4. Finite Element Model Validation and Parameter Analysis
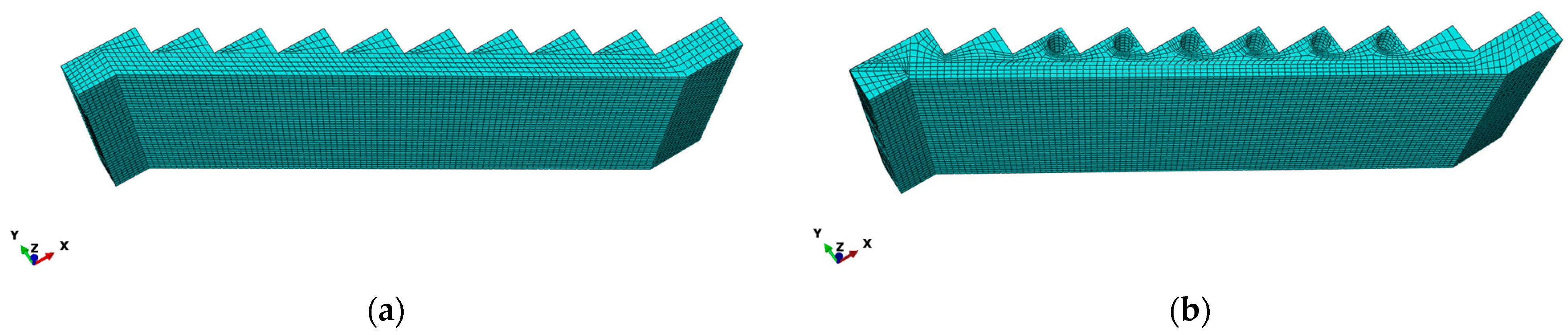
4.1. Model Establishment
4.2. Validation of the Model
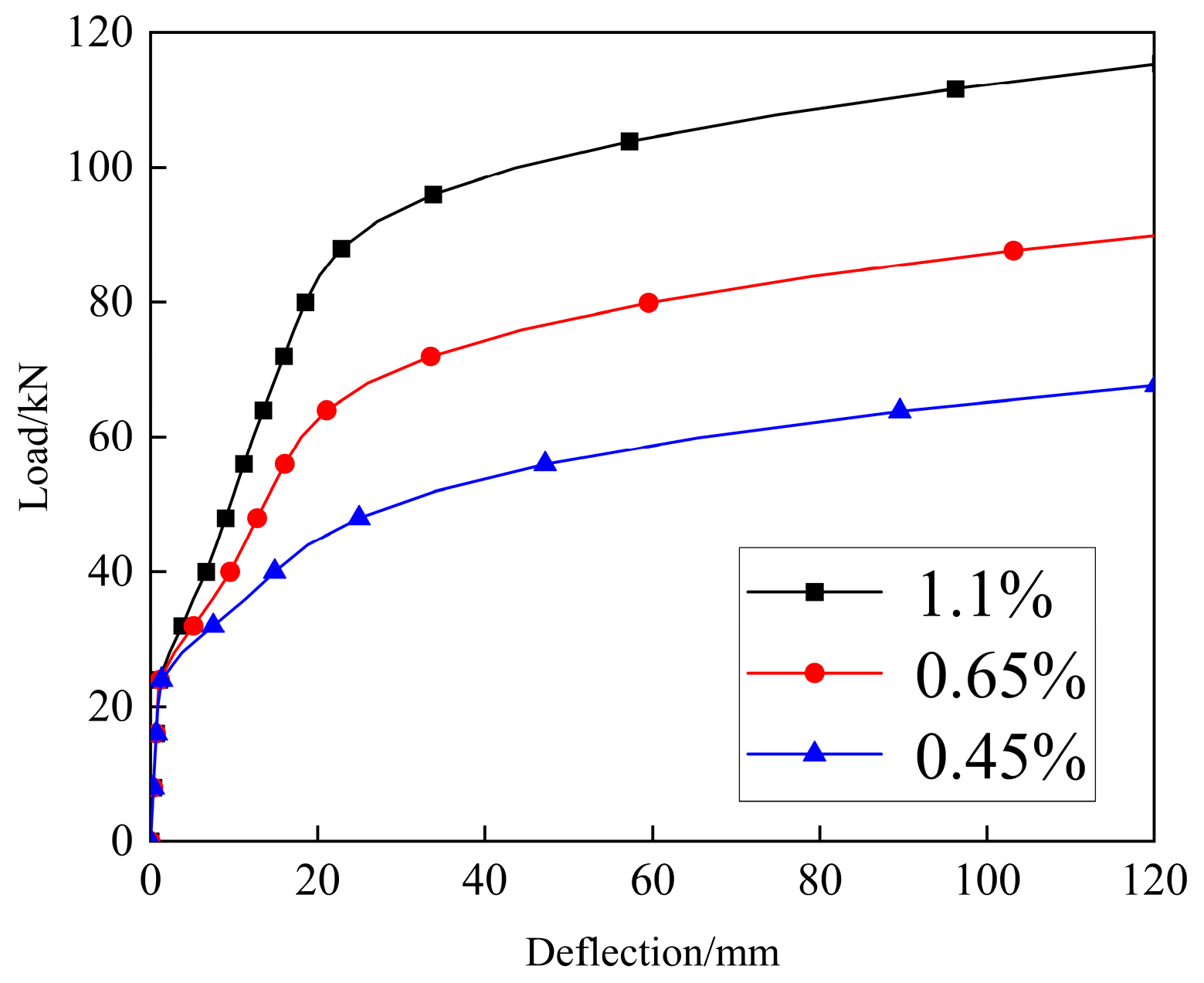
4.3. Analysis of Parameters
5. Conclusions
- (1)
- Experimental observations indicate that both types of staircase slabs mainly exhibit through cracks, which eventually propagate along the inner corners of the prefabricated steps, identifying these corners as weak points. Additionally, the KXB staircase shows significantly fewer cracks compared to the CG staircase, highlighting its stronger structural integrity.
- (2)
- Analysis of load-deflection curves, tensile reinforcement load-strain curves at the slab’s mid-span underside, and mid-span concrete load-strain curves for the two prefabricated staircases reveals that, at a 16% weight reduction, the KXB staircase’s load-bearing capacity is 28.6% higher than the CG staircase. Moreover, under identical loads, the CG staircase exhibits significantly greater strain in its reinforcement and concrete, reflecting its weaker capacity and higher failure susceptibility.
- (3)
- Experimental results for the two prefabricated staircases indicate that the maximum error between test and finite element analysis results for yield and ultimate loads is within 10%, confirming the accuracy of the developed models.
- (4)
- Parametric analysis shows that increasing the tensile reinforcement ratio at the underside markedly improves the KXB staircase’s load-bearing capacity, with a maximum increase of 50%, while the effect on weight reduction remains negligible.
- (5)
- Compared to conventional staircases, the innovative lightweight staircase offers a significantly reduced weight, streamlining construction logistics and on-site installation. It is well-suited for rapid construction projects, complies with practical engineering requirements, and supports the trend of lightweight development in prefabricated buildings.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Zhang, F.Q.; Zhang, H. Comparative analysis of off-site precast concrete and cast-in-place concrete in low-carbon built environment. Fresenius Environ. Bull. 2020, 29, 1804–1812. [Google Scholar]
- Chen, X.A.; Su, S.; Yuan, J.; Li, J.; Lou, F.; Wang, Q. Analyzing the Environmental, Economic, and Social Sustainability of Prefabricated Components: Modeling and Case Study. Sustainability 2023, 16, 342. [Google Scholar] [CrossRef]
- Liu, H.; Zainul Abidin, N. A Review on Research of Prefabricated Building Costs: Exploring Collaborations, Intellectual Basis, and Research Trends. Sustainability 2024, 16, 9823. [Google Scholar] [CrossRef]
- Xin, G.; Long, G.; Zhao, J.; Zhang, Z. The Effect of Steel Trusses on the Mechanical Performance of Laminated Precast Slabs. Buildings 2023, 13, 1653. [Google Scholar] [CrossRef]
- Sah, T.P.; Lacey, A.W.; Hao, H.; Chen, W. Prefabricated Concrete Sandwich and Other Lightweight Wall Panels for Sustainable Building Construction: State-of-the-Art Review. J. Build. Eng. 2024, 89, 109391. [Google Scholar] [CrossRef]
- Wu, X.C.; Han, J.Y.; Cui, H.; Li, T.; Bai, X.; He, Y.; Liu, N. A Comparative Review of Recent Research Progress in Prefabricated Buildings in China and Other Countries. Buildings 2024, 14, 1062. [Google Scholar] [CrossRef]
- Mir, F.U.H.; Rai, D.C. Experimental and parametric investigation of effects of built-in staircases on the dynamics of RC buildings. Earthq. Eng. Struct. Dyn. 2020, 49, 527–542. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, A.; Cao, J. Earthquake response analysis for stairs about frame structure. Eng. Fail. Anal. 2013, 33, 490–496. [Google Scholar] [CrossRef]
- Wang, X.; Astroza, R.; Hutchinson, T.C.; Conte, J.P.; Restrepo, J.I. Dynamic characteristics and seismic behavior of prefabricated steel stairs in a full-scale five-story buildings hake table test program. Earthq. Eng. Struct. Dyn. 2015, 44, 2507–2527. [Google Scholar] [CrossRef]
- Sezen, H.; Acar, R.; Dogangun, A.; Livaoglu, R. Dynamic analysis and seismic performance of reinforced concrete minarets. Eng. Struct. 2008, 30, 2253–2264. [Google Scholar] [CrossRef]
- Higgins, C. Prefabricated Steel Stair Performance under Combined Seismic and Gravity Loads. J. Struct. Eng. 2009, 135, 122–129. [Google Scholar] [CrossRef]
- Zhang, R.F.; Zhao, Z.P.; Dai, K.S. Seismic response mitigation of a wind turbine tower using a tuned parallel inerter mass system. Eng. Struct. 2019, 180, 29–39. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Tan, P.; Ma, H.T.; Dona, M. Improving the Seismic Performance of Staircases in Building Structures with a Novel Isolator. Cmes-Comp. Model. Eng. 2020, 124, 415–431. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, C.; Zhou, Y.; Wang, G.; Shi, F.; Huang, W. Seismic behavior of prefabricated reinforced concrete stair isolated by high damping rubber bearings. Bull. Earthq. Eng. 2022, 21, 1325–1352. [Google Scholar] [CrossRef]
- Luo, D.Z.; Deng, X.S.; Zhou, Y.; Zhang, C. Seismic performance analysis of frame structures with damped staircases. Build. Struct. 2019, 49, 80–85. (In Chinese) [Google Scholar]
- Deng, X.S.; Luo, D.Z.; Zhou, Y.; Chen, Z.Y. Analysis of energy dissipating performance of damped staircase with different constructions and design parameters. Earthq. Eng. Eng. D 2018, 32, 1–9. (In Chinese) [Google Scholar]
- Cong, S.P.; Zhang, Z.; Zheng, Q.; Xu, Z. Seismic behavior of reinforced concrete frame staircase with separated slab stairs. Structures 2021, 34, 4284–4296. [Google Scholar] [CrossRef]
- Hu, H.; Li, Z.L.; Liu, H.J.; Jiang, Q.B. Experimental study and finite element analysis on sliced prefabricated staircases. Build. Struct. 2018, 48, 97–106. (In Chinese) [Google Scholar]
- Liu, J.M.; Wang, X.J.; Qin, K.; Wei, L.S.; Zhang, H. Research and application of longitudinal segment technology for prefabricated stairs. Struct. Constr. 2020, 42, 1160–1162. (In Chinese) [Google Scholar]
- Liu, W.Z.; Cui, S.Q. Experimental study on the flexural performance of prefabricated prestressed concrete stairs. Build. Struct. 2021, 51, 8–15. (In Chinese) [Google Scholar]
- Song, S.F. Response Analysis of a New Prefabricated Hollow Slab Staircase under Seismic Action. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2014. (In Chinese). [Google Scholar]
- Li, N.; Xu, Q.G.; Huang, L.P.; Wei, S. Research on type selection and static loading test of lightweight assembled stairs. Eng. Construct. Design 2021, 15, 16–18+40. (In Chinese) [Google Scholar]
- Wang, Y.; Sheng, D.; Wang, Y. Research on the Performance of Lightweight Prefabricated Concrete Stairs with a Special-Shaped Hollow Landing Slab. Buildings 2024, 14, 1314. [Google Scholar] [CrossRef]
- White, J.; Pleau, R.; Bouchard, F. Innovative Design with Ultra-High Performance Concrete: A Case Study. In Proceedings of the fib Symposium 2004, Avignon, France, 26–28 May 2004. [Google Scholar]
- Shan, Y.; Gong, Y.; Wang, Y.; Zhou, Q.; Li, X.; Ding, F.; Kuang, Y. Flexural behavior of ultra-high performance concrete (UHPC) shaped thin-plate ribbed staircases: An experimental and numerical study. Mater. Struct. 2024, 57, 18. [Google Scholar] [CrossRef]
- Shen, Y.J.; Wang, Q.; Zhou, Q.; Li, X.; Xiang, Z. Experimental Study on Fire Resistance of Geopolymer High-Performance Concrete Prefabricated Stairs. Buildings 2024, 14, 3783. [Google Scholar] [CrossRef]
- Marcinkiewicz, K.; Wells, M. Staircase showcase for ultra-high-strength fibre-reinforced concrete. Proc. Inst. Civil Eng.-Civil Eng. 2014, 167, 131–137. [Google Scholar] [CrossRef]
- Mobaraki, B.; Vaghefi, M. The Effect of Protective Barriers on the Dynamic Response of Underground Structures. Buildings 2024, 14, 3764. [Google Scholar] [CrossRef]
- Wang, A.; Gao, R.; Chen, Q.; Jin, W.; Fang, P.; Wu, D. An Optimization Study on Continuous Steel Box Girder Bridge Components. Buildings 2025, 15, 124. [Google Scholar] [CrossRef]
- Bai, L.; Liang, X.; Xin, L.; Liu, M.; Yu, Z.; Chu, Y. Investigation on the Seismic Performance of RC Frame Buildings with Rubber Isolation Bearing Installed in Staircases. Buildings 2023, 13, 616. [Google Scholar] [CrossRef]
- GB50010-2010; Code for Design of Concrete Structures. China Architecture Publishing & Media Co., Ltd.: Beijing, China, 2010. (In Chinese)
- 15G310-1~2; Prefabricated Concrete Joint Structure Collection. China Planning Press: Beijing, China, 2015. (In Chinese)
- GB50009-2012; Load Code for the Design of Building Structures. China Architecture Publishing & Media Co., Ltd.: Beijing, China, 2012. (In Chinese)
- Liang, X.W.; Shi, Q.X. Concrete Structure Design Principle; China Architecture & Building Press: Beijing, China, 2019; pp. 99–108. (In Chinese) [Google Scholar]
- GB/T50152-2012; Standard for Test Methods of Concrete Structures. China Architecture Publishing & Media Co., Ltd.: Beijing, China, 2014. (In Chinese)
- Chen, H.T.; Sun, Z.; Zhang, X.; Zhang, W. Equivalent Fatigue Constitutive Model Based on Fatigue Damage Evolution of Concrete. Appl. Sci. 2024, 14, 8721. [Google Scholar] [CrossRef]
- Shang, F.L. Fundamental of Plasticity; Xi’an Jiao Tong University Press: Xi’an, China, 2018; pp. 14–17. (In Chinese) [Google Scholar]

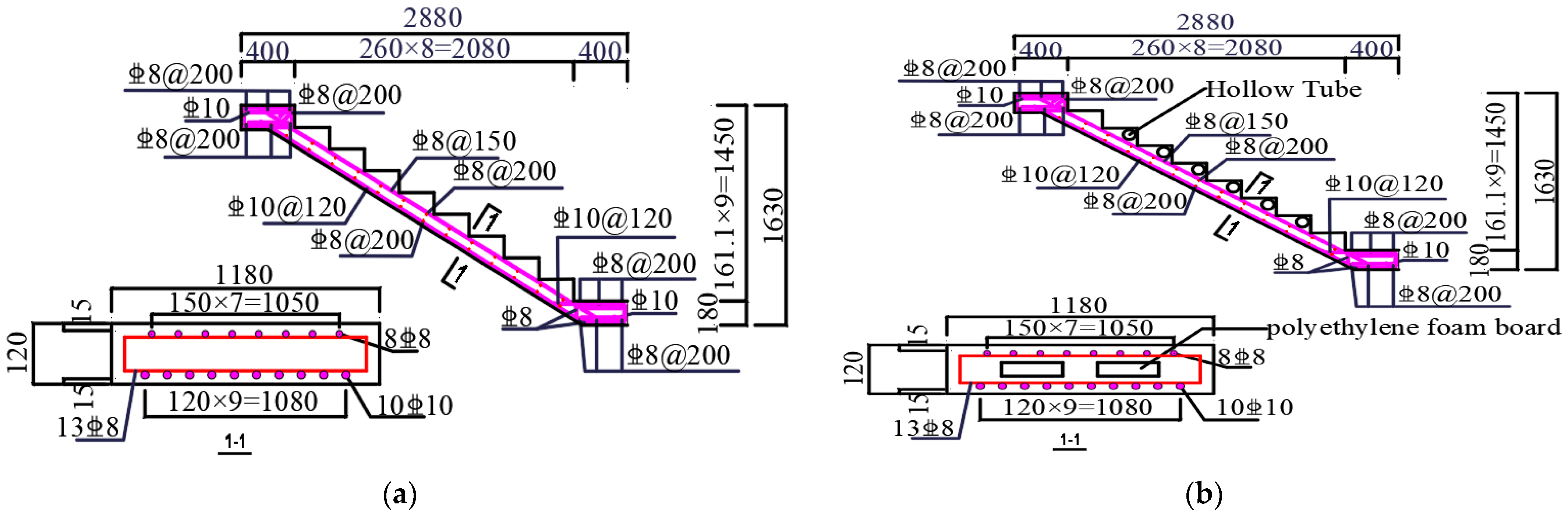


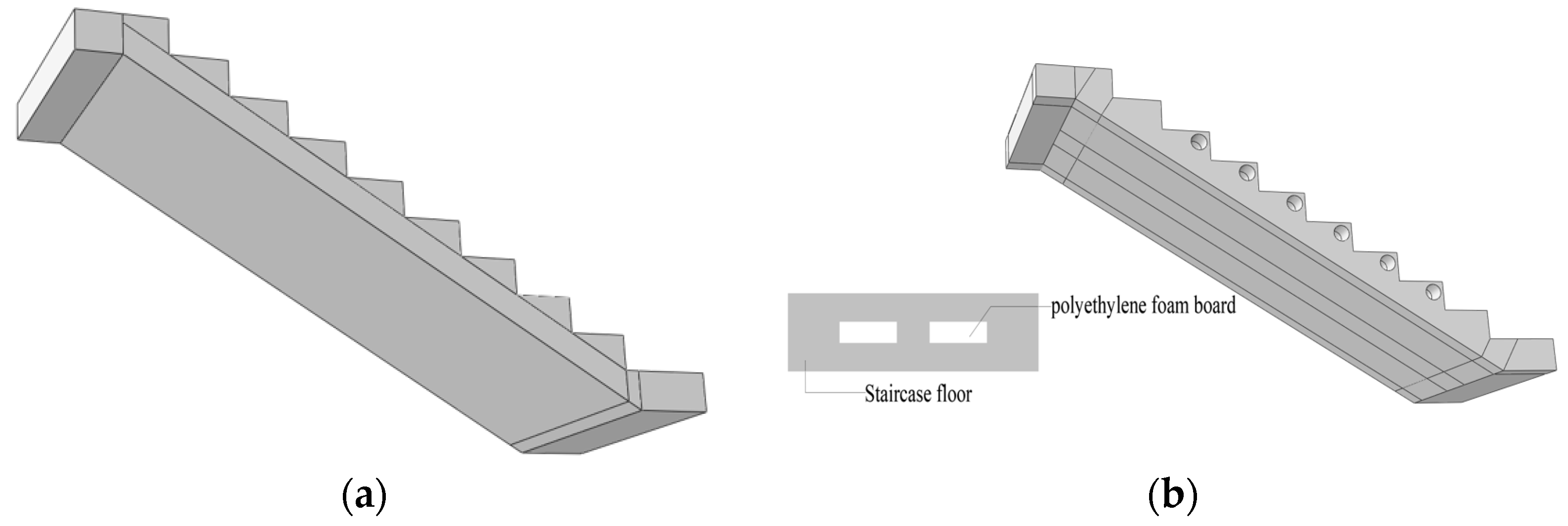

| Specimen Number | CG | KXB |
|---|---|---|
| Upper Longitudinal Reinforcement | 8 8@150 8@150 | 8 8@150 8@150 |
| Lower Longitudinal Reinforcement | 10 10@120 10@120 | 10 10@120 10@120 |
| Distribution Reinforcement | 13 8@200 8@200 | 13 8@200 8@200 |
| Total Weight | 1830 kg | 1530 kg |
| Reduced Weight | \ | 299 kg |
| Weight Reduction Rate | \ | 16% |
| Specimen Number | CG | KXB |
|---|---|---|
| Average compressive strength of cube/MPa | 32 | 30.5 |
| Specification |  8 8 |  10 10 |
|---|---|---|
| Yield Strength/MPa | 422 | 436 |
| Tensile Strength/MPa | 618 | 627 |
| Specimen Number | Yield Load | Ultimate Load | ||||
|---|---|---|---|---|---|---|
| Experiment/kN | FEA/kN | Error/% | Experiment/kN | FEA/kN | Error/% | |
| CG | 22.7 | 25.2 | 9.9 | 62.5 | 67.9 | 8.0 |
| KXB | 25.5 | 27.9 | 8.6 | 87.2 | 91.4 | 4.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Bao, Y.; Qin, K. Experimental and Finite Element Analysis on the Structural Performance of Lightweight Hollow Slab Prefabricated Staircases. Buildings 2025, 15, 245. https://doi.org/10.3390/buildings15020245
Liu J, Bao Y, Qin K. Experimental and Finite Element Analysis on the Structural Performance of Lightweight Hollow Slab Prefabricated Staircases. Buildings. 2025; 15(2):245. https://doi.org/10.3390/buildings15020245
Chicago/Turabian StyleLiu, Jingmin, Yiming Bao, and Kang Qin. 2025. "Experimental and Finite Element Analysis on the Structural Performance of Lightweight Hollow Slab Prefabricated Staircases" Buildings 15, no. 2: 245. https://doi.org/10.3390/buildings15020245
APA StyleLiu, J., Bao, Y., & Qin, K. (2025). Experimental and Finite Element Analysis on the Structural Performance of Lightweight Hollow Slab Prefabricated Staircases. Buildings, 15(2), 245. https://doi.org/10.3390/buildings15020245





