Seismic Failure Assessment Using Energy Outputs of Finite Element Analysis: A Strategy for Complex Heritage Masonry Structures Modeled with Concrete Damaged Plasticity Material
Abstract
:1. Introduction and Objectives
- In the context of the so-called “displacement-based design”, predicting the displacement that a structure can reach at limit state conditions is fundamental. The substantial inability of finite element models conceived in the static field to accurately predict the ultimate displacements for historical buildings is well documented in the literature [10,11,12,13]. The Italian guidelines for cultural heritage (probably the most advanced for numerical analysis of monumental structures), address this limitation by suggesting nonlinear static analyses—in the absence of a clear drop in the load-bearing capacity and for materials unable to withstand tensile stresses—up to “relevant displacements” of the pushover curve (§ 5.2.4 [14]). Thus, a quantitative measure of failure is missing.
- Nonlinear static analyses often exhibit a lack of convergence for applied loads far from the collapse limit state and/or premature halting. These issues can be solved by using dynamic analyses in which the equations of motion are solved at each load step by means of well-known integration schemes that do not require sub-iterations based on return mapping procedures. This easily justifies the potentially high cost of using the explicit formulation adopted here instead of a standard formulation.
- Relative distributions of inertial forces acting on a structure are often based on modal superposition and are imposed a priori. For a nonlinear static analysis, the hypothesis of a linear elastic material for masonry is used for these calculations, but it is unrealistic, especially when masonry is subjected to progressively increasing horizontal accelerations. Such an assumption, already questionable at the beginning of the analyses for monumental historic masonry buildings (which are often damaged by previous seismic events and may exhibit pre-existing states of cracking that occurred over a long period of time, for example induced by foundation settlements) would require adaptive procedures, as for instance adaptive pushover analyses, which are typically carried out in a static fashion. Indeed, with the progressive application of the horizontal loads, crack spreads and damage patterns tend to evolve, with the progressive shift of the period of the structure towards the right portion of the spectrum. The presence of evolving crack patterns changes the natural frequencies and the corresponding participating mass, and potentially invalidates the originally determined force distributions.
2. Materials and Methods
2.1. Validation with a 3D Static Pushover Test
2.2. Validation with a Dynamic Ground Acceleration Test
2.3. Validation with an Axial Loading and Shear Displacement Test
3. Application Cases
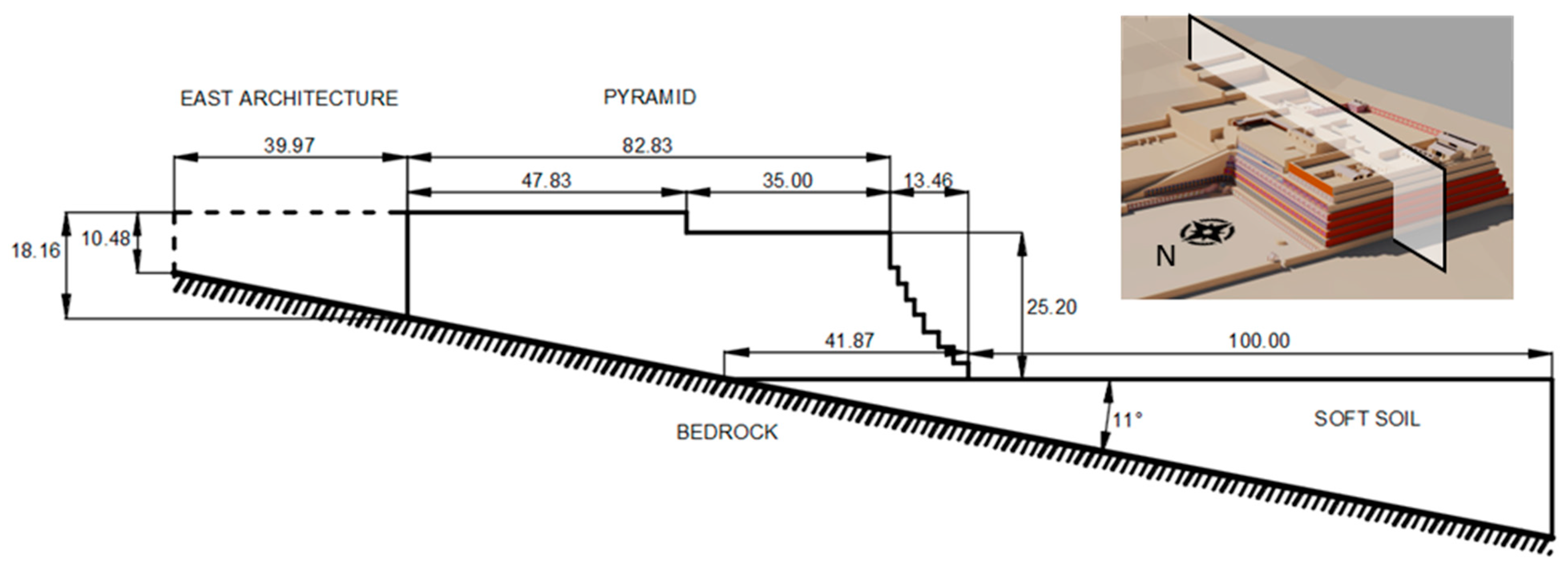
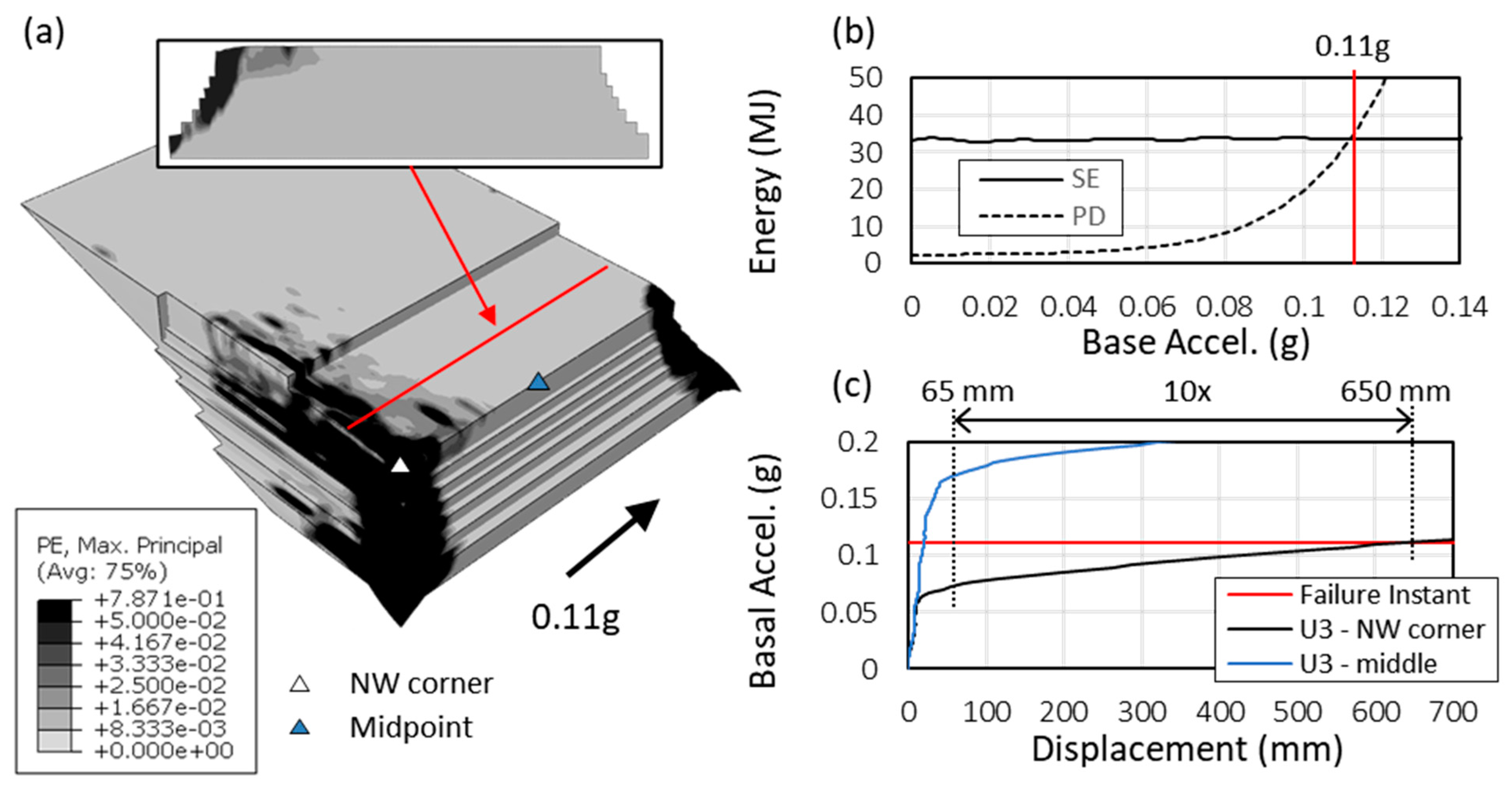
3.1. Huaca de la Luna, Trujillo, Perú
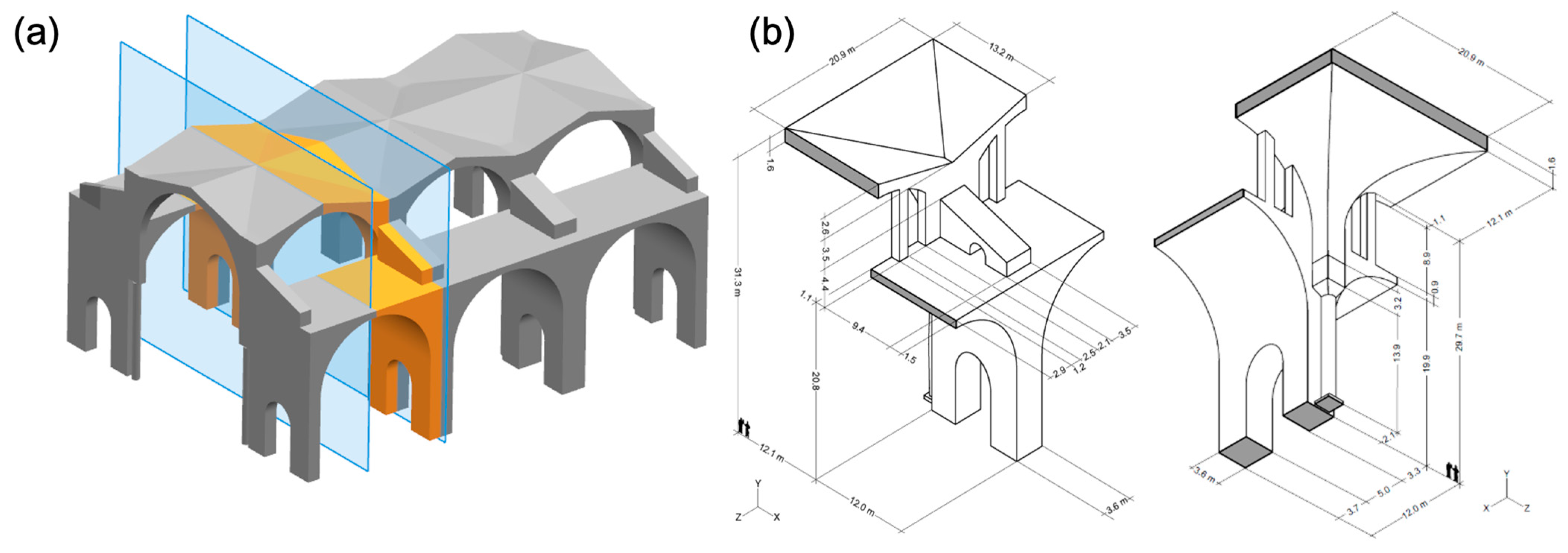
3.2. Frigidarium of the Baths of Diocletian, Rome, Italy
3.3. Church of San Pedro de Andahuaylillas, Perú
4. Conclusions
- The response from initial damage up to complete structural failure can be traced by using nonlinear dynamic analysis solved with an explicit algorithm. The inherent stability of the explicit analysis coupled with the concrete damaged plasticity (CDP) material formulation allows the correct modeling of large fracture propagations, which yields an accurate assessment of complex built heritage structures.
- Quantitatively predicting the displacement that a structure can reach in its ultimate limit state conditions becomes possible, even in the absence of softening of the global pushover curve. This feature makes the proposed procedure particularly suitable and appealing in the context of the so-called “displacement-based design”.
- Most importantly, for the dynamic assessment of masonry structures, it is not necessary to impose static load distributions a priori, based on modal superposition. In fact, the relative distributions of inertial forces acting on the superstructure are a direct consequence of the application of accelerations (or, alternatively, of velocities) directly at the base. In the context of a nonlinear dynamic analysis, such inertial forces are automatically computed and considered in the step-by-step solution of the nonlinear equations of motion. In this way, the use of slow dynamic analyses solves to some extent the issues related to calculating modal participation factors and to adapting them to reflect progressive damage.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- D’Ayala, D.; Lagomarsino, S. Performance-Based Assessment of Cultural Heritage Assets: Outcomes of the European FP7 PERPETUATE Project. Bull. Earthq. Eng. 2015, 13, 5–12. [Google Scholar] [CrossRef]
- Diaferio, M.; Foti, D.; Sabbà, M.F.; Lerna, M. A Procedure for the Seismic Risk Assessment of the Cultural Heritage. Bull. Earthq. Eng. 2021, 19, 1027–1050. [Google Scholar] [CrossRef]
- Spoldi, E.; Russo, S. Damage Assessment and Dynamic Characteristics of Temples in Nepal Post Gorkha 2015 Earthquake. Int. J. Archit. Herit. 2021, 15, 479–493. [Google Scholar] [CrossRef]
- Karanikoloudis, G.; Lourenço, P.B.; Alejo, L.E.; Mendes, N. Lessons from Structural Analysis of a Great Gothic Cathedral: Canterbury Cathedral as a Case Study. Int. J. Archit. Herit. 2021, 15, 1765–1794. [Google Scholar] [CrossRef]
- Rainone, L.S.; Tateo, V.; Casolo, S.; Uva, G. About the Use of Concrete Damage Plasticity for Modeling Masonry Post-Elastic Behavior. Buildings 2023, 13, 1915. [Google Scholar] [CrossRef]
- Schiavoni, M.; Giordano, E.; Roscini, F.; Clementi, F. Advanced Numerical Insights for an Effective Seismic Assessment of Historical Masonry Aggregates. Eng. Struct. 2023, 285, 115997. [Google Scholar] [CrossRef]
- Schiavoni, M.; Giordano, E.; Roscini, F.; Clementi, F. Numerical Assessment of Interacting Structural Units on the Seismic Damage: A Comparative Analysis with Different Modeling Approaches. Appl. Sci. 2023, 13, 972. [Google Scholar] [CrossRef]
- Karimi, A.H.; Karimi, M.S.; Kheyroddin, A.; Shahkarami, A.A. Experimental and Numerical Study on Seismic Behavior of An Infilled Masonry Wall Compared to An Arched Masonry Wall. Structures 2016, 8, 144–153. [Google Scholar] [CrossRef]
- Clementi, F. Failure Analysis of Apennine Masonry Churches Severely Damaged during the 2016 Central Italy Seismic Sequence. Buildings 2021, 11, 58. [Google Scholar] [CrossRef]
- Milani, G.; Valente, M. Comparative Pushover and Limit Analyses on Seven Masonry Churches Damaged by the 2012 Emilia-Romagna (Italy) Seismic Events: Possibilities of Non-Linear Finite Elements Compared with Pre-Assigned Failure Mechanisms. Eng. Fail. Anal. 2015, 47, 129–161. [Google Scholar] [CrossRef]
- Vitorino, S.; Corazzi, R.; Doz, G. Seismic Performance Assessment of the Historical Cathedral of Santa Maria Del Fiore Dome by Numerical Analysis. Eng. Fail. Anal. 2024, 165, 108734. [Google Scholar] [CrossRef]
- Nastri, E.; Tenore, M.; Todisco, P. Calibration of Concrete Damaged Plasticity Materials Parameters for Tuff Masonry Types of the Campania Area. Eng. Struct. 2023, 283, 115927. [Google Scholar] [CrossRef]
- Kalkbrenner, P.; Pelà, L.; Sandoval, C. Multi Directional Pushover Analysis of Irregular Masonry Buildings without Box Behavior. Eng. Struct. 2019, 201, 109534. [Google Scholar] [CrossRef]
- Direttiva del Presidente del Consiglio dei Ministri; DPCM Gazzetta Ufficiale della Repubblica Italiana G.U. Valutazione e Riduzione del Rischio Sismico del Patrimonio Culturale con Riferimento Alle Norme Tecniche per le Costruzioni di cui al Decreto Ministeriale 14 Gennaio 2008; 2011; Volume 54. [Google Scholar]
- Bayraktar, A.; Hökelekli, E.; Yang, T.T.Y. Seismic Failure Behavior of Masonry Domes under Strong Ground Motions. Eng. Fail. Anal. 2022, 142, 106749. [Google Scholar] [CrossRef]
- Valente, M.; Milani, G. Seismic Response and Damage Patterns of Masonry Churches: Seven Case Studies in Ferrara, Italy. Eng. Struct. 2018, 177, 809–835. [Google Scholar] [CrossRef]
- Misir, I.S.; Yucel, G. Numerical Model Calibration and a Parametric Study Based on the Out-of-Plane Drift Capacity of Stone Masonry Walls. Buildings 2023, 13, 437. [Google Scholar] [CrossRef]
- Shehu, R. Implementation of Pushover Analysis for Seismic Assessment of Masonry Towers: Issues and Practical Recommendations. Buildings 2021, 11, 71. [Google Scholar] [CrossRef]
- Malcata, M.; Ponte, M.; Tiberti, S.; Bento, R.; Milani, G. Failure Analysis of a Portuguese Cultural Heritage Masterpiece: Bonet Building in Sintra. Eng. Fail. Anal. 2020, 115, 104636. [Google Scholar] [CrossRef]
- Valente, M. Seismic Behavior and Damage Assessment of Two Historical Fortified Masonry Palaces with Corner Towers. Eng. Fail. Anal. 2022, 134, 106003. [Google Scholar] [CrossRef]
- Milani, G.; Valente, M. Failure Analysis of Seven Masonry Churches Severely Damaged during the 2012 Emilia-Romagna (Italy) Earthquake: Non-Linear Dynamic Analyses vs Conventional Static Approaches. Eng. Fail. Anal. 2015, 54, 13–56. [Google Scholar] [CrossRef]
- Fortunato, G.; Funari, M.F.; Lonetti, P. Survey and Seismic Vulnerability Assessment of the Baptistery of San Giovanni in Tumba (Italy). J. Cult. Herit. 2017, 26, 64–78. [Google Scholar] [CrossRef]
- Funari, M.F.; Silva, L.C.; Mousavian, E.; Lourenço, P.B. Real-Time Structural Stability of Domes through Limit Analysis: Application to St. Peter’s Dome. Int. J. Archit. Herit. 2021, 17, 915–937. [Google Scholar] [CrossRef]
- Tezcan, S.; Pando, M.A.; Aguilar, R.; Perucchio, R. Nonlinear 2D and 3D Finite Element Static and Dynamic Analysis of the Main Pyramid of Huaca de La Luna, Peru. In Proceedings of the 13th International Conference on Structural Analysis of Historical Construction (SAHC 2023), Kyoto, Japan, 12–15 September 2023; Springer International Publishing: Cham, Switzerland, 2023; Volume 47. [Google Scholar]
- Sadholz, A.; Muir, C.; Perucchio, R. Limit Analysis to Assess the Seismic Capacity of Diocletian’s Frigidarium. In Proceedings of the Structural Analysis of Historical Constructions: Anamnesis, Diagnosis, Therapy, Controls, Leuven, Belgium, 13–15 September 2016; Van Balen, K., Verstrynge, E., Eds.; Taylor & Francis Group: London, UK, 2016; pp. 272–278. [Google Scholar]
- Tezcan, S.; Tambe, N.; Muir, C.; Aguilar, R.; Perucchio, R. Nonlinear FE Analysis of the Response to Lateral Accelerations of the Triumphal Arch of the Church of Andahuaylillas, Peru. In Structural Analysis of Historical Constructions; RILEM Bookseries; Aguilar, R., Torrealva, D., Moreira, S., Pando, M.A., Ramos, L.F., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 18, pp. 1301–1309. ISBN 978-3-319-99440-6. [Google Scholar]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A Plastic-Damage Model for Concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Dassault Systemes Abaqus/CAE User’s Guide. Available online: http://130.149.89.49:2080/v2016/pdf_books/CAE.pdf (accessed on 27 February 2024).
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering, 3rd ed.; Prentice-Hall International Series in Civil Engineering and Engineering Mechanics; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2007; ISBN 978-0-13-156174-8. [Google Scholar]
- Pinho, R. Using Pushover Analysis for Assessment of Buildings and Bridges. In Advanced Earthquake Engineering Analysis; Pecker, A., Ed.; Springer: Vienna, Austria, 2007; pp. 91–120. ISBN 978-3-211-74214-3. [Google Scholar]
- Aguilar, R.; Pando, M.A.; Briceño, C.; Zavala, G.; Castañeda, B.; Perucchio, R.; Uceda, S. Structural and Geotechnical Engineering Assessment of Huaca de La Luna—A Massive Earthen Moche Culture Pyramid in Northern Peru. J. Cult. Herit. 2018, 34, 83–94. [Google Scholar] [CrossRef]
- D’Altri, A.M.; Cannizzaro, F.; Petracca, M.; Talledo, D.A. Nonlinear Modelling of the Seismic Response of Masonry Structures: Calibration Strategies. Bull. Earthq. Eng. 2022, 20, 1999–2043. [Google Scholar] [CrossRef]
- Silva, V.; Crowley, H.; Varum, H.; Pinho, R.; Sousa, R. Evaluation of Analytical Methodologies Used to Derive Vulnerability Functions. Earthq. Eng. Struct. Dyn. 2014, 43, 181–204. [Google Scholar] [CrossRef]
- Ferretti, F.; Simoni, E.; Buratti, N.; Mazzotti, C. Typological Fragility Analysis of Masonry Buildings in Emilia Romagna Region (Italy). Bull. Earthq. Eng. 2023, 21, 3321–3356. [Google Scholar] [CrossRef]
- Aşıkoğlu, A.; Vasconcelos, G.; Lourenço, P.B.; Pantò, B. Pushover Analysis of Unreinforced Irregular Masonry Buildings: Lessons from Different Modeling Approaches. Eng. Struct. 2020, 218, 110830. [Google Scholar] [CrossRef]
- Gaggero, M.B.; Korswagen, P.A.; Esposito, R.; Rots, J.G. In-Plane Behaviour of Unreinforced Masonry Strengthened with a Structural Glass Window: A Proof of Concept. Buildings 2023, 13, 361. [Google Scholar] [CrossRef]
- Cannizzaro, F.; Pantò, B.; Lepidi, M.; Caddemi, S.; Caliò, I. Multi-Directional Seismic Assessment of Historical Masonry Buildings by Means of Macro-Element Modelling: Application to a Building Damaged during the L’Aquila Earthquake (Italy). Buildings 2017, 7, 106. [Google Scholar] [CrossRef]
- Betti, M.; Galano, L.; Vignoli, A. Time-History Seismic Analysis of Masonry Buildings: A Comparison between Two Non-Linear Modelling Approaches. Buildings 2015, 5, 597–621. [Google Scholar] [CrossRef]
- Tezcan, S.; Pando, M.A.; Aguilar, R.; Castañeda, B.; Rojas, C.; Perucchio, R. Preliminary Nonlinear Static and Dynamic Analysis of the Main Pyramid of Huaca de La Luna, Peru. In Proceedings of the COMPDYN 2021: 8th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Athens, Greece, 28–30 June 2021; Papadrakakis, M., Fragiadakis, M., Eds.; Athens, Greece, 2021; pp. 244–257. [Google Scholar]
- Riccio, C.; Remus, A.; Tezcan, S.; Silva, L.C.; Milani, G.; Perucchio, R. A Macroblock 2D Finite Element Model for Assessing the Roots of Failure of Huaca de La Luna’s Main Pyramid (Peru) under Seismic Action. Eng. Fail. Anal. 2023, 151, 107417. [Google Scholar] [CrossRef]
- Remus, A.; Yılmaz, L.; Tezcan, S.; Perucchio, R. Effect of Eastern Architecture and Sloping Foundation Conditions on the Static and Dynamic Response of the Adobe Pyramid Huaca De La Luna (Perú). In Proceedings of the 13th International Conference on the Structural Analysis and Historical Constructions (SAHC 2023), Kyoto, Japan, 12–15 September 2023; Springer International Publishing: Cham, Switzerland, September 2023; Volume 47. [Google Scholar]
- Remus, A.; Tezcan, S.; Pando, M.A.; Aguilar, R.; Perucchio, R. 2D and 3D Nonlinear Finite Element Sensitivity Analysis of the Static and Dynamic Behavior of the Adobe Pyramid of Huaca de La Luna, Trujillo, Perú. Int. J. Archit. Herit. 2024, 1–29. [Google Scholar] [CrossRef]
- Sadholz, A.; Muir, C.; Perucchio, R. A 3D Kinematic Model for Assessing the Seismic Capacity of the Frigidarium of the Baths of Diocletian. In Proceedings of the 2015 Digital Heritage, Granada, Spain, 28 September–2 October 2015; Volume 2, pp. 89–92. [Google Scholar]
- Faleri, F. Structural Analysis of Concrete Vaulted Monuments in Imperial Rome; Politecnico di Milano: Milan, Italy, 2019. [Google Scholar]
- Faleri, F. Seismic Vulnerability of Roman Concrete Vaulted Monuments: Two Case Studies Dating Back to Imperial Rome. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2019. [Google Scholar]
- Ivancic, S.; Brune, P.; Perucchio, R. A Concrete Damage Plasticity Model for Ancient Roman Pozzolanic Concrete. In Proceedings of the 9th International Masonry Conference, Guimarães, Portugal, 7–9 July 2014; International Masonry Society: Guimarães, Portugal, 2014. [Google Scholar]
- Brune, P. The Mechanics of Imperial Roman Concrete and the Structural Design of Vaulted Monuments. Ph.D. Thesis, University of Rochester, Rochester, NY, USA, 2010. [Google Scholar]
- Vargas, J.; Aguilar, R.; Gonzales, M.; Briceño, C. Structural Intervention in Saint Peter the Apostle Church of Andahuaylillas in Cusco, Peru. In Proceedings of the 13th Ibero-American Seminar on Earthen Architecture and Construction (XXIII SIACOT), Valparaiso, Chile, 19–23 November 2013. [Google Scholar]
- Wang, Y.; Qiao, Z.; Dong, Y.; Briceño, C.; Aguilar, R.; Perucchio, R. Nonlinear Finite Element Evaluation of the Structural Response to Lateral Accelerations of the Adobe Church of Andahuaylillas, Peru. In Proceedings of the Second International Conference on Performance-based and Life-cycle Structural Engineering (PLSE 2015), Portland, OR, USA, 9–11 December 2015; School of Civil Engineering, The University of Queensland: Brisbane, QLD, Australia, 2015; pp. 358–367. [Google Scholar]
- Briceño, C.; Wang, Y.; Qiao, Z.; Dong, Y.; Perucchio, R. Seismic Analysis of Earthen Churches: The Triumphal Arch at Andahuaylillas, Peru. In Proceedings of the CIVIL-COMP Proceedings, Prague, Czech Republic, 1–4 September 2015. [Google Scholar]
- Remus, A.; Tezcan, S.; Pando, M.A.; Aguilar, R.; Perucchio, R. Damage Assessment via Time History Analysis of the Massive Earthen Pyramid of Huaca de La Luna (Huacas de Moche, Perú). In Proceedings of the 18th World Conference on Earthquake Engineering, Milan, Italy, 30 June–5 July 2024. [Google Scholar]
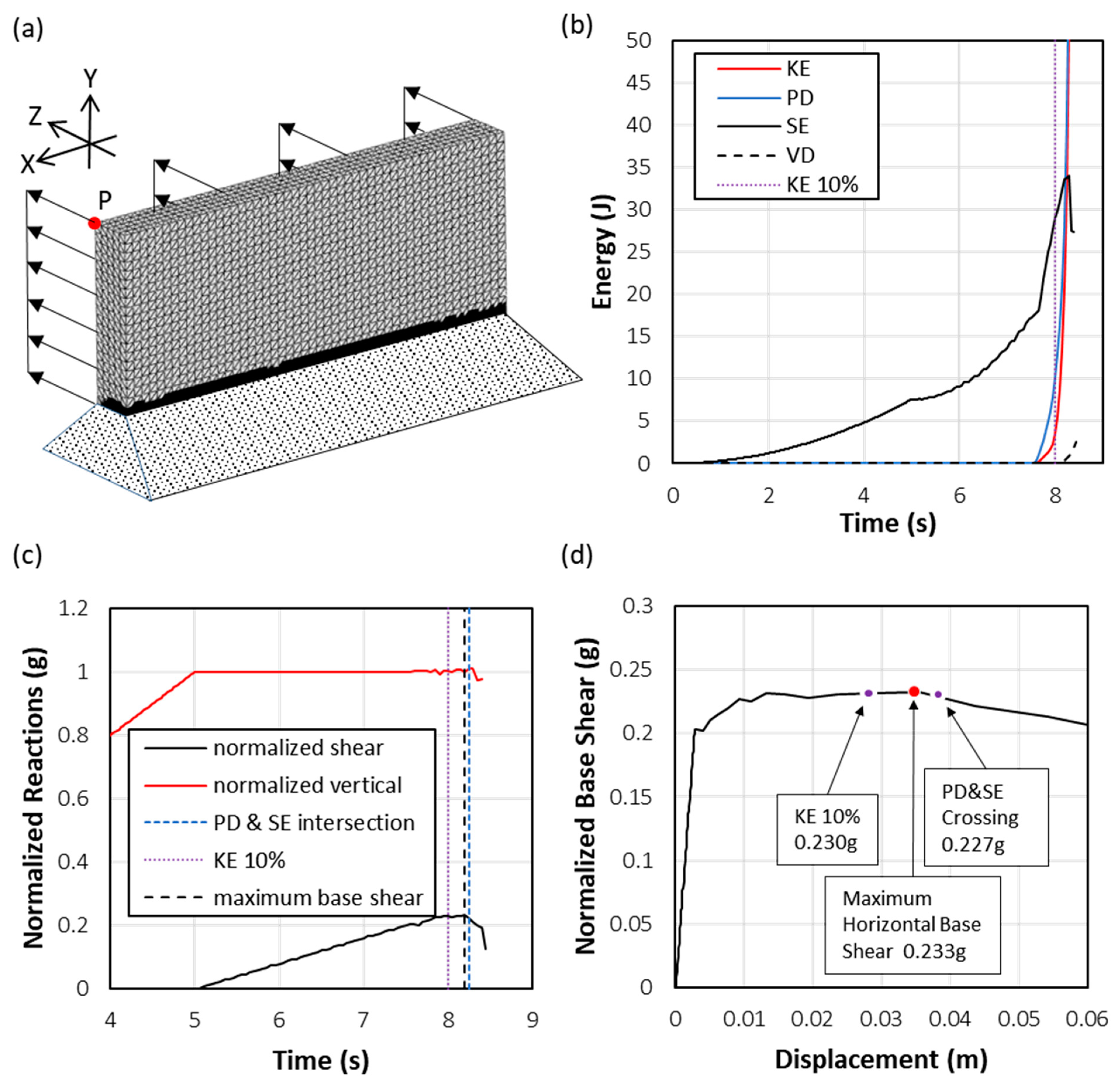
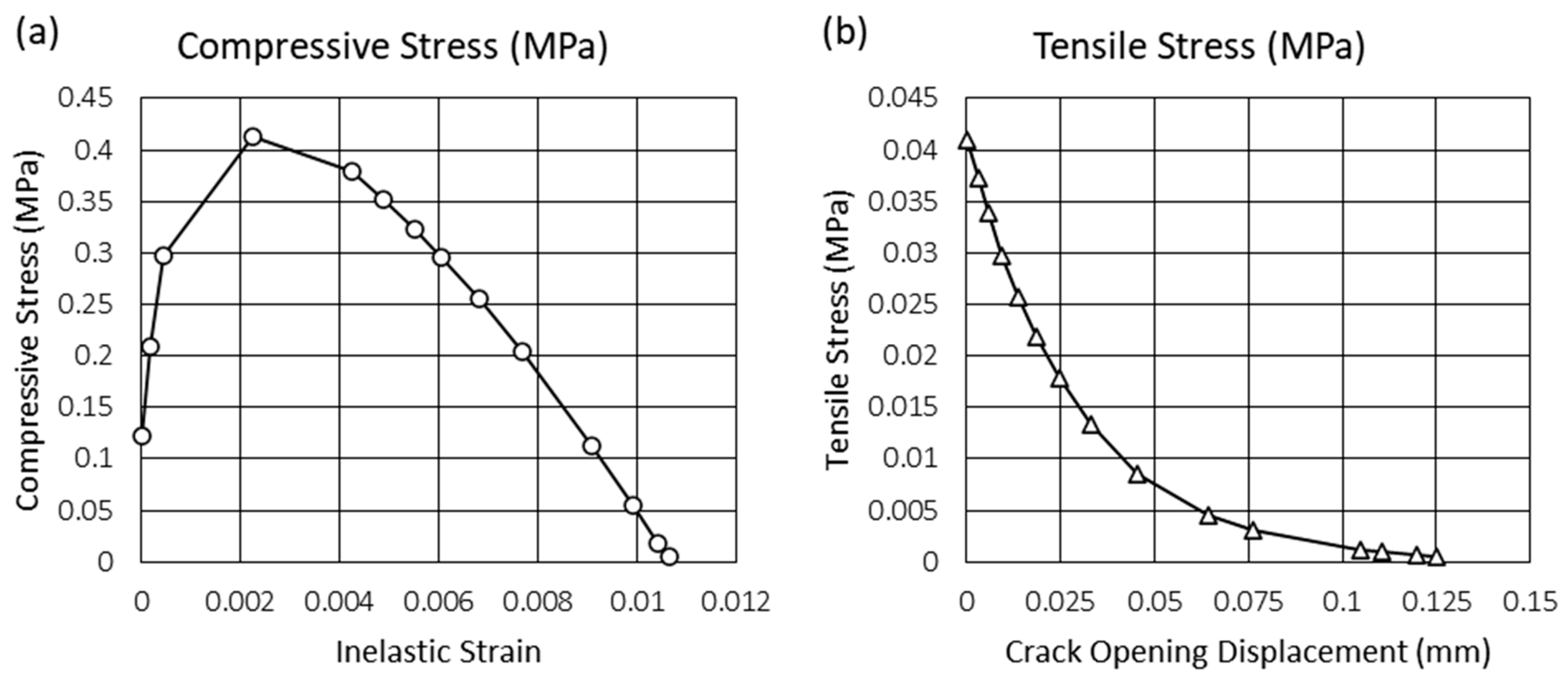
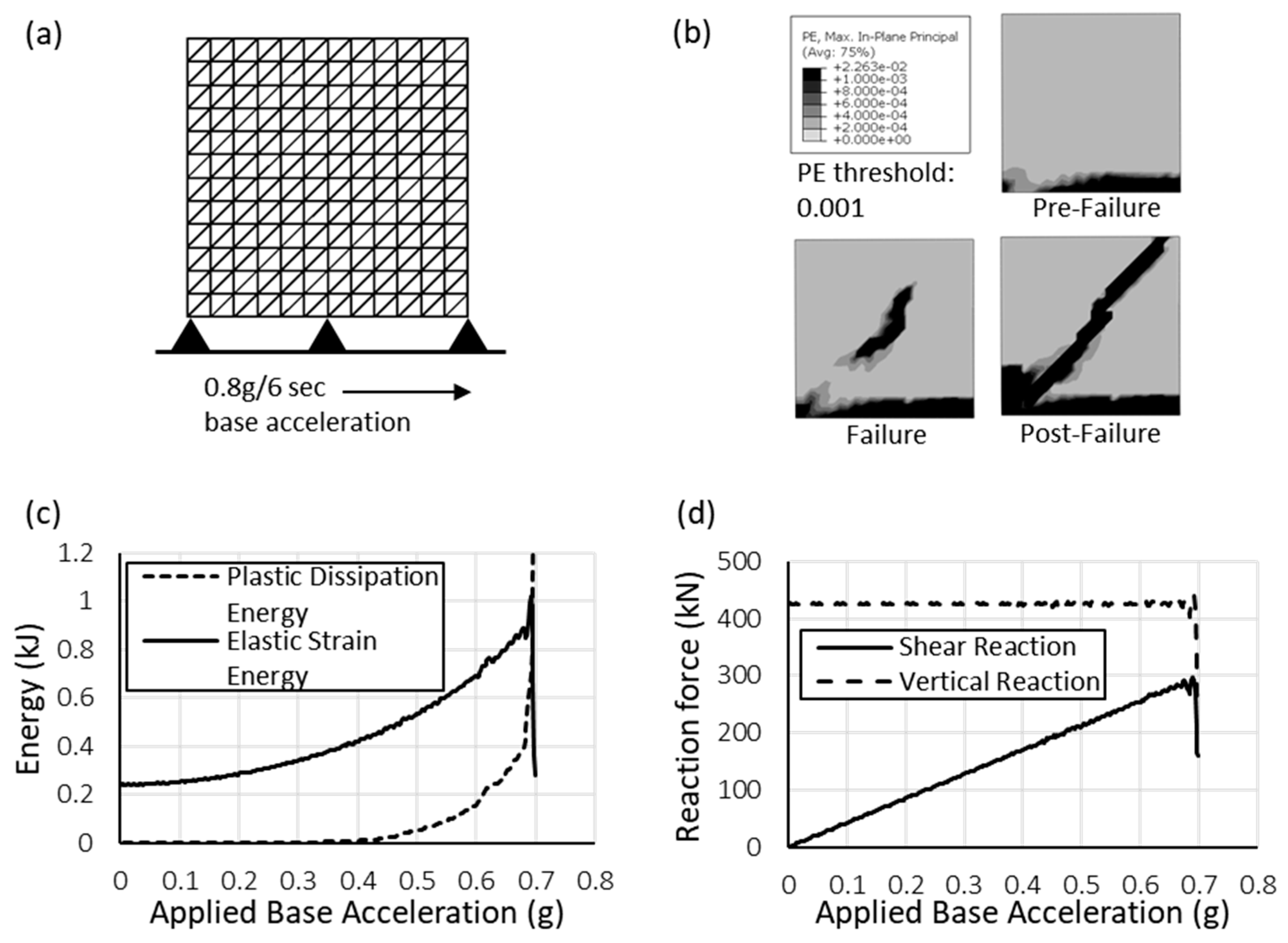
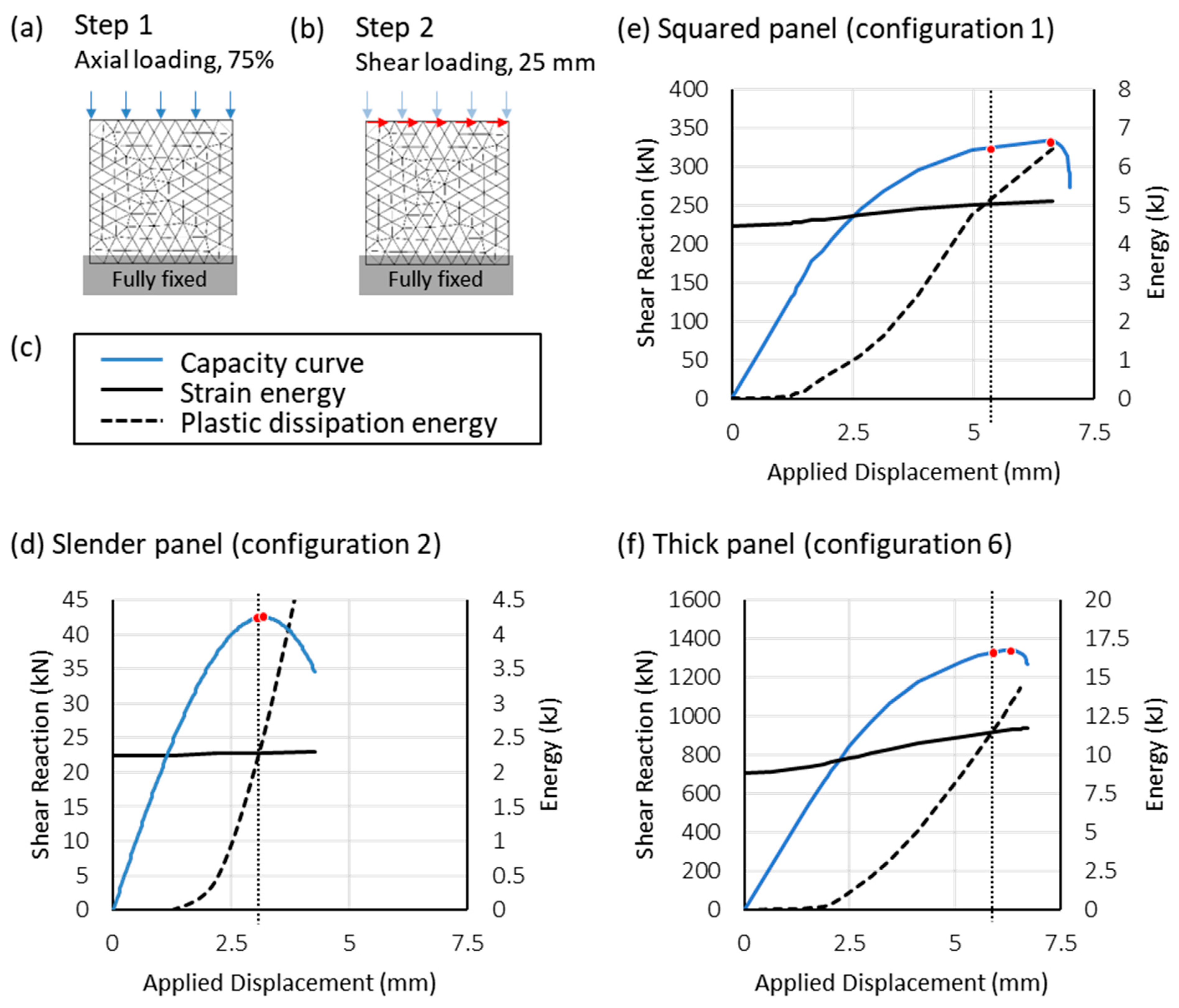




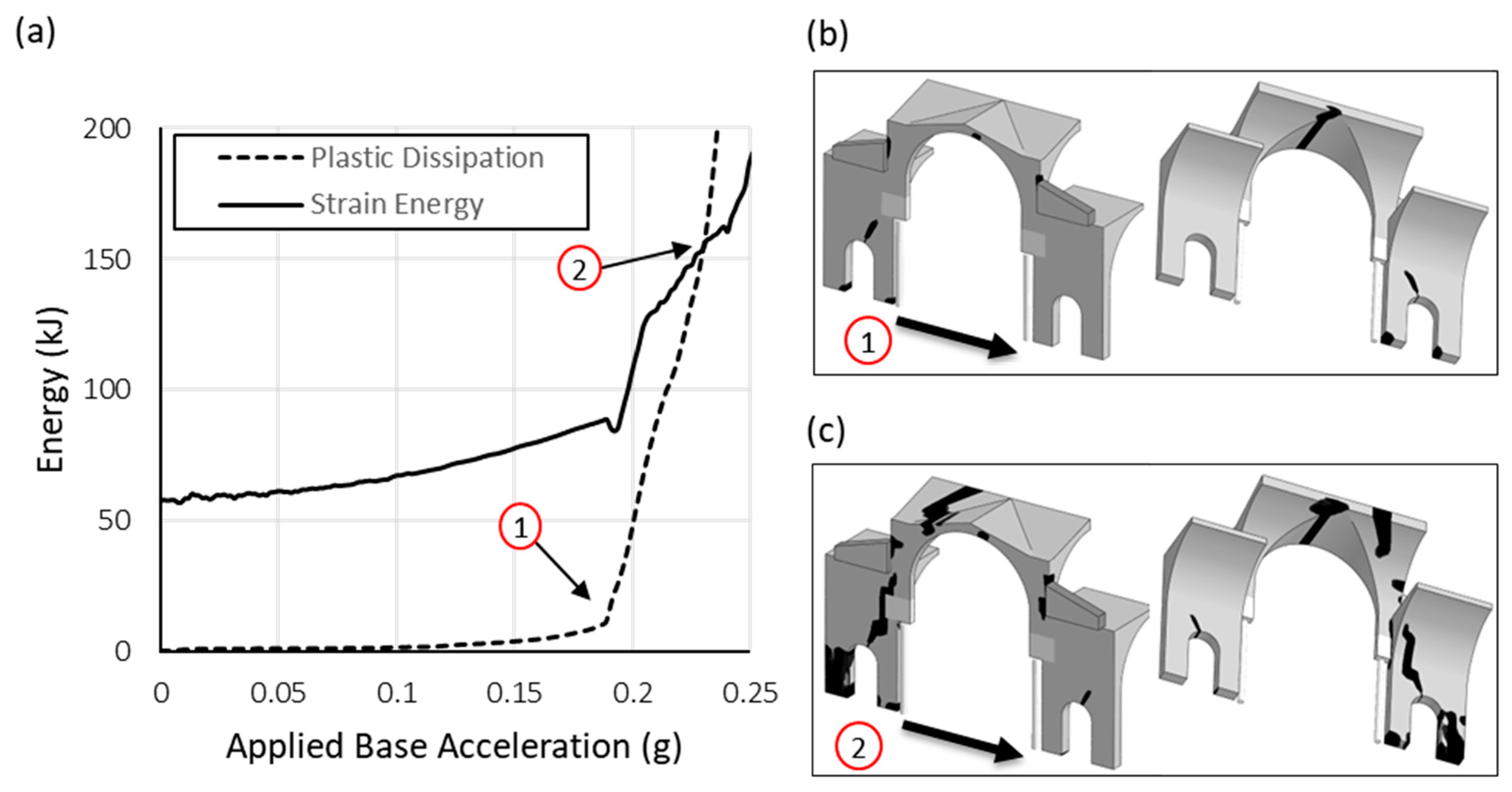
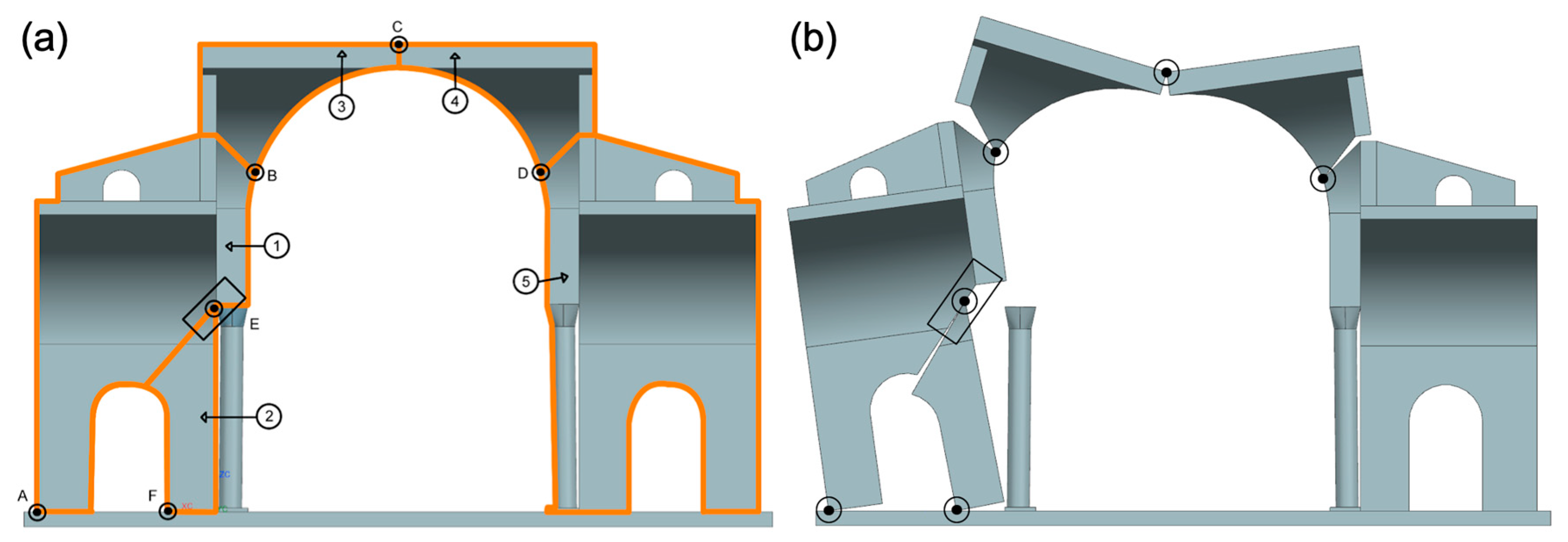
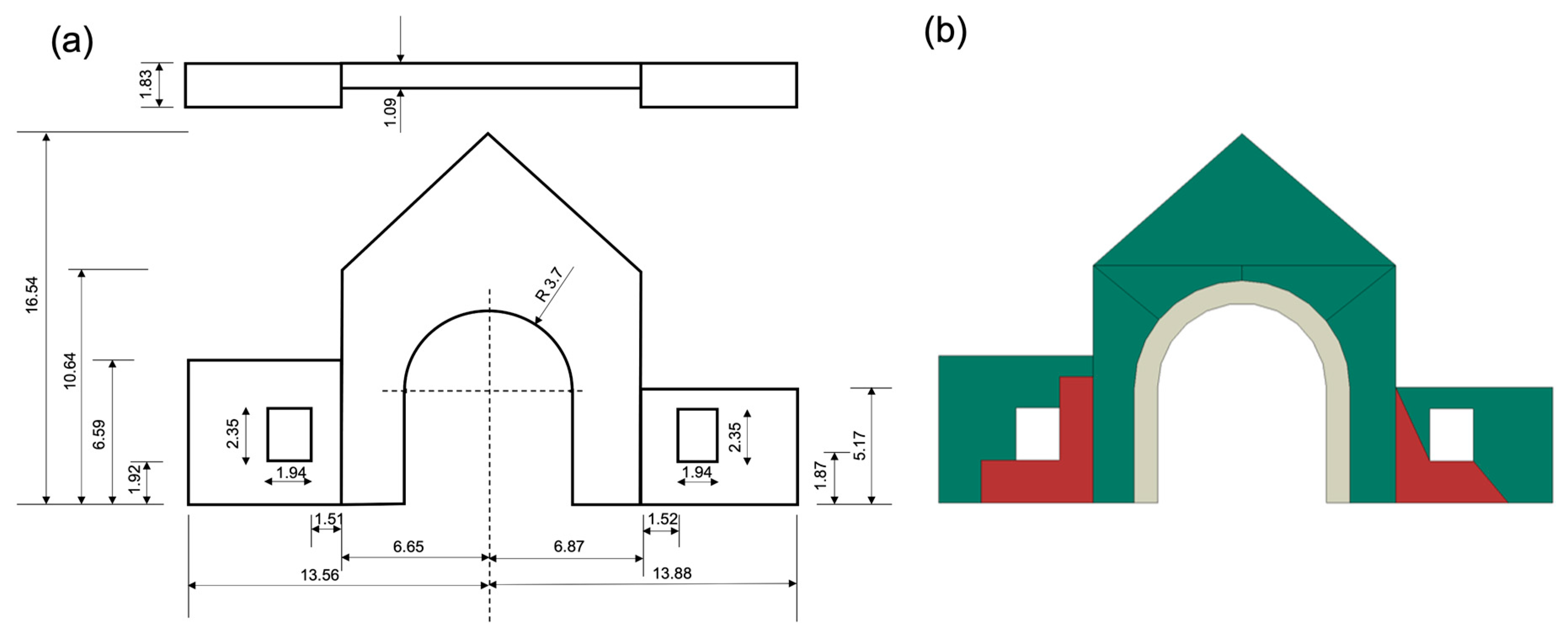

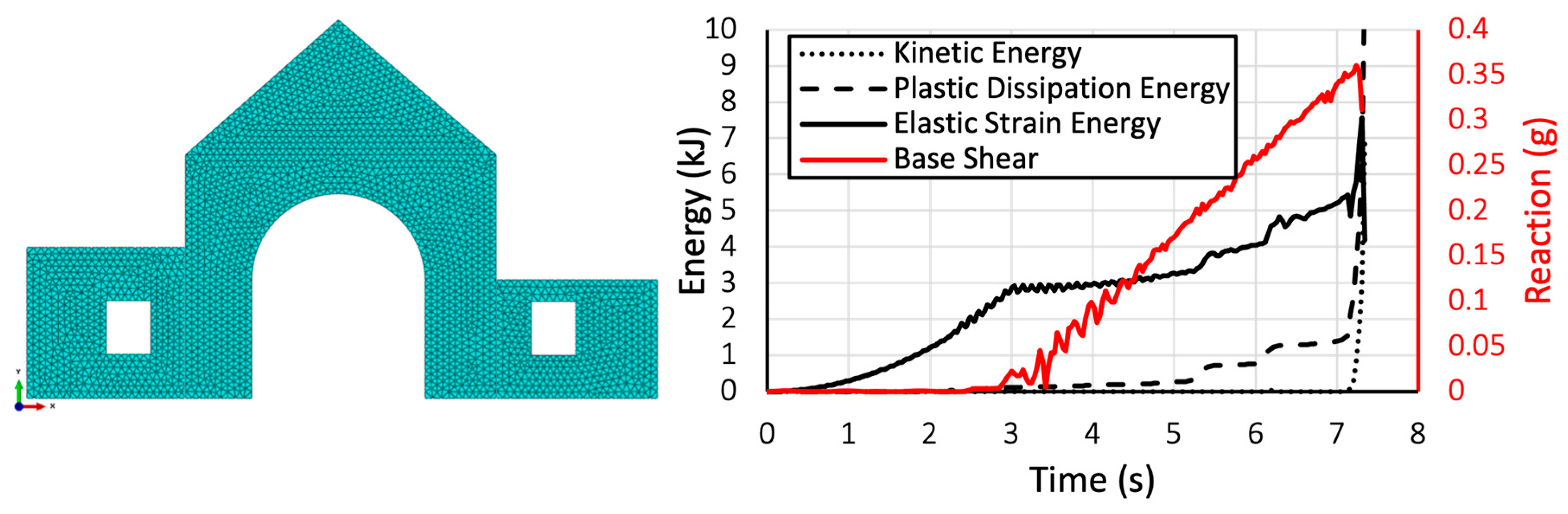

| Element Type | Element Size [m] | Number of Elements |
|---|---|---|
| Quadratic tetrahedral (C3D10M) | 0.1 | 31,351 |
| Density and Elastic Behavior | ||||
|---|---|---|---|---|
| Mass Density [kg/m3] | Young’s Modulus [MPa] | Poisson’s Ratio | ||
| 1735 | 123 | 0.2 | ||
| Plasticity Parameters | ||||
| Dilation Angle | Eccentricity | Fb0/fc0 | K | Viscosity Parameter |
| 18 | 0.1 | 1.16 | 0.67 | 5 × 10−4 |
| Element Type | Element Size [m] | Number of Elements |
|---|---|---|
| Quadratic triangles (CPS6M) | 0.42 | 288 |
| Element Type | Element Size | Number of Elements |
|---|---|---|
| Linear tetrahedron | 0.25 m | 13,107 |
| Density and Elastic Behavior | ||||
|---|---|---|---|---|
| Mass Density [kg/m3] | Young’s Modulus [MPa] | Poisson’s Ratio | ||
| 2100 | 1392 | 0.2 | ||
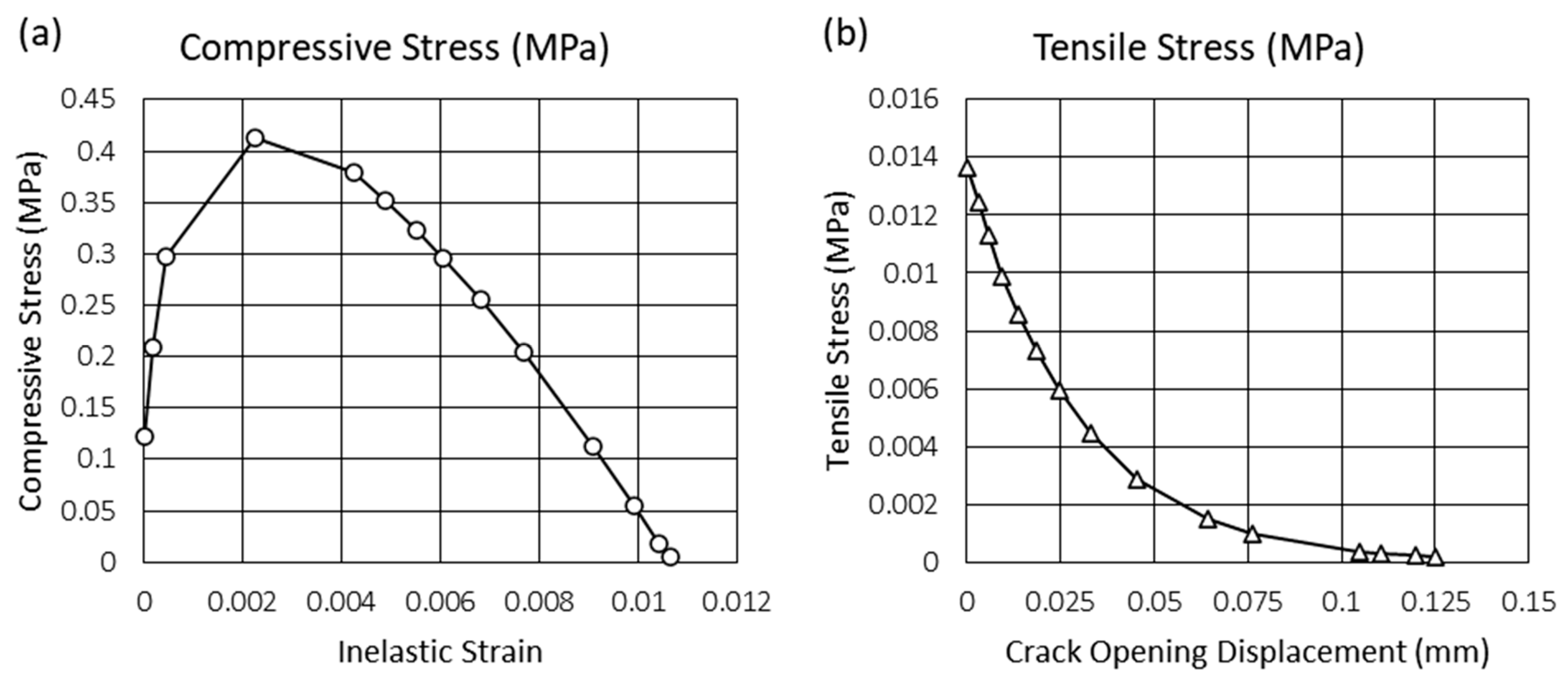
| Compressive Behavior | ||||
| Stress [MPa] | Inelastic Strain | Damage Parameter | ||
| 2.67 | 0 | 0 | ||
| 2.67 | 0.003 | 0 | ||
| 0.8 | 0.01 | 0.9 | ||
| Tensile Behavior | ||||
| Stress [MPa] | Cracking Strain | Damage Parameter | ||
| 0.054 | 0 | 0 | ||
| 0.007 | 0.0015 | 0.9 | ||
| Plasticity Parameters | ||||
| Dilation Angle | Eccentricity | Fb0/fc0 | K | Viscosity Parameter |
| 10 | 0.1 | 1.16 | 0.667 | 0 |
| Density and Elastic Behavior | ||||
|---|---|---|---|---|
| Mass Density [kg/m3] | Young’s Modulus [MPa] | Poisson’s Ratio | ||
| 1735 | 123 | 0.2 | ||
| Plasticity Parameters | ||||
| Dilation Angle | Eccentricity | Fb0/fc0 | K | Viscosity Parameter |
| 1 | 0.1 | 1.16 | 0.67 | 1 × 10−8 |
| Element Type | Element Size | Number of Elements |
|---|---|---|
| Quadratic plane strain triangle (CPE6M) | 0.75 m | 8175 |
| Element Type | Element Size | Number of Elements |
|---|---|---|
| Linear brick element (C3D8R) | 1 m | 233,604 |
| Element Type | Element Size [m] | Number of Elements |
|---|---|---|
| Linear hexahedral | ~0.45 | 33,312 |
| Linear quadrilateral plate | ~0.45 | 288 |
| Linear line (beam) | ~0.35 | 80 |
| Density and Elastic Behavior | ||||
|---|---|---|---|---|
| Mass Density [kg/m3] | Young’s Modulus [GPa] | Poisson’s Ratio | ||
| 1500 | 3.37 | 0.2 | ||
| Plasticity Parameters | ||||
| Dilation Angle | Eccentricity | Fb0/fc0 | K | Viscosity Parameter |
| 31 | 0.1 | 1.16 | 0.67 | 1 × 10−4 |
| Density and Elastic Behavior | ||||
|---|---|---|---|---|
| Material | Mass Density [kg/m3] | Young’s Modulus [MPa] | Poisson’s Ratio | |
| Adobe | 1539 | 350 | 0.25 | |
| Brick | 1800 | 1200 | 0.25 | |
| Stone masonry | 2200 | 2350 | 0.25 | |
| Postcritical behavior | ||||
| Material | σc [MPa] | σf [MPa] | GIC [N/m] | GIF [N/m] |
| Adobe | 0.875 | 0.0875 | 1400 | 4 |
| Brick | 2.4 | 0.12 | 3840 | 2.16 |
| Stone masonry | 5.3 | 0.176 | 8480 | 5.104 |
| Plasticity parameters (common to all materials) | ||||
| Dilation angle | Eccentricity | Fb0/fc0 | K | Viscosity parameter |
| 1 | 0.1 | 1.16 | 0.67 | 1 × 10−8 |
| Element Type | Element Size | Number of Elements |
|---|---|---|
| Quadratic triangular plane stress | ~0.3 m | 4680 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Remus, A.; Tezcan, S.; Sun, J.; Milani, G.; Perucchio, R. Seismic Failure Assessment Using Energy Outputs of Finite Element Analysis: A Strategy for Complex Heritage Masonry Structures Modeled with Concrete Damaged Plasticity Material. Buildings 2025, 15, 318. https://doi.org/10.3390/buildings15030318
Remus A, Tezcan S, Sun J, Milani G, Perucchio R. Seismic Failure Assessment Using Energy Outputs of Finite Element Analysis: A Strategy for Complex Heritage Masonry Structures Modeled with Concrete Damaged Plasticity Material. Buildings. 2025; 15(3):318. https://doi.org/10.3390/buildings15030318
Chicago/Turabian StyleRemus, Anna, Selman Tezcan, Jiacheng Sun, Gabriele Milani, and Renato Perucchio. 2025. "Seismic Failure Assessment Using Energy Outputs of Finite Element Analysis: A Strategy for Complex Heritage Masonry Structures Modeled with Concrete Damaged Plasticity Material" Buildings 15, no. 3: 318. https://doi.org/10.3390/buildings15030318
APA StyleRemus, A., Tezcan, S., Sun, J., Milani, G., & Perucchio, R. (2025). Seismic Failure Assessment Using Energy Outputs of Finite Element Analysis: A Strategy for Complex Heritage Masonry Structures Modeled with Concrete Damaged Plasticity Material. Buildings, 15(3), 318. https://doi.org/10.3390/buildings15030318







