Seismic Damage Quantification of RC Short Columns from Crack Images Using the Enhanced U-Net
Abstract
1. Introduction
2. Cyclic Test of RC Short Columns
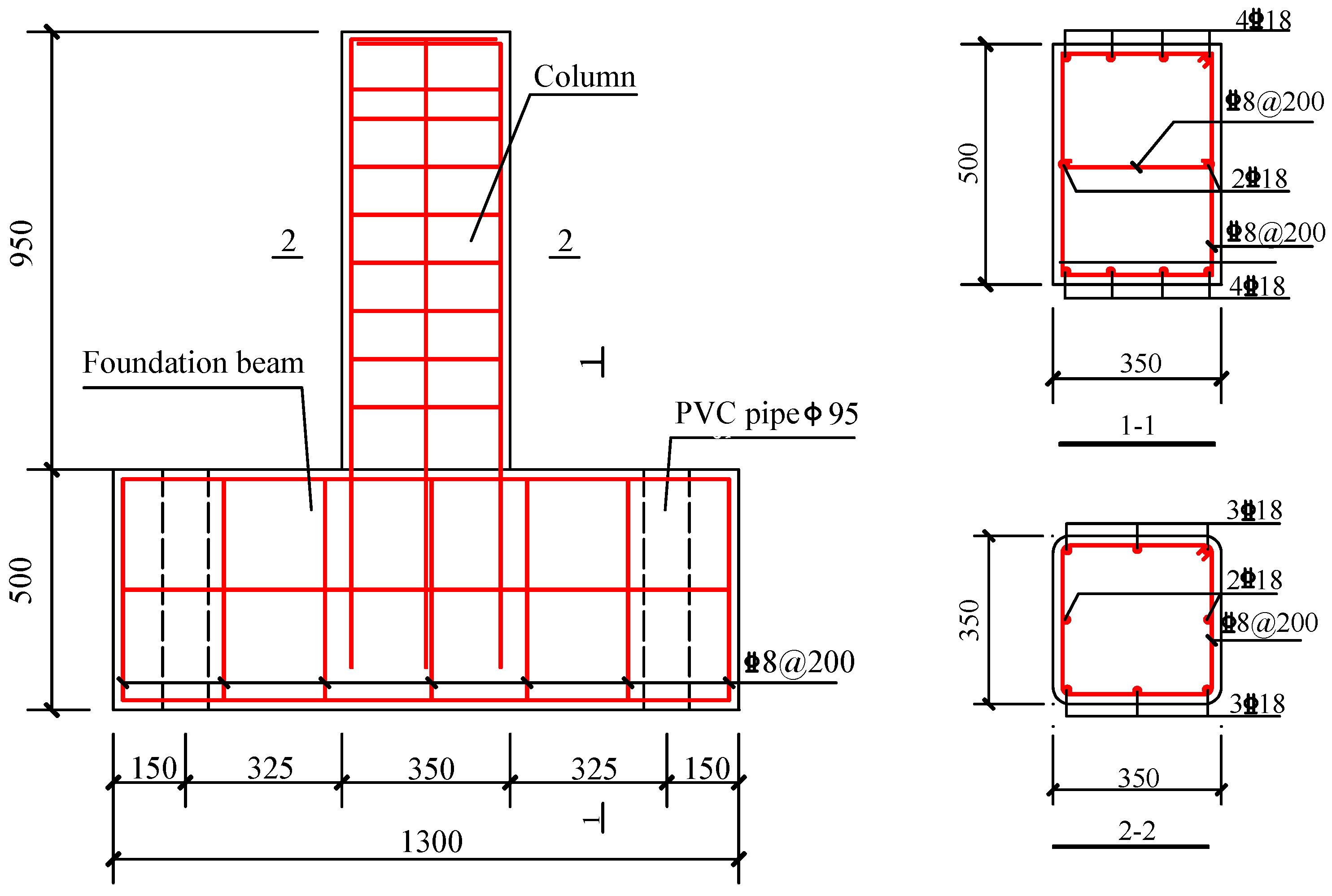
2.1. Preparation of the Specimens
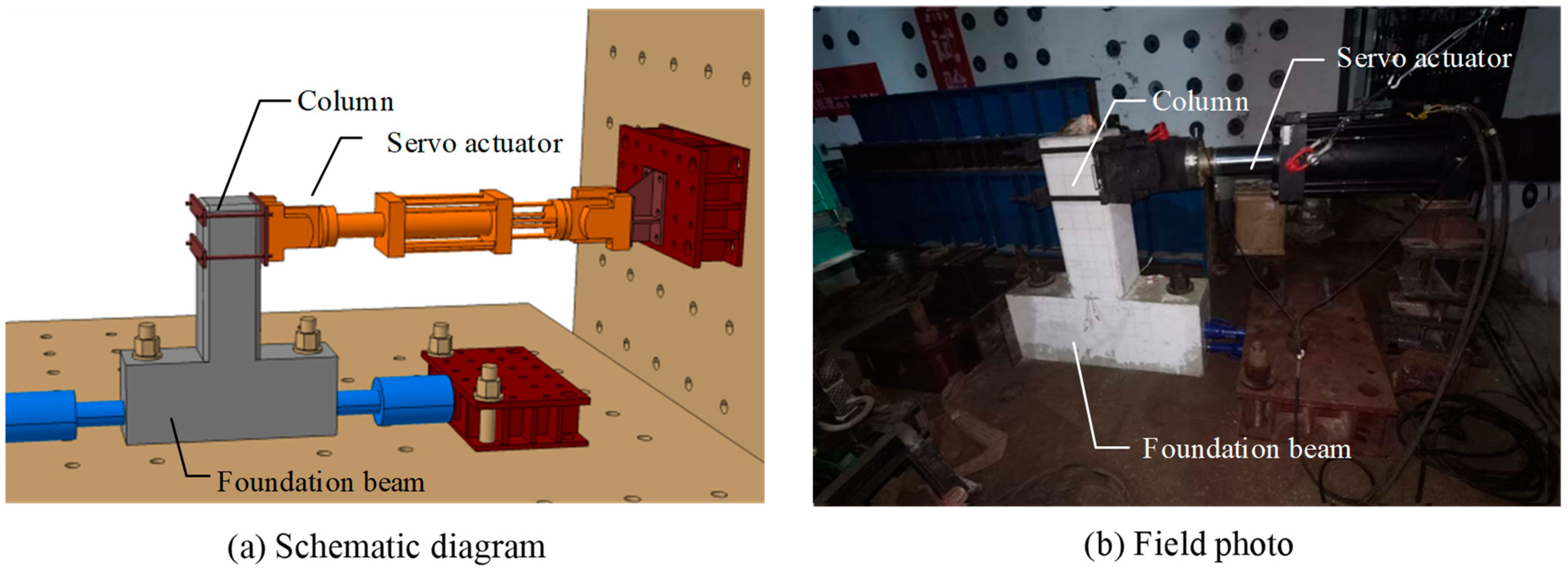
2.2. Testing Device and Measurements
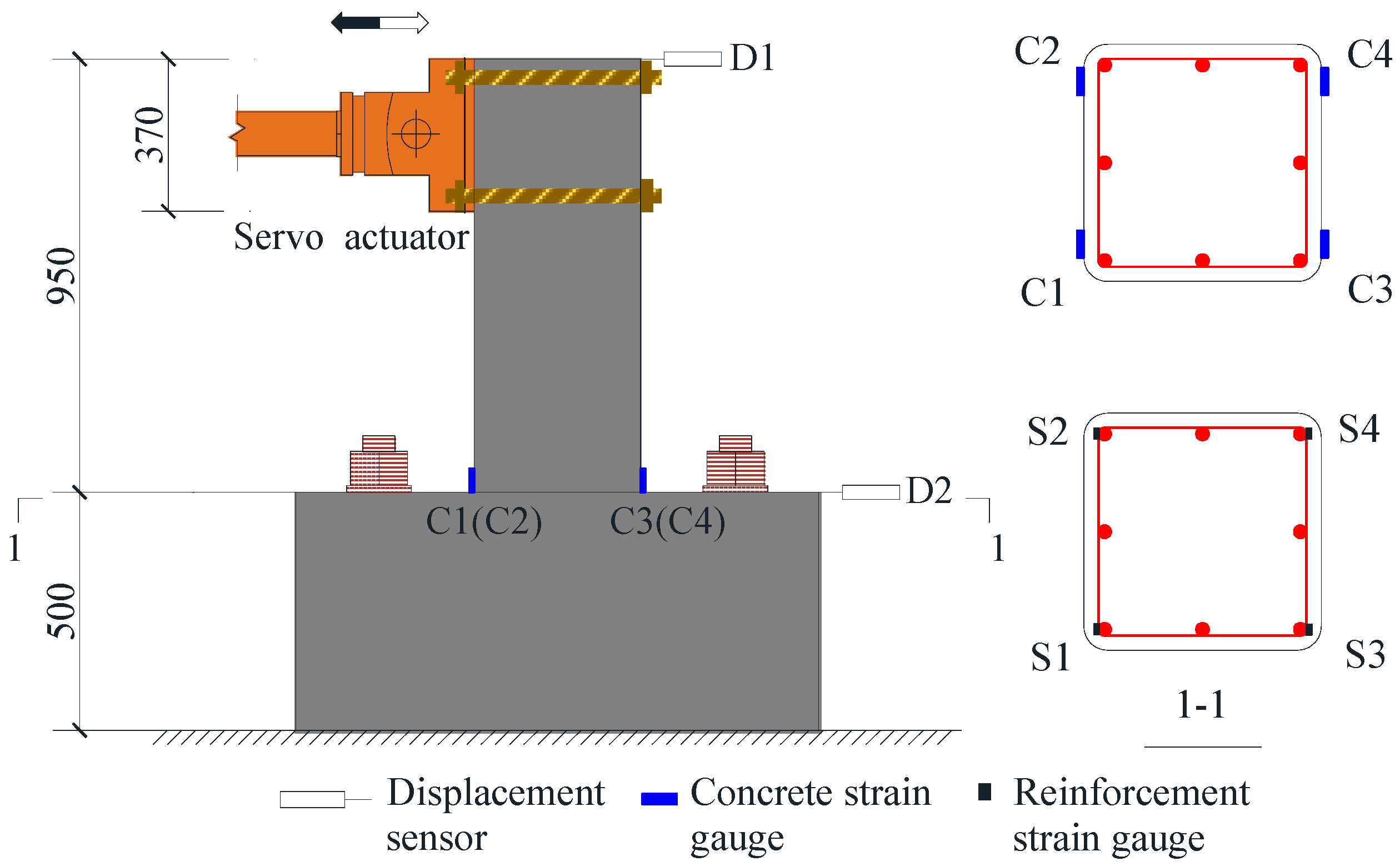
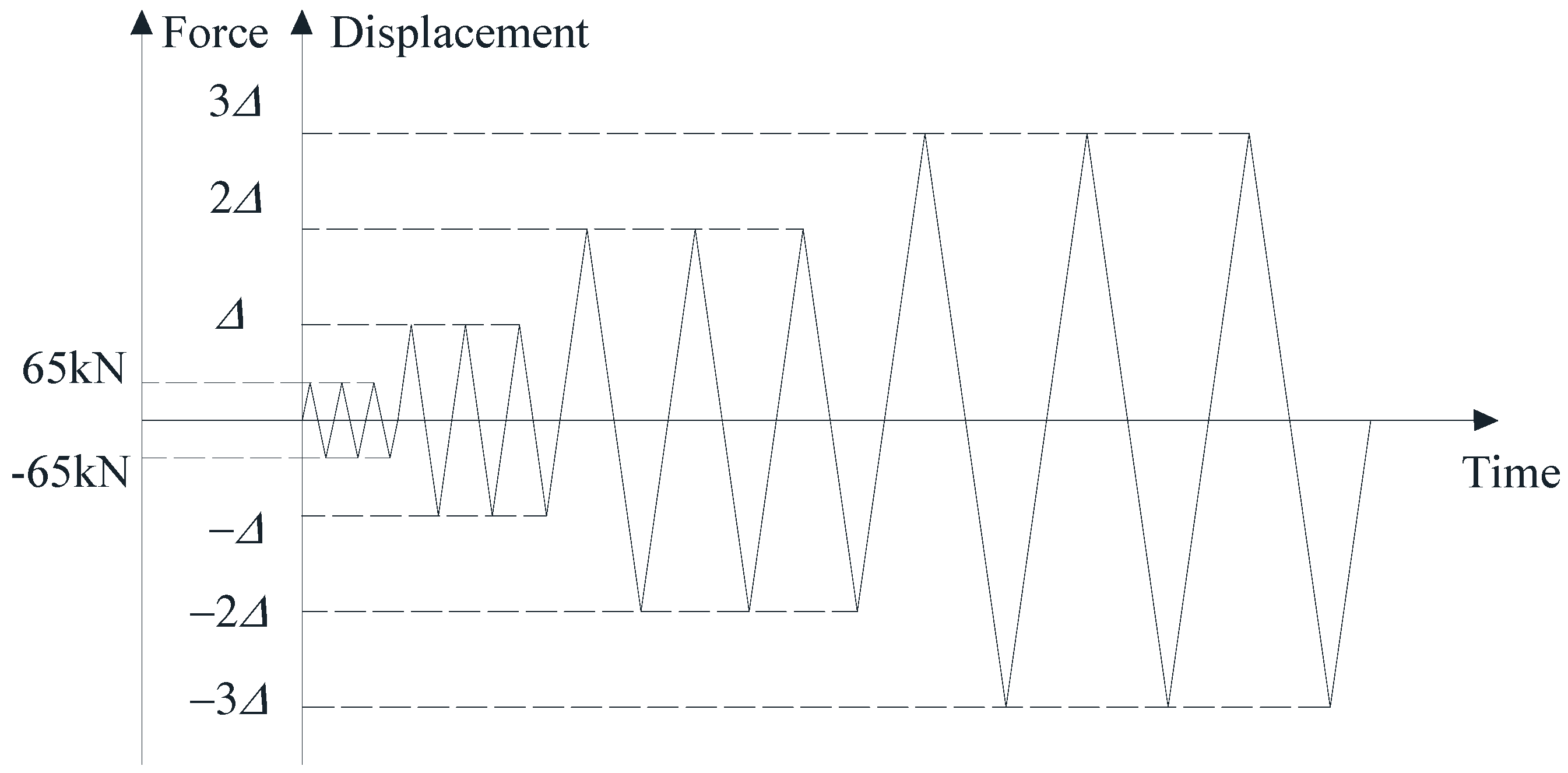
2.3. Test Procedure
2.4. Test Results
2.4.1. Damage Process
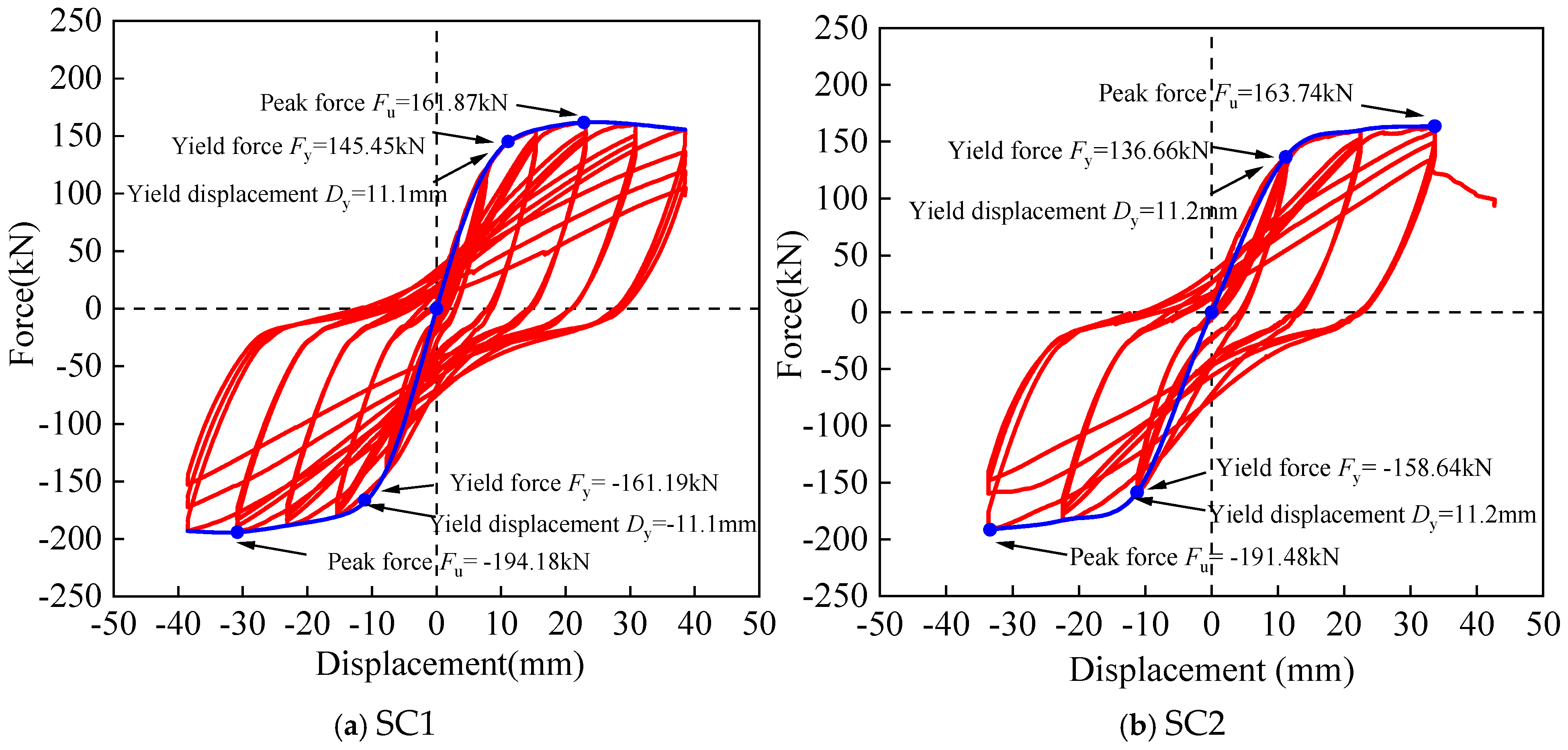
2.4.2. Load-Displacement Curves
3. Crack Image Acquisition
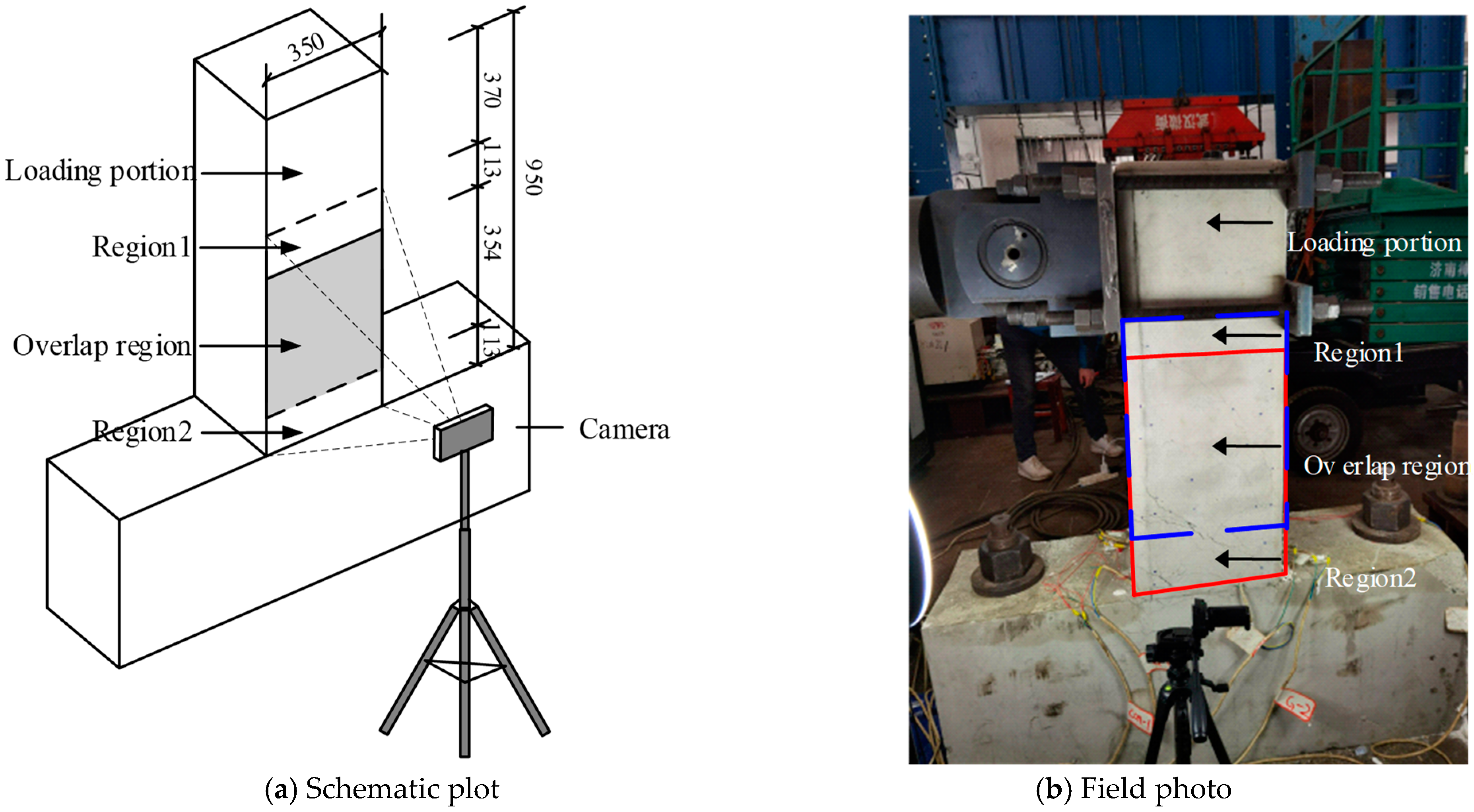
3.1. Photographing Scheme
3.2. Crack Image Stitching
4. Crack Segmentation Based on the Enhanced U-Net
4.1. Architecture of the Network
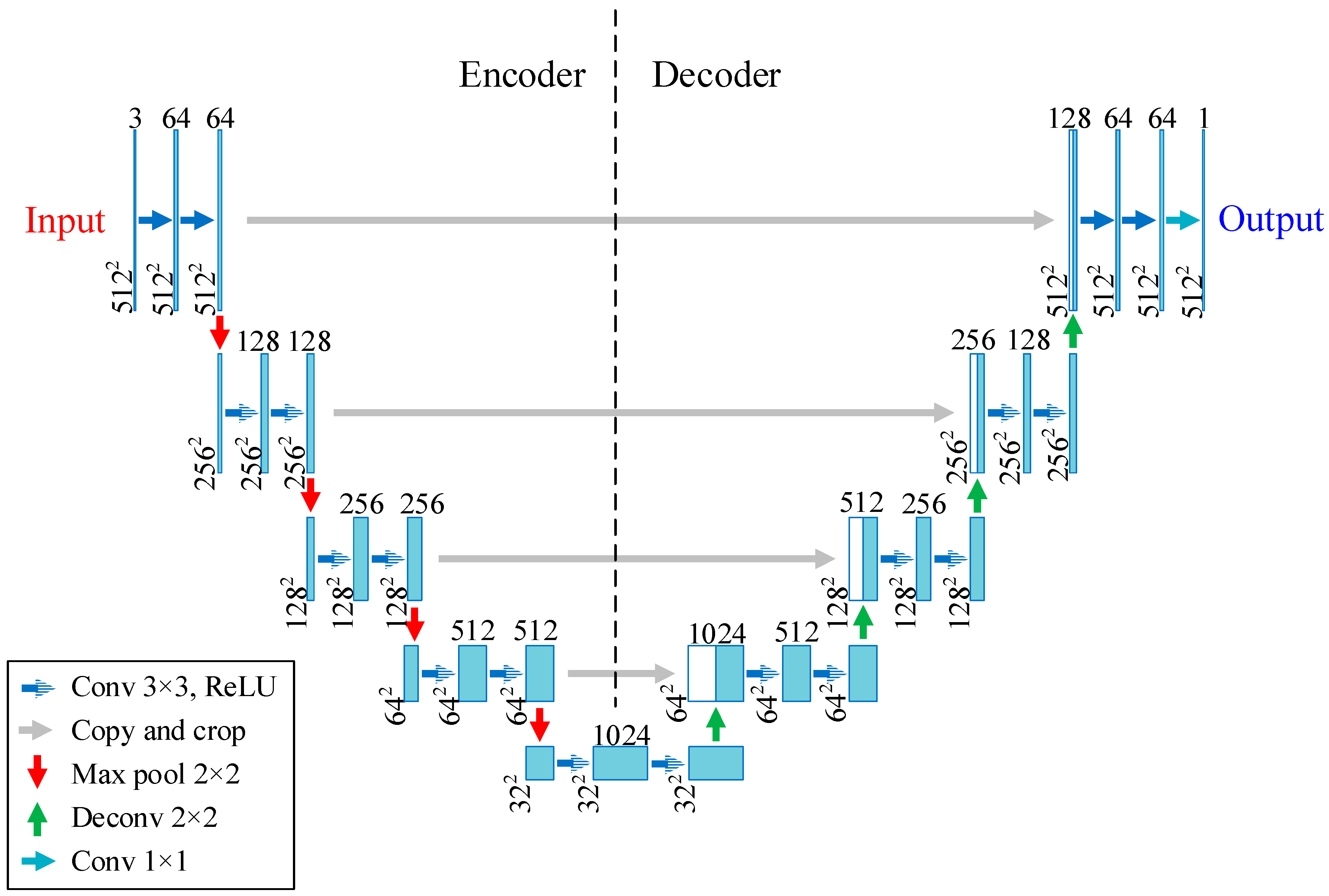
4.1.1. Architecture of the Original U-Net
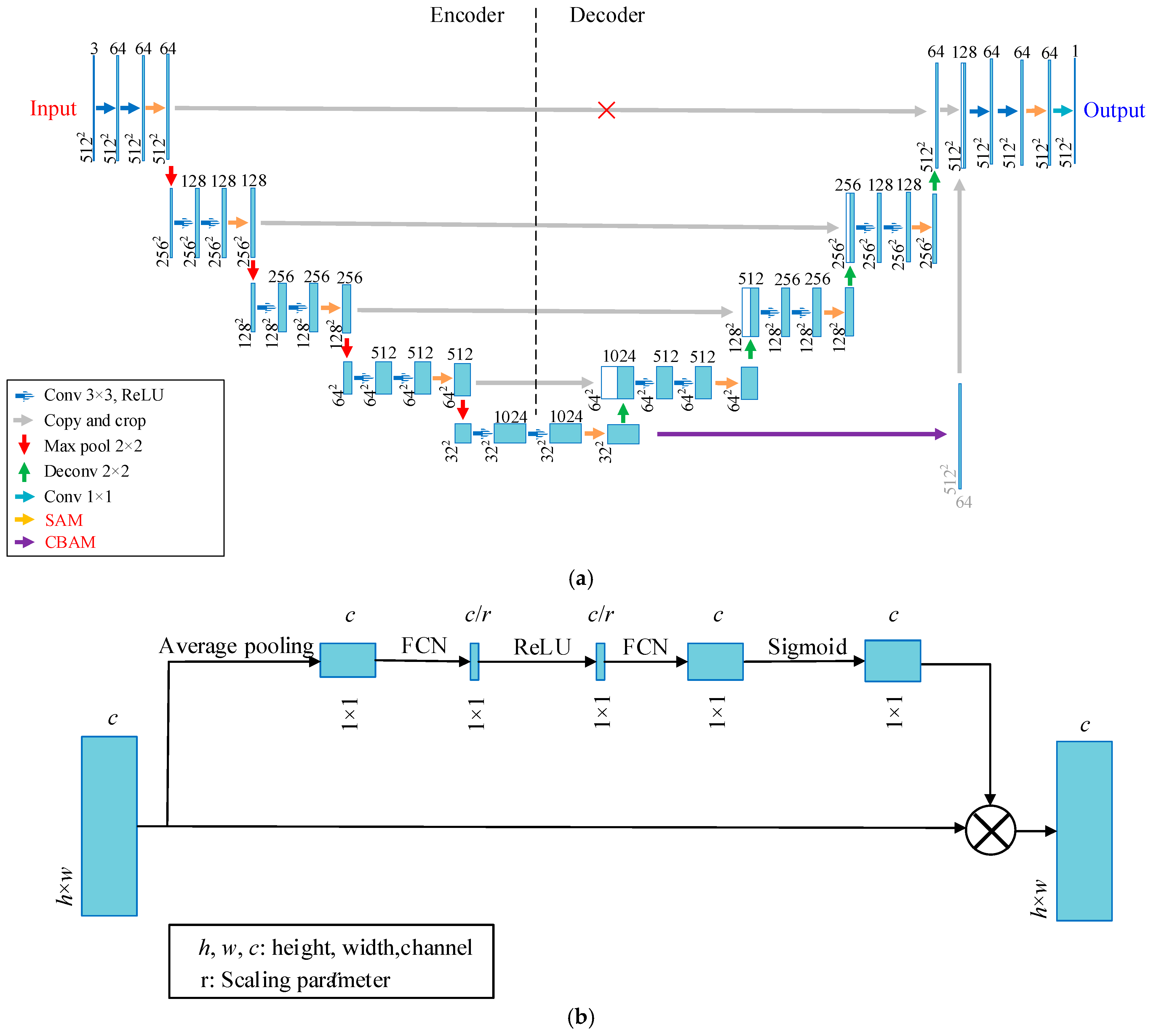
4.1.2. Architecture of the Proposed DA-CrackNet
4.2. Training and Testing of the Network
4.2.1. Preparation of the Dataset
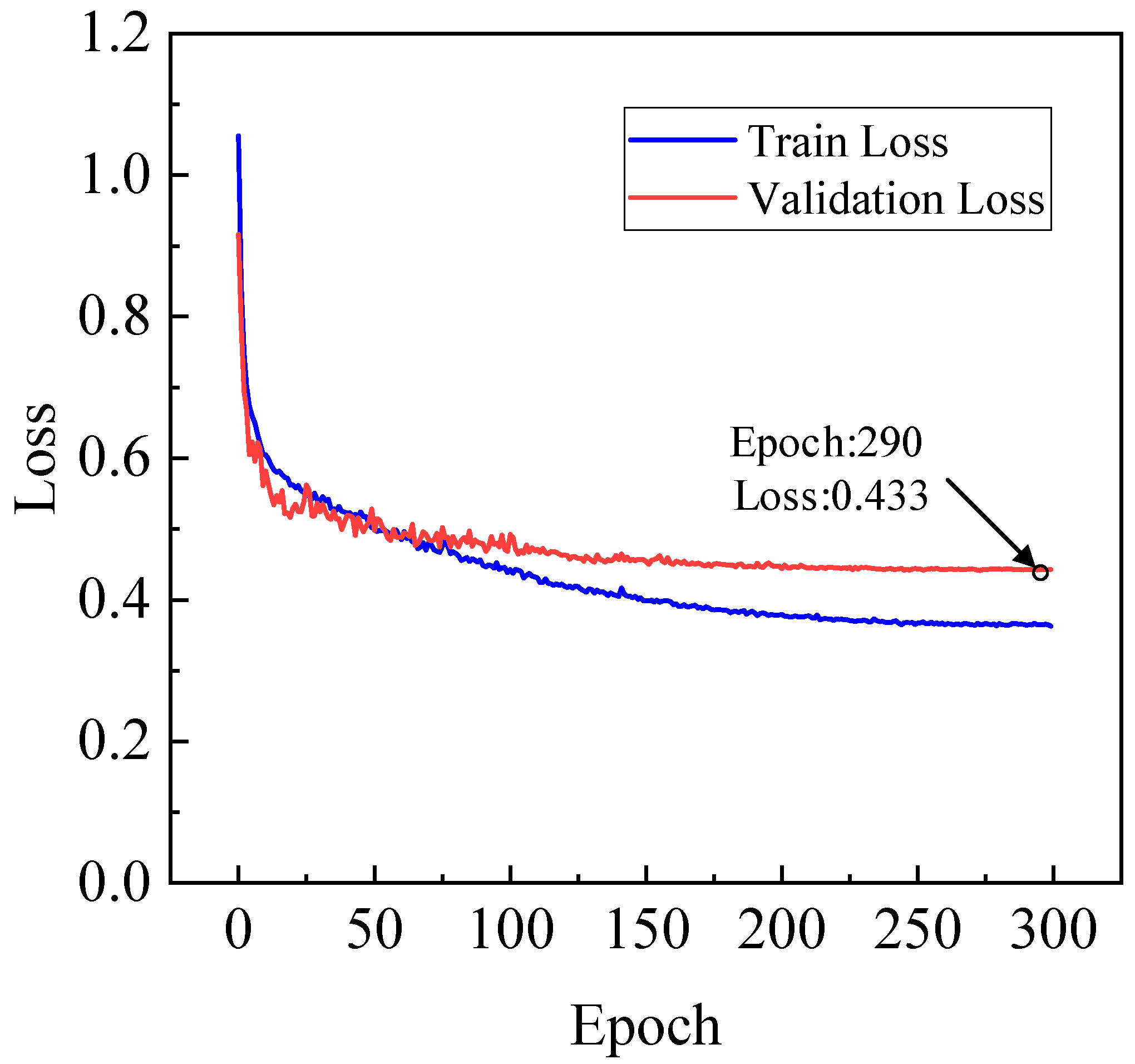
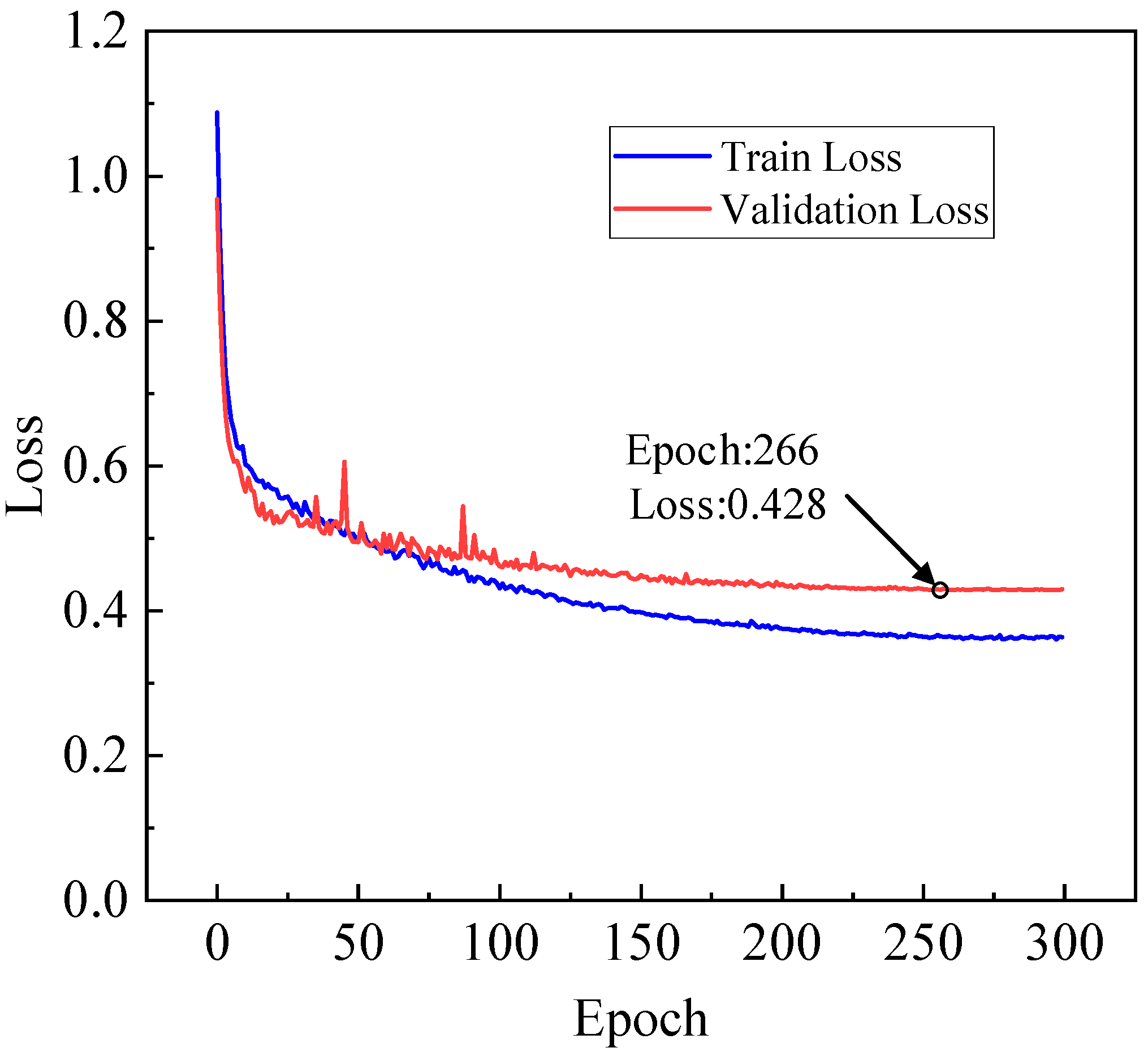
4.2.2. Training of the Network
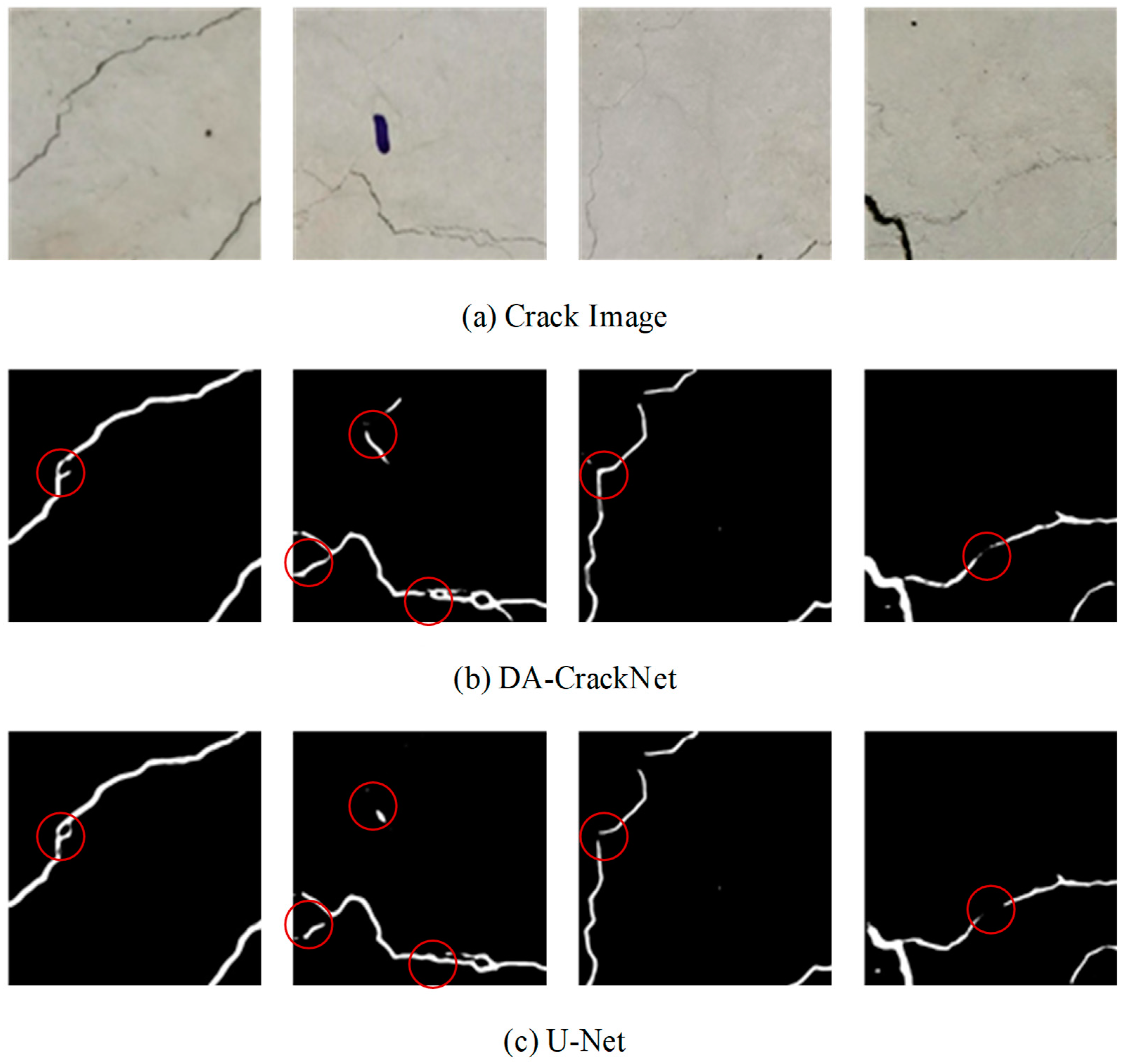
4.2.3. Testing of the Network
5. Seismic Damage Evaluation of RC Short Columns Based on Crack Information
5.1. Damage Development During the Test
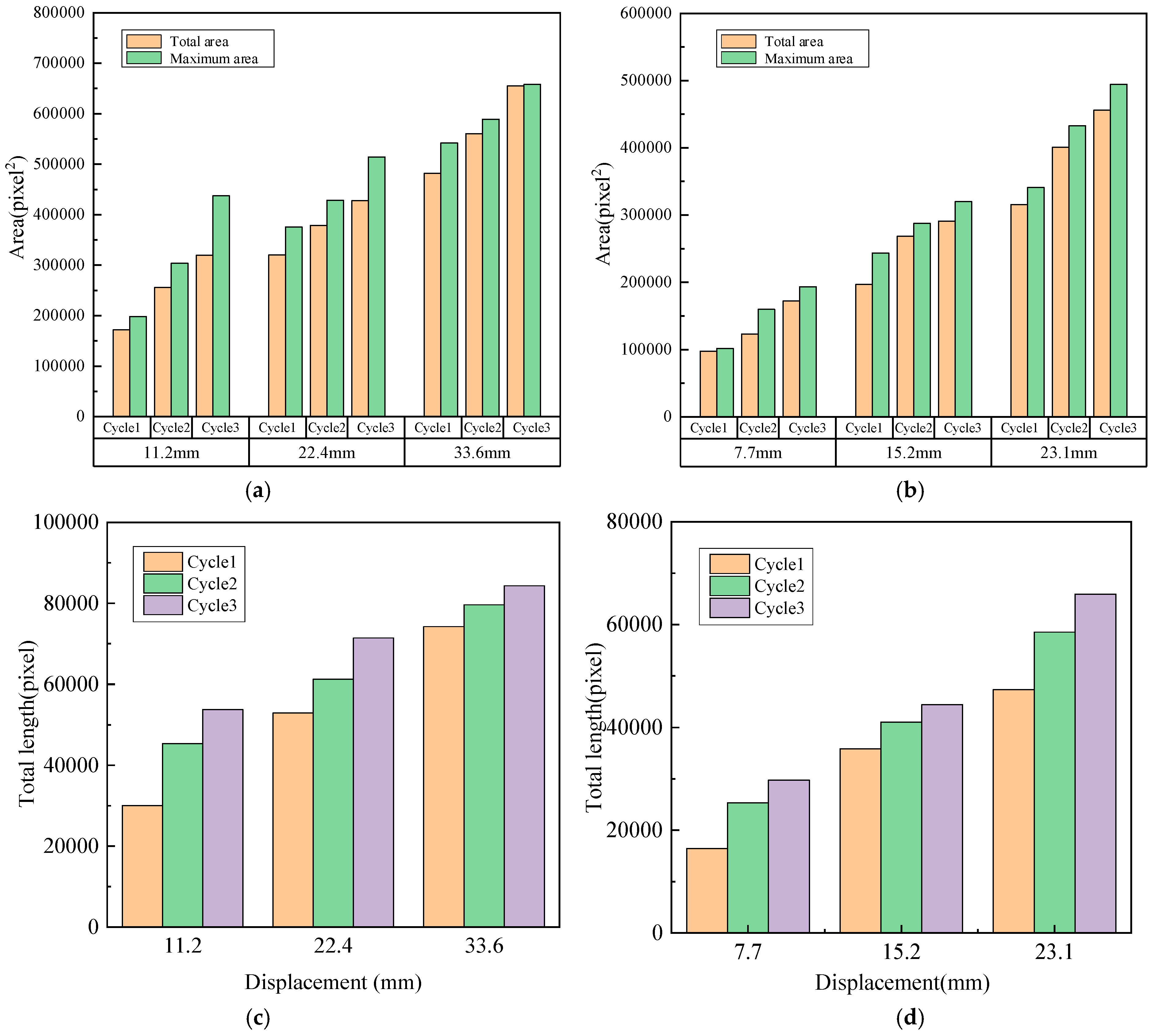
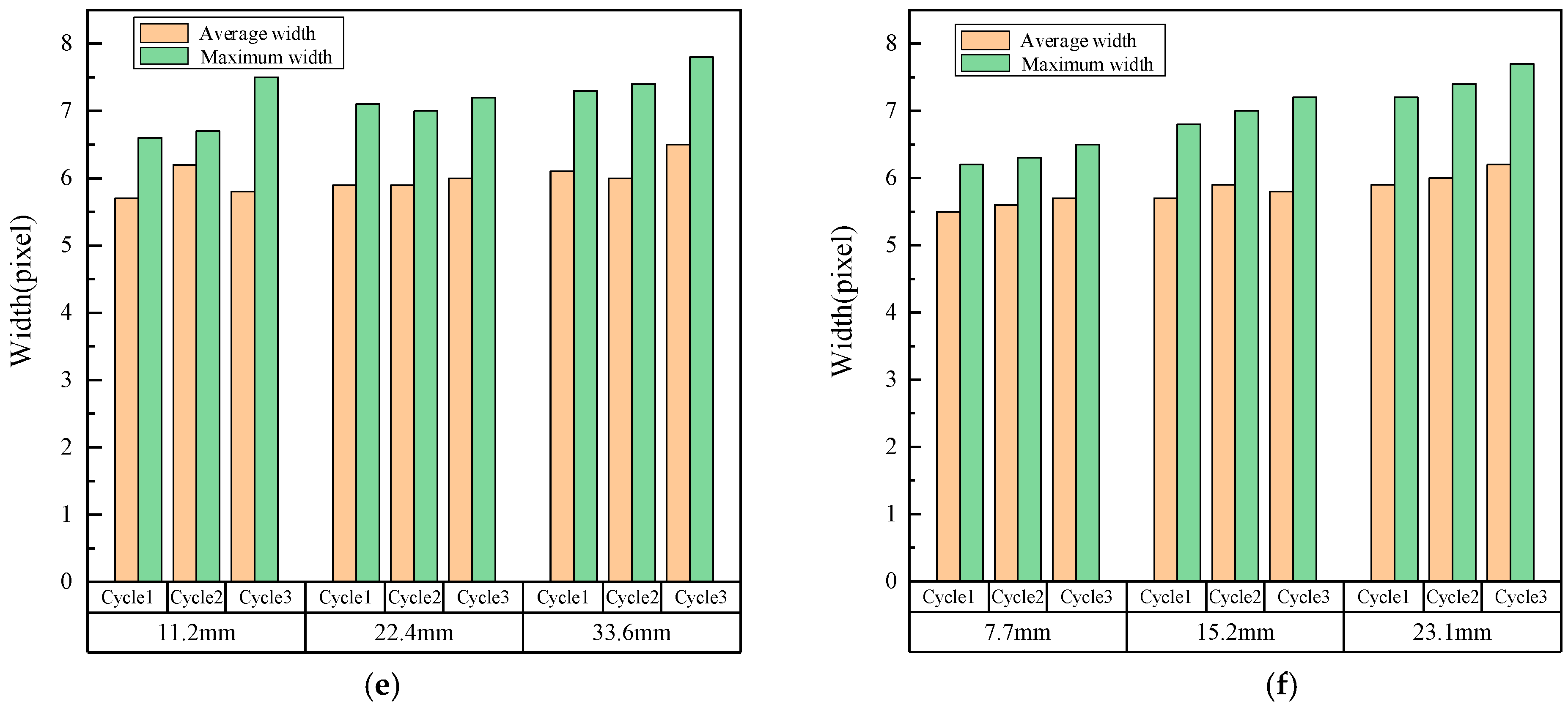
5.2. Crack Development During the Test
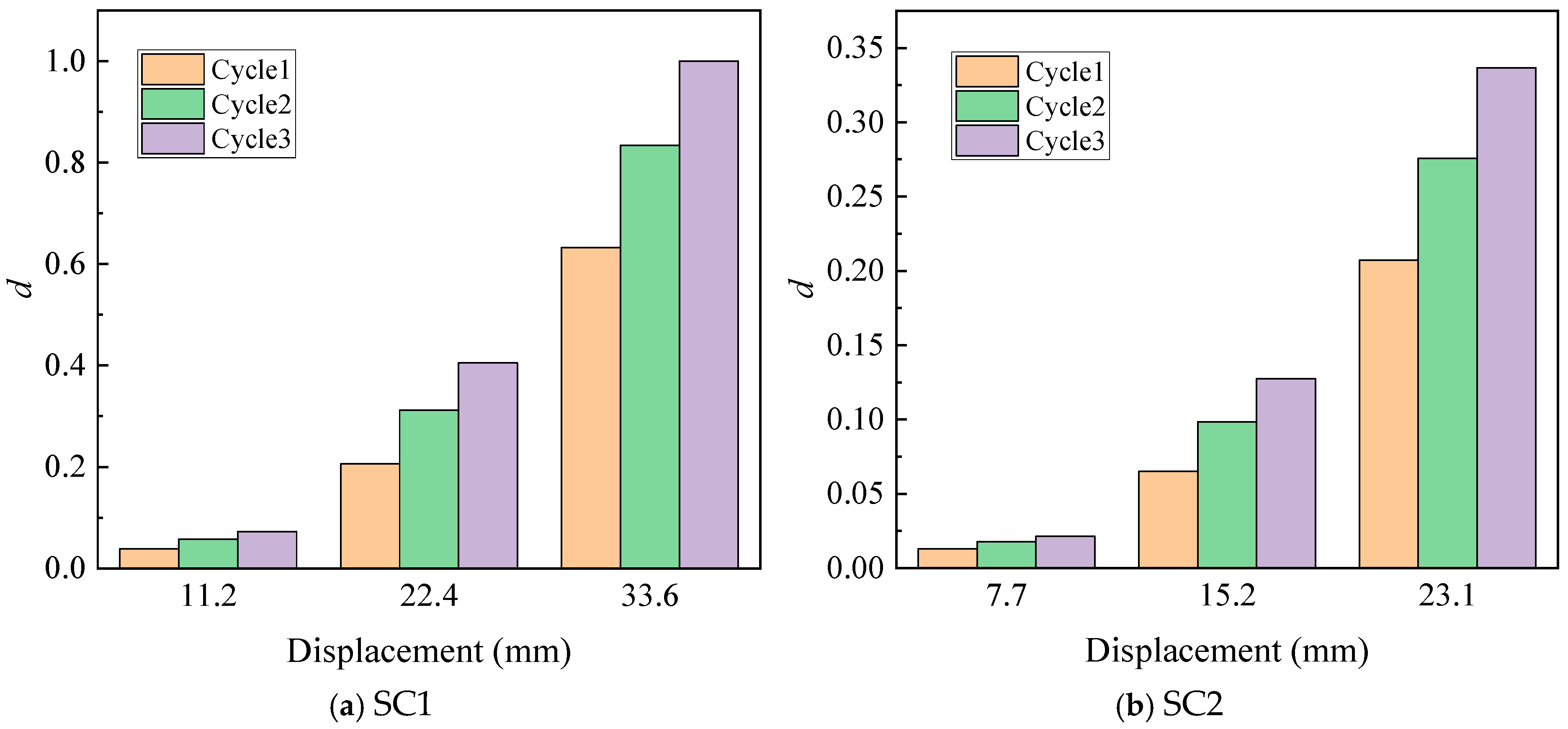
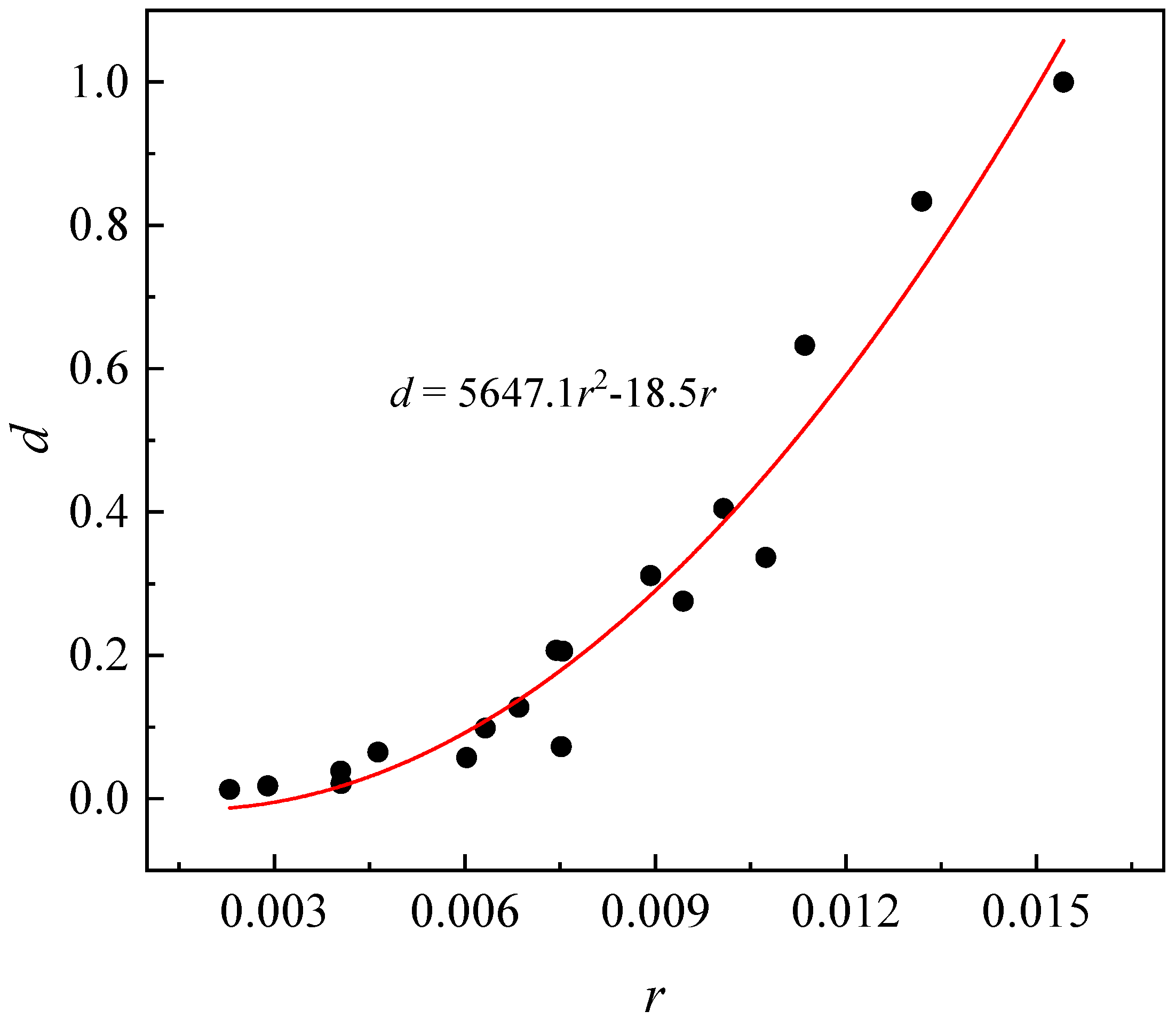
5.3. Correlation Between Seismic Damage and Crack Information
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rirong, F.U.; Liu, K.; Men, G.; Hui, L. The Impact Analysis of Seismic Performance of Setting Up the Core Column Strengthening Measures on Short Column Structure; Atlantis Press: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef][Green Version]
- Promis, G.; Ferrier, E.; Hamelin, P. Effect of external FRP retrofitting on reinforced concrete short columns for seismic strengthening. Compos. Struct. 2009, 88, 367–379. [Google Scholar] [CrossRef]
- Kam, W.Y.; Pampanin, S.; Elwood, K. Seismic Performance of Reinforced Concrete Buildings in the 22 February Christchurch (Lyttleton) Earthquake. Bull. N. Z. Soc. Earthq. Eng. 2011, 44, 223–233. [Google Scholar]
- Ricci, P.; Luca, F.D.; Verderame, G.M. 6th April 2009 L’Aquila earthquake, Italy: Reinforced concrete building performance. Bull. Earthq. Eng. 2011, 9, 285–305. [Google Scholar] [CrossRef]
- Vicente, R.S.; Rodrigues, H.; Varum, H.; Costa, A.; da Silva, J.A.R.M. Performance of masonry enclosure walls: Lessons learned from recent earthquakes. Earthq. Eng. 2012, 11, 23–34. [Google Scholar] [CrossRef]
- Hamidia, M.; Sheikhi, M.; Asjodi, A.H.; Dolatshahi, K.M. Computer vision-based quantification of updated stiffness for damaged RC columns after earthquake. Adv. Eng. Softw. 2024, 190, 103597. [Google Scholar] [CrossRef]
- Ji, X.D.; Miao, Z.H.; Kromanis, R. Vision-based measurements of deformations and cracks for RC structure tests. Eng. Struct. 2020, 212, 110508. [Google Scholar] [CrossRef]
- Kim, B.; Cho, S. Automated Vision-Based Detection of Cracks on Concrete Surfaces Using a Deep Learning Technique. Sensors 2018, 18, 3452. [Google Scholar] [CrossRef] [PubMed]
- Hoang, N.D.; Huynh, T.C.; Tran, V.D. Concrete Spalling Severity Classification Using Image Texture Analysis and a Novel Jellyfish Search Optimized Machine Learning Approach. Adv. Civ. Eng. 2021, 2021, 5551555. [Google Scholar] [CrossRef]
- Cao, M.T.; Nguyen, N.M.; Chang, K.T.; Tran, X.-L.; Hoang, N.-D. Automatic recognition of concrete spall using image processing and metaheuristic optimized Logit Boost classification tree. Adv. Eng. Softw. 2021, 159, 103031. [Google Scholar] [CrossRef]
- Paal, S.G.; Brilakis, I.; Desroches, R. Automated computer vision-based detection of exposed transverse reinforcement for post-earthquake safety assessments. In Proceedings of the World Conference of Structural Control & Monitoring, Barcelona, Spain, 15–17 July 2014. [Google Scholar]
- Xu, Y.; Wei, S.; Bao, Y.; Li, H. Automatic seismic damage identification of reinforced concrete columns from images by a region-based deep convolutional neural network. Struct. Control Health Monit. 2019, 26, e2313. [Google Scholar] [CrossRef]
- Bae, H.; An, Y.K. Computer vision-based statistical crack quantification for concrete structures. Measurement 2023, 211, 112632. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Kam, T.Y.; Cheng, P.Y. An Automatic Approach for Accurate Edge Detection of Concrete Crack Utilizing 2D Geometric Features of Crack. J. Signal Process. Syst. Signal Image Video Technol. 2014, 77, 221–240. [Google Scholar] [CrossRef]
- Vashpanov, Y.; Son, J.Y.; Heo, G.; Podousova, T.; Kim, Y.S. Determination of Geometric Parameters of Cracks in Concrete by Image Processing. Adv. Civ. Eng. 2019, 2019, 2398124. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. [Google Scholar]
- He, K.M.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 386–397. [Google Scholar] [CrossRef]
- Zhang, J.M.; Lu, C.Q.; Wang, J.; Wang, L.; Yue, X.-G. Concrete Cracks Detection Based on FCN with Dilated Convolution. Appl. Sci. 2019, 9, 2686. [Google Scholar] [CrossRef]
- Zhang, L.X.; Shen, J.K.; Zhu, B.J. A research on an improved Unet-based concrete crack detection algorithm. Struct. Health Monit. Int. J. 2021, 20, 1864–1879. [Google Scholar] [CrossRef]
- Yu, C.; Du, J.; Li, M.; Li, Y.; Li, W. An Improved U-Net Model for Concrete Crack Detection. Mach. Learn. Appl. 2022, 10, 100436. [Google Scholar]
- Xiang, C.; Guo, J.J.; Cao, R.; Deng, L. A crack-segmentation algorithm fusing transformers and convolutional neural networks for complex detection scenarios. Autom. Constr. 2023, 152, 104894. [Google Scholar] [CrossRef]
- Shamsabadi, E.A.; Xu, C.; Rao, A.S.; Nguyen, T.; Ngo, T.; Dias-Da-Costa, D. Vision transformer-based autonomous crack detection on asphalt and concrete surfaces. Autom. Constr. 2022, 140, 104316. [Google Scholar] [CrossRef]
- Liu, Z.; Yeoh, J.; Gu, X.Y.; Dong, Q.; Chen, Y.; Wu, W.; Wang, L.; Wang, D. Automatic pixel-level detection of vertical cracks in asphalt pavement based on GPR investigation and improved mask R-CNN. Autom. Constr. 2023, 146, 104689. [Google Scholar] [CrossRef]
- Zhang, C.G.; Shu, J.P.; Zhang, H.; Ning, Y.; Yu, Y. Estimation of load-carrying capacity of cracked RC beams using 3D digital twin model integrated with point clouds and images. Eng. Struct. 2024, 310, 118126. [Google Scholar] [CrossRef]
- Miao, Z.H.; Ji, X.D.; Okazaki, T.; Takahashi, N. Pixel-level multicategory detection of visible seismic damage of reinforced concrete components. Comput. Aided Civ. Infrastruct. Eng. 2021, 36, 620–637. [Google Scholar] [CrossRef]
- Zou, D.J.; Zhang, M.; Bai, Z.L.; Liu, T.; Zhou, A.; Wang, X.; Cui, W.; Zhang, S. Multicategory damage detection and safety assessment of post-earthquake reinforced concrete structures using deep learning. Comput. Aided Civ. Infrastruct. Eng. 2022, 37, 1188–1204. [Google Scholar] [CrossRef]
- Han, X.; Zhao, Z.; Chen, L.; Hu, X.; Tian, Y.; Zhai, C.; Wang, L.; Huang, X. Structural damage-causing concrete cracking detection based on a deep-learning method. Constr. Build. Mater. 2022, 337, 127562. [Google Scholar] [CrossRef]
- Dunphy, K.; Sadhu, A.; Wang, J. Multiclass damage detection in concrete structures using a transfer learning-based generative adversarial networks. Struct. Control Health Monit. 2022, 19, e3079. [Google Scholar] [CrossRef]
- Hamidia, M.; Afzali, M.; Jamshidian, S.; Safi, M. Post-earthquake stiffness loss estimation for reinforced concrete columns using fractal analysis of crack patterns. Struct. Concr. J. FIB 2023, 24, 3933–3951. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, K.; Huang, J.W.G. Fully decouple convolutional network for damage detection of rebars in RC beams. Eng. Struct. 2023, 285, 116023. [Google Scholar] [CrossRef]
- Zhang, G.; Sun, B.; Wang, S.; Xu, J.; Zhang, H. RC column damaged classification based on deep contrasted attention. J. Civ. Struct. Health Monit. 2023, 13, 15–33. [Google Scholar] [CrossRef]
- Yilmaz, M.; Dogan, G.; Arslan, M.H.; Ilki, A. Categorization of Post-Earthquake Damages in RC Structural Elements with Deep Learning Approach. J. Earthq. Eng. 2024, 28, 2620–2651. [Google Scholar] [CrossRef]
- Bazrafshan, P.; On, T.; Basereh, S.; Okumus, P.; Ebrahimkhanlou, A. A graph-based method for quantifying crack patterns on reinforced concrete shear walls. Comput. Aided Civ. Infrastruct. Eng. 2024, 39, 498–517. [Google Scholar] [CrossRef]
- Dung, C.V.; Anh, L.D. Autonomous concrete crack detection using deep fully convolutional neural network. Autom. Constr. 2019, 99, 52–58. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Cao, Y.W.; Wang, Y.Z.; Wang, W. Computer vision-based concrete crack detection using U-net fully convolutional networks. Autom. Constr. 2019, 104, 129–139. [Google Scholar] [CrossRef]
- Xu, S.; Tang, H.; Wang, X.; Wang, D. Assessment of geometric parameters of segmented crack on concrete building facade using deep learning. Structures 2023, 57, 105188. [Google Scholar] [CrossRef]
- Chu, H.; Chun, P. Fine-grained crack segmentation for high-resolution images via a multiscale cascaded network. Comput. -Aided Civ. Infrastruct. Eng. 2024, 39, 575–594. [Google Scholar] [CrossRef]
- GB50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2010. (In Chinese)
- JGJ/T 101-2015; Specification for Seismic Test Buildings. China Architecture & Building Press: Beijing, China, 2015. (In Chinese)
- Feng, P.; Qiang, H.L.; Ye, L.P. Discussion and Definition on Yield Points of Materials, Members and Structures. Eng. Mech. 2017, 34, 36–46. [Google Scholar] [CrossRef]
- Belloni, V.; Sjölander, A.; Ravanelli, R.; Crespi, M.; Nascetti, A. Crack Monitoring from Motion (CMfM): Crack detection and measurement using cameras with non-fixed positions. Autom. Constr. 2023, 156, 105072. [Google Scholar] [CrossRef]
- Harris, C. A combined corner and edge detector. In Proceedings of the Fourth Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; pp. 147–151. [Google Scholar]
- Toyama, F.; Shoji, K. Image mosaicing from a set of images without configuration information. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 26 August 2004; pp. 899–902. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Key points. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Brown, M.; Lowe, D.G. Automatic Panoramic Image Stitching using Invariant Features. Int. J. Comput. Vis. 2007, 74, 59–73. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Chen, K.L.; Wang, M.L. Image stitching algorithm research based on OpenCV. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 7292–7297. [Google Scholar]
- Ju, H.Y.; Li, W.; Tighe, S.S.; Xu, Z.; Zhai, J. CrackU-net: A novel deep convolutional neural network for pixelwise pavement crack detection. Struct. Control Health Monit. 2020, 27, e2551. [Google Scholar]
- Tang, Y.Z.; Zhang, A.A.; Luo, L.; Wang, G.; Yang, E. Pixel-level pavement crack segmentation with encoder-decoder network. Measurement 2021, 184, 109914. [Google Scholar] [CrossRef]
- Schlemper, J.; Oktay, O.; Schaap, M.; Heinrich, M.; Kainz, B.; Glocker, B.; Rueckert, D. Attention gated networks: Learning to leverage salient regions in medical images. Med. Image Anal. 2019, 53, 197–207. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Proceedings of the 4th Deep Learning in Medical Image Analysis (DLMIA) Workshop, Granada, Spain, 20 September 2018. [Google Scholar]
- Huang, H.; Lin, L.; Tong, R.; Hu, H.; Zhang, Q.; Iwamoto, Y.; Han, X.; Chen, Y.-W.; Wu, J. UNet 3+: A Full-Scale Connected UNet for Medical Image Segmentation. arXiv 2020, arXiv:2004.08790. [Google Scholar]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. TransUNet: Transformers Make Strong Encoders for Medical Image Segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef]
- Woo, S.H.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer: Cham, Switzerland, 2018; Volume 11211, pp. 3–19. [Google Scholar]
- Russell, B.C.; Torralba, A.; Murphy, K.P.; Freeman, W.T. LabelMe: A database and web-based tool for image annotation. Int. J. Comput. Vis. 2008, 77, 157–173. [Google Scholar] [CrossRef]
- Zhong, Z.; Zheng, L.; Kang, G.L.; Li, S.; Yang, Y. Random Erasing Data Augmentation. In Proceedings of the 34th AAAI Conference on Artificial Intelligence/32nd Innovative Applications of Artificial Intelligence Conference/10th AAAI Symposium on Educational Advances in Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 13001–13008. [Google Scholar]
- Telea, A. An Image Inpainting Technique Based on the Fast Marching Method. J. Graph. Tools 2004, 9, 23–34. [Google Scholar] [CrossRef]
- Sudre, C.H.; Li, W.Q.; Vercauteren, T.; Ourselin, S.; Cardoso, M.J. Generalised Dice Overlap as a Deep Learning Loss Function for Highly Unbalanced Segmentations. In Proceedings of the 3rd MICCAI International Workshop on Deep Learning in Medical Image Analysis (DLMIA)/7th International Workshop on Multimodal Learning for Clinical Decision Support (ML-CDS), Québec City, QC, Canada, 14 September 2017; Cardoso, M.J., Arbel, T., Eds.; Springer: Cham, Switzerland, 2017; Volume 10553, pp. 240–248. [Google Scholar]
- Yadav, S.; Shukla, S. Analysis of k-fold cross-validation over hold-out validation on colossal datasets for quality classification. In Proceedings of the 2016 IEEE 6th International Conference on Advanced Computing (IACC), Bhimavaram, India, 27–28 February 2016; pp. 78–83. [Google Scholar]
- Rajput, V. Robustness of different loss functions and their impact on networks learning capability. arXiv 2021, arXiv:2110.08322. [Google Scholar]
- Trucco, E. Computer and Robot Vision. AI Commun. 1995, 8, 50–51. [Google Scholar] [CrossRef]







| Type | Strength Grade | Ec or Es (GPa) | fy (MPa) | fcu or fu (MPa) | εy |
|---|---|---|---|---|---|
| Concrete | C60 | 35 | - | 54.49 | - |
| Longitudinal reinforcement | HRB400 | 200 | 395.62 | 590.39 | 2.95 × 10−3 |
| Stirrup | HRB400 | 201 | 467.71 | 534.40 | 2.66 × 10−3 |
| Sensor Size/Inch | Effective Pixels per Million | Image Resolution |
|---|---|---|
| 1/1.28 | 5000 | 6144 × 8192 |
| Network | Precision (%) | Recall (%) | F1 Score (%) | mIoU (%) | Time (s) |
|---|---|---|---|---|---|
| DA-CrackNet | 94.05 | 79.03 | 76.27 | 69.16 | 53.97 |
| U-Net | 93.84 | 76.99 | 75.76 | 68.77 | 47.56 |
| Specimen | Total Area | Maximum Area | Total Length | Average Width | Maximum Width |
|---|---|---|---|---|---|
| SC1 | 0.973 | 0.968 | 0.960 | 0.936 | 0.938 |
| SC2 | 0.970 | 0.902 | 0.913 | 0.902 | 0.899 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Chen, Q.; Dai, Z.; Song, C.; Hu, X. Seismic Damage Quantification of RC Short Columns from Crack Images Using the Enhanced U-Net. Buildings 2025, 15, 322. https://doi.org/10.3390/buildings15030322
Chen Z, Chen Q, Dai Z, Song C, Hu X. Seismic Damage Quantification of RC Short Columns from Crack Images Using the Enhanced U-Net. Buildings. 2025; 15(3):322. https://doi.org/10.3390/buildings15030322
Chicago/Turabian StyleChen, Zixiao, Qian Chen, Zexu Dai, Chenghao Song, and Xiaobin Hu. 2025. "Seismic Damage Quantification of RC Short Columns from Crack Images Using the Enhanced U-Net" Buildings 15, no. 3: 322. https://doi.org/10.3390/buildings15030322
APA StyleChen, Z., Chen, Q., Dai, Z., Song, C., & Hu, X. (2025). Seismic Damage Quantification of RC Short Columns from Crack Images Using the Enhanced U-Net. Buildings, 15(3), 322. https://doi.org/10.3390/buildings15030322







