Optimization of Thermal Insulation Parameters for Vertical Perimeters in Buildings with Single-Layer Walls
Abstract
:1. Introduction
1.1. Thermal Protection Requirements
1.2. Study of the Variability of Thermal Bridge Parameters
2. Description of the Research Object
3. Procedure for Determining the Temperature Fields Within the Thermal Bridge Formation
- -
- For the external surface of the wall, the external air temperature te = −22 °C and Rse = 0.04 [m2·K/W];
- -
- For the external surface of the ground, the outdoor air temperature te = −22 °C and Rse = 0.04 [m2·K/W];
- -
- For internal wall surface, the indoor air temperature ti = 20 °C and Rsi = 0.13 [m2·K/W];
- -
- For the floor on the ground inside the building from above, the indoor air temperature ti = 20 °C and Rsi = 0.17 [m2·K/W].
4. Method of Determining the Temperature Fields Within the Thermal Bridge Formed and the Linear Heat Transfer Coefficient
5. Mathematical Modeling of the Temperature Dependence at the Thermal Bridge Location and the Linear Heat Transfer Coefficient
- -
- The temperature of the inner surface at the thermal bridge ϑimg:
- -
- The linear heat transfer coefficient of the thermal bridge site ψim:
6. Test Results, Their Interpretation, and Optimization
6.1. Results of This Study
6.2. Interpretation
6.3. Discussion
6.4. Optimization
7. Conclusions
- This article presents a study on the temperature field in the ground-floor zone elements of a heated building at the contact point “external wall-foundation wall-ground floor slab-ground” under significant variations in internal and external temperatures. The results of this study confirmed the complex nature of the influence of selected parameters and the necessity of performing an optimization procedure. Temperature distribution data were obtained through computational experiments. The calculations were performed using THERM 7.6 software. The obtained data were used to develop deterministic mathematical models of the studied functions. These models enabled the estimation of the degree and nature of the influence of the analyzed factors on the temperature ϑimg and the linear thermal transmittance coefficient ψim. Furthermore, the models allowed for determining the safe operating conditions of the external wall with the above-described solution for the linear thermal bridge in the ground-floor zone;
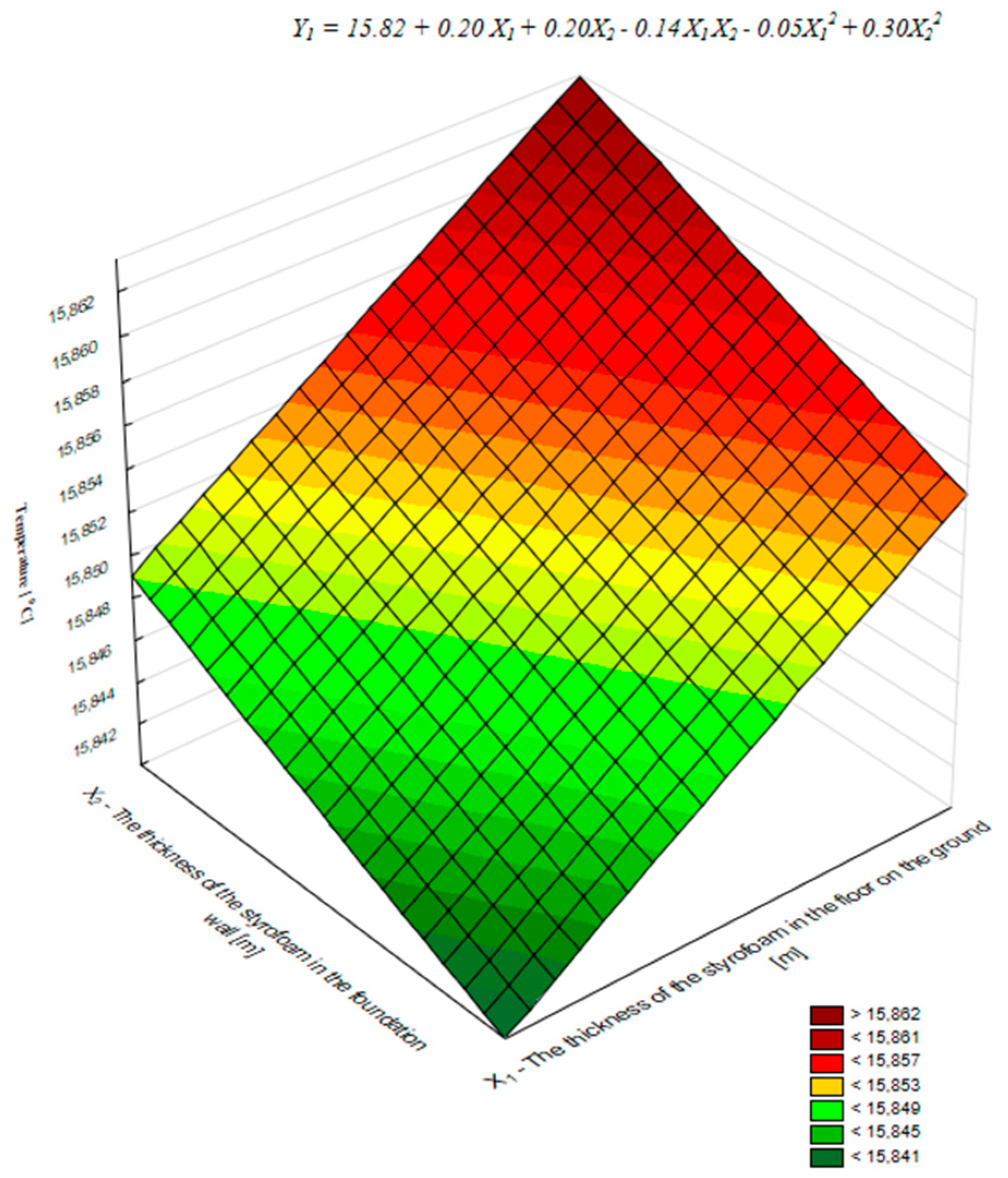
- From the temperature dependence model ϑimg at the thermal bridge location, it was detected that factors X1, X2, and X4 show favorable effects and increase the magnitude of ϑimg. The effects of their influence when changing from lower to upper levels are, respectively, +2.57, +2.51, and +4.17%. The effects of the other two factors, X3 and X5, are associated with a decrease in ϑimg. Their contributions were, respectively, −12.01 and −4.66%, and the total contribution of the factors to the lowering of ϑimg. was −16.67%. It was also detected that a change in the location of the thermal insulation layers in the considered partitions with a shift to the internal boundaries of these partitions (level X3 = 1; level X4 = 3) with the other factors unchanged could increase the temperature at the thermal bridging site by about 2.5 °C;
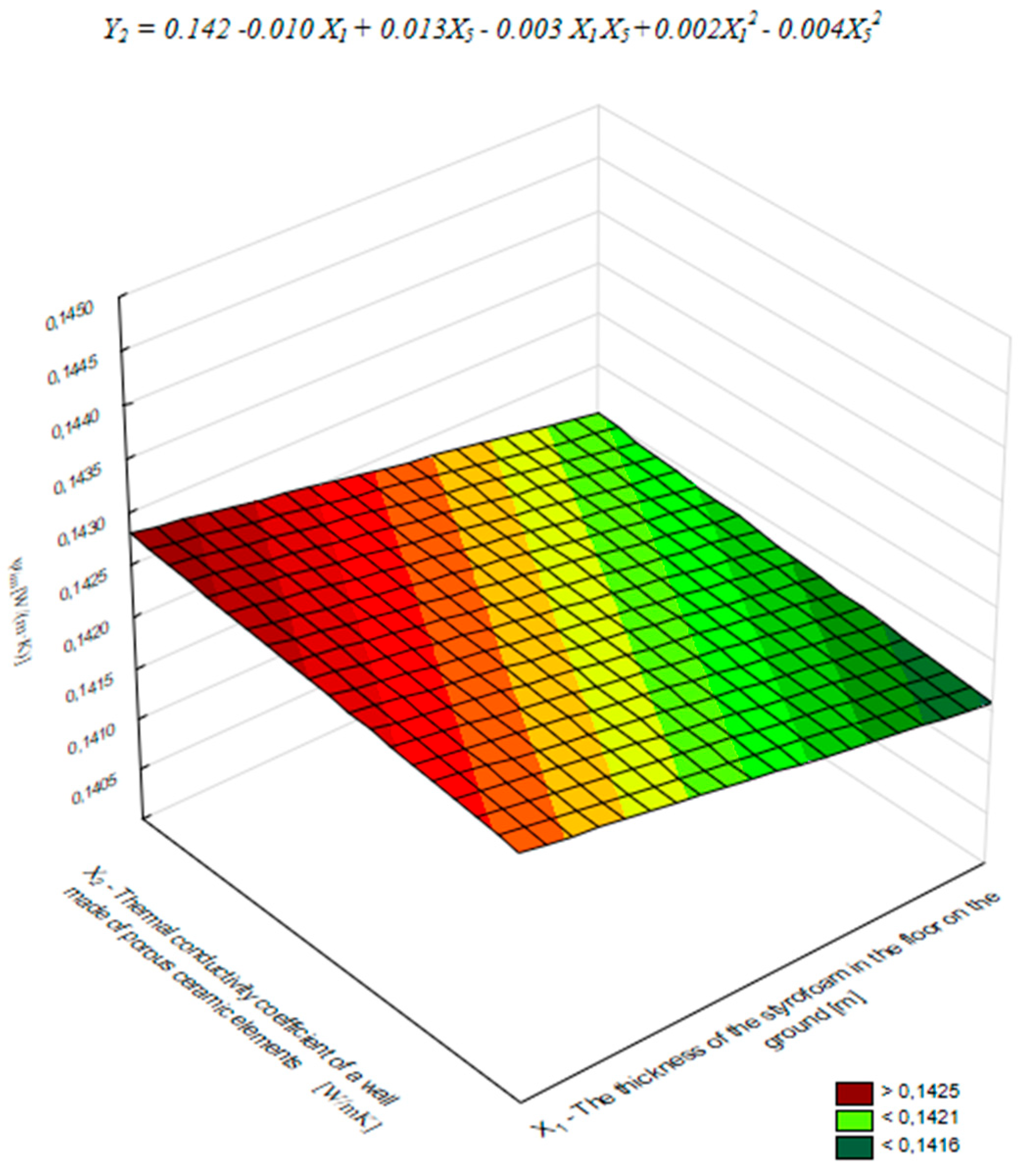
- From the dependence model of the ψim coefficient of the analyzed thermal bridge, it was detected that the factors X1, X2, and X4 also show favorable effects of influencing the linear heat transfer coefficient ψim, lowering it to −13.00; −9.93; −8.63%, respectively. On the other hand, unfavorable effects related to increasing the linear heat transfer coefficient ψim are shown by factors X3 and X5 with contributions of +50.39 and +20.80%, respectively;
- On the basis of the temperature dependence model ϑimg at the thermal bridge location, mathematical descriptions were proposed for two conditions for the safe operation of the external wall with the above-described solution of the linear thermal bridge on the ground floor, namely: operation condition I preventing the occurrence of condensation on the bridge surface and operation condition II preventing the occurrence of relative humidity of 80% on the bridge surface (mold development). The mathematical descriptions created make it possible to assess the suitability of the numerous combinations of solutions and materials of the elements of the thermal bridge under consideration in terms of temperature and humidity;
- Based on the model of the relationship for the ψim coefficient of the analyzed thermal bridge, an optimization of the considered parameters was carried out according to an energy efficiency criterion. An iterative search method was applied, exploring the relevant parameter space with an appropriate sampling step for each factor within the MATLAB environment. The optimization aimed to find parameter values that ensure the minimum value of the linear thermal transmittance coefficient ψim. Three alternative sets of optimal parameter values were identified, all providing the same minimum coefficient value of ψimmin = 0.078 [W/(m K)]. The determined optimal parameter values ensure a temperature ϑimg at the thermal bridge location of approximately 17.3 °C, which guarantees safe operational conditions for the wall in terms of moisture protection.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- European Commission–Department: Energy–In Focus, Energy Efficiency of Buildings Brussels. 17 February 2020, pp. 154–196. Available online: https://commission.europa.eu/news/focus-energy-efficiency-buildings-2020-02-17_pl (accessed on 28 March 2024).
- BPIE—Buildings Performance Institute Europe, Europe’s Buildings Under The Microscope. A Country-by-Country Review of the Energy Performance of Buildings. 2011. Available online: https://bpie.eu/wp-content/uploads/2015/10/HR_EU_B_under_microscope_study.pdf (accessed on 4 December 2016).
- Regulation of the Minister of Develpmant, Work and Technology of 21 December 2020 on Technical Conditions, Which Should Correspond to the Buildings and Their Location. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20200002351 (accessed on 28 March 2024).
- Priority Program of the National Fund for Environmental Protection and Water Management “Improvement of Energy Efficiency” Part:2: Subsidies to Credits for Construction of Energy-Saving Houses, Years 2012–2015.
- Passivhause Institut. Available online: https://passipedia.org/basics/building_physics_-_basics/what_defines_thermal_bridge_free_design (accessed on 1 April 2024).
- ISO 10211:2017; Thermal Bridges in Building Construction—Heat Flows and Surface Temperatures–Detailed Calculations. ISO: London, UK, 2007.
- Chruściel, W.; Sulik, P. Wytyczne do projektowania konstrukcji murowych w systemie Porotherm Dryfix. 2012, 1, 38–47. Available online: https://www.wienerberger.pl/content/dam/wienerberger/poland/marketing/documents-magazines/brochures/PL_MKT_DOC_POR_wytyczne_do_projektowania_konstrukcji_murowych_w_systemie_porotherm_dry%EF%AC%81x.pdf (accessed on 10 June 2024).
- Technical notebook. In Projektowanie Architektoniczne i Konstrukcyjne Budynków w Systemie Ytong, wyd; Xella Polska sp. z o.o: Warszawa, Poland, 2017.
- Theodosiou, T.G.; Papadopoulos, A.M. The impact of thermal bridges on the energy demand of buildings with double brick wall constructions. Energy Build. 2008, 40, 2083–2089. [Google Scholar] [CrossRef]
- Kim, M.-Y.; Kim, H.-G.; Kim, J.-S.; Hong, G. Investigation of Thermal and Energy Performance of the Thermal Bridge Breaker for Reinforced Concrete Residential Buildings. Energies 2022, 15, 2854. [Google Scholar] [CrossRef]
- Smusz, R.; Korzeniowski, M. Experimental investigation of thermal bridges in building at real conditions, E3S Web Conf. In Proceedings of the 17th International Conference Heat Transfer and Renewable Sources of Energy, Międzyzdroje, Poland, 3 December 2018; Volume 70. [Google Scholar] [CrossRef]
- ISO 14683:2017; Thermal Bridges in Building Construction—Linear Thermal Transmittance—Simplified Methods and Default Values. ISO: London, UK, 2017.
- Evola, G.; Gagliano, A. Experimental and Numerical Assessment of the Thermal Bridging Effect in a Reinforced Concrete Corner Pillar. Buildings 2024, 14, 378. [Google Scholar] [CrossRef]
- Chandrasiri, D.; Gatheeshgar, P.; Ahmadi, H.M.; Simwanda, L. Numerical Study of Thermal Efficiency in Light-Gauge Steel Panels Designed with Varying Insulation Ratios. Buildings 2024, 14, 300. [Google Scholar] [CrossRef]
- Michálková, D.; Ďurica, P. Measured Impact of Material Settlement in a Timber-Frame Wall with Loose Fill Insulation. Buildings 2023, 13, 1622. [Google Scholar] [CrossRef]
- Milovanović, B.; Bagarić, M.; Gaši, M.; Vezilić Strmo, N. Case Study in Modular Lightweight Steel Frame Construction: Thermal Bridges and Energy Performance Assessment. Appl. Sci. 2022, 12, 10551. [Google Scholar] [CrossRef]
- Zhang, X.; Jung, G.-J.; Rhee, K.-N. Performance Evaluation of Thermal Bridge Reduction Method for Balcony in Apartment Buildings. Buildings 2022, 12, 63. [Google Scholar] [CrossRef]
- Capozzoli, A.; Gorrino, A.; Corrado, V. A building thermal bridges sensitivity analysis. Appl. Energy 2013, 107, 229–243. [Google Scholar] [CrossRef]
- Sedlakova, A.; Majdeln, P.; Tazky, L. Energy efficient buildings—lower structure. Tech. J. 2014, 425–432. Available online: https://suw.biblos.pk.edu.pl/downloadResource&mId=1149294 (accessed on 10 June 2024).
- Deru, M. A Model for Ground-Coupled Heat and Moisture Transfer from Buildings. Technical Report; 2003; pp. 66–72. Available online: https://www.nrel.gov/docs/fy01osti/29693.pdf (accessed on 10 June 2024).
- Stolarska, A.; Strzałkowski, J. Modelling of Edge insulation depending on bounduary conditions for the ground level. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 042003. [Google Scholar] [CrossRef]
- Brzyski, P.; Grudzińska, M.; Majerek, D. Analysis of the Occurrence of Thermal Bridges in Several Variants of Connections of the Wall and the Ground Floor in Construction Technology with the Use of a Hemp–Lime Composite. Materials 2019, 12, 2392. [Google Scholar] [CrossRef] [PubMed]
- El Saied, A.; Maalouf, C.; Bejat, T. Etienne Wurtz c Slab-on-grade thermal bridges: A thermal behavior and solution review. Energy Build. 2022, 257, 111770. [Google Scholar] [CrossRef]
- Godlewski, T.; Mazur, Ł.; Szlachetka, O.; Witowski, M.; Łukasik, S.; Koda, E. Design of Passive Building Foundations in the Polish Climatic Conditions. Energies 2021, 14, 7855. [Google Scholar] [CrossRef]
- Wesołowska, M.; Hołownia, P. Izolacje termiczne posadzek budynków niepodpiwniczonych ze ścianami jednowarstwowymi. In Proceedings of the VII Ogólnopolska Konferencja Naukowo-Techniczna Energodom 2004, Kraków, Poland, 13 October 2004. [Google Scholar]
- EN ISO 13788:2012; Hygrothermal Performance of Building Components and Building Elements—Internal Surface Temperature to Avoid Critical Surface Humidity and Interstitial Condensation—Calculation Methods. ISO: London, UK, 2012; ISO 13788:2012, Corrected version 2020-05.
- Available online: https://windows.lbl.gov/therm-software-downloads (accessed on 1 January 2024).
- PN-EN ISO 10211-1; Mostki Cieplne w Budynkach. Obliczanie Strumieni Cieplnych i Temperatury Powierzchni. Część 1:Metody ogólne. ISO: London, UK, 2008.
- Finlayson, E.; Mitchell, R.; Arasteh, D.; Windows and Daylighting Group. THERM 2.0: Program Description, A PC Program for Analyzing the Two-Dimensional Heat Transfer Through Building Products; Building Technologies Department Environmental Energy Technologies Division, Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1998.
- PN-EN ISO 13370:2017; Thermal Performance of Buildings. Heat Transfer via the Ground. Calculation Methods. ISO: London, UK, 2017.
- Brodsky, V.Z. Tables of Experimental Plans for Factor and Polymial Models; Metallurgy: Moscow, Russia, 1982. [Google Scholar]
- Available online: https://www.statsoft.pl/textbook/stathome.html (accessed on 1 January 2024).
- Korzyński, M. Methodology of the Experiment. Planning, Implementation, and Statistical Analysis of the Results of Technological Experiments; WNT: Warsaw, Poland, 2006. [Google Scholar]
- Durakovic, B. Design of Experiments Application, Concepts, Examples: State of the Art. Period. Eng. Nat. Sci. 2017, 5, 421–439. [Google Scholar] [CrossRef]
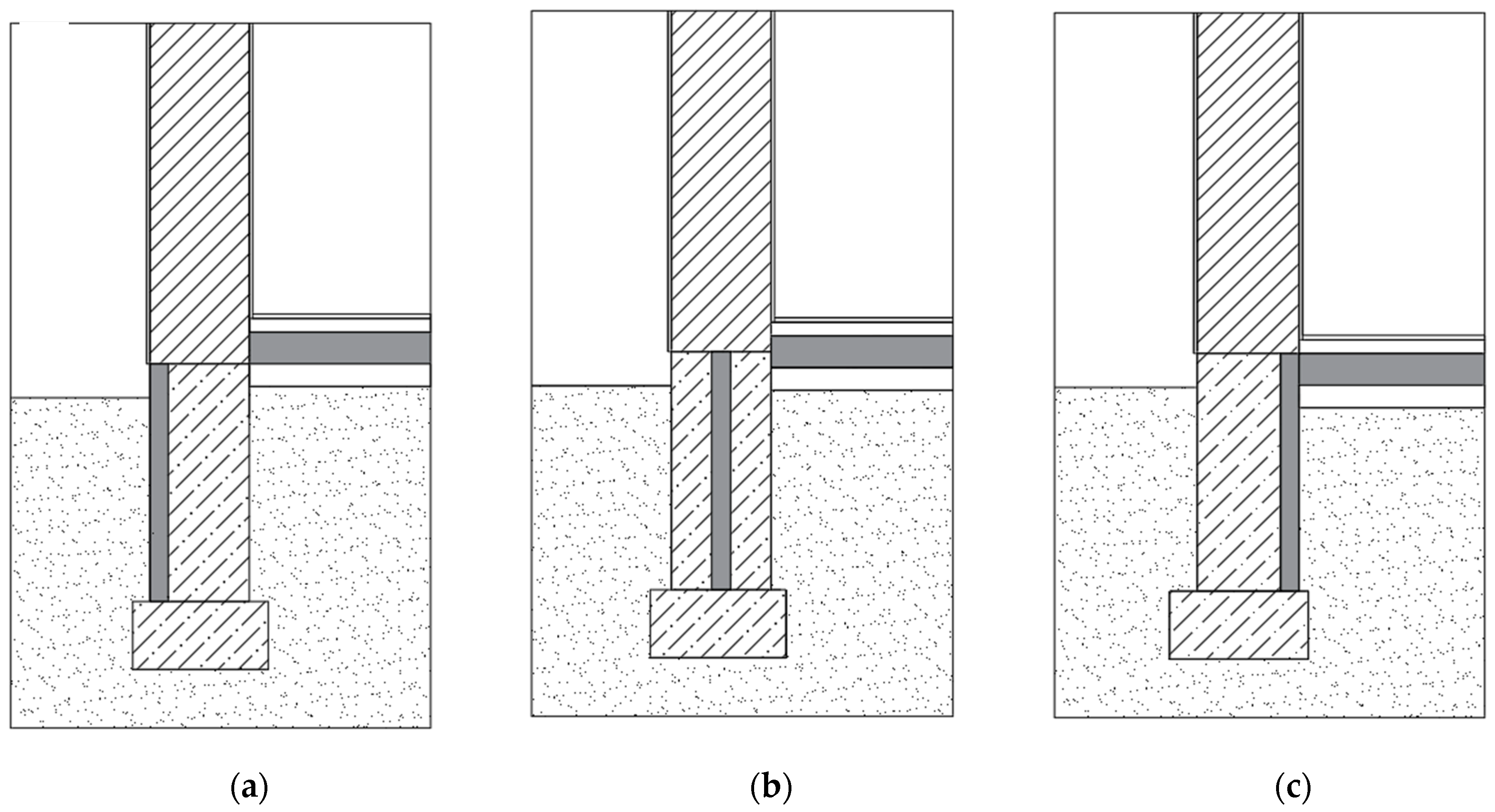

| Heat Transfer Coefficient U [W/(m2·K)] | Polish Building Regulations [3] from 01.01.2021 Introducing the Definition of a Low-Energy Building | National Subsidy Programs for New Energy-Efficient Buildings * [4] | Passive Building Standard [5] | |
|---|---|---|---|---|
| EUco,max = 40 kWh/(m2year) | EUco,max = 15 kWh/(m2year) | |||
| wall (Ti > 16 °C) | 0.20 | 0.15 | 0.12 | 0.15 |
| floor on the ground | 0.30 | 0.20 | ||
| Linear Heat Transfer Coefficient Ψ [W/(m·K)] | Polish Building Regulations [3] from 01.01.2021 Introducing the Definition of a Low-Energy Building | National Subsidy Programs for New Energy-Efficient Buildings [4] | Passive Building Standard [5] | |
|---|---|---|---|---|
| EUco,max = 40 kWh/(m2year) | EUco,max = 15 kWh/(m2year) | |||
| balcony | no requirements | 0.20 | 0.01 | 0.01 |
| other | 0.10 | |||
| Material | Porous Ceramic Filling Mineral Wool [6] | Autoclaved Aerated Concrete [7] | ||
|---|---|---|---|---|
| Modular dimensions of the element [mm] | 248 × 380 × 249 248 × 440 × 249 | 599 × 480 × 199 | 599 × 400 × 249 | 599 × 480 × 249 |
| Thermal conductivity λ [W/(m·K)] | 0.077 | 0.095 | 0.075 | 0.077 |
| Wall thickness [cm] | 38 | 44 | 48 | 40 |
| Heat transfer coefficient [W/(m2·K)] | 0.20 | 0.17 | 0.19 | 0.18 |
| Material | Thickness [m] | Factor λ [W/(m∙K)] | ||||
|---|---|---|---|---|---|---|
| Foundation wall | ||||||
| Cement–lime plaster | 0.015 | 0.82 | ||||
| Concrete | 0.36 | |||||
| Polystyrene | 0.04 | 0.06 | 0.08 | 0.04 | ||
| Above-ground wall | ||||||
| Cement–lime plaster | 0.015 | 0.82 | ||||
| Wall made of porous ceramic elements | 0.44 | 0.077 | 0.095 | 0.113 | ||
| Cement–lime plaster | 0.015 | 0.82 | ||||
| Floor on the ground | ||||||
| Terracotta | 0.02 | 1.05 | ||||
| Polystyrene | 0.06 | 0.1 | 0.14 | 0.04 | ||
| Concrete leveling layer | 0.1 | 1.15 | ||||
| Sand | 0.5B’/2.5B’ | 2 | ||||
| Factor | Name of the Factor | Natural Values of Ximin, X0, Ximax Corresponding to the Coded Values: | ||
|---|---|---|---|---|
| Xi = −1 | Xi = 0 | Xi = +1 | ||
| Factor X1 | Thickness of polystyrene foam in the floor on the ground, dp [m] | 0.06 | 0.10 | 0.14 |
| Factor X2 | Thickness of polystyrene foam in the foundation wall, df [m] | 0.04 | 0.06 | 0.08 |
| Factor X3 | Location of the thermal insulation layer in the floor on the ground, t [-] | 1 (up) | 2 (middle) | 3 (down) |
| Factor X4 | Location of the vertical perimeter thermal insulation layer in the foundation wall, r [-] | 1 (outside) | 2 (middle) | 3 (inside) |
| Factor X5 | Thermal conductivity coefficient of expanded clay masonry, λs [W/mK] | 0.077 | 0.095 | 0.113 |
| Nr | X1 | X2 | X3 | X4 | X5 | Y1 ϑimg | () ϑimg | Y2 ψim | () ψim |
|---|---|---|---|---|---|---|---|---|---|
| 1 | +1 | +1 | +1 | +1 | +1 | 16.0 | 16.01 | 0.145 | 0.145 |
| 2 | −1 | −1 | −1 | −1 | +1 | 16.1 | 15.88 | 0.145 | 0.148 |
| 3 | +1 | −1 | +1 | +1 | +1 | 15.0 | 14.87 | 0.176 | 0.177 |
| 4 | −1 | −1 | +1 | +1 | +1 | 14.8 | 15.01 | 0.181 | 0.175 |
| 5 | −1 | −1 | −1 | +1 | −1 | 16.5 | 16.43 | 0.123 | 0.129 |
| 6 | +1 | +1 | +1 | −1 | −1 | 14.3 | 14.36 | 0.188 | 0.187 |
| 7 | −1 | +1 | 0 | −1 | 0 | 16.3 | 16.12 | 0.132 | 0.133 |
| 8 | 0 | −1 | −1 | −1 | 0 | 16.8 | 16.96 | 0.107 | 0.102 |
| 9 | −1 | +1 | −1 | −1 | −1 | 17.1 | 17.19 | 0.091 | 0.092 |
| 10 | 0 | 0 | 0 | +1 | −1 | 16.7 | 16.88 | 0.113 | 0.111 |
| 11 | +1 | 0 | −1 | −1 | −1 | 17.3 | 17.35 | 0.078 | 0.075 |
| 12 | +1 | −1 | +1 | −1 | +1 | 13.5 | 13.51 | 0.191 | 0.191 |
| 13 | +1 | −1 | −1 | +1 | +1 | 16.6 | 16.65 | 0.118 | 0.117 |
| 14 | +1 | 0 | +1 | 0 | 0 | 14.2 | 14.21 | 0.189 | 0.190 |
| 15 | −1 | −1 | +1 | +1 | 0 | 14.9 | 14.91 | 0.179 | 0.182 |
| 16 | −1 | 0 | −1 | +1 | +1 | 15.8 | 15.59 | 0.153 | 0.161 |
| 17 | −1 | −1 | +1 | −1 | −1 | 14.4 | 14.43 | 0.187 | 0.187 |
| 18 | +1 | −1 | +1 | +1 | −1 | 15.8 | 15.85 | 0.153 | 0.150 |
| 19 | +1 | −1 | 0 | −1 | −1 | 17.1 | 16.89 | 0.091 | 0.098 |
| 20 | 0 | +1 | −1 | 0 | +1 | 16.6 | 16.39 | 0.118 | 0.125 |
| 21 | −1 | +1 | +1 | +1 | −1 | 16.5 | 16.43 | 0.123 | 0.125 |
| 22 | +1 | +1 | −1 | +1 | −1 | 17.3 | 17.21 | 0.078 | 0.080 |
| 23 | +1 | −1 | −1 | 0 | −1 | 17.3 | 17.31 | 0.078 | 0.079 |
| 24 | −1 | +1 | +1 | −1 | +1 | 13.9 | 13.96 | 0.191 | 0.191 |
| 25 | −1 | +1 | −1 | +1 | +1 | 16.1 | 16.38 | 0.141 | 0.131 |
| 26 | −1 | 0 | +1 | 0 | −1 | 14.7 | 14.68 | 0.182 | 0.179 |
| 27 | +1 | +1 | −1 | −1 | +1 | 16.8 | 16.86 | 0.107 | 0.105 |
| Nr | dp [m] (X1) | df [m] (X2) | t [-] (X3) | r [-] (X4) | λs [W/mK] (X5) | ψimmin |
|---|---|---|---|---|---|---|
| 1 | 0.14 m (+1) | 0.08 m (+1) | 1 (−1) | 3 (+1) | 0.077 (−1) | 0.078 |
| 2 | 0.14 m (+1) | 0.06 m (0) | 1 (−1) | 1 (−1) | 0.077 (−1) | 0.078 |
| 3 | 0.14 m (+1) | 0.04 m (−1) | 1 (−1) | 2 (0) | 0.077 (−1) | 0.078 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jezierski, W.; Szczepaniak, P.; Leszczyński, C. Optimization of Thermal Insulation Parameters for Vertical Perimeters in Buildings with Single-Layer Walls. Buildings 2025, 15, 405. https://doi.org/10.3390/buildings15030405
Jezierski W, Szczepaniak P, Leszczyński C. Optimization of Thermal Insulation Parameters for Vertical Perimeters in Buildings with Single-Layer Walls. Buildings. 2025; 15(3):405. https://doi.org/10.3390/buildings15030405
Chicago/Turabian StyleJezierski, Walery, Paula Szczepaniak, and Cezary Leszczyński. 2025. "Optimization of Thermal Insulation Parameters for Vertical Perimeters in Buildings with Single-Layer Walls" Buildings 15, no. 3: 405. https://doi.org/10.3390/buildings15030405
APA StyleJezierski, W., Szczepaniak, P., & Leszczyński, C. (2025). Optimization of Thermal Insulation Parameters for Vertical Perimeters in Buildings with Single-Layer Walls. Buildings, 15(3), 405. https://doi.org/10.3390/buildings15030405






