Assessment of RC Columns Under Axial Compression for Un-Corroded and Corroded Stirrups Scenarios: A Practice-Oriented Numerical Approach
Abstract
1. Introduction
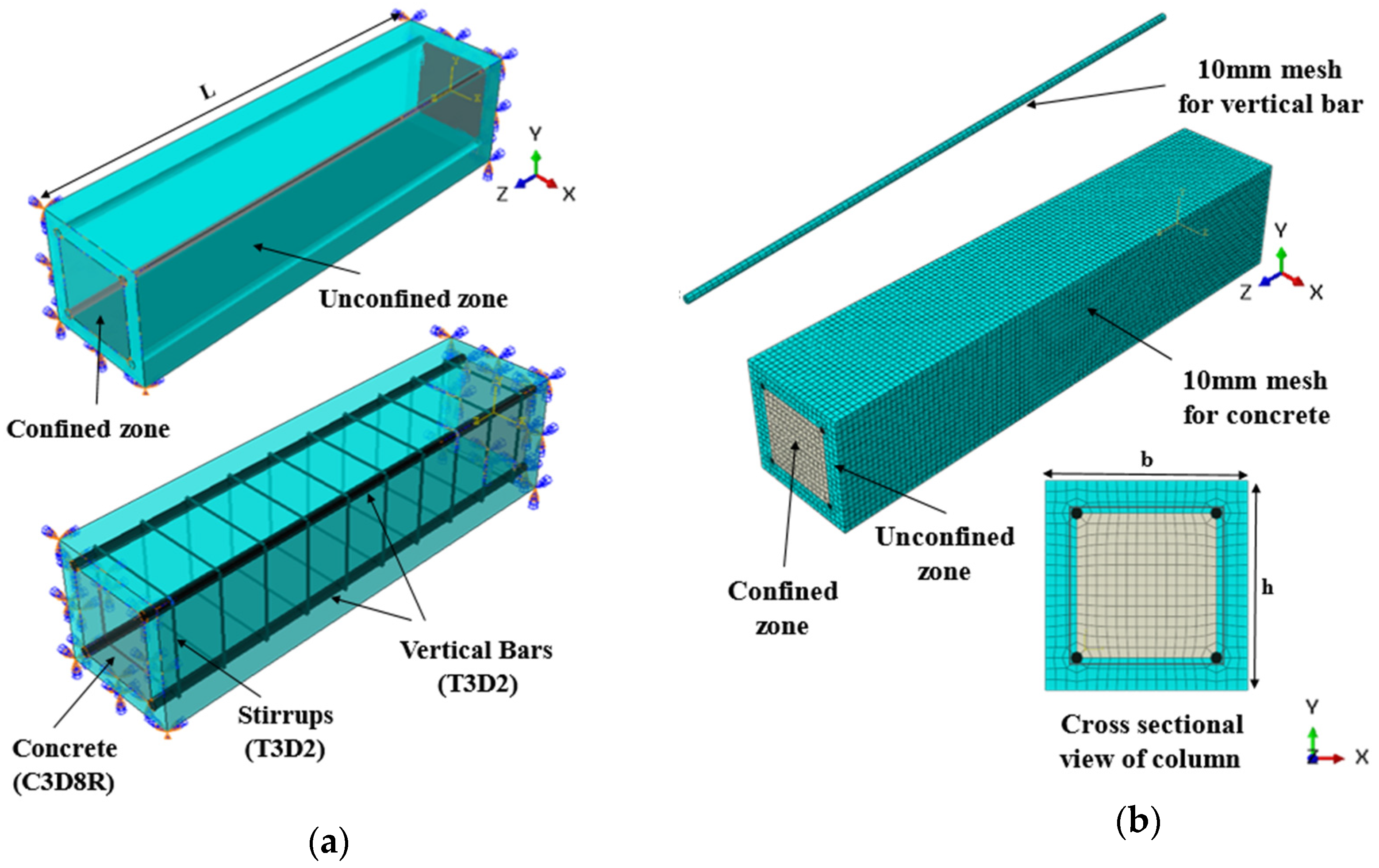
2. Finite Element Modelling Method
2.1. Modelling Procedure
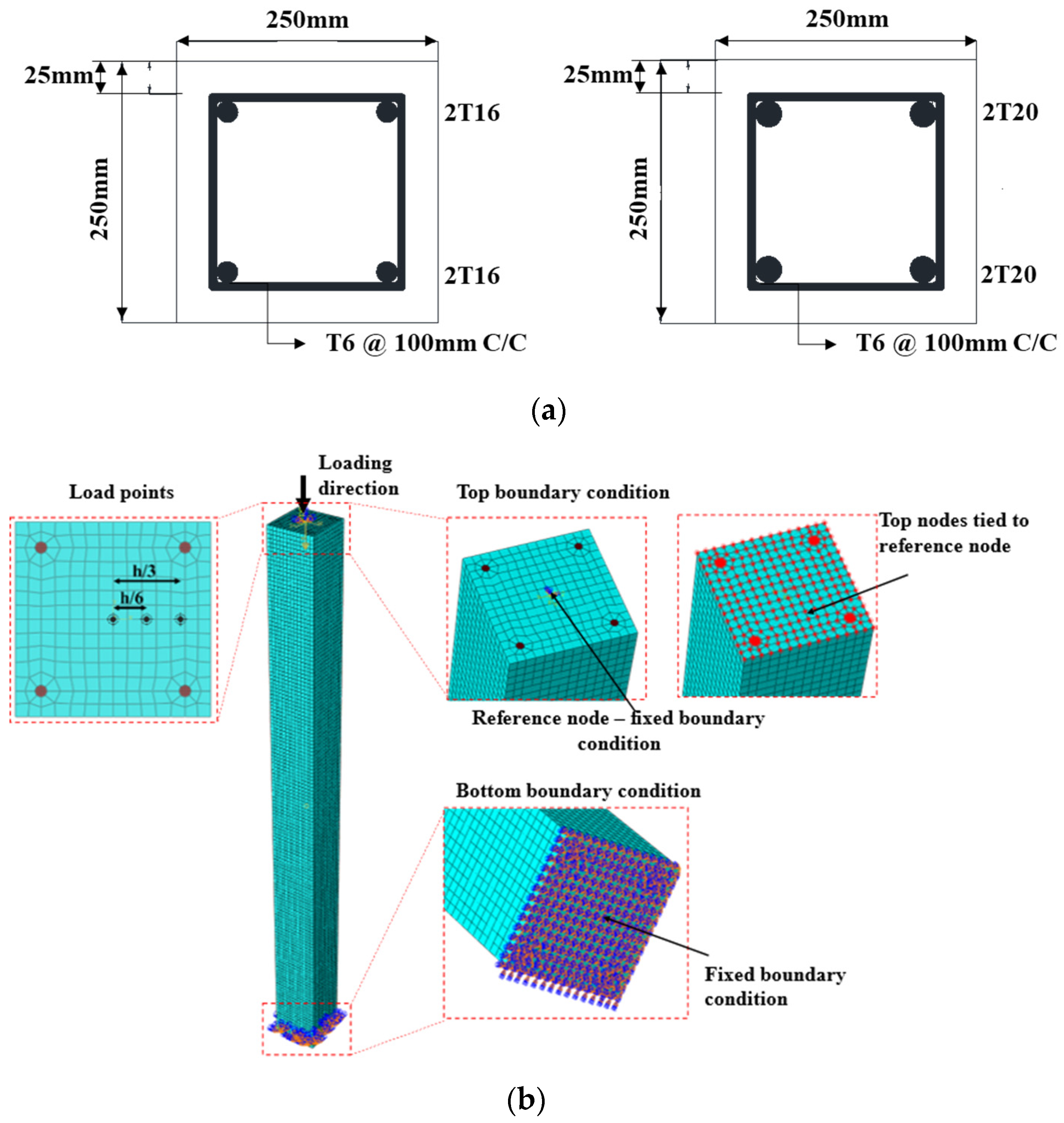
2.2. FE Model of RC Column
2.3. Modelling the Corroded Stirrup RC Columns
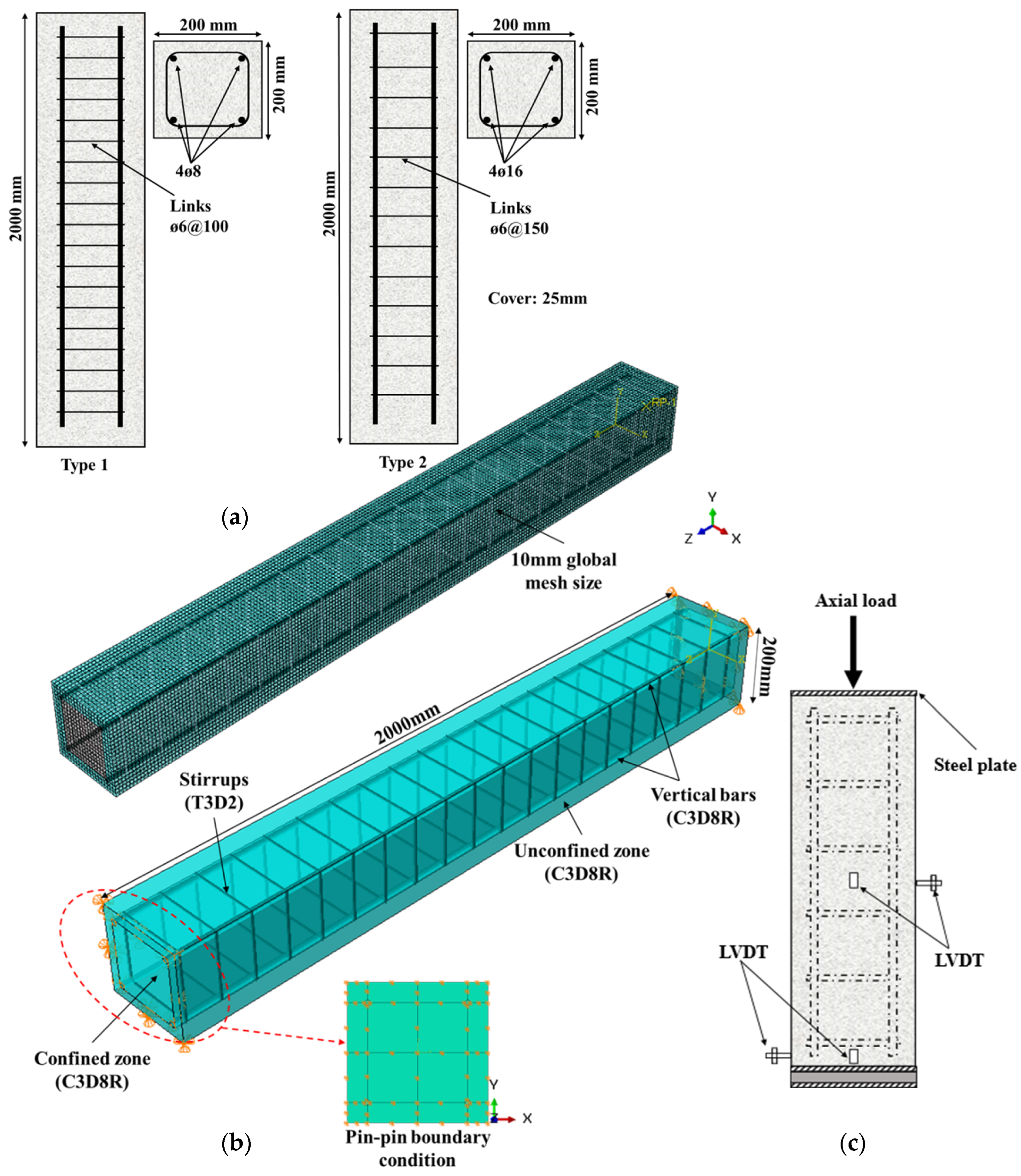
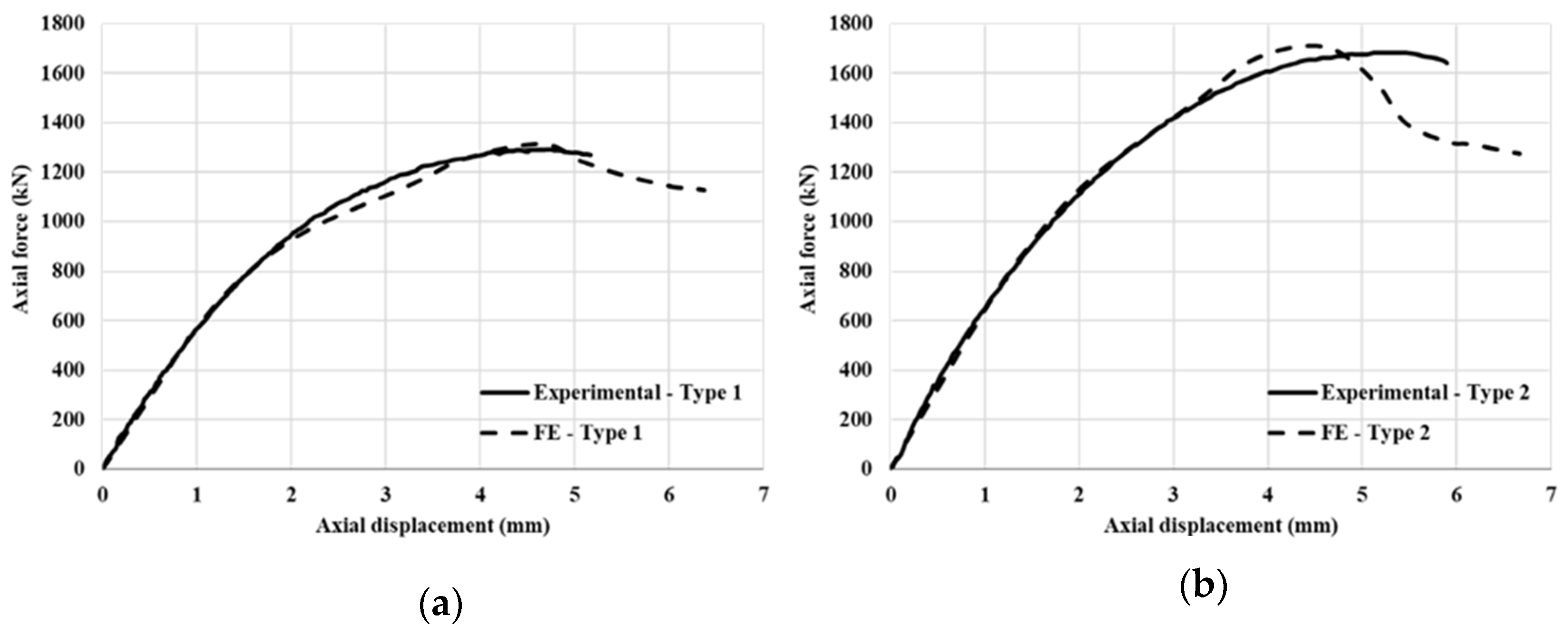
3. Verification of the Modelling Method
3.1. Experimental Description
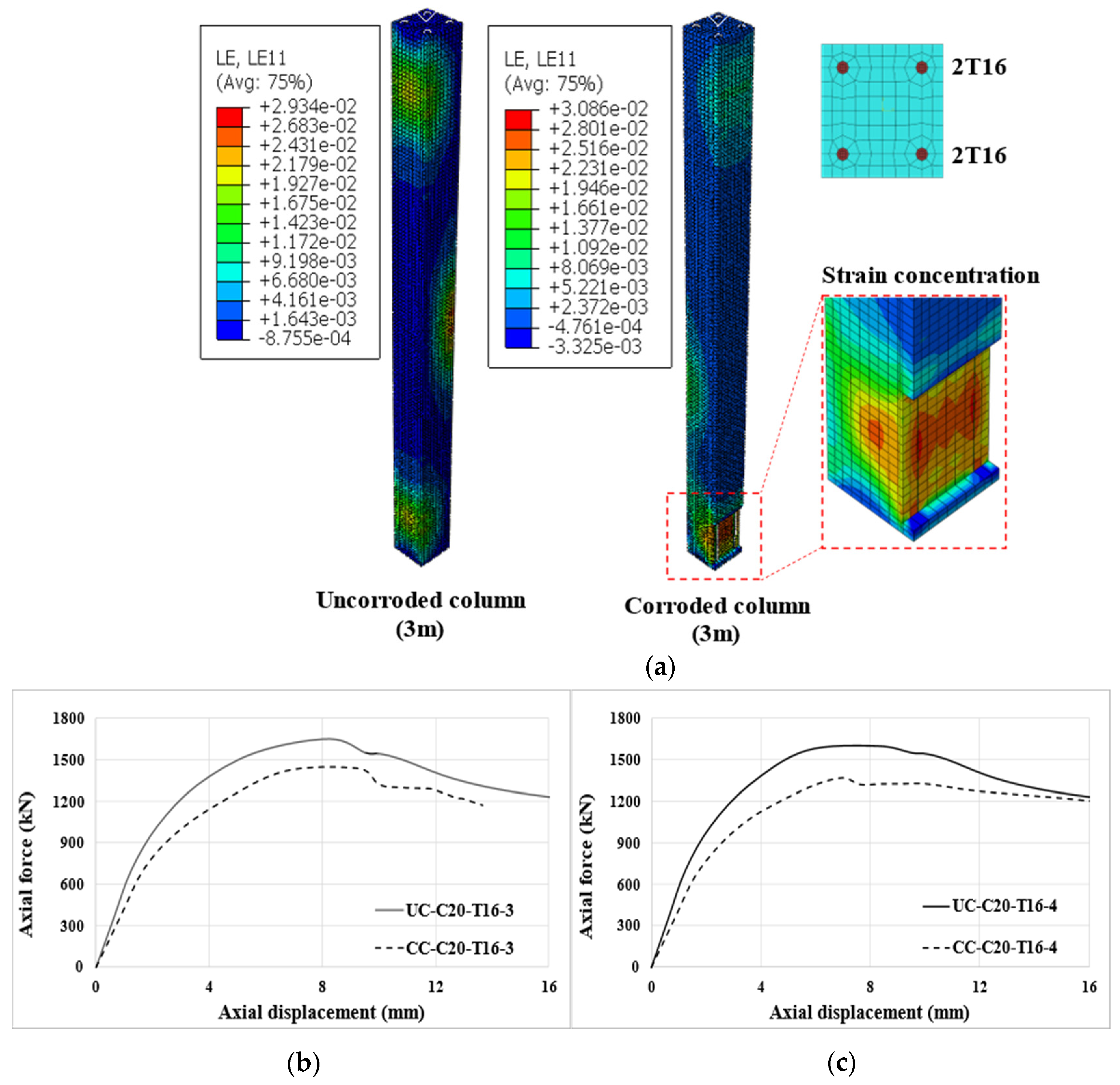
3.2. Validation Results
4. Parametric Analyses
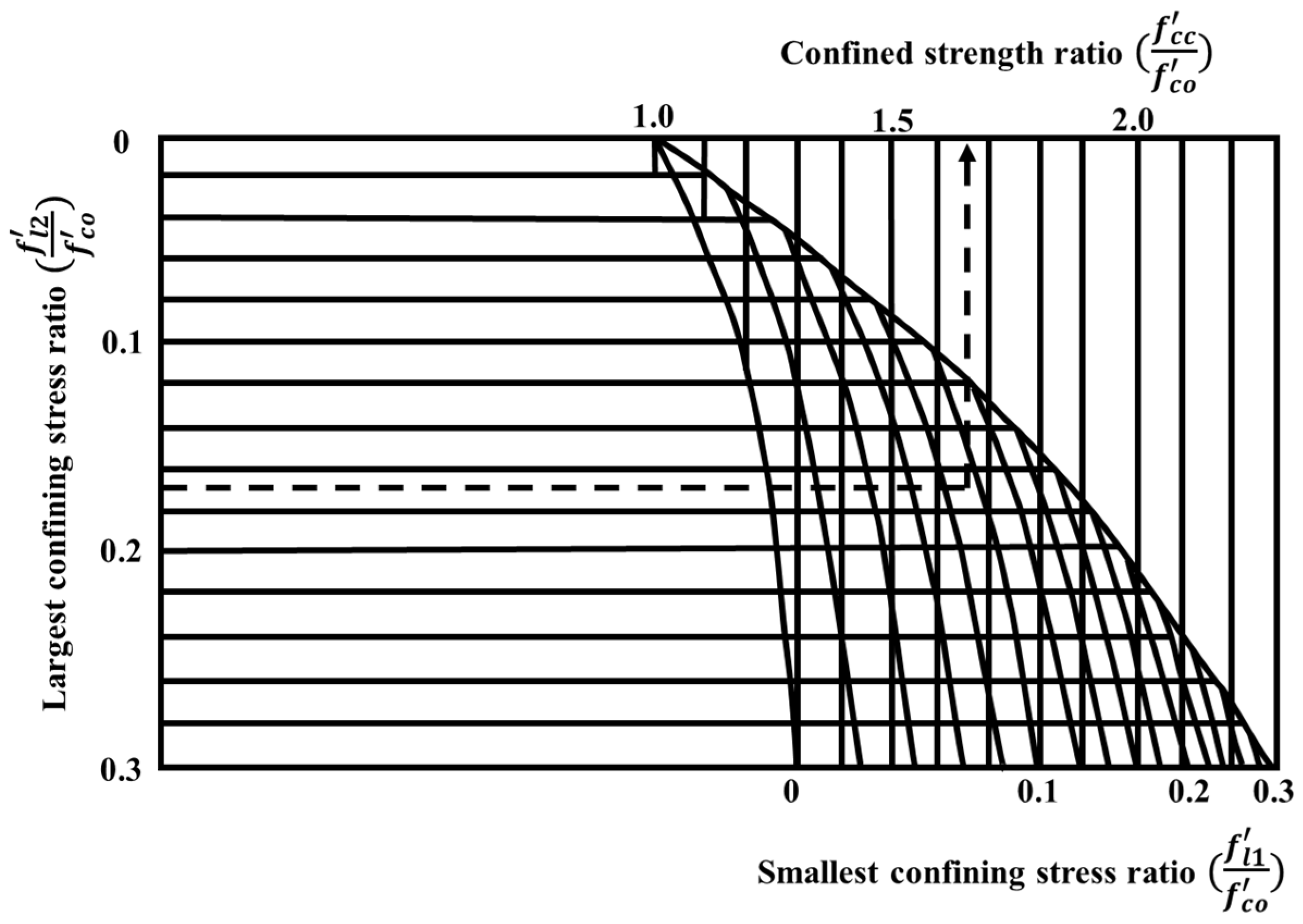
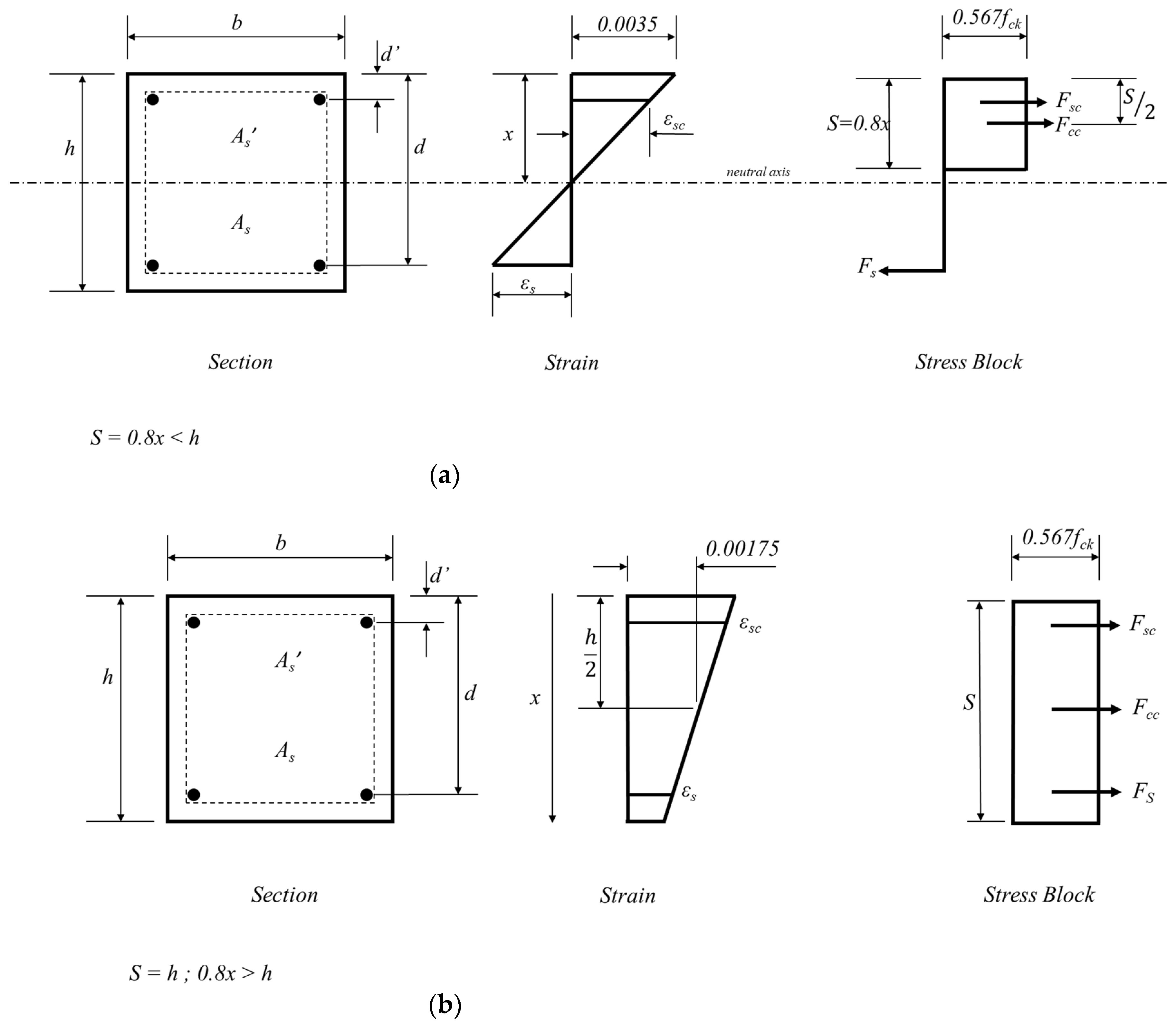
4.1. Modified (M–N) Interaction Diagrams
4.2. Comparison of Analytical and FE Predicted Results
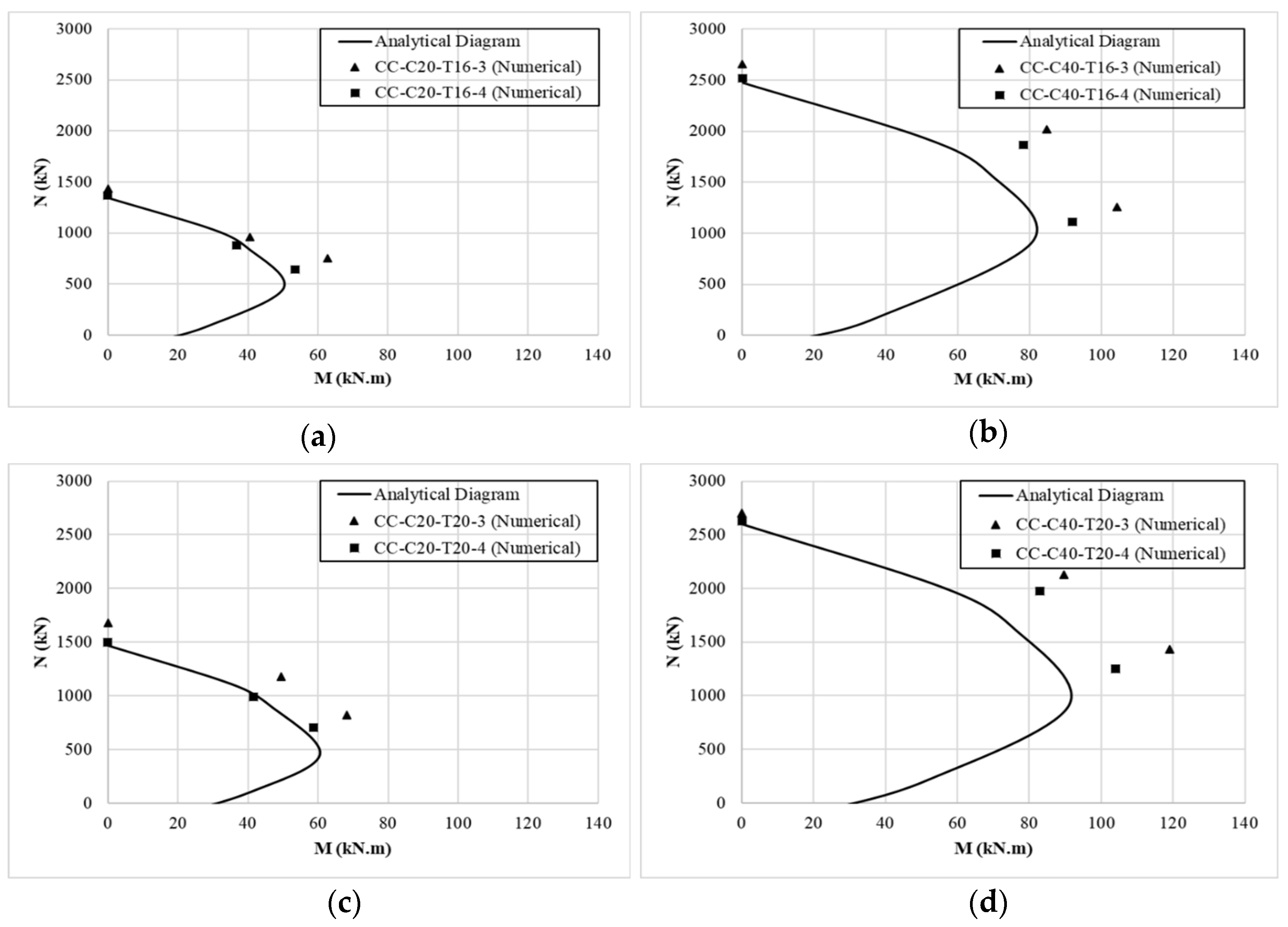
4.2.1. Un-Corroded RC Columns
4.2.2. Corroded RC Columns
4.2.3. Comparisons of Un-Corroded and Corroded Columns
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Notations
| RC | Reinforced concrete |
| FE | Finite element |
| CDP | Concrete damage plasticity |
| KNM | Tangential stiffness matrix |
| VM | Trivial displacement solution of buckling modes |
| λi | Eigenvalue of an ith mode |
| Pcr | Critical buckling load |
| Q | Total axial load |
| σcr | Euler’s critical buckling load |
| n | Restraint factor |
| E | Young’s modulus |
| I | Moment of inertia |
| le | Effective length of the column |
| fr,eff | Effective lateral confining stresses |
| ke | Confinement effectiveness coefficient |
| Ae | Area of effectively confined concrete core |
| ACC | Area of core concrete |
| fr | Lateral confining stress |
| Atr | Total area of transverse bars running in the respective directions (x and y) |
| fy | Yield strength of the transverse reinforcement |
| s | Centre-to-centre spacing of stirrups |
| dC | Core dimensions to centrelines of perimeter hoop |
| fcc′ | Maximum concrete stress |
| εcc | Strain corresponding to maximum concrete stress |
| fc | Confined concrete stress |
| εc | Longitudinal compressive concrete strain |
| Ec | Tangent modulus of elasticity of concrete |
| h | Width of the column |
| ϕ | Diameter of the vertical bar |
| b | Length of the column cross-section |
| As′ | Cross-sectional area of compression reinforcement |
| As | Cross-sectional area of tension reinforcement |
| εsc | Compressive strain in reinforcement As′ |
| εs | Tensile or compressive strain in reinforcement As |
| x | Neutral axis depth |
| d′ | Depth of compression reinforcement |
| d | Effective depth of tension reinforcement |
| Fcc | Compressive force acting through the centroid of the stress block |
| Fsc | Compressive force in the reinforcement area As′ and acting through its centroid |
| Fs | Tensile or compressive force in the reinforcement acting through its centroid |
| fck,uncon | Characteristic unconfined concrete compressive strength |
| fck,confined | Characteristic confined concrete compressive strength |
| Auncon″ | Area corresponding to unconfined concrete zone |
| Acon″ | Area corresponding to confined concrete zone |
| N | Axial compressive force |
| M | Moment |
| Plastic centroid depth | |
| l0 | Effective height of column |
| r | Radius of gyration |
| λs | Slenderness of the column |
Appendix A
| Grade of Concrete | ||
|---|---|---|
| Unconfined Strength (MPa) | ||
| 16 mm Bar | 20 mm Bar | |
| 20 | 24.4 | 25 |
| 40 | 44.8 | 46 |
Appendix B
| Nomenclature | Axial Capacity (kN) | Lateral Deflection (mm) | Nomenclature | Axial Capacity (kN) | Lateral Deflection (mm) |
|---|---|---|---|---|---|
| UC-C20-T16-3 | 1653 | 2.02 | CC-C20-T16-3 | 1436 | 2.32 |
| UC-C20-T16-4 | 1602 | 2.49 | CC-C20-T16-4 | 1367 | 2.91 |
| UC-C40-T16-3 | 2899 | 2.16 | CC-C40-T16-3 | 2654 | 2.65 |
| UC-C40-T16-4 | 2727 | 2.92 | CC-C40-T16-4 | 2513 | 3.14 |
| UC-C20-T20-3 | 1857 | 2.16 | CC-C20-T20-3 | 1678 | 2.74 |
| UC-C20-T20-4 | 1687 | 3.05 | CC-C20-T20-4 | 1497 | 3.28 |
| UC-C40-T20-3 | 2976 | 1.96 | CC-C40-T20-3 | 2703 | 2.69 |
| UC-C40-T20-4 | 2765 | 2.85 | CC-C40-T20-4 | 2630 | 3.33 |
| Nomenclature | Axial Capacity (kN) | Lateral Deflection (mm) | Nomenclature | Axial Capacity (kN) | Lateral Deflection (mm) |
|---|---|---|---|---|---|
| UC-C20-T16-3-h/6 | 1125 | 2.81 | CC-C20-T16-3-h/6 | 965 | 3.03 |
| UC-C20-T16-4-h/6 | 1014 | 3.35 | CC-C20-T16-4-h/6 | 876 | 3.69 |
| UC-C40-T16-3-h/6 | 2278 | 2.72 | CC-C40-T16-3-h/6 | 2019 | 3.12 |
| UC-C40-T16-4-h/6 | 2057 | 3.20 | CC-C40-T16-4-h/6 | 1867 | 3.82 |
| UC-C20-T20-3-h/6 | 1308 | 2.95 | CC-C20-T20-3-h/6 | 1178 | 2.99 |
| UC-C20-T20-4-h/6 | 1156 | 3.26 | CC-C20-T20-4-h/6 | 987 | 3.81 |
| UC-C40-T20-3-h/6 | 2376 | 2.55 | CC-C40-T20-3-h/6 | 2132 | 3.16 |
| UC-C40-T20-4-h/6 | 2107 | 3.02 | CC-C40-T20-4-h/6 | 1976 | 4.05 |
References
- Li, J.; Hao, H.; Wu, C. Numerical study of precast segmental column under blast loads. Eng. Struct. 2017, 134, 125–137. [Google Scholar] [CrossRef]
- Li, C.; Bi, K.; Hao, H. Seismic performances of precast segmental column under bidirectional earthquake motions: Shake table test and numerical evaluation. Eng. Struct. 2019, 187, 314–328. [Google Scholar] [CrossRef]
- Thilakarathna, H.M.I.; Thambiratnam, D.P.; Dhandasekar, M.; Perera, N. Numerical simulation of axially loaded concrete columns under transverse impact and vulnerability assessment. Int. J. Impact Eng. 2010, 37, 1100–1112. [Google Scholar] [CrossRef]
- Chauhan, A.; Sharma, U.K. Influence of temperature and relative humidity variations on non-uniform corrosion of reinforced concrete. Structures 2019, 19, 296–308. [Google Scholar] [CrossRef]
- Li, D.; Wei, R.; Li, L.; Guan, X.; Mi, X. Pitting corrosion of reinforcing steel bars in chloride contaminated concrete. Constr. Build. Mater. 2019, 199, 359–368. [Google Scholar] [CrossRef]
- Suzuki, A.; Liao, W.; Shibata, S.; Yoshino, Y.; Kimura, Y.; Shimoi, N. Structural damage detection technique of secondary building components using piezoelectric sensors. Buildings 2023, 13, 2368. [Google Scholar] [CrossRef]
- Vu, N.S.; Li, B. Seismic performance assessment of corroded reinforced concrete short columns. Eng. Struct. 2018, 144, 04018018. [Google Scholar] [CrossRef]
- Firouzi, A.; Abdolhosseini, M.; Ayazian, R. Service life prediction of corrosion-affected reinforced concrete columns based on time-dependent reliability analysis. Eng. Fail. Anal. 2020, 117, 104944. [Google Scholar] [CrossRef]
- Li, D.; Wei, R.; Xing, F.; Sui, L.; Zhou, Y.; Wang, W. Influence of Non-uniform corrosion of steel bars on the seismic behavior of reinforced concrete columns. Constr. Build. Mater. 2018, 167, 20–23. [Google Scholar] [CrossRef]
- Wu, X.; Chen, L.; Li, H.; Xu, J. Experimental study of the mechanical properties of reinforced concrete compression members under the combined action of sustained load and corrosion. Constr. Build. Mater. 2019, 202, 11–22. [Google Scholar] [CrossRef]
- Chotickai, P.; Tongya, P.; Jantharaksa, S. Performance of corroded rectangular RC columns strengthened with CFRP composite under eccentric loading. Constr. Build. Mater. 2021, 268, 121134. [Google Scholar] [CrossRef]
- Tapan, M.; Aboutaha, R.S. Effect of steel corrosion and loss of concrete cover on strength of deteriorated RC Columns. Constr. Build. Mater. 2011, 25, 2596–2603. [Google Scholar] [CrossRef]
- Li, P.; Ren, Y.; Zhou, Y.; Zhu, Z.; Chen, Y. Experimental study on the mechanical properties of corroded RC columns repaired with large rupture strain FRP. J. Build. Eng. 2022, 54, 104413. [Google Scholar] [CrossRef]
- Cao, Q.; Jia, J.; Zhang, L.; Ye, H.; Lv, X. Experimental study of axial compression of reinforced concrete columns made by environment-friendly post-filling coarse aggregate process. Struct. Concr. 2021, 22, 1671–1687. [Google Scholar] [CrossRef]
- Li, Q.; Huang, L.; Ye, H.; Fu, C.; Jin, X. Mechanical degradation of reinforced concrete columns corroded under sustained loads. Int. J. Civ. Eng. 2020, 18, 883–901. [Google Scholar] [CrossRef]
- Zhang, G.; Cao, X.; Fu, Q. Experimental study on residual strength of concrete confined with corroded stirrups. Can. J. Civ. Eng. 2016, 43, 583–590. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.; Park, R. Observed stress-strain behavior of confined concrete. J. Struct. Eng. 1988, 114, 1827–1849. [Google Scholar] [CrossRef]
- Rajput, A.S.; Sharma, U.K. Corroded reinforced concrete columns under simulated seismic loading. Eng. Struct. 2018, 171, 453–463. [Google Scholar] [CrossRef]
- Yang, S.Y.; Song, X.B.; Jia, H.X.; Chen, X.; Liu, X.L. Experimental research on hysteretic behaviors of corroded reinforced concrete columns with different maximum amounts of corrosion of Rebar. Constr. Build. Mater. 2016, 121, 319–327. [Google Scholar] [CrossRef]
- Feng, R.; Zhang, J.; Li, Y.; Zhu, J.H. Experimental study on hysteretic behavior for corroded circular RC columns retrofitted by ICCP-SS. Structures 2022, 35, 421–435. [Google Scholar] [CrossRef]
- Guo, L.; Guo, W.; Chen, D.; Wang, K.; Yu, L. Experimental study on reinforced concrete small-eccentricity compressive column after acid rain corrosion. J. Build. Eng. 2024, 83, 108331. [Google Scholar] [CrossRef]
- Suzuki, A.; Shibata, D.; Zhong, X.; Kimura, Y. Buckling strength of compression members considering mechanical performance variations by heat exposure. J. Constr. Steel Res. 2025, 226, 109269. [Google Scholar] [CrossRef]
- Rao, A.S.; Lepech, M.D.; Kiremidjian, A.S.; Sun, X.Y. Simplified structural deterioration model for reinforced concrete bridge piers under cyclic loading. Struct. Infrastruct. Eng. 2016, 13, 55–66. [Google Scholar] [CrossRef]
- Vu, N.S.; Yu, B.; Li, B. Prediction of strength and drift capacity of corroded reinforced concrete columns. Constr. Build. Mater. 2016, 115, 304–318. [Google Scholar] [CrossRef]
- Mohammed, A.; Almansour, H.; Martín-Pérez, B. Simplified finite element model for evaluation of ultimate capacity of corrosion-damaged reinforced concrete beam-columns. Int. J. Adv. Struct. 2018, 10, 381–400. [Google Scholar] [CrossRef]
- Alabduljabbar, H.; Haido, J.H.; Alyousef, R.; Yousif, S.T.; McConnell, J.; Wakil, K.; Jermsittiparsert, K. Prediction of the flexural behavior of corroded concrete beams using combined method. Structures 2020, 25, 1000–1008. [Google Scholar] [CrossRef]
- Kagermanov, A.; Markovic, I. An overview on finite element-modelling techniques for structural capacity assessment of corroded reinforced concrete structures. Struct. Infrastruct. Eng. 2022, 19, 1585–1599. [Google Scholar] [CrossRef]
- BaniAsad, E.; Dehestani, M. Incorporation of corrosion and bond-slip effects in properties of reinforcing element embedded in concrete beams. Structures 2019, 20, 105–115. [Google Scholar] [CrossRef]
- Kyaure, M.; Abed, F. Finite element parametric analysis of RC columns strengthened with FRCM. Compo. Struct. 2021, 275, 114498. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Wang, Z.; Su, Y. Axial compression mesoscale modelling of RC columns after reinforcement-electrochemical chloride extraction. Structures 2021, 31, 876–890. [Google Scholar] [CrossRef]
- Asad, M.; Zahra, T.; Thamboo, J.; Song, M. Finite element modelling of reinforced masonry walls under axial compression. Eng. Struct. 2022, 252, 113594. [Google Scholar] [CrossRef]
- ABAQUS, Finite Element Software Documentation; Dassault Systèmes, Simulia: Johnston, RI, USA, 2017.
- Mohamed, M.S.; Thamboo, J.A.; Jeyakaran, T. Experimental and numerical assessment of the flexural behaviour of semi-precast-reinforced concrete slabs. Adv. Struct. Eng. 2020, 23, 1865–1879. [Google Scholar] [CrossRef]
- Le Minh, H.; Khatir, S.; Abdel Wahab, M.; Cuong-Le, T. A concrete damage plasticity model for predicting the effects of compressive high-strength concrete under static and dynamic loads. J. Build. Eng. 2021, 44, 103239. [Google Scholar] [CrossRef]
- Halahla, A.M.; Abu Tahnat, Y.B.; Almasri, A.H.; Voyiadjis, G.Z. The effect of shape memory alloys on the ductility of exterior reinforced concrete beam-column joints using the damage plasticity model. Eng. Struct. 2019, 200, 109676. [Google Scholar] [CrossRef]
- Kang, S.B.; Tan, K.H. Bond–slip behaviour of deformed reinforcing bars embedded in well-confined concrete. Mag. Concr. Res. 2016, 68, 515–529. [Google Scholar] [CrossRef]
- ElMandooh Galal, K.; Ghobarah, A. Flexural and shear hysteretic behaviour of reinforced concrete columns with variable axial load. Eng. Struct. 2003, 25, 1353–1367. [Google Scholar] [CrossRef]
- Rodriguez, J.; Ortega, L.M.; Casal, J. Load bearing capacity of concrete columns with corroded reinforcement. In Proceedings of the 4th International Symposium on Corrosion of Reinforcement in Concrete Construction, Cambridge, UK, 1–4 July 1996; pp. 220–230. [Google Scholar]
- Liu, Y.; Hao, H.; Hao, Y. Damage prediction of RC columns with various levels of corrosion deteriorations subjected to blast loading. J. Build. Eng. 2023, 83, 108019. [Google Scholar] [CrossRef]
- EN 1992-1-1; Eurocode 2. Design of Concrete Structures—Part 1–1: General Rules and Rules for Buildings. British Standards Institution: London, UK, 2004.
- Mander, J.B.; Priestley, M.J.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Massicotte, B.; Elwi, A.E.; MacGregor, J.G. Tension-stiffening model for planar reinforced concrete members. J. Struct. Eng. 1990, 116, 3039–3058. [Google Scholar] [CrossRef]
- Mosley, W.H.; Bungey, J.H.; Hulse, R. Reinforced Concrete Design; Macmillan: Basingstoke: UK, 1999. [Google Scholar]






| Mode of Buckling | Axial Load Q (kN) | Eigenvalue () | FE Result (kN) | Theoretical (kN) | Error (%) |
|---|---|---|---|---|---|
| 1 | 0.201 | 7.9 | 1.58 | 1.59 | 0.77 |
| 2 | 0.201 | 31.4 | 6.31 | 6.36 | 0.79 |
| 3 | 0.201 | 70.6 | 14.19 | 14.30 | 0.82 |
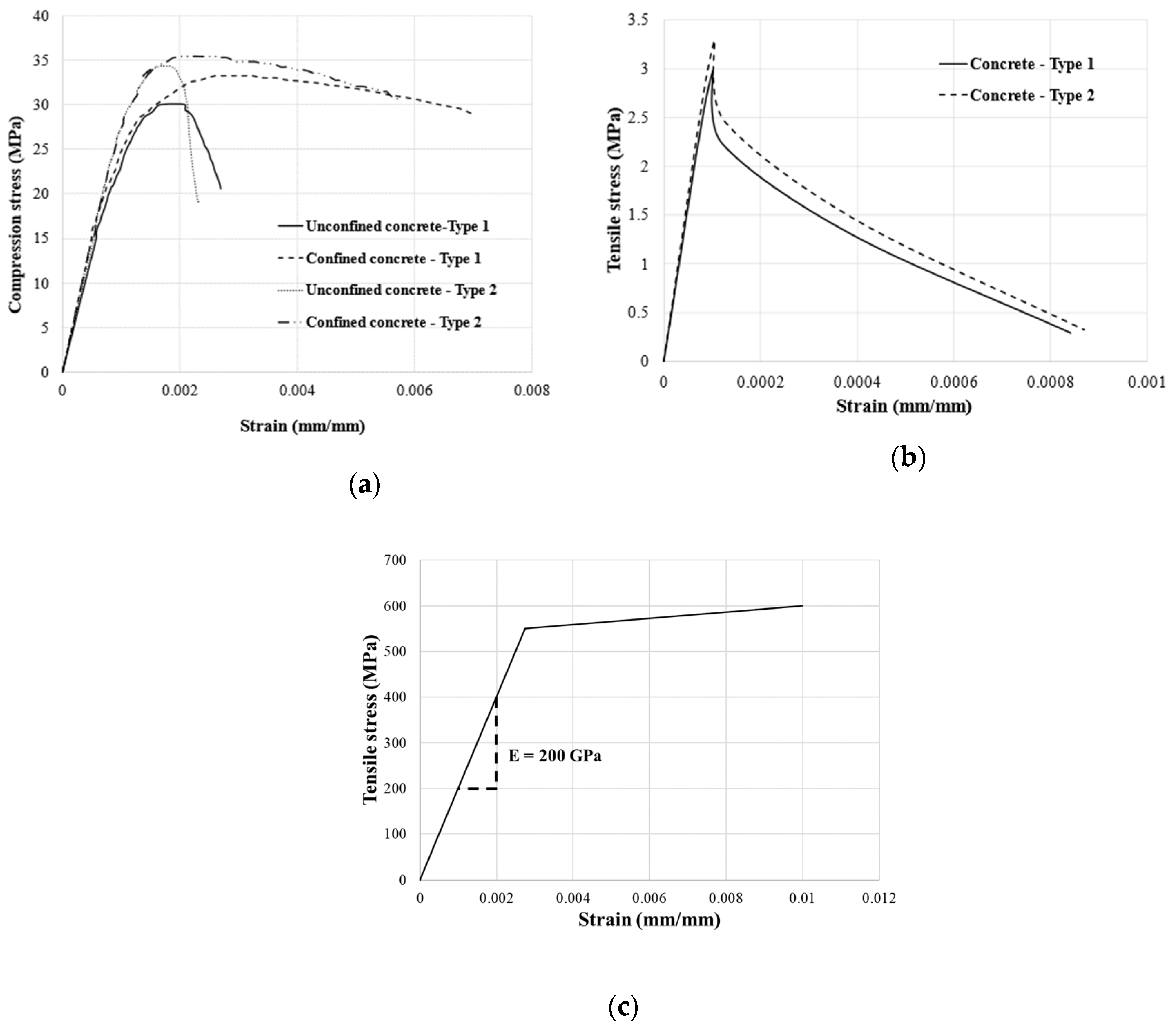
| Material | Parameters (MPa) | Values | |
|---|---|---|---|
| Type 1 | Type 2 | ||
| Unconfined concrete | Compressive strength | 30 | 34 |
| Tensile strength | 2.9 | 3.2 | |
| Young’s modulus | 26,000 | 28,000 | |
| Confined concrete | Compressive strength | 33 | 35.4 |
| Tensile strength | 2.9 | 3.2 | |
| Young’s modulus | 30,000 | 30,000 | |
| Main reinforcement | Yield strength | 550 | 550 |
| Young’s modulus | 200,000 | 200,000 | |
| Stirrups | Yield strength | 550 | 550 |
| Young’s modulus | 200,000 | 200,000 | |
| CDP model parameters | |||
| Concrete | Dilation angle | 36° | 36° |
| Eccentricity | 0.1 | 0.1 | |
| Strength ratio | 1.16 | 1.16 | |
| Shape factor | 0.67 | 0.67 | |
| Viscosity | 0.002 | 0.002 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahamed, A.; Nifla, F.; Thamboo, J.; Asad, M.; Zahra, T. Assessment of RC Columns Under Axial Compression for Un-Corroded and Corroded Stirrups Scenarios: A Practice-Oriented Numerical Approach. Buildings 2025, 15, 579. https://doi.org/10.3390/buildings15040579
Ahamed A, Nifla F, Thamboo J, Asad M, Zahra T. Assessment of RC Columns Under Axial Compression for Un-Corroded and Corroded Stirrups Scenarios: A Practice-Oriented Numerical Approach. Buildings. 2025; 15(4):579. https://doi.org/10.3390/buildings15040579
Chicago/Turabian StyleAhamed, Aabith, Fathima Nifla, Julian Thamboo, Mohammad Asad, and Tatheer Zahra. 2025. "Assessment of RC Columns Under Axial Compression for Un-Corroded and Corroded Stirrups Scenarios: A Practice-Oriented Numerical Approach" Buildings 15, no. 4: 579. https://doi.org/10.3390/buildings15040579
APA StyleAhamed, A., Nifla, F., Thamboo, J., Asad, M., & Zahra, T. (2025). Assessment of RC Columns Under Axial Compression for Un-Corroded and Corroded Stirrups Scenarios: A Practice-Oriented Numerical Approach. Buildings, 15(4), 579. https://doi.org/10.3390/buildings15040579









