Assessing Wall Tie Deterioration in Masonry Veneer Wall Through Vibration-Based Damage Identification Methods †
Abstract
:1. Introduction
2. Vibration-Based Damage Identification
2.1. Natural Frequency-Based Method
2.2. Coordinate Modal Assurance Criteria (COMAC)
2.3. Parameter-Based Method (PM)
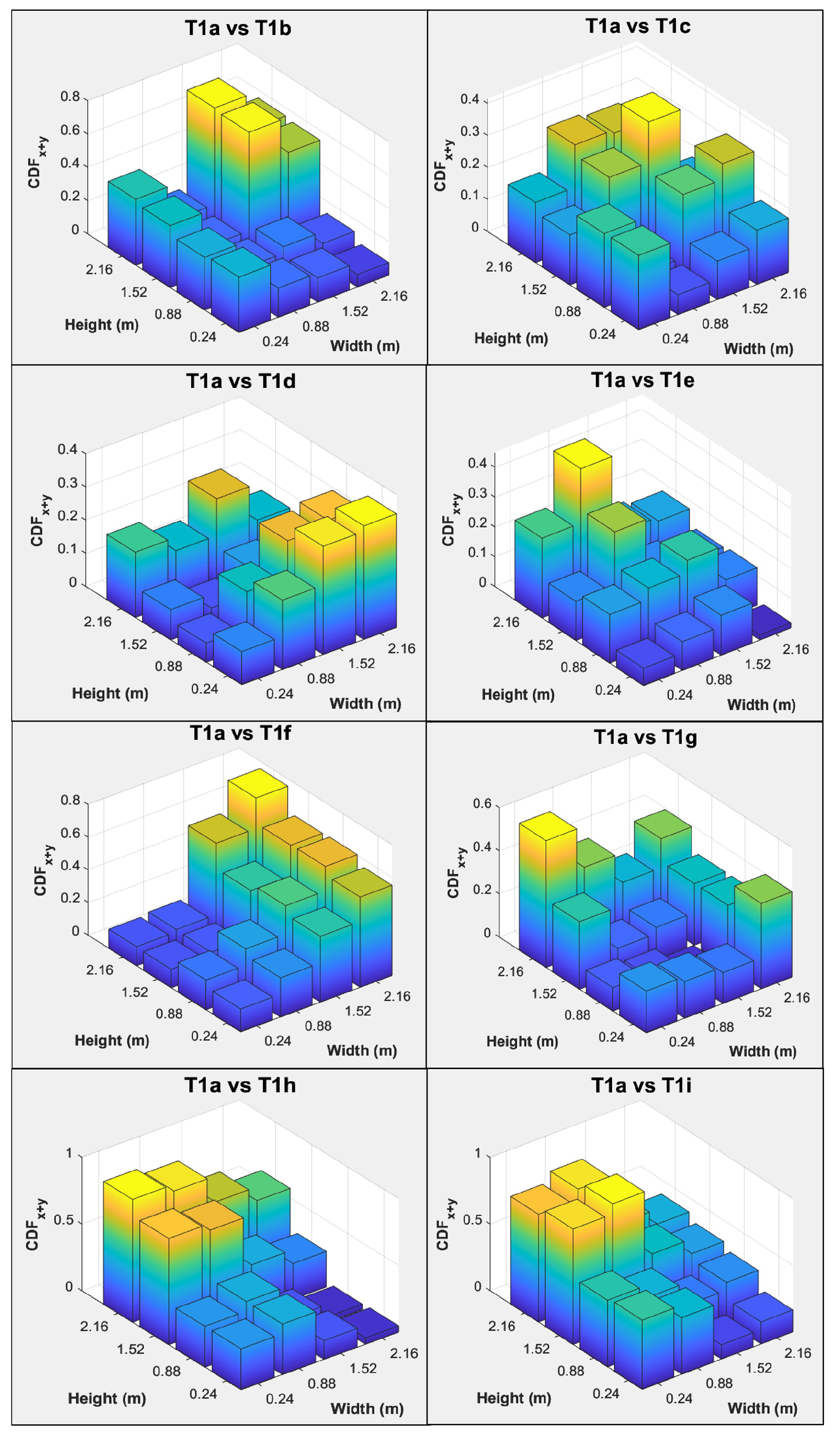
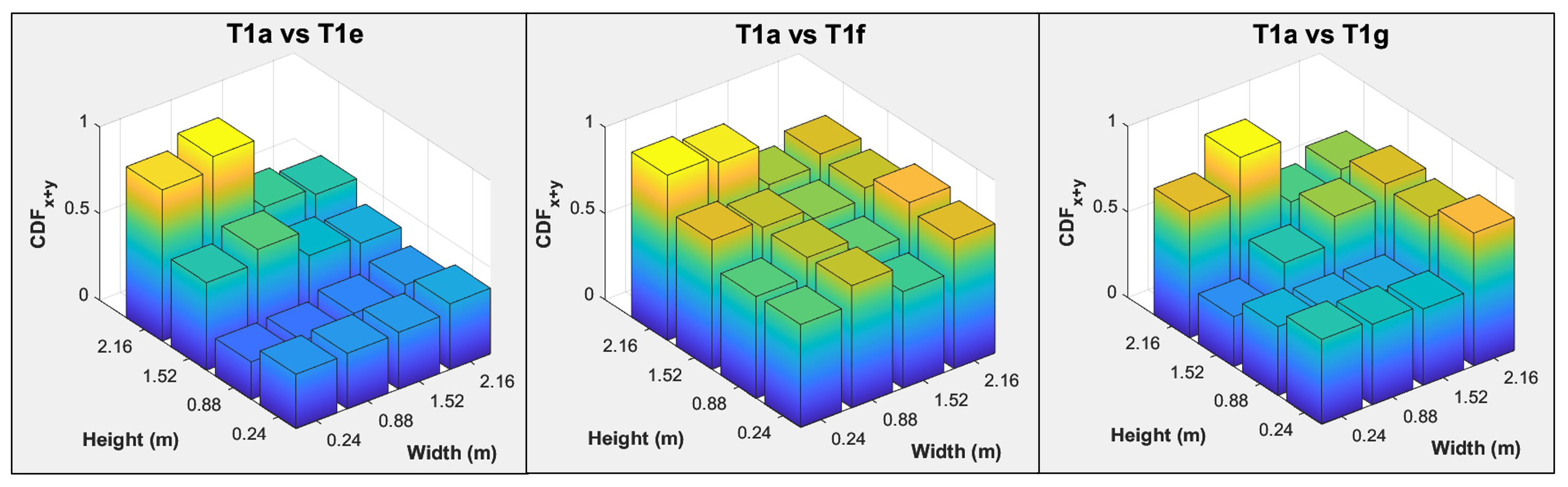
2.4. Curvature Damage Factor (CDF)
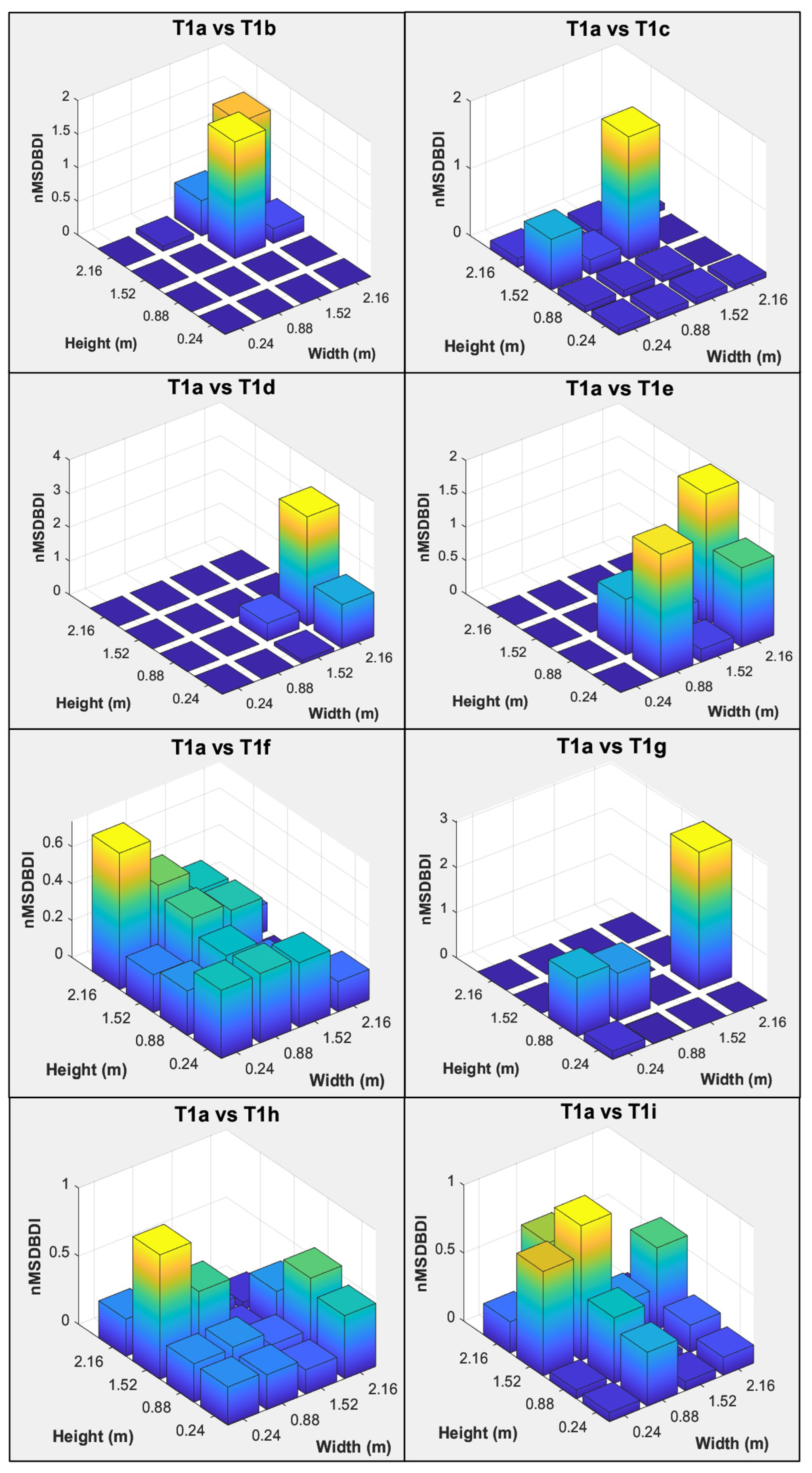
2.5. Mode-Shape-Derivative-Based Damage Identification Method (MSDBDI)
3. Experimental Testing Program
3.1. Masonry Veneer Wall Description
3.2. Preliminary Finite Element Modelling of Masonry Veneer Wall
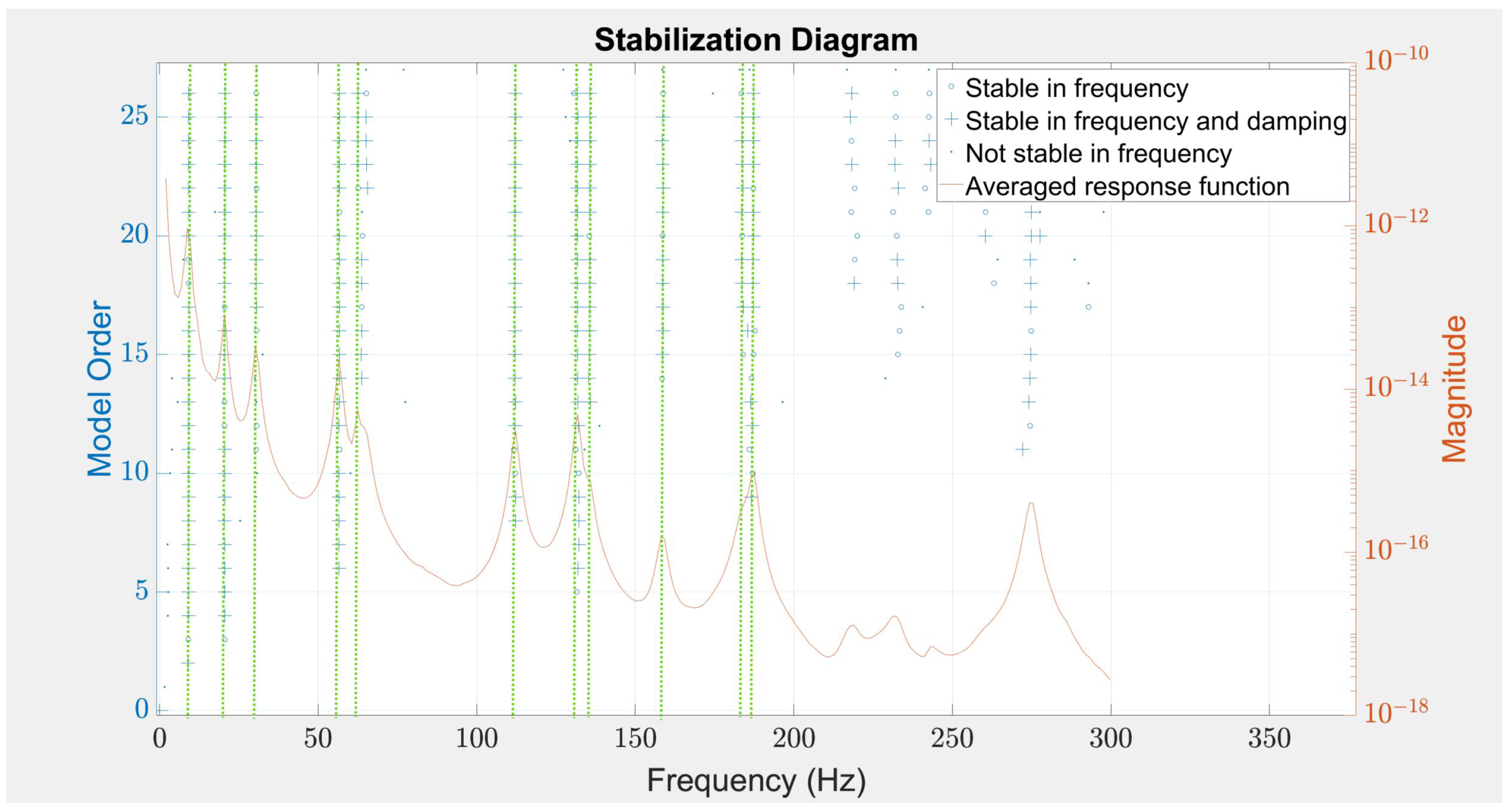
3.3. Impact Hammer Testing
4. Results and Discussion
4.1. Damage Detection
4.2. Damage Localisation
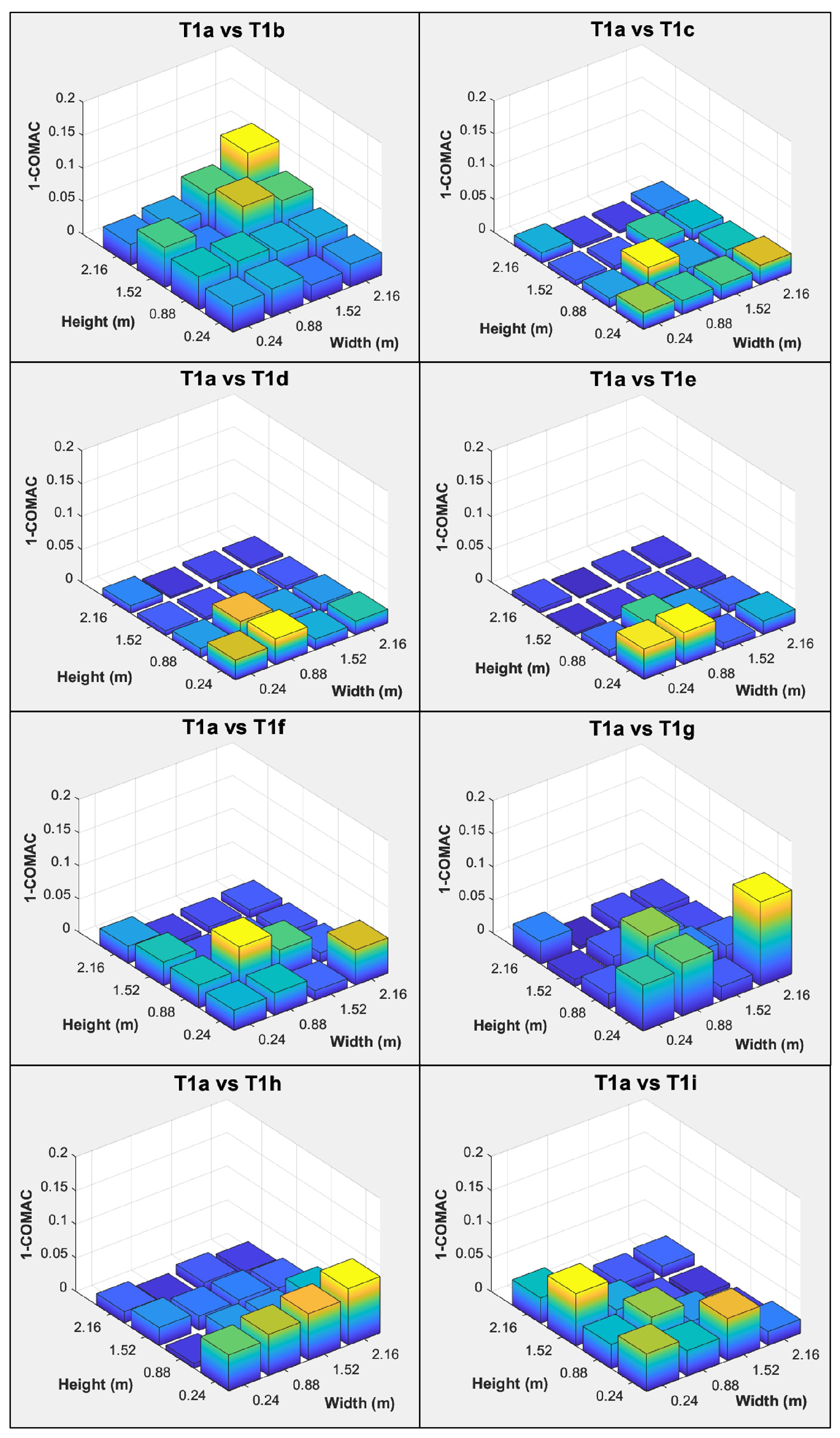
4.2.1. COMAC
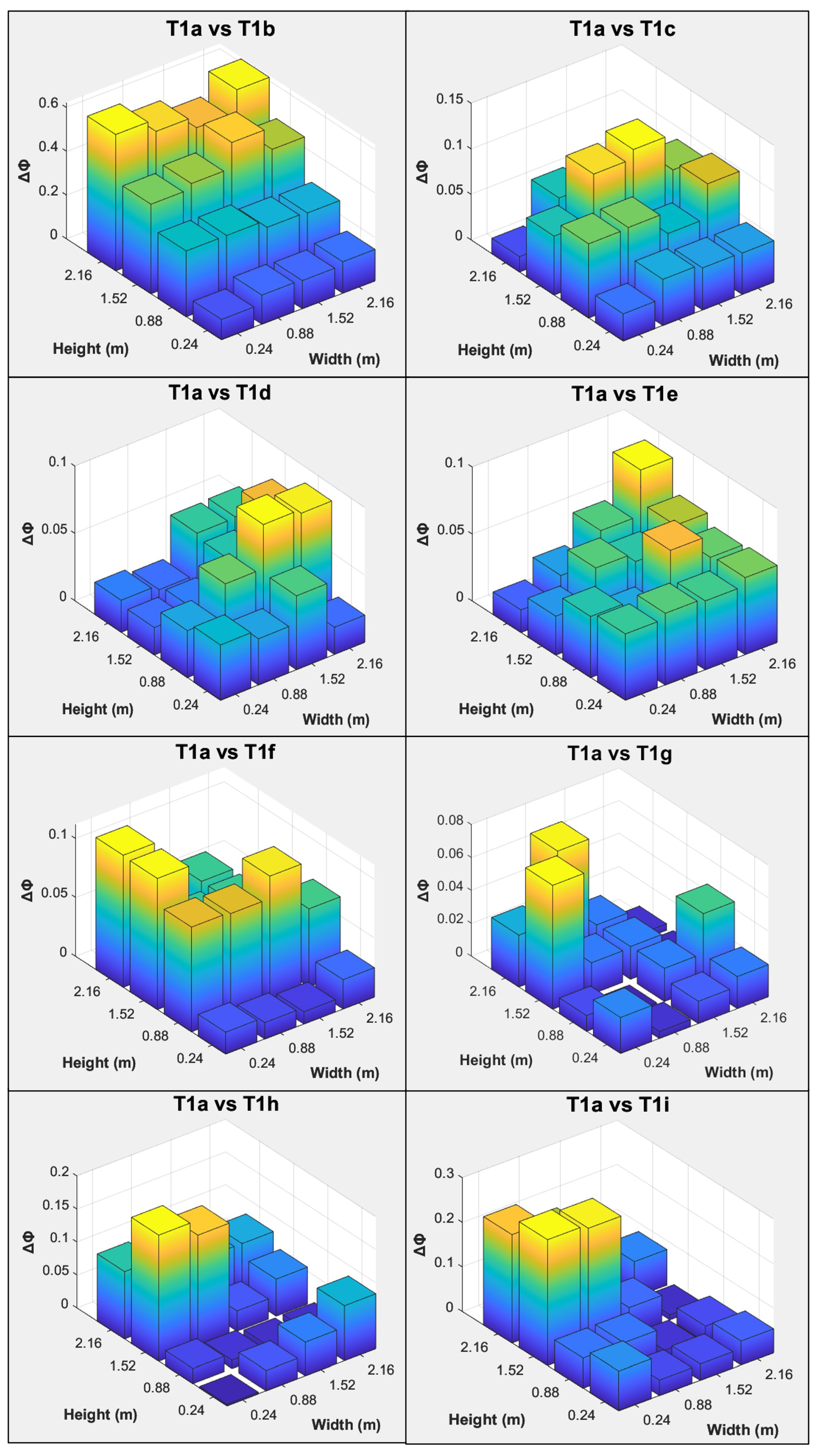
4.2.2. PM
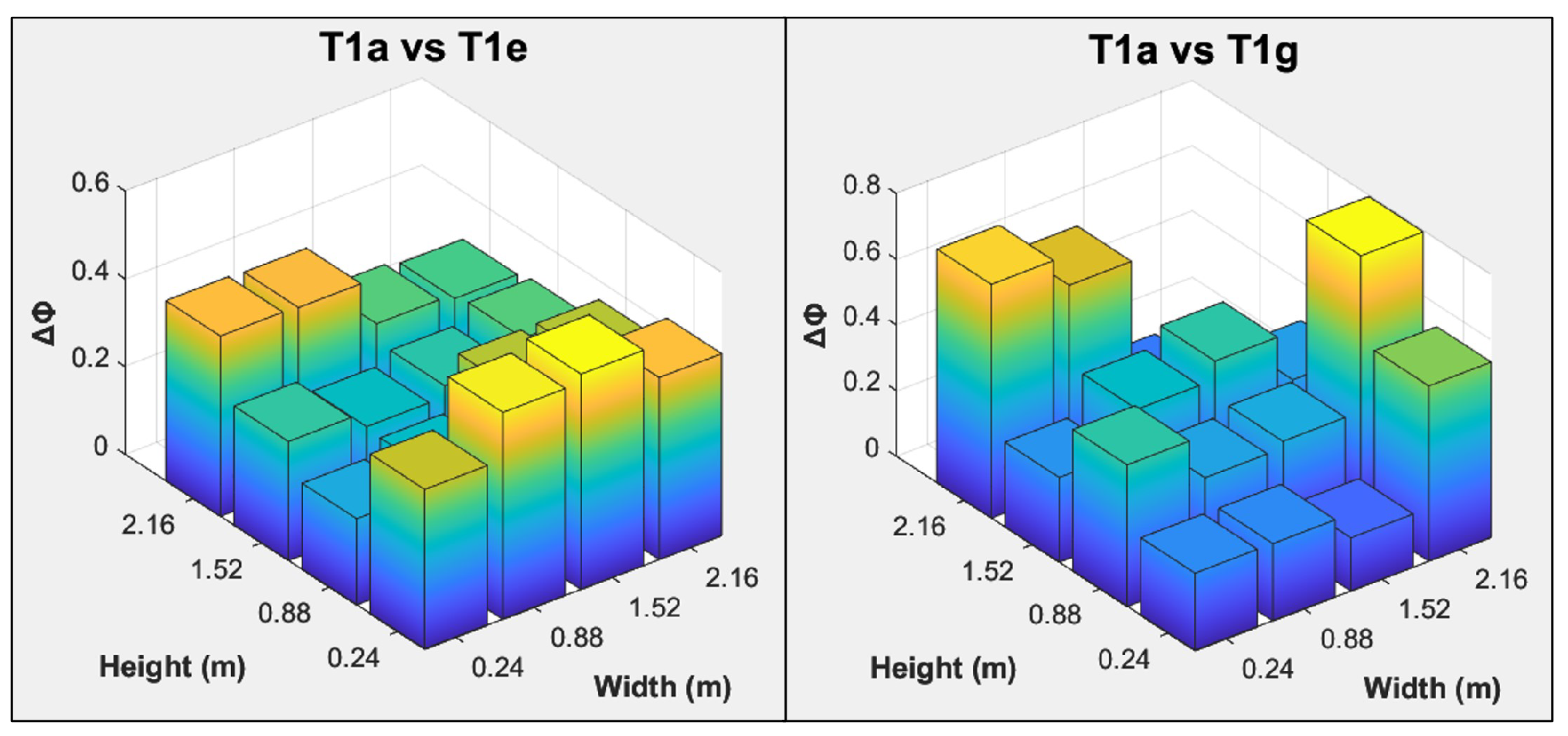
4.2.3. CDF
4.2.4. MSDBDI
4.2.5. Comparisons of All Damage Localisation Methods
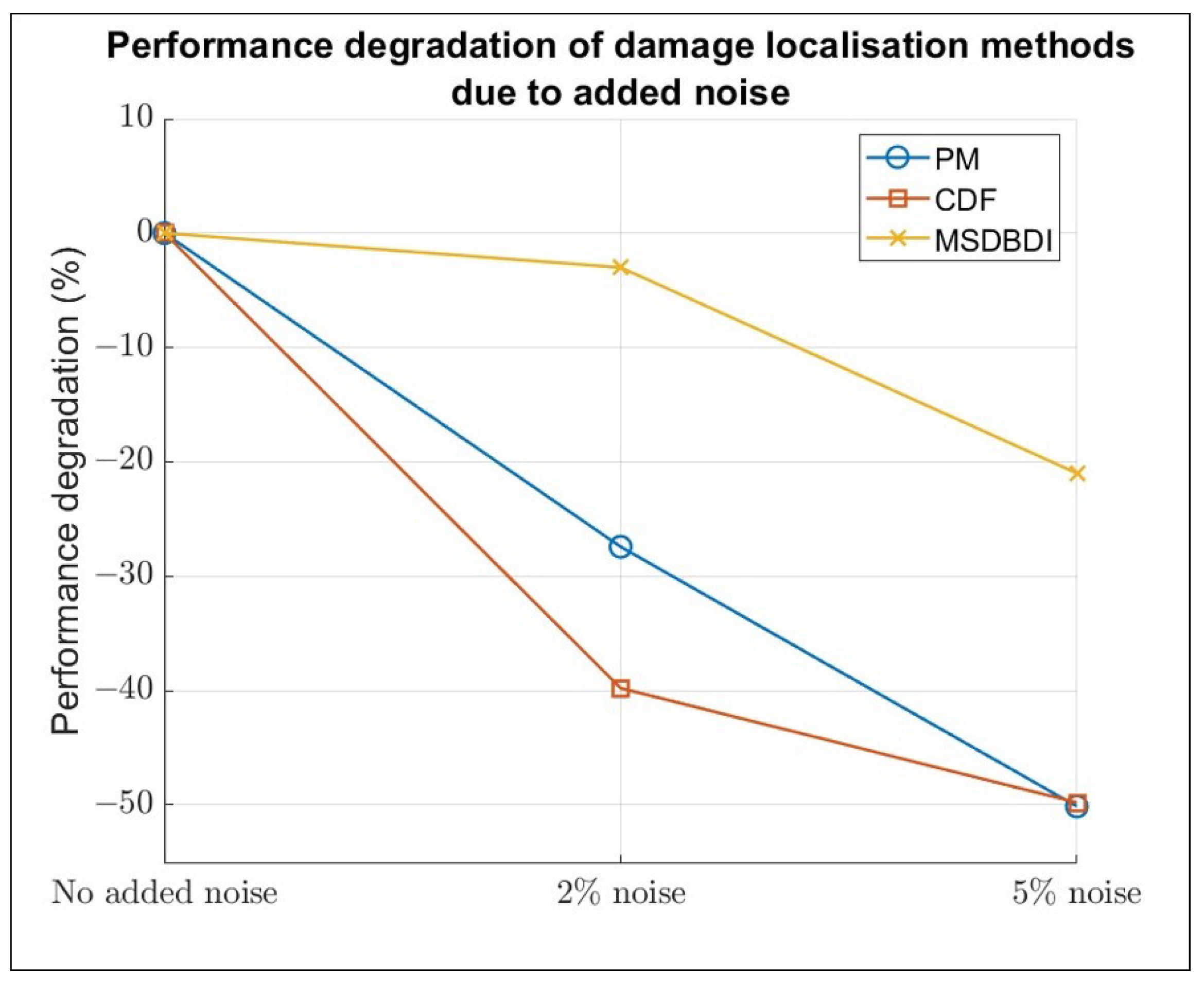
4.2.6. Noise Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chaves, I.; Masia, M.; Terry, L.; Lam, C.Y.; Hossain, M.A.; Smith, B.; de Prazer, S.; Vazey, J.; Melchers, R.; Chen, W. Estimating stability and resilience of ageing masonry walls for enhanced infrastructure management and public safety. Aust. J. Struct. Eng. 2025, 26, 20–29. [Google Scholar] [CrossRef]
- Page, A.; Kleeman, P.; Stewart, M.; Melchers, R. Structural aspects of the Newcastle earthquake. In Proceedings of the Second National Structural Engineering Conference 1990: Preprints of Papers, Barton, ACT, Australia, 3–5 October 1990; pp. 305–312. [Google Scholar]
- Chaves, I.A.; de Prazer, S.; Jardim do Nascimento, B.; Flowers, G. Empirical Coastal Atmospheric Corrosion of Masonry Metal Wall Ties. Corros. Mater. Degrad. 2021, 2, 657–665. [Google Scholar] [CrossRef]
- Page, A.W. The Newcastle earthquake and the masonry structures code AS3700. In Proceedings of the 2019 AEES Conference. Australian Earthquake Engineering Society, Newcastle, NSW, Australia, 29 November–1 December 2019. [Google Scholar]
- Maurenbrecher, A.; Brousseau, R. Review of Corrosion Resistance of Metal Components in Masonry Cladding on Buildings; National Research Council Canada, Institute for Research in Construction: Ottawa, ON, Canada, 1993. [Google Scholar]
- Ramos, L.F.; De Roeck, G.; Lourenço, P.B.; Campos-Costa, A. Damage identification on arched masonry structures using ambient and random impact vibrations. Eng. Struct. 2010, 32, 146–162. [Google Scholar] [CrossRef]
- Oyarzo-Vera, C.; Chouw, N. Damage Identification of Unreinforced Masonry Panels Using Vibration-Based Techniques. Shock Vib. 2017, 2017, 1–14. [Google Scholar] [CrossRef]
- Bernat-Masó, E.; Gil, L. Assessing the performance of CFRP strengthening on masonry walls using experimental modal analysis. Eng. Struct. 2019, 193, 184–193. [Google Scholar] [CrossRef]
- Cakir, F.; Uysal, H. Experimental modal analysis of brick masonry arches strengthened prepreg composites. J. Cult. Herit. 2015, 16, 284–292. [Google Scholar] [CrossRef]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B.; Shevitz, D.W. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review; Technical Report; Los Alamos National Lab: Los Alamos, NM, USA, 1996. [Google Scholar]
- Fan, W.; Qiao, P. Vibration-based Damage Identification Methods: A Review and Comparative Study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Ramos, L.F. Damage Identification on Masonry Structures Based on Vibration Signatures. Ph.D. Thesis, University of Minho, Guimarães, Portugal, 2007. [Google Scholar]
- Ewins, D.J. Modal Testing: Theory, Practice and Application; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Dong, C.; Zhang, P.; Feng, W.; Huang, T. The sensitivity study of the modal parameters of a cracked beam. In Proceedings of the 12th International Modal Analysis Conference, Honolulu, HI, USA, 31 January–3 February 1994; Volume 2251, p. 98. [Google Scholar]
- Abdel Wahab, M.M.; De Roeck, G. Damage detection in bridges using modal curvatures: Application to a real damage scenario. J. Sound Vib. 1999, 226, 217–235. [Google Scholar] [CrossRef]
- Navabian, N.; Bozorgnasab, M.; Taghipour, R.; Yazdanpanah, O. Damage identification in plate-like structure using mode shape derivatives. Arch. Appl. Mech. 2016, 86, 819–830. [Google Scholar] [CrossRef]
- Pepi, C.; Cavalagli, N.; Gusella, V.; Gioffrè, M. Damage detection via modal analysis of masonry structures using shaking table tests. Earthq. Eng. Struct. Dyn. 2021, 50, 2077–2097. [Google Scholar] [CrossRef]
- Avitabile, P. Modal Testing: A Practitioner’s Guide, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Ho, Y.; Ewins, D. On the structural damage identification with mode shapes. In Proceedings of the European COST F3 Conference on System Identification and Structural Health Monitoring, Madrid, Spain, 6–9 June 2000; Volume 1. [Google Scholar]
- Pandey, A.; Biswas, M.; Samman, M. Damage detection from changes in curvature mode shapes. J. Sound Vib. 1991, 145, 321–332. [Google Scholar] [CrossRef]
- Salawu, O.; Williams, C. Damage location using vibration mode shapes. In Proceedings of the 12th International Modal Analysis Conference, Honolulu, HI, USA, 31 January–3 February 1994; Volume 2251, p. 933. [Google Scholar]
- Logan, D.L. A First Course in the Finite Element Method; Thomson: Toronto, ON, Canada, 2011; Volume 4. [Google Scholar]
- Li, J.; Stewart, M.; Masia, M. Probabilistic modeling of unreinforced masonry walls subjected to lateral out-of-plane loading. In Numerical Modeling of Masonry and Historical Structures; Elsevier: Amsterdam, The Netherlands, 2019; pp. 91–140. [Google Scholar]
- AS3700:2018; Masonry Structures. Standards Australia: Sydney, Australia, 2018.
- AS2699.1:2020; Built-In Components for Masonry Construction, Part 1: Wall Ties. Standards Australia: Sydney, Australia, 2020.
- Sugo, H.; Page, A.; Lawrence, S. Characterization and bond strengths of mortars with clay masonry units. In Proceedings of the 11th International Brick/Block Masonry Conference (IB2MAC), Shanghai, China, 14–16 October 1997; pp. 14–16. [Google Scholar]
- DIANA FEA BV. DIANA Finite Element Analysis, Release Note 10.8; DIANA FEA BV: The Hague, The Netherlands, 2024. [Google Scholar]
- Heffler, L.M.; Stewart, M.G.; Masia, M.J.; Corrêa, M.R.S. Statistical analysis and spatial correlation of flexural bond strength for masonry walls. Mason. Int. 2008, 21, 59–70. [Google Scholar]
- Muhit, I.B.; Stewart, M.G.; Masia, M.J. Probabilistic constitutive law for masonry veneer wall ties. Aust. J. Struct. Eng. 2022, 23, 97–118. [Google Scholar] [CrossRef]
- Muhit, I.B. Stochastic Assessment of Unreinforced Masonry Veneer Wall Systems Subjected to Lateral Out-of-Plane Loading. Ph.D. Thesis, The University of Newcastle, Newcastle, Australia, 2021. [Google Scholar]
- Lourenço, P.B. Structural masonry analysis: Recent developments and prospects. In Proceedings of the 14th International Brick and Block Masonry Conference (14IBMAC), Sydney, Australia, 17–20 February 2008; pp. 17–20. [Google Scholar]
- Heffler, L. Variability of Unit Flexural Bond Strength and Its Effect on Strength in Clay Brick Unreinforced Masonry Walls Subject to Vertical Bending. Master’s Thesis, The University of Newcastle, Newcastle, Australia, 2009. [Google Scholar]
- Petersen, R.B. In-Plane Shear Behaviour of Unreinforced Masonry Panels Strengthened with Fibre Reinforced Polymer Strips. Ph.D. Thesis, The University of Newcastle, Newcastle, Australia, 2009. [Google Scholar]
- Lourenço, P.B.; Rots, J.G. Multisurface Interface Model for Analysis of Masonry Structures. J. Eng. Mech. 1997, 123, 660–668. [Google Scholar] [CrossRef]
- Chaves, I.A.; Melchers, R.E.; Barbara Jardim do, N.; Philips, J.; Masia, M. Effects of inter-cavity corrosion on metallic wall ties in masonry structures. AIMS Mater. Sci. 2022, 9, 311–324. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. Signal processing techniques for vibration-based health monitoring of smart structures. Arch. Comput. Methods Eng. 2016, 23, 1–15. [Google Scholar] [CrossRef]
- Ozdemir, A.A.; Gumussoy, S. Transfer function estimation in system identification toolbox via vector fitting. IFAC-PapersOnLine 2017, 50, 6232–6237. [Google Scholar] [CrossRef]
- Akers, J.C.; Winkel, J.P.; Chin, A.W.; Parks, R.A.; Chandler, D.E.; Stasiunas, E.C.; Allen, M.S. Operational Modal Analysis of the Artemis I Dynamic Rollout Test and Wet Dress Rehearsal. In Proceedings of the IMAC, A Conference and Exposition on Structural Dynamics, Orlando, FL, USA, 29 January–1 February 2024; pp. 91–112. [Google Scholar]
- Lam, C.Y.; Hossain, M.A.; Masia, M.; Chaves, I.; Vazey, J. Detecting corroded wall ties through non-destructive means. In Proceedings of the Corrosion and Prevention 2024, Cairns, Australia, 10–14 November 2024. [Google Scholar]
- Ručevskis, S.; Chate, A. Damage identification in a plate-like structure using modal data. Aviation 2013, 17, 45–51. [Google Scholar] [CrossRef]
- Ho, L.V.; Trinh, T.T.; De Roeck, G.; Bui-Tien, T.; Nguyen-Ngoc, L.; Wahab, M.A. An efficient stochastic-based coupled model for damage identification in plate structures. Eng. Fail. Anal. 2022, 131, 105866. [Google Scholar] [CrossRef]
- Cornwell, P.; Doebling, S.W.; Farrar, C.R. Application of the strain energy damage detection method to plate-like structures. J. Sound Vib. 1999, 224, 359–374. [Google Scholar] [CrossRef]
- Yoon, M.; Heider, D.; Gillespie, J., Jr.; Ratcliffe, C.; Crane, R. Local damage detection using the two-dimensional gapped smoothing method. J. Sound Vib. 2005, 279, 119–139. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. A 2-D continuous wavelet transform of mode shape data for damage detection of plate structures. Int. J. Solids Struct. 2009, 46, 4379–4395. [Google Scholar] [CrossRef]
- Xia, Y.; Hao, H.; Zanardo, G.; Deeks, A. Long term vibration monitoring of an RC slab: Temperature and humidity effect. Eng. Struct. 2006, 28, 441–452. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, K.; Ye, Z.; Liu, C.; Lu, K.; Wang, L. Influence of temperature on the natural vibration characteristics of simply supported reinforced concrete beam. Sensors 2021, 21, 4242. [Google Scholar] [CrossRef]
- Yan, W.; Ren, W. A direct algebraic method to calculate the sensitivity of element modal strain energy. Int. J. Numer. Methods Biomed. Eng. 2011, 27, 694–710. [Google Scholar] [CrossRef]
- Pajan, J.; Duvnjak, I.; Bartolac, M.; Ereiz, S. Mode shape area difference method for sparse damage detection in beam-like structures. Struct. Concr. 2024. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, J.; Wei, Z.; Lu, Z. A two-step approach for damage identification in plates. J. Vib. Control. 2016, 22, 3018–3031. [Google Scholar] [CrossRef]
- Fleming, A.J.; Moheimani, S.R. Spatial system identification of a simply supported beam and a trapezoidal cantilever plate. IEEE Trans. Control. Syst. Technol. 2003, 11, 726–736. [Google Scholar] [CrossRef]
- Jiang, X.; Ma, Z.J.; Ren, W. Crack detection from the slope of the mode shape using complex continuous wavelet transform. Comput. Civ. Infrastruct. Eng. 2012, 27, 187–201. [Google Scholar] [CrossRef]
- Pakrashi, V.; O’Connor, A.; Basu, B. A study on the effects of damage models and wavelet bases for damage identification and calibration in beams. Comput. Civ. Infrastruct. Eng. 2007, 22, 555–569. [Google Scholar] [CrossRef]
- Xiang, J.; Liang, M. Wavelet-based detection of beam cracks using modal shape and frequency measurements. Comput. Civ. Infrastruct. Eng. 2012, 27, 439–454. [Google Scholar] [CrossRef]
- Rainieri, C.; Fabbrocino, G.; Brigante, D. Differentiating Local and Global Vibration Modes of Heritage Masonry Buildings through the Spatial Correlation of Modal Displacements. Int. J. Archit. Herit. 2022, 16, 597–615. [Google Scholar] [CrossRef]
- Weng, S.; Zhu, H.; Xia, Y.; Li, J.; Tian, W. A review on dynamic substructuring methods for model updating and damage detection of large-scale structures. Adv. Struct. Eng. 2020, 23, 584–600. [Google Scholar] [CrossRef]
- Xiao, F.; Sun, H.; Mao, Y.; Chen, G.S. Damage identification of large-scale space truss structures based on stiffness separation method. Structures 2023, 53, 109–118. [Google Scholar] [CrossRef]

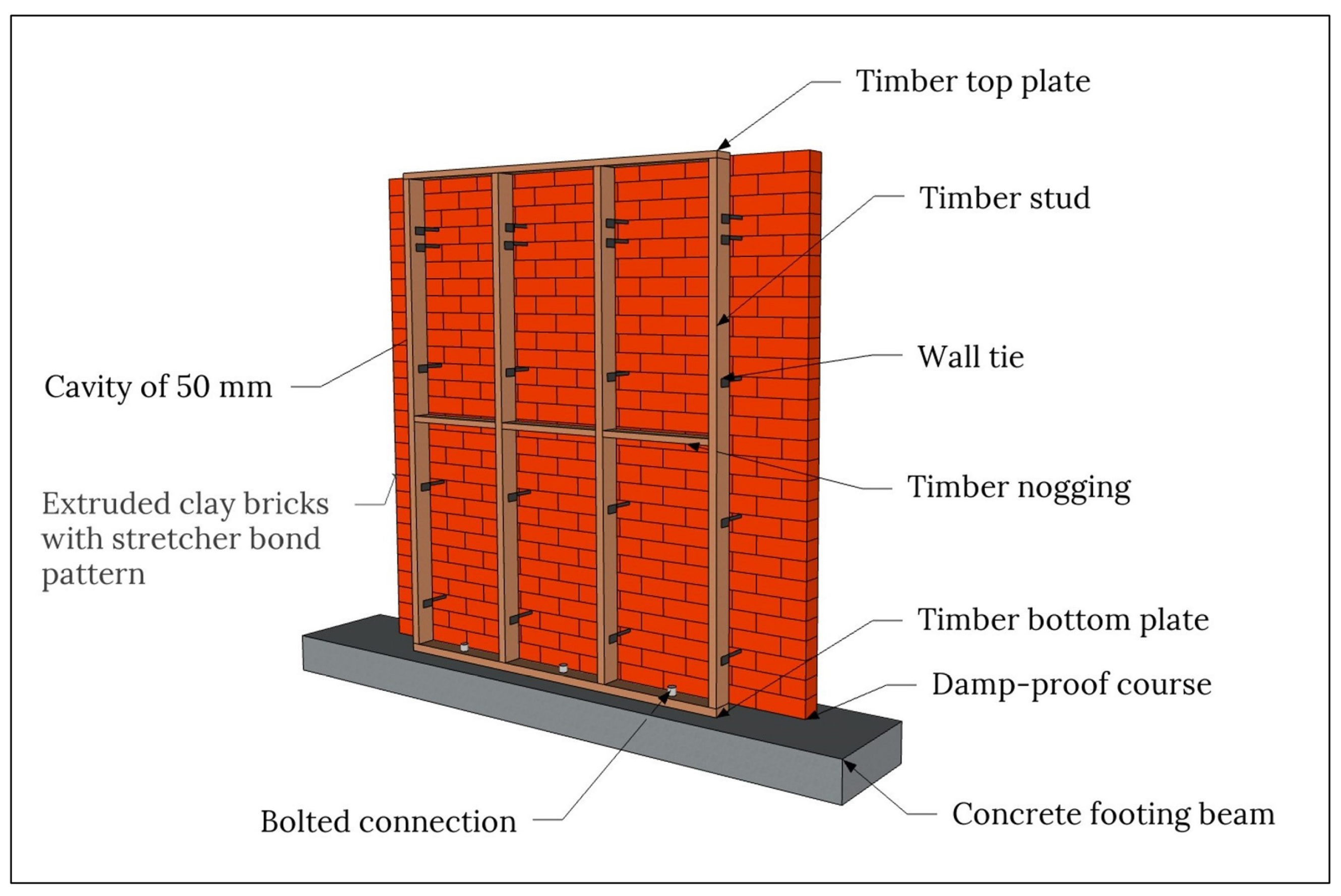

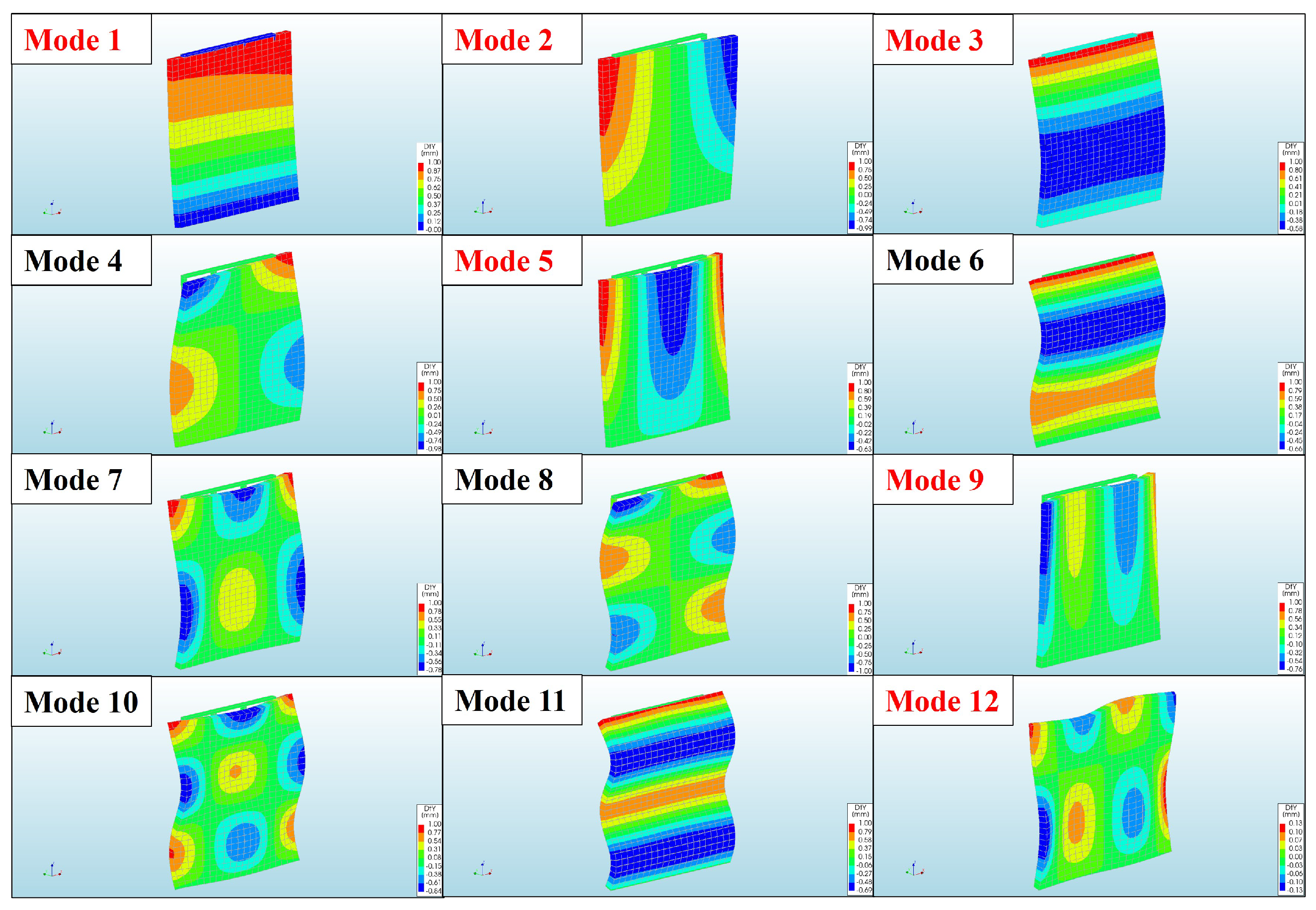
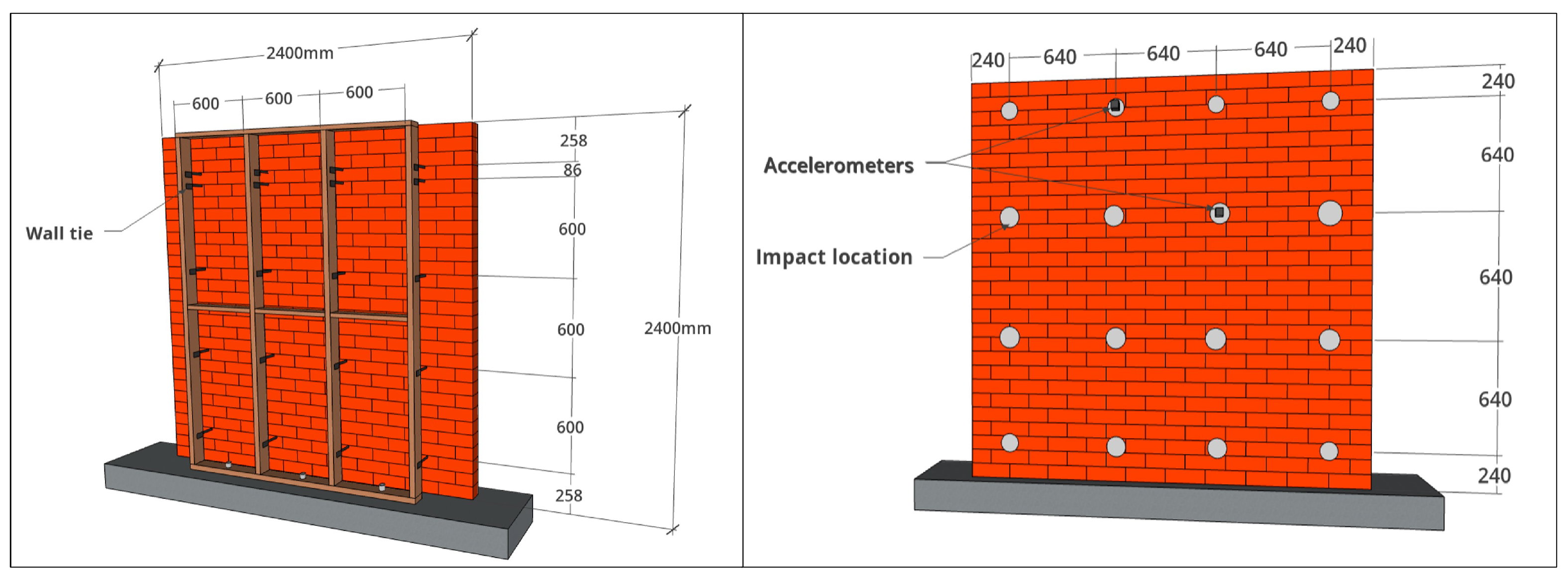


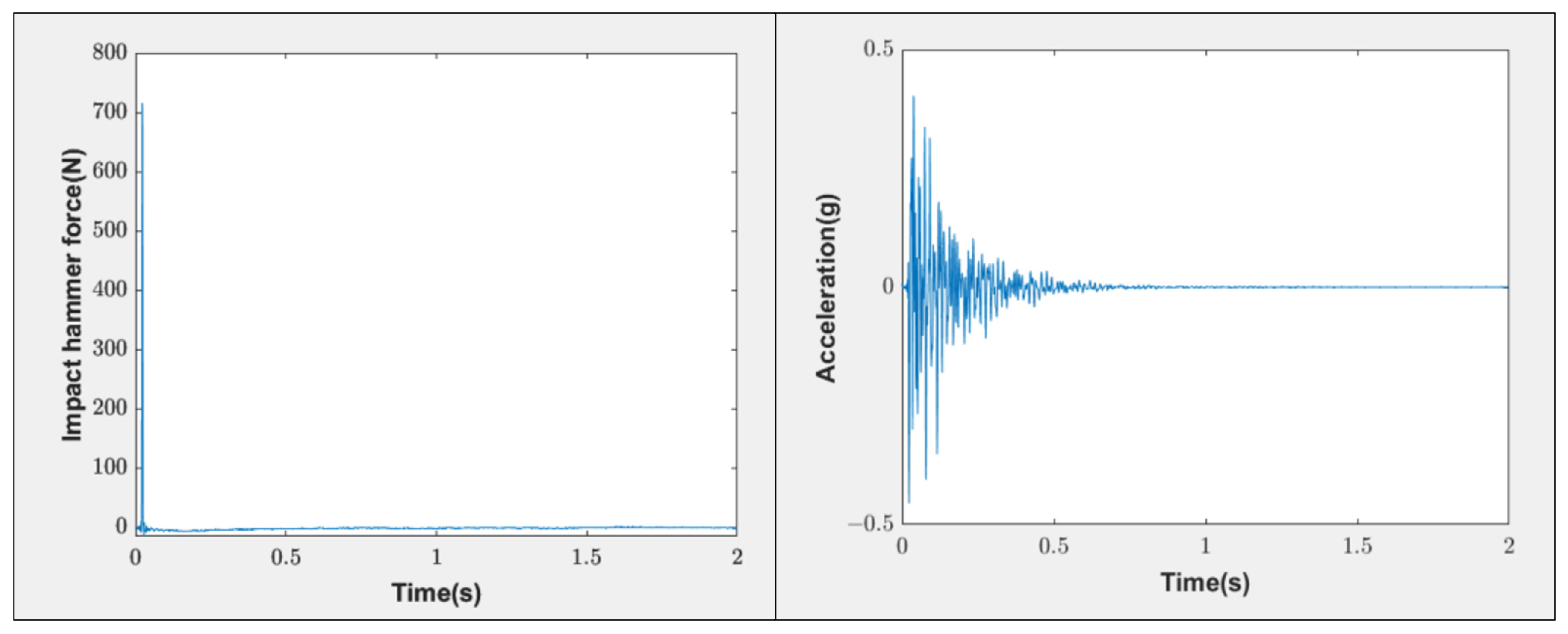
| Parameter | Value | Unit | Source |
|---|---|---|---|
| Brick unit | |||
| Elastic modulus | 31,338 | N/mm2 | MC |
| Poisson’s ratio | 0.15 | - | Assumed |
| Density | 1.8 × | T/mm3 | Assumed |
| Brick crack | |||
| Linear normal stiffness | 1000 | N/mm3 | Assumed |
| Linear shear stiffness | 1000 | N/mm3 | Assumed |
| Direct tensile strength | 1.332 | N/mm2 | RT |
| Fracture energy | 0.037 | Nmm/mm2 | [31] |
| Mortar joint | |||
| Linear normal stiffness | 231 | N/mm3 | MC |
| Linear shear stiffness | 96 | N/mm3 | MC |
| Flexural tensile strength | 0.26 | N/mm2 | BW |
| Tensile fracture energy | 0.0048 | Nmm/mm2 | [32] |
| Cohesion (shearing) | 0.40 | N/mm2 | ST |
| Friction angle (shearing) | 0.86 | Radian | ST |
| Dilatancy angle (shearing) | 0.55 | Radian | [33] |
| Residual friction angle (shearing) | 0.86 | Radian | Assumed |
| Confining normal stress (shearing) | −1.0 | N/mm2 | [33] |
| Exponential degradation coefficient (shearing) | 1.9 | - | [33] |
| Masonry compressive strength (crushing) | 12.37 | N/mm2 | MC |
| Compressive fracture energy | 23.56 | Nmm/mm2 | [31] |
| Shear traction control factor () | 9.0 | - | [34] |
| Equivalent plastic relative displacement | 0.014 | mm | MC |
| Mode-II fracture energy factor, a | −0.8 | mm | [33] |
| Mode-II fracture energy factor, b | 0.05 | N/mm | [33] |
| Test Case | Description of Simulated Wall Tie Deterioration | Disconnected Wall Tie Locations |
|---|---|---|
| T1a | Reference state, all wall ties are fully intact. | - |
| T1b | Top two rows of wall ties are disconnected. | Near Points 1 to 4 |
| T1c | The third row (from the top) of wall ties is disconnected. | Near Points 5 to 8 |
| T1d | The fourth row (from the top) of wall ties is disconnected. | Near Points 9 to 12 |
| T1e | Bottom row of wall ties is disconnected. | Near Points 13 to 16 |
| T1f | Wall ties at the top left corner of the wall are disconnected. | Near Point 1 |
| T1g | Wall tie at the bottom left corner of the wall is disconnected. | Near Point 13 |
| T1h | Wall ties at the outer most left column are disconnected. | Near Points 1, 5, 9 and 13 |
| T1i | Two columns of wall ties are disconnected. | Near Points 1, 2, 5, 6, 9, 10, 13 and 14 |
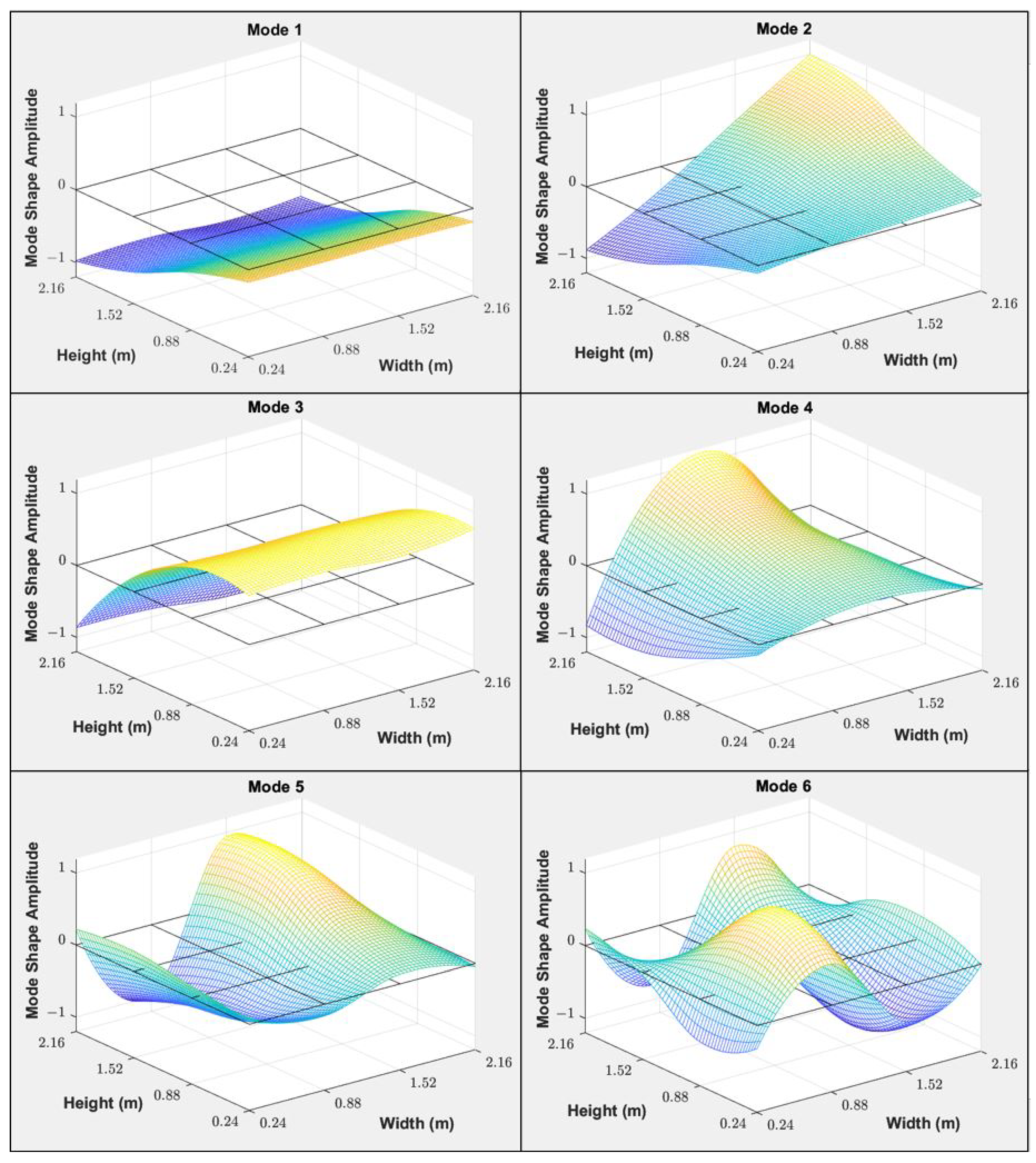
| Natural Frequencies (Hz) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Modes | T1a | T1b | T1c | T1d | T1e | T1f | T1g | T1h | T1i |
| 1 | 9.12 | 5.64 | 8.64 | 8.69 | 8.68 | 8.32 | 8.95 | 8.19 | 7.37 |
| 2 | 20.52 | 17.94 | 19.79 | 19.93 | 19.95 | 19.06 | 20.02 | 18.76 | 18.41 |
| 3 | 30.54 | 28.17 | 29.33 | 29.52 | 29.54 | 29.72 | 30.40 | 29.46 | 29.01 |
| 4 | 56.66 | 55.58 | 55.72 | 56.12 | 56.09 | 55.73 | 55.87 | 55.65 | 55.10 |
| 5 | 131.86 | 131.36 | 128.51 | 130.72 | 131.03 | 130.01 | 130.02 | 129.25 | 129.57 |
| 6 | 187.06 | 186.75 | 185.63 | 187.31 | 186.22 | 184.76 | 185.16 | 183.17 | 183.48 |
| Relative Difference in Natural Frequencies (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Modes | T1a | T1b | T1c | T1d | T1e | T1f | T1g | T1h | T1i |
| 1 | - | −38.12 | −5.27 | −4.70 | −4.81 | −8.81 | −1.84 | −10.18 | −19.14 |
| 2 | - | −12.55 | −3.54 | −2.86 | −2.77 | −7.09 | −2.43 | −8.59 | −10.29 |
| 3 | - | −7.75 | −3.98 | −3.34 | −3.29 | −2.67 | −0.45 | −3.55 | −5.00 |
| 4 | - | −1.91 | −1.65 | −0.95 | −1.00 | −1.65 | −1.39 | −1.78 | −2.76 |
| 5 | - | −0.37 | −2.54 | −0.86 | −0.62 | −1.40 | −1.39 | −1.97 | −1.73 |
| 6 | - | −0.17 | −0.77 | 0.13 | −0.45 | −1.23 | −1.02 | −2.08 | −1.91 |
| Modal assurance criteria (MAC) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Modes | T1a | T1b | T1c | T1d | T1e | T1f | T1g | T1h | T1i |
| 1 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.97 | 0.96 |
| 2 | 0.97 | 0.98 | 0.97 | 0.97 | 0.96 | 0.99 | 0.96 | 0.99 | 0.96 |
| 3 | 0.90 | 0.84 | 0.87 | 0.88 | 0.88 | 0.91 | 0.92 | 0.84 | 0.85 |
| 4 | 0.98 | 0.97 | 0.97 | 0.97 | 0.97 | 0.98 | 0.99 | 0.94 | 0.97 |
| 5 | 0.97 | 0.98 | 0.98 | 0.96 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 |
| 6 | 0.95 | 0.97 | 0.98 | 0.99 | 0.97 | 0.96 | 0.95 | 0.91 | 0.95 |
| Category | Category Description | Number of Identified Test Cases (Out of 8) | ||
|---|---|---|---|---|
| PM | CDF | MSDBDI | ||
| Correct | Highest damage index at the correct damage location | 7 | 5 | 5 |
| Vicinity | Highest damage index at one column or row away from the exact damage location | 0 | 1 | 2 |
| False | Highest damage index far away from the damage location | 1 | 2 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lam, C.Y.; Masia, M.; Chaves, I.; Hossain, M.A.; Vazey, J. Assessing Wall Tie Deterioration in Masonry Veneer Wall Through Vibration-Based Damage Identification Methods. Buildings 2025, 15, 1226. https://doi.org/10.3390/buildings15081226
Lam CY, Masia M, Chaves I, Hossain MA, Vazey J. Assessing Wall Tie Deterioration in Masonry Veneer Wall Through Vibration-Based Damage Identification Methods. Buildings. 2025; 15(8):1226. https://doi.org/10.3390/buildings15081226
Chicago/Turabian StyleLam, Chee Yin, Mark Masia, Igor Chaves, Md Akhtar Hossain, and John Vazey. 2025. "Assessing Wall Tie Deterioration in Masonry Veneer Wall Through Vibration-Based Damage Identification Methods" Buildings 15, no. 8: 1226. https://doi.org/10.3390/buildings15081226
APA StyleLam, C. Y., Masia, M., Chaves, I., Hossain, M. A., & Vazey, J. (2025). Assessing Wall Tie Deterioration in Masonry Veneer Wall Through Vibration-Based Damage Identification Methods. Buildings, 15(8), 1226. https://doi.org/10.3390/buildings15081226








