Experimental Research and Analysis of Influencing Factors on Hysteresis Properties of Common Steel Bars with Unbonded Sections

Abstract

With the aim of investigating the factors influencing the hysteretic behavior of common steel bars with unbonded sections (CS-US), hysteresis tests of six CS-US specimens were conducted, taking unbonded length, the location of the unbonded section, steel bar diameter, steel bar strength grade, and concrete strength grade as study variables. The results show that there exist necking phenomena in steel bars and different degrees of damage to concrete in all specimens. A 3D fine model was established by Solid works and ABAQUS software and verified according to the experimental results. The results show that the simulated values are close to the experimental values. Subsequent to the validation of the model, a thorough analysis was performed to assess the energy dissipation capacity and ductility of CS-US. The findings indicate that the implementation of an unbonded section can remarkably enhance the energy dissipation capacity and ductility of CS-US. It was demonstrated that the larger the unbonded length, the greater the ductility and energy dissipation capacity of CS-US. An alteration in the bonded length at the loading end exerts minimal influence on the energy dissipation capacity and ductility of CS-US. The energy dissipation capacity and ductility of CS-US decrease with an increasing steel bar diameter or strength grade. Concrete strength grades lower than C40 have minimal impact on the energy dissipation capacity and ductility of CS-US; concrete with a strength grade higher than C40 exhibits a decrease in energy dissipation capacity and ductility initially, followed by an increase. However, the values of these parameters remain lower than those observed in concrete with a strength grade below C40. Finally, the proposed design values of the above parameters are provided as a reference for engineering applications.

1. Introduction

In reinforced concrete structures, the bond performance of steel bars and concrete is a critical factor in determining the mechanical performance of the entire structure. The factors influencing bond performance are numerous and include the loading mode, the properties of the steel bar, the characteristics of the concrete, and the environmental factors that may be present. In terms of loading mode, relevant researchers mainly study the influences of loading form, loading rate, and test method on bond performance [1,2]. For example, Yang et al. [3] studied the bond performance of geopolymer-based ultrahigh-performance concrete (G-UHPC) and steel bars under cyclic loading. Li et al. [4] studied the bond performance of steel bars and rubber concrete under different loading rates through a center draw test. Wang et al. [5,6] studied the influence of different test methods on the bond performance of high-strength steel bars and concrete through a center draw test and a beam test.

With regard to steel bars, relevant researchers have focused on the impacts of various parameters on bond performance. These parameters include the type, strength, grade, diameter, corrosion degree, and location of the steel bar [7,8,9,10]. For example, Zheng et al. [11] investigated the impacts of the corrosion degree and diameter of a rebar on the bond performance of the rebar and ordinary concrete. Qu et al. [12] investigated the impacts of the steel bar diameter and length-to-diameter ratio on the hysteretic properties of a stainless steel clad rebar. Li et al. [13] investigated the impacts of the stirrup ratio, steel bar diameter, and steel bar types on the bond performance of high-strength stainless steel bars and ultrahigh-performance concrete (UHPC). Rabi et al. [14,15,16,17] used artificial neural networks to predict the bond properties between stainless steel bars and concrete and proposed a constitutive model of stainless steel bars based on a series of tensile tests.

With regard to concrete, relevant studies primarily focus on the impacts of concrete protective layer thickness and concrete types on bond performance [18]. Concrete types include recycled concrete [19], high-performance concrete [20,21,22], fiber-reinforced high-performance concrete [23,24,25], etc. For instance, Fayed et al. [26] investigated the impacts of recycled concrete aggregate and the reinforcement ratio on the bond performance of steel bars and recycled concrete. Gao et al. [27] investigated the effects of concrete protective layer thickness and steel fiber volume fraction on the bond performance of steel bars in UHPC through a center draw test. Piotr [28] investigated the impacts of concrete protective layer thickness and fiber volume content on the bond performance of steel bars in basalt fiber-reinforced high-performance concrete (BFRHPC) using a center draw test. Shamass et al. [29] studied the bond properties between carbonated aggregates, basalt fiber-reinforced polymers, and concrete. Al-Kheetan et al. [30] applied Nano-ZnO to concrete with recycled concrete aggregate to evaluate the properties of the concrete mixture in terms of its physical and mechanical properties and durability.

In terms of the environment, Hu et al. [31,32] studied the influence of a freezing environment on the bond performance of steel bars in early-age frozen concrete. Zhou et al. [33] investigated the impact of temperature on the bond performance of steel bars and concrete using a center draw test of steel bars at normal temperature and elevated temperature.

The aforementioned studies demonstrate that multiple factors significantly impact the bonding behavior between steel bars and concrete, including but not limited to the following: bar diameter, anchorage length, corrosion characteristics (location and progression rate), thickness of the concrete protective layer, proportion of recycled aggregates, environmental temperature variations, and applied load configurations.

The abovementioned rebars are all fully bonded rebars. However, compared with bonded rebars, the bond properties of the CS-US proposed in this paper are different, and they are not only affected by the above factors but also by the unbonded length and location of the unbonded section due to the existence of the unbonded section. Therefore, it is necessary to further study the key factors affecting the bond properties of CS-US.

In addition, when our research group set the unbonded section on the steel bars of the edge components of the shear wall (Figure 1), it was found that the ductility and energy dissipation capacity of the shear wall were greatly improved after a pseudo-static test on the wall was conducted [34]. Therefore, in order to further study the energy dissipation mechanism of CS-US, an in-depth study on a single CS-US was conducted to explore its hysteretic performance and influencing factors, and finally, design recommendations are put forward to provide a theoretical basis for engineering applications.

2. Experimental Program

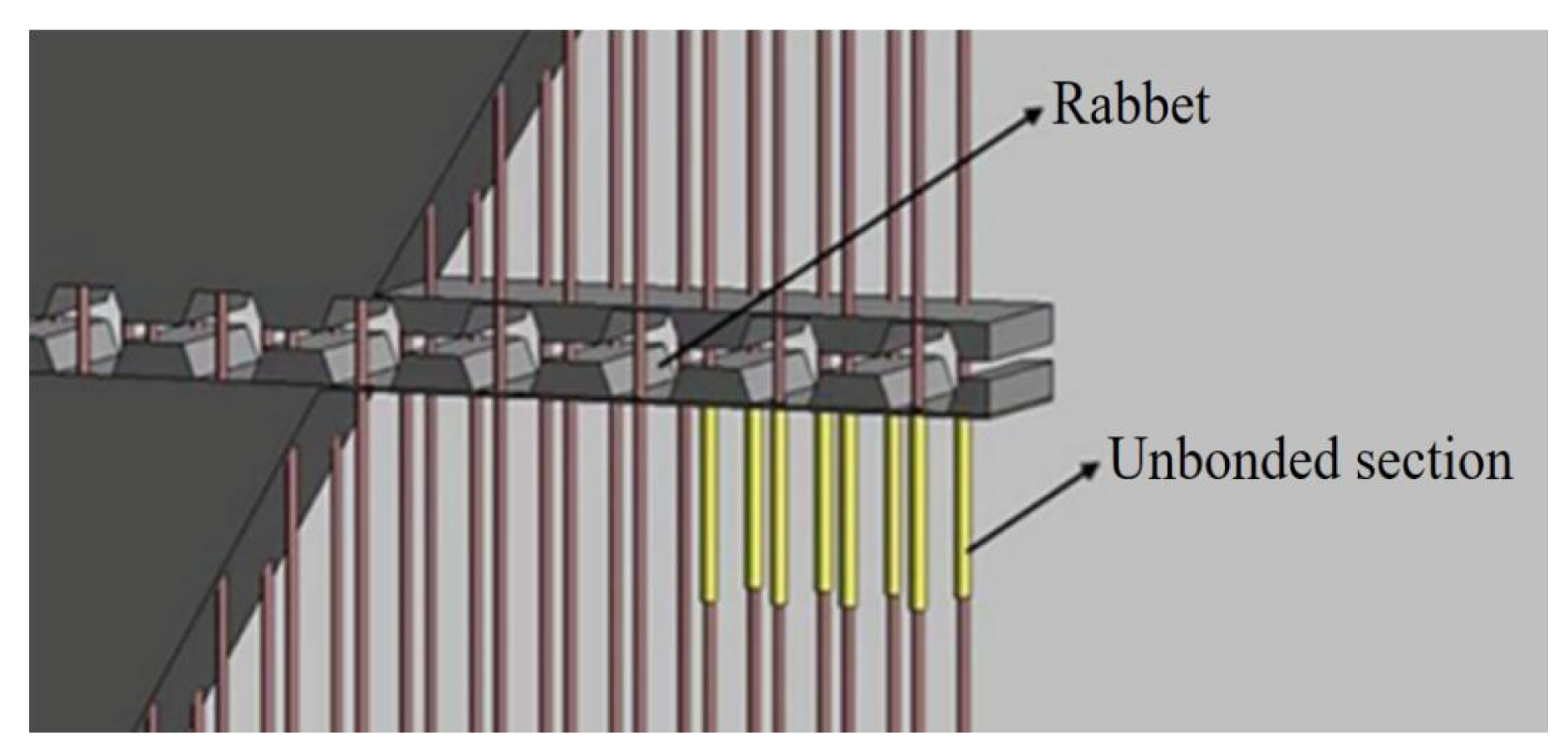
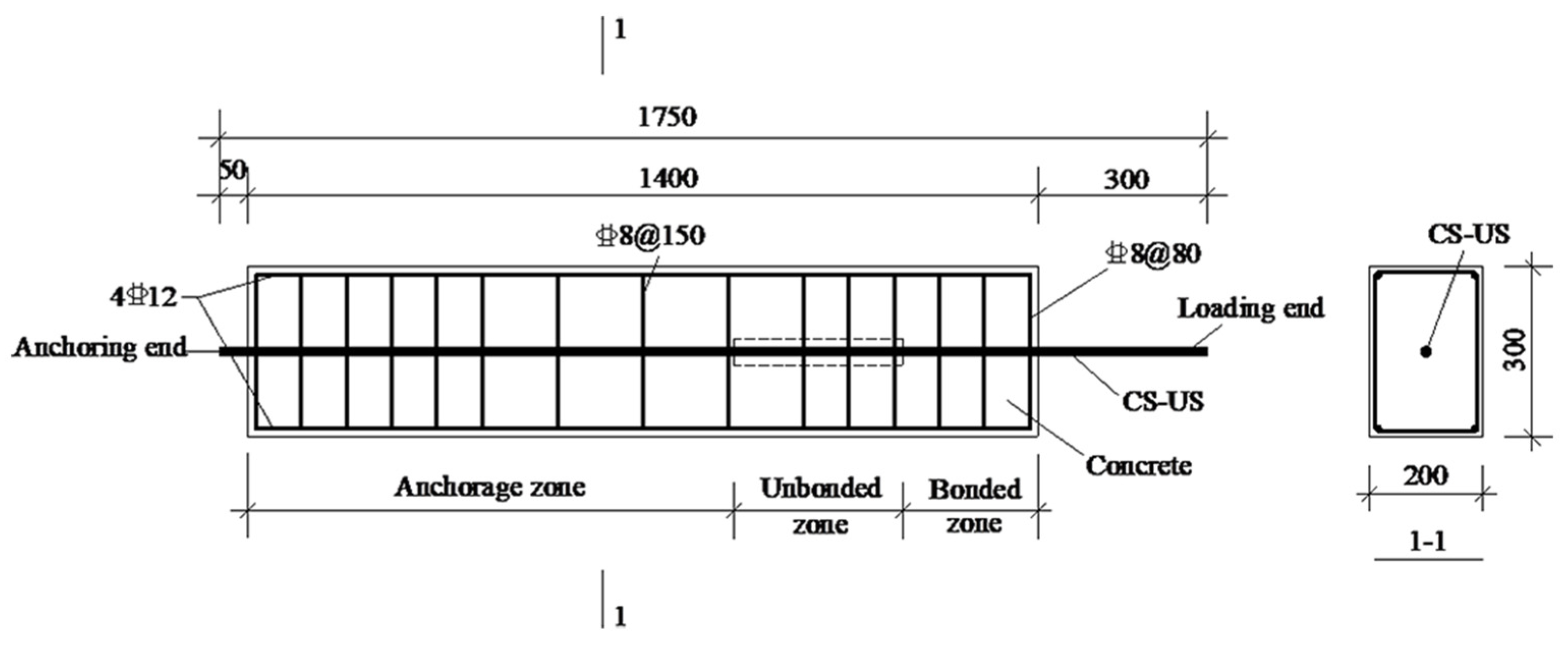
2.1. Specimen Design

Six CS-US specimens were made for conducting hysteresis tests, taking the unbonded length, the location of the unbonded section, steel bar diameter, steel bar strength grade, and concrete strength grade as the studied variables. The specimens’ parameters are enumerated in

Table 1. Test specimen parameters.

Specimen Name	Unbonded Length (mm)	Bonded Length at Loading End (mm)	Steel Bar Diameter (mm)	Steel Bar Strength Grade	Concrete Strength Grade
JD	300	240	16	HRB400	C35
WC	400	240	16	HRB400	C35
YC	300	320	16	HRB400	C35
GZ	300	240	20	HRB400	C35
GQ	300	240	16	HRB500	C35
HQ	300	240	16	HRB400	C30

. The length of the bonded steel bar at the loading end is reflective of the location of the unbonded section. Specimen JD is the control specimen, and specimens WC, YC, GZ, GQ, and HQ are compared in terms of the unbonded length, location of the unbonded section, steel bar diameter, steel bar strength grade, and concrete strength grade, respectively. As illustrated in Figure 2, the specimen’s dimensions are specified in detail. The exterior concrete portion of the steel bar measures 1400 mm, encompassing the anchorage zone, the unbonded zone, and the bonded zone at the loading end. The installation and loading of the specimen are facilitated by the length of the steel bar at the loading end, which measures 300 mm. To ensure the accuracy of the measurement, a 50 mm segment is allocated at the anchored end for quantifying the horizontal displacement of the steel bar. The horizontal displacement of CS-US is the difference between the displacement of the steel bar at the loading end and the steel bar at the anchored end.

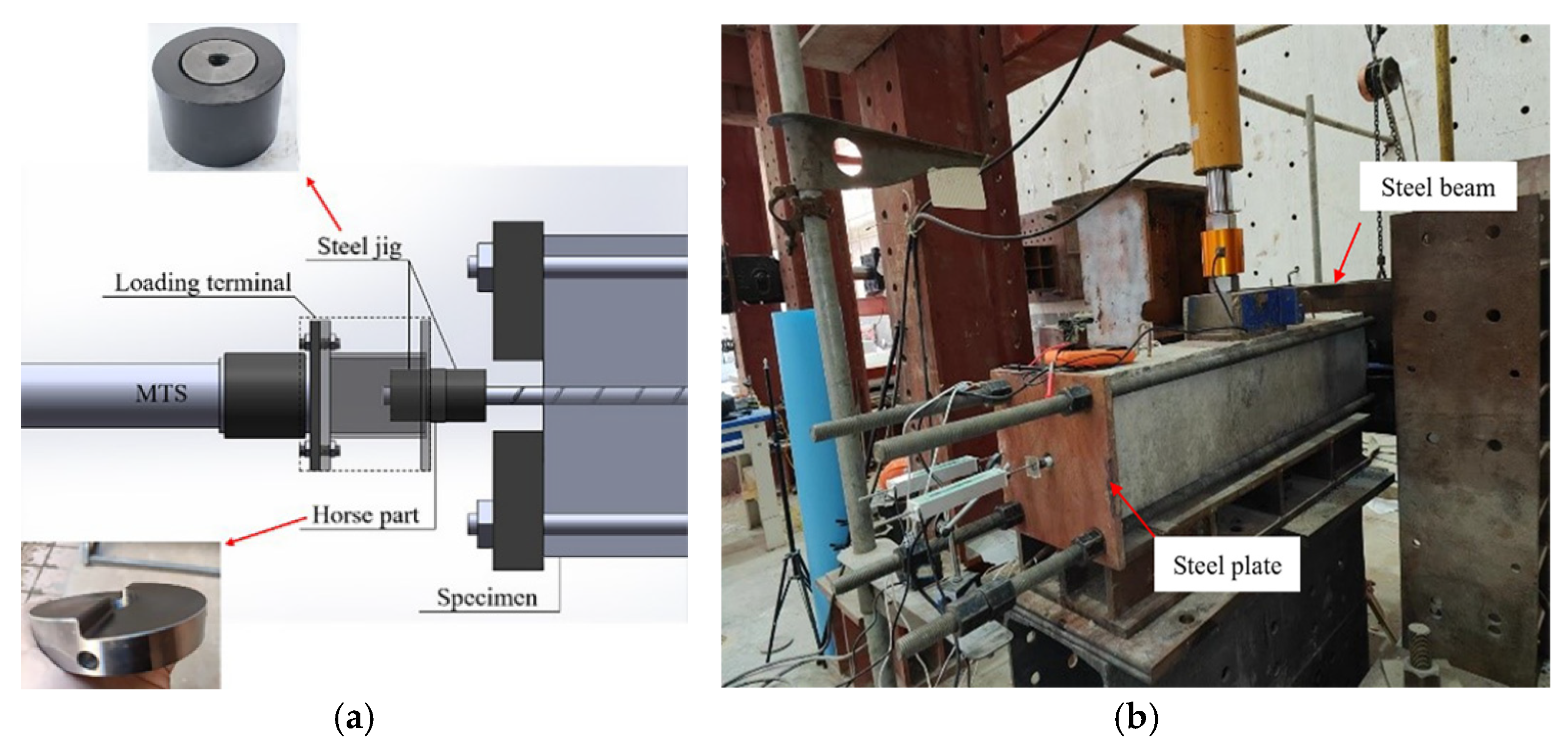
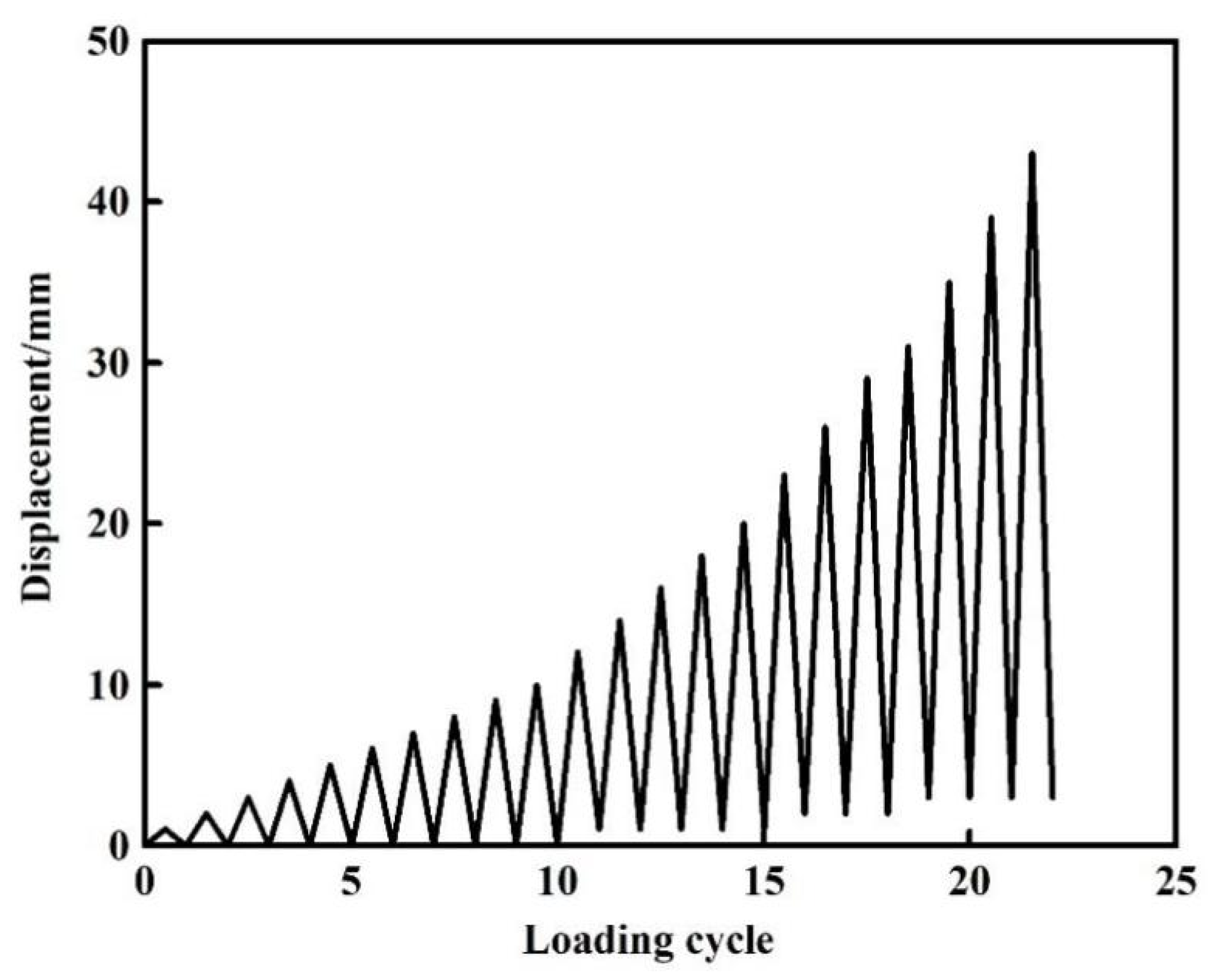
2.2. Test Setup and Loading Regime

The test device (Figure 3) consists of a loaded device and a fixed device. The loading device (Figure 3a), mainly set at the loading end, includes the loading terminal, the steel jig, and the horse part. The horse part is used to facilitate the disassembly of the steel bar and enable the recycling of the steel jig. Moreover, the combination of the two steel jigs and the horse part ensures a tight connection between the steel bar and the loading terminal, enabling the steel bar to effectively transmit force. The fixed device is shown in Figure 3b. The specimen is fixed horizontally with four long screws by the steel beam at the loading end and the steel plate at the anchored end. The steel beam is affixed to the reaction frame at the loading end, and the horizontal loading device adopts a 25 t MTS actuator. The specimen is fixed vertically by applying 40 kN pressure through a 20 t jack.

This test adopted a displacement loading regime. As the loading displacement increased, the elongation of the steel bar increased. To prevent the steel bar from bending under compression, this paper used a positive hysteresis loading method, setting the tension of the steel bar as positive. In accordance with the “Standard for Test Method of Concrete Structures” (GB/T 50152-2012) [35] and the results of previous numerical simulations, when the positive tensile displacement is within 10 mm, the tensile displacement of each stage is set to 1 mm, and then the positive compression should return to zero. When the positive tensile displacement is within the range of 10 mm to 20 mm, the tensile displacement of each stage is 2 mm, and then the positive compression should return to 1 mm. When the positive tensile displacement is within the range of 20 mm to 30 mm, the tensile displacement of each stage is 3 mm, and then the positive compression should return to 2 mm, and so on. Each stage is cycled once, and the loading regime can be observed in Figure 4. To avoid the possibility of the impact load from the broken steel bar affecting the normal operation of the MTS actuator, based on the pretest numerical simulation results, all tests were terminated when the unbonded steel bar yielded and the displacement of CS-US suddenly increased (the bond between the steel bar and the concrete was not effective).

3. Establishment and Verification of Finite Element Model

3.1. Contact Setting of CS-US with Concrete

During the loading process of the structure, the contact surface of the steel bar and concrete undergoes constant modification. Evidence was presented by several researchers indicating that cohesive units are capable of effectively ensuring the mechanical performance of steel bars and concrete under a complex stress state [36]. For the purpose of simulating the contact interface of the steel bar and concrete, the cohesive interaction attribute is assigned to CS-US and concrete in the bonded section. In the unbonded section, the concrete portion corresponding to the unbonded steel bar is cut away, and the excised portion is an elongated cylinder with a cross-sectional diameter of 1.5 times the diameter of the unbonded steel bar. This procedure is essential for achieving the unbonding of the steel bar.

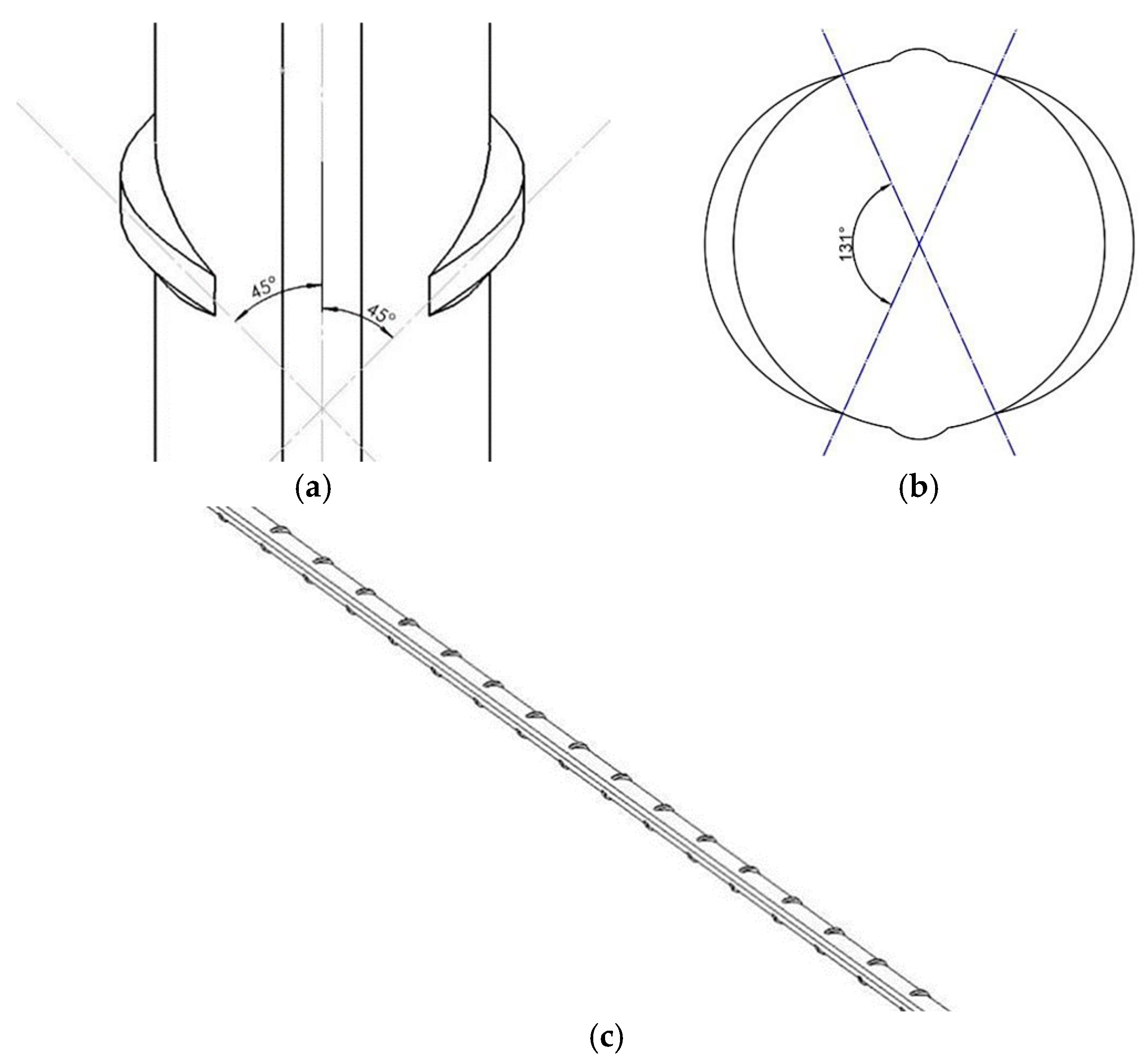
3.2. Unit Type and Size

(1)

CS-US

In this study, 3D Solid works software (SolidWorks 2024) was utilized in the establishment of the refined CS-US model. As demonstrated in Figure 5, the angle between the initial position of the outer rib of the steel bar and the radial axis is 45° (Figure 5a), while the crawling angle of the outer rib of the steel bar along the surface is approximately 130° (Figure 5b), and the refined model of CS-US is shown in Figure 5c.

The model was implemented in ABAQUS software (ABAQUS 6.14.4), and to unveil the fracture of CS-US, a 3D solid tetrahedral unit (C3D4) was utilized to represent the steel bar, with a unit size of 4 mm, as illustrated in Figure 6.

(2)

The Remaining Steel Bars and Concrete

As this paper focused on the performance of CS-US, the truss element T3D2 was used for the remaining steel bars with a unit size of 50 mm. The 3D solid tetrahedral unit (C3D4) was utilized for concrete with a unit size designated as 50 mm, and the unit size assigned to the cut part of the unbonded section was 10 mm, as illustrated in Figure 7. The finite element model of the final specimen is depicted in Figure 8.

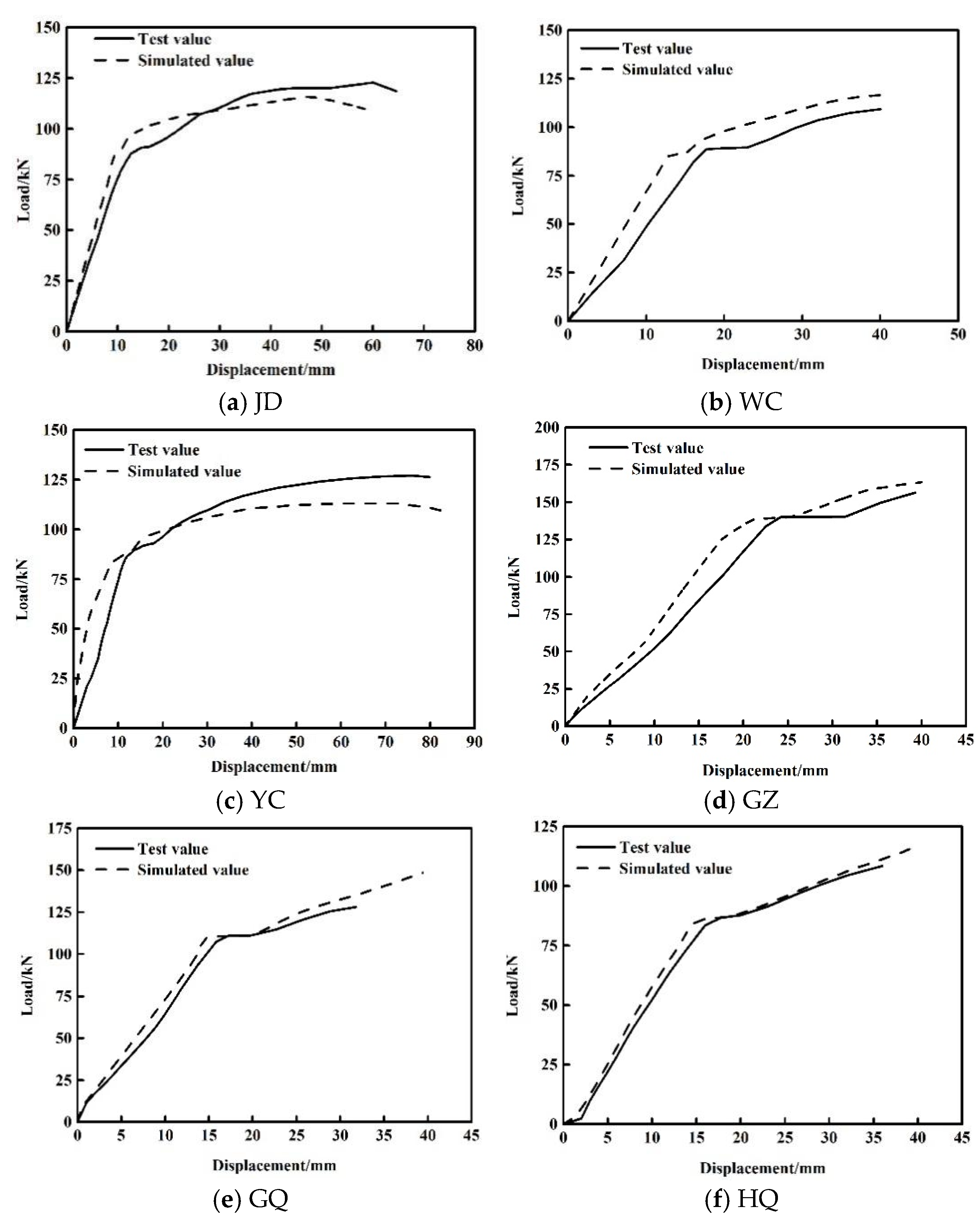
3.3. Verification of Finite Element Model

(1)

Failure pattern

In accordance with the aforementioned modeling method, the ultimate failure pattern of the entire specimen collection was obtained and subsequently evaluated in comparison with the test results, as illustrated in Figure 9. The PEEQ value is greater than 0, which indicates that the specimens yielded.

As illustrated in Figure 9, the simulation outcomes of the ultimate failure patterns of the specimens exhibit a marked similarity with the experimental results. There exists the phenomenon of necking in all specimens. The concrete destruction of the specimen HQ is more serious.

(2)

Load–Displacement Curves

Pursuant to the aforementioned methodology of model construction, the load–displacement curves of specimens are obtained. Subsequently, the aforementioned curves are evaluated in comparison with the test results. The ensuing data are displayed in Figure 10.

As illustrated in Figure 10, the simulated values in the elastic phase are all larger than the test values because necking was generated by the stretching of the steel bars during the test process, resulting in different degrees of slippage in the steel bars at the steel jig. Overall, the simulated values of the specimens are similar to the test values.

4. Parameter Analysis of CS-US Hysteresis Properties

Due to the limited number of test specimens, it is necessary to establish CS-US models with varying parameters. These models will be utilized to investigate the influence laws of unbonded length, the location of the unbonded section, steel bar diameter, steel bar strength grade, and concrete strength grade on the hysteresis properties of CS-US. This investigation will employ the modeling method proposed in the previous section. The establishment of these models will allow for the analysis of the influence laws of each parameter on the energy dissipation capacity and ductility of CS-US.

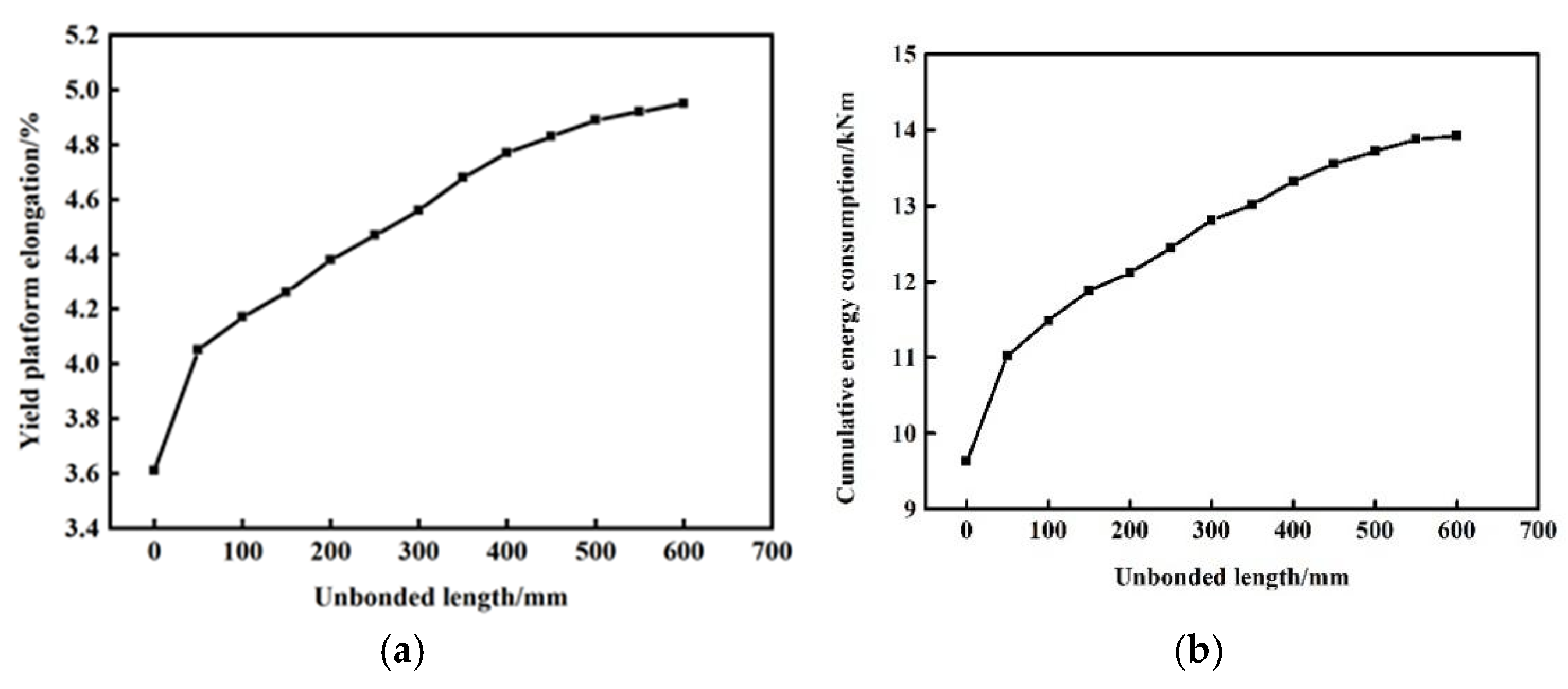
4.1. Unbonded Length

The following parameters were used: The concrete strength grade was set as C35, and the steel bar strength grade was designated as HRB400. The diameter of the steel bar was set as 16 mm, and the bonded length at the loading end was set as 240 mm. The unbonded length ranged from 0 to 600 mm at an interval of 50 mm, and thirteen CS-US models were fabricated. For ordinary steel bars, if the yielding platform segment of the steel bar is ignored, it is considered that the steel bar enters the strengthening stage immediately after yielding. Thus, the deformation capacity of the steel bar will be underestimated, and it cannot provide an accurate basis for the seismic design. Therefore, this paper adopts the yield platform elongation rate [37] $\alpha$ as the ductility index of the steel bar (the same as the following), which is calculated by the following formula:

$$\alpha =∆l/l$$

(1)

where $∆l$ is the elongation of the steel bar at yielding in the bonded zone at the loading end, and $l$ is the sum of the length of the outwardly extended stress section at the loading end of the steel bar and the bonded length at the loading end.

After calculation, the influence law of the unbonded length on the energy dissipation capacity (cumulative energy dissipation, the same below) and ductility of CS-US was obtained, as illustrated in Figure 11.

As illustrated in Figure 11, the energy dissipation capacity and ductility of CS-US exhibit more significant increases as the unbonded length is extended from 0 mm to 50 mm. This observation suggests that the strategic placement of the unbonded section can be an effective method for enhancing the energy dissipation capacity and ductility of CS-US. It was demonstrated that the ductility and energy dissipation capacity of CS-US increase with an increase in unbonded length. When the unbonded length is in the range of 50 mm to 400 mm, the ductility and energy dissipation capacity of CS-US exhibit more pronounced increases, while in the range of 400 mm to 600 mm, the aforementioned properties of CS-US undergo more gradual increases. Therefore, taking into consideration the effects of unbonded length on the ductility and energy dissipation capacity of the steel bar, it is preferable to set the unbonded length between 50 mm and 400 mm, and the specific value depends on the needs of the project.

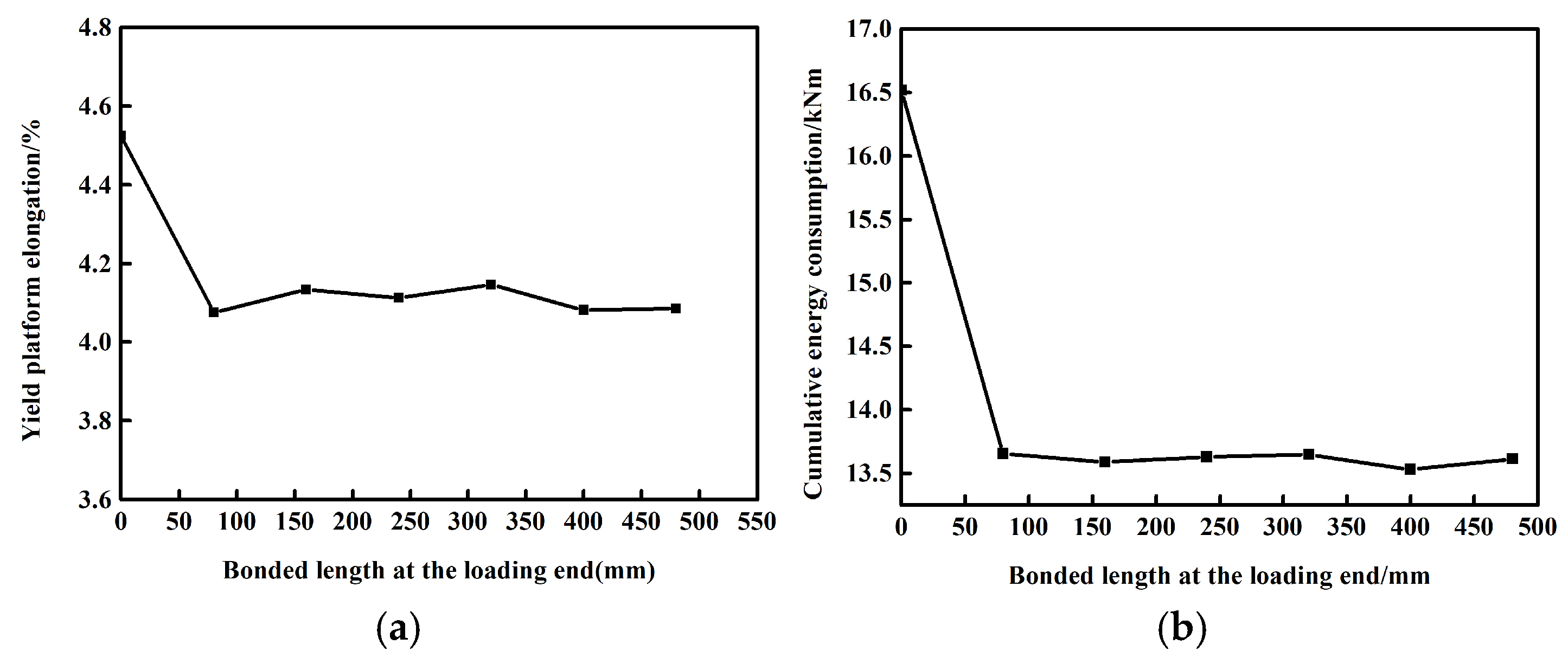
4.2. Location of Unbonded Section

Take the concrete strength grade as C35, the steel bar strength grade as HRB400, the steel bar diameter as 16 mm, and the unbonded length as 300 mm, for example, then the bonded length at the loading end ranged from 0 to 480 mm at an interval of 80 mm, and seven CS-US models were made. After calculation, the influencing laws of the unbonded section location on the energy dissipation capacity and ductility of CS-US were obtained, as shown in Figure 12.

As illustrated in Figure 12, when the bonded length at the loading end is 0 mm, the energy dissipation capacity and ductility of CS-US are larger. This is because the unbonded section is directly connected to the extended length of the steel bar, so the deformation of the steel bar is larger. However, this may affect the displacement of the structure. When the bonded length at the loading end is larger than 0 mm, the energy dissipation capacity and ductility of CS-US vary less.

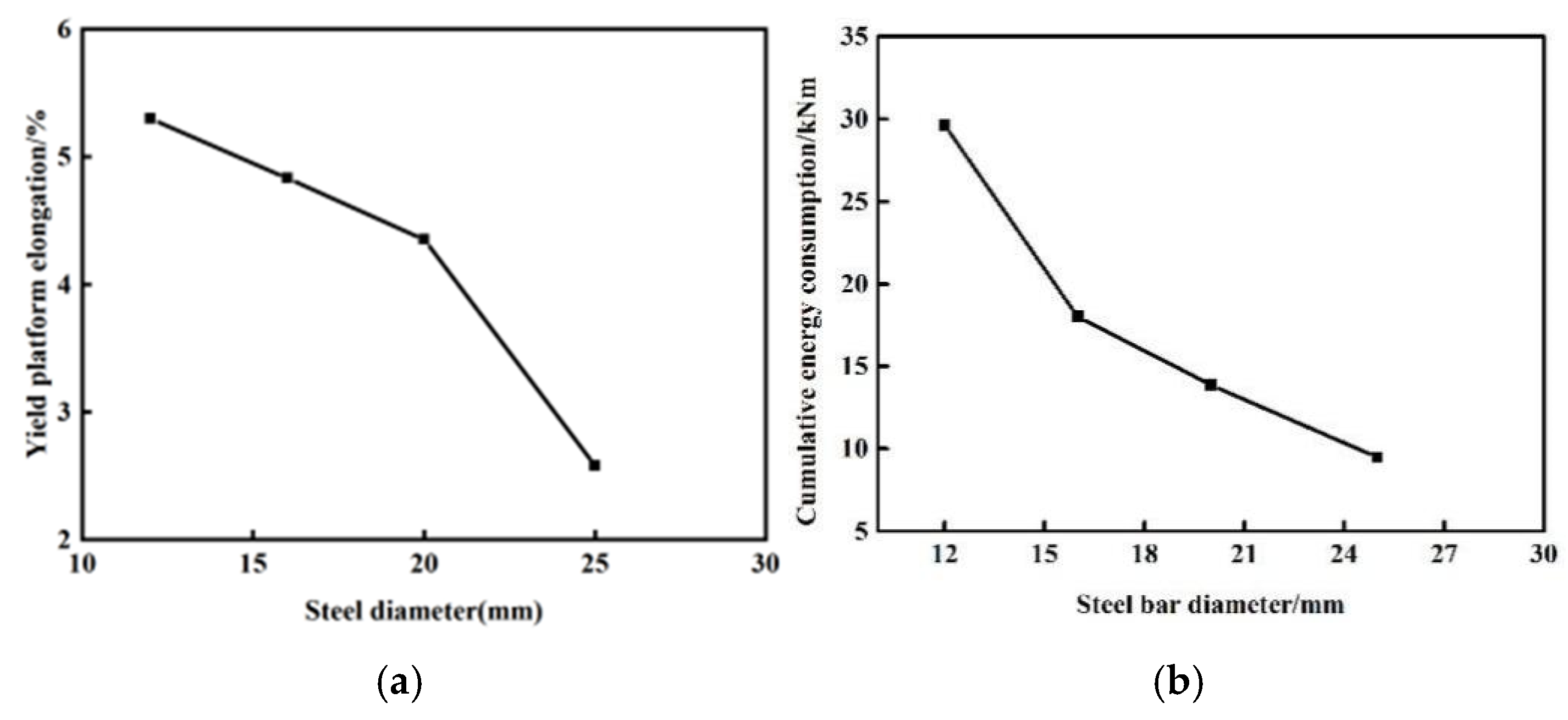
4.3. Steel Bar Diameter

By taking the concrete strength grade as C35, the steel bar strength grade as HRB400, the unbonded length as 300 mm, and the bonded length at the loading end as 240 mm, for example, and taking the steel bar diameters as 12 mm, 16 mm, 20 mm, and 25 mm, four CS-US models were made. Through calculations, the influence of steel bar diameter on the energy dissipation capacity and ductility of CS-US was derived. This relationship is demonstrated in Figure 13.

As illustrated in Figure 13, an augmentation in the diameter of steel bars is concomitant with a diminution in both the energy dissipation capacity and ductility of CS-US. This phenomenon can be ascribed to the principle that an augmentation in the diameter of steel bars leads to an increase in the contact area of steel bars and concrete. Consequently, the bond strength increases, leading to a diminution in the extended length of the steel bar and a concomitant decline in ductility. However, an increase in the specimen’s bearing capacity is observed, while the subsequent calculations indicate a decline in cumulative energy dissipation with increasing steel bar diameter.

4.4. Steel Bar Strength Grade

By taking the concrete strength grade as C35, the steel bar diameter as 16 mm, the unbonded length as 300 mm, and the bonded length at the loading end as 240 mm, for example, and taking the steel bar strength grades as HRB335, HRB400, and HRB500, three CS-US models were made. After calculation, the influence law of steel bar strength grade on the energy dissipation capacity and ductility of CS-US is obtained, as shown in

Table 2. Effects of steel bar strength grade on energy dissipation capacity and ductility of CS-US.

Steel Bar Strength Grade	Yield Platform Elongation (%)	Cumulative Energy Dissipation (kNm)
HRB335	4.9	15.4
HRB400	4.4	13.8
HRB500	3.8	12.5

.

As can be seen from Table 2, with an increase in steel bar strength grade, the energy dissipation capacity and ductility of CS-US decrease. This is because an increase in the steel bar strength grade leads to a decrease in the extended length of the steel bar and its ductility. However, the specimen’s bearing capacity increases, and upon calculation, the cumulative energy dissipation capacity of the specimen exhibits a decreasing trend.

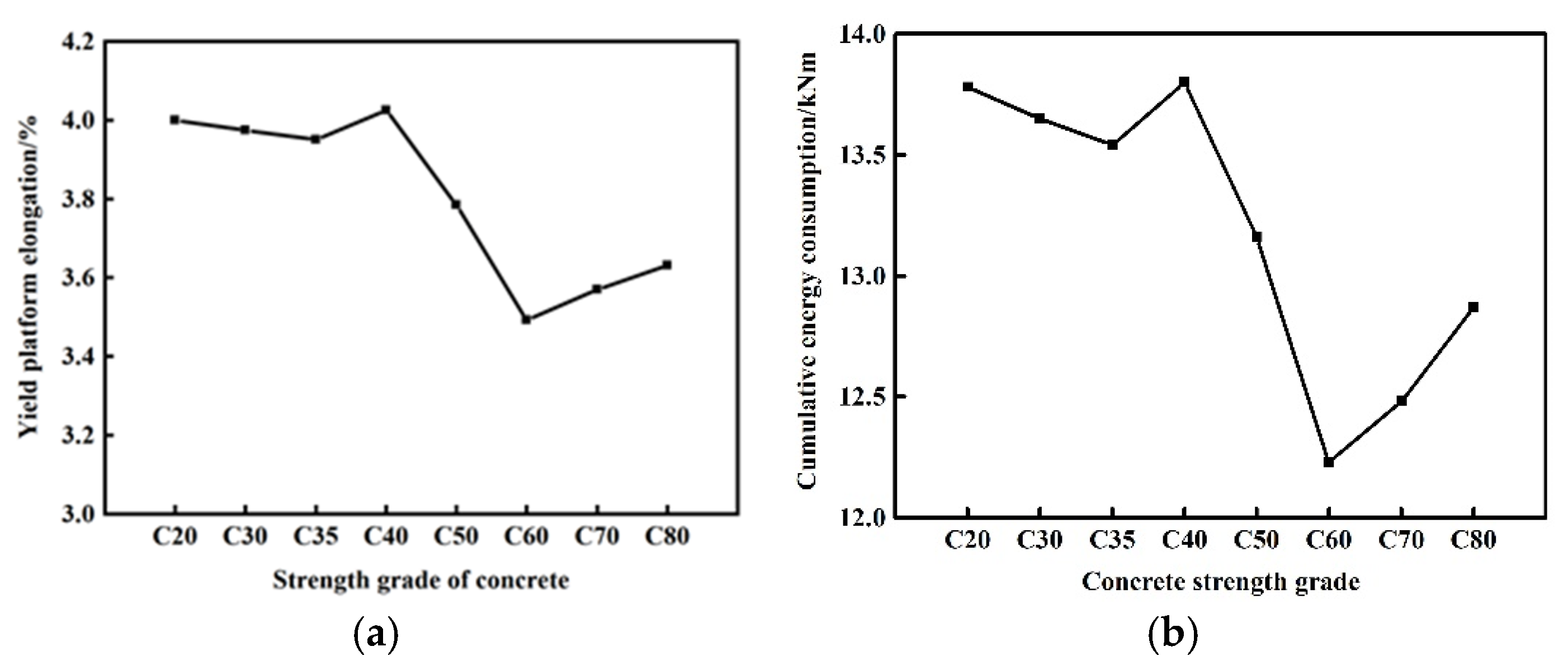
4.5. Concrete Strength Grade

By taking the steel bar diameter as 16 mm, the steel bar strength grade as HRB400, the unbonded length as 300 mm, and the bonded length at the loading end as 240 mm, for example, and taking the concrete strength grades as C20, C30, C35, C40, C50, C60, C70, and C80, eight CS-US models were made. After calculations, the influence laws of concrete strength grade on the energy dissipation capacity and ductility of CS-US were obtained, as shown in Figure 14.

As illustrated in Figure 14, for concrete strengths inferior to C40, the energy dissipation capacity and ductility of CS-US exhibit minimal variations. When the concrete strength grade varies between C40 and C60, the energy dissipation capacity and ductility of CS-US decrease faster. In the range of concrete strength grades from C60 to C80, the ductility increases at a slower rate, while the energy dissipation capacity increases at a faster rate. However, both of these remain lower than those of steel bars. In the range of concrete strength grades from C20 to C50, it can be observed that high-strength concrete can lead to decreases in energy dissipation capacity and ductility.

4.6. Design Recommendations

In consideration of the impacts of the aforementioned parameters on the energy dissipation capacity and ductility of CS-US, the following design recommendations are proposed: The unbonded length should be selected within the range of 50–400 mm, and the concrete strength grade should be designated between C20 and C50. The bonded length at the loading end, the diameter of the steel bar, and the steel strength grade should be determined in accordance with the specific circumstances.

5. Conclusions

With reference to the hysteresis test of CS-US, the use of Solid works and ABAQUS finite element software was proposed for the simulation and analysis of CS-US. The failure patterns and load–displacement curves of CS-US were then verified according to the test results. A parametric analysis of energy dissipation capacity and ductility was conducted, taking into account the effects of the unbonded length, the location of the unbonded section, the steel bar diameter, the steel bar strength grade, and the concrete strength grade. Specific conclusions are drawn as follows.

(1)

The simulated values in the elastic phase are larger than the test values because of the necking of steel bars. Overall, the simulated values of the specimens are similar to the test values.

(2)

The efficacy of the unbonded section in enhancing the energy dissipation capacity and ductility of CS-US was demonstrated; furthermore, an increase in the unbonded length corresponds to enhancements in both energy dissipation capacity and ductility. When the unbonded length is in the range of 50 mm to 400 mm, the ductility and energy dissipation capacity of CS-US exhibit more pronounced increases, while in the range of 400 mm to 600 mm, the aforementioned properties of CS-US undergo a more gradual increase.

(3)

The setting of the bonded length at the loading end significantly reduces the energy dissipation capacity and ductility of CS-US, and its change has less influence on these parameters.

(4)

The larger the steel bar diameter is, the lower the energy dissipation capacity and ductility of CS-US are.

(5)

The larger the steel bar strength grade is, the lower the energy dissipation capacity and ductility of CS-US are.

(6)

When the concrete strength grade is below C40, the energy dissipation capacity and ductility of CS-US show minimal variations. However, when the concrete strength grade exceeds C40, the energy dissipation capacity and ductility of CS-US initially decrease and then increase, yet they remain lower than those observed in steel bars with concrete strength grades below C40.

(7)

Based on the influencing laws of the above parameters, the parameter design recommendations of CS-US are proposed as follows. The unbonded length should be selected within the range of 50–400 mm, and the concrete strength grade should be designated between C20 and C50. The bonded length at the loading end, the diameter of the steel bar, and the steel strength grade should be determined in accordance with the specific circumstances.