Interfacial Shear Behavior of Novel Connections Between Concrete Bridge Piers and Anti-Overturning Steel Supporting Joists
Abstract
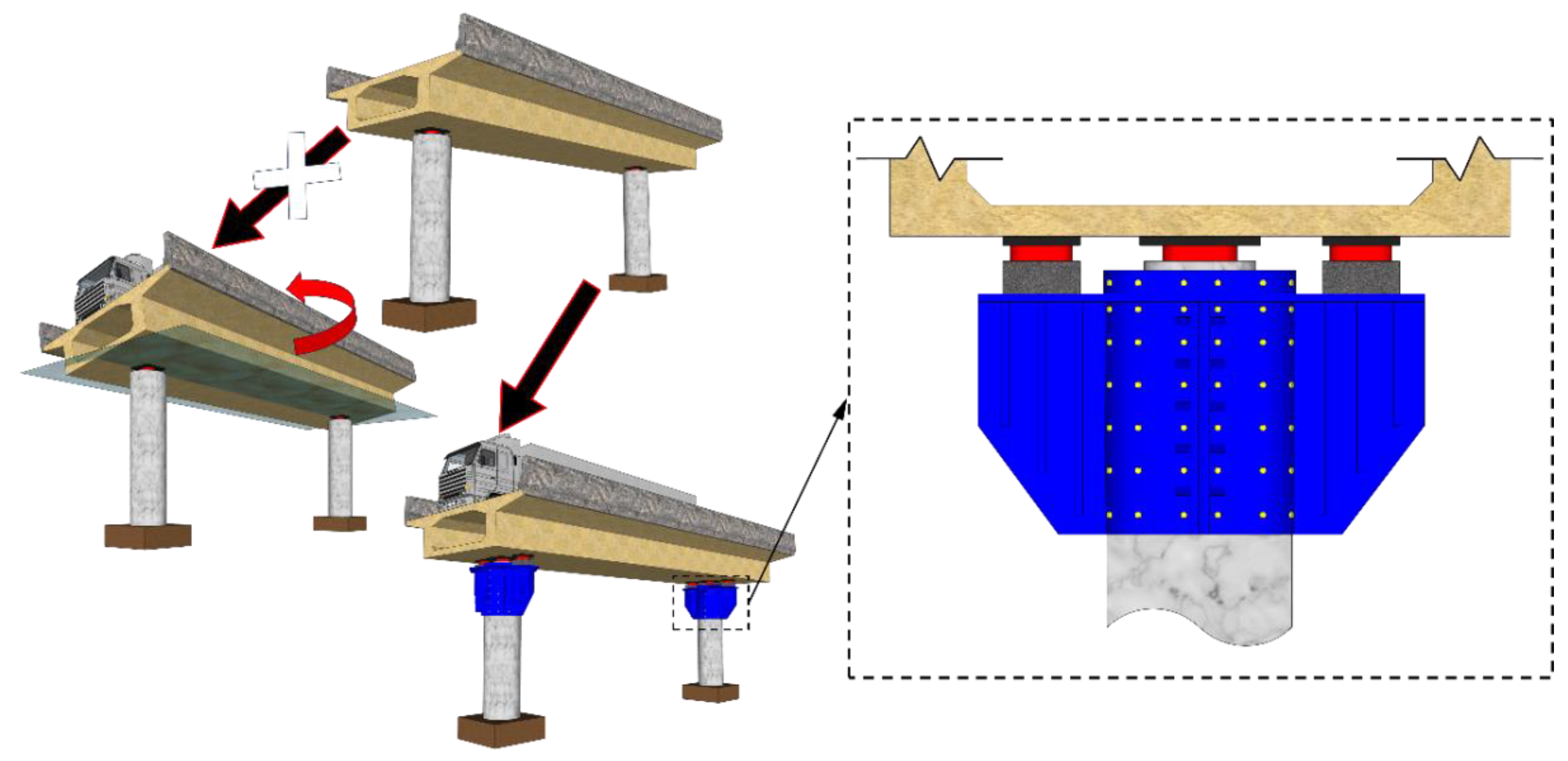
1. Introduction
2. Experimental Program
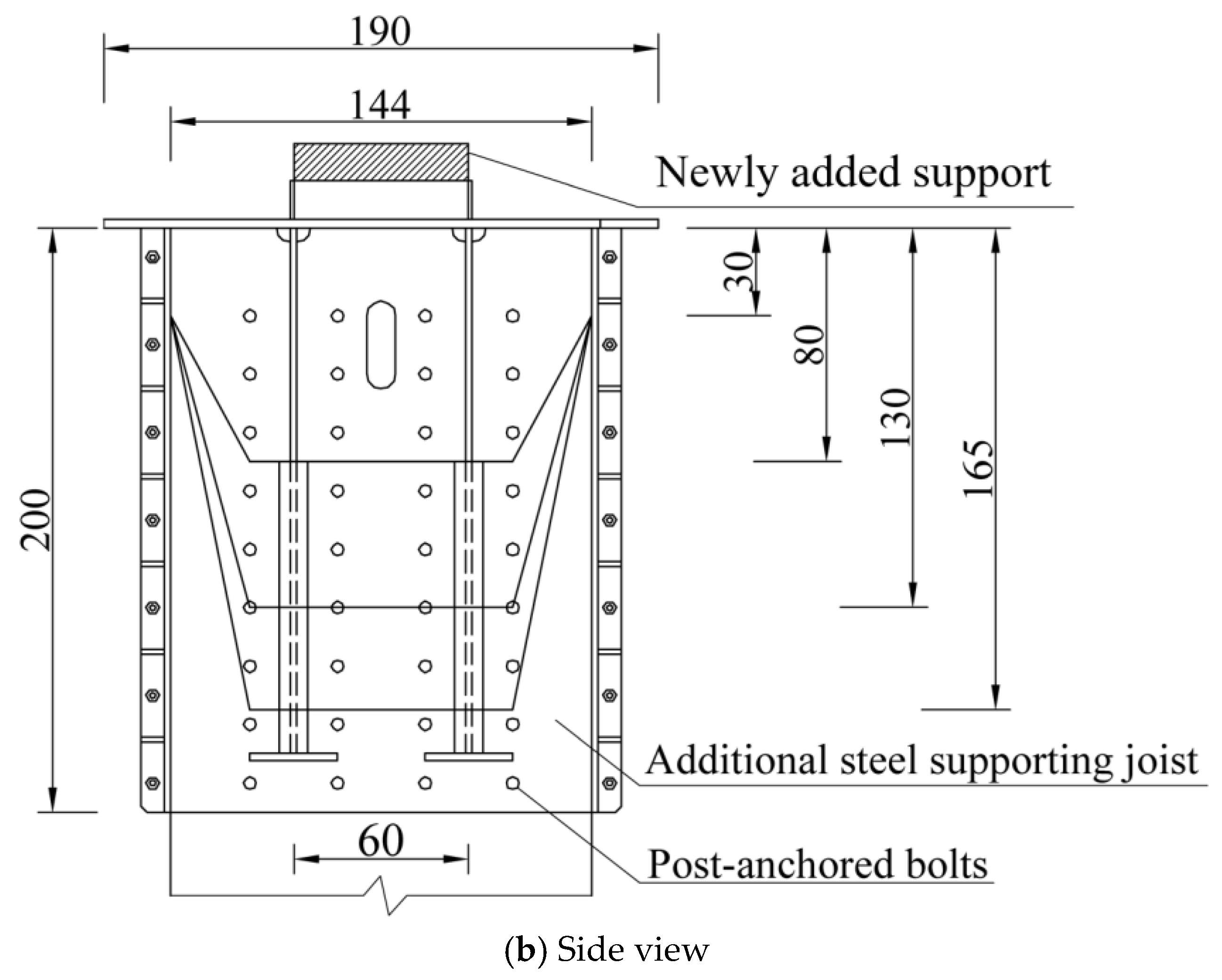
2.1. Specimen Design
2.2. Specimen Fabrication
2.3. Material Properties
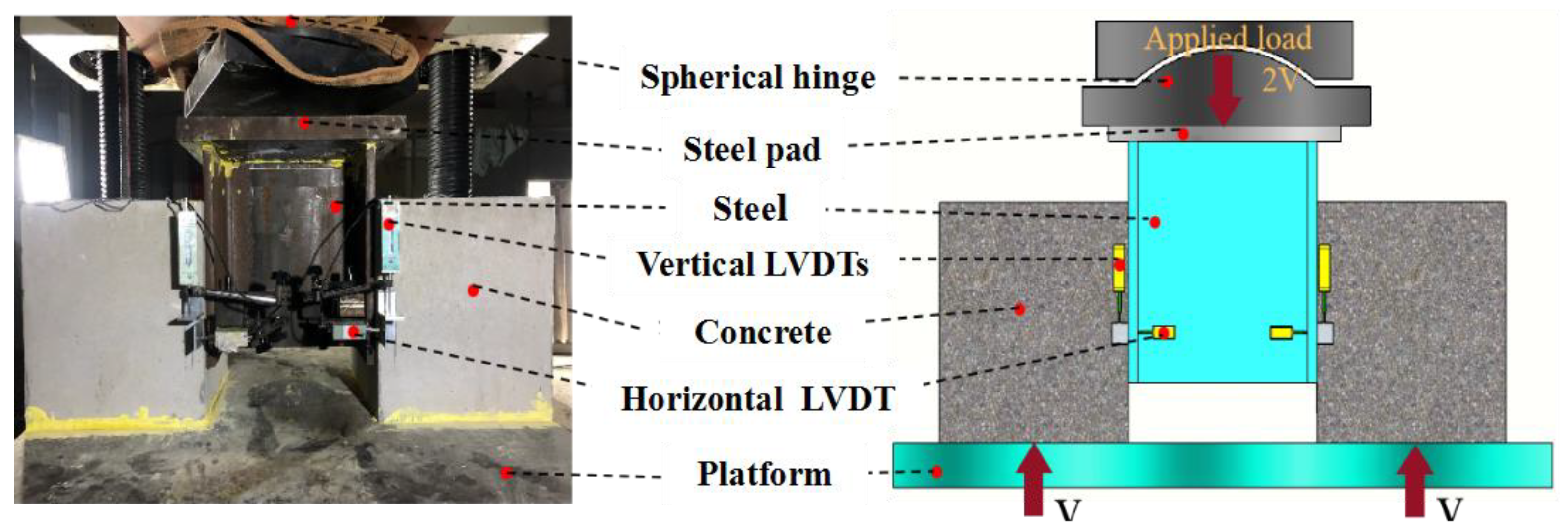
2.4. Test Setup and Instruments
3. Test Results and Discussions
3.1. Observed Phenomena
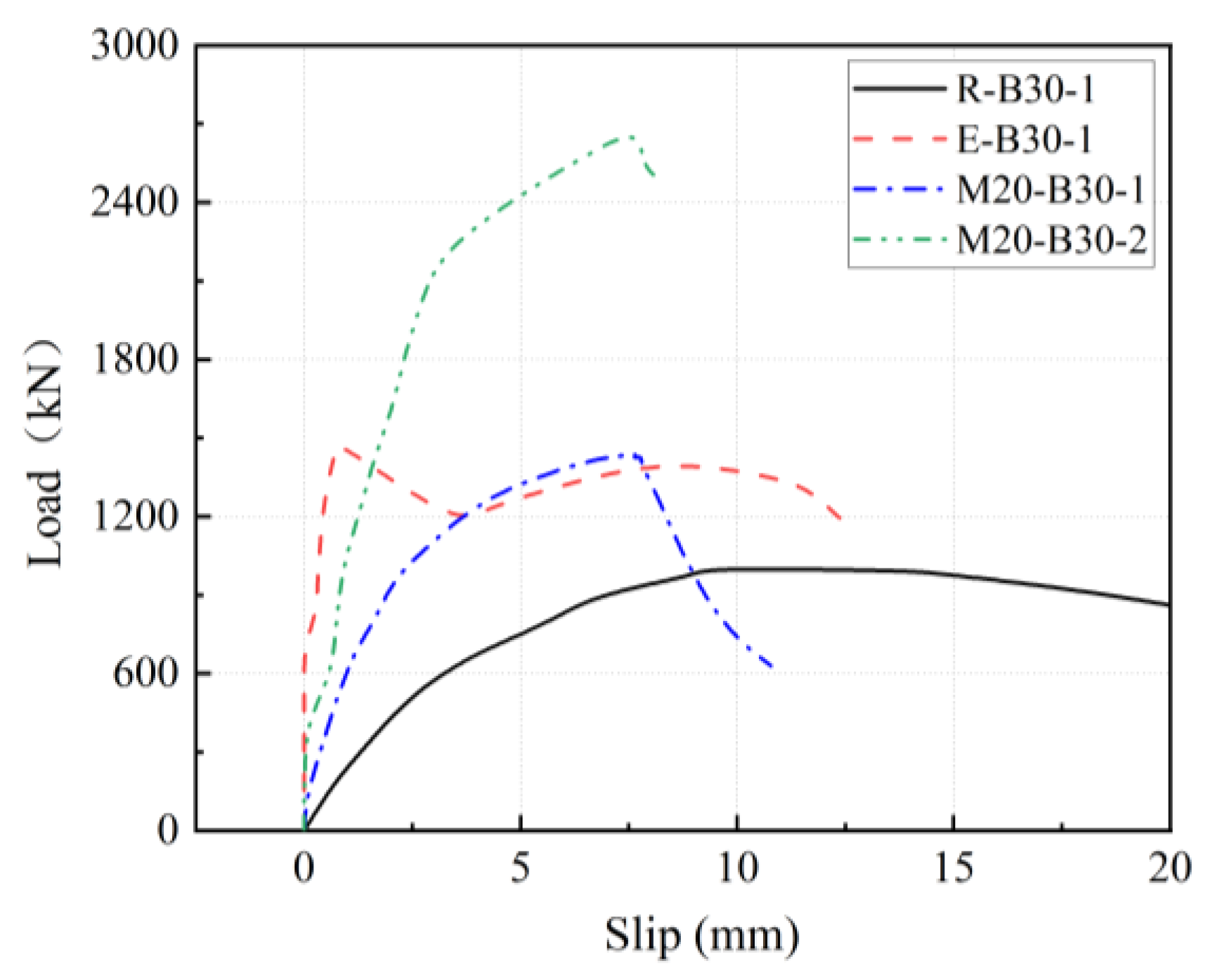
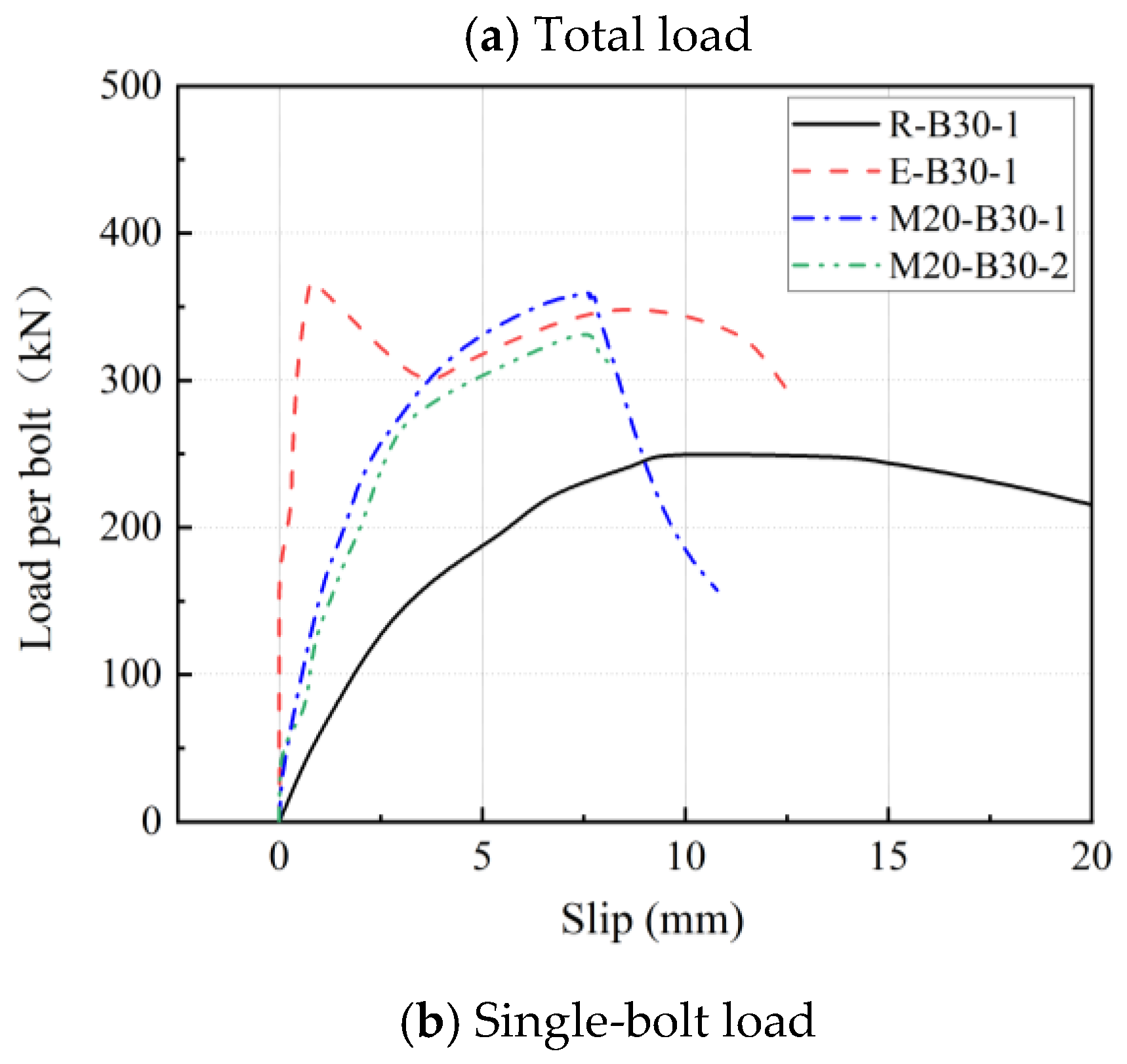
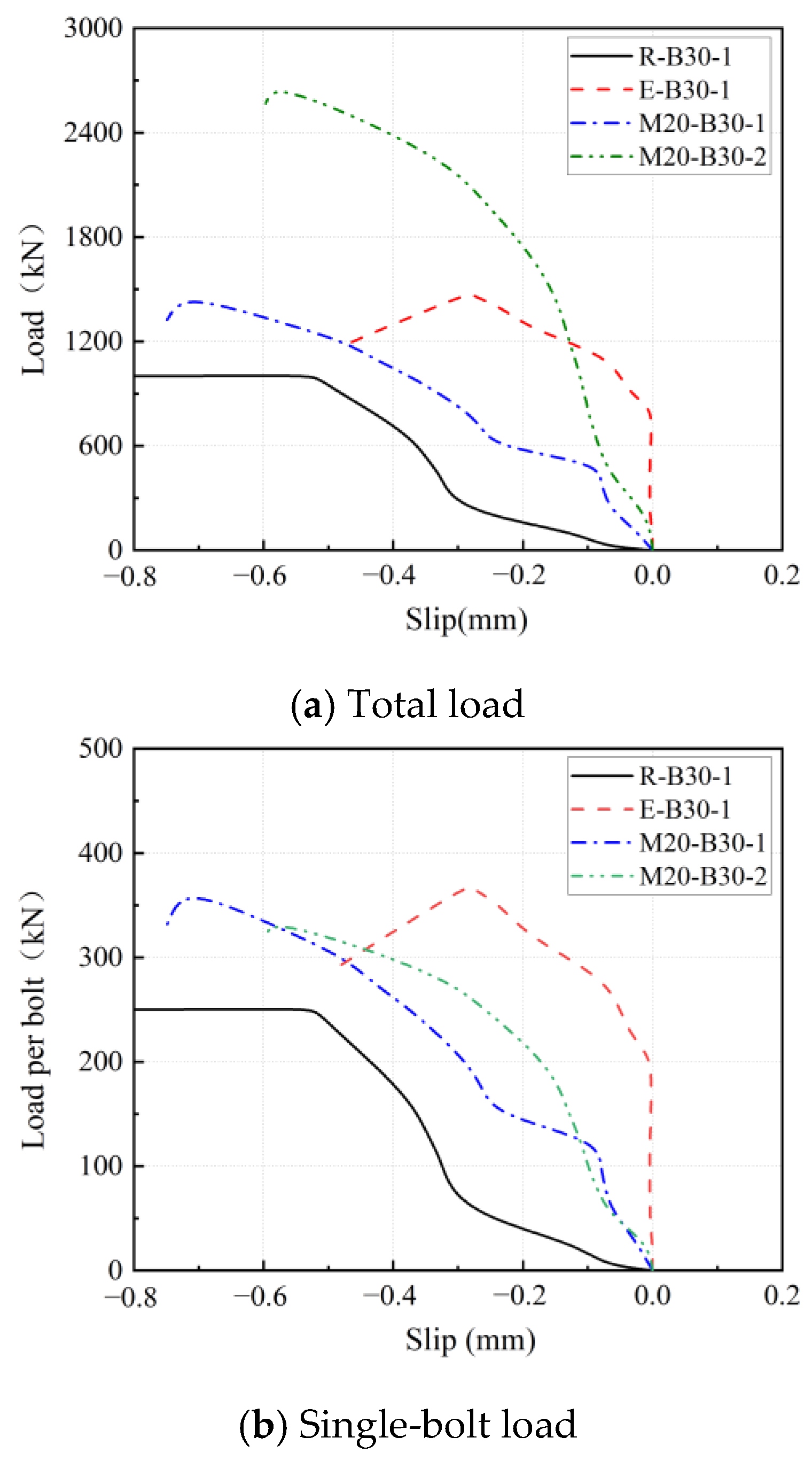
3.2. Load–Slip Relationships
3.3. Load–Dilatancy Curves
3.4. Ultimate Loads
4. Applicability of Theoretical Formulae
5. Verification of Interfacial Shear-Bearing Capacity of ASSJ Design
6. Conclusions
- (1)
- Compared with specimens with barely roughened interfaces, epoxy resin and epoxy mortar employed at the steel–concrete interface can increase the shear-bearing capacity of connections by approximately 47.71% and 43.46%, respectively. The interface treatment method using epoxy mortar can also improve the ductility and stiffness, while the specimen smeared with epoxy resin has excessive stiffness, and the failure mode belongs to brittle failure. The slippage of the specimen smeared with epoxy resin was 0.78 mm at peak load, which was significantly lower than the 8.23 mm slippage of the specimen with the epoxy mortar layer.
- (2)
- Compared with the specimen with a single row of bolts, the shear-bearing capacity of a single bolt in the specimen with two rows of bolts exhibited approximately an 8% reduction, due to the uneven transmission of stress and concrete overstressing.
- (3)
- By comparing the relevant formulae for shear connectors with the test value, it is shown that the shear-bearing capacity of high-strength bolt connections calculated by the formulae of EC 4, AASHTO, and GB50017 can accurately predict the shear-bearing capacity of large-diameter bolt connectors with an epoxy resin or epoxy mortar layer. The GB50017 formula was recommended for calculating the shear-bearing capacity of the novel bolt connection in this study.
- (4)
- Under the most unfavorable load on one side, the maximum vertical and horizontal shear force borne by bolts in the ASSJ of an actual rehabilitation project was 49.4 kN and 148.0 kN, respectively, which is less than the calculated GB50017 formula value of 286.8 kN. The connection design of the ASSJ can meet the requirements of load-bearing capacity under the combined action of vertical load and eccentric moment.
- (5)
- In future work, the long-term performance of the proposed connection under various environmental conditions (e.g., cyclic loading, temperature variations, and moisture exposure) should be investigated to achieve a comprehensive understanding of the structural behaviors of the proposed novel shear connection. This research would provide valuable insights into the durability and aging behavior of the connection, thereby further enhancing its practical application in bridge rehabilitation projects.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Al-Kheetan, M.J.; Al-Tarawneh, M.; Ghaffar, S.H.; Chougan, M.; Jweihan, Y.S.; Rahman, M.M. Resistance of hydrophobic concrete with different moisture contents to advanced freeze–thaw cycles. Struct. Concr. 2021, 22, E1050–E1061. [Google Scholar] [CrossRef]
- Li, P.; Han, P.; Ma, Y.L.; Chen, C.J. Analysis of Accident Mechanism and Reinforcement Measures for Single Column Pier Ramp Bridge. Urban Roads Bridges Flood Control 2016, 2, 78–81 + 10–11. (In Chinese) [Google Scholar]
- Wang, F.; Wu, H.Y.; Zhao, R.X. Causes and lessons of bridge collapse accidents in past three years at home and abroad. Urban Roads Bridges Flood Control 2020, 12, 73–76. (In Chinese) [Google Scholar]
- Makhaik, R. 4 Loaded Trucks Overturn Defense Bridge in Himachal; Hill Post: Shimla, India, 2010. [Google Scholar]
- Zhang, J.; Cheng, H.L. Inspiration from the “12.18” Production Safety Responsibility Accident at the Huahu Interchange of the Shanghai Chongqing Expressway. China Highw. 2022, 20, 20–21. (In Chinese) [Google Scholar]
- Xi, C. Design and numerical simulation of adding steel cover beams to curved beam single column piers. Transp. World 2022, 35, 132–135. (In Chinese) [Google Scholar]
- Kwon, G.; Engelhardt, M.D.; Klingner, R.E. Behavior of post-installed shear connectors under static and fatigue loading. J. Constr. Steel Res. 2010, 66, 532–541. [Google Scholar] [CrossRef]
- Kwon, G.; Engelhardt, M.D.; Klingner, R.E. Experimental behavior of bridge beams retrofitted with postinstalled shear connectors. J. Bridge Eng. 2011, 16, 536–545. [Google Scholar] [CrossRef]
- Kwon, G.; Engelhardt, M.D.; Klingner, R.E. Parametric studies and preliminary design recommendations on the use of postinstalled shear connectors for strengthening noncomposite steel bridges. J. Bridge Eng. 2012, 17, 310–317. [Google Scholar] [CrossRef]
- Chen, Y.T.; Zhao, Y.; West, J.S.; Walbridge, S. Behaviour of steel–precast composite girders with through-bolt shear connectors under static loading. J. Constr. Steel Res. 2014, 103, 168–178. [Google Scholar] [CrossRef]
- Guo, S.Y.; Zhang, X.; Chen, J.Z.; Mou, B.; Shang, H.S.; Wang, P.; Zhang, L.; Ren, J. Mechanical and interface bonding properties of epoxy resin reinforced Portland cement repairing mortar. Constr. Build. Mater. 2020, 264, 120715. [Google Scholar] [CrossRef]
- Chen, P.; Li, Y.; Zhou, X.; Wang, H.; Li, J. Study on the Bond Performance of Epoxy Resin Concrete with Steel Reinforcement. Buildings 2024, 14, 2905. [Google Scholar] [CrossRef]
- Wang, C.; Fan, Z.; Li, C.; Zhang, H.; Xiao, X. Preparation and engineering properties of low-viscosity epoxy grouting materials modified with silicone for microcrack repair. Constr. Build. Mater. 2021, 290, 123270. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, Z.; Fang, Z.; Fang, S.; Tu, W.; Mo, F.; Xie, S.; Liu, J. Rapid hardening high performance concrete (RHHPC) for bridge expansion joints: From material properties to interfacial shear performance. Constr. Build. Mater. 2025, 458, 139638. [Google Scholar] [CrossRef]
- Zou, S.; Chen, R.; Wang, H.; Fang, Z.; Qu, C.; Zhang, C. Effect of shear key geometrical dimensions on seismic performance of prefabricated concrete piers with shallow socket connections. Structures 2025, 71, 107975. [Google Scholar] [CrossRef]
- Weng, K.F.; Zhu, J.X.; Huang, B.T.; Dai, J.G.; Chen, J.F. Interfacial shear behavior between prefabricated Strain-Hardening Ultra-High-Performance Concrete (SH-UHPC) and cast-in-place concrete. Eng. Struct. 2025, 325, 119405. [Google Scholar] [CrossRef]
- Fang, Z.; Hu, L.; Jiang, H.; Fang, S.; Zhao, G.; Ma, Y. Shear performance of high-strength friction-grip bolted shear connector in prefabricated steel–UHPC composite beams: Finite element modelling and parametric study. Case Stud. Constr. Mater. 2023, 18, e01860. [Google Scholar] [CrossRef]
- Tu, W.; Ke, Y.; Shen, R.; Jiang, H.; Zhang, S.; Tian, Y.; Cao, Z. Interfacial shear behavior of PBL deeply embedded in UHPC considering end-bearing effect. J. Constr. Steel Res. 2025, 226, 109242. [Google Scholar] [CrossRef]
- Xiao, J.; Liu, L.; Zeng, H.; Zhai, K.; Fu, J.; Jiang, H.; Pang, L. Research on the bond performance between glass fiber reinforced polymer (GFRP) bars and Ultra-high performance concrete (UHPC). J. Build. Eng. 2024, 98, 111340. [Google Scholar] [CrossRef]
- Ataei, A.; Zeynalian, M.; Yazdi, Y. Cyclic behaviour of bolted shear connectors in steel-concrete composite beams. Eng. Struct. 2019, 198, 109455. [Google Scholar] [CrossRef]
- Fang, Z.; Wu, J.; Zhao, G.; Fang, S.; Ma, Y.; Jiang, H. Shear performance and design recommendations of single embedded nut bolted shear connectors in prefabricated steel–UHPC composite beams. Steel Compos. Struct. 2024, 50, 319–336. [Google Scholar]
- Xu, Q.; Sebastian, W.; Lu, K.; Yao, Y.; Wang, J. Longitudinal shear performance of lightweight steel-UHPC composite connections based on large-diameter high strength friction-grip bolts. Eng. Struct. 2022, 260, 114220. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, Z.; Wu, C.; Wang, H.; Yang, J.; Zou, Y. Shear performance of high-strength bolt-epoxy bonding composite connector in steel-concrete composite structure. Structures 2024, 61, 106085. [Google Scholar] [CrossRef]
- Zhang, L.; Deng, B.; He, B.; Jiang, H.; Xiao, J.; Tian, Y.; Fang, J. Experimental Investigation on Shear Behavior of Non-Stirrup UHPC Beams under Larger Shear Span–Depth Ratios. Buildings 2024, 14, 1374. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, L.; Deng, B.; Gao, X.; Xie, S.; Sha, Z.; Chen, M. The direct shear behavior of the ultra-high performance concrete-filled socket connections between the bridge piers and footings. Structures 2024, 66, 106888. [Google Scholar] [CrossRef]
- Chen, X.; Yang, Y.; Xue, Y.; Yu, Y.; Feng, S. Shear behavior of large studs and novel bolted connectors in steel-UHPC composite beams. Structures 2022, 45, 2091–2103. [Google Scholar] [CrossRef]
- Pavlović, M.; Marković, Z.; Veljković, M.; Buđevac, D. Bolted shear connectors vs. headed studs behaviour in push-out tests. J. Constr. Steel Res. 2013, 88, 134–149. [Google Scholar] [CrossRef]
- Jiang, J.; Zhou, Z.; Wang, H.; Zou, Y.; Zhang, Z.; Liang, H. Shear properties of composite steel plate connectors for prefabricated steel–concrete composite beams. Structures 2023, 58, 105360. [Google Scholar] [CrossRef]
- Sithara, K.P.; Shajee, S. Analysis of High Strength Friction Grip Bolted Shear Connectors in Composite Beam Section. Int. J. Innov. Res.Sci. Eng. Technol. 2016, 5, 13382–13387. [Google Scholar]
- Dallam, L.N. High strength bolt shear connectors-pushout tests. J. Proc. 1968, 65, 767–769. [Google Scholar]
- Luo, J.; Wu, G.; Zhao, G.; Fang, S.; Jiang, H.; Xiao, J. Experimental and numerical analysis on shear performance of single embedded nut bolted shear connectors in prefabricated steel-UHPC composite structures under cyclic loading. Structures 2025, 73, 108446. [Google Scholar] [CrossRef]
- Jiang, H.; Fang, H.; Wu, J.; Fang, Z.C.; Fang, S.; Chen, G.F. Push-out tests on demountable high-strength friction-grip bolt shear connectors in steel–precast UHPC composite beams for accelerated bridge construction. Steel Compos. Struct. 2022, 45, 797–818. [Google Scholar]
- Xian, B.; Wang, G.; Ma, F.; Fang, S.; Jiang, H.; Xiao, J. Shear performance of single embedded nut bolted shear connectors in precast steel–UHPC composite beams under combined tension-shear loads. Case Stud. Constr. Mater. 2024, 21, e03558. [Google Scholar] [CrossRef]
- Ataei, A.; Mahmoudy, S.A.; Zeynalian, M.; Chiniforush, A.A.; Ngo, T.D. Experimental study of innovative bolted shear connectors in demountable cold-formed steel–concrete composite beams. Thin-Walled Struct. 2023, 192, 111116. [Google Scholar] [CrossRef]
- Fang, Z.; Fang, H.; Li, P.; Jiang, H.; Chen, G. Interfacial shear and flexural performances of steel–precast UHPC composite beams: Full-depth slabs with studs vs. demountable slabs with bolts. Eng. Struct. 2022, 260, 114230. [Google Scholar] [CrossRef]
- Gesoğlu, M.; Güneyisi, E.M.; Güneyisi, E.; Yılmaz, M.E.; Mermerdaş, K. Modeling and analysis of the shear capacity of adhesive anchors post-installed into uncracked concrete. Compos. Part B Eng. 2014, 60, 716–724. [Google Scholar] [CrossRef]
- Porcarelli, S.; Shedde, D.; Wang, Z.; Ingham, J.M.; Giongo, I.; Dizhur, D. Tension and shear anchorage systems for limestone structures. Constr. Build. Mater. 2021, 272, 121616. [Google Scholar] [CrossRef]
- Mahrenholtz, P.; Eligehausen, R. Post-installed concrete anchors in nuclear power plants: Performance and qualification. Nucl. Eng. Des. 2015, 287, 48–56. [Google Scholar] [CrossRef]
- Siamakani, S.Y.M.; Jiradilok, P.; Nagai, K.; Sahamitmongkol, R. Discrete mesoscale analysis of adhesive anchors under tensile load taking into account post-installed reinforcement. Constr. Build. Mater. 2020, 262, 120778. [Google Scholar] [CrossRef]
- Epackachi, S.; Esmaili, O.; Mirghaderi, S.R.; Behbahani, A.A.T. Behavior of adhesive bonded anchors under tension and shear loads. J. Constr. Steel Res. 2015, 114, 269–280. [Google Scholar] [CrossRef]
- Alhaidary, H.; Al-Tamimi, A.K. Importance of performance certification for post-installed anchors: An experimental assessment. Structures 2021, 29, 273–285. [Google Scholar] [CrossRef]
- Ceroni, F.; Darban, H.; Luciano, R. Analysis of bond behavior of injected anchors in masonry elements by means of Finite Element Modeling. Compos. Struct. 2020, 241, 112099. [Google Scholar] [CrossRef]
- Berthet, J.F.; Yurtdas, I.; Delmas, Y.; Li, A. Evaluation of the adhesion resistance between steel and concrete by push out test. Int. J. Adhes. Adhes. 2011, 31, 75–83. [Google Scholar] [CrossRef]
- Luo, Y.; Li, A.; Kang, Z. Parametric study of bonded steel–concrete composite beams by using finite element analysis. Eng. Struct. 2012, 34, 40–51. [Google Scholar] [CrossRef]
- Meaud, C.; Jurkiewiez, B.; Ferrier, E. Steel–concrete bonding connection: An experimental study and non-linear finite element analysis. Int. J. Adhes. Adhes. 2014, 54, 131–142. [Google Scholar] [CrossRef]
- Jurkiewiez, B.; Meaud, C.; Ferrier, E. Non-linear models for steel–concrete epoxy-bonded beams. J. Constr. Steel Res. 2014, 100, 108–121. [Google Scholar] [CrossRef]
- Larbi, A.S.; Ferrier, E.; Jurkiewiez, B.; Hamelin, P. Static behaviour of steel concrete beam connected by bonding. Eng. Struct. 2007, 29, 1034–1042. [Google Scholar] [CrossRef]
- Rauscher, S.; Hegger, J. Modern composite structures made of high performance materials. Compos. Constr. Steel Concr. VI 2008, 19, 691–702. [Google Scholar]
- Johnson, R.P.; Anderson, D. Designers’ Guide to EN 1994-1-1: Eurocode 4: Design of Composite Steel and Concrete Structures. General Rules and Rules for Buildings; Thomas Telford: London, UK, 2004. [Google Scholar]
- ASTM C1231/C1231M-15; Standard Practice for Use of Unbond Caps in Determination of Compressive Strength of Hardened Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2015.
- ASTM C469/C469M-14; Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM A370-14; Standard Test Methods and Definitions for Mechanical Testing of Steel Products. ASTM International: West Conshohocken, PA, USA, 2014.
- Dai, X.H.; Lam, D.; Saveri, E. Effect of concrete strength and stud collar size to shear capacity of demountable shear connectors. J. Struct. Eng. 2015, 141, 04015025. [Google Scholar] [CrossRef]
- AASHTO LRFD. Bridge Design Specifications, 8th ed.American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2017. [Google Scholar]
- GB 50017-2017; Standard for Design of Steel Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China, China Architecture & Building Press: Beijing, China, 2017. (In Chinese)
- JSCE. Standard Specifications for Steel and Composite Structures; Japan Society of Civil Engineers (JSCE): Tokyo, Japan, 2007. [Google Scholar]
- Liu, X.; Bradford, M.A.; Lee, M.S.S. Behavior of high-strength friction-grip bolted shear connectors in sustainable composite beams. J. Struct. Eng. 2015, 141, 04014149. [Google Scholar] [CrossRef]
- JTG 3362-2018; Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts. Ministry of Transport of the People’s Republic of China: Beijing, China, 2017. (In Chinese)

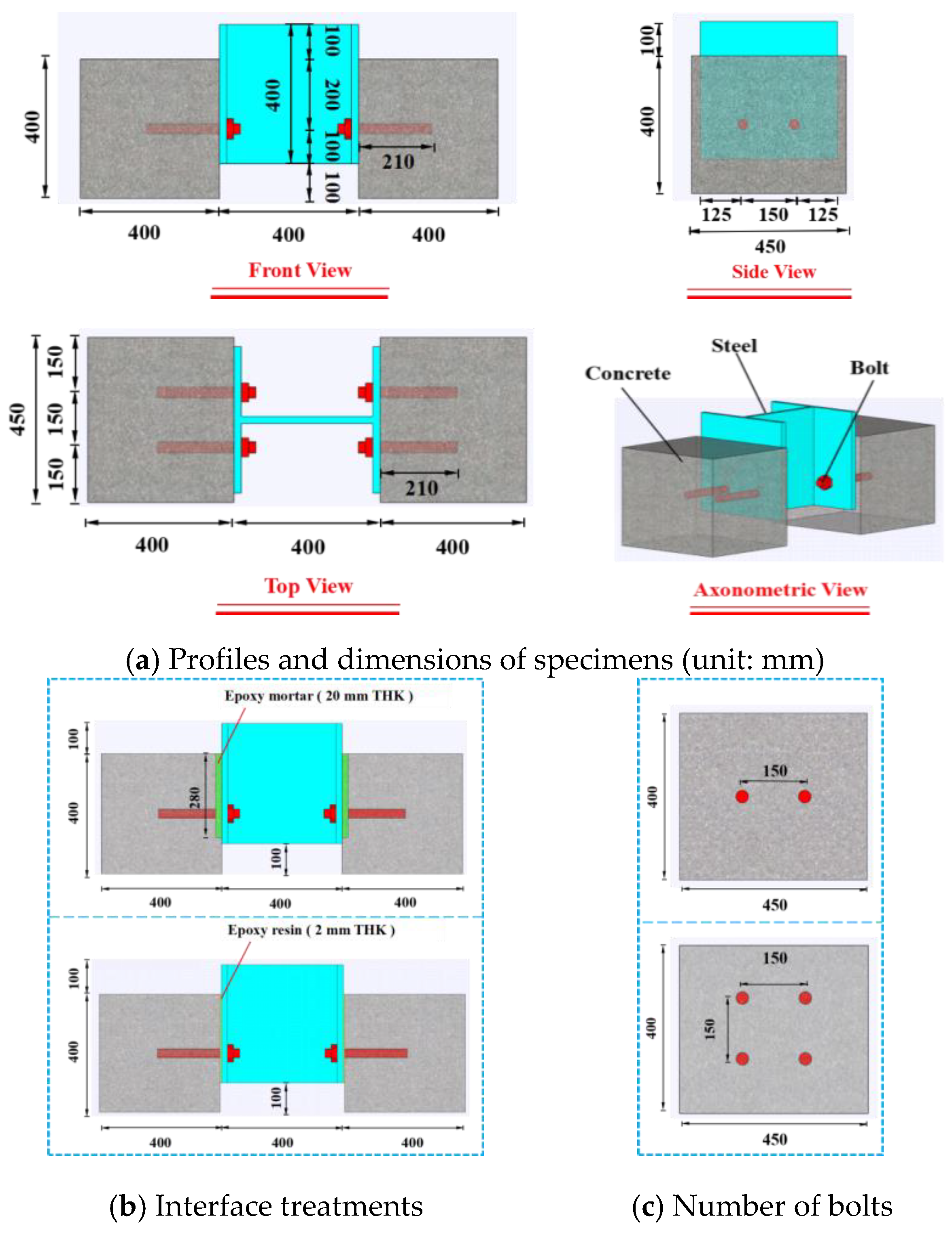





| No. | Specimen Name | Concrete Grade | Bolt Diameter D (mm) | Bolt Row/Bolt Number | Surface Treatment Method | Steel Grade |
|---|---|---|---|---|---|---|
| 1 | R-B30-1 | C40 | 30 | 1/4 | Barely rough | Q355 |
| 2 | E-B30-1 | C40 | 30 | 1/4 | Rough + epoxy resin | Q355 |
| 3 | M20-B30-1 | C40 | 30 | 1/4 | Rough + epoxy mortar | Q355 |
| 4 | M20-B30-2 | C40 | 30 | 2/8 | Rough + epoxy mortar | Q355 |
| Material Types | Compressive Strength fcu (MPa) | Elastic Modulus Ec (MPa) | Poisson’s Ratio |
|---|---|---|---|
| Concrete | 42.2 | 32345 | 0.204 |
| Epoxy mortar | 94.5 | 38837 | 0.237 |
| Material types | Compressive strength fcu (MPa) | Tensile strength ftu (MPa) | Bonding strength fs (MPa) |
| Epoxy resin | 122.9 | 44.2 | 4.4 |
| Material types | Yield strength fy (MPa) | Ultimate Strength fu (MPa) | |
| Bolt | 602.41 | 664.23 | |
| Steel beam | 363.29 | 515.03 |
| Specimens | Pu (kN) | (mm) | Failure Mode |
|---|---|---|---|
| R-B30-1 | 1003.85 | 14.06 | Bolt fracture and concrete spalling |
| E-B30-1 | 1482.86 | 0.78 | Bolt fracture |
| M20-B30-1 | 1440.14 | 8.23 | Bolt fracture |
| M20-B30-2 | 2654.56 | 7.77 | Bolt fracture and concrete spalling |
| Source | Formula | Parameter |
|---|---|---|
| EC4 | : Ultimate shear-bearing capacity of bolts (N) : Nominal bolt diameter (mm) : Concrete compressive strength (MPa) : Effective cross-sectional area of bolts (mm2) : Elastic modulus of concrete (MPa) : Yield strength of bolts (MPa) : Ultimate strength of bolts (MPa) : Bolt depth : Aspect ratio factor, taken as 1.0 in this article : Coefficient, here set as 0.75 : Design safety factor, usually taken as 1.25, here set as 1.0 | |
| AASHTO-LFRD | ||
| GB50017-2017 | ||
| JSCE | ||
| Kwon | ||
| Liu |
| Specimen | PE (kN) | PA (kN) | PG (kN) | PJ (kN) | PK (kN) | PL (kN) | PT (kN) | PT/PE | PT/PA | PT/PG | PT/PJ | PT/PK | PT/PL |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R-B30-1 | 241.9 (298.0) | 245.8 (279.4) | 281.8 (286.8) | 261.6 | 186.3 | 245.9 | 250.96 | 1.04 | 1.02 | 0.89 | 0.96 | 1.35 | 1.02 |
| E-B30-1 | 241.0 (298.0) | 245.8 (279.4) | 281.8 (286.8) | 261.6 | 186.3 | 245.9 | 370.72 | 1.53 (1.24) | 1.51 (1.33) | 1.32 (1.29) | 1.42 | 1.99 | 1.51 |
| M20-B30-1 | 241.9 (298.0) | 245.8 (279.4) | 281.8 (286.8) | 261.6 | 186.3 | 245.9 | 360.04 | 1.49 (1.21) | 1.46 (1.29) | 1.28 (1.26) | 1.38 | 1.93 | 1.46 |
| M20-B30-2 | 241.9 (298.0) | 245.8 (279.4) | 281.8 (286.8) | 261.6 | 186.3 | 245.9 | 331.82 | 1.37 (1.11) | 1.35 (1.19) | 1.18 (1.16) | 1.27 | 1.78 | 1.35 |
| AVG (remove R-B30-1) | 1.46 (1.19) | 1.44 (1.27) | 1.26 (1.23) | 1.36 | 1.90 | 1.44 | |||||||
| STDEV (remove R-B30-1) | 0.083 | 0.082 | 0.072 | 0.078 | 0.108 | 0.082 | |||||||
| COV (remove R-B30-1) | 0.057 | 0.057 | 0.057 | 0.057 | 0.057 | 0.057 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, G.; Zhou, C.; Wu, S.; Zhang, L.; Xiao, J.; Li, P.; Chen, Z.; Shi, Q.; Hu, J.; Jiang, H. Interfacial Shear Behavior of Novel Connections Between Concrete Bridge Piers and Anti-Overturning Steel Supporting Joists. Buildings 2025, 15, 1299. https://doi.org/10.3390/buildings15081299
Mei G, Zhou C, Wu S, Zhang L, Xiao J, Li P, Chen Z, Shi Q, Hu J, Jiang H. Interfacial Shear Behavior of Novel Connections Between Concrete Bridge Piers and Anti-Overturning Steel Supporting Joists. Buildings. 2025; 15(8):1299. https://doi.org/10.3390/buildings15081299
Chicago/Turabian StyleMei, Gongyong, Chengan Zhou, Shengze Wu, Lifeng Zhang, Jie Xiao, Peisen Li, Zhenkan Chen, Quan Shi, Jiaxin Hu, and Haibo Jiang. 2025. "Interfacial Shear Behavior of Novel Connections Between Concrete Bridge Piers and Anti-Overturning Steel Supporting Joists" Buildings 15, no. 8: 1299. https://doi.org/10.3390/buildings15081299
APA StyleMei, G., Zhou, C., Wu, S., Zhang, L., Xiao, J., Li, P., Chen, Z., Shi, Q., Hu, J., & Jiang, H. (2025). Interfacial Shear Behavior of Novel Connections Between Concrete Bridge Piers and Anti-Overturning Steel Supporting Joists. Buildings, 15(8), 1299. https://doi.org/10.3390/buildings15081299










