Theoretical Model for Circular Concrete-Filled Steel Tubes Reinforced with Latticed Steel Angles Under Eccentric Loading
Abstract
:1. Introduction
2. Summary of Eccentric Compression Tests of CFST-LSA
3. Proposed Theoretical Model for Axial Compression Resistance of CFST-LSA
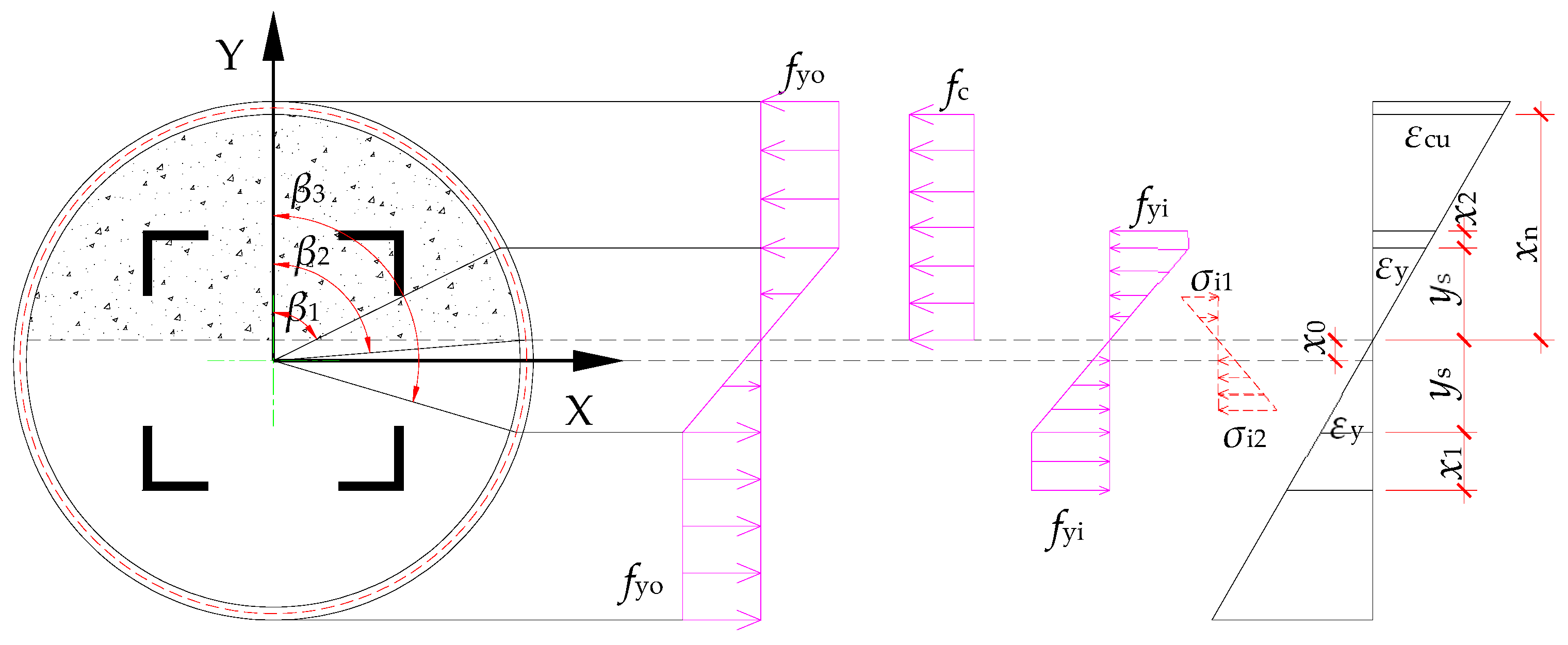
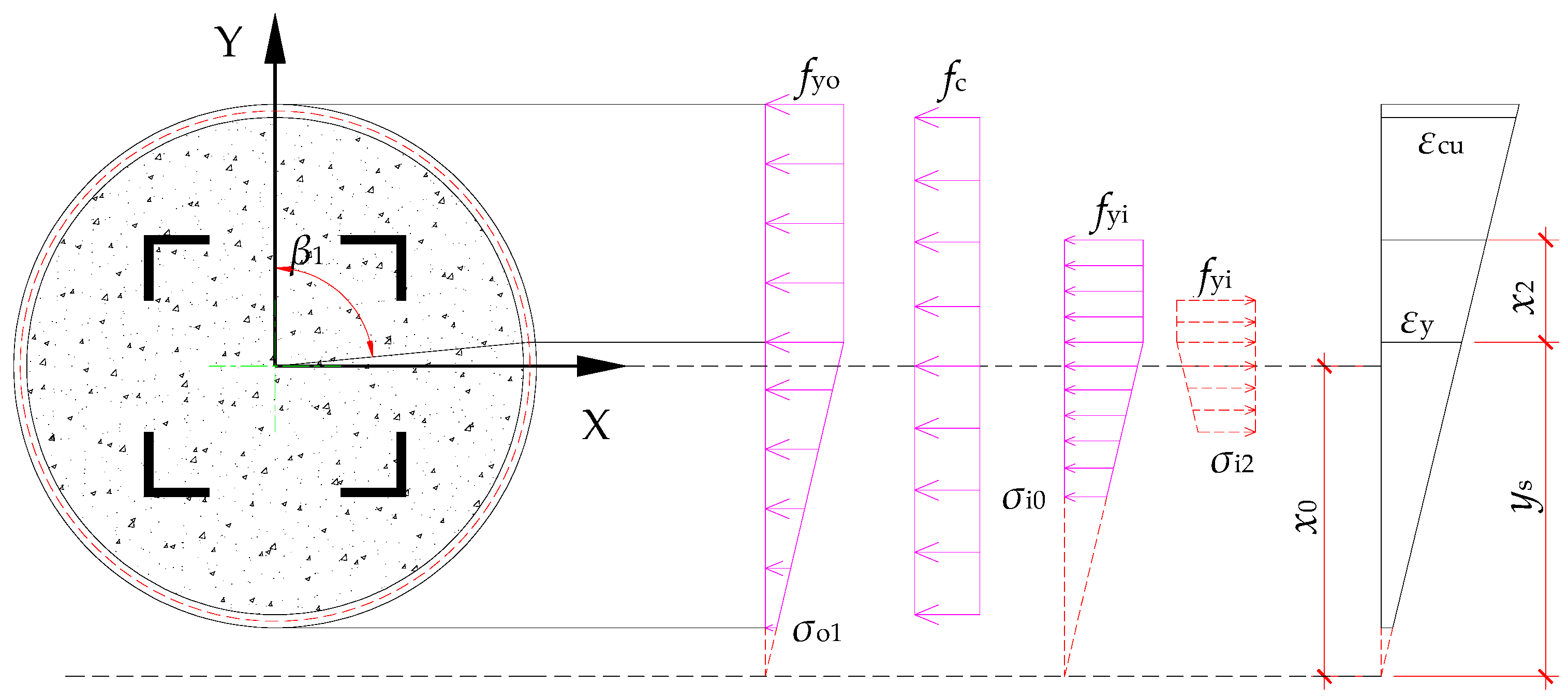
3.1. Case I: Outer Steel Tube and Inner Steel Angles Partially Yield
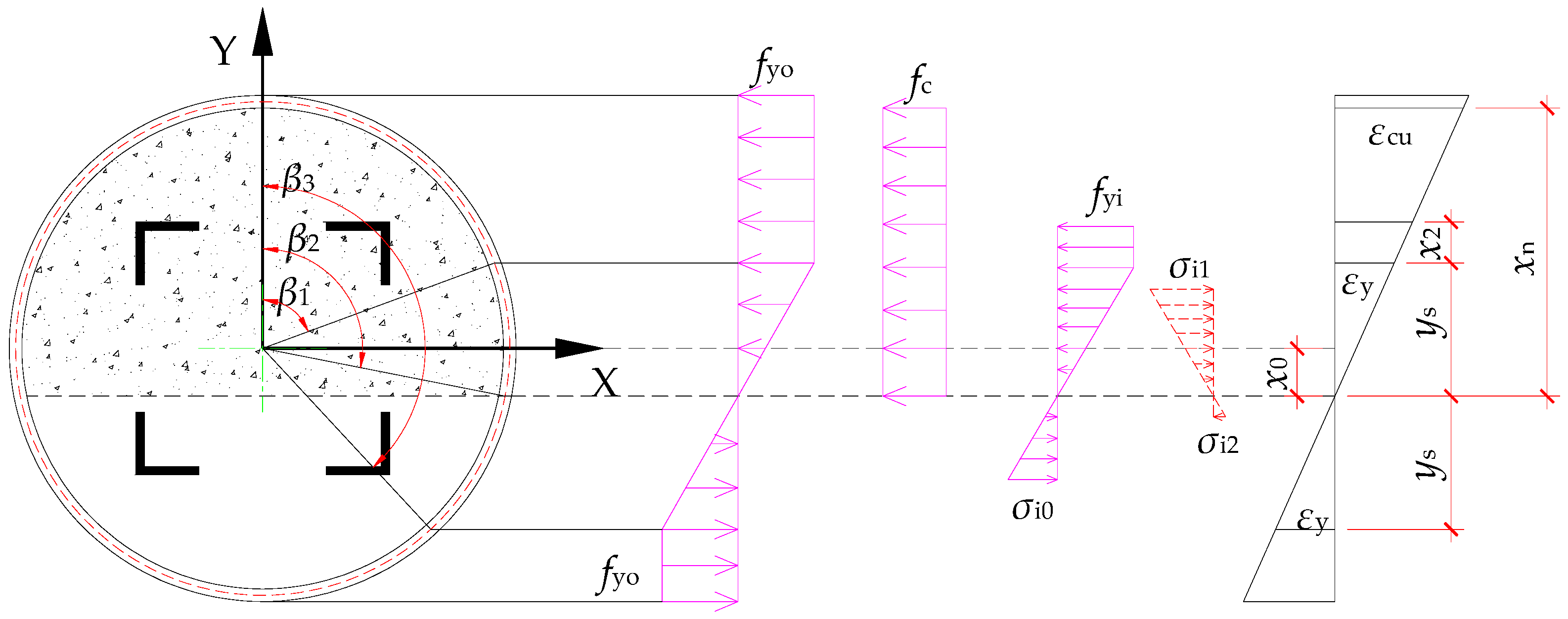
3.2. Case II: Outer Steel Tube Partially Yield and Inner Steel Angles Remain Elastic
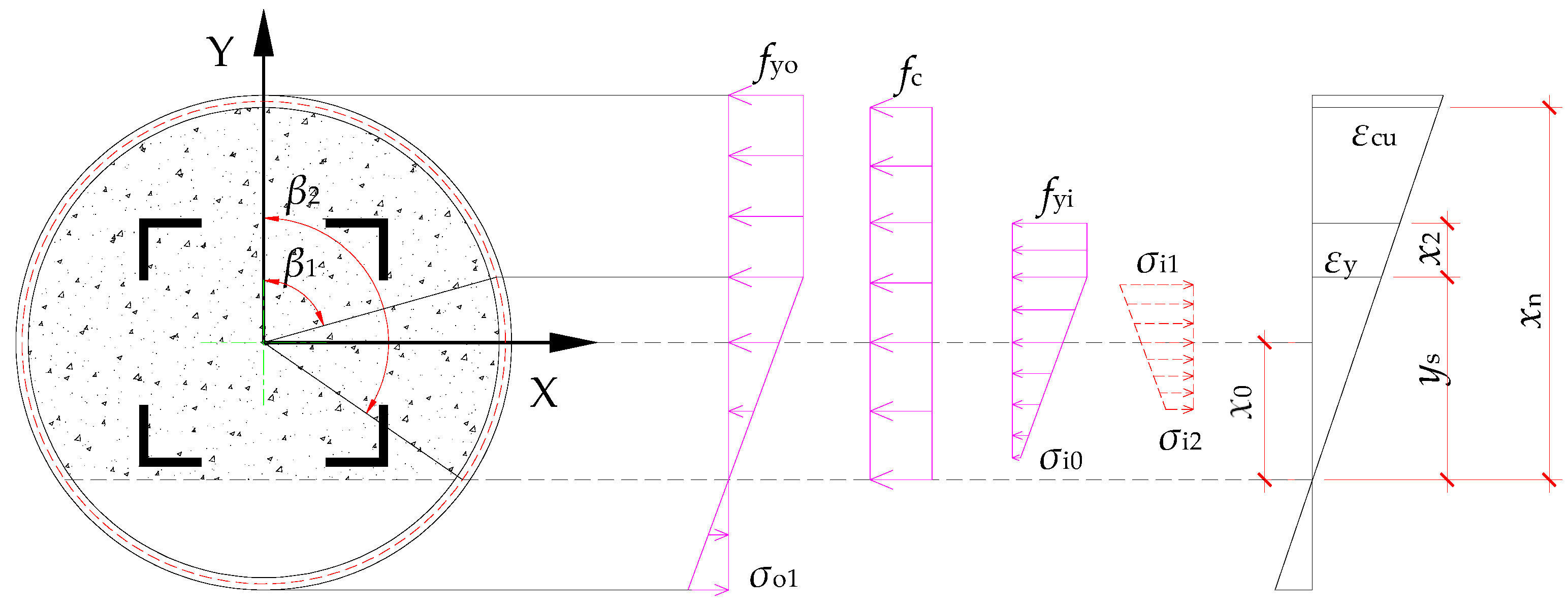
3.3. Case III: Outer Steel Tube and Inner Steel Angles Remain Elastic
3.4. Case IV: Neutral Axis Does Not Pass Through the Outer Steel Tube
3.5. Effect of Second-Order Moment
4. Validation of the Theoretical Model for CFST-LSA
5. Conclusions
- (1)
- According to the four critical states proposed in this paper, the ultimate state of CFST-LSA columns and the position of the neutral axis are closely related to the magnitude of the eccentricity.
- (2)
- The contribution of the steel angles to the eccentric capacity of CFST-LSA columns under eccentric loading conditions is relatively limited.
- (3)
- The proposed theoretical model offers relatively conservative predictions for the experimental and numerical outcomes regarding the eccentric capacity of CFST-LSA columns; the average ratio of experimental results to predicted values is 1.085, with a coefficient of variation of 0.022.
- (4)
- Specimens with an eccentricity of 30 mm experienced failure under Case IV, while those with an eccentricity of 60 mm failed under Case III; hence, the steel tube did not undergo tensile yield failure when the tested specimens reached their ultimate bearing capacity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ac | The area of concrete subjected to compressive stress |
| b | Width of a single steel angle |
| Do | The outer diameter of the steel tube |
| e0 | The eccentric distance |
| Esi | Elastic modulus of steel angle |
| Eso | Elastic modulus of steel tube |
| fc | Cylinder compressive strength of concrete |
| fyi | Yield strength of steel angle |
| fyo | Yield strength of steel tube |
| h | Spacing between the outer edge of two steel angles |
| L0 | Total length of specimen |
| l0 | Effective length of specimen |
| Mc | Bending moment of concrete in the compression zone about the section centroid axis |
| Mi | Bending moment of the steel angles about the section centroid axis |
| Muo | Bending moment of outer steel tube about the section centroid axis |
| Nc | Resultant force of concrete in the compression zone |
| Nexp | Experimental value of the eccentric compressive capacity |
| Ni | Resultant force of steel angles |
| Np | Calculated value of the eccentric compressive capacity using the proposed theoretical model |
| Nuo | Resultant force of steel tube |
| ri | Radius of rotation for the cross-sectional profile of the specimen |
| ro | The radius of the central region of the steel tube wall |
| Ro | The radius of the outer edge of steel tube wall |
| ti | Thickness of a single steel angle |
| to | Wall thickness of steel tube |
| x0 | Distance between the neutral axis and the section centroid axis |
| x1 | The height of the yield zone of the steel angles in the tension region |
| x2 | The height of the yield zone of the steel angles in the compression region |
| xn | Distance between the section centroid axis and the maximum compressive strain of concrete |
| ys | The height of the unyielded region of the steel angles located in the tension or compression zone |
| αsc | The ratio between the yield strain of steel and the ultimate compressive strain of concrete, αsc = εy/εcu |
| εcu | Ultimate compressive strain of concrete |
| εy | Yield strain of steel |
| η | Eccentricity amplification factor |
| σs | Stress of steel tube |
References
- Liu, H.Q.; Liu, Y.Z.; Huo, J.S.; Zhu, D.J. Cyclic behaviour of a novel steel beam-to-prefabricated CFST column connection with threaded sleeve bolts. Structures 2021, 34, 615–629. [Google Scholar] [CrossRef]
- Hu, H.S.; Wang, H.Z.; Guo, Z.X.; Shahrooz, B.M. Axial Compressive Behavior of Square Spiral-Confined High-Strength Concrete-Filled Steel-Tube Columns. ASCE J. Struct. Eng. 2020, 146, 04020136. [Google Scholar] [CrossRef]
- Wang, F.Y.; Young, B.; Gardner, L. Experimental Study of Square and Rectangular CFDST Sections with Stainless Steel Outer Tubes under Axial Compression. ASCE J. Struct. Eng. 2019, 145, 04019139. [Google Scholar] [CrossRef]
- Inai, E.; Mukai, A.; Kai, M.; Tokinoya, H.; Fukumoto, T.; Mori, K. Behavior of concrete-filled steel tube beam columns. ASCE J. Struct. Eng. 2004, 130, 189–202. [Google Scholar] [CrossRef]
- Yu, Z.W.; Ding, F.X.; Lin, S. Researches on mechanical behavior of high-performance concrete filled tubular steel stub columns after high temperature. J. China Railw. Soc. 2003, 25, 71–79. (In Chinese) [Google Scholar]
- Ma, H.; Liu, X.Y.; Chen, Y.C.; Zhao, Y.L. Seismic damage evaluation of steel reinforced recycled concrete filled circular steel tube composite columns. Earthq. Struct. 2022, 23, 445–462. [Google Scholar]
- Ding, F.X.; Pan, Z.C.; Lai, Z.C.; Yu, Z.W. Experimental Study on the Seismic Behavior of Tie Bar Stiffened Round-Ended Concrete-Filled Steel Tube Columns. ASCE J. Bridge Eng. 2020, 25, 04020071. [Google Scholar] [CrossRef]
- Han, L.H.; An, Y.F. Performance of concrete-encased CFST stub columns under axial compression. J. Constr. Steel Res. 2014, 93, 62–76. [Google Scholar] [CrossRef]
- Han, L.H.; Li, W.; Bjorhovde, R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures: Members. J. Constr. Steel Res. 2014, 100, 211–228. [Google Scholar] [CrossRef]
- Shen, L.; Yang, B.; Ding, M.; Feng, C.; Alqawzai, S.; Elchalakani, M.; Chen, K. Experimental Study on the Behavior of a Novel Stiffened Hexagonal CFDST Stub Column under Axial Load. ASCE J. Struct. Eng. 2022, 148, 04021231. [Google Scholar] [CrossRef]
- Yan, Y.X.; Xu, L.H.; Li, B.; Chi, Y.; Yu, M.; Zhou, K.K.; Song, Y. Axial behavior of ultra-high performance concrete (UHPC) filled stocky steel tubes with square sections. J. Constr. Steel Res. 2019, 158, 417–428. [Google Scholar] [CrossRef]
- Zhou, K.; Han, L.H. Experimental and numerical study of temperature developments of composite joints between concrete-encased concrete-filled steel tube columns and reinforced concrete beams. Fire Saf. J. 2020, 116, 103187. [Google Scholar] [CrossRef]
- Zhou, K.; Han, L.H. Modelling the behaviour of concrete-encased concrete-filled steel tube (CFST) columns subjected to full-range fire. Eng. Struct. 2019, 183, 265–280. [Google Scholar] [CrossRef]
- Zhou, K.; Han, L.H. Experimental performance of concrete-encased CFST columns subjected to full-range fire including heating and cooling. Eng. Struct. 2018, 165, 331–348. [Google Scholar] [CrossRef]
- Cai, J.M.; Pan, J.L.; Wu, Y.F. Mechanical behavior of steel-reinforced concrete-filled steel tubular (SRCFST) columns under uniaxial compressive loading. Thin-Walled Struct. 2015, 97, 1–10. [Google Scholar] [CrossRef]
- Wei, J.G.; Luo, X.; Lai, Z.C.; Varma, A.H. Experimental Behavior and Design of High-Strength Circular Concrete-Filled Steel Tube Short Columns. ASCE J. Struct. Eng. 2020, 146, 04019184. [Google Scholar] [CrossRef]
- Varma, A.H.; Ricles, J.M.; Sause, R.; Lu, L.W. Experimental behavior of high strength square concrete-filled steel tube beam-columns. ASCE J. Struct. Eng. 2002, 128, 309–318. [Google Scholar] [CrossRef]
- Shafighfard, T.; Kazemi, F.; Bagherzadeh, F.; Mieloszyk, M.; Yoo, D.Y. Chained machine learning model for predicting load capacity and ductility of steel fiber-reinforced concrete beams. Comput.-Aided Civ. Infrastruct. Eng. 2024, 39, 3573–3594. [Google Scholar] [CrossRef]
- Kazemi, F.; Shafighfard, T.; Yoo, D.Y. Data-driven modeling of mechanical properties of fiber-reinforced concrete: A critical review. Arch. Comput. Methods Eng. 2024, 31, 2049–2078. [Google Scholar] [CrossRef]
- Zhou, X.H.; Yan, B.; Liu, J.P. Behavior of square tubed steel reinforced-concrete (SRC) columns under eccentric compression. Thin-Walled Struct. 2015, 91, 129–138. [Google Scholar] [CrossRef]
- Zhang, S.M.; Li, X.Z.; Li, J.; Lu, W.; Chen, J. Behavior comparison of seven-types of steel-concrete composite stub columns under axial compression. Eng. Struct. 2022, 252, 113637. [Google Scholar] [CrossRef]
- Yang, J.L.; Wang, J.Z.; Zhang, S.; Wang, Z.R. Behavior of eccentrically loaded circular CFRP-steel composite tubed steel-reinforced high-strength concrete columns. J. Constr. Steel Res. 2020, 170, 106101. [Google Scholar] [CrossRef]
- Qi, H.T.; Guo, L.H.; Liu, J.P.; Gan, D.; Zhang, S.M. Axial load behavior and strength of tubed steel reinforced-concrete (SRC) stub columns. Thin-Walled Struct. 2011, 49, 1141–1150. [Google Scholar] [CrossRef]
- Shi, Y.L.; Xian, W.; Wang, W.D.; Li, H.W. Mechanical behaviour of circular steel-reinforced concrete-filled steel tubular members under pure bending loads. Structures 2020, 25, 8–23. [Google Scholar] [CrossRef]
- Xu, F.; Wang, J.; Chen, J.; Wang, Y.H. Load-transfer mechanism in angle-encased CFST members under axial tension. Eng. Struct. 2019, 178, 162–178. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, X.F.; Yan, L.B.; Wu, C. Numerical study on I-section steel-reinforced concrete-filled steel tubes (SRCFST) under bending. Eng. Struct. 2020, 225, 111276. [Google Scholar] [CrossRef]
- Wang, X.D.; Liu, J.P.; Zhou, X.H. Behaviour and design method of short square tubed-steel-reinforced-concrete columns under eccentric loading. J. Constr. Steel Res. 2016, 116, 193–203. [Google Scholar] [CrossRef]
- Ma, H.; Qiang, J.Q.; Xi, J.C.; Zhao, Y.L. Cyclic loading tests and horizontal bearing capacity of recycled concrete filled circular steel tube and profile steel composite columns. J. Constr. Steel Res. 2022, 199, 107572. [Google Scholar] [CrossRef]
- Xu, C.; Wei, Y.-Y.; Yun, Y.-C. Analysis of steel-reinforced concrete-filled-steel tubular (SRCFST) columns under cyclic loading. Constr. Build. Mater. 2012, 28, 88–95. [Google Scholar]
- Liu, J.; Abdullah, J.A.; Zhang, S. Hysteretic behavior and design of square tubed reinforced and steel reinforced concrete (STRC and/or STSRC) short columns. Thin-Walled Struct. 2011, 49, 874–888. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Zang, X.; Chen, Y.F.; Wang, X. Hysteretic behavior and modified design of square TSRC columns with shear studs. Thin-Walled Struct. 2018, 129, 265–277. [Google Scholar] [CrossRef]
- Gan, D.; Guo, L.; Liu, J.; Zhou, X. Seismic behavior and moment strength of tubed steel reinforced-concrete (SRC) beam-columns. J. Constr. Steel Res. 2011, 67, 1516–1524. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, J. Seismic behavior and strength of tubed steel reinforced concrete (SRC) short columns. J. Constr. Steel Res. 2010, 66, 885–896. [Google Scholar] [CrossRef]
- Wang, W.D.; Wei, X.; Hou, C.; Shi, Y.L. Experimental investigation and FE modelling of the flexural performance of square and rectangular SRCFST members. Structures 2020, 27, 2411–2425. [Google Scholar] [CrossRef]
- Wang, Z.B.; Zhang, B.H.; Chen, Z.; Tan, E.L.; Qiu, R.M.; Zheng, T.B. Steel-reinforced concrete-filled rectangular stainless steel tubular columns: Tests, analysis and design. J. Constr. Steel Res. 2025, 226, 109212. [Google Scholar] [CrossRef]
- Chen, J.; Hu, L.; Wang, J.; Song, S.S. Eccentric compression behavior of circular concrete-filled steel tubes reinforced with internal latticed steel angles. Struct. Concr. 2024, 25, 169–184. [Google Scholar] [CrossRef]
- Xu, F.; Chen, J.; Chan, T.M. Numerical investigation on compressive performance of CFST columns with encased built-up lattice-angles. J. Constr. Steel Res. 2017, 137, 242–253. [Google Scholar] [CrossRef]
- Xu, F.; Chen, J.; Jin, W.L. Experimental investigation of thin-walled concrete-filled steel tube columns with reinforced lattice angle. Thin-Walled Struct. 2014, 84, 59–67. [Google Scholar] [CrossRef]
- Wang, J.; Qiu, W.J.; Kong, S.C.; Zhu, J.H. Investigation of the axial compressive behaviour of CFRP-confined circular CFST stub columns with inner latticed steel angles. Compos. Struct. 2022, 280, 114895. [Google Scholar] [CrossRef]
- Hu, L.; Song, S.S.; Chen, J.; Wang, J. Flexural behavior of circular section concrete-filled steel tubes with embedded latticed angles. J. Constr. Steel Res. 2022, 196, 107401. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.R.; Li, H.; Lv, L.Y. Behaviour of square concrete-filled steel tubes reinforced with internal latticed steel angles under bending. Structures 2023, 48, 1436–1454. [Google Scholar] [CrossRef]
- Du, P.; Gan, D.; Yang, Y.; Tan, K.H. Simplified method for analysis of circular steel tubed-reinforced-concrete columns under eccentric compression. Eng. Struct. 2019, 198, 109524. [Google Scholar] [CrossRef]
- Ran, J.; Li, T.; Wang, H.; Zhu, Q.; Zhang, H.; Du, Y.; Li, W. Behavior and design of circular concrete columns strengthened with textile-reinforced mortar subjected to eccentric compression. Structures 2023, 51, 242–257. [Google Scholar] [CrossRef]
- Zeng, J.J.; Guo, Y.C.; Liao, J.J.; Shi, S.W.; Bai, Y.L.; Zhang, L. Behavior of hybrid PET FRP confined concrete-filled high-strength steel tube columns under eccentric compression. Case Stud. Constr. Mater. 2022, 16, e00967. [Google Scholar] [CrossRef]
- Gao, D.; Du, Y.; Chen, Z.; Zhao, B.Z. Behavior of CFRP confined rectangular high-strength concrete-filled steel tubular columns under eccentric compression. Eng. Struct. 2024, 321, 119006. [Google Scholar] [CrossRef]
- Yan, J.B.; Chen, A.; Zhu, J.S. Tests and analysis on circular UHPFRC-filled steel tubular stub columns under eccentric compression. J. Constr. Steel Res. 2021, 178, 106501. [Google Scholar] [CrossRef]
- Hu, H.S.; Xu, L.; Guo, Z.X.; Shahrooz, B.M. Behavior of eccentrically loaded square spiral-confined high-strength concrete-filled steel tube columns. Eng. Struct. 2020, 216, 110743. [Google Scholar] [CrossRef]
- Ahmed, M.; Liang, Q.Q.; Patel, V.I.; Hadi, M.N.S. Behavior of eccentrically loaded double circular steel tubular short columns filled with concrete. Eng. Struct. 2019, 201, 109790. [Google Scholar] [CrossRef]
- Zhao, T.F. Mechanical Behaviors Study of Square Tube Components Filled with Steel Reinforced Concrete. Ph.D. Thesis, Northeastern University, Shenyang, China, 2009. (In Chinese). [Google Scholar]
- Liu, X. Mechanical Behaviors Study of Steel Tube Filled with Steel-Reinforced High-Strength Concrete. Ph.D. Thesis, Northeastern University, Shenyang, China, 2009. (In Chinese). [Google Scholar]
- Xue, L.; Zhang, J.X.; Ruan, C.T.; Wang, X.F. A New Method of Calculating Normal Section Bearing Capacity of SRC Bending Members. Ind. Constr. 2003, 33, 65–70. (In Chinese) [Google Scholar]
- Wang, J. Research and Application on the Mechanical Properties of Concrete-Filled Circular Steel Tubes with Latticed Steel Angles Inside. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2018. (In Chinese). [Google Scholar]
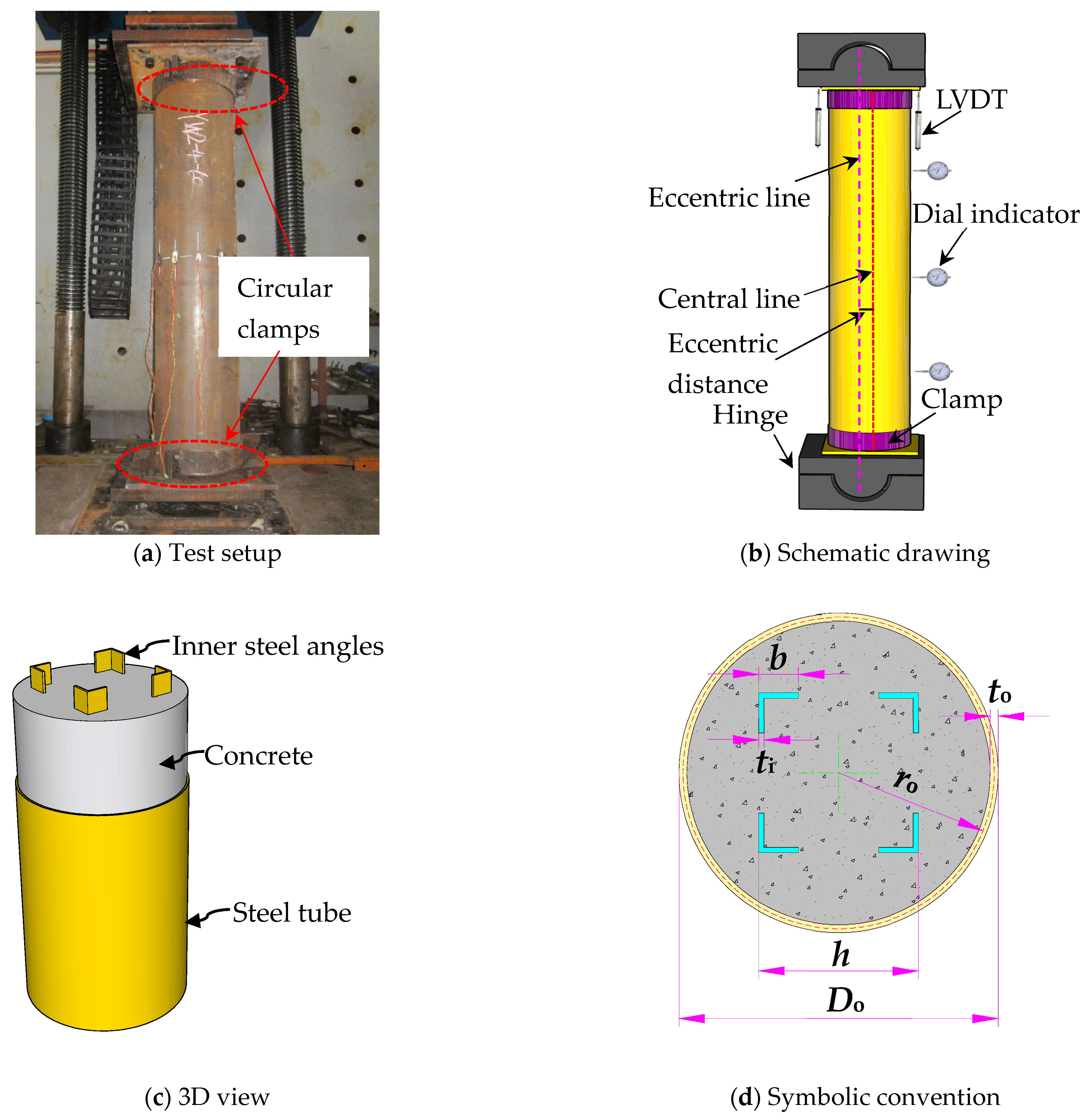
| Specimen Group | Repeated Specimens | L/mm | Do × to/mm | h/mm | b × ti/mm | e0/mm |
|---|---|---|---|---|---|---|
| CFST-30 | / | 2000 | 400 × 5 | / | / | 30 |
| CFST-LSA-A-30 | CFST-LSA-A-30-1 | 2000 | 400 × 5 | 200 | L40 × 4 | 30 |
| CFST-LSA-A-30-2 | 2000 | 400 × 5 | 200 | L40 × 4 | 30 | |
| CFST-LSA-B-30 | CFST-LSA-B-30-1 | 2000 | 400 × 5 | 200 | L50 × 6 | 30 |
| CFST-LSA-B-30-2 | 2000 | 400 × 5 | 200 | L50 × 6 | 30 | |
| CFST-LSA-B-30-3 | 2000 | 400 × 5 | 200 | L50 × 6 | 30 | |
| CFST-60 | / | 2000 | 400 × 5 | / | / | 60 |
| CFST-LSA-A-60 | CFST-LSA-A-60-1 | 2000 | 400 × 5 | 200 | L40 × 4 | 60 |
| CFST-LSA-A-60-2 | 2000 | 400 × 5 | 200 | L40 × 4 | 60 | |
| CFST-LSA-B-60 | CFST-LSA-B-60-1 | 2000 | 400 × 5 | 200 | L50 × 6 | 60 |
| CFST-LSA-B-60-2 | 2000 | 400 × 5 | 200 | L50 × 6 | 60 |
| Failure Type | Neutral Axis Position | Stress State in the Tensile Region | |
|---|---|---|---|
| Outer Steel Tube | Inner Steel Angles | ||
| Case I | √ | Partially yielding | Partially yielding |
| Case II | Partially yielding | Elastic | |
| Case III | Elastic | Elastic | |
| Case IV | × | - | - |
| Reference | Specimen | Experimental or Numerical Failure Mode [52] | Theoretical Failure Mode | η | Nexp/kN | Np/kN | Nexp/Np |
|---|---|---|---|---|---|---|---|
| Chen et al. [36] | CFST-LSA-A-30-1 | Bending-buckling | Case IV | 1.210 | 5811 | 5521 | 1.053 |
| CFST-LSA-A-30-2 | 5921 | 1.072 | |||||
| NM-1 | 6126 | 1.110 | |||||
| CFST-LSA-B-30-1 | Bending-buckling | Case IV | 1.210 | 6383 | 5710 | 1.118 | |
| CFST-LSA-B-30-2 | 6354 | 1.113 | |||||
| CFST-LSA-B-30-3 | 6078 | 1.064 | |||||
| NM-2 | 6408 | 1.122 | |||||
| CFST-LSA-A-60-1 | Bending-buckling | Case III | 1.105 | 5099 | 4691 | 1.087 | |
| CFST-LSA-A-60-2 | 4967 | 1.059 | |||||
| NM-3 | 5031 | 1.072 | |||||
| CFST-LSA-B-60-1 | Bending-buckling | Case III | 1.105 | 5658 | 5229 | 1.082 | |
| CFST-LSA-B-60-2 | 5725 | 1.095 | |||||
| NM-4 | 5529 | 1.057 | |||||
| Mean | 1.085 | ||||||
| COV | 0.022 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wang, J. Theoretical Model for Circular Concrete-Filled Steel Tubes Reinforced with Latticed Steel Angles Under Eccentric Loading. Buildings 2025, 15, 1319. https://doi.org/10.3390/buildings15081319
Li Z, Wang J. Theoretical Model for Circular Concrete-Filled Steel Tubes Reinforced with Latticed Steel Angles Under Eccentric Loading. Buildings. 2025; 15(8):1319. https://doi.org/10.3390/buildings15081319
Chicago/Turabian StyleLi, Zhongpei, and Jun Wang. 2025. "Theoretical Model for Circular Concrete-Filled Steel Tubes Reinforced with Latticed Steel Angles Under Eccentric Loading" Buildings 15, no. 8: 1319. https://doi.org/10.3390/buildings15081319
APA StyleLi, Z., & Wang, J. (2025). Theoretical Model for Circular Concrete-Filled Steel Tubes Reinforced with Latticed Steel Angles Under Eccentric Loading. Buildings, 15(8), 1319. https://doi.org/10.3390/buildings15081319





