Experimental and Numerical Study on Mechanical Performance of Half-Tenon Beam–Column Joint Under Different Reinforcement of Energy Dissipation Plate and Steel Sleeve

Abstract

Two types of reinforcing the half-tenon wood joints, one reinforced with an energy dissipation plate (SW-1) and the other by a steel sleeve with energy dissipation plate (SW-2), were designed. The pure wood beam–column joint specimen SW-0, specimen SW-1 and specimen SW-2 were experimented by the monotonic loading test, and the corresponding failure mode of joints and load–displacement curve were obtained. Based on the reliability of the verified finite element numerical model, the impact of thickness of the energy dissipation plate on the seismic performance of the SW-2 joint was analyzed. The research results show that the SW-0 and SW-1 joints exhibited significant tenon pulling phenomena, while the SW-2 joint did not show this phenomenon. The initial stiffness of the joints is significantly improved after reinforcement, and the initial stiffness of the SW-1 and SW-2 specimens is 2.64 and 7.24 times that of the SW-0 specimen, respectively. The ultimate loads of specimens SW-0, SW-1 and SW-2 are, respectively, 2.8 kN, 6.2 kN and 24.9 kN. The enclosed area of hysteresis loop and the slope of skeleton curve gradually increase as the thickness of the energy dissipation plate increases, resulting in a significant enhancement in energy dissipation capacity. The ultimate bearing capacity of the joint and the slope of skeleton curve exhibit negligible variation when the thickness of energy dissipation plate exceeds 2.0 mm, and the corresponding optimal thickness is obtained as 2 mm.

1. Introduction

Wood possesses excellent thermal insulation properties and better biocompatibility and is recognized as one of the oldest building materials in China. However, natural wood has certain disadvantages, such as initial defects and significant differences in mechanical properties along and across the grain. Considering that China has a large steel production and that steel has advantages such as high strength and stable properties, combining wood and steel at the component level not only results in a light-weight structure with enhanced strength but also integrates modern and cultural elements.

Half-tenon joints reinforced with steel plates were subjected to monotonic loading tests and compared mechanical properties by Karel’Skiy, A. et al. [1], Masaeli, M. et al. [2], and Michele, M. et al. [3] who concluded that the flexural stiffness and bending capacity of the joints were improved by reinforcing the steel plates. The seismic performance of mortise and tenon joints reinforced with FRP material was studied by La Rosa Pilar, D. et al. [4], Gribanov, A.S. et al. [5], and Karagoz, Ü.I. et al. [6] through low-cycle fatigue tests. The results showed that the hysteresis curve of the reinforced joint was more plump than that of the pure one, and the stiffness was improved. Meanwhile, Chen, G. et al. [7] have also used FRP to strengthen concrete–steel double-skin tubular columns and concluded that the hoop rupture strain of cyclically loaded columns was reduced by 10% due to possible damage accumulation. Wooden joints reinforced with self-tapping screws and pure ones were subjected to low-cycle repeated load tests by Kamyar, K. et al. [8], Elbashir, D. et al. [9], and Dar, M.A. et al. [10] who concluded that the withdrawal of the tenon was effectively reduced and the initial stiffness, ductility, and bending capacity of the joint were enhanced by the application of self-tapping screws for reinforcement. The steel tube was reinforced with foam material and subjected to quasi-static test by Shao, J. et al. [11,12,13,14,15,16,17] who concluded that the bearing capacity and deformation capacity of the steel tube significantly increased. Wood joints reinforced with adhesives were designed and conducted under the axial loading tests by Shaimaa, S. et al. [18,19] to investigate the mechanical properties of the joints, who discovered that the tenon pulling phenomenon in the joints was improved after reinforcement, and the most suitable bonding length was found to be 350 mm. The mechanical properties of integrated sleeve mortise and tenon steel–wood composite joints were investigated through experimental and numerical simulation methods by Wang, Z. et al. [20], revealing significant improvements in initial stiffness and ultimate load-carrying capacity after reinforcement. A light steel–wood frame system, braced with oriented strand board (OSB) and featuring a composite gypsum bracing board with an external gypsum filling board, was designed and executed seismic testing by Scotta, R. et al. [21], where this innovative system had high ductility and excellent energy dissipation capabilities to make the structural system suitable for applications in multiple earthquake areas. The one-dimensional steel-wood composite frame was simulated by Chiniforush, A.A. et al. [22,23] using finite element software, and the composite frame model was verified with experimental data, which indicated that both the shear connection stiffness of the wood and the wood shrinkage rate had a certain impact on the long-term performance of the connections. A ten-story benchmark steel–timber hybrid (STH) structure was designed by Offerman, T. et al. [24] to investigate the response of the lateral stability system in high-rise steel–timber hybrid structures, wherein the STH structure exhibited greater lateral deformation compared to steel–concrete structures, and both remained within the code-specified limits.

Currently, the reinforcement methods of mortise–tenon joints that are being considered by researchers include self-tapping screws, metal connectors, and FRP materials. However, the improvements in the overall integrity, load-bearing capacity, and seismic performance of the joints after reinforcement are relatively limited. Therefore, an innovative reinforcement method is necessary to seek to address this issue. Two different types of energy dissipation plates and steel sleeve reinforcement for beam–column half-tenon joints were designed in this paper to enhance the overall integrity of mechanical performance. Three types of beam–column joints including the pure wood joint (SW-0), the joint reinforced with two energy dissipation plates (SW-1), and the joint reinforced with a steel sleeve and two energy dissipation plates (SW-2) were designed and fabricated. Monotonic loading tests were conducted on these three groups of specimens to obtain the failure modes and load–displacement curves of the joint. The ABAQUS V6.11 finite element software was utilized to perform numerical simulations on these specimens to verify the reliability of the model and to investigate the effects of different thicknesses of energy dissipation plates on the hysteresis curves, skeleton curves, and stress distribution in various components of the SW-2 joint, such as wooden columns, wooden beams, and steel sleeves.

2. Design and Fabrication of the Joints

2.1. Test Materials

Chinese fir, Q235B steel and high-strength bolts with a grade of 10.9 and a nominal diameter of 10 mm were selected as the materials for the monotonic loading experiment.

(1)

Chinese fir

The physical and mechanical properties of Chinese fir were tested in accordance with the standards [25,26]. Standard-sized Chinese fir specimens were used in groups of 5 for testing the bending strength, elastic modulus, compressive strength of the specimen. The average values and standard deviations of the mechanical properties of Chinese fir are presented in

Table 1. The average values and standard deviations of the mechanical properties of Chinese fir.

Mechanical Properties	Average Value	Standard Deviation
Elastic modulus	11,059.71 MPa	58.61 MPa
Compressive strength	38.14 MPa	1.15 MPa
Poisson’s ratio	0.54	0.03
Density	247.21 kg/m3	0.42 kg/m3

.

(2)

Q235B steel

According to the reference [27], the mechanical properties of Q235B steel were tested using five sets of standard tensile specimens. The average values and standard deviations of the mechanical properties of Q235B steel are shown in

Table 2. The average values and standard deviations of the mechanical properties of Q235B steel.

Mechanical Properties	Average Value	Standard Deviation
Elastic modulus	205.85 GPa	5.26 GPa
Yield strength	233.87 MPa	2.72 MPa
Ultimate strength	372.21 MPa	3.85 MPa

.

(3)

High-strength bolt

According to the reference [28], the mechanical properties of five sets of standard high-strength bolt specimens were tested. The average values and standard deviations of the mechanical properties of high-strength bolts are shown in

Table 3. The average values and standard deviations of the mechanical properties of high-strength bolts.

Mechanical Properties	Average Value	Standard Deviation
Yield strength	958.62 MPa	5.11 MPa
Tensile strength	1042.51 MPa	3.72 MPa

.

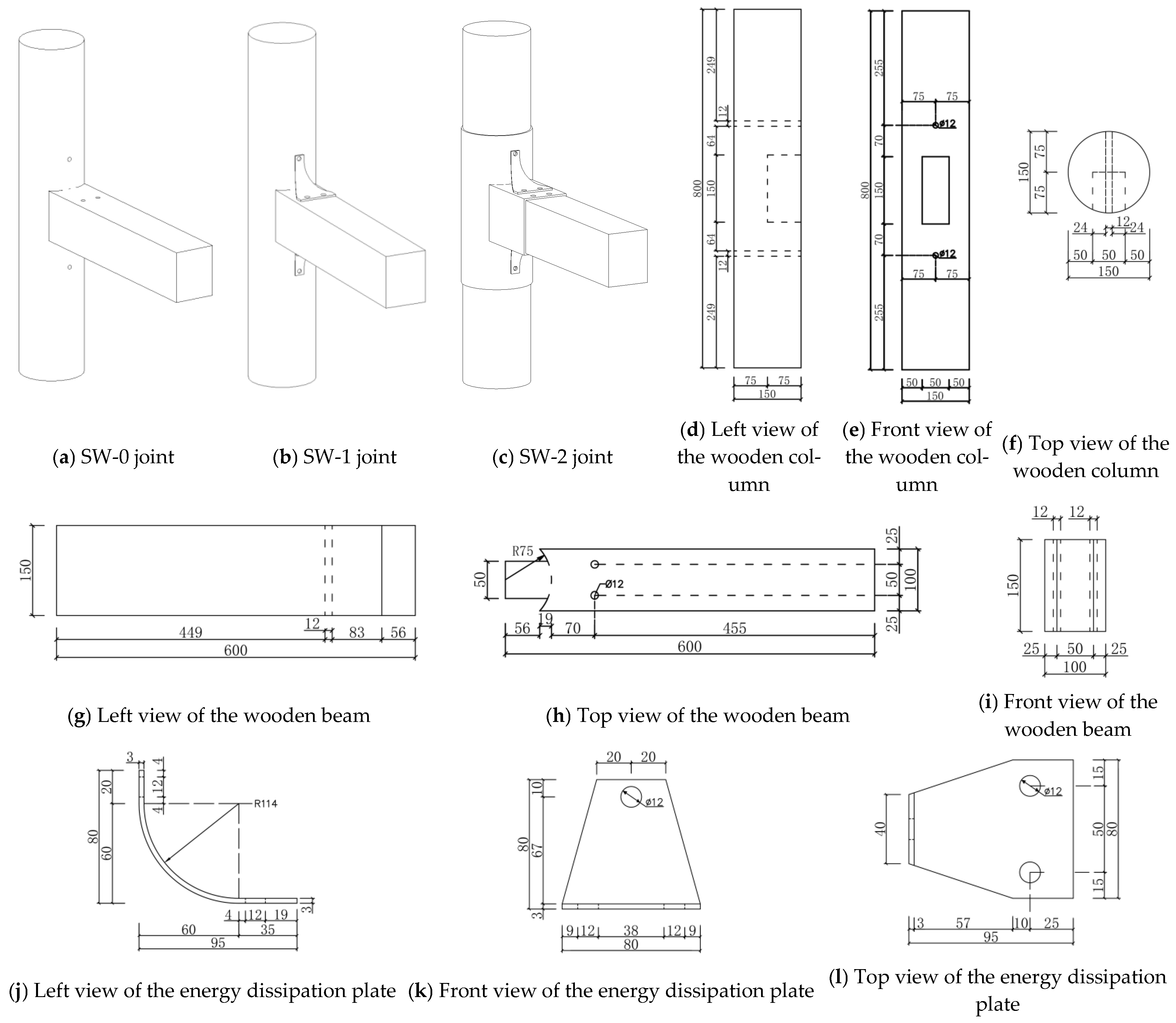
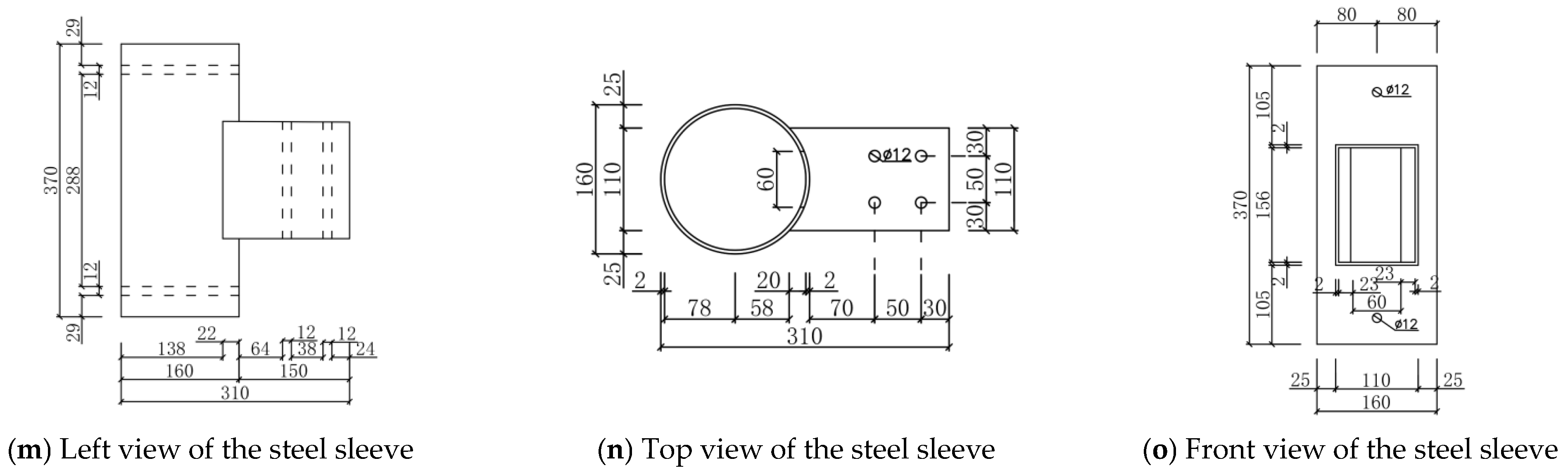
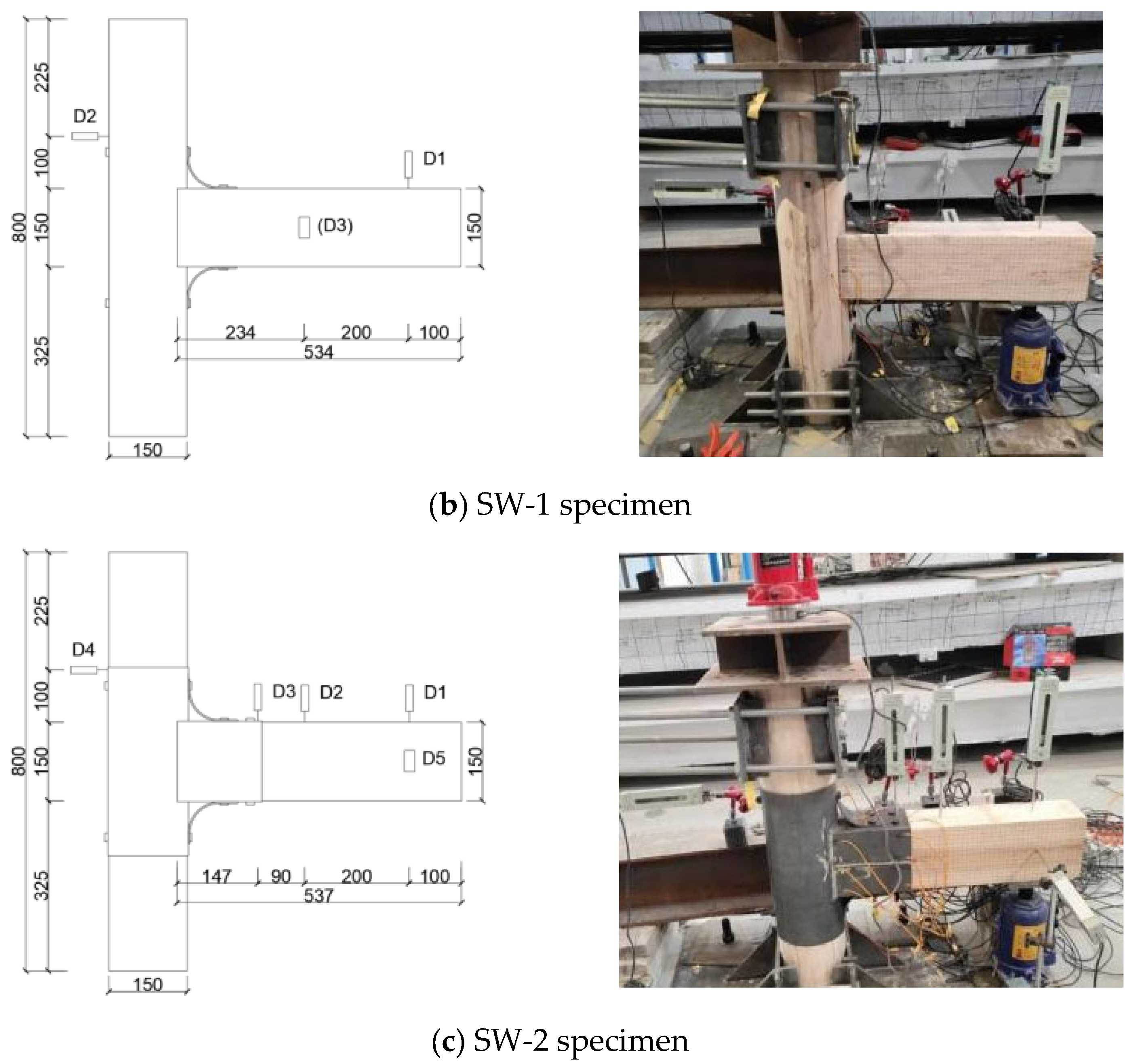
2.2. Design of the Test Joints

The survey data of traditional wooden structural joints from the southeastern Guizhou region were collected and analyzed by the research team, and then the specific dimensions and proportional relationships of the wooden components of the half-tenon joints were obtained. Taking into account factors such as the thermal expansion and contraction of wood, as well as the actual processing errors of wood and steel, the final manufacturing dimensions of the beams, columns, steel sleeves and energy dissipation plates were determined.

The SW-0 specimen is defined as a pure wooden beam–column joint without any steel reinforcement, relying solely on mortise–tenon connections to transfer internal forces. The joint of SW-1 specimen is reinforced with energy dissipation plates, while the joint of SW-2 specimen is reinforced by steel sleeve with energy dissipation plates based on the SW-0 joint. The processing dimensions of the wooden beam and columns, energy dissipation plates, and steel sleeves are shown in Figure 1.

2.3. Fabrication and Assembly of the Joints

Based on the above designed component machining dimensions, the wooden beams, wooden columns, steel sleeves, and other components are fabricated in wood and steel workshops, respectively. The assembly steps for the SW-2 wood specimen reinforced with a steel sleeve and two energy dissipation plates are as follows: firstly, the steel sleeve was placed at the top of the wooden column, and the mortise and tenon were aligned. Then, the steel sleeve was gently tapped by a rubber mallet to ensure it was centered on the wooden column. Secondly, the wooden beam was inserted into the beam end of the steel sleeve, and the beam end was lightly tapped with the rubber mallet to ensure tight contact with both the steel sleeve and the wooden column. Thirdly, the energy dissipation plates were placed above and below the steel sleeve and temporarily secured to ensure the bolt holes were aligned. Finally, high-strength bolts were employed for the bolt connection to complete the assembly. The final assembly of the SW-0, SW-1, and SW-2 specimens is illustrated in Figure 2.

3. Monotonic Loading Test

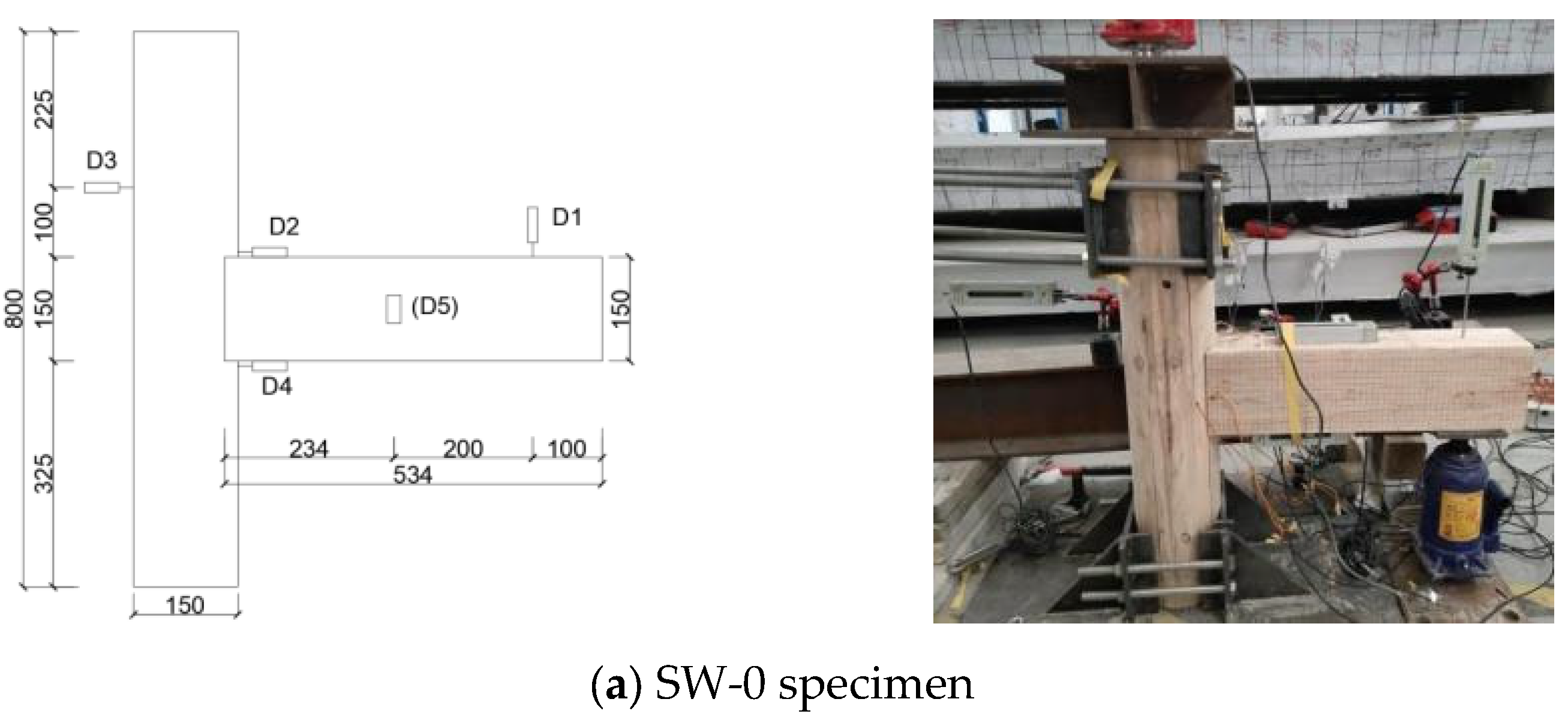
3.1. Experimental Loading Device

The monotonic loading experiment was conducted in the Heavy Equipment Laboratory of the Jiangsu University of Science and Technology. According to the laboratory space conditions, the reaction frame was erected and fixed to the ground with threaded rods. The base fixing steel plate was positioned according to the diameter of the wooden column, and then the fixing plate was secured to the ground with threaded rods. The specimen column end was inserted between two back-to-back steel plates of the column base, and then the plates and the specimen were tightened and fixed with bolts. Meanwhile, the horizontal displacement of the specimen was restrained by reinforcing the top with a threaded rod and a steel plate to complete the fixation of the specimen. A hydraulic jack with a ten-ton capacity was placed above the specimen column to apply an axial force to the top of the column, and a steel plate was installed between the column top and the hydraulic jack to ensure that the load applied to the column top was uniform. Additionally, a hydraulic jack with a twenty-ton capacity was positioned under the beam end of the specimen to facilitate the application of displacement loads at the beam end, as plotted in Figure 3.

3.2. Displacement Gauge Layout

The installation locations of the displacement gauges for the SW-0, SW-1 and SW-2 specimens are shown in Figure 4. The SW-0 specimen is equipped with five displacement gauges. D1, D5 and D3 are used to measure the vertical displacement of the wooden beam, the out-of-plane displacement of the wooden beam and the lateral displacement of the wooden column, respectively. The SW-1 specimen is equipped with three displacement gauges. D1, D2 and D3 are, respectively, utilized to monitor the vertical displacement of the wooden beam, the lateral displacement of the wooden column and the out-of-plane displacement of the wooden beam. Five displacement gauges are installed on the SW-2 specimen. D1 and D2 are used to measure the vertical displacement of the wooden beam, D3 and D5 is severally employed to measure the vertical and out-of-plane displacement of the steel sleeve of the wooden beam and D4 is used to measure the lateral displacement of the steel sleeve of the wooden column.

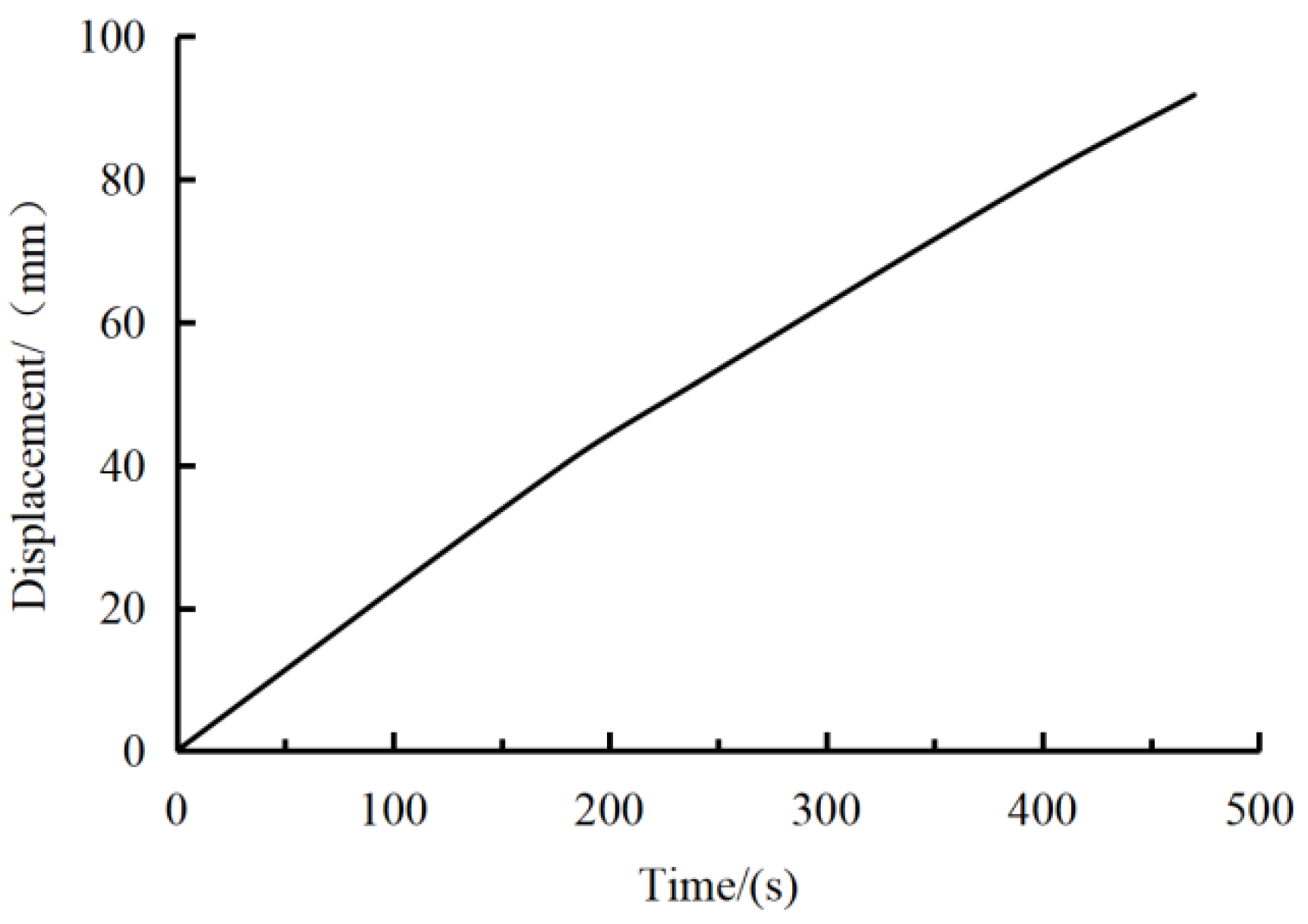
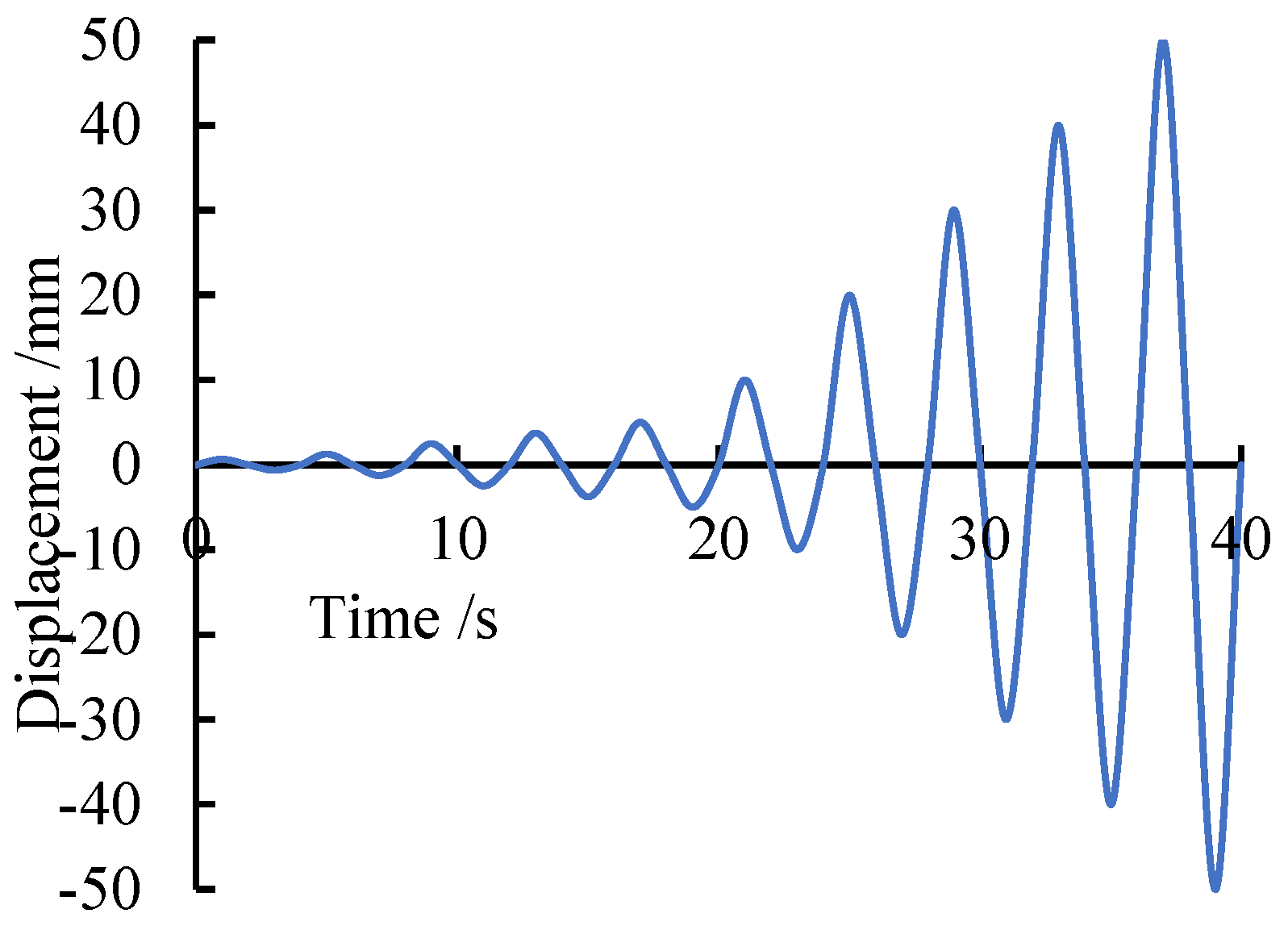
3.3. Loading Scheme

A displacement control method was employed at the beam end during the monotonic loading test, with the entire loading process divided into two stages including the pre-loading and normal loading.

(1)

Pre-loading stage. The main purpose is to check whether the measuring equipment employed in the experiment is working properly and to eliminate any potential imperfect contacts between the components of the joint specimen. The preload value of the SW-0 specimen is applied at 5% of the estimated ultimate load, whereas the SW-1 and SW-2 joints are installed at 10% of the estimated ultimate load.

(2)

Normal loading stage. This stage is divided into two steps for load application. First, a 25 kN axial load is applied at the top of the column. Second, a displacement-controlled loading method is used at the beam end to apply the load. The initial displacement amplitude is 5 mm with each subsequent level increasing by 5 mm as the controlled displacement until the specimen fails, and the loading scheme is illustrated in Figure 5.

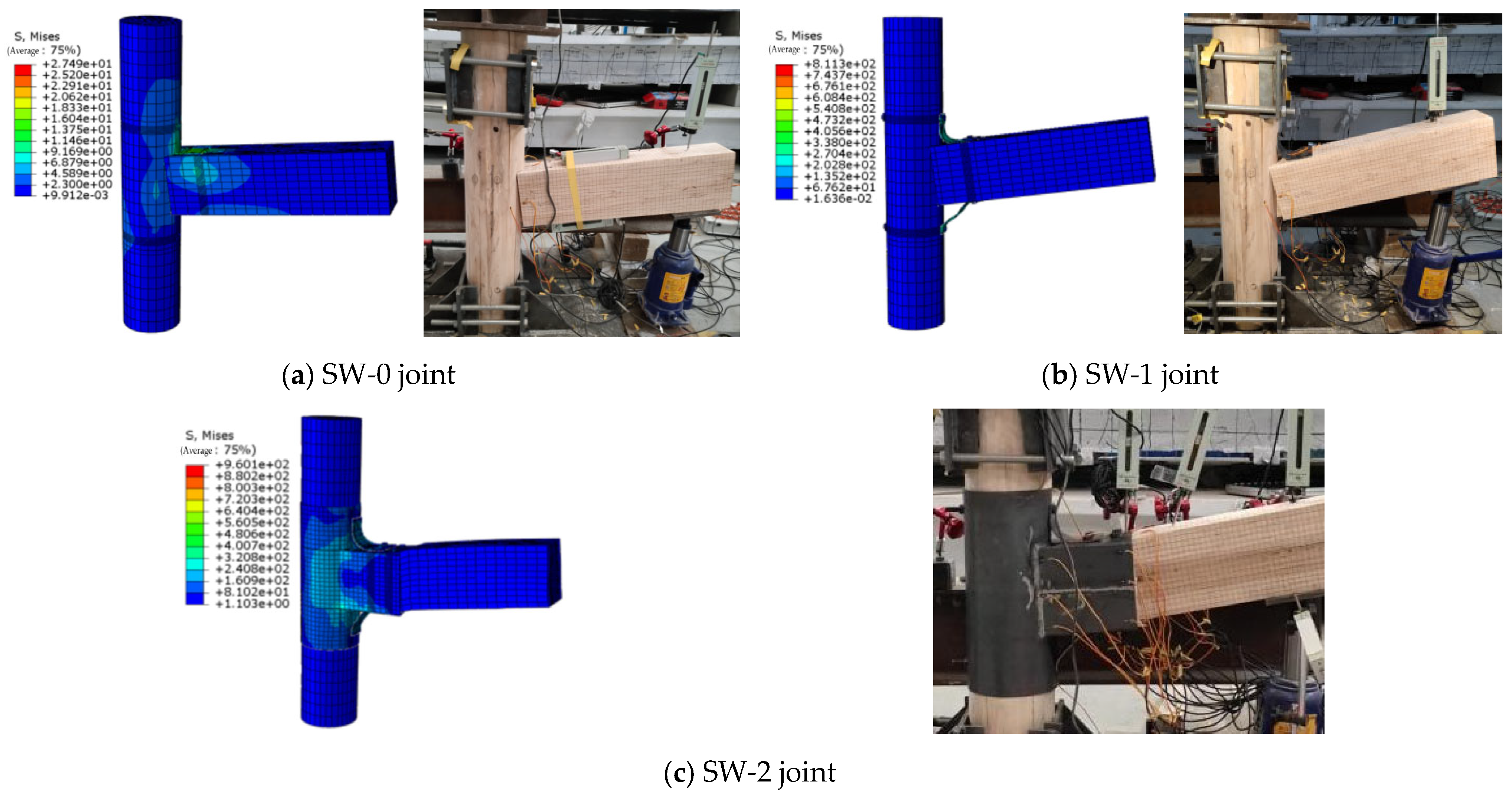
3.4. Analysis of Joint Failure Modes

(1)

SW-0 specimen

At the beginning of the test, the SW-0 specimen showed no apparent change under minimal load. With the increase in the vertical displacement at the beam end, there was a small compression between the joint and the mortise, accompanied by a “squeaking” sound that lasted for 1 to 2 s and the tenon withdrawal phenomenon of the joint was not obvious at this stage. There was a slight separation between the beam and column of the specimen when the vertical displacement reached 10 mm, along with a minor squeezing phenomenon between the mortise and the tenon, as shown in Figure 6a. This was accompanied by a continuous “squeaking” sound lasting for about 3 to 4 s, and the horizontal distance from the lower edge of the beam to the wooden column at the tenon location was approximately 5 mm at this time. The mutual squeezing action between the mortise and the tenon of the joint gradually intensified when the vertical load was further increased to 30 mm, as plotted in Figure 6b, and the joint emitted a louder “squeaking” sound with each application of displacement load, which lasted for 4 to 5 s.

A severe separation occurred between the beam and column of the specimen when the vertical displacement at the beam end was further loaded to 59 mm, and the serious squeezing phenomenon appeared between the mortise and the tenon. The wood fibers at the tenon emitted a clear sound of fracture as a gap of about 5 mm formed, accompanied by a loud “cracking” noise. Small cracks appeared with a small amount of wood shavings falling off between the mortise and the tenon at this point. No visible lateral displacement of the column or out-of-plane displacement of the beam was observed throughout the loading process of the specimen. The final failure mode of the SW-0 specimen is shown in Figure 7.

(2)

SW-1 specimen

At the beginning of the test, the SW-1 specimen showed no apparent change under minimal load. With the vertical displacement at the beam end reached 30 mm, as shown in Figure 8a, the mortise and tenon head experienced a slight mutual compression, accompanied by a faint sound of wood fiber cracking and a continuous “creaking” noise lasting for 2 to 3 s. A significant separation occurred between the beam and column of the joint when the displacement was further increased to 50 mm, as plotted in Figure 8b. The horizontal distance between the tenon head at the lower edge of the beam and the wooden column was approximately 20 mm, and the energy-dissipating plate on the upper side was significantly compressed and bent. The mutual compression between the mortise and tenon head intensified sharply, and the energy-dissipating plate on the lower side experienced severe tensile deformation. The nut of the high-strength bolt at the bottom of the wooden column had a slight indentation with a depth of about 1 mm. A small gap existed between the top of the high-strength bolt at the upper part of the wooden column and the wooden column. The grating sound of wood fiber cracking occurred repeatedly as the load continued to increase, accompanied by a loud “cracking” noise that lasted for 3 to 4 s.

The specimen was no longer able to bear the load and was completely destroyed when the vertical displacement at the beam end reached 86 mm. Therefore, the ultimate loading displacement value for the SW-1 joint was taken as 86 mm. The SW-1 specimen joint reinforced with energy dissipation plate experienced significant separation in the final destruction mode. The horizontal distance between the tenon head at the lower edge of the beam and the wooden column was approximately 25 mm. Severe compression occurred between the mortise and tenon head, accompanied by the dropping of a small amount of wood chips. The upper energy-dissipating plate was bent to almost match the angle between the wooden beam and column, while the lower energy dissipation plate experienced extremely severe tension. The area around the bolt holes in the energy dissipation plate underwent severe deformation, resulting in out-of-plane bulging. The bolt hole around the back lower part of the wooden column exhibited significant inward deformation. The bolt hole in the wooden column connected to the lower energy dissipation plate underwent extremely severe deformation, with the hole expanding downward by about 14 mm. Several small, elongated wood strips were sheared and compressed below the bolt hole. Meanwhile, the top of the high-strength bolt at the upper part of the wooden column was pushed out by about 3 mm. The final failure mode of the SW-1 specimen is illustrated in Figure 9.

(3)

SW-2 specimen

The SW-2 specimen showed no apparent change under minimal load at the beginning of the experiment. Due to the slight gap between the steel sleeve on the beam and the wooden beam, the joint emitted a continuous slight “squeaking” sound for 1 to 2 s as the vertical displacement increased. The beam steel sleeve subjected to vertical compression from the wooden beam and gradually exhibited a slight upward bulging phenomenon during the process of loading the displacement to 10 mm, accompanied by a continuous “squeaking” sound lasting 1 to 2 s. The front edge of the steel sleeve on the beam arose a slight mutual squeezing action with the wooden beam when the vertical displacement reached 10 mm, as shown in Figure 10, which caused a tiny upward bulge of approximately 0.3 mm at the front of the steel sleeve on the beam, and the wooden beam appeared slight compressive deformation. The upper and lower sides of the energy dissipation plate, respectively, exhibited slight bending and stretching. The high-strength bolts connecting the wooden beam and the steel sleeve on the beam primarily bore an upward tensile force along the bolt shaft, which caused the lower side of the steel sleeve on the beam to raise an upward pull, and the small upward indentation with a maximum value of approximately 0.4 mm occurred on the lower side of the beam steel sleeve.

The upward bulging phenomenon of the steel sleeve on the beam under the vertical compression of the wooden beam increased during the process of loading the displacement to 30 mm, accompanied by a larger “squeaking” sound lasting for 2 to 3 s, and the deformation degree of the fan-shaped energy dissipation plates on the upper and lower sides continuously increased. The mutual squeezing action between the front edge of the steel sleeve on the beam and the wooden beam intensified when the displacement was loaded to 30 mm, as illustrated in Figure 11, causing a noticeable upward bulge of approximately 1 mm at the front of the steel sleeve on the beam, and the wooden beam appeared a slight compressive deformation to form an internal pressure phenomenon. The upward concave phenomenon with a concave value of approximately 2.5 to 3 mm on the lower side of the steel sleeve on the beam increasingly intensified, and the lower end of the steel sleeve on the column was subjected to tensile force, causing the horizontal direction of the wooden beam to raise a slight tensile deformation of approximately 0.5 to 1 mm. Simultaneously, a trivial indentation phenomenon occurred at the upper corner of the steel sleeve joint, and the upper and lower fan-shaped energy dissipation plates individually exhibited significant bending and stretching phenomena.

The front end of the steel sleeve on the beam further severely bulged with the bulge value being approximately 1.5 to 2 mm when the displacement was loaded to 50 mm, as plotted in Figure 12, and the internal pressure phenomenon of the wrapped wooden beam was increasingly intensified. The lower side of the steel sleeve on the beam showed the upward concave deformation with the concave value of about 3 to 3.5 mm, and the lower end of the steel sleeve on the column exhibited tensile deformation of approximately 1 to 1.5 mm due to tensile force. Additionally, a noticeable indentation phenomenon occurred at the pressure side corner of the steel sleeve node.

Occasional minor sounds of wood fiber rupture and a loud “dada” sound lasting 2 to 3 s can be heard during the process of loading the displacement to 80 mm, and the specimen was unable to carry the load and was completely destroyed when the vertical displacement reached 80 mm. Therefore, the ultimate load displacement value for the SW-2 specimen was taken as 80 mm. The front end of the steel sleeve on the beam had a severe bulge with a value of approximately 3.5 to 4 mm at that moment, while the internal pressure phenomenon within the wrapping of the wooden beam was intense. The lower side of the steel sleeve on the beam concave upward had a concave value of about 5 to 6 mm, and the degree of tensile deformation of the wooden beam at the lower end of the steel sleeve on the beam also significantly increased, with the tensile deformation amount being approximately 3 to 4 mm. No visible lateral displacement of the column or out-of-plane displacement of the beam was observed throughout the loading process of the specimen, and the final failure mode of the SW-2 specimen is shown in Figure 13.

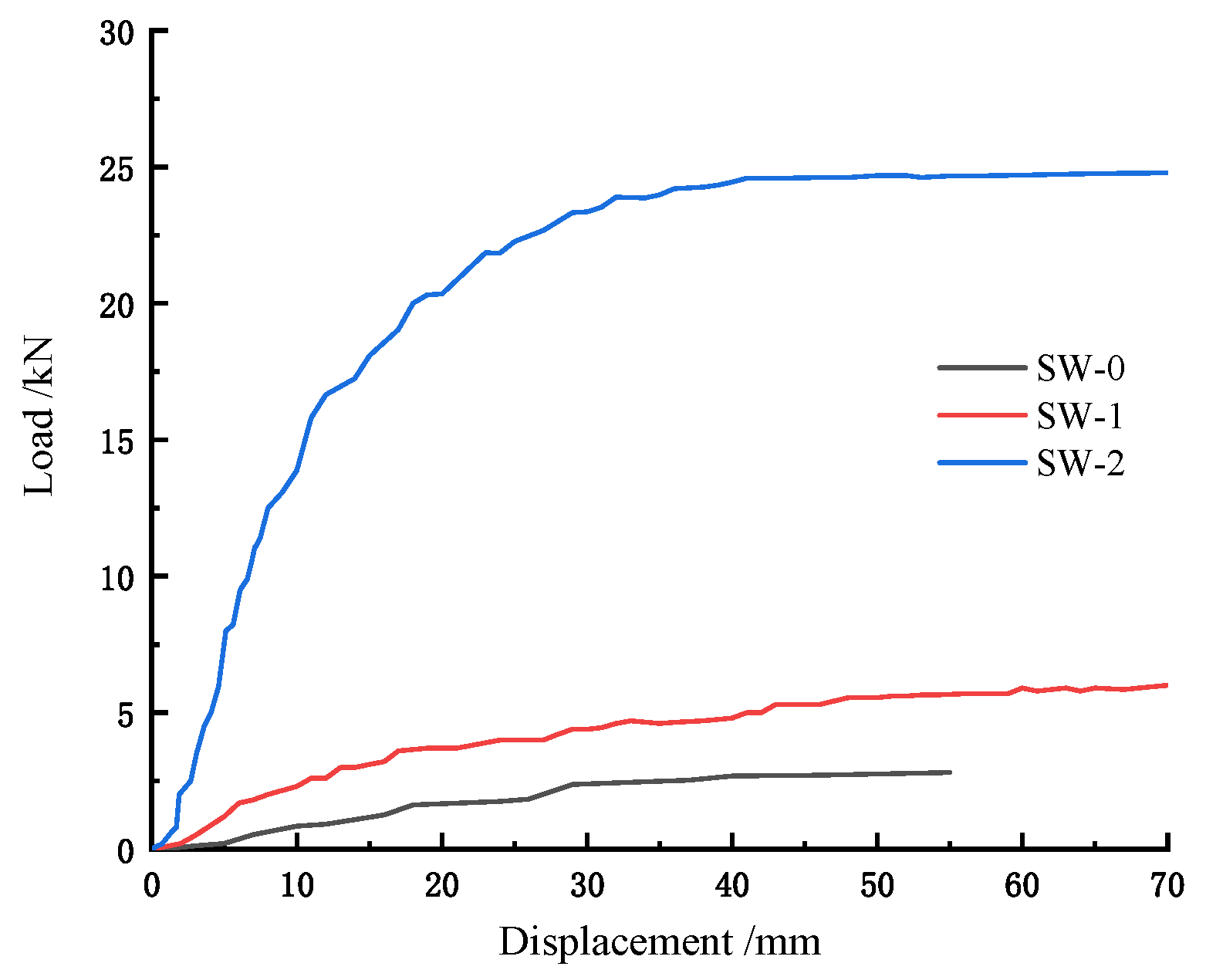
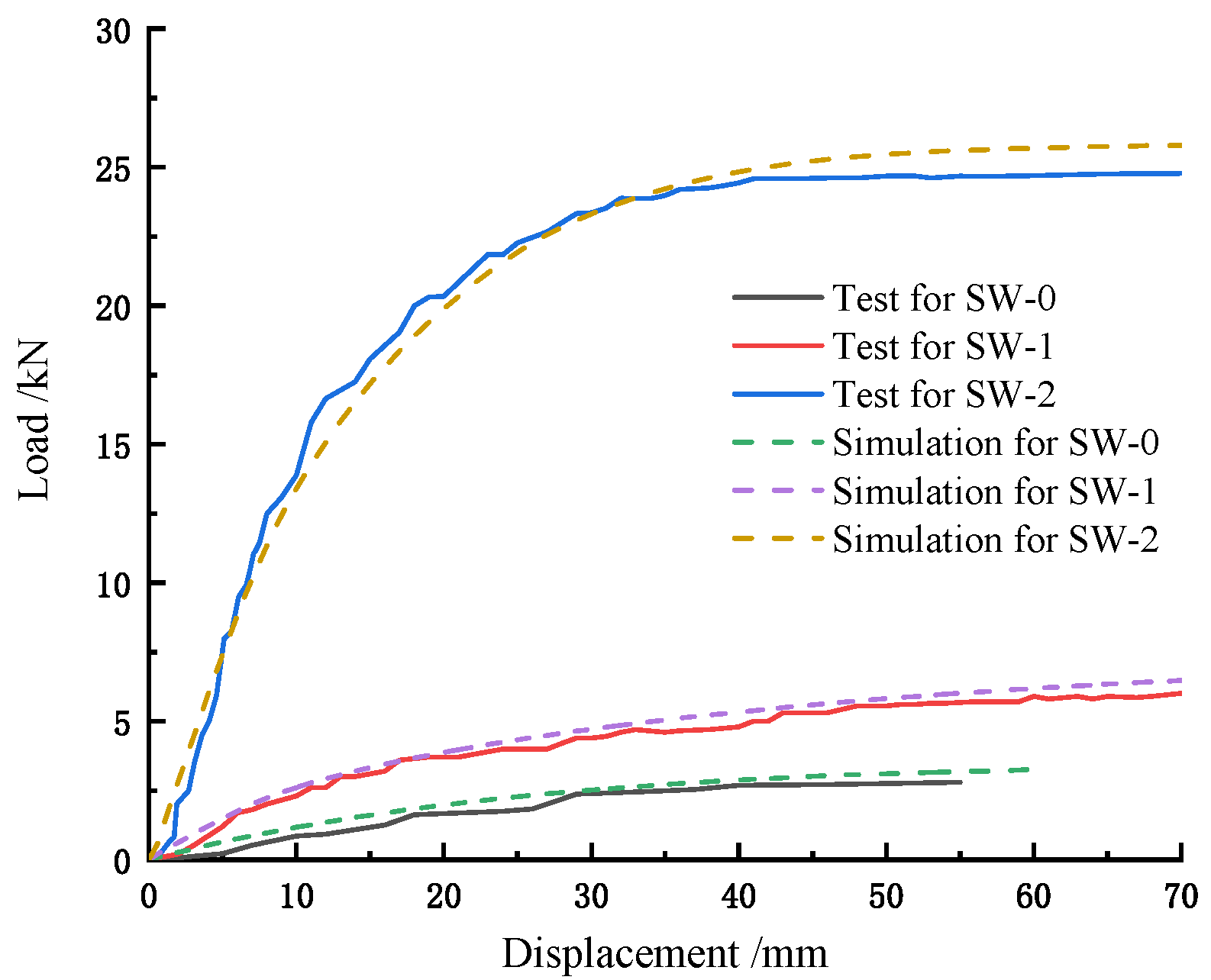
3.5. Load–Displacement Curve

The load–displacement curves of the specimens were obtained by organizing and analyzing the loading displacements and loads for the SW-0, SW-1 and SW-2 specimens, as illustrated in Figure 14.

It can be seen from the figure that the load–displacement curve of the joint is divided into three stages: the elastic ascending phase, the elastoplastic curve phase, and the plastic horizontal phase. The curve shows slight slippage in the beginning, which exists due to errors in the fabrication of the beam–column half-tenon joint and the presence of certain gaps during assembly. The curve trends of the SW-0 and SW-1 specimens are approximately the same and lack an obvious yield phase, while the SW-2 specimen exhibits distinct yield phases.

The ultimate load for each specimen was taken as the load corresponding to its final loading displacement. A straight line parallel to the initial elastic slope was drawn on the load–displacement relationship of the specimen, intersecting the curve at two points, such that the area under the curve above the line equals the area above the curve below that line. The load value at which the areas on both sides are balanced was the yield load, as plotted in Figure 15. The comparison of the mechanical properties of the three groups of specimens is shown in

Table 4. Comparison of the mechanical properties of the three groups of specimens.

Comparison Joint	SW-0	SW-1	SW-2
Proportional limit displacement/mm	7.13	5.35	8.06
Proportional limit load/kN	0.61	1.21	4.99
Initial stiffness/(kN/m)	85.55	226.17	619.11
Initial displacement at the onset of the horizontal segment/mm	40.35	51.37	43.62
Initial load at the onset of the horizontal segment/kN	2.76	5.16	24.71
Ultimate displacement/mm	59.33	86.16	80.12
Ultimate load/kN	2.80	6.20	24.90

.

As shown in the above table, the initial stiffness of the SW-1 and SW-2 specimens is 2.64 and 7.24 times that of the SW-0 specimen, respectively, and ultimate loads are 2.21 and 8.89 times. The effects of the two different reinforcement methods are distinct, which provides a variety of reinforcement options for the building structures in different environments, with various functions, load types and owner needs.

4. Finite Element Numerical Simulation

4.1. Modeling Process

The numerical model of the beam–column half-tenon joint was established in the “Part” module of the ABAQUS finite element software at a 1:1 scale according to the dimensions of the test specimen. The components of the joint were created using the “3D-Solid-Extrude” function.

The bolt holes at the upper and lower ends of the wooden column and the high-strength tie bolts exhibited invisible deformation. Therefore, in simulating the steel sleeve-reinforced beam–column half-tenon joint, the model was simplified by omitting the high-strength tie bolts at the upper and lower ends of the wooden column. Instead, binding constraints were applied between the wooden column and the steel sleeve in the areas where the high-strength tie bolts should have been installed. The threads on the high-strength tie bolts in the wooden beam have a negligible effect on the mechanical properties of the entire beam–column half-tenon joint and can be ignored. Therefore, the bolt shaft is modeled as smooth, and the nut is considered as an integral part of the bolt shaft.

A structured meshing technique with hexahedral elements was employed for the mesh generation of the components. Specifically, the wooden column, beam, steel sleeve, energy-dissipation plate and high-strength tie bolt were meshed with element sizes of 20 mm, 15 mm, 10 mm, 4 mm and 2 mm, respectively. The contact type in the beam–column joint model was set as “General Contact”, and the pressure-overclosure was set to “Hard Contact” for the “Normal Behavior”. The friction model is based on the penalty method for the “Tangential Behavior”, and the friction coefficients are determined according to the literature [29]. The friction coefficients for wood–wood contact, wood–steel contact, and steel–steel contact are 0.4, 0.35 and 0.3, respectively. Additionally, the high-strength tie bolts are constrained using the “Binding” type. The boundary conditions at the bottom of the column are set to be fully fixed, while the displacements U1 and U2 at the top of the column are constrained. The loading method is the same as that used in the experiment.

4.2. Constitutive Relation of Material

The relationship between external excitation and internal response is referred to by the constitutive relationship of a material, describing how a material deforms under external loading and the connection between the load and deformation.

(1)

Material property of wood during the elastic stage

The research group had calculated and transformed the physical and mechanical property indices of Chinese fir through experimental testing. The resulting material property values for Chinese fir during the elastic stage are shown in

Table 5. Material property values of Chinese fir during the elastic phase.

Representative Value	Input Value	Value
$E_{\mathrm{L}}$	$E_1$	11,059.71 MPa
$E_{\mathrm{R}}$	$E_2$	242.72 MPa
$E_{\mathrm{T}}$	$E_3$	217.13 MPa
$G_{\mathrm{L}\mathrm{R}}$	$G_{12}$	822.75 MPa
$G_{\mathrm{L}\mathrm{T}}$	$G_{13}$	658.23 MPa
$G_{\mathrm{R}\mathrm{T}}$	$G_{23}$	197.36 MPa
$v_{\mathrm{L}\mathrm{R}}$	$v_{12}$	0.54
$v_{\mathrm{L}\mathrm{T}}$	$v_{13}$	0.46
$v_{\mathrm{R}\mathrm{T}}$	$v_{23}$	0.41

The subscripts L, R and T, respectively, represent the longitudinal, radial and tangential directions of Chinese fir. The local coordinate system’s axes 1, 2 and 3 correspond to the global coordinate system’s X, Y and Z axes.

.

(2)

Yield strength value of Chinese fir during the plastic stage

The material properties of Chinese fir during the plastic stage are determined based on the Hill yield criterion to obtain the yield stress values in different directions. The σ₀ represents the reference value of yield strength (the compressive strength along the grain is selected in the paper), σ_ij denotes the yield stress values of Chinese fir in different directions, and R₁₁, R₂₂, R₃₃, R₁₂, R₁₃, R₂₃ represent the ratios of yield strength in different directions of Chinese fir. The yield strength values of Chinese fir during the plastic stage are plotted in

Table 6. Yield strength values of Chinese fir during the plastic phase.

Yield Strength (MPa)	σ11	σ22	σ33	σ12	σ13	σ23	σo
	29	1.6	1.6	3.51	3.51	3.51	29
Yield Strength Coefficient	R11	R22	R33	R12	R13	R23
	1	0.06	0.06	0.12	0.12	0.12

.

(3)

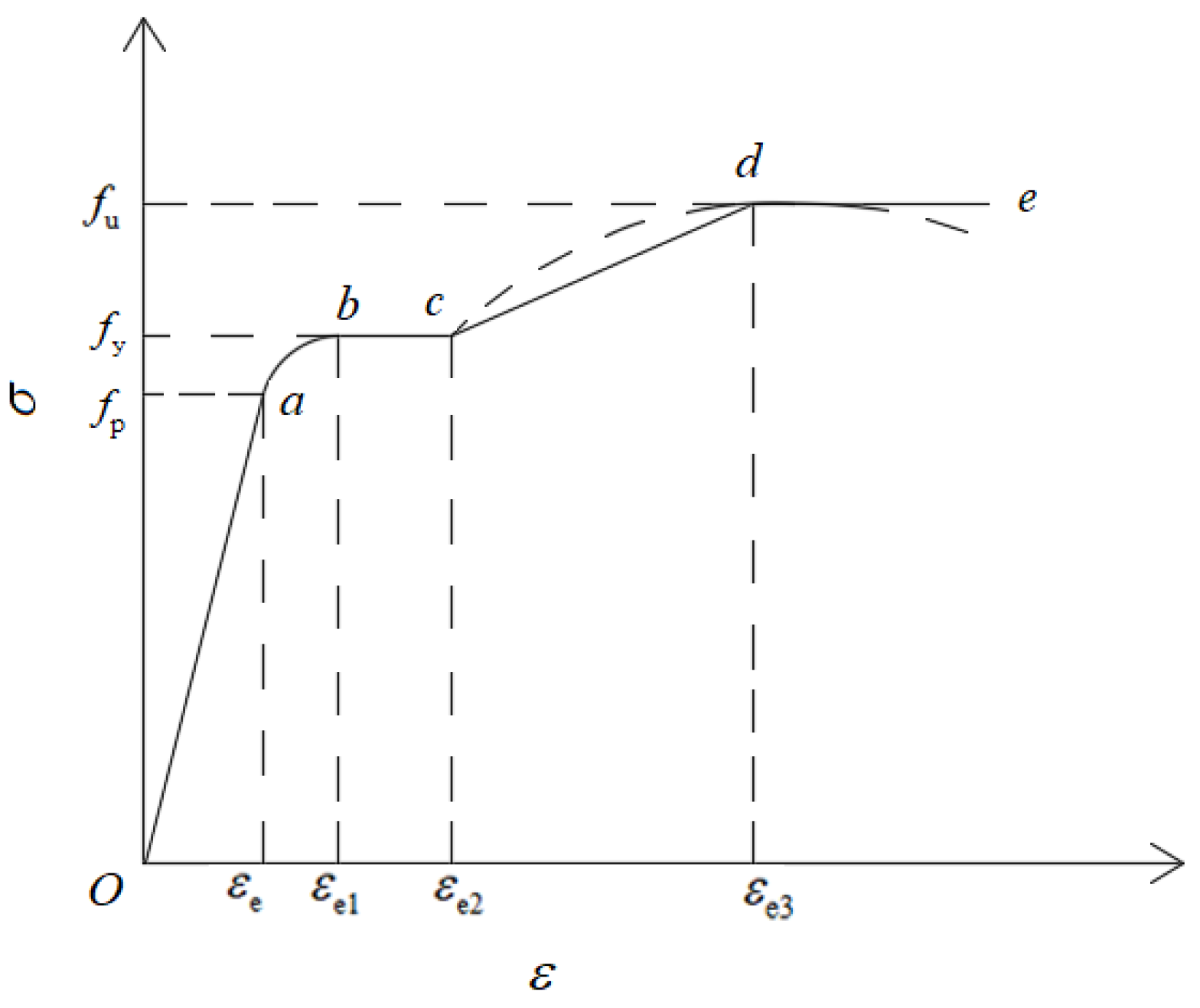
Constitutive relation of steel

The Mises yield criterion and hardening rule were generally adopted to calculate the constitutive relation of steel by the mathematical expression represented in Equation (1). The stress–strain curve of steel under the uniaxial tensile experiment is illustrated in Figure 16, where the f_p, f_y and f_u are, respectively, the proportional limit, yield strength and tensile strength. The a, b, c, d and e in the figure respectively represent the proportional limit, yield limit, yield platform end, ultimate strength and fracture point. The elastic modulus of steel with the Poisson’s ratio of 0.3 was 2.06 × 10⁵ N/mm². The high-strength bolts are hexagonal bolts with a diameter of 10 mm and a grade of 10.9, featuring a yield strength of 960 MPa and a density of 7800 kg/m³.

$$\sigma =\left\{\begin{array}{cc}\hfill E_{\mathrm{s}}{\epsilon }_{\mathrm{s}}\hfill & {\epsilon }_{\mathrm{s}}\le {\epsilon }_e\hfill \\ \hfill -A{{\epsilon }_{\mathrm{s}}}^2+B{\epsilon }_{\mathrm{s}}+C\hfill & {\epsilon }_e<{\epsilon }_{\mathrm{s}}\le {\epsilon }_{e1}\hfill \\ \hfill f_{\mathrm{y}}\hfill & {\epsilon }_{e1}<{\epsilon }_{\mathrm{s}}\le {\epsilon }_{e2}\hfill \\ \hfill f_{\mathrm{y}}\left[1+0.6{\displaystyle \frac{{\epsilon }_{\mathrm{s}}-{\epsilon }_{e2}}{{\epsilon }_{e3}-{\epsilon }_{e2}}}\right]\hfill & {\epsilon }_{e2}<{\epsilon }_{\mathrm{s}}\le {\epsilon }_{e3}\hfill \\ \hfill 1.6f_{\mathrm{y}}\hfill & {\epsilon }_{\mathrm{s}}>{\epsilon }_{e3}\hfill \end{array}\right.$$

(1)

$${\epsilon }_{\mathrm{e}}=0.8\frac{f_{\mathrm{y}}}{E_{\mathrm{s}}}$$

$${\epsilon }_{\mathrm{e}1}=1.5{\epsilon }_{\mathrm{e}}$$

$${\epsilon }_{\mathrm{e}2}=10{\epsilon }_{\mathrm{e}1}$$

$$A=0.2{\displaystyle \frac{f_{\mathrm{y}}}{{({\epsilon }_{\mathrm{e}1}-{\epsilon }_{\mathrm{e}})}^2}}$$

$$B=2A{\epsilon }_{\mathrm{e}1}$$

$$C=0.8f_{\mathrm{y}}+A{\epsilon }_{\mathrm{e}}^2-B{\epsilon }_{\mathrm{e}}$$

where:

• f_y—Yield strength of steel
• E_s—Elasticity modulus of steel
• ε_e—The corresponding strain value for the proportional limit
• ε_e1—The corresponding strain value for entering the yield platform
• ε_e2—The corresponding strain value for the end yield platform
• ε_e3—The corresponding strain value for the strength limit

Figure 16. Stress–strain relationship of steel under uniaxial action.

Figure 16. Stress–strain relationship of steel under uniaxial action.

4.3. Comparison on Simulation and Experiment

(1)

Comparison of failure modes

The comparison of failure modes between simulation and experiment for the three groups of joints are illustrated in Figure 16. Figure 17a,b show that the failure modes of the SW-0 and SW-1 joints in both the experiment and numerical simulation are tenon pull-out failures. The amount of tenon pull-out increases gradually with the increase in the vertical displacement load at the beam end. Additionally, the energy-dissipating plates at the upper and lower ends of the SW-1 joint undergo compressive and tensile deformations. Figure 17c reveals that the failure modes of the SW-3 joint in both the experiment and numerical simulation are characterized by the inward deformation of the steel sleeve and the compression failure of the wooden beam. In summary, the finite element simulation results for the three groups of joint models shows respectable agreement with the actual monotonic loading test phenomena.

(2)

Comparison of load–displacement curves

The comparison of displacement–load curves between simulation and experiment for the three groups of joints are illustrated in Figure 18. The figure illustrates that the load–displacement and rotation-moment curves derived from the finite element simulation and the experimental results exhibit similar trends. The initial slip observed in the experimental curves is due to the small gaps that exist between the assembled components of the joint, which arise from uncertainties such as material processing and thermal expansion and contraction. Therefore, during the initial loading phase of the experiment, the wooden beam experiences a relatively large displacement under a small load value.

Relative error between simulated and testing mechanical properties of the specimen is plotted in

Table 7. Relative error between simulated and testing mechanical properties of the specimen.

Comparison	Proportional Limit Load/kN		Ultimate Displacement/mm		Relative Error/%
	Simulation	Test	Simulation	Test	Proportional Limit Load	Ultimate Displacement
SW-0	0.64	0.61	3.21	2.80	4.92	14.64
SW-1	1.38	1.21	6.96	6.20	14.05	12.26
SW-2	5.78	4.99	26.9	24.90	15.83	8.03

. It can be seen from the table that there is some deviation between the simulated and experimental results, which is because the friction coefficient is significantly influenced by the surface roughness and moisture content variations in wood. Factors such as the microstructure of wood, changes in moisture content and internal defects are not considered in the finite element model. Additionally, the lower end of the specimen in the experimental setup is not perfectly fixed, and there may be deviations in the loading points at the beam ends, the dimensions of the specimen, and the contact conditions during assembly. These factors may lead to discrepancies between the simulation and the experimental results. The relative errors of ultimate displacements and loads between the simulated and experimental results were between 5% and 16%, which meet the accuracy requirements of engineering. Therefore, it was further concluded that the mechanical performance of the half-lap joints unreinforcement and reinforcement under monotonic loading test was accurately simulated by adopting the finite element model, and the numerical methodology was commendably applied to the parametric analysis.

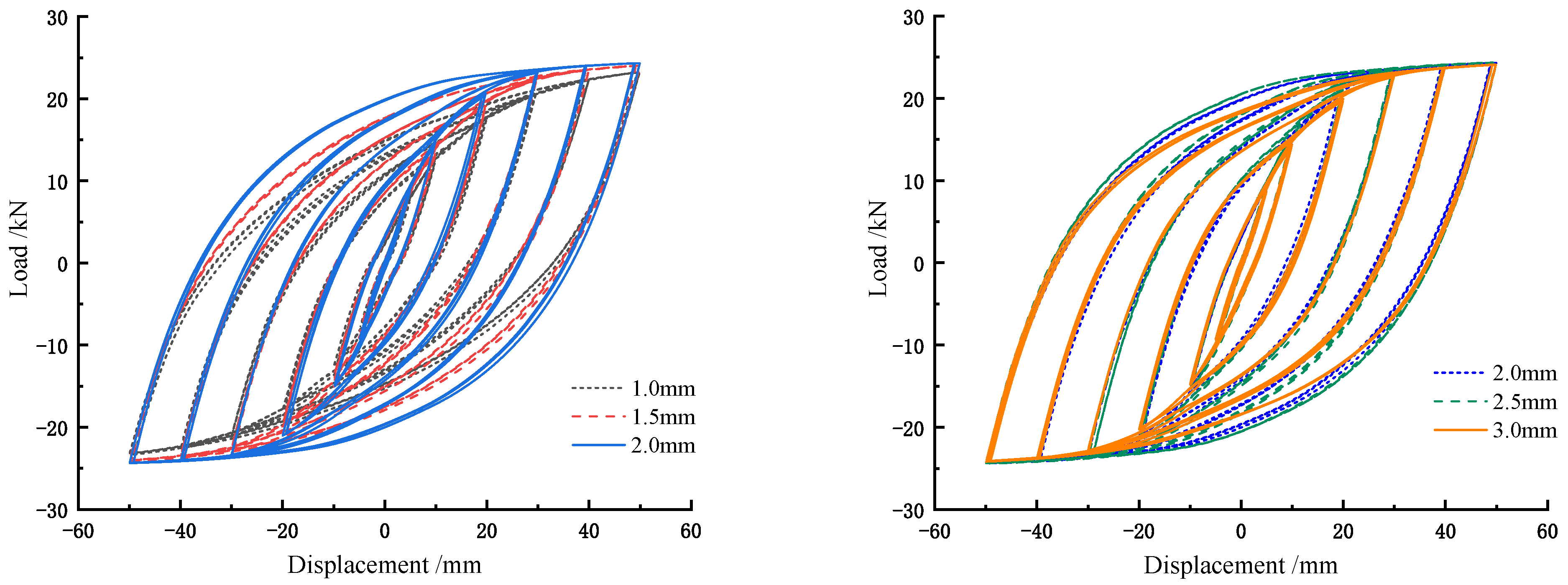
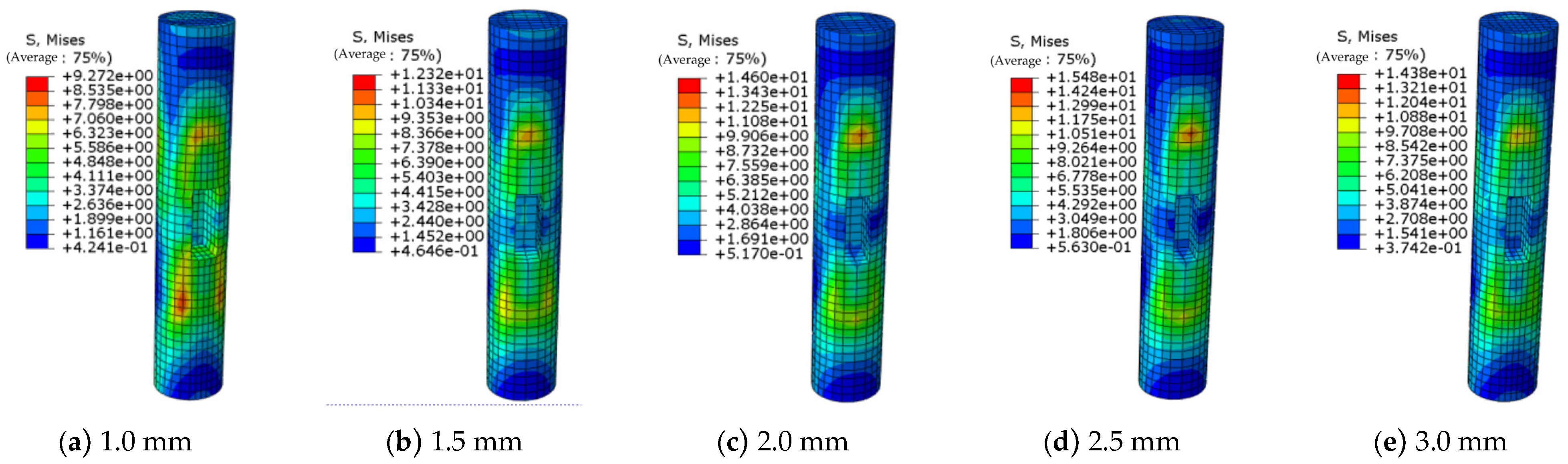
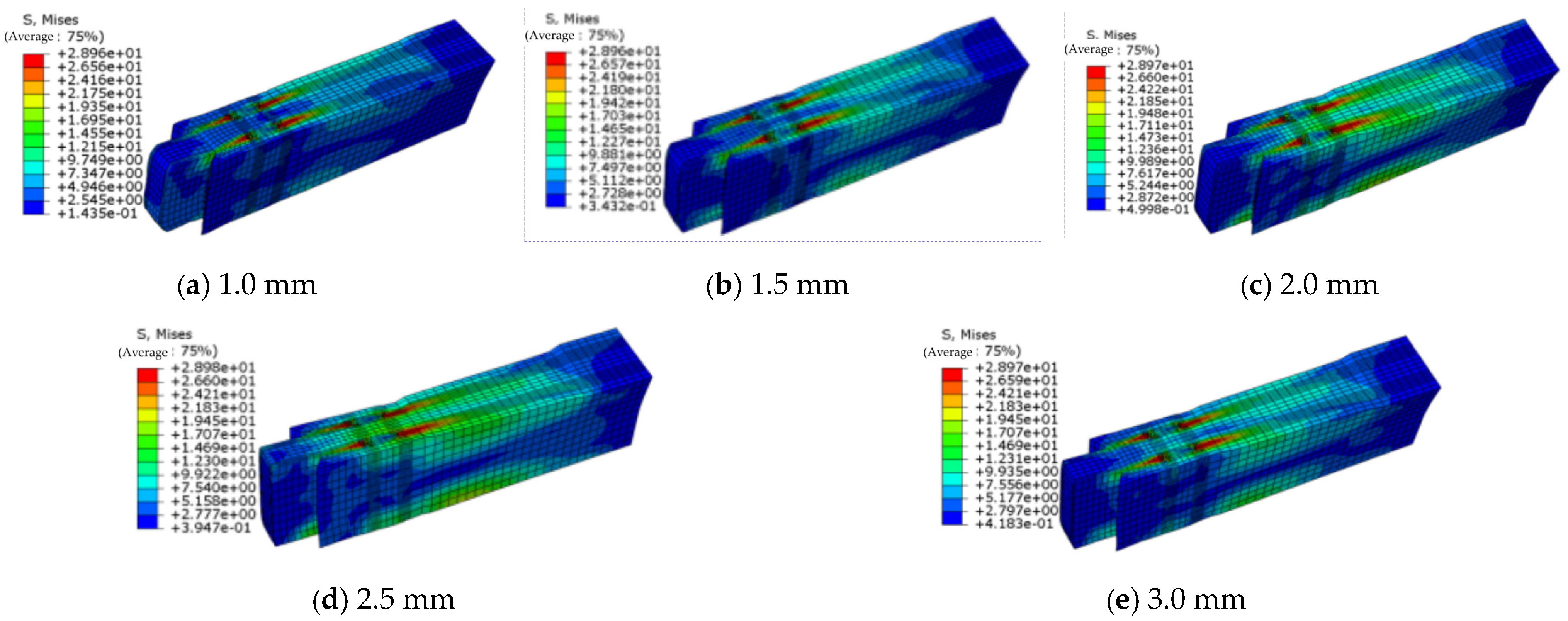
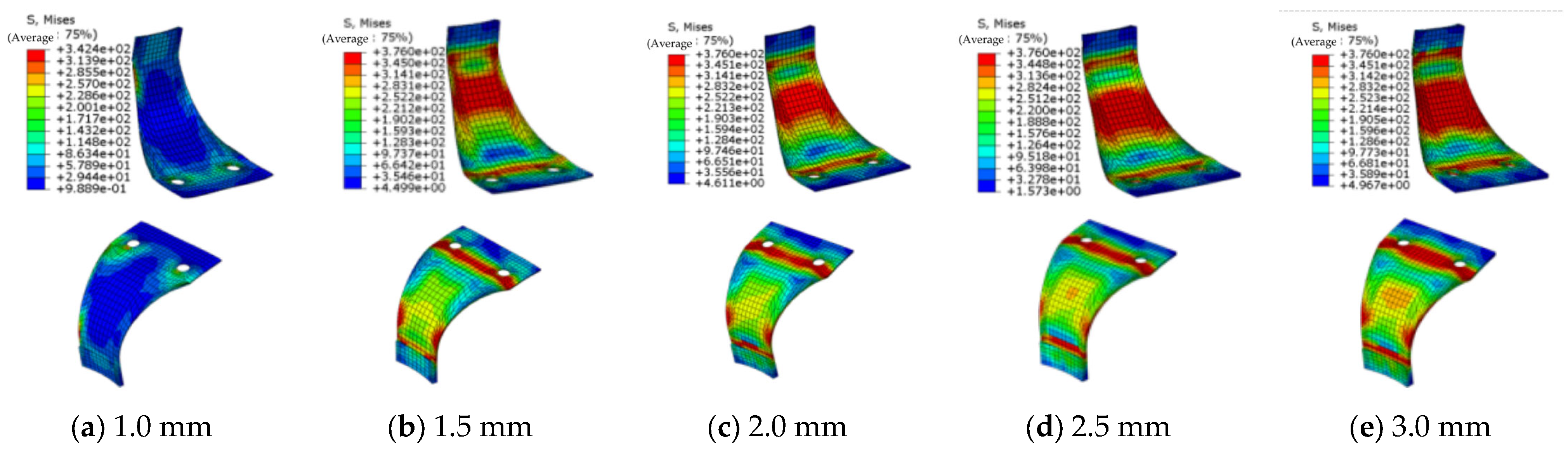
4.4. Finite Element Simulation of the SW-2 Joint with Different Thicknesses of Energy Dissipation Plate

In this simulation, the dimensions of the finite element model of the SW-2 joint are identical to the experimental dimensions for all components except for the thickness of the energy dissipation plate, which is the only variable. The thicknesses of the energy dissipation plates are 1.0 mm, 1.5 mm, 2.0 mm, 2.5 mm and 3.0 mm. Low-cycle reversed cyclic loading was employed for the simulation, as shown in Figure 19.

(1)

Analysis of joint hysteresis curves

The hysteresis curves of the joints with different thicknesses of energy-dissipation plates are illustrated in Figure 20. The figure shows that the envelope area of the hysteresis curves increases gradually with the increase in the thickness of the energy-dissipation plates, indicating a significant improvement in their energy-dissipation capacity. The ultimate bearing capacity of the joint remains almost unchanged when the thickness of the energy-dissipating plate exceeds 2.0 mm. However, the fullness for the hysteresis curve of joint decreases and the ultimate bearing capacity is reduced when the thickness reaches 3.0 mm. This is because the increase in the weight of structure due to the increased plate thickness, leads to a degradation in the seismic performance of joint. In summary, the optimal thickness of the energy-dissipating plate is 2 mm.

(2)

Analysis of joint skeleton curves

The skeleton curves of the joints with different thicknesses of energy-dissipation plates are plotted in Figure 21. All thicknesses of energy-dissipation plates exhibit relatively linear elastic behavior in the initial stage, followed by a nonlinear phase. Before the thickness of the energy-dissipation plates reaches 2.5 mm, the slope for the skeleton curve of joint increases with the raising of thickness, and the starting point of the nonlinear stage gradually shifts towards higher load values. When the thickness of the energy-dissipation plates is 3.0 mm, both the slope of the skeleton curve and the ultimate load-bearing capacity of the joint decrease as the displacement increases. This is because an increase in the thickness of the plates also leads to an increase in the self-weight of the structure, resulting in a reduction in the seismic performance of the joint.

(3)

Stress cloud diagram for wooden columns

The stress cloud diagrams of wooden columns with different thicknesses of energy-dissipation plates are shown in Figure 22. It can be observed from the figure that the stress of the wooden columns with energy-dissipation plates of 1.0 mm and 1.5 mm thickness covers the entire mortise area, while the stress of the wooden columns with energy-dissipation plates of 2.0 mm, 2.5 mm and 3.0 mm thickness is mainly concentrated on the upper and lower sides of the mortise. Wooden columns with energy-dissipation plates of 1.0 mm and 1.5 mm thickness exhibit slight deformation at the mortise. The deformation of the wooden column mortise becomes almost negligible with the thickness of the energy-dissipation plates gradually increases. This is because thinner energy-dissipation plates have lower stiffness and a weaker capacity to bear internal forces, which requires the wooden columns to bear more of the internal forces. In contrast, thicker energy-dissipation plates have greater stiffness and can withstand larger internal forces without yielding or breaking, which results in less deformation for the wooden columns.

(4)

Stress cloud diagram for wooden beams

The stress cloud diagrams of wooden beams with different thicknesses of energy-dissipation plates are illustrated in Figure 23. It can be observed from the figure that the high-stress areas and deformation on the upper and lower flanges of wooden beams with 1.0 mm and 1.5 mm thick energy-dissipation plates are relatively small. When the thickness of the energy-dissipation plates increases to 2.5 mm, large areas of high stress appear on the upper and lower flanges of the wooden beams, and the deformation also becomes increasingly severe. The areas with high stress on the upper and lower flanges of the wooden beams become relatively small when the thickness of the energy-dissipation plates reaches 3.0 mm. This is because thinner energy-dissipation plates have lower stiffness and a weaker capacity to bear internal forces, which require the wooden beams to bear more of the internal forces. In contrast, thicker energy-dissipation plates have greater stiffness and can withstand larger internal forces without yielding or breaking, which reduce stress concentration and deformation. The thickness of the energy-dissipation plates was further increased to enhance the restraining effect of the plates on the wooden beams, and the increase in stress concentration and deformation was suppressed to a certain extent. However, the impact of the plates on both the overall and local stiffness of the wooden beams may have reached saturation due to the thickness of the energy-dissipation plates is thicker. Therefore, the reduction in stress and deformation is relatively small.

(5)

Stress cloud diagram for steel sleeves

The stress cloud diagrams of steel sleeves with different thicknesses of energy-dissipation plates are shown in Figure 24. It can be observed from the figure that the stress concentration phenomenon in steel sleeves is mainly focused at the connections between beams and columns with steel sleeves, and the phenomenon gradually decreases as the thickness of the energy-dissipation plates increases. This is because the energy-dissipation plates as an energy-absorbing device effectively absorb and dissipate energy through that deformation capabilities, which reduces stress concentration in the main structure. The energy-absorbing capacity of the plates is enhanced as the thickness increases, allowing the plates to more effectively absorb and disperse stress, and alleviate the stress concentration phenomenon.

(6)

Stress cloud diagram for energy-dissipation plates

The stress cloud diagrams of energy-dissipation plates with different thicknesses of energy-dissipation plates are plotted in Figure 25. It can be observed from the figure that the stress value of the energy-dissipation plate with a thickness of 1 mm is lower, and the yield strength of the plates does not reach. This is because the plate is thin and has low stiffness, which causes the plates to break before reaching yield at smaller displacements. As the thickness of the energy-dissipation plates gradually increases, the stress concentration around the bolt holes and in the curved areas becomes increasingly severe, with the maximum stress value reaching 376 MPa, which indicates that the energy-dissipation plates have all reached yield strength and entered the plastic stage. This is because the stiffness is enhanced with the increased thickness of the plates, which further improves the load-bearing capacity of the energy-dissipation plates and allows the plates to share more of the internal forces. Consequently, the stress concentration phenomenon in the energy-dissipation plates gradually intensifies.

(7)

Stress cloud diagram for high-strength bolt

The stress cloud diagrams of high-strength bolt with different thicknesses of energy-dissipation plates are plotted in Figure 26. It can be observed from the figure that as the thickness of the energy-dissipation plates gradually increases, the stress concentration and deformation around the upper and lower threads of the high-strength tension bolts become more severe. This is because the contribution of the plates to the overall stiffness of the structure also increases with the thickness of the energy-dissipation plates, and the connection areas of the bolts are subjected to greater stress under the same external forces. Additionally, the load transfer path within the structure may be altered by the thicker energy-dissipation plates, which leads to more load being transferred through the bolts, causing greater stress concentration and deformation in the upper and lower thread areas of the bolts. In actual structures, threads can increase local stress, especially in the area where the bolt contacts the connecting components. Since the threads of high-strength tension bolts are ignored in numerical simulations, the simulation results of the stress levels, stiffness and strength of the bolts in these areas may be underestimated, thereby affecting the stiffness and deformation behavior of the entire joint. Although the details of the bolt threads were ignored in this study, such simplification is reasonable in the preliminary analysis stage, especially when it comes to the evaluation of the overall structural performance.

4.5. Limitation of Study

(1)

Material properties and variability. The mechanical properties of wood are significantly influenced by factors such as moisture content, grain orientation, and inherent material defects. Therefore, the generalizability of the findings in this study may be limited due to the inherent stochastic nature of wood properties.

(2)

Simplified numerical model. The contact friction coefficients and the material constitutive models of the finite element model were simplified. The complex interactions between wood and steel components under dynamic loading conditions may not be fully captured due to the simplifications of the model.

(3)

Loading condition. This study focused on monotonic loading tests, which means that the cyclic loading conditions typically encountered in seismic events may not be fully represented.

(4)

General applicability. The materials, dimensions, and reinforcement methods used in this study is specific. Therefore, the research results may not be directly applied to other types of steel-wood composite joints or different reinforcement materials and configurations.

5. Conclusions

Two types of energy-dissipation plates and steel sleeve-reinforced beam–column semi-tenon joints were designed and conducted for experiments and numerical simulations. The conclusions are as follows:

Firstly, the pure steel–wood beam–column joint (SW-0) and joint reinforced with an energy dissipation plate (SW-1) exhibited significant tenon pulling phenomena at load values of approximately 2 kN and 3.8 kN, respectively, while the joint reinforced by a steel sleeve with energy dissipation plates (SW-2) did not show this phenomenon. In the final failure pattern of the joints, the bolt holes at column bottom of the SW-1 specimen expanded downward by approximately 14 mm, and several small, elongated wooden strips were sheared off just below the bolt holes due to compression. In contrast, the bolt holes of the SW-2 specimen experienced only minimal vertical stretching. Both reinforcement methods can effectively enhance the deformation capacity of the joint by allowing the energy-dissipation plates to absorb some energy through plastic deformation of the plates.

Secondly, the initial stiffness of the joints is significantly improved after reinforcement and the initial stiffness of the SW-1 and SW-2 specimens is 2.64 and 7.24 times that of the SW-0 specimen, respectively. The ultimate loads of specimens SW-0, SW-1 and SW-2 are, respectively, 2.8 kN, 6.2 kN and 24.9 kN. The effects of the two different reinforcement methods are distinct, which provides a variety of reinforcement options for the building structures in different environments, with various functions, load types and owner needs.

Thirdly, with the thickness of the energy dissipation plate increases, the enclosed area of the hysteresis loop and the slope of the skeleton curve gradually increase, resulting in a significant enhancement in energy dissipation capacity. The ultimate bearing capacity of the joint and the slope of the skeleton curve exhibit negligible variation when the thickness of the energy dissipation plate exceeds 2.0 mm, and the corresponding optimal thickness is obtained as 2 mm.

Lastly, thinner energy-dissipation plates (1.0 mm, 1.5 mm) have lower stiffness, which results in a wider distribution of stress and greater deformation in the wooden columns and beams, and it makes the energy-dissipation plates work well in conjunction with the wooden beams to reduce stress concentration and deformation. Thicker energy-dissipation plates (2.0 mm, 2.5 mm, 3.0 mm) have greater stiffness, causing stress concentration in local areas of the wooden columns and beams, with less deformation to make the structural stiffness tends to be saturated. The stress in the energy-dissipation plates becomes more concentrated as the thickness increases, and the stress concentration of the high-strength bolts worsens with the growth in thickness of the energy-dissipation plates.