Spatial Characteristic Analysis of Near-Fault Velocity Pulses Based on Simulation of Earthquake Ground Motion Fields
Abstract
:1. Introduction
2. Ground Motion Simulation Method
3. Simulation of Ground Motion Fields and Pulse Identification
3.1. Simulation of Ground Motion Fields
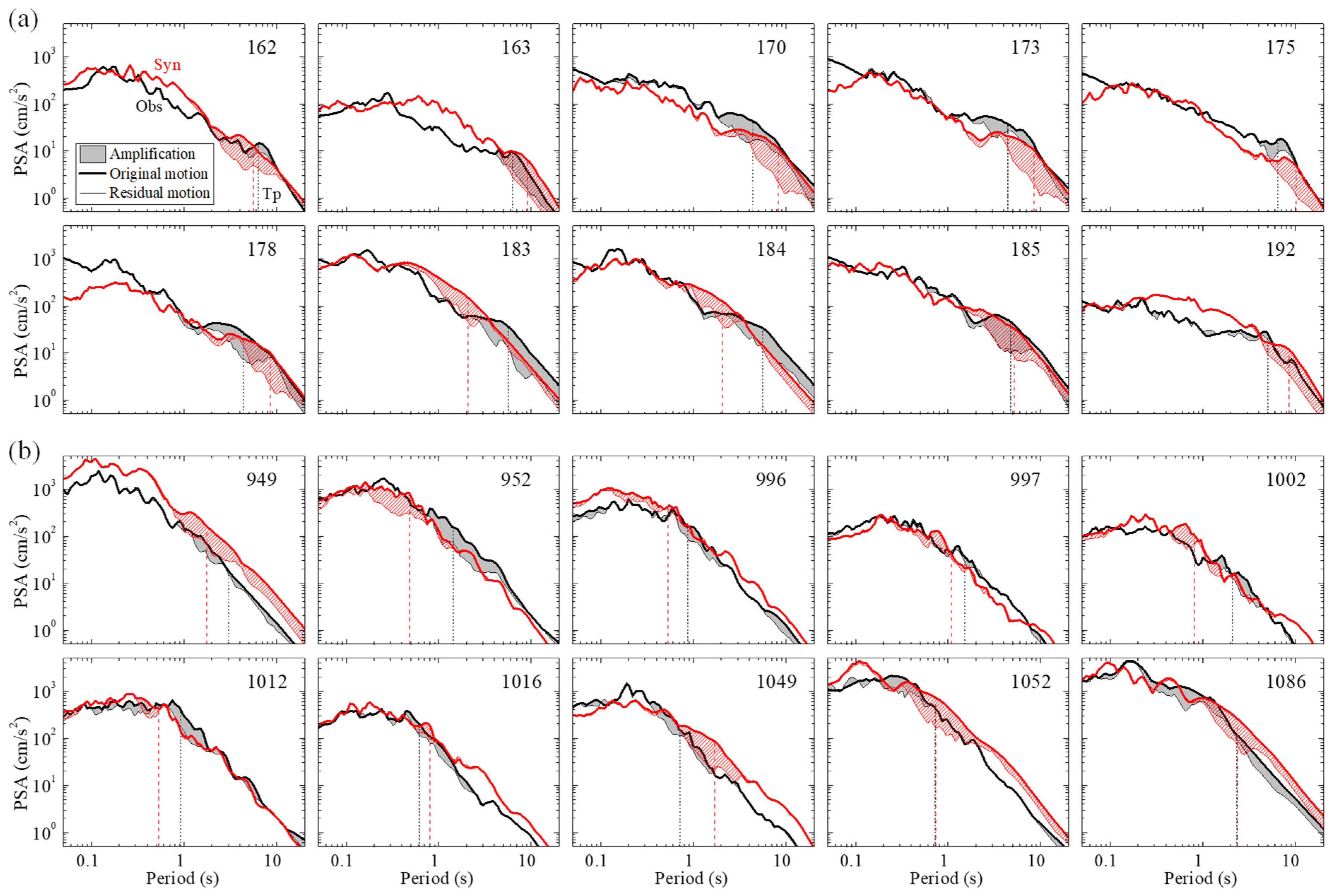
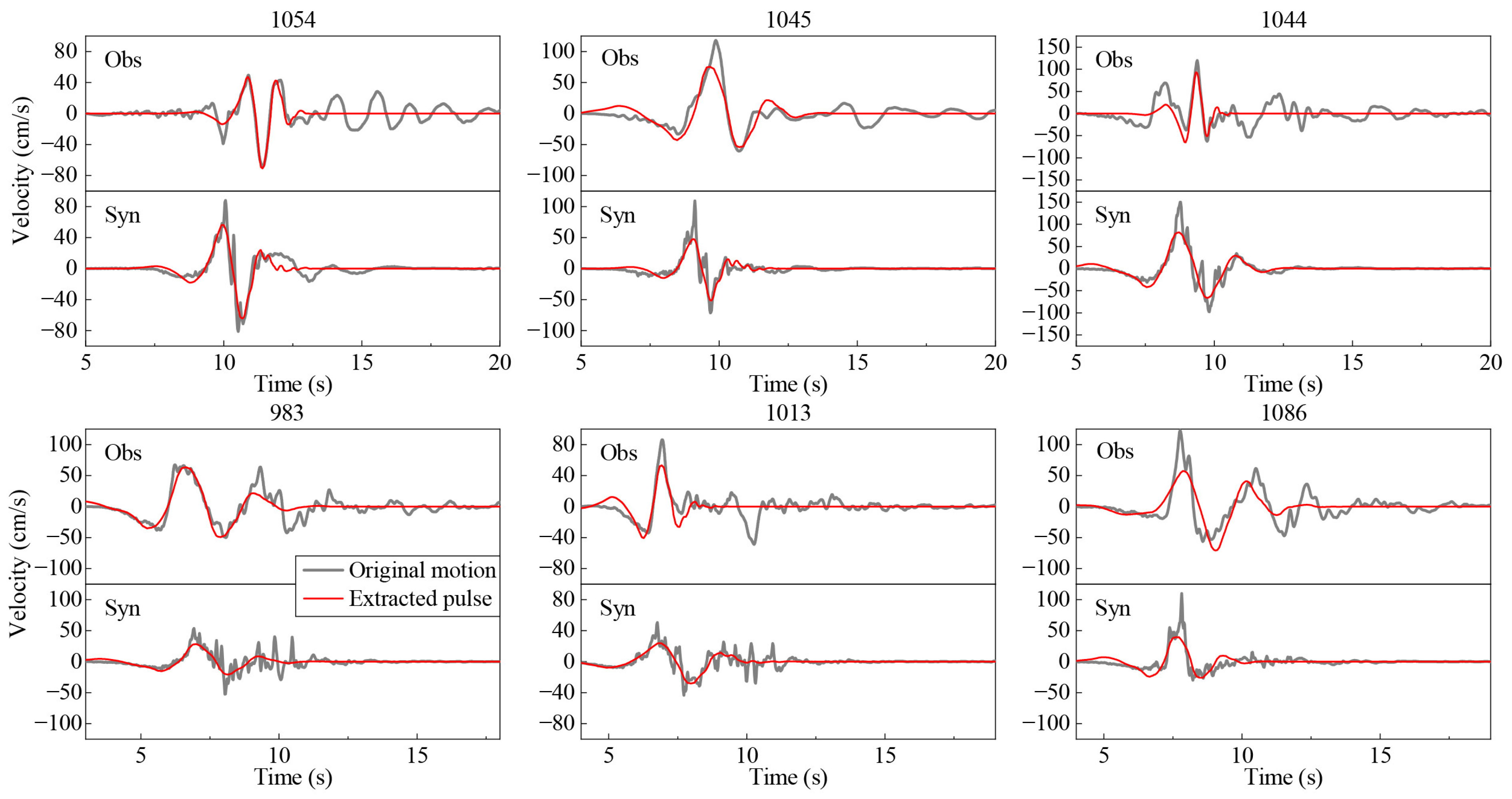
3.2. Pulse Identification of Ground Motion Fields
4. Spatial Characteristic Analysis of Near-Fault Pulses
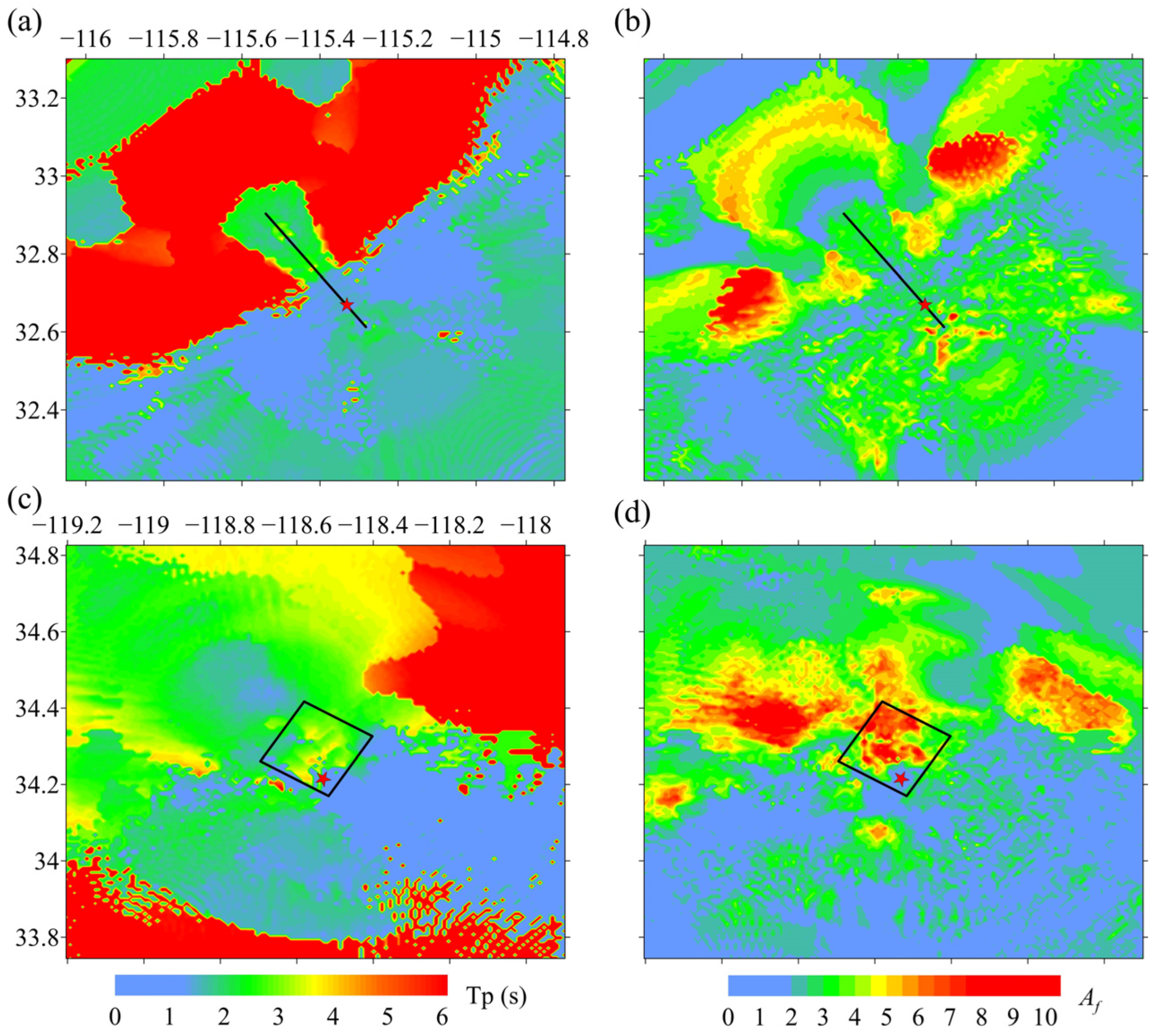
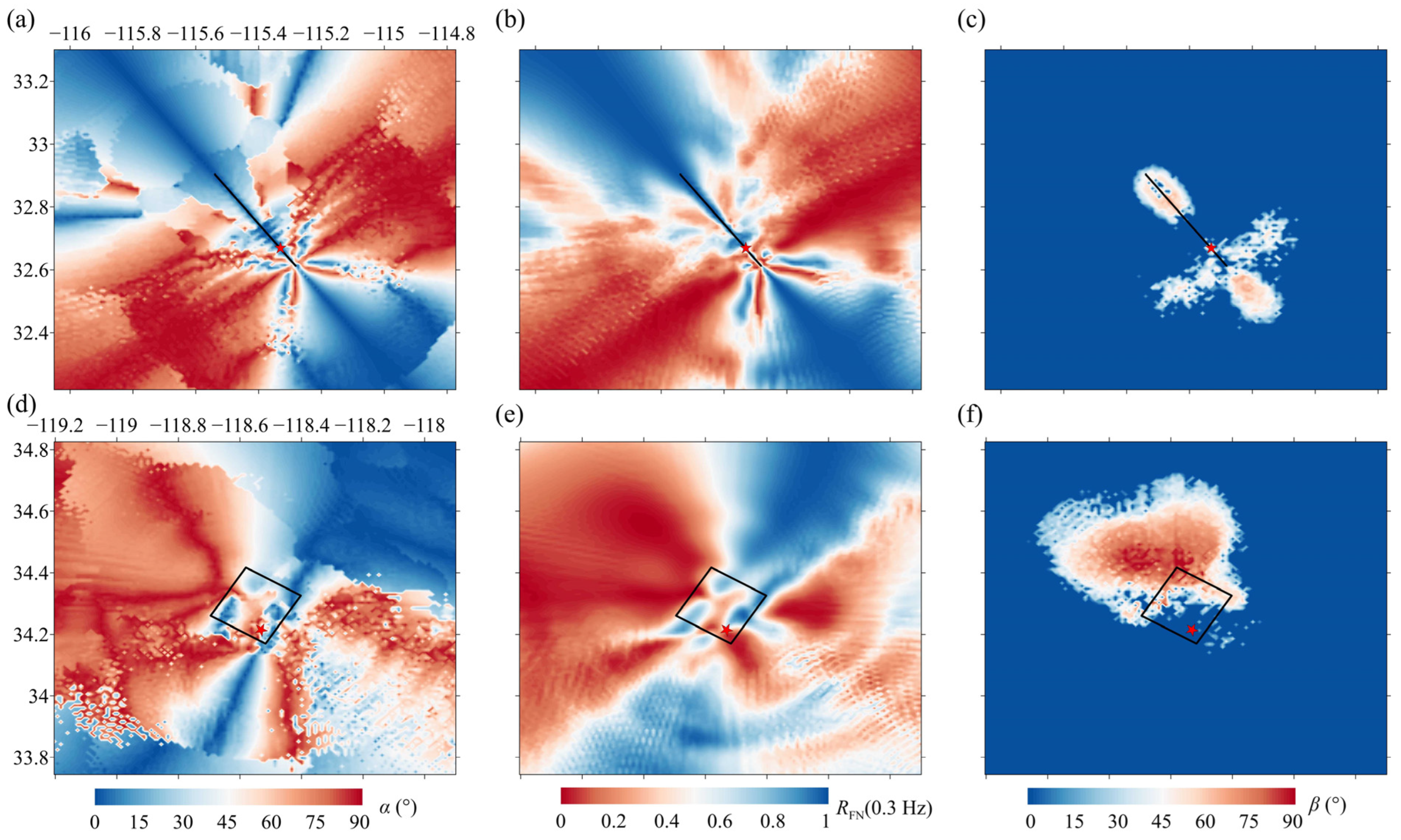
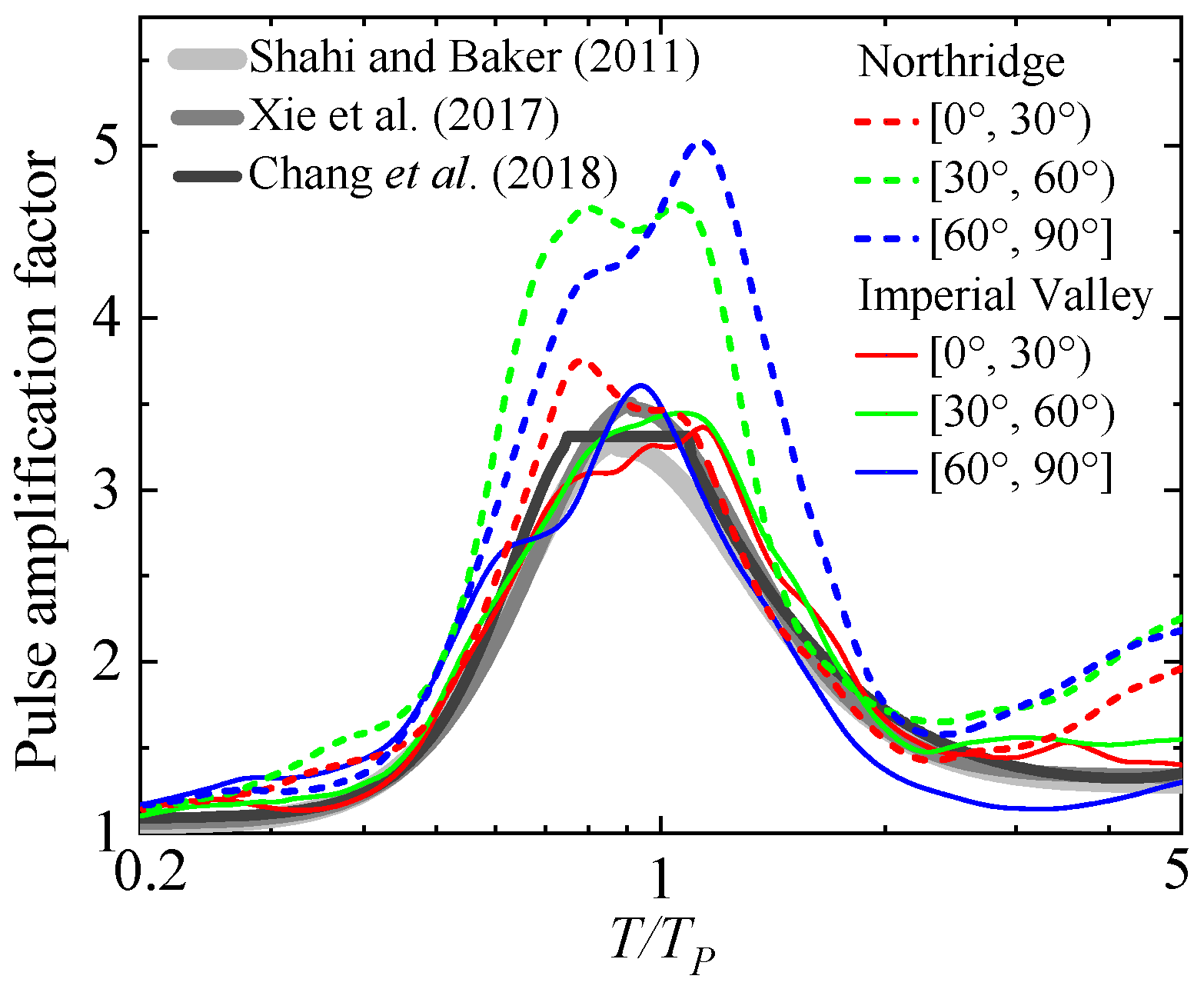
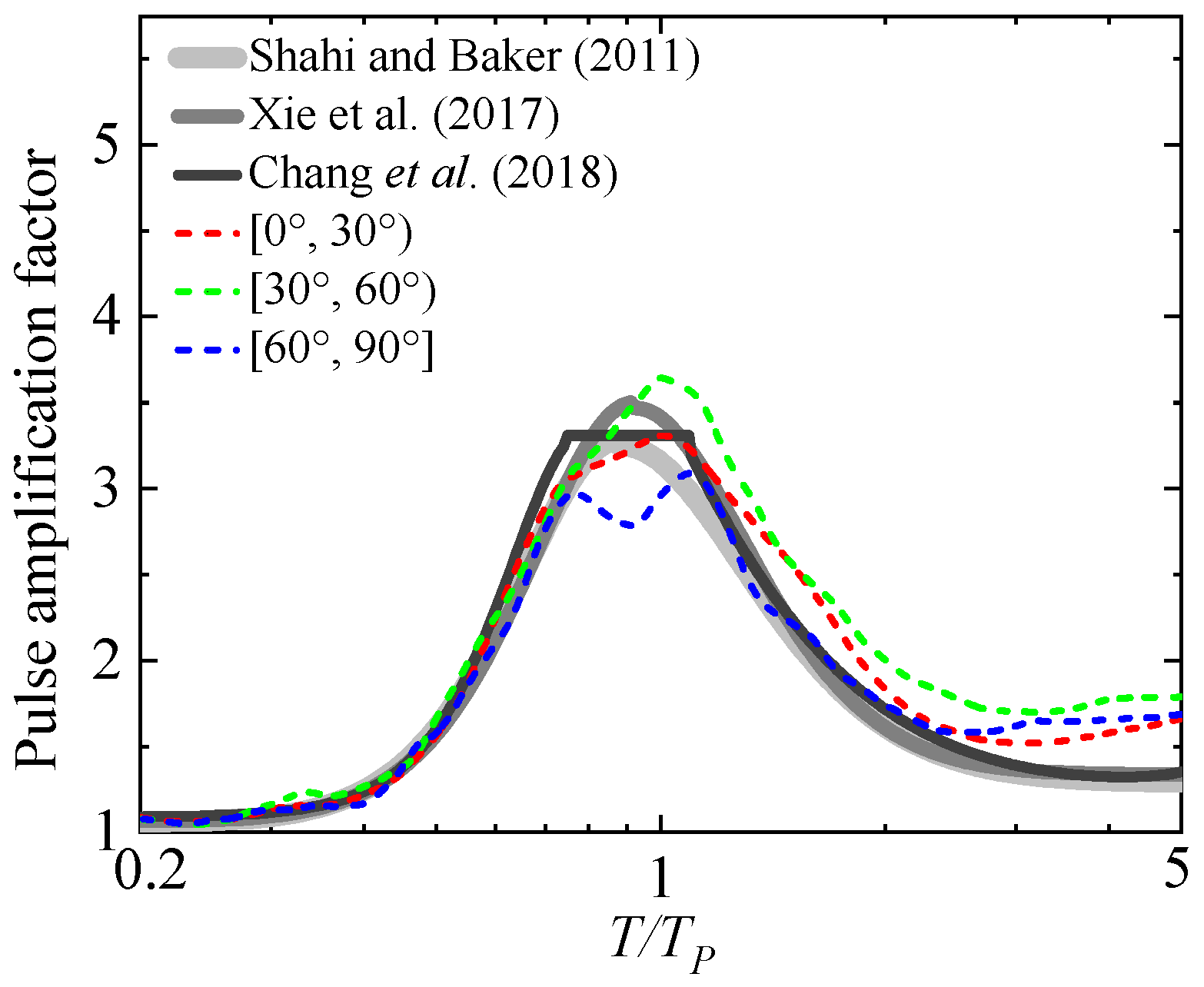
4.1. Spatial Analysis of the Pulse Period and Amplification Factor
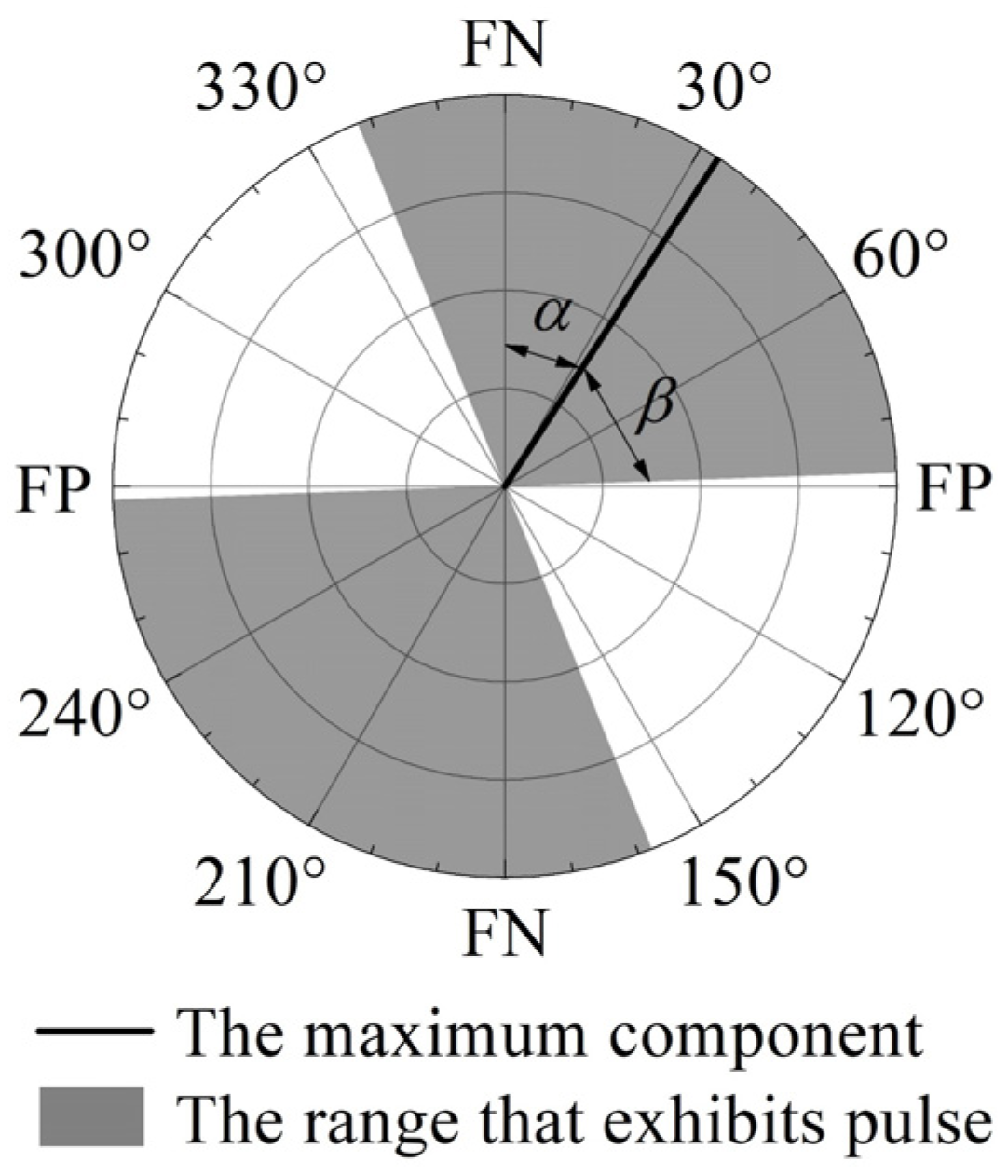
4.2. Spatial Analysis of Orientation of the Maximum Pulse Component
4.3. Relationship Between , , and
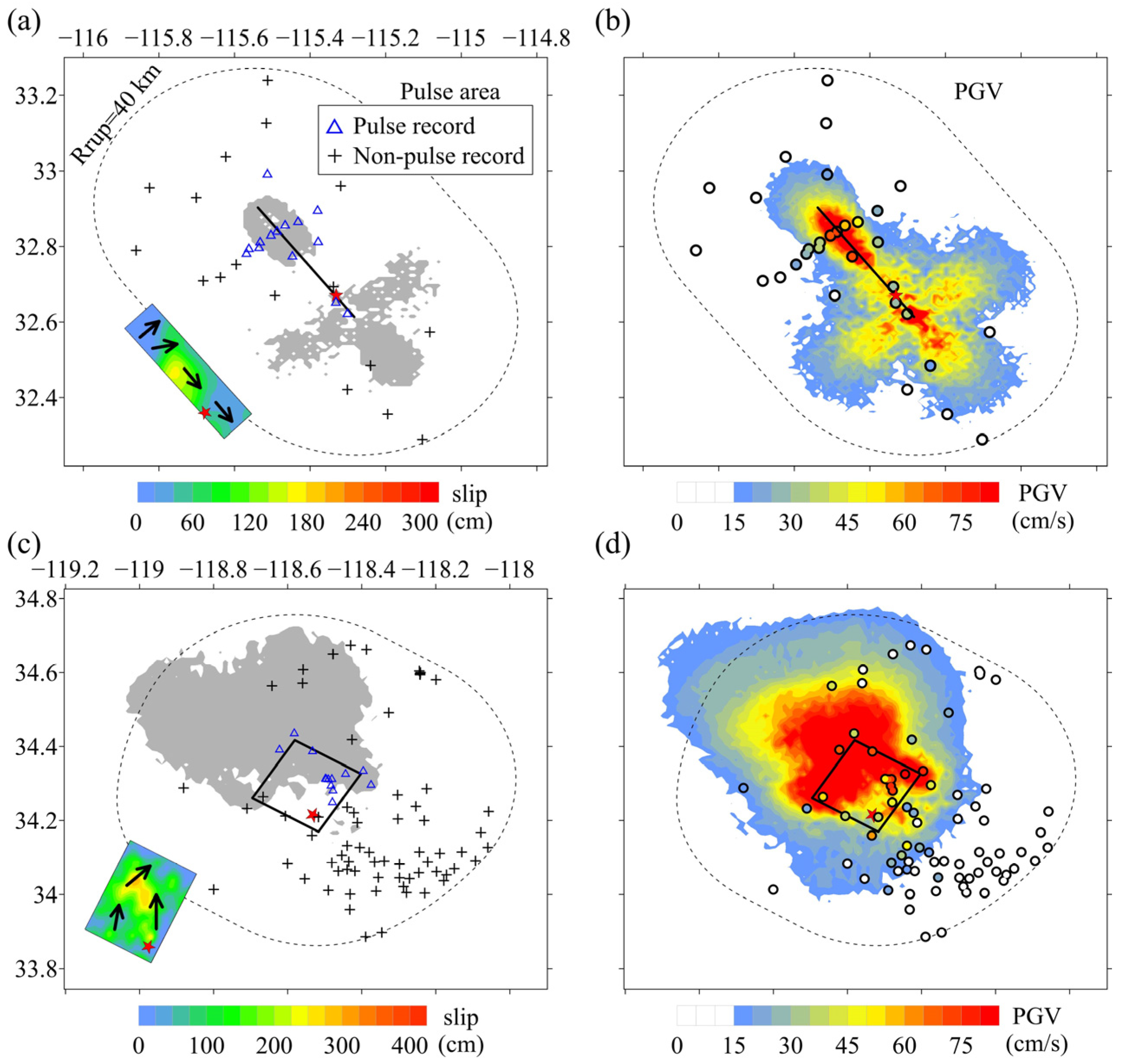
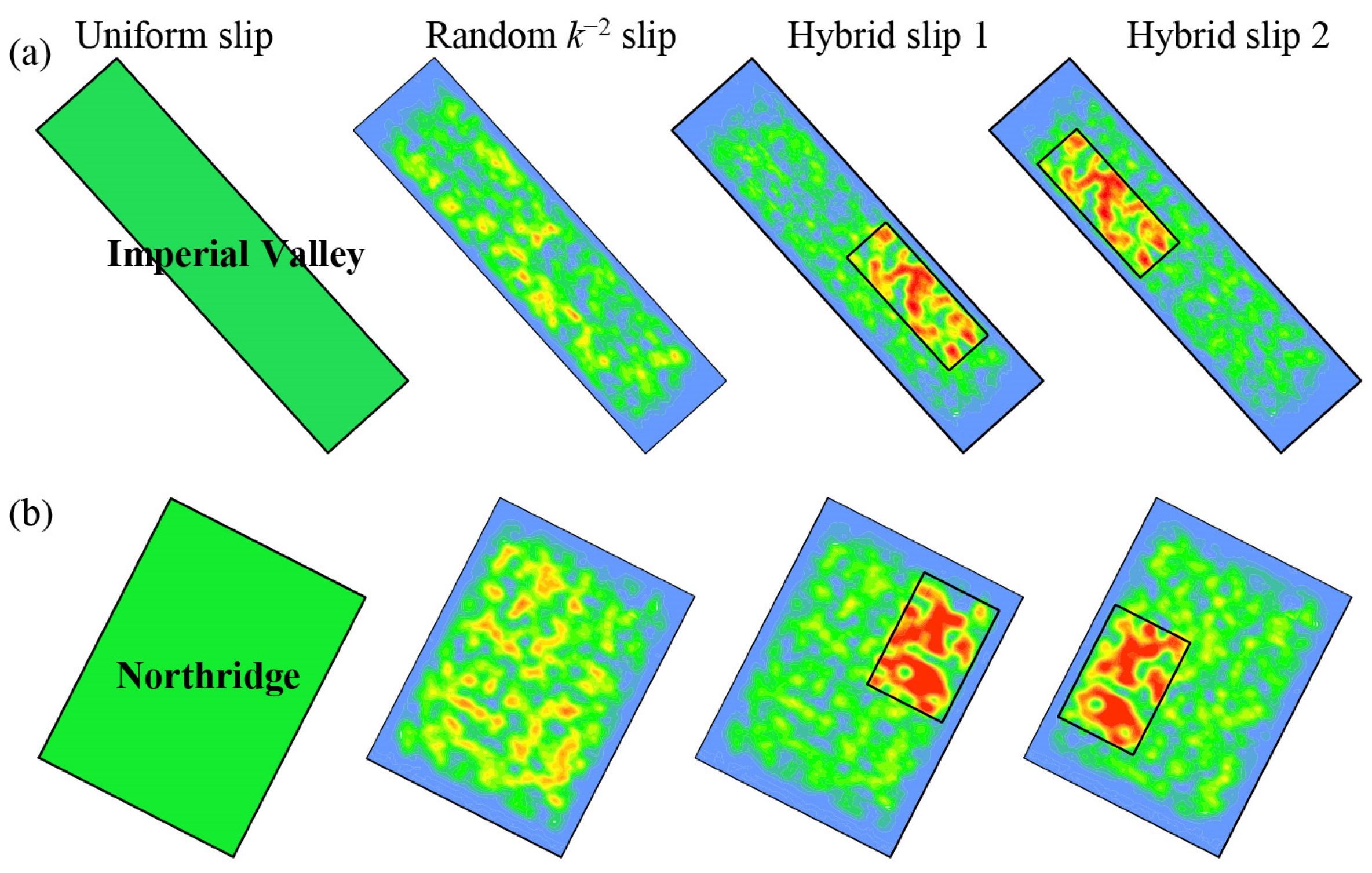
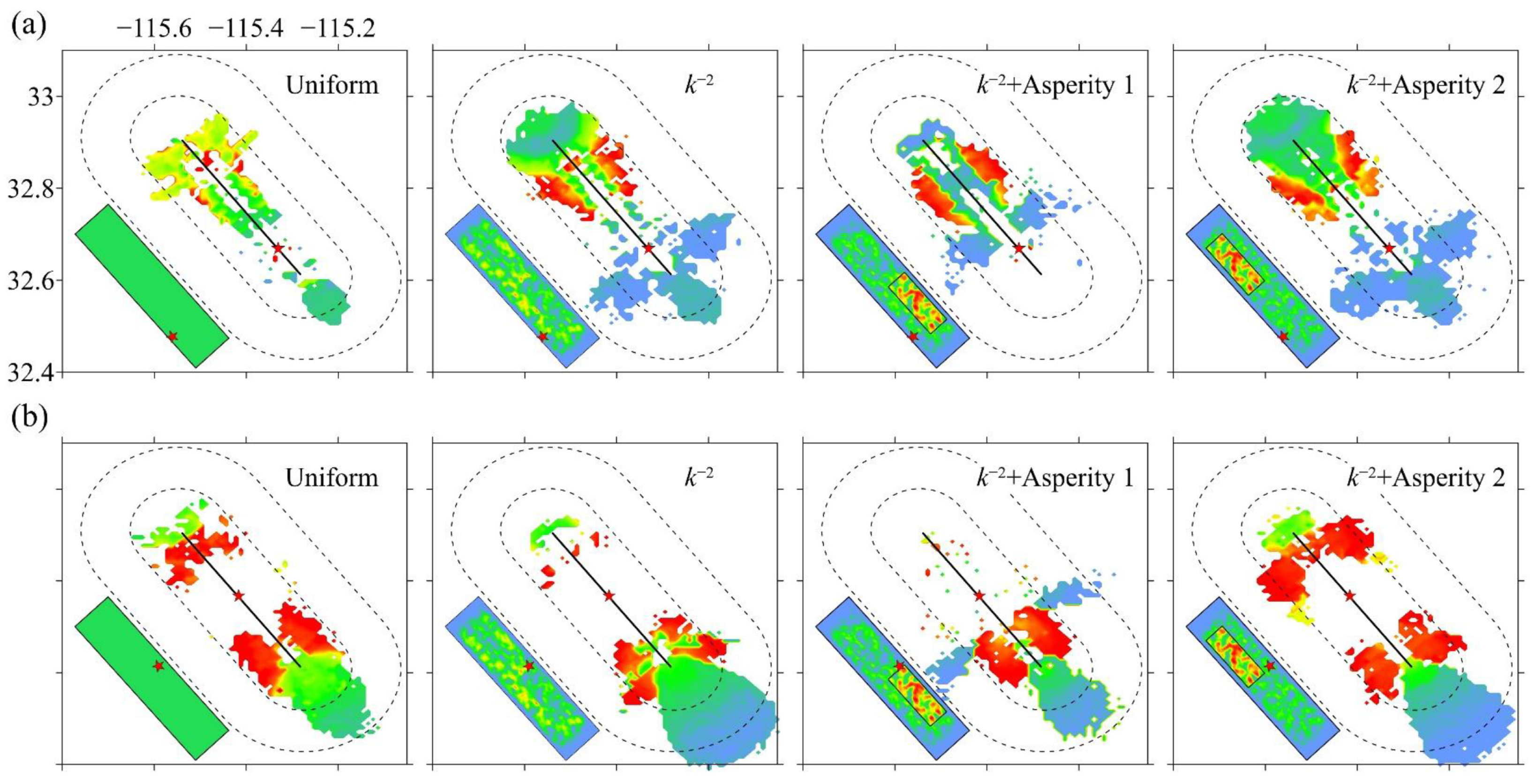
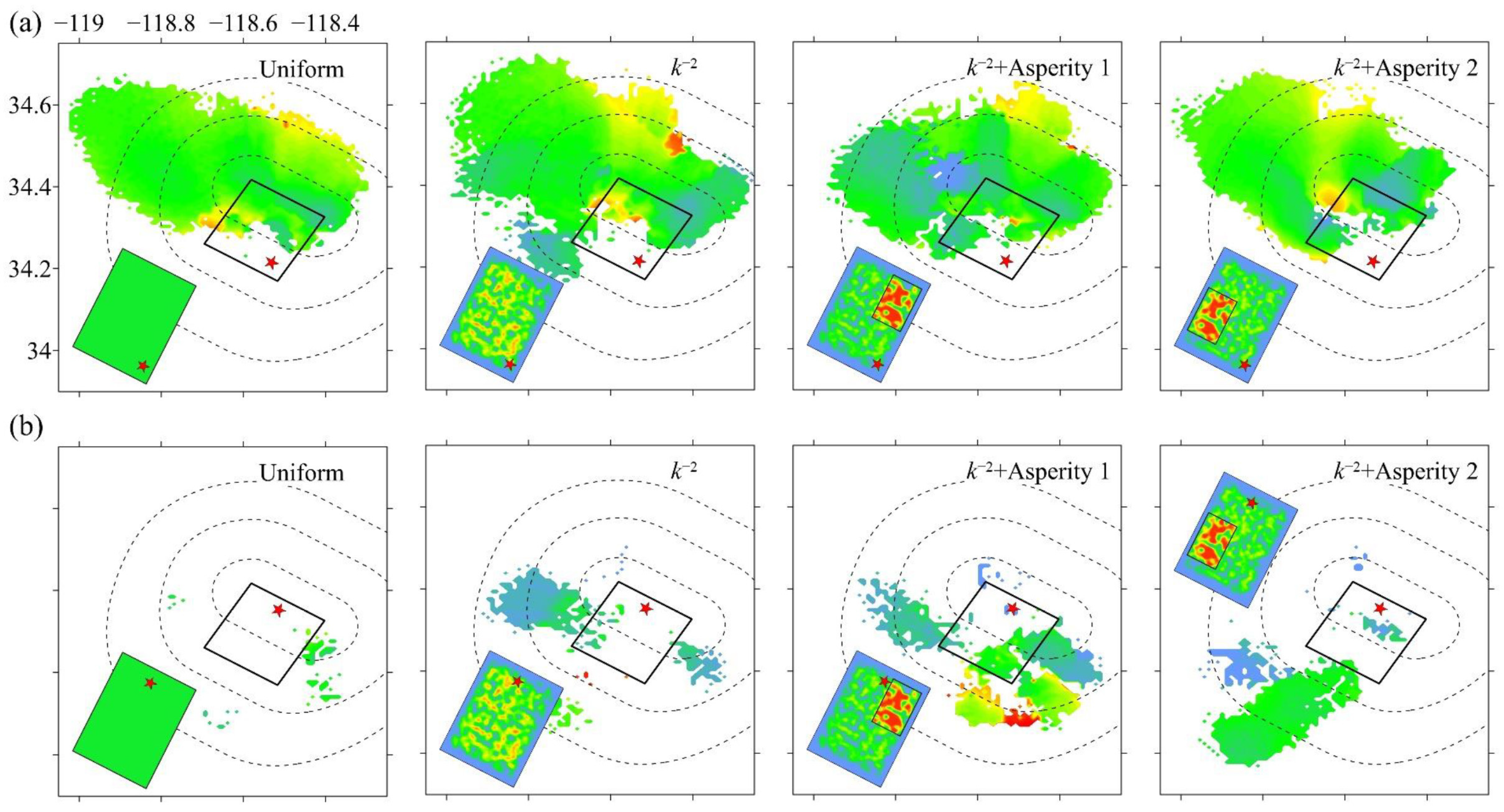
5. Influence of Slip Distribution on Area of Near-Fault Pulses
5.1. Type of Slip Distribution
5.2. Influence of Slip Distribution
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shahi, S.K.; Baker, J.W. An Empirically Calibrated Framework for Including the Effects of Near-Fault Directivity in Probabilistic Seismic Hazard Analysis. Bull. Seismol. Soc. Am. 2011, 101, 742–755. [Google Scholar] [CrossRef]
- Chioccarelli, E.; Iervolino, I. Near-Source Seismic Hazard and Design Scenarios. Earthq. Eng. Struct. Dyn. 2013, 42, 603–622. [Google Scholar] [CrossRef]
- Withers, K.; Moschetti, M.; Powers, P.; Petersen, M.; Graves, R.; Aagaard, B.T.; Baltay, A.; Luco, N.; Wirth, E.; Rezaeian, S.; et al. Integration of Rupture Directivity Models for the US National Seismic Hazard Model. Earthq. Spectra 2024, 40, 1066–1098. [Google Scholar] [CrossRef]
- Iervolino, I.; Cornell, C.A. Probability of Occurrence of Velocity Pulses in Near-Source Ground Motions. Bull. Seismol. Soc. Am. 2008, 98, 2262–2277. [Google Scholar] [CrossRef]
- Estacio, J.L.P.; De Risi, R. Historical Evolution of the Input Parameters of Ergodic and Non-Ergodic Ground Motion Models (GMMs): A Review. Earth-Sci. Rev. 2025, 105074. [Google Scholar] [CrossRef]
- Spudich, P.; Bayless, J.; Baker, J.; Chiou, S.; Somerville, A. Final Report of the NGA-West2 Directivity Working Group; Pacific Earthquake Engineering Research Center (PEER): Berkeley, CA, USA, 2013. [Google Scholar]
- Weatherill, G.; Lilienkamp, H. Capturing Directivity in Probabilistic Seismic Hazard Analysis for New Zealand: Challenges, Implications, and a Machine Learning Approach for Implementation. Bull. Seismol. Soc. Am. 2024, 114, 373–398. [Google Scholar] [CrossRef]
- Somerville, P.G. Magnitude Scaling of the near Fault Rupture Directivity Pulse. Phys. Earth Planet. Inter. 2003, 137, 201–212. [Google Scholar] [CrossRef]
- Bayless, J.; Abrahamson, N.A.; Somerville, P.G. A Rupture Directivity Adjustment Model and Its Application in Seismic Hazard. Earthq. Spectra 2025, 41, 753–781. [Google Scholar] [CrossRef]
- Xie, J.; Li, X.; Wen, Z. The Amplification Effects of Near-Fault Distinct Velocity Pulses on Response Spectra. Eng. Mech. 2017, 34, 194–211. [Google Scholar]
- Chang, Z.; Sun, X.; Zhai, C.; Zhao, J.X.; Xie, L. An Empirical Approach of Accounting for the Amplification Effects Induced by Near-Fault Directivity. Bull. Earthq. Eng. 2018, 16, 1871–1885. [Google Scholar] [CrossRef]
- Chang, Z.; Wu, H.; Goda, K. Automated Parameterization of Velocity Pulses in Near-fault Ground Motions. Earthq. Eng. Struct. Dyn. 2024, 53, 1006–1027. [Google Scholar] [CrossRef]
- Shahi, S.K.; Baker, J.W. An Efficient Algorithm to Identify Strong-Velocity Pulses in Multicomponent Ground Motions. Bull. Seismol. Soc. Am. 2014, 104, 2456–2466. [Google Scholar] [CrossRef]
- Withers, K.B.; Olsen, K.B.; Day, S.M.; Shi, Z. Ground Motion and Intraevent Variability from 3D Deterministic Broadband (0–7.5 Hz) Simulations along a Nonplanar Strike-Slip Fault. Bull. Seismol. Soc. Am. 2019, 109, 229–250. [Google Scholar] [CrossRef]
- Dadras, E.Y.; Yazdani, A.; Nicknam, A.; Eftekhari, S.N. Incorporating Source Rupture Characteristics into the Near-Fault Pulse Prediction Model. Bull. Seismol. Soc. Am. 2018, 108, 200–209. [Google Scholar] [CrossRef]
- Somerville, P.G.; Smith, N.F.; Graves, R.W.; Abrahamson, N.A. Modification of Empirical Strong Ground Motion Attenuation Relations to Include the Amplitude and Duration Effects of Rupture Directivity. Seismol. Res. Lett. 1997, 68, 199–222. [Google Scholar] [CrossRef]
- Rowshandel, B. Incorporating Source Rupture Characteristics into Ground-Motion Hazard Analysis Models. Seismol. Res. Lett. 2006, 77, 708–722. [Google Scholar] [CrossRef]
- Yu, H.; Zhu, C.; Chen, Q. Intelligent Identification Method for Pulse-like Ground Motions and Field Distribution of Three-Dimensional Orientation-Independent Pulse Characteristics. Soil Dyn. Earthq. Eng. 2024, 182, 108722. [Google Scholar] [CrossRef]
- Lin, Y.Y.; Kanamori, H.; Zhan, Z.; Ma, K.F.; Yeh, T.Y. Modelling of Pulse-like Velocity Ground Motion during the 2018 Mw6.3 Hualien Earthquake, Taiwan. Geophys. J. Int. 2020, 223, 348–365. [Google Scholar] [CrossRef]
- Yen, M.H.; von Specht, S.; Lin, Y.Y.; Cotton, F.; Ma, K.F. Within-and Between-Event Variabilities of Strong-Velocity Pulses of Moderate Earthquakes within Dense Seismic Arrays. Bull. Seismol. Soc. Am. 2022, 112, 361–380. [Google Scholar] [CrossRef]
- Han, L.; Tao, Z.; Cao, Z.; Tao, X. Relationship Between Asperities and Velocity Pulse Generation Mechanism. Front. Earth Sci. 2022, 10, 843532. [Google Scholar] [CrossRef]
- Cao, Z.; Tao, X.; Tao, Z.; Tang, A. Kinematic Source Modeling for the Synthesis of Broadband Ground Motion Using the F-k Approach. Bull. Seismol. Soc. Am. 2019, 109, 1738–1757. [Google Scholar] [CrossRef]
- Hartzell, S.; Liu, P.; Mendoza, C.; Ji, C.; Larson, K.M. Stability and Uncertainty of Finite-Fault Slip Inversions: Application to the 2004 Parkfield, California, Earthquake. Bull. Seismol. Soc. Am. 2007, 97, 1911–1934. [Google Scholar] [CrossRef]
- Zhu, L.; Rivera, L.A. A Note on the Dynamic and Static Displacements from a Point Source in Multilayered Media. Geophys. J. Int. 2002, 148, 619–627. [Google Scholar] [CrossRef]
- Gallovič, F.; Brokešová, J. On Strong Ground Motion Synthesis with k−2 Slip Distributions. J. Seismol. 2004, 8, 211–224. [Google Scholar] [CrossRef]
- Crempien, J.G.F.; Archuleta, R.J. UCSB Method for Simulation of Broadband Ground Motion from Kinematic Earthquake Sources. Seismol. Res. Lett. 2015, 86, 61–67. [Google Scholar] [CrossRef]
- Baker, J.W. Quantitative Classification of Near-Fault Ground Motions Using Wavelet Analysis. Bull. Seismol. Soc. Am. 2007, 97, 1486–1501. [Google Scholar] [CrossRef]
- Hartzell, S.H.; Heaton, T.H. Inversion of Strong Ground Motion and Teleseismic Waveform Data for the Fault Rupture History of the 1979 Imperial Valley, California, Earthquake. Bull. Seismol. Soc. Am. 1983, 73, 1553–1583. [Google Scholar] [CrossRef]
- Wald, D.J.; Heaton, T.H.; Hudnut, K.W. The Slip History of the 1994 Northridge, California, Earthquake Determined from Strong-Motion, Teleseismic, GPS, and Leveling Data. Bull. Seismol. Soc. Am. 1996, 86, S49–S70. [Google Scholar] [CrossRef]
- Cao, Y.; Mavroeidis, G.P. Simulation of Near-Fault Ground Strains and Rotations from Actual Strike-Slip Earthquakes: Case Studies of the 2004 Mw 6.0 Parkfield, the 1979 Mw 6.5 Imperial Valley and the 1999 Mw 7.5 Izmit Earthquakes. Geophys. J. Int. 2021, 226, 1920–1947. [Google Scholar] [CrossRef]
- Luo, Q.; Zhang, G.; Ding, B.; Ji, Z. Evaluation of Strongest Ground Motions under Strike-Slip Rupture for the Luding and Imperial Valley Earthquakes. Soil Dyn. Earthq. Eng. 2025, 194, 109390. [Google Scholar] [CrossRef]
- Hough, S.E.; Graves, R.W.; Cochran, E.S.; Yoon, C.E.; Blair, L.; Haefner, S.; Wald, D.J.; Quitoriano, V. The 17 January 1994 Northridge, California, Earthquake: A Retrospective Analysis. Seism. Rec. 2024, 4, 151–160. [Google Scholar] [CrossRef]
- McGarr, A.; Fletcher, J. Mapping Apparent Stress and Energy Radiation over Fault Zones of Major Earthquakes. Bull. Seismol. Soc. Am. 2002, 92, 1633–1646. [Google Scholar] [CrossRef]
- Graves, R.W.; Pitarka, A. Broadband Ground-Motion Simulation Using a Hybrid Approach. Bull. Seismol. Soc. Am. 2010, 100, 2095–2123. [Google Scholar] [CrossRef]
- Ancheta, T.D.; Darragh, R.B.; Stewart, J.P.; Seyhan, E.; Silva, W.J.; Chiou, B.S.-J.; Wooddell, K.E.; Graves, R.W.; Kottke, A.R.; Boore, D.M.; et al. NGA-West2 Database. Earthq. Spectra 2014, 30, 989–1005. [Google Scholar] [CrossRef]
- Boore, D.M.; Stewart, J.P.; Seyhan, E.; Atkinson, G.M. NGA-West2 Equations for Predicting PGA, PGV, and 5% Damped PSA for Shallow Crustal Earthquakes. Earthq. Spectra 2014, 30, 1057–1085. [Google Scholar] [CrossRef]
- Pitarka, A.; Graves, R.; Irikura, K.; Miyakoshi, K.; Wu, C.; Kawase, H.; Rodgers, A.; McCallen, D. Refinements to the Graves–Pitarka Kinematic Rupture Generator, Including a Dynamically Consistent Slip-Rate Function, Applied to the 2019 Mw 7.1 Ridgecrest Earthquake. Bull. Seismol. Soc. Am. 2022, 112, 287–306. [Google Scholar] [CrossRef]
- Boore, D.M. Orientation-Independent, Nongeometric-Mean Measures of Seismic Intensity from Two Horizontal Components of Motion. Bull. Seismol. Soc. Am. 2010, 100, 1830–1835. [Google Scholar] [CrossRef]
- Howard, J.K.; Tracy, C.A.; Burns, R.G. Comparing Observed and Predicted Directivity in Near-Source Ground Motion. Earthq. Spectra 2005, 21, 1063–1092. [Google Scholar] [CrossRef]
- Somerville, P.; Irikura, K.; Graves, R.; Sawada, S.; Wald, D.; Abrahamson, N.; Iwasaki, Y.; Kagawa, T.; Smith, N.; Kowada, A. Characterizing Crustal Earthquake Slip Models for the Prediction of Strong Ground Motion. Seismol. Res. Lett. 1999, 70, 59–80. [Google Scholar] [CrossRef]
- Takenaka, H.; Mamada, Y.; Futamure, H. Near-Source Effect on Radiation Pattern of High-Frequency S Waves: Strong SH-SV Mixing Observed from Aftershocks of the 1997 Northwestern Kagoshima, Japan, Earthquakes. Phys. Earth Planet. Inter. 2003, 137, 31–43. [Google Scholar] [CrossRef]
- Castro, R.; Franceschina, G.; Pacor, F.; Bindi, D.; Luzi, L. Analysis of the Frequency Dependence of the S-Wave Radiation Pattern from Local Earthquakes in Central Italy. Bull. Seismol. Soc. Am. 2006, 96, 415–426. [Google Scholar] [CrossRef]
- Takemura, S.; Furumura, T.; Saito, T. Distortion of the Apparent S-Wave Radiation Pattern in the High-Frequency Wavefield: Tottori-Ken Seibu, Japan, Earthquake of 2000. Geophys. J. Int. 2009, 178, 950–961. [Google Scholar] [CrossRef]
- Sandeep; Joshi, A.; Kamal; Kumar, P.; Kumar, A. Effect of Frequency-Dependent Radiation Pattern in the Strong Motion Simulation of the 2011 Tohoku Earthquake, Japan, Using Modified Semi-Empirical Method. Nat. Hazards 2014, 73, 1499–1521. [Google Scholar] [CrossRef]
- Li, C.; Zuo, Z.; Kunnath, S.; Chen, L. Orientation of the Strongest Velocity Pulses and the Maximum Structural Response to Pulse-like Ground Motions. Soil Dyn. Earthq. Eng. 2020, 136, 106240. [Google Scholar] [CrossRef]


| Parameters | Imperial Valley | Northridge |
|---|---|---|
| Moment magnitude | 6.58 | 6.8 |
| Energy magnitude | 6.6 | 6.7 |
| Source mechanism | Strike-slip | Dip-slip |
| Strike | 323° | 122° |
| Dip | 90° | 40° |
| Average rake | 180° | 101° |
| Fault depth | 0 km | 5 km |
| Fault length and width | 42 km × 10.4 km | 18 km × 24 km |
| Number of subsources | 16 × 8 | 16 × 16 |
| Stress drop | 2.5 MPa | 6 MPa |
| Velocity structure | [34] | [34] |
| Slip and rake distributions | [28] | [29] |
| Number of records | 31 | 83 |
| Number of pulse-like records | 14 | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Z.; Wei, J.; Sun, Z.; Song, W. Spatial Characteristic Analysis of Near-Fault Velocity Pulses Based on Simulation of Earthquake Ground Motion Fields. Buildings 2025, 15, 1363. https://doi.org/10.3390/buildings15081363
Cao Z, Wei J, Sun Z, Song W. Spatial Characteristic Analysis of Near-Fault Velocity Pulses Based on Simulation of Earthquake Ground Motion Fields. Buildings. 2025; 15(8):1363. https://doi.org/10.3390/buildings15081363
Chicago/Turabian StyleCao, Zelin, Jia Wei, Zhiyu Sun, and Weiju Song. 2025. "Spatial Characteristic Analysis of Near-Fault Velocity Pulses Based on Simulation of Earthquake Ground Motion Fields" Buildings 15, no. 8: 1363. https://doi.org/10.3390/buildings15081363
APA StyleCao, Z., Wei, J., Sun, Z., & Song, W. (2025). Spatial Characteristic Analysis of Near-Fault Velocity Pulses Based on Simulation of Earthquake Ground Motion Fields. Buildings, 15(8), 1363. https://doi.org/10.3390/buildings15081363





