Deformation Analysis of Nuclear Power Shield Tunnel by Longitudinal Response Displacement Method Considering Fluid–Solid Coupling
Abstract
:1. Introduction
2. Methods
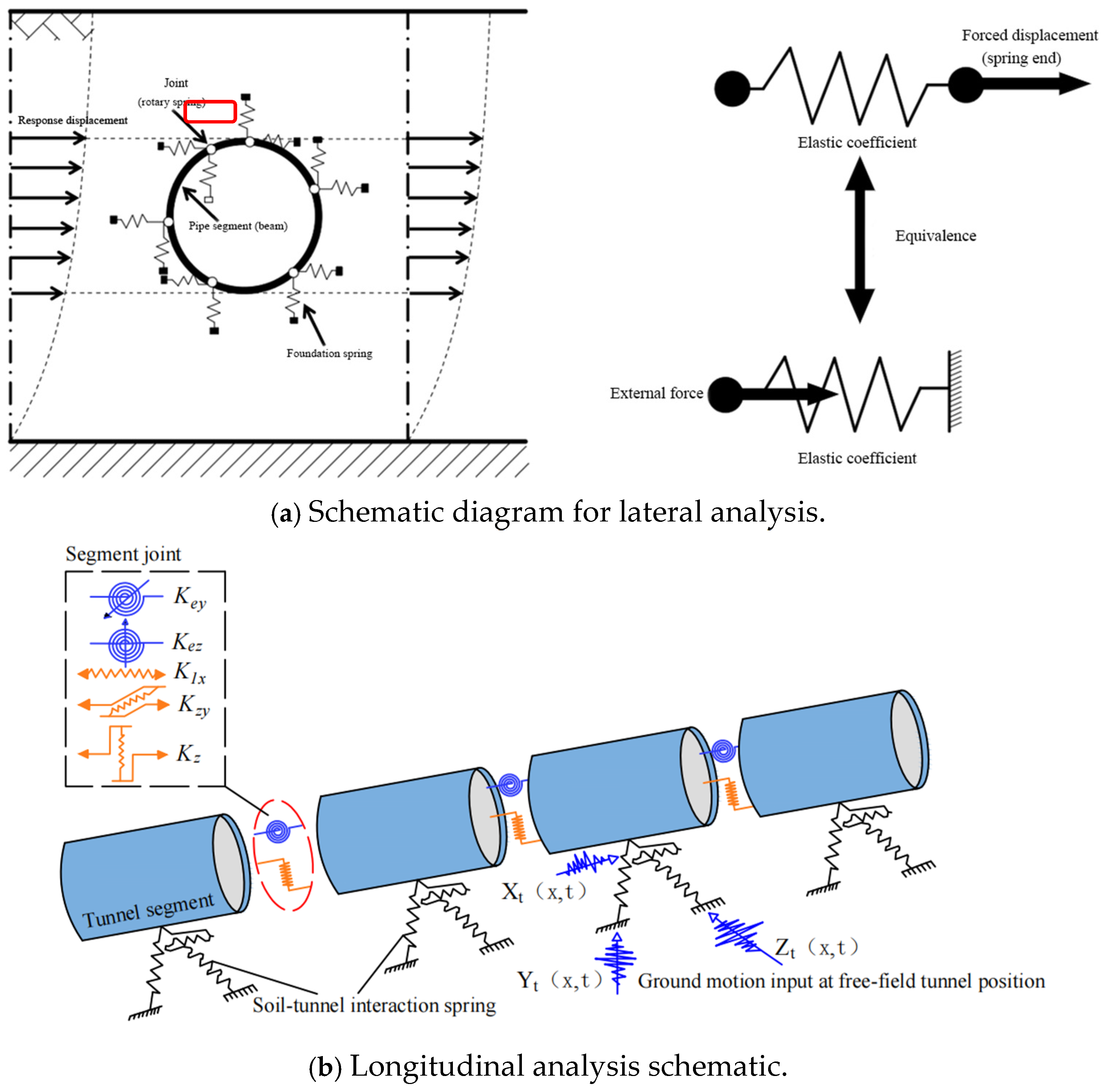
2.1. Response Displacement Method
2.2. Fluid–Solid Coupling
2.3. Engineering Cases
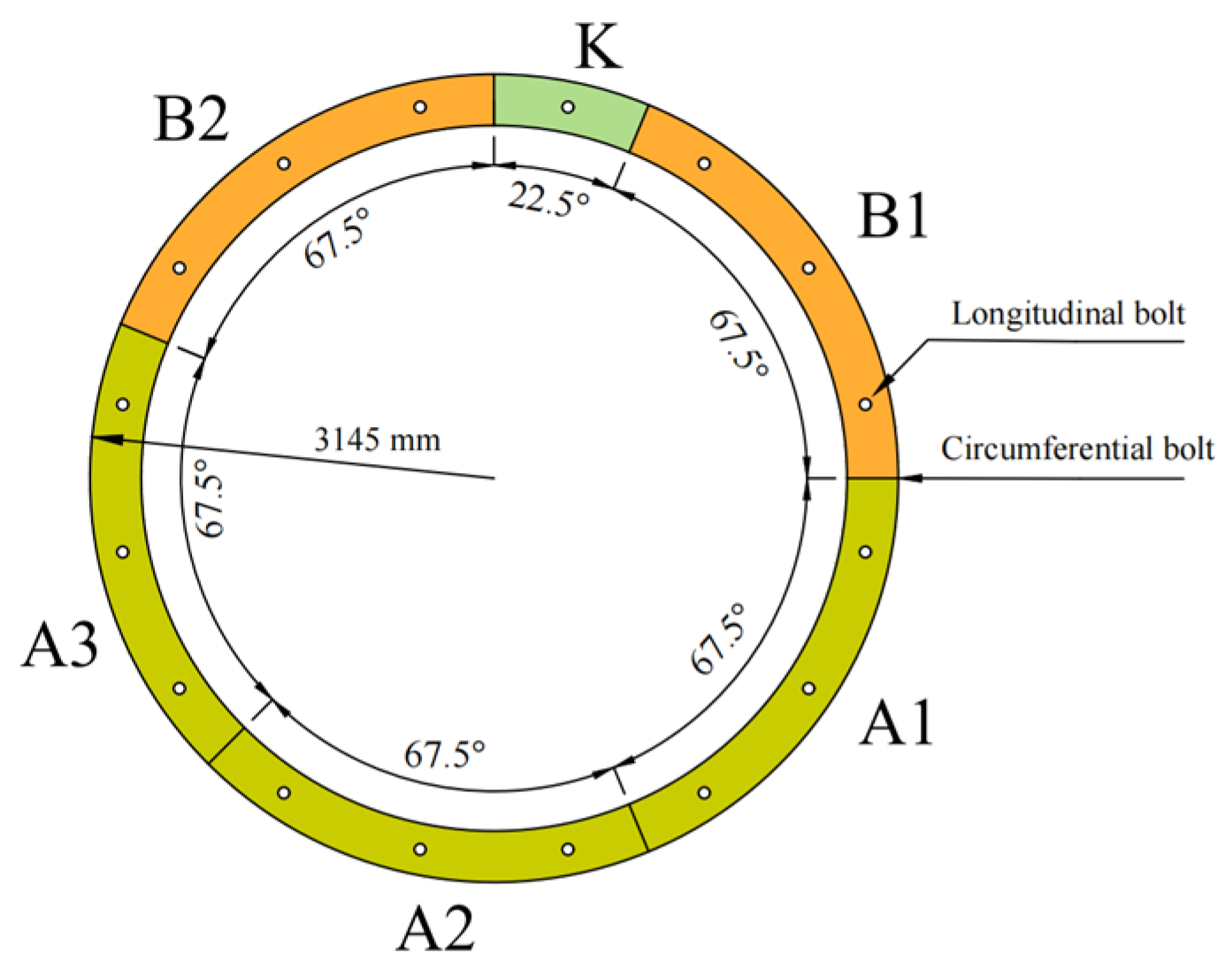
2.3.1. Engineering Overview
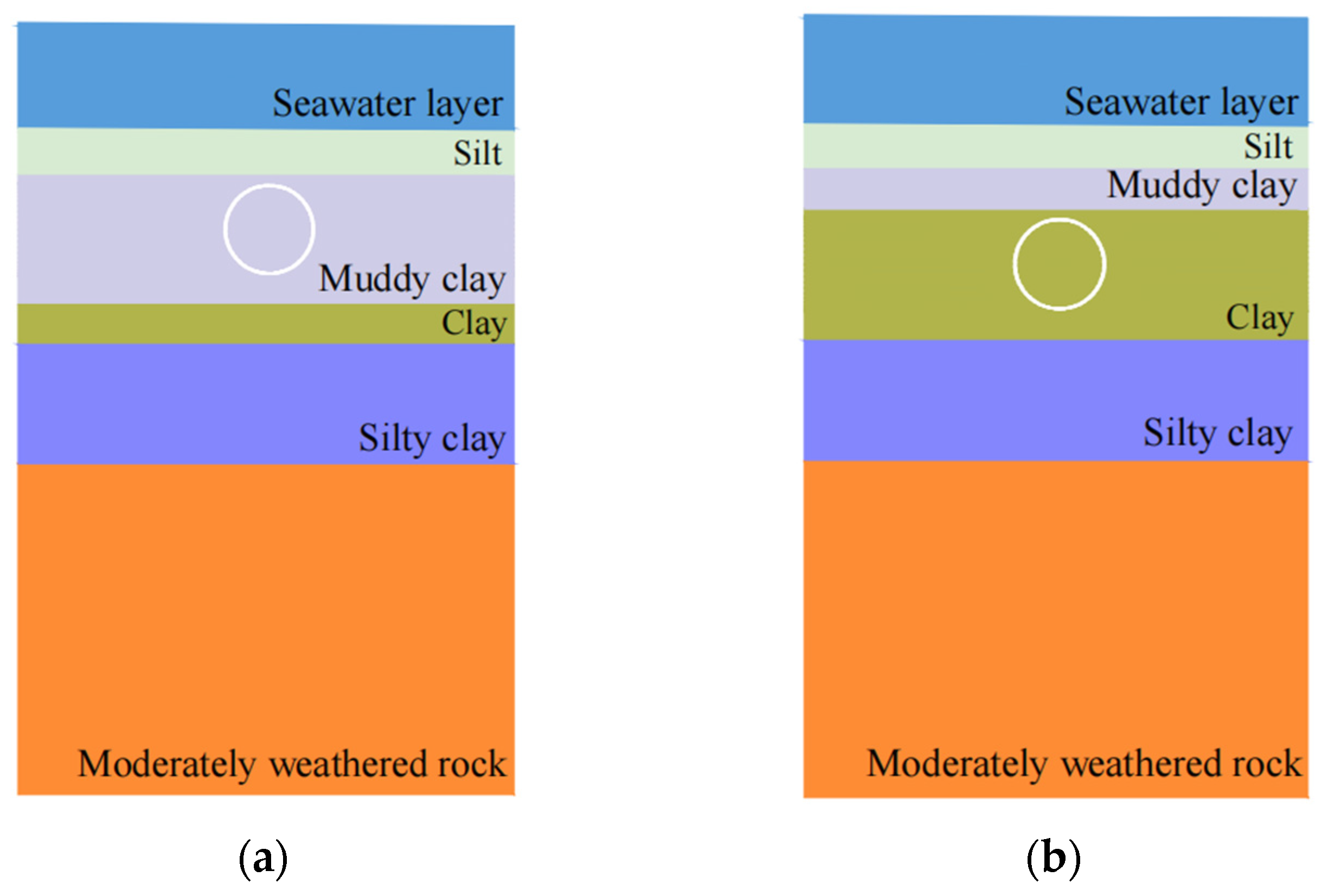
2.3.2. Soil Calculation Parameters
2.3.3. Design Ground Motion Parameters
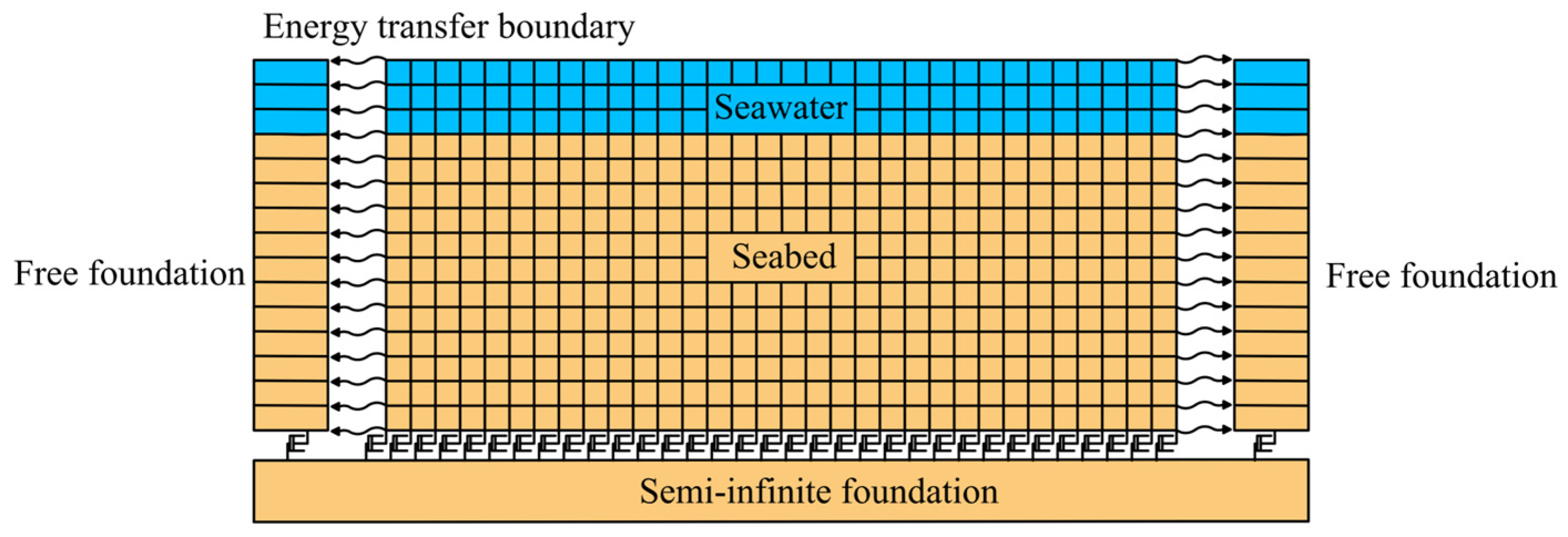
2.4. Numerical Analysis Model
2.4.1. Lateral Analysis Model
2.4.2. Longitudinal Analysis Model
2.4.3. Free-Field Analysis
3. Results
3.1. Results of Lateral Analysis
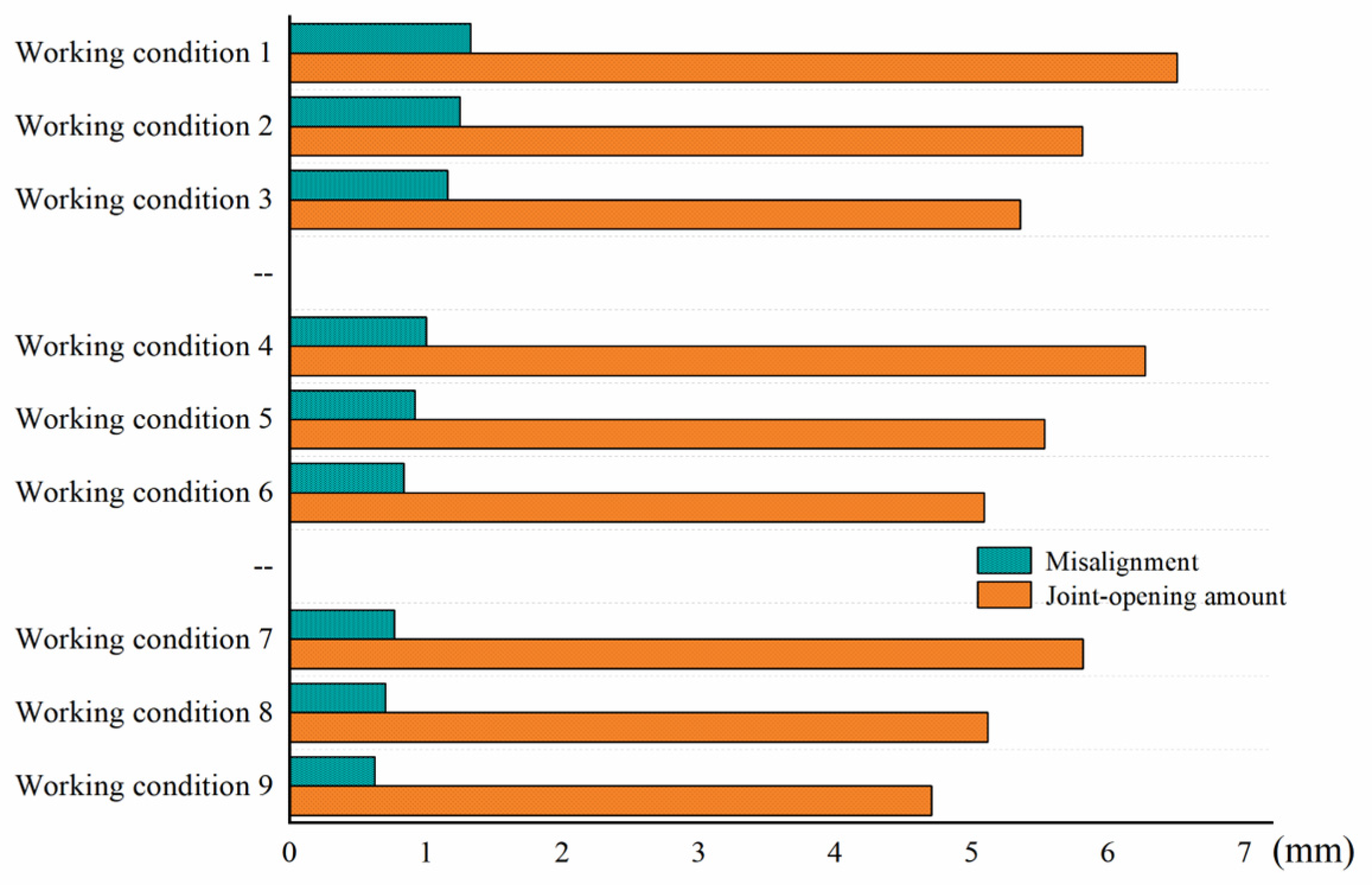
3.2. Results of Longitudinal Analysis
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; Tao, L.; Chen, X. Study on the Transverse Seismic Response of Underwater Tunnel Shaft. Sci. Technol. Eng. 2016, 16, 273–278. [Google Scholar]
- Ding, Z.; Peng, L.; Li, X. Study on Seismic Response of Connectional Passages for Underwater Shield Tunnel. J. Zhengzhou Univ. (Eng. Sci.) 2010, 31, 65–69. [Google Scholar]
- Yu, H.; Zhao, G.; Xu, L.; Dai, J.; Tao, X. Analysis of Submarine Tunnel Linings in Rising Region Crossing Upper Soft and Lower Hard Stratum to Transversal Seismic Load. Earthq. Eng. Eng. Dyn. 2021, 41, 211–218. [Google Scholar]
- Wu, X.; Xu, J.; Wang, S.; Sha, P.; Han, Z.; Chen, X.; Shu, S.; Qiao, W.; Zeng, X. Ground Deformation of Shield Tunneling through Composite Strata in Coastal Areas. Buildings 2024, 14, 1236. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, Y.; Chen, C. Correlation Analysis of Tunnel Deformation and Internal Force in the Earthquake Based on Tunnel Inclination. Buildings 2024, 14, 1395. [Google Scholar] [CrossRef]
- Chang, X.; Sun, J.; Guo, L. Mechanical Performances of Concrete-Filled Steel Pipe Composite Segments in Complex Geological Conditions. Buildings 2024, 14, 2961. [Google Scholar] [CrossRef]
- He, R.; Zhou, Z.; Li, S.; Vanapalli, S. Investigating Surface Settlements During Shield Tunneling Using Numerical Analysis. Sustainability 2025, 17, 20. [Google Scholar] [CrossRef]
- Cai, X.; Liang, J.; Xu, A.; Li, D.; Wu, Z.; Yan, Q. Longitudinal Seismic Analysis of Mawan Sea-crossing Large Diameter Shield Tunnels. J. Nat. Disasters 2020, 29, 13–20. [Google Scholar]
- Chen, G.X.; Ruan, B.; Zhao, K.; Chen, W.Y.; Zhuang, H.Y.; Du, X.L.; Khoshnevisan, S.; Juang, C.H. Nonlinear Response Characteristics of Undersea Shield Tunnel Subjected to Strong Earthquake Motions. J. Earthq. Eng. 2018, 24, 351–380. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, G.; Kong, M. Seismic Response of Undersea Tunnels to Hydrodynamic and Hydrostatic Pressures. Chin. J. Geotech. Eng. 2013, 35, 357–362. [Google Scholar]
- Cheng, X.S.; Xu, W.W.; Yue, C.Q.; Du, X.L.; Charles, H. Dowding. Seismic Response of Fluid–structure Interaction of Undersea Tunnel During Bidirectional Earthquake. Ocean. Eng. 2014, 75, 64–70. [Google Scholar] [CrossRef]
- Chen, W.; Lv, Z.; Xu, L.; Ruan, B.; Ma, J.; Chen, G. Seismic Responce of Subsea Tunnels Consideing Seawater Seabed Coupling Effect. J. Eng. Geol. 2021, 29, 1878–1886. [Google Scholar]
- He, C.; Geng, P. Research on Practical Seismic Analysis Methods of Shield Tunnel. China J. Highw. Transp. 2020, 33, 15–25. [Google Scholar]
- Zhou, Y.; Xia, C.; Shi, Z.; Lu, G.; Liu, L.; Liu, M. Progressive Failure of Water-Resistant Stratum in Karst Tunnel Construction Using an Improved Meshfree Method Considering Fluid–Solid Interaction. Buildings 2024, 14, 3140. [Google Scholar] [CrossRef]
- Huang, W.; Xu, G.; He, C.; Li, B. Seismic Response Analysis of Subsea Tunnels Considering Fluid-Solid Coupling Effect. Tunn. Constr. 2024, 44, 739–749. [Google Scholar]
- Li, Y.; Wang, Y.; Ren, J.; Dong, Q.; Chen, L.; Wang, Z. Research on the Determination and Law of Formation Seepage Pressure of Slurry Shield Tunnel. Yellow River 2024, 46, 138–144. [Google Scholar]
- Jiang, J.; Huang, W.; Xun, Z.; Zhao, K.; Li, Z.; Du, X. Seismic Elasto-plastic Response Analysis of Subsea Immersed Tunnel of Hong Kong-Zhuhai-Macao Bridge. J. Build. Struct. 2023, 44, 359–366. [Google Scholar]
- Wang, W.; He, C.; Geng, P. Longitudinal Seismic Analysis of Shield Tunnels in Homogeneous Ground. Mod. Tunn. Technol. 2016, 53, 73–79. [Google Scholar]
- Geng, P.; Wang, Q.; Guo, X.; He, C.; Lu, S.; Xiao, M. Force Characteristics of Longitudinal Joints of Shield Tunnel under Seismic Action. J. Southwest Jiaotong Univ. 2020, 55, 704–712. [Google Scholar]
- Yan, Q.; Zhang, Y.; Wang, C.; Geng, P. Quasi-static Analysis Method for Seismic Effect of Shear Waves on Shield Tunnel. Eng. Mech. 2015, 32, 184–191. [Google Scholar]
- Liang, J.; Wu, Z.; Xin, Y.; Ba, Z. Seismic Countermeasures of Shield Tunnel under Fault Movement. Earthq. Eng. Eng. Dyn. 2020, 40, 1–11. [Google Scholar]
- Zhang, G.; Zhang, W.; Qi, J.; Niu, R.; Zhang, C. Seismic Response Analysis of Anchor Joint in Shield–Driven Tunnel Considering Soil–Structure Interaction. Appl. Sci. 2022, 12, 6362. [Google Scholar] [CrossRef]
- Wang, X.; Meng, M.; Li, J.; Zhang, L.; Wang, S. Comparative Analysis of Reaction Displacement Method and Time History Analysis Method in Seismic Design of Tunnel. Railw. Eng. 2015, 7, 35–38. [Google Scholar]
- Liang, J.; Zhu, Y.; Zhao, H. Applicability of Integral Forced Response Displacement Method Inseismic Analysis of Shield Tunnels. Earthq. Eng. Eng. Dyn. 2020, 40, 1–10. [Google Scholar]
- Fu, X.; Chang, S.; Chen, G. Comparison of Pseudo Static Method and Nonlinear Dynamic Method of Subway Station Structure Seismic Response Analysis. Earthq. Eng. Eng. Dyn. 2016, 36, 44–51. [Google Scholar]
- GB 50267-2019; Standard for Seismic Design of Nuclear Power Plants. China Architecture & Building Press: Beijing, China, 2019. (In Chinese)
- Gu, Y.; Liu, J.; Du, Y. 3D Consistent Viscous-spring Artificial Boundary and Viscous-spring Boundary Element. Eng. Mech. 2007, 12, 31–37. [Google Scholar]
- Yin, X.; Li, J.; Lin, G. 3D Compact Viscous-spring Boundary Element Based on UPFs. World Earthq. Eng. 2012, 28, 95–100. [Google Scholar]
- Zhao, J.; Gan, C.; Lan, W. Three Dimensional Seismic Analysis of Immersed Tunnel in Sea Area of Nuclear Power Plant Considering Soil Structure Interaction. Nucl. Sci. Eng. 2023, 43, 402–411. [Google Scholar]
- GB 50909-2014; Code for Seismic Design of Urban Rail Transit Structures. China Planning Press: Beijing, China, 2014. (In Chinese)
- GB/T 51336-2018; Standard for Seismic Design of Underground Structure. Architecture and Building Press: Beijing, China, 2018.
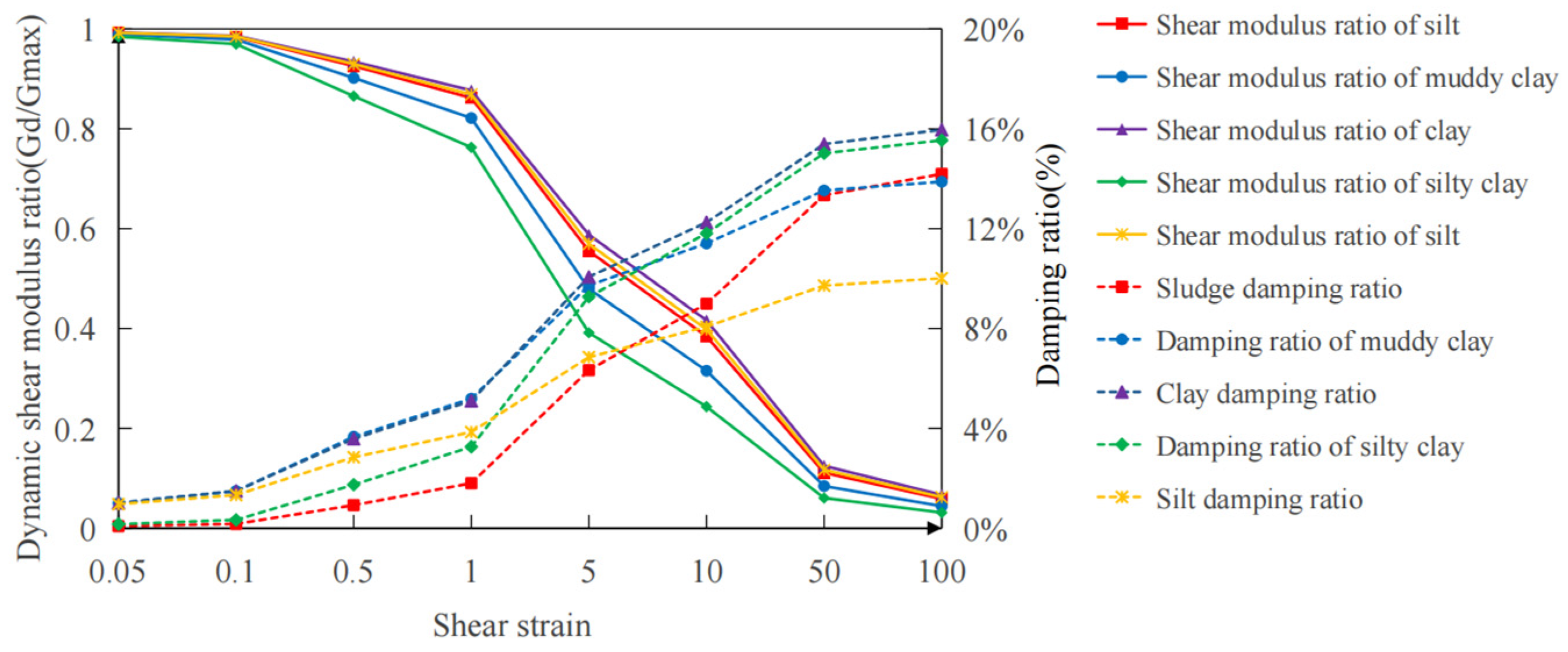

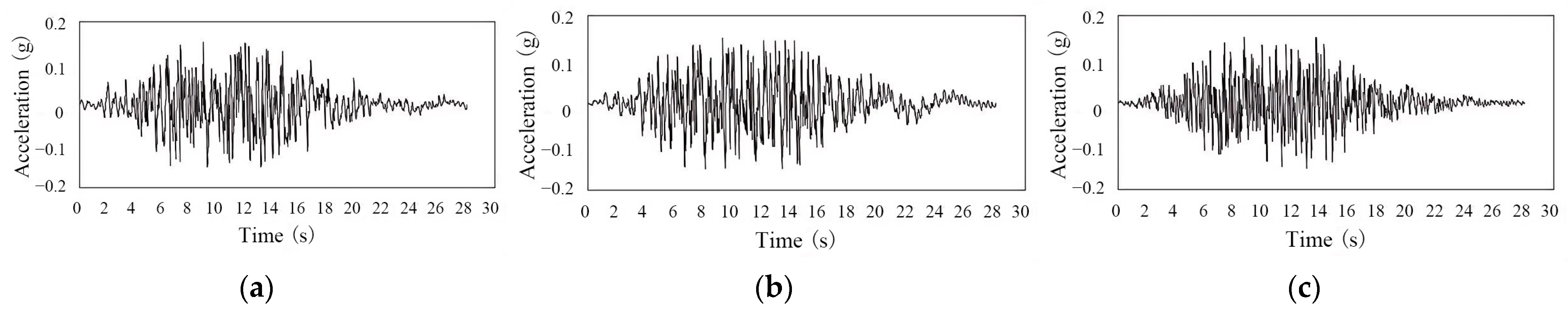
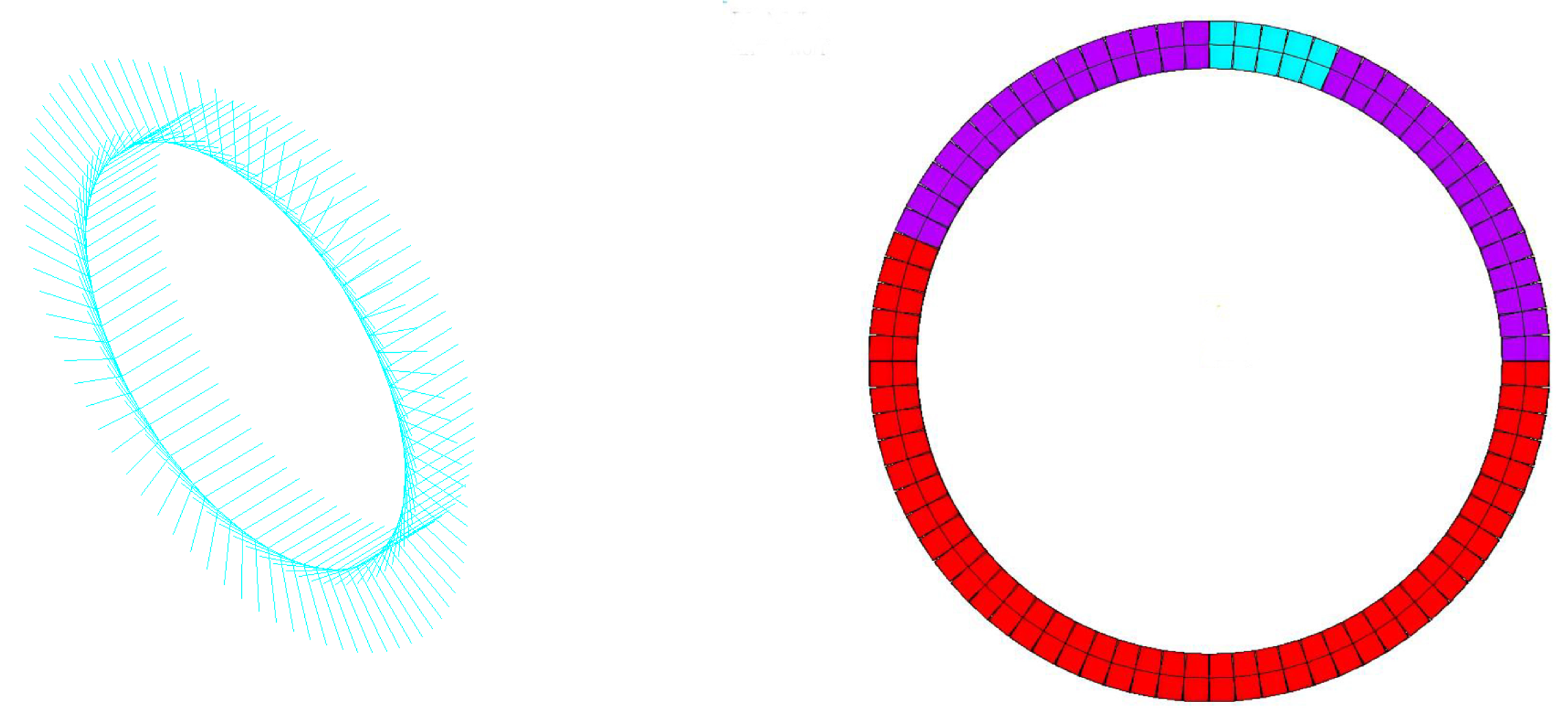
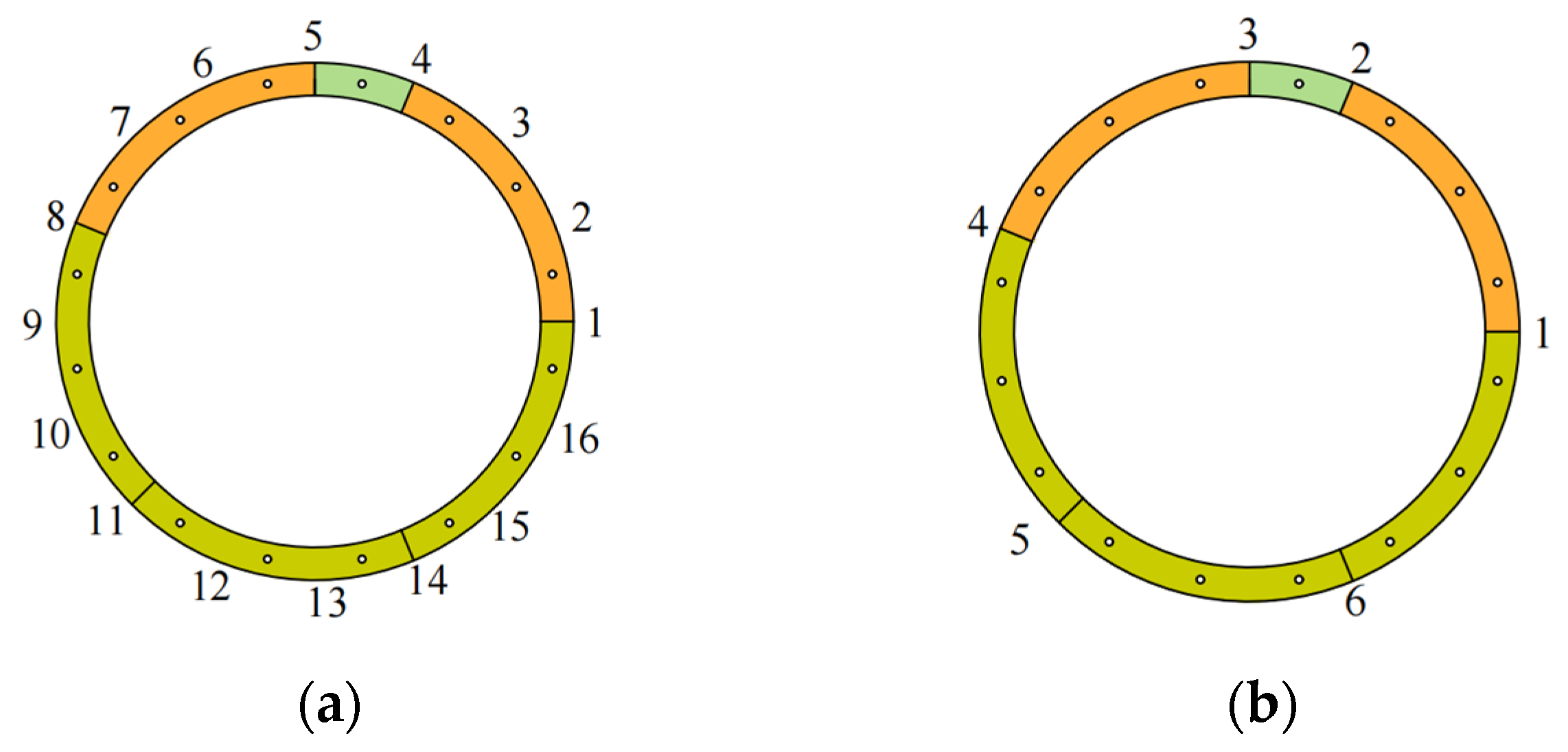
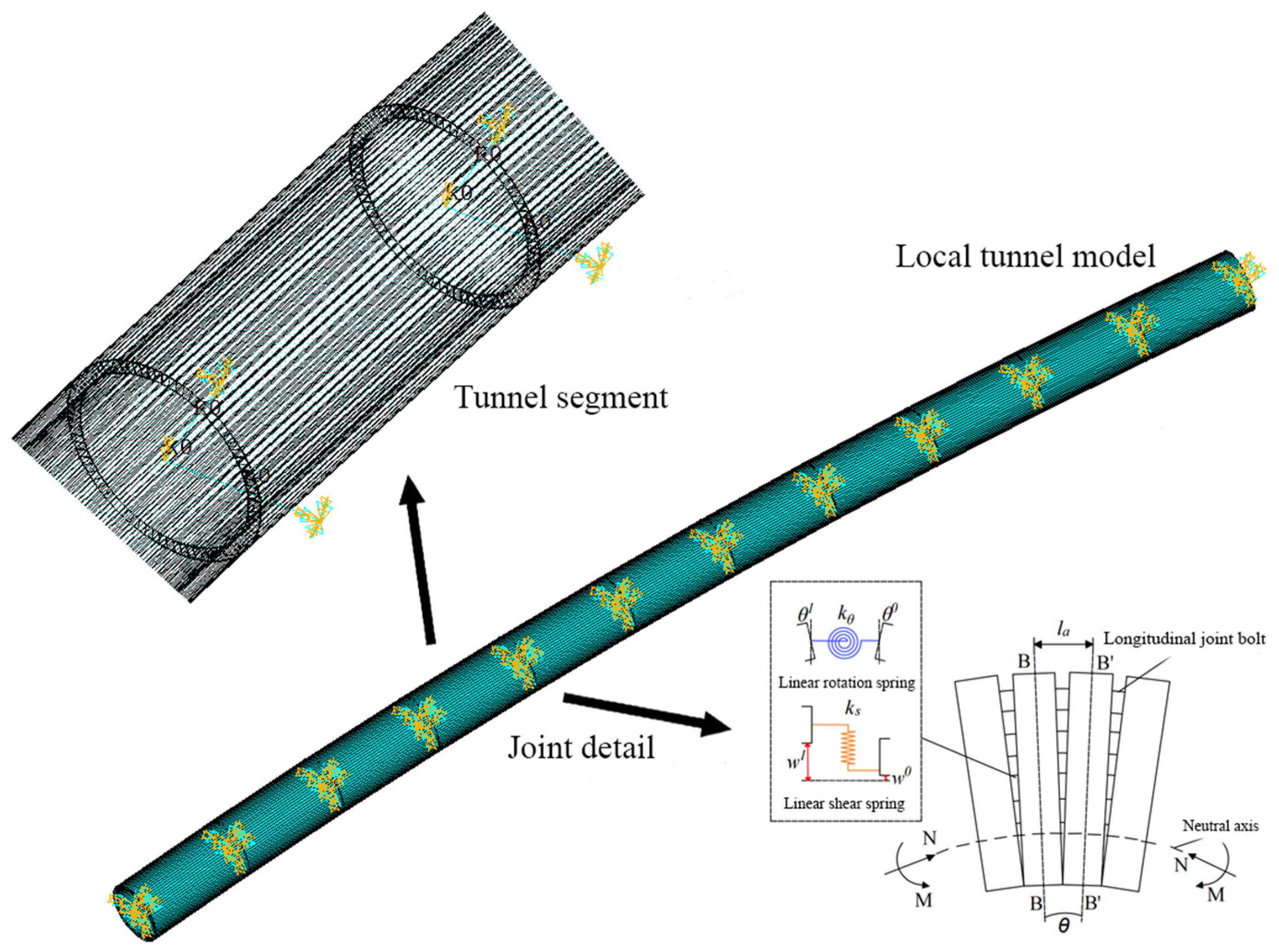
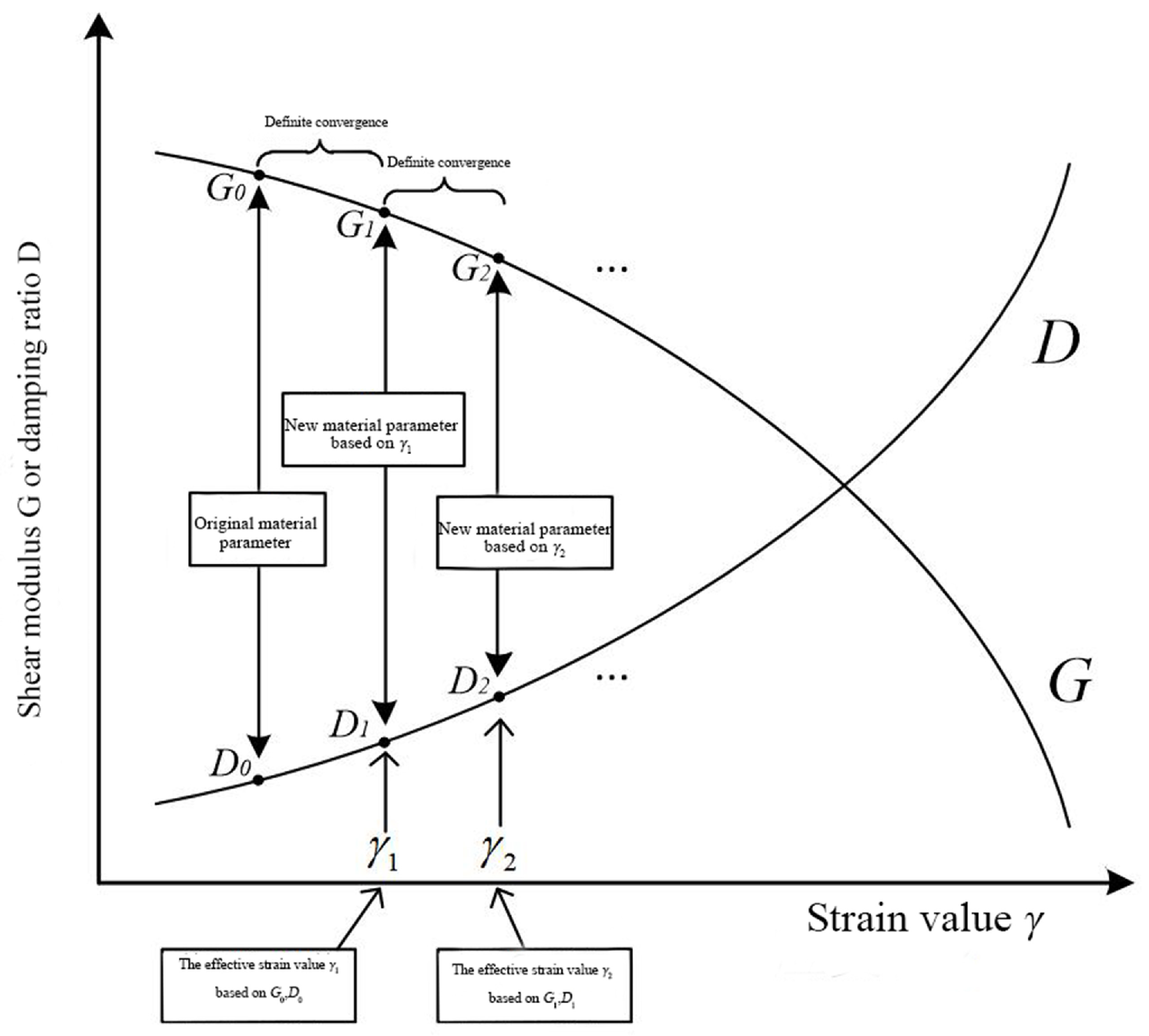
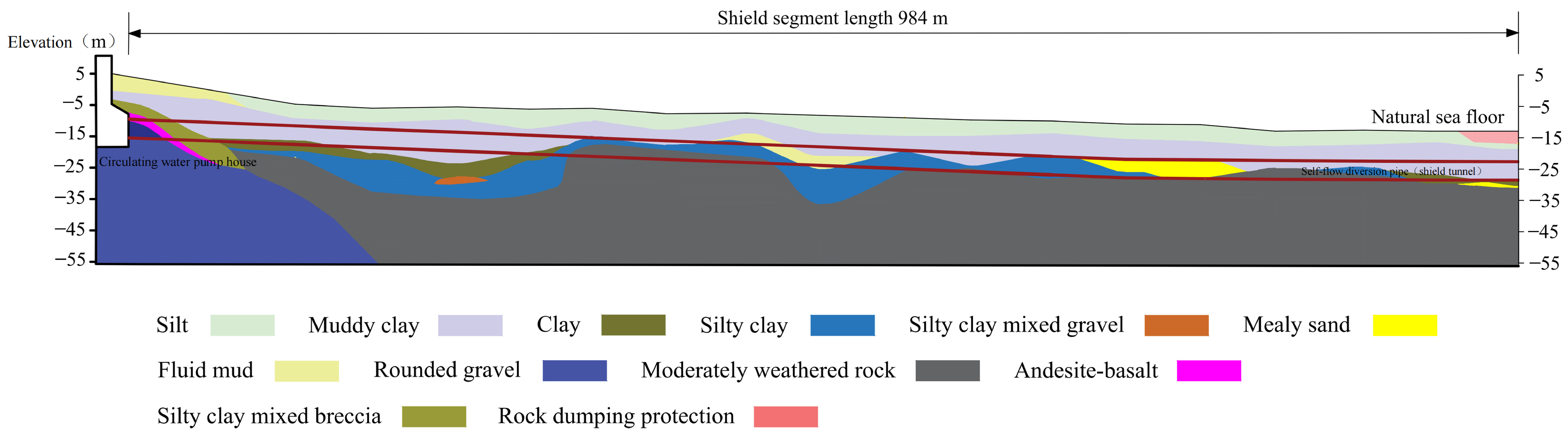







| Number | Soil Layer Name | Density (kg/m3) | Static Elastic Modulus (E/Pa) | Static Poisson’s Ratio (μ) | Dynamic Elastic Modulus (Ed/Pa) | Dynamic Poisson’s Ratio (μd) |
|---|---|---|---|---|---|---|
| 1 | Concrete | 2500 | 3.25 × 1010 | 0.20 | 4.225 × 1010 | 0.20 |
| 2 | Silt | 1610 | 1.00 × 107 | 0.30 | 1.95 × 107 | 0.45 |
| 3 | Muddy clay | 1750 | 1.30 × 107 | 0.30 | 2.91 × 107 | 0.45 |
| 4 | Clay | 1830 | 2.07 × 107 | 0.32 | 1.68 × 108 | 0.45 |
| 5 | Silty clay | 1950 | 2.61 × 107 | 0.30 | 1.49 × 108 | 0.45 |
| 6 | Moderately weathered rock | 2550 | 2.46 × 107 | 0.24 | 4.60 × 1010 | 0.21 |
| Bolt Type | Tensile Strength 106(N/m3) | Shear Resistance 106(N/m3) | Bending Stiffness 1 106(N·m)/rad | Bending Stiffness 2 106(N·m)/rad | Working Condition |
|---|---|---|---|---|---|
| M24 | 192 | 80 | 25 | 40 | 1 |
| 50 | 80 | 2 | |||
| 75 | 100 | 3 | |||
| M30 | 300 | 125 | 25 | 40 | 4 |
| 50 | 80 | 5 | |||
| 75 | 100 | 6 | |||
| M36 | 432 | 180 | 25 | 40 | 7 |
| 50 | 80 | 8 | |||
| 75 | 100 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Zhao, J.; Yu, X.; Fan, C.; Qian, B. Deformation Analysis of Nuclear Power Shield Tunnel by Longitudinal Response Displacement Method Considering Fluid–Solid Coupling. Buildings 2025, 15, 1365. https://doi.org/10.3390/buildings15081365
Fan Y, Zhao J, Yu X, Fan C, Qian B. Deformation Analysis of Nuclear Power Shield Tunnel by Longitudinal Response Displacement Method Considering Fluid–Solid Coupling. Buildings. 2025; 15(8):1365. https://doi.org/10.3390/buildings15081365
Chicago/Turabian StyleFan, Yijiang, Jie Zhao, Xiaodong Yu, Cheng Fan, and Bo Qian. 2025. "Deformation Analysis of Nuclear Power Shield Tunnel by Longitudinal Response Displacement Method Considering Fluid–Solid Coupling" Buildings 15, no. 8: 1365. https://doi.org/10.3390/buildings15081365
APA StyleFan, Y., Zhao, J., Yu, X., Fan, C., & Qian, B. (2025). Deformation Analysis of Nuclear Power Shield Tunnel by Longitudinal Response Displacement Method Considering Fluid–Solid Coupling. Buildings, 15(8), 1365. https://doi.org/10.3390/buildings15081365





