Study on the Engineering Characteristics of Alluvial Silty Sand Embankment Under Vehicle Loads
Abstract
:1. Introduction
2. Analytical Basis
2.1. Simplification of Vehicle Load
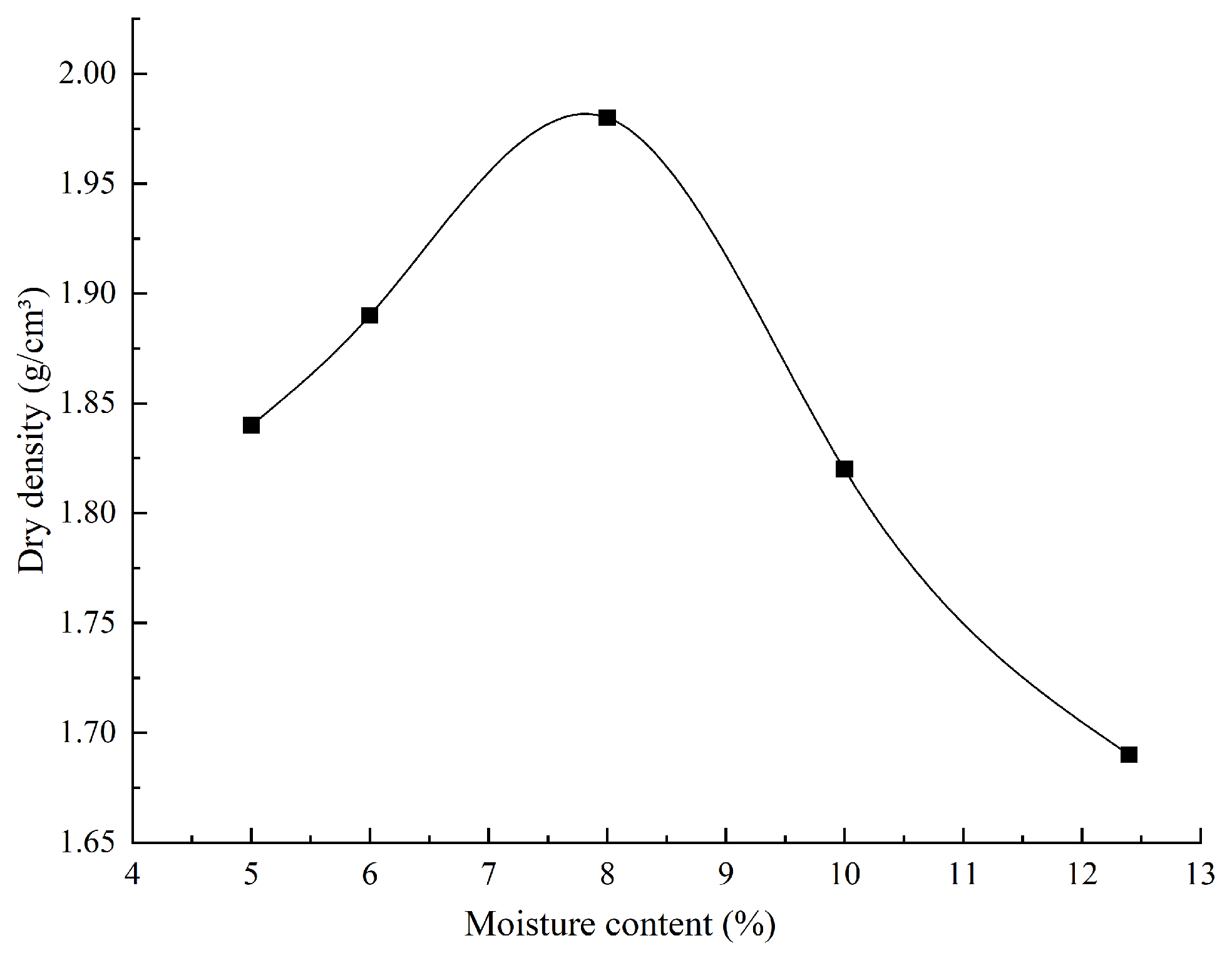
2.2. Basic Soil Properties
3. Dynamic Triaxial Test Study
3.1. Test Equipment
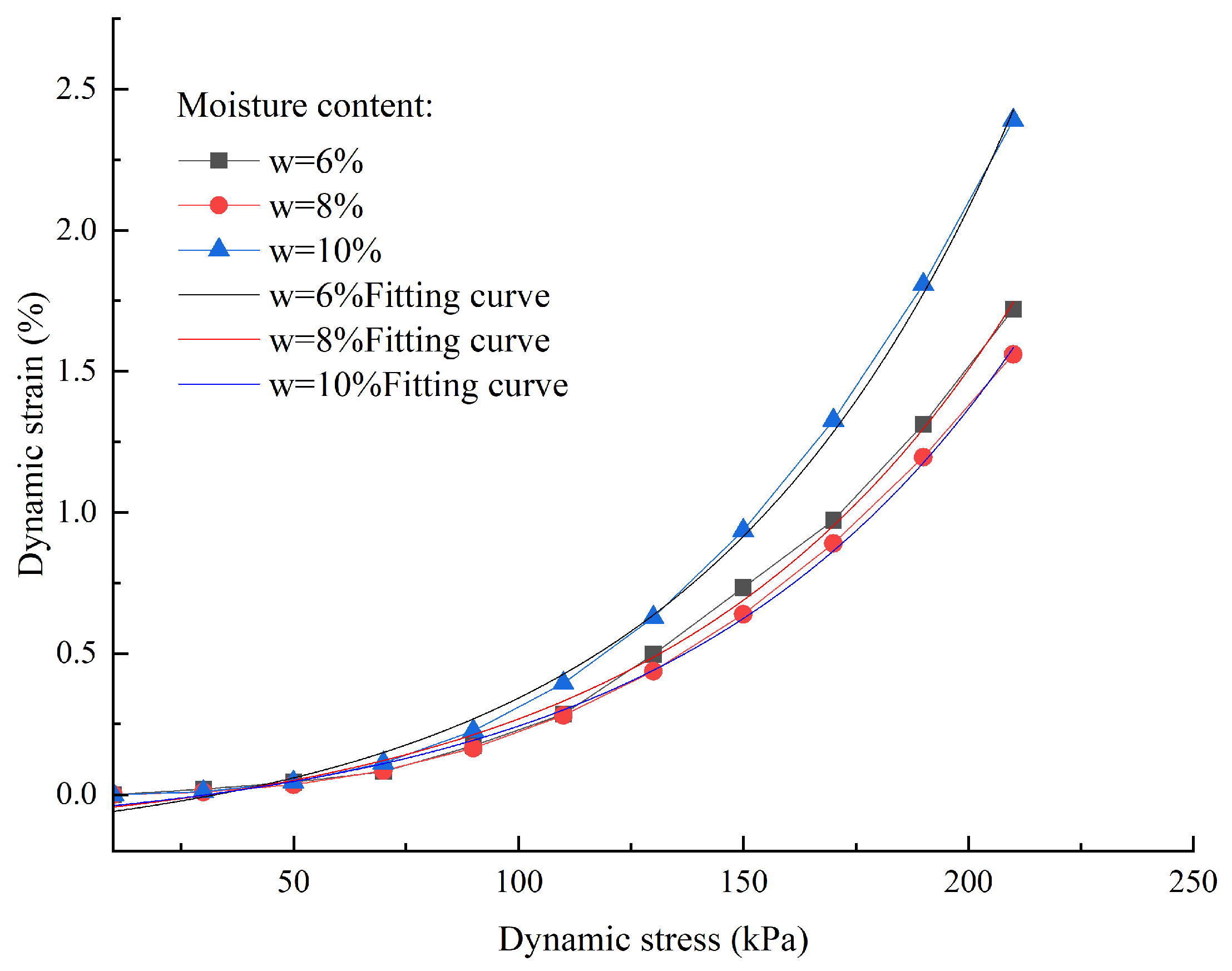
3.2. Stress–Strain Fitting of Soil Samples
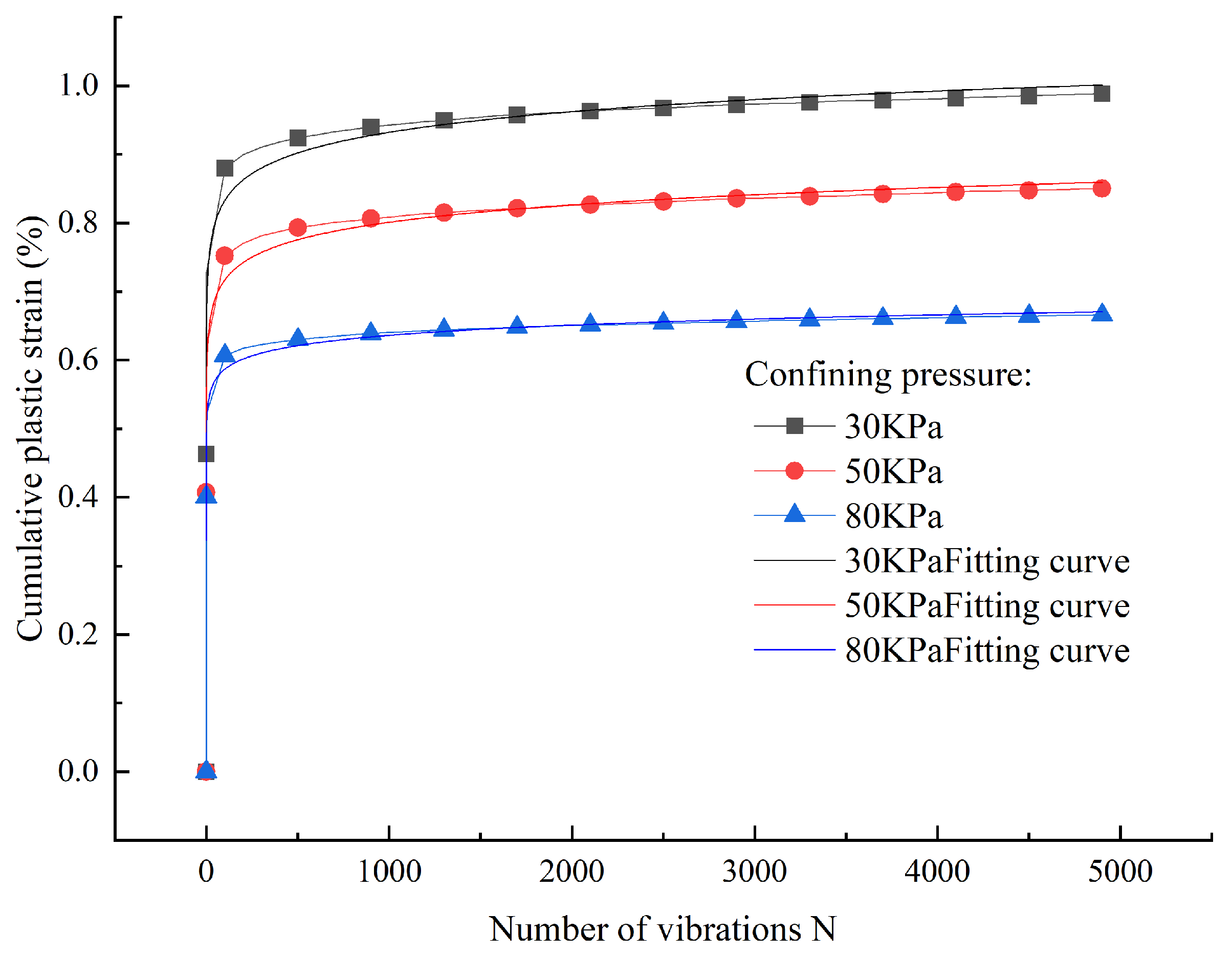
3.3. Fitting Relationship Between Dynamic Elastic Modulus and Dynamic Strain
4. Finite Element Analysis
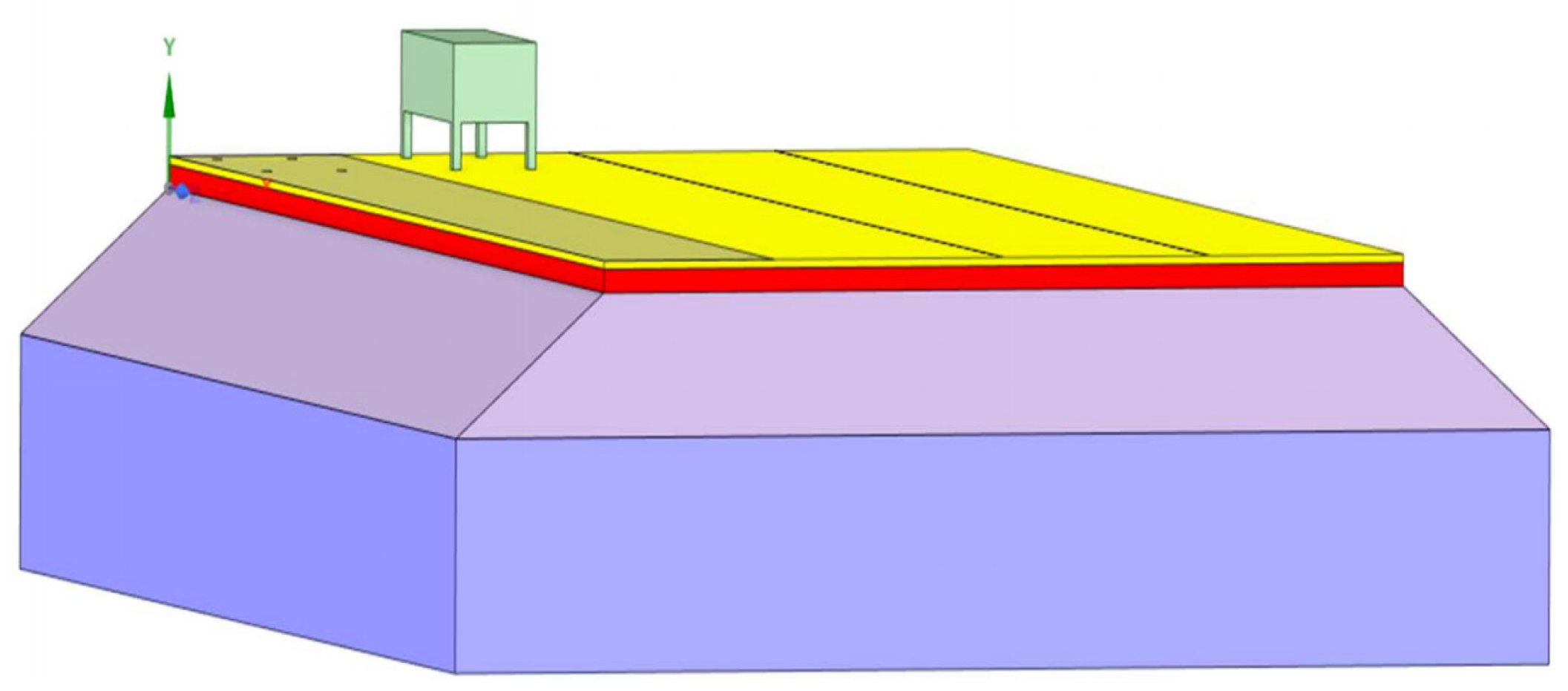
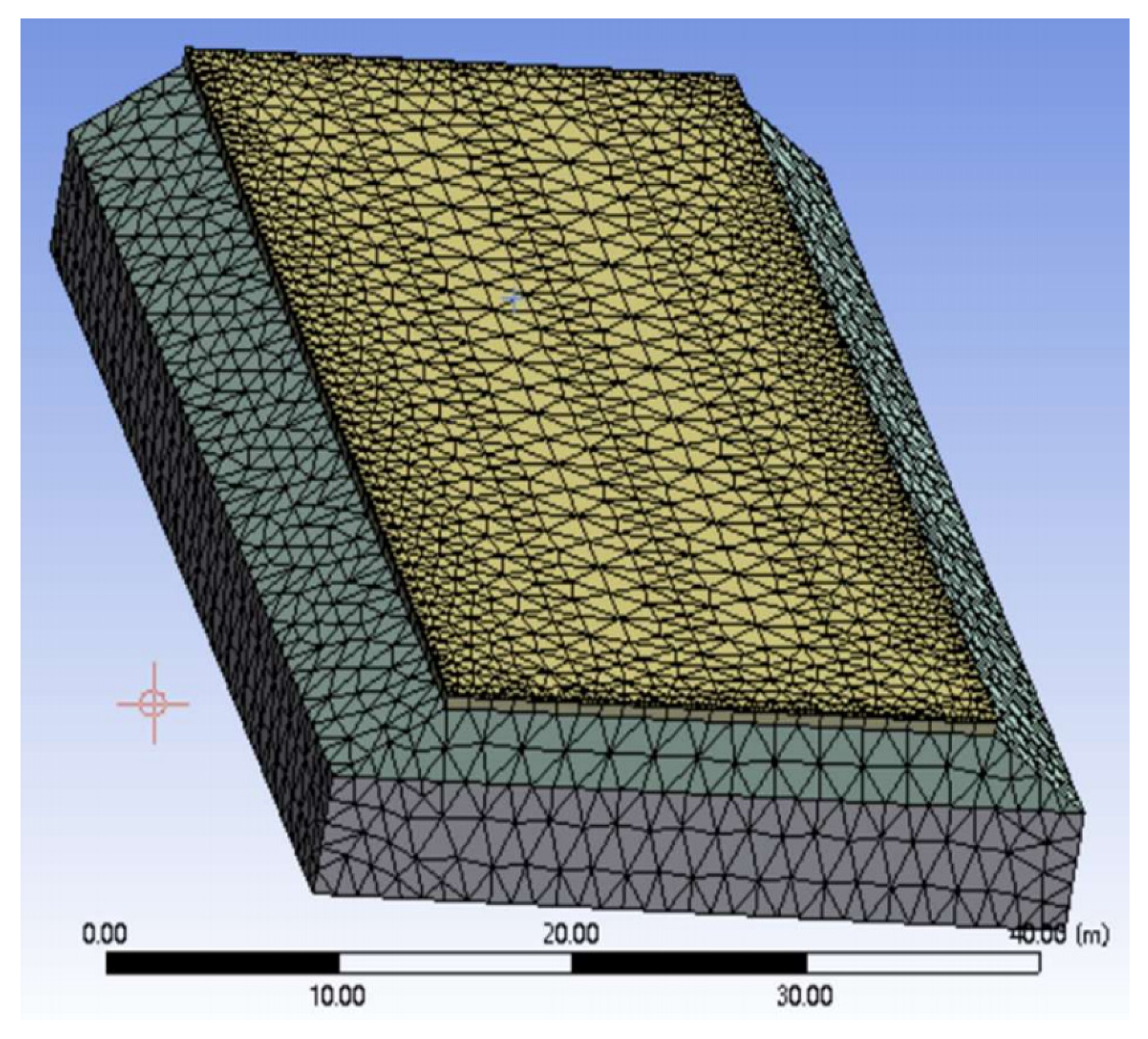
4.1. Model Determination
4.2. Simulation Conditions
4.3. Model Validation
5. Analysis of Engineering Characteristics Results
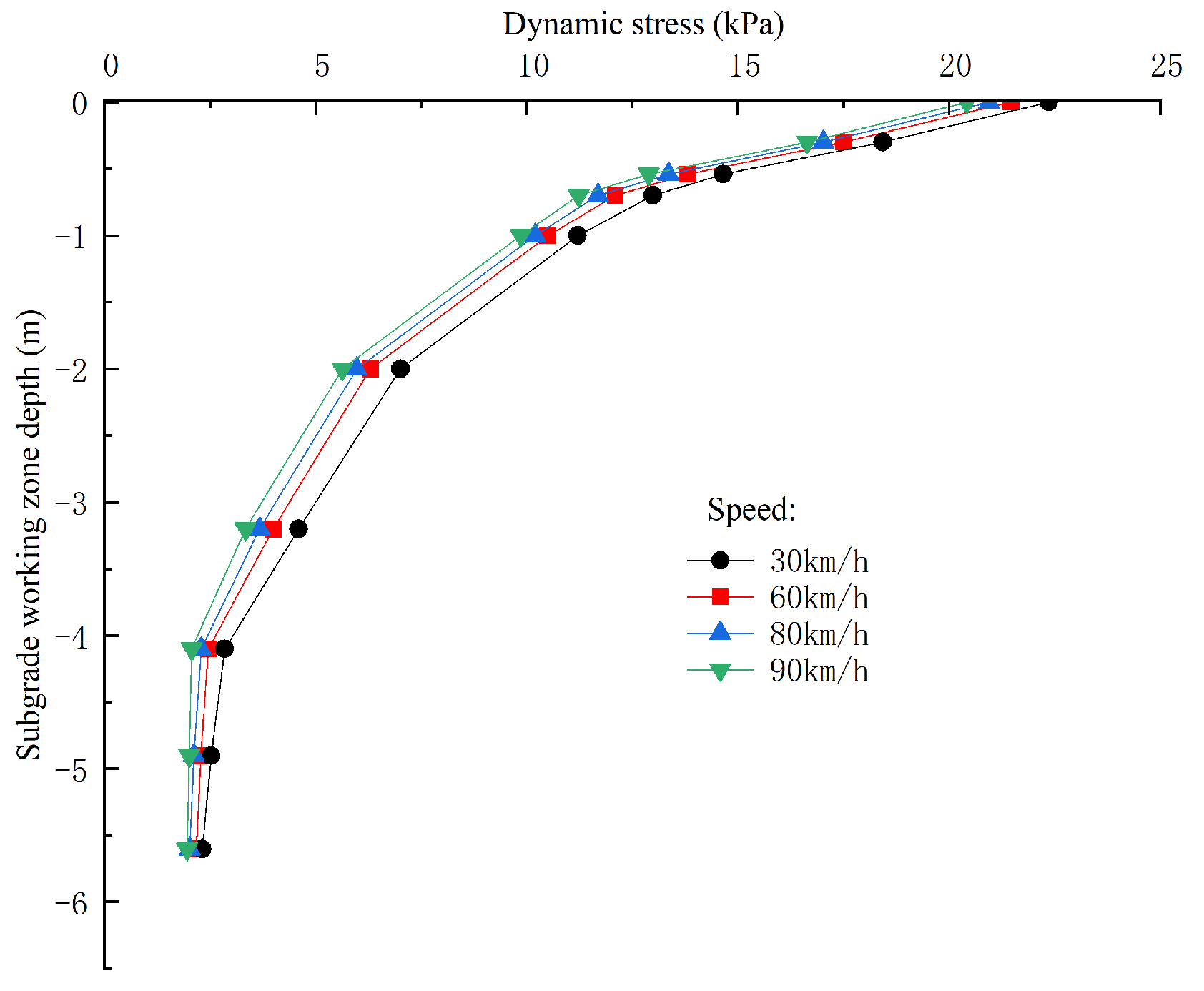
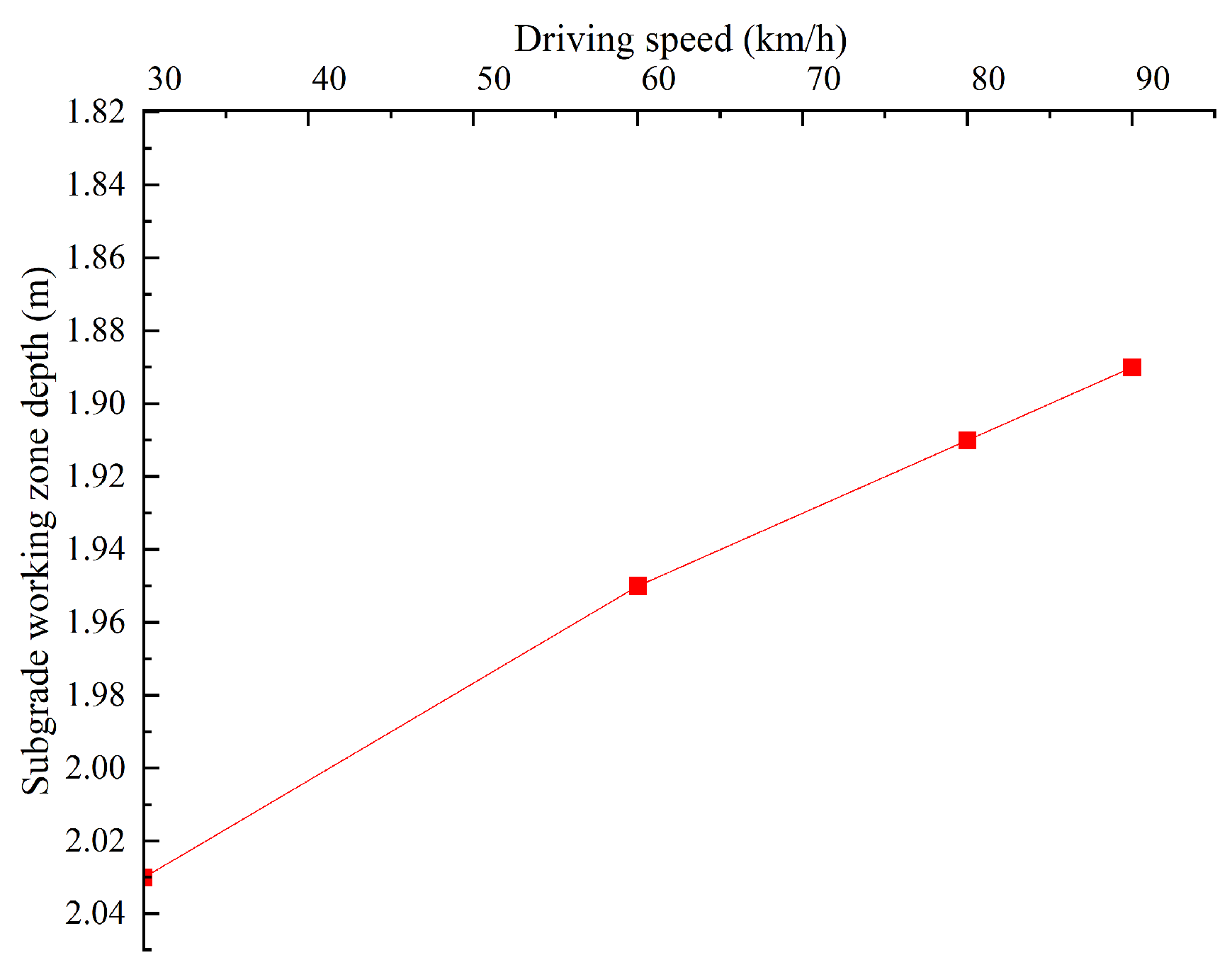
5.1. Influence of Speed
5.2. Influence of Moisture Content and Compaction Degree
5.2.1. Moisture Content
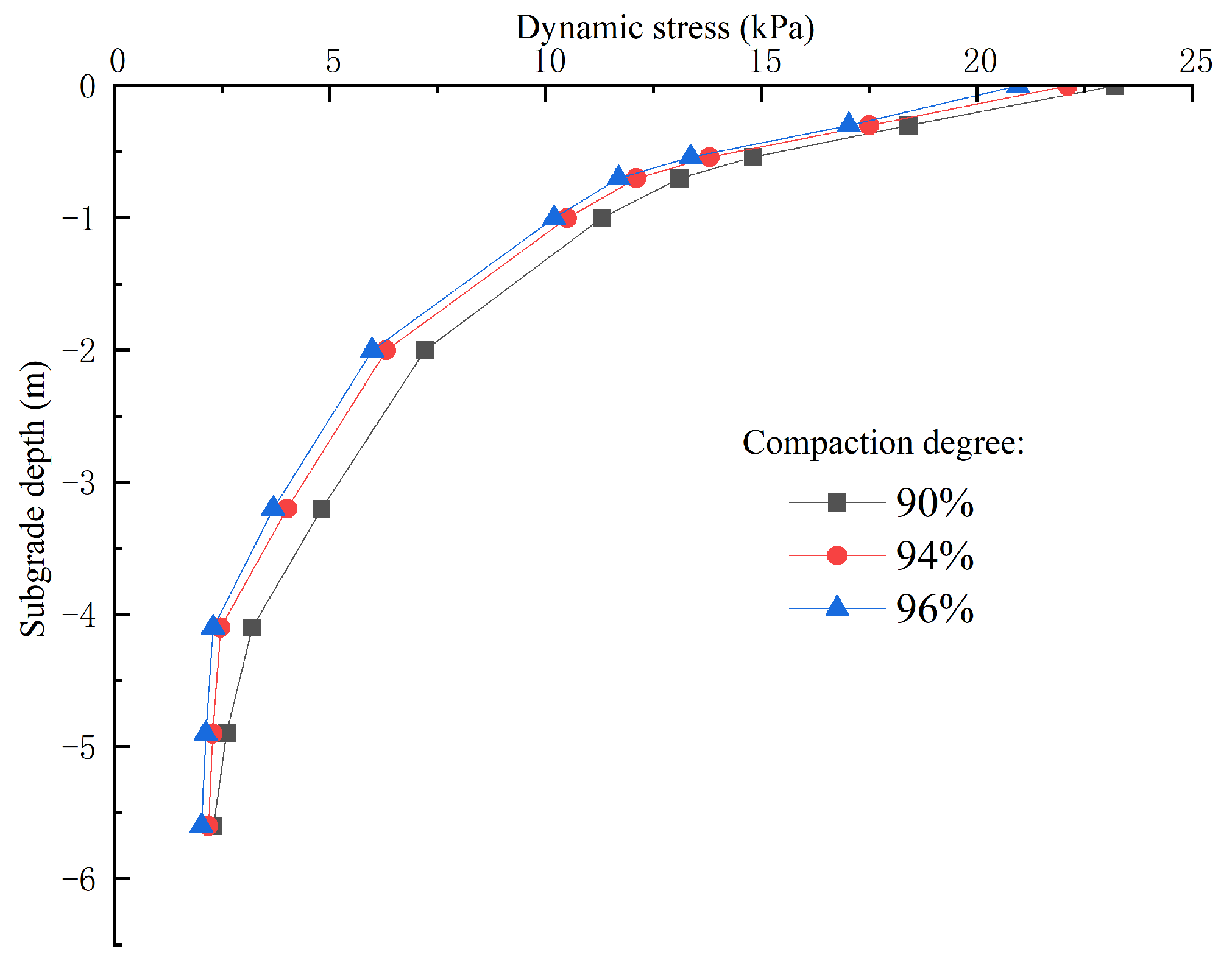
5.2.2. Compaction Degree
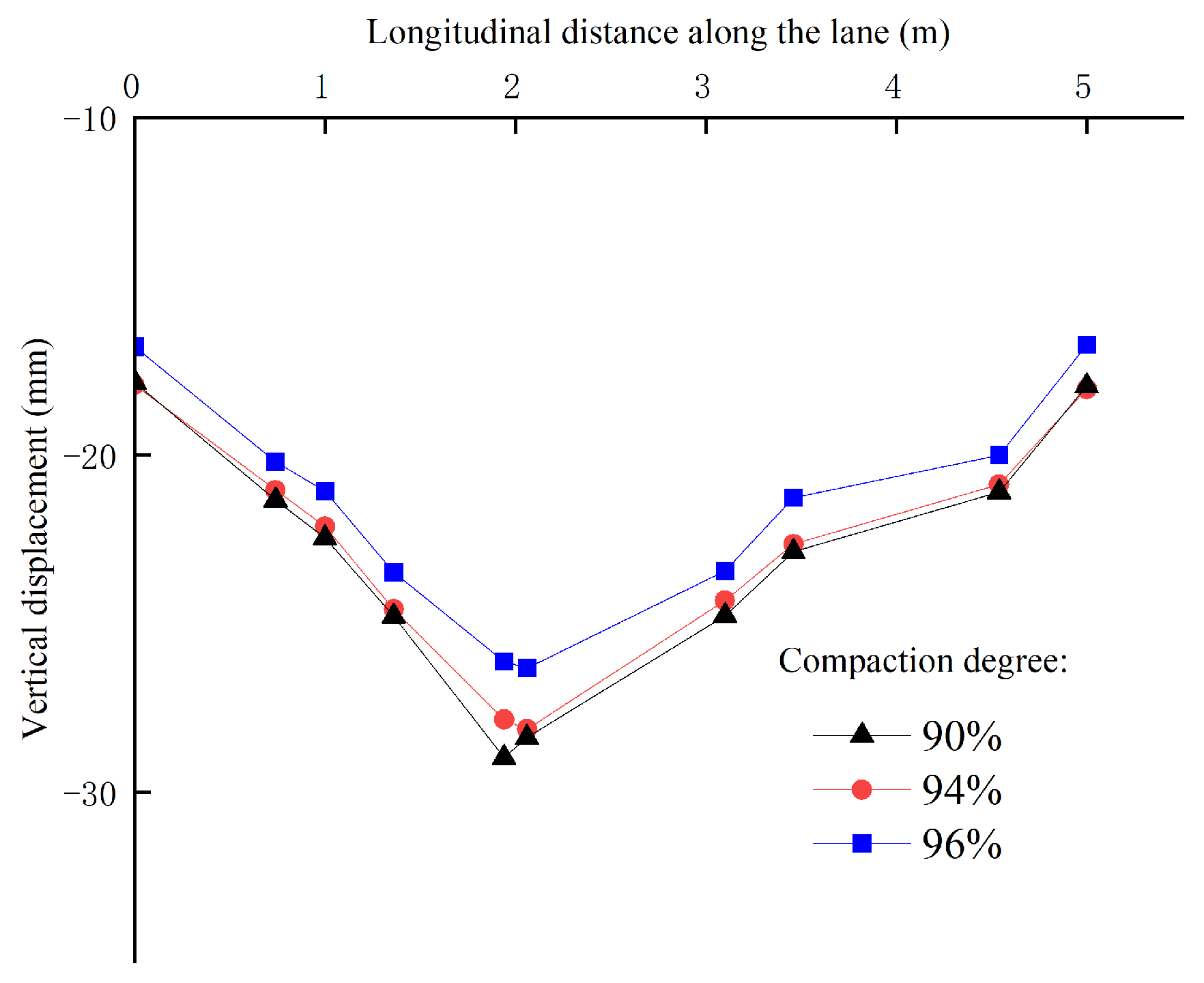
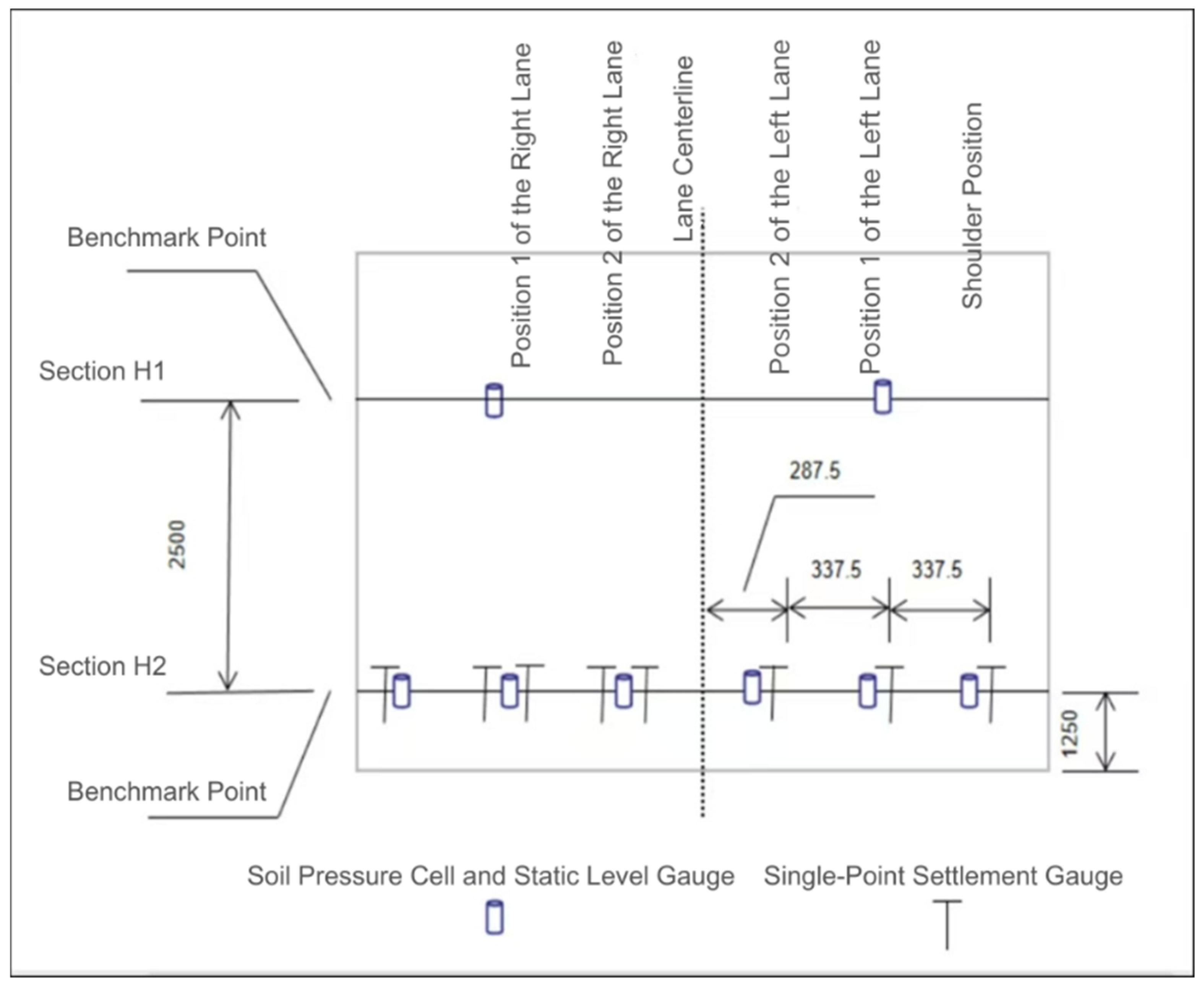
6. Field Monitoring
6.1. Instrument Selection and Principles
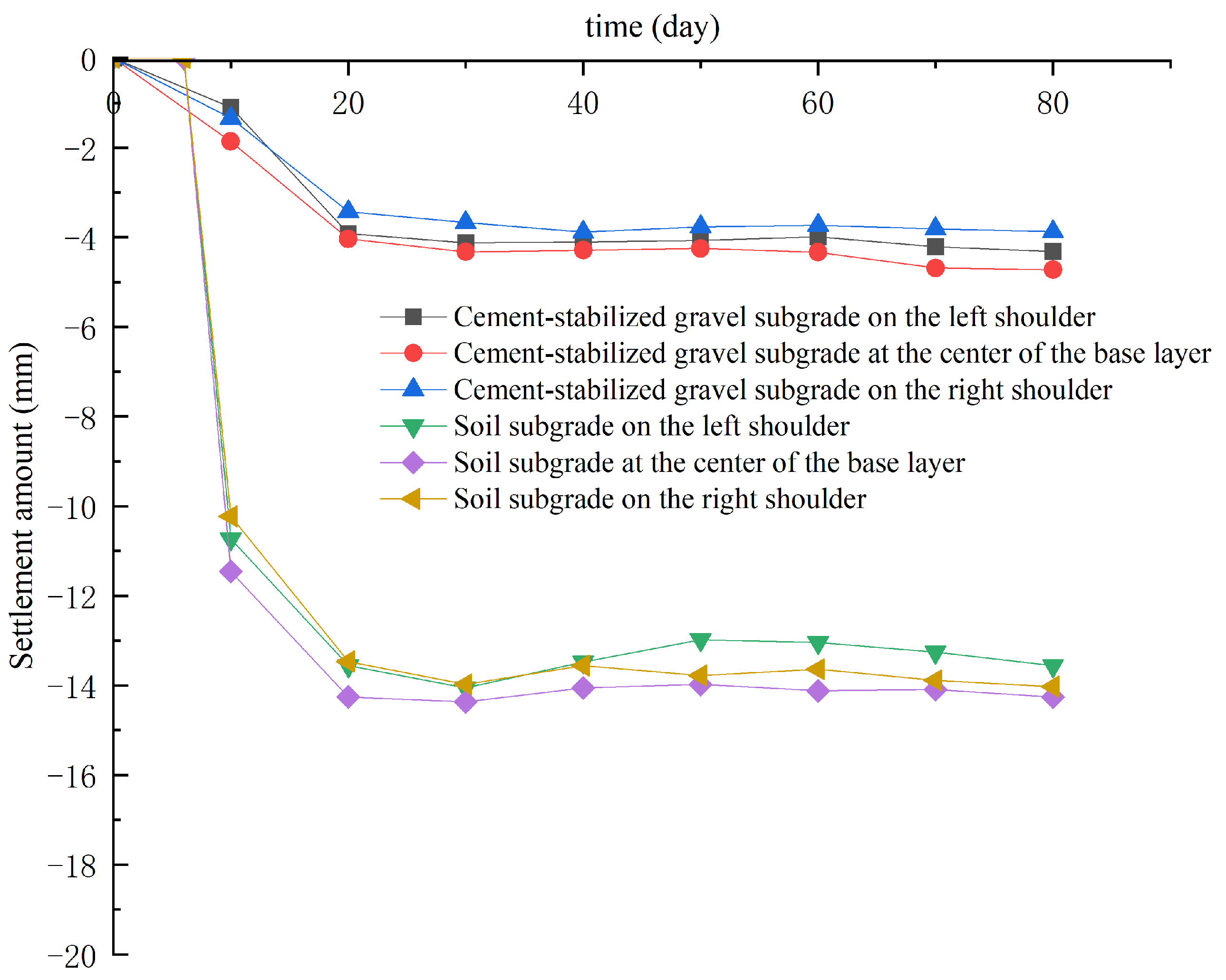
6.2. Results Analysis
7. Conclusions
- (1)
- The change in vehicle speed has a relatively small effect on the distribution and depth of dynamic stress. Under high-speed conditions (such as 90 km/h), dynamic stress attenuation is faster and the impact depth is shallower. Therefore, the design of roadbed thickness can be appropriately optimized and drainage measures can be strengthened to improve the economic efficiency of the project.
- (2)
- Moisture content and compaction degree are key factors affecting the performance of alluvial silty sand subgrade. Research has shown that an increase in soil moisture content can lead to a decrease in its shear strength, an increase in dynamic stress, and a significant increase in displacement at the top of the roadbed (for example, when it increases from 8% to 10%, the displacement at the top increases by 104.8%). Improving compaction can help reduce roadbed settlement and enhance the overall stability and safety of the roadbed.
- (3)
- The finite element simulation results are in good agreement with the on-site monitoring data, verifying the reliability of the model and providing an effective analysis tool for similar projects. However, the assumption of the homogeneous subgrade used in the model may to some extent underestimate the impact of actual soil layer stratification effects.
- (4)
- The initial settlement of alluvial silty sand filling is relatively large, but the settlement rate is fast and can stabilize within 24 days, and its long-term performance meets the engineering requirements. Compared with cement crushed stone filling, although its settlement is significantly increased, it has no significant impact on overall stability and can be used as an economic alternative material for non-critical road sections. Xu et al. [28], based on life cycle theory and the Sobol method, further analyzed the carbon emissions of ecological slope protection. Their results indicate that the rational selection of filler materials can significantly reduce the environmental impact of engineering projects. This provides theoretical support for the application of alluvial silty sand in the field of environmental protection.
- (5)
- The use of alluvial silty sand as roadbed filling material is feasible, but it is necessary to strictly control the moisture content and compaction degree during construction, and strengthen drainage design. Its environmental and economic benefits further support its potential application in sustainable engineering. It is suggested that future research be conducted to test the performance of alluvial silt under different geological conditions (such as coastal or mountainous areas), analyze the influence of factors such as salinity or geological structure, and make the results applicable to more engineering scenarios.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, L. Model Experimental Study on Mechanical Characteristics of Support Structures for Highway Tunnels in Granite Residual Soil. J. Hunan Univ. Arts Sci. (Nat. Sci. Ed.) 2023, 35, 76–80. [Google Scholar]
- Sun, J. Some Advances in Rock Rheological Mechanics and Its Engineering Applications. Chin. J. Rock Mech. Eng. 2007, 26, 1081–1106. [Google Scholar]
- Wang, X. Experimental Study on Engineering Mechanical Properties of Silty Soil Deposited by the Yellow River in the Yellow River Floodplain. Build. Technol. Dev. 2022, 49, 114–116. [Google Scholar]
- Long, J. Application of Cement Mixing Piles in Soft Soil Foundation Construction of Municipal Roads. Sichuan Build. Mater. 2022, 48, 186–187, 224. [Google Scholar]
- Min, J.; Zou, Y. Application of foam lightweight soil in rapid reconstruction of urban roads. Urban Roads Bridges Flood Control 2022, 12, 233–235+28. [Google Scholar] [CrossRef]
- Deng, T.; Ma, B.; Zou, Y.; Wang, Q.; Song, C. Influence of sample preparation methods on road performance indicators of red clay. Subgrade Eng. 2022, 6, 90–95. [Google Scholar] [CrossRef]
- Wang, X.; Yang, J. Physical and Mechanical Properties of Red Sandstone and Its Compaction Energy for Subgrade Construction. J. Zhejiang Univ. Sci. Technol. 2022, 34, 551–558. [Google Scholar]
- Wang, C. Study on Mechanical Properties of Cement-Modified Sedimentary Silty Sand Roadbed. Highway 2023, 68, 75–79. [Google Scholar]
- Xu, J.; Zhao, D.; Wang, S.; Chen, X.; Wu, X.; Han, Z.; Liu, Y. Quantitative analysis of pore structure’s impact on early mechanical properties and durability of foam concrete: Macroscopic and mesoscopic insights. Constr. Build. Mater. 2025, 459, 139775. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Yang, G.; Chen, X. Dynamic stress testing of highway subgrade and base layer under heavy loads. J. Vib. Shock 2007, 26, 169–173. [Google Scholar]
- Wang, X. Study on Dynamic Response of Flexible Pavement Structure and Subgrade Under Random Loads. Ph.D. Thesis, Central South University, Changsha, China, 2006. [Google Scholar]
- Jiang, Y.; Li, S.; Wang, T. Numerical method of dynamic triaxial test on graded crushed rock. J. Southeast Univ. (Nat. Sci. Ed.) 2013, 43, 604–609. [Google Scholar]
- Ni, X.; Ye, B. Unit test and simulation of liquid-solid phase transition mechanism after sand liquefaction. J. Tongji Univ. (Nat. Sci. Ed.) 2023, 51, 16–22. [Google Scholar]
- Lou, Q.; Tao, T.; Tian, X.; Xie, C. Numerical simulation method for impact failure patterns of limestone based on HJC constitutive model. Blasting 2022, 39, 71–79. [Google Scholar]
- Weng, L.; Zhang, H.; Zhang, Y.; Chu, Z.; Xu, X. Dynamic mechanical properties and constitutive model of water-saturated siltstone under low temperature. Chin. J. Appl. Mech. 2022, 39, 1096–1107, 1134. [Google Scholar]
- Sun, D.; Wu, B. Study on dynamic elastic modulus and damping ratio of unsaturated silt. J. Hydraul. Eng. 2012, 43, 1108–1113, 1120. [Google Scholar]
- Chen, G.; Wang, B.; Liu, J. Experimental study on dynamic shear modulus and damping ratio of recently deposited soils. J. Undergr. Space Eng. 2008, 4, 539–543, 594. [Google Scholar]
- Xie, Y.; Chen, T.; Wang, J.; Gu, S.; Zhu, F. Dynamic shear characteristics of frozen clay-concrete interface. J. Railw. Sci. Eng. 2022, 19, 2637–2646. [Google Scholar]
- Tang, Y.; Wang, Y.; Huang, Y.; Zhou, Z. Dynamic strength and dynamic stress-strain relationship of soil under subway traffic loads. J. Tongji Univ. (Nat. Sci. Ed.) 2004, 32, 701–704. [Google Scholar]
- Chen, Y.; Huang, B.; Chen, Y. Deformation and strength characteristics of structured soft clay under cyclic loading. Chin. J. Geotech. Eng. 2005, 27, 1065–1071. [Google Scholar]
- Chen, S. Study on Engineering Characteristics and Treatment Techniques of Expansive Soil. Doctoral Dissertation, Huazhong University of Science and Technology, Wuhan, China, 2006. [Google Scholar]
- Dai, S.; Van Deusen, D. Field study of in situ subgrade soil response under flexible pavements. Transp. Res. Rec. 1998, 1639, 23–35. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, Y.; Gong, W.; Feng, Q. Dynamic Analysis Method for Vehicle-Track Vertical Coupling System Based on Transfer Matrix Method. J. Vib. Shock 2022, 41, 31–38. [Google Scholar]
- Sun, J.; Li, M.; Tian, H. Dynamic Load Response Analysis of Heavy-Duty Vehicles on Uneven Road Surfaces. J. Chongqing Jiaotong Univ. (Nat. Sci. Ed.) 2019, 38, 48–53. [Google Scholar]
- Xu, L.; Guo, W.; Wang, J.; Fang, C.; Zhang, Z. Performance of recycled aggregate concrete based on a new classification method. Constr. Build. Mater. 2016, 101, 469–477. [Google Scholar]
- Dai, G.; Huang, M.; Xu, Q.; Qiu, Y. Dynamic response of saturated porous media under cyclic loading. Soil Dyn. Earthq. Eng. 2018, 113, 1–11. [Google Scholar]
- Xu, J.; Wu, X.; Qiao, W.; Wang, S.; Shu, S.; Zhao, D.; Chen, X. Life cycle carbon emission assessment for ecological protection slopes: Focus on construction and maintenance phases. J. Clean. Prod. 2025, 497, 145174. [Google Scholar] [CrossRef]
- Xu, J.B.; Wu, X.; Qiao, W.; Wang, S.; Chen, X.; Zhao, D.; Zeng, X.; Shu, S. Carbon emission analysis of ecological slope protection based on lifecycle theory and sobol method. Ecol. Eng. 2025, 215, 107584. [Google Scholar] [CrossRef]
- ASTM D2487-17; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). ASTM International: West Conshohocken, PA, USA, 2017.
- GB/T 50145-2007; Standard for Engineering Classification of Soils. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2007.
- ASTM D6913/D6913M-17; Standard Test Methods for Particle-Size Distribution (Gradation) of Soils Using Sieve Analysis. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM D4318-17; Standard Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM D698-12; Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Standard Effort (12,400 ft-lbf/ft3 (600 kN-m/m3)). ASTM International: West Conshohocken, PA, USA, 2012.
- JTG D30-2015; Specifications for Design of Highway Subgrades. Ministry of Transport of the People’s Republic of China: Beijing, China, 2015.
- Guo, G.; Ding, W.; Zhang, C. Analysis of stochastic dynamic load acting on rough road by heavy-duty traffic. In Proceedings of the 12th International Conference of Chinese Transportation Professionals (CICTP 2012): Multimodal Transportation Systems—Convenient, Safe, Cost-Effective, Efficient; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2012; pp. 3194–3205. [Google Scholar] [CrossRef]
- Wang, S.W.; Xu, J.B.; Wu, X.; Qi, Y.; Chen, X.; Zeng, X.; Qiao, W.; Dong, T. Creep constitutive model of coral sand. Bull. Eng. Geol. Environ. 2025, 84, 85. [Google Scholar] [CrossRef]
- JTG/T D31-02-2023; Technical Specifications for Highway Subgrade Monitoring. Ministry of Transport of the People’s Republic of China: Beijing, China, 2023.

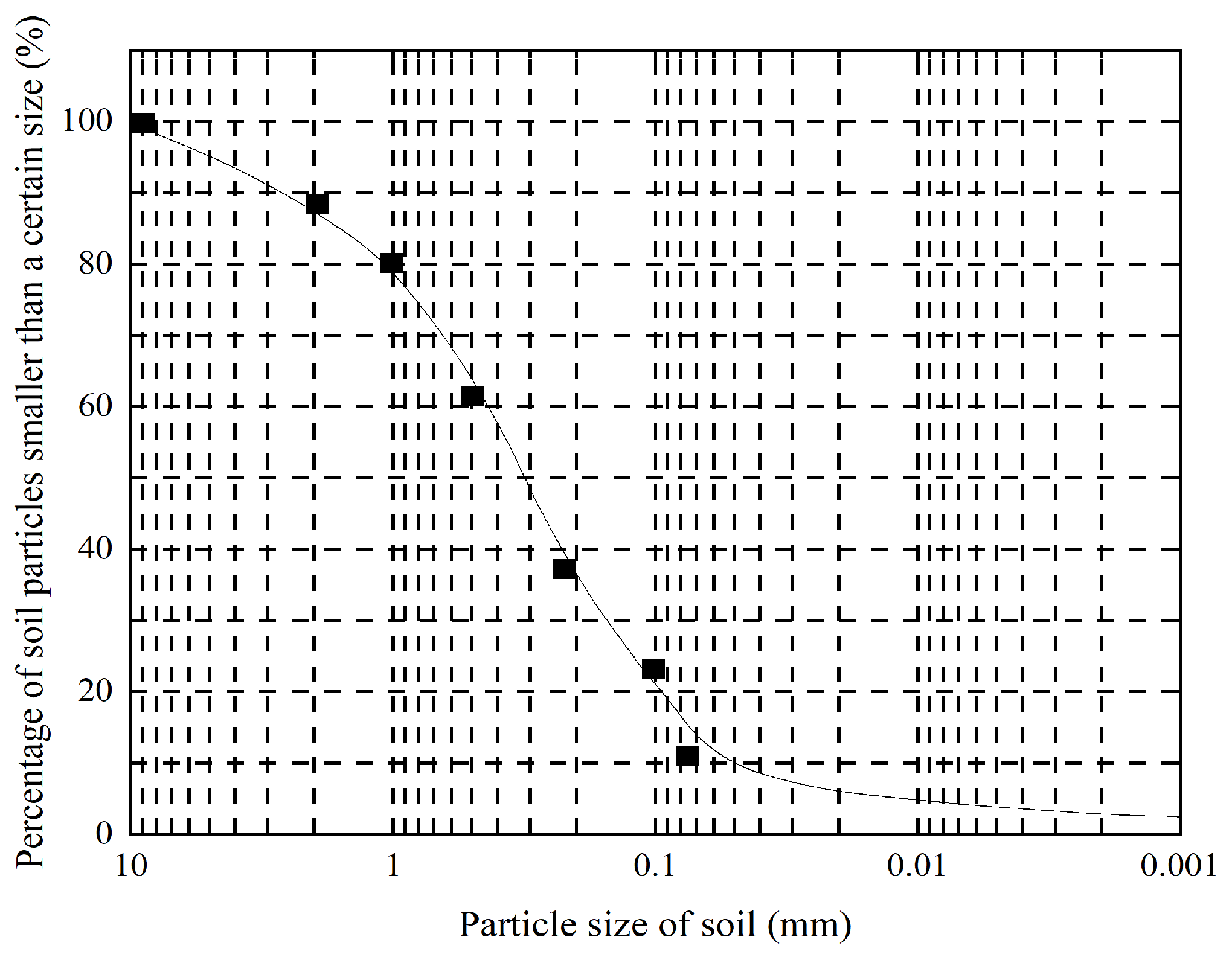




| Size/mm | >2 | 2~1 | 1~0.5 | 0.5~0.25 | 0.25~0.075 | <0.075 |
| Distribution | 11.9% | 11% | 17.8% | 26.9% | 27.8% | 4.6% |
| Parameter | Liquid Limit (WL, %) | Plastic Limit (WP, %) | Plasticity Index (Ip) |
|---|---|---|---|
| Value | 29.6 | 8.4 | 2.62 |
| No. | Confining Pressure (kPa) | Moisture Content (%) | a | b | R2 |
|---|---|---|---|---|---|
| 1 | 30 | 8 | 8.47 × 10−6 | 4.31 × 10−3 | 0.9686 |
| 2 | 50 | 8 | 6.32 × 10−6 | 6.32 × 10−3 | 0.9535 |
| 3 | 80 | 8 | 5.19 × 10−6 | 7.12 × 10−3 | 0.969 |
| 4 | 50 | 6 | 6.89 × 10−6 | 6.73 × 10−3 | 0.9578 |
| 5 | 50 | 10 | 7.64 × 10−6 | 4.69 × 10−3 | 0.9610 |
| No. | Confining Pressure (kPa) | Moisture Content | Loading Frequency | A | B | R2 |
|---|---|---|---|---|---|---|
| 1 | 30 | 6% | 1 | 71.975 | −0.22487 | 0.98843 |
| 2 | 50 | 6% | 1 | 104.486 | −0.2296 | 0.97314 |
| 3 | 80 | 6% | 1 | 134.70 | −0.21617 | 0.98643 |
| 4 | 30 | 8% | 1 | 105.3363 | −0.22637 | 0.95928 |
| 5 | 30 | 10% | 1 | 62.37651 | −0.25859 | 0.97944 |
| 6 | 30 | 8% | 3 | 105.678 | −0.22638 | 0.95936 |
| 7 | 30 | 8% | 5 | 101.10384 | −0.23329 | 0.96086 |
| Layer | Parameter | |||||
|---|---|---|---|---|---|---|
| Elastic Modulus (MPa) | Poisson’s Ratio | Density (kg/m3) | Cohesion (kPa) | Internal Friction Angle | Damping Ratio | |
| Surface Layer | 1200 | 0.25 | 2300 | - | - | 0.12 |
| Base Layer | 1500 | 0.25 | 2200 | - | - | 0.1 |
| Subgrade | 120 | 0.32 | 2120 | 22.4 | 32.5 | 0.15 |
| Foundation | 38 | 0.35 | 1600 | 27.6 | 28.4 | 0.2 |
| Driving Speed (km/h) | Moisture Content (%) | Base Layer Modulus (MPa) | Base Layer Thickness (cm) | Compaction Degree (%) |
|---|---|---|---|---|
| 30, 60, 80, 90 | 8 | 1300 | 56 | 96 |
| 8, 10 | 1500 | 56, 64, 72 | 96 | |
| 8 | 1700 | 56 | 96 |
| Driving Speed (km/h) | Dynamic Stress Variation Range (kPa) |
|---|---|
| 30 | 2.32~22.64 |
| 60 | 2.13~21.38 |
| 80 | 2.02~20.95 |
| 90 | 1.96~20.42 |
| Moisture Content (%) | Dynamic Stress Variation Range (kPa) |
|---|---|
| 8 | 2.63~24.62 |
| 10 | 2.54~22.35 |
| Compaction Degree (%) | Dynamic Stress Variation Range (kPa) |
|---|---|
| 90 | 2.33~23.62 |
| 94 | 2.18~22.13 |
| 96 | 2.02~20.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, T.; Chen, J.; Zhang, Y.; Shen, J.; Yue, X. Study on the Engineering Characteristics of Alluvial Silty Sand Embankment Under Vehicle Loads. Buildings 2025, 15, 1375. https://doi.org/10.3390/buildings15081375
Qiu T, Chen J, Zhang Y, Shen J, Yue X. Study on the Engineering Characteristics of Alluvial Silty Sand Embankment Under Vehicle Loads. Buildings. 2025; 15(8):1375. https://doi.org/10.3390/buildings15081375
Chicago/Turabian StyleQiu, Tangtang, Junwen Chen, Ying Zhang, Jiang Shen, and Xiabing Yue. 2025. "Study on the Engineering Characteristics of Alluvial Silty Sand Embankment Under Vehicle Loads" Buildings 15, no. 8: 1375. https://doi.org/10.3390/buildings15081375
APA StyleQiu, T., Chen, J., Zhang, Y., Shen, J., & Yue, X. (2025). Study on the Engineering Characteristics of Alluvial Silty Sand Embankment Under Vehicle Loads. Buildings, 15(8), 1375. https://doi.org/10.3390/buildings15081375




