Advanced Investigation into Active Control Force Requirements for Seismic Damage Mitigation of Inelastic Structures
Abstract
:1. Introduction and Scope
2. State of the Art Review
3. Structural Response Simulation Procedure
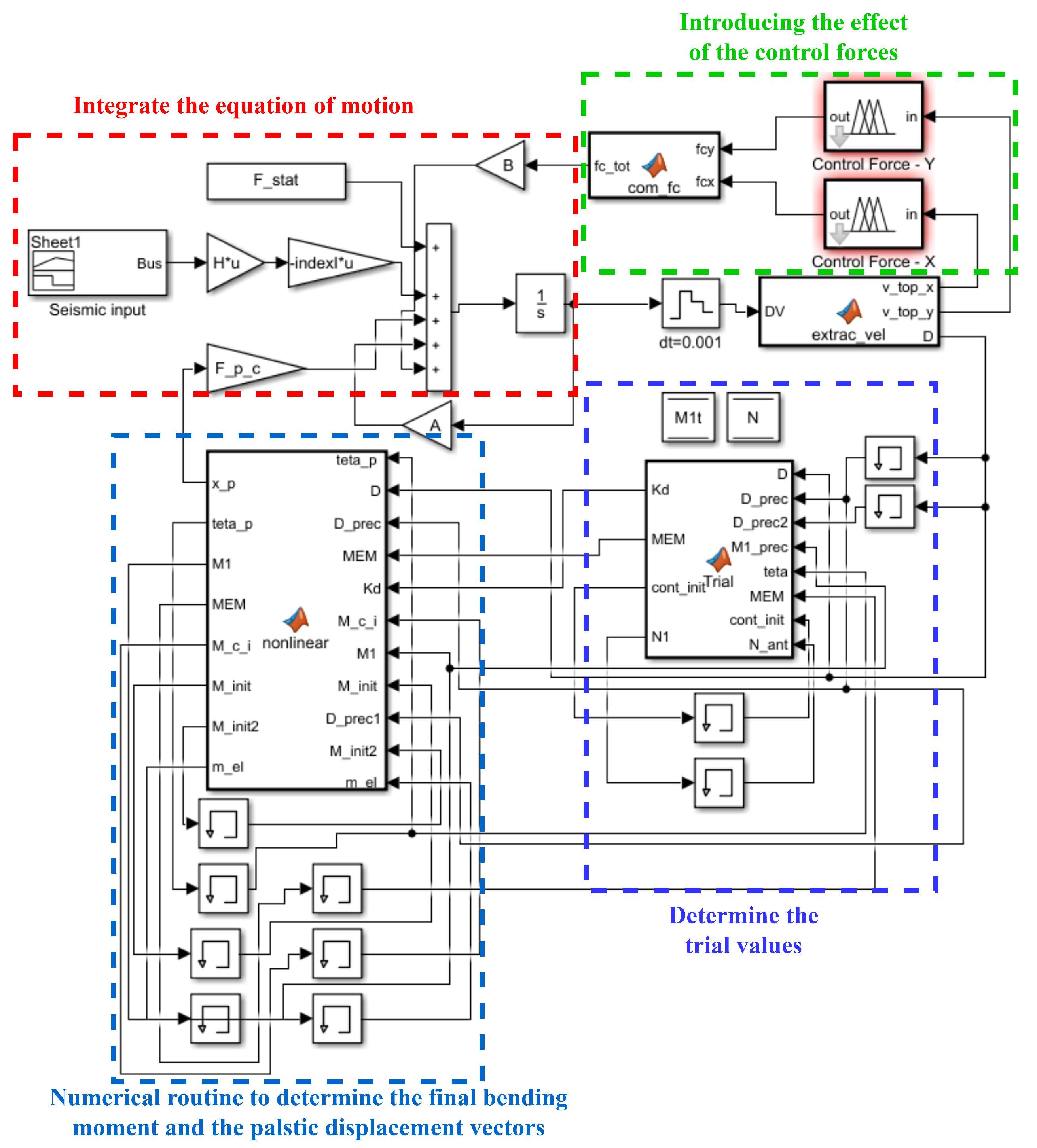
3.1. Simulation of the Nonlinear Dynamic Response
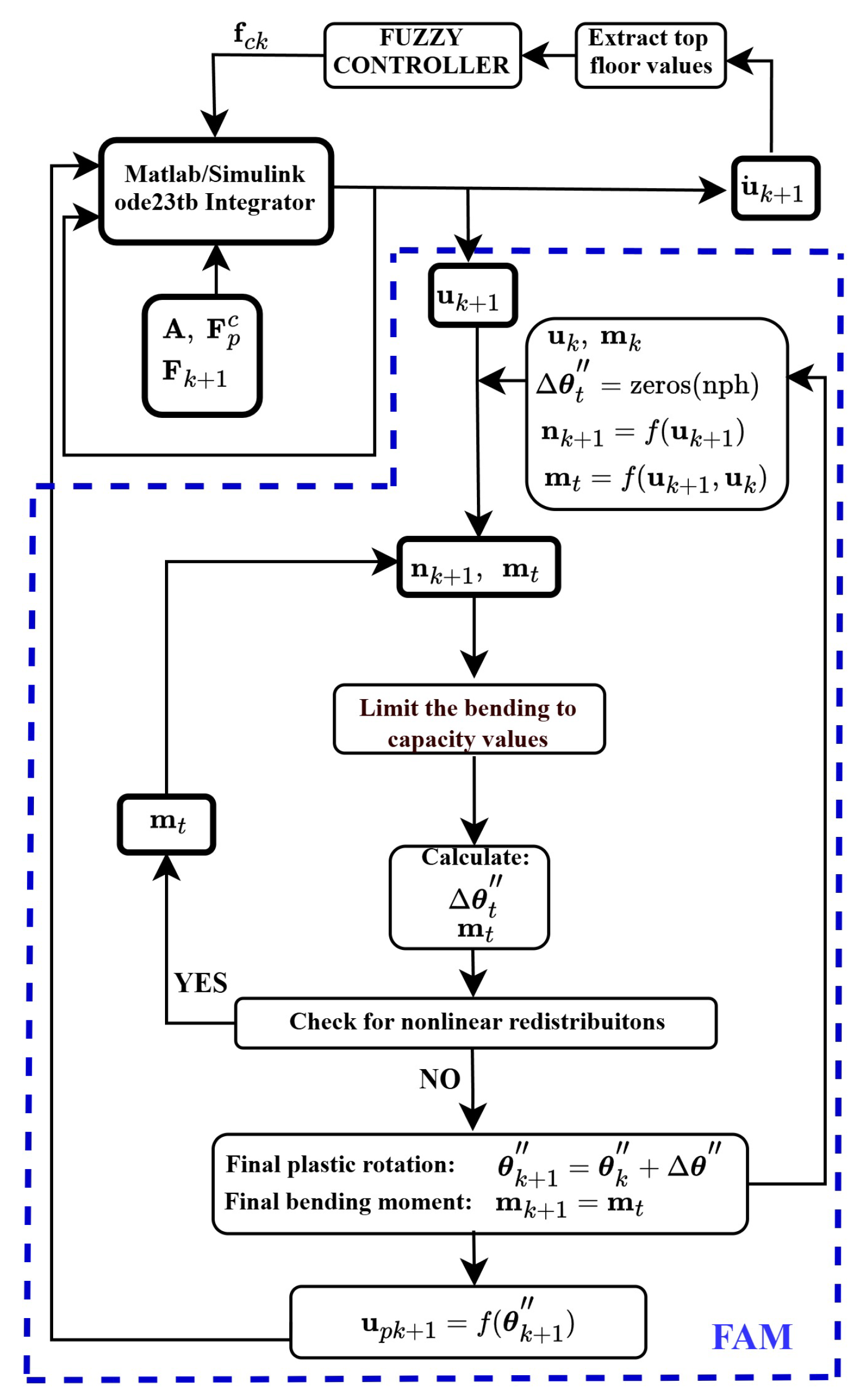
3.2. The Active Control Algorithm
3.3. Damage Quantification
4. Case Study
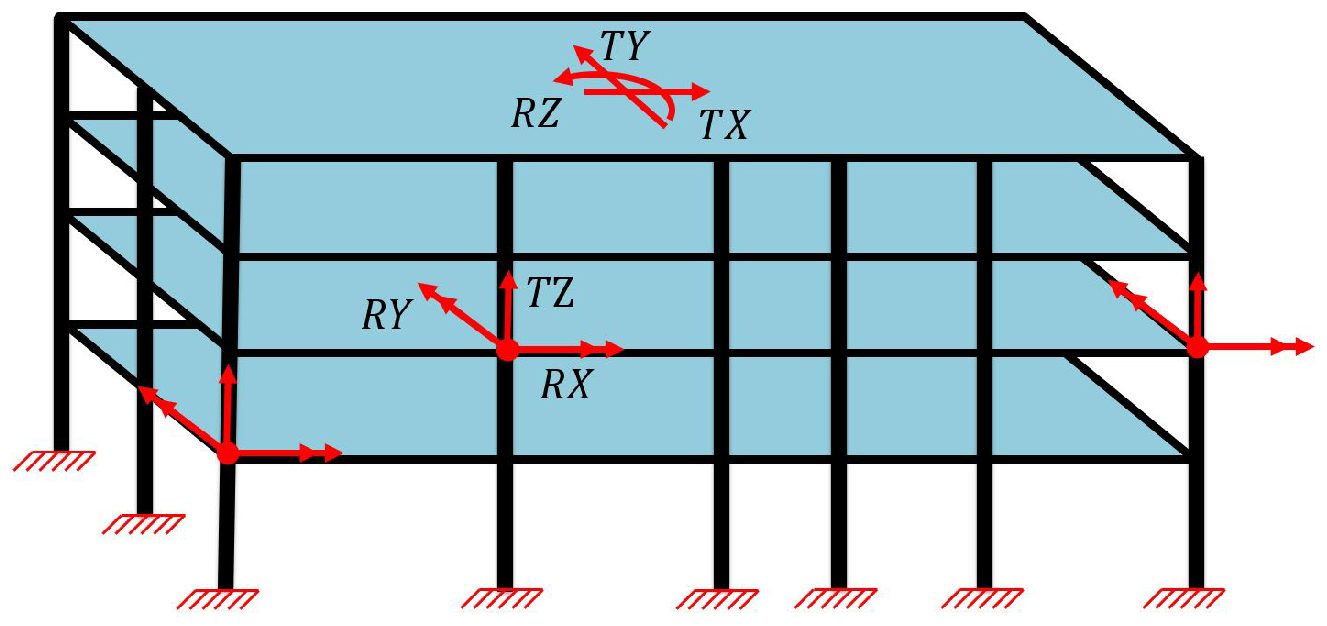
4.1. Description of Structural Models
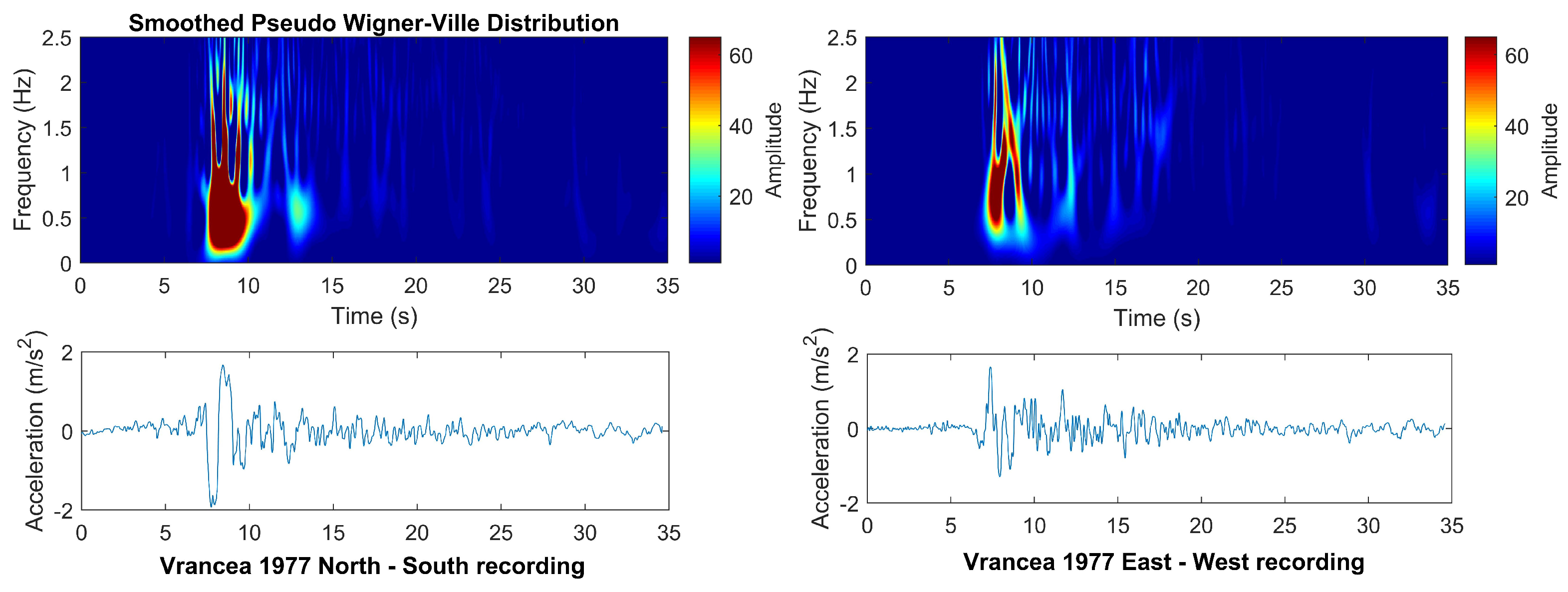
4.2. Seismic Inputs
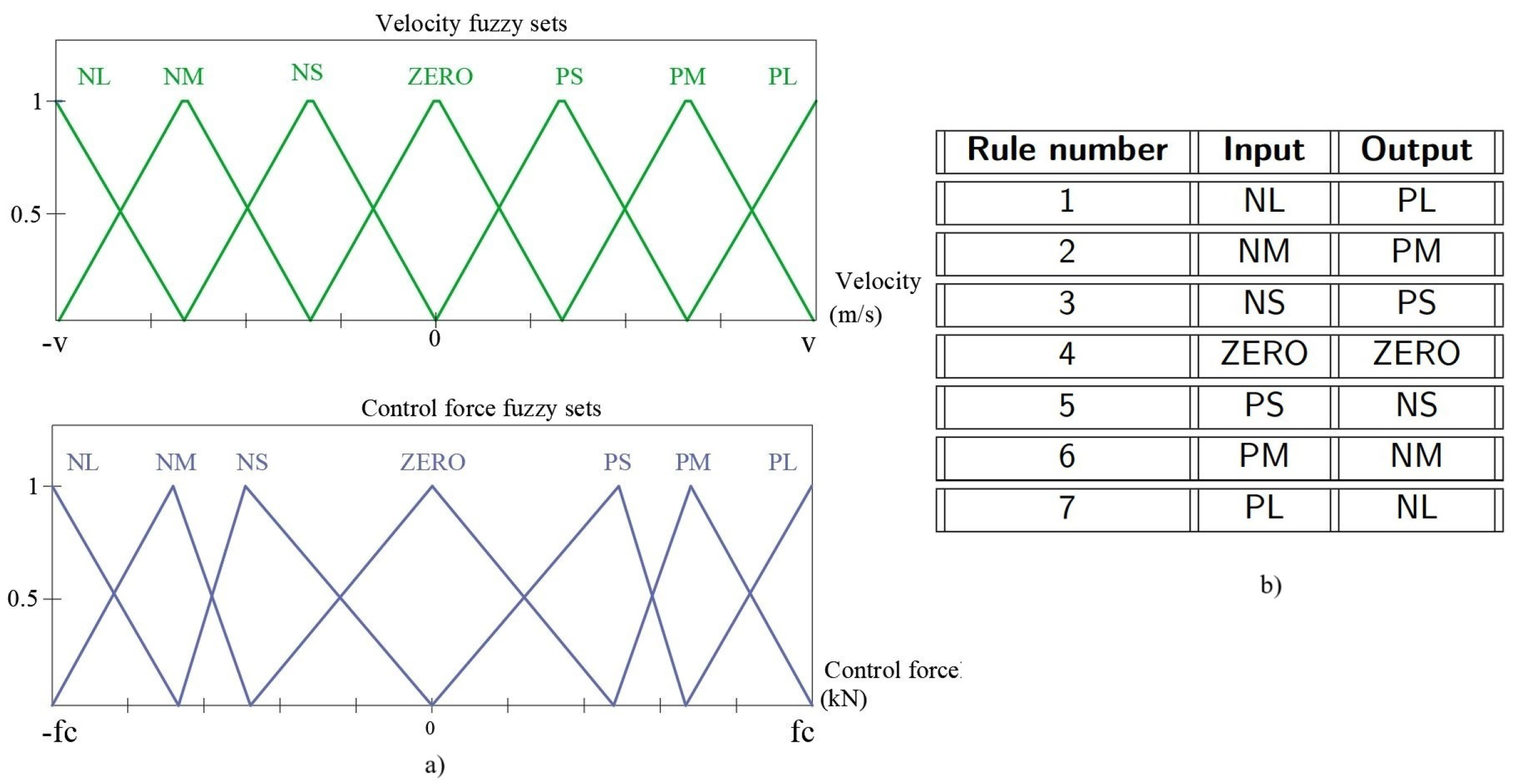
4.3. Fuzzy Control Algorithm
4.4. Results
5. Research Significance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Description |
| Global structural damage index | |
| Damage index of plastic hinge i | |
| Damage index for story j | |
| Damage index for the entire structure | |
| , , | Max, recoverable, and ultimate plastic rotation |
| Yield bending moment capacity | |
| , , | Dissipated hysteresis energy (total, hinge-level, or story-level) |
| , | Weighting factors based on relative dissipated energy |
| , , | First, second, and third natural periods |
| , , | Displacement, velocity, acceleration vectors describing structural response |
| , , | Mass, stiffness, damping matrices describing the structural model |
| Ground acceleration input vector | |
| Plastic displacement vector | |
| Plastic rotation vector at plastic hinge locations | |
| State vector for state-space model | |
| , , , | State-space matrices |
| P, , | Axial force and bending moments on y and z axes of the cross section |
| , | Peak axial capacity and axial force at balance point |
| , | Bending moment capacities on y and z directions of the cross section |
| Total number of plastic hinges | |
| AMD | Active Mass Damper |
| PGA | Peak Ground Acceleration |
| FAM | Force Analogy Method |
| SPWVD | Smoothed Pseudo Wigner–Ville Distribution |
Appendix A
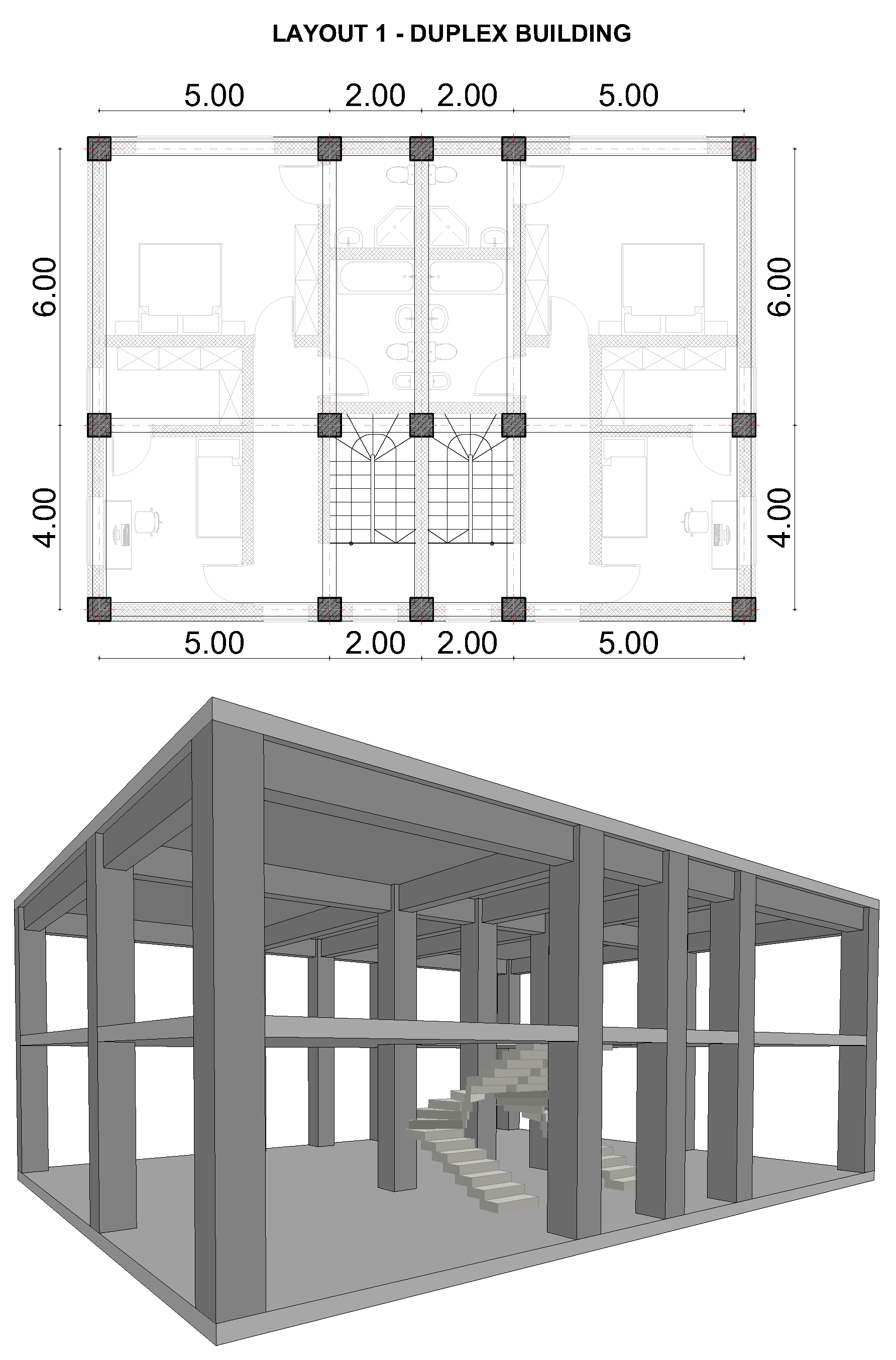

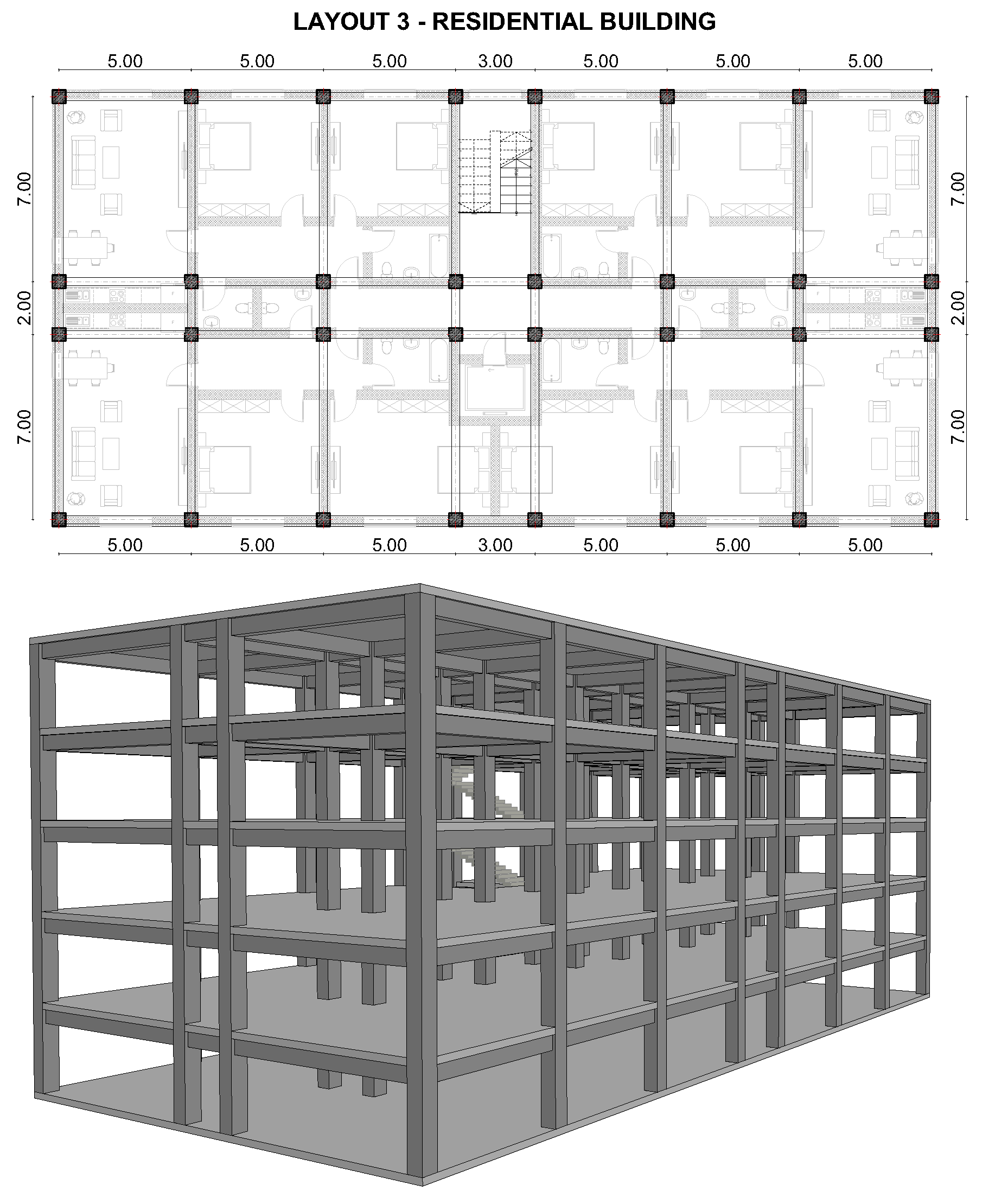

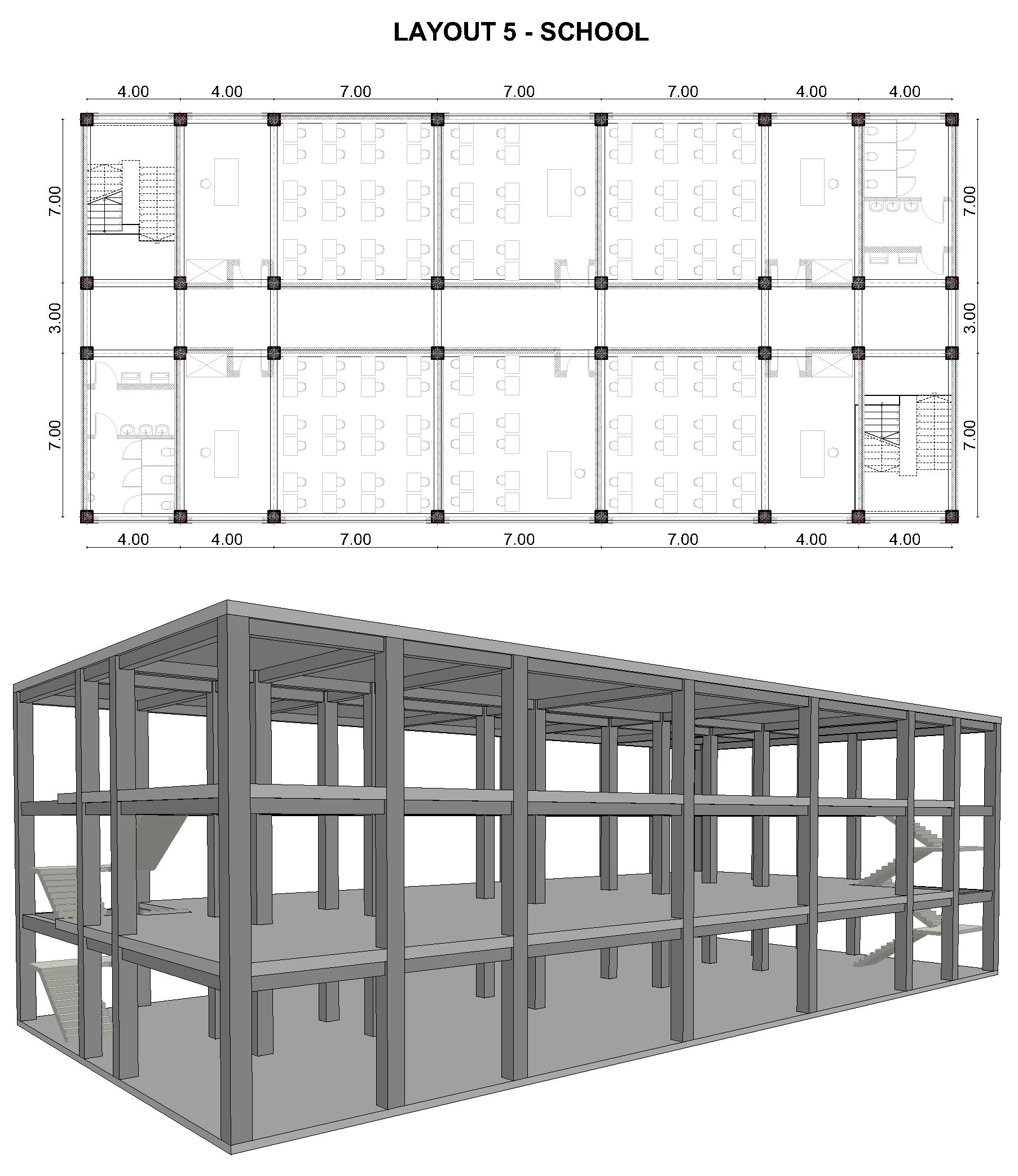
References
- Mobaraki, B.; Vaghefi, M. The Effect of Protective Barriers on the Dynamic Response of Underground Structures. Buildings 2024, 14, 3764. [Google Scholar] [CrossRef]
- Koutsoloukas, L.; Nikitas, N.; Aristidou, P. Passive, semi-active, active and hybrid mass dampers: A literature review with associated applications on building-like structures. Dev. Built Environ. 2022, 12, 100094. [Google Scholar] [CrossRef]
- Nica, G.B.; Munteanu Ruben, I.; Calofir, V.; Iancovici, M. Modelling nonlinear behavior of 3D frames using the Force Analogy Method. Structures 2022, 35, 1162–1174. [Google Scholar] [CrossRef]
- Munteanu, R.I.; Moţa, F.; Calofir, V.; Baciu, C. New Approach to Nonlinear Dynamic Analysis of Reinforced Concrete 3D Frames; An Accurate and Computational Efficient Mathematical Model. Appl. Sci. 2022, 12, 1692. [Google Scholar] [CrossRef]
- Munteanu, R.I.; Ruxandra, E.; Cătălin, B.; Vasile, C. A new perspective into torsional inelastic response of actively controlled irregular multistorey buildings. Alex. Eng. J. 2023, 71, 691–706. [Google Scholar] [CrossRef]
- Soong, T.T.; Spencer, B.F. Active Structural Control: Theory and Practice. J. Eng. Mech. 1992, 118, 1282–1285. [Google Scholar] [CrossRef]
- Spencer, B.; Nathan, M.; Newmark; Newmark;Nagarajaiah, S. State of the Art of Structural Control. J. Struct. Eng.-ASCE 2003, 129, 845–856. [Google Scholar] [CrossRef]
- Saaed, T.E.; Nikolakopoulos, G.; Jonasson, J.E.; Hedlund, H. A state of the art review of structural control systems. J. Vib. Control 2015, 21, 919–937. [Google Scholar] [CrossRef]
- Venanzi, I. A Review on Adaptive Methods for Structural Control. Open Civ. Eng. J. 2016, 10, 653–667. [Google Scholar] [CrossRef]
- Dyke, S.J.; Spencer, B.F., Jr.; Quast, P.; Kaspari, D.C., Jr.; Sain, M.K. Implementation of an Active Mass Driver Using Acceleration Feedback Control. Comput.-Aided Civ. Infrastruct. Eng. 1996, 11, 305–323. [Google Scholar] [CrossRef]
- Nagashima, I.; Shinozaki, Y. Variable gain feedback control technique of active mass damper and its application to hybrid structural control. Earthq. Eng. Struct. Dyn. 1997, 26, 815–838. [Google Scholar] [CrossRef]
- López-Almansa, F.; Andrade, R.; Rodellar, J.; Reinhorn, A.M. Modal Predictive Control of Structures. II: Implementation. J. Eng. Mech.-ASCE 1994, 120, 1761–1772. [Google Scholar] [CrossRef]
- Yang, C.S.W.; Chung, L.L.; Wu, L.Y.; Chung, N.H. Modified predictive control of structures with direct output feedback. Struct. Control Health Monit. 2011, 18, 922–940. [Google Scholar] [CrossRef]
- Li, L.; Song, G.; Ou, J. Hybrid active mass damper (AMD) vibration suppression of nonlinear high-rise structure using fuzzy logic control algorithm under earthquake excitations. Struct. Control Health Monit. 2011, 18, 698–709. [Google Scholar] [CrossRef]
- Ramírez-Neria, M.; Morales-Valdez, J.; Yu, W. Active vibration control of building structure using active disturbance rejection control. J. Vib. Control 2022, 28, 2171–2186. [Google Scholar] [CrossRef]
- Azimi, M.; Pan, H.; Abdeddaim, M.; Lin, Z. Optimal Design of Active Tuned Mass Dampers for Mitigating Translational–Torsional Motion of Irregular Buildings. In Proceedings of the International Conference on Experimental Vibration Analysis for Civil Engineering Structures, San Diego, CA, USA, 12–14 July 2017; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Rebecchi, G.; Menardo, F.; Rosti, M.; Bussini, A.; Diamanti, P.; Viva, F.D.; Masiello, G.; Sguazzo, S. An Innovative Active Control System for The Seismic Retrofit of a Precast R.C. Wall-Bearing Building. Procedia Struct. Integr. 2023, 44, 1180–1187. [Google Scholar] [CrossRef]
- Liu, S.; Chen, S.; Zeng, S.; Zhang, B.; Hu, S. Seismic performance analysis of K-shaped EBF with an innovative crack-resistant composition beam. J. Build. Eng. 2025, 101, 111818. [Google Scholar] [CrossRef]
- Hu, S.; Liu, S.; Zeng, S.; Zhang, B.; Xu, Z. Investigating seismic performance of a novel self-centering shear link in EBF utilizing experimental and numerical simulation. J. Constr. Steel Res. 2025, 224, 109129. [Google Scholar] [CrossRef]
- Xue, Z.; Cui, X.; Pei, Q.; Zhong, J.; He, Y.; Zhang, Y. Seismic Isolation Performance of Nuclear Power Plant Containment Structures. Buildings 2024, 14, 1650. [Google Scholar] [CrossRef]
- Pei, Q.; Qi, P.; Xue, Z.; Zhong, J.; Zhang, Y. Design and Experimental Analysis of Seismic Isolation Bearings for Nuclear Power Plant Containment Structures. Buildings 2023, 13, 2366. [Google Scholar] [CrossRef]
- Pei, Q.; Wu, C.; Cheng, Z.; Ding, Y.; Guo, H. The Seismic Performance of New Self-Centering Beam-Column Joints of Conventional Island Main Buildings in Nuclear Power Plants. Materials 2022, 15, 1704. [Google Scholar] [CrossRef] [PubMed]
- Moutsopoulou, A.; Petousis, M.; Vidakis, N.; Pouliezos, A.; Stavroulakis, G.E. Advancement in Intelligent Control for Dampening Structural Vibrations. Vibration 2024, 7, 844–862. [Google Scholar] [CrossRef]
- Li, M.; Xie, R. Optimal Control Based on Reinforcement Learning for Flexible High-Rise Buildings with Time-Varying Actuator Failures and Asymmetric State Constraints. Buildings 2025, 15, 841. [Google Scholar] [CrossRef]
- Koutsoloukas, L.; Nikitas, N.; Aristidou, P. Robust structural control of a real high-rise tower equipped with a hybrid mass damper. Struct. Des. Tall Spec. Build. 2022, 31, e1941. [Google Scholar] [CrossRef]
- Zhu, Q.; Yang, W.; Zhang, Q.; Du, Y. A hybrid vibration mitigation method based on the crowd flow control and tuned mass damper on a footbridge. Eng. Struct. 2021, 245, 112972. [Google Scholar] [CrossRef]
- Kobori, T.; Koshika, N.; Yamada, K.; Ikeda, Y. Seismic-response-controlled structure with active mass driver system. Part 1: Design. Earthq. Eng. Struct. Dyn. 1991, 20, 133–149. [Google Scholar] [CrossRef]
- Kobori, T.; Koshika, N.; Yamada, K.; Ikeda, Y. Seismic-response-controlled structure with active mass driver system. Part 2: Verification. Earthq. Eng. Struct. Dyn. 1991, 20, 151–166. [Google Scholar] [CrossRef]
- Cao, H.; Reinhorn, A.; Soong, T. Design of an active mass damper for a tall TV tower in Nanjing, China. Eng. Struct. 1998, 20, 134–143. [Google Scholar] [CrossRef]
- Yamamoto, M.; Higashino, M.; Toyama, K.; Aizawa, S. Five years of wind and earthquake observation results from a building with AMD. In Proceedings of the Conference: Structural Engineers World Congress, San Francisco, CA, USA, 19–23 July 1998. [Google Scholar]
- Yamamoto, M.; Sone, T. Behavior of active mass damper (AMD) installed in high-rise building during 2011 earthquake off Pacific coast of Tohoku and verification of regenerating system of AMD based on monitoring. Struct. Control Health Monit. 2014, 21, 634–647. [Google Scholar] [CrossRef]
- Chen, C.J.; Li, Z.H.; Teng, J.; Wu, Q.G.; Lin, B.C. A variable gain state-feedback technique for an AMD control system with stroke limit and its application to a high-rise building. Struct. Des. Tall Spec. Build. 2021, 30, e1816. [Google Scholar] [CrossRef]
- Rebecchi, G.; Menardo, F.; Rosti, M.; Bussini, A.; Calvi, P. Full-Scale Shake Table Tests of A R.C. Building Equipped with an Active Mass Damper: Experimental Results and Numerical Simulations. J. Earthq. Eng. 2023, 27, 2702–2725. [Google Scholar] [CrossRef]
- Hart, G.; Wong, K. Structural Dynamics for Structural Engineers; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Li, G.; Wong, K. Theory of Nonlinear Structural Analysis; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Carrillo, J.; Oyarzo-Vera, C.; Blandón, C. Damage assessment of squat, thin and lightly-reinforced concrete walls by the Park & Ang damage index. J. Build. Eng. 2019, 26, 100921. [Google Scholar] [CrossRef]
- Cao, S.; Jiang, L.; Wei, B. Numerical and experimental investigations on the Park-Ang damage index for high-speed railway bridge piers with flexure failures. Eng. Struct. 2019, 201, 109851. [Google Scholar] [CrossRef]
- Ghosh, S.; Datta, D.; Katakdhond, A.A. Estimation of the Park–Ang damage index for planar multi-storey frames using equivalent single-degree systems. Eng. Struct. 2011, 33, 2509–2524. [Google Scholar] [CrossRef]
- Nica, G.B.; Pavel, F.; Hojda, G. A fast nonlinear dynamic analysis automated approach to produce fragility curves for 3D RC frames. Eng. Struct. 2023, 281, 115695. [Google Scholar] [CrossRef]
- Park, Y.; Ang, A.H. Mechanistic Seismic Damage Model for Reinforced Concrete. J. Struct. Eng. 1985, 111, 722–739. [Google Scholar] [CrossRef]
- Kunnath, S.K.; Reinhorn, a.M.; Lobo, R.F. IDARC Version 3.0: A Program for the Inelastic Damage Analysis of Reinforced Concrete Structures; Technical Report NCEER-92-0022; U.S. National Center for Earthquake Engineering Research: New York, NY, USA, 1992. [Google Scholar]
- Powell, G.H.; Chen, P.F. 3D Beam-Column Element with Generalized Plastic Hinges. J. Eng. Mech. 1986, 112, 627–641. [Google Scholar] [CrossRef]
- Cotovanu, A.; Vacareanu, R. Local site conditions modeling in stochastic simulation of ground motions generated by Vrancea (Romania) intermediate-depth seismic source. J. Seismol. 2020, 24, 229–241. [Google Scholar] [CrossRef]
- Munteanu, R.I.; Stamatescu, I.; Calofir, V.; Nica, G.B.; Iliescu, S.S. Structural damage mitigation using a fuzzy controller. In Proceedings of the 2021 23rd International Conference on Control Systems and Computer Science (CSCS), Bucharest, Romania, 26–28 May 2021; pp. 393–400. [Google Scholar] [CrossRef]
- Munteanu, R.I.; Nica, G.B.; Calofir, V.; Iliescu, S.S.; Sîrbu, O.T. Building seismic behavior improvement using an optimal control algorithm. In Proceedings of the 2020 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 21–23 May 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Park, Y.J.; Ang, A.H.S.; Wen, Y.K. Damage-Limiting Aseismic Design of Buildings. Earthq. Spectra 1987, 3, 1–26. [Google Scholar] [CrossRef]
- Gharehbaghi, S. Damage controlled optimum seismic design of reinforced concrete framed structures. Struct. Eng. Mech. 2018, 65, 53–68. [Google Scholar]




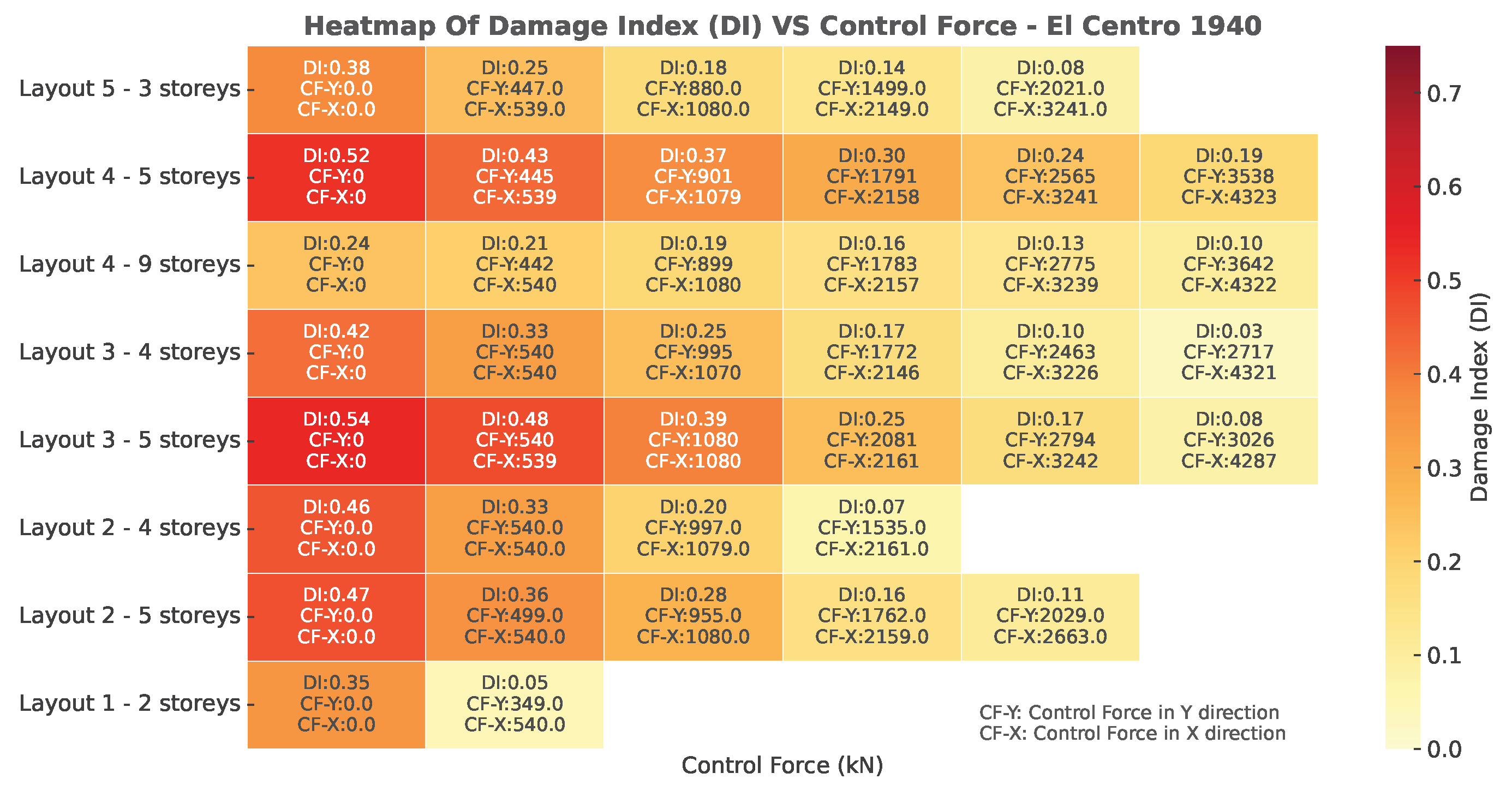
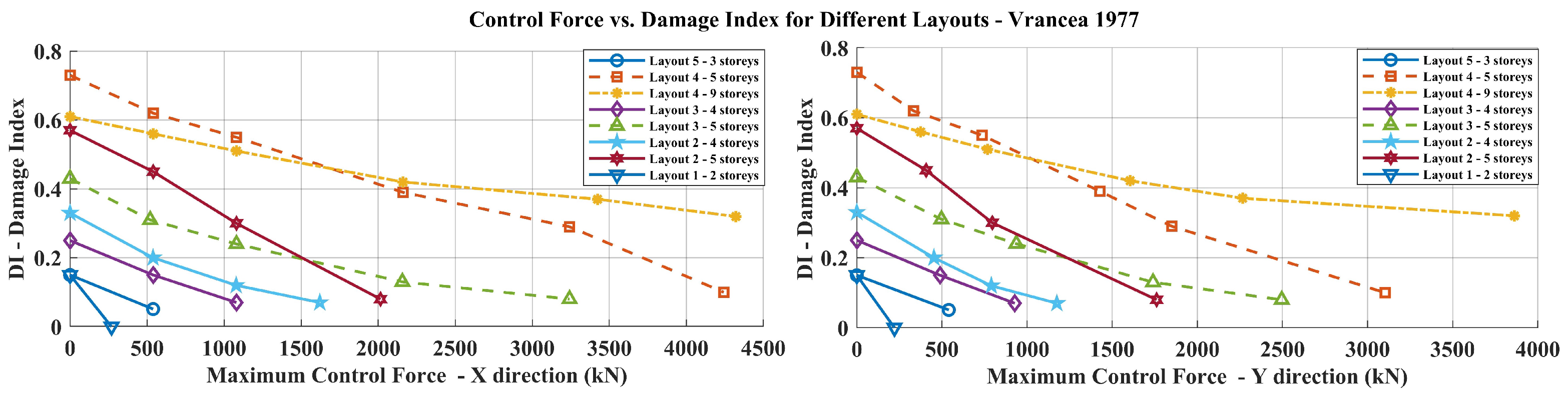
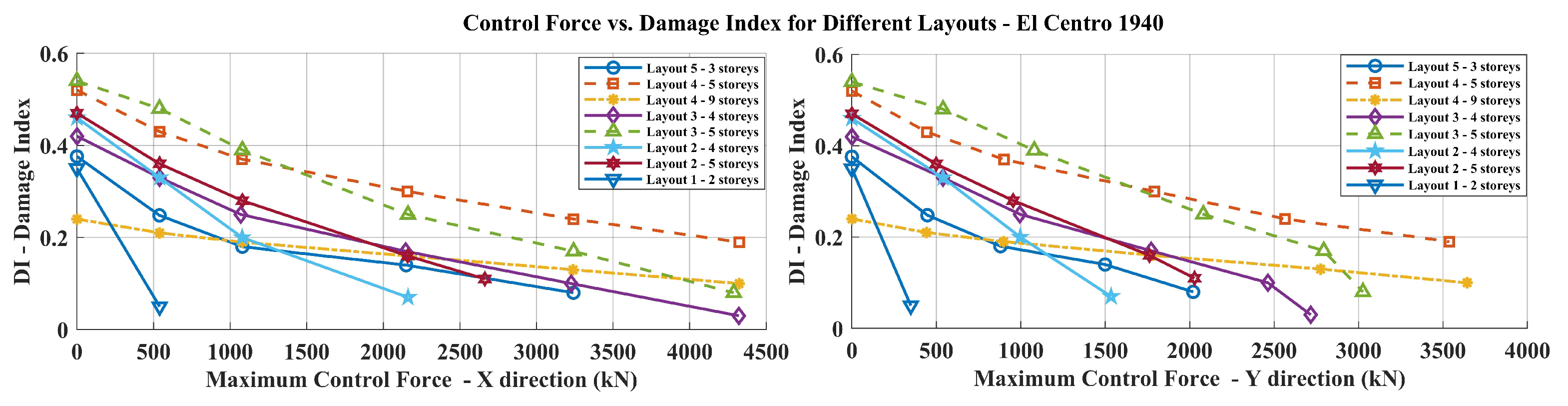
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Young’s modulus | E | ||
| Density | 2.5035 | ||
| Damping ratio | 0.05 | – | |
| Poisson’s ratio | 0.2 | – | |
| Shear modulus | G | ||
| Live load | – | 15 | kN/m |
| Parameter | Layout 1 | Layout 2 | Layout 3 | ||
|---|---|---|---|---|---|
| Type | 2 Story | 4 Story | 5 Story | 4 Story | 5 Story |
| (s) | 0.35 | 0.53 | 0.68 | 0.45 | 0.58 |
| (s) | 0.32 | 0.50 | 0.64 | 0.42 | 0.52 |
| (s) | 0.30 | 0.46 | 0.58 | 0.41 | 0.52 |
| (m) | 0.35 | 0.55 | 0.55 | 0.55 | 0.55 |
| (m) | 0.35 | 0.55 | 0.55 | 0.55 | 0.55 |
| (m) | 0.25 | 0.3 | 0.3 | 0.3 | 0.3 |
| (m) | 0.45 | 0.55 | 0.55 | 0.55 | 0.55 |
| 208 | 448 | 560 | 928 | 1160 | |
| (kNm) | 90 | 165 | 165 | 165 | 165 |
| (kNm) | 290 | 980 | 1040 | 980 | 0.37 |
| (kNm) | −3172 | −7012 | −7318 | −7012 | −7318 |
| (kNm) | −2289 | −5687 | −5782 | −5687 | −5782 |
| Parameter | Layout 4 | Layout 5 | |
|---|---|---|---|
| Type | 5 Story | 9 Story | 3 Story |
| (s) | 0.59 | 1.1 | 0.37 |
| (s) | 0.52 | 0.94 | 0.34 |
| (s) | 0.51 | 0.92 | 0.33 |
| (m) | 0.7 | 1 | 0.55 |
| (m) | 0.7 | 1 | 0.55 |
| (m) | 0.3 | 0.3 | 0.3 |
| (m) | 0.65 | 0.75 | 0.65 |
| 1160 | 2088 | 696 | |
| (kNm) | 190 | 420 | 200 |
| (kNm) | 1900 | 5400 | 980 |
| (kNm) | −11,000 | −21,000 | −7012 |
| (kNm) | −9400 | −18,400 | −5687 |
| Parameter | Layout 1 | Layout 2 | Layout 3 | Layout 4 | Layout 5 |
|---|---|---|---|---|---|
| Type | 2-Story | 4/5-Story | 4/5-Story | 5/9-Story | 3-Story |
| length (m) | 14 | 18 | 33 | 30 | 37 |
| width (m) | 10 | 21 | 16 | 21 | 17 |
| number of spans | 4 | 3 | 7 | 6 | 7 |
| number of bays | 2 | 3 | 3 | 3 | 3 |
| area per floor () | 140 | 378 | 528 | 630 | 216 |
| function | Duplex home | Residential | Residential | Office | School |
| story height (m) | 3 | 3 | 3 | 4 | 3.5 |
| Damage Level | Visual Indicators | Damage Index | Damage State |
|---|---|---|---|
| Collapse | Total or partial collapse | >1.0 | Building collapse |
| Severe | Extensive crashing of concrete. Disclosure of buckled reinforcements | 0.4–1.0 | Damage beyond repair |
| Moderate | Extensive large cracks. Spalling of concrete in weaker elements | 0.25–0.4 | Repairable damage |
| Low | Minor cracks throughout building. Partial crashing of concrete columns | 0.1–0.25 | Minor damage |
| Slight | Sporadic occurrence of cracking | <0.1 | No damage |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munteanu, R.I.; Calofir, V.; Lemnaru, K.-C.; Ponta, C. Advanced Investigation into Active Control Force Requirements for Seismic Damage Mitigation of Inelastic Structures. Buildings 2025, 15, 1402. https://doi.org/10.3390/buildings15091402
Munteanu RI, Calofir V, Lemnaru K-C, Ponta C. Advanced Investigation into Active Control Force Requirements for Seismic Damage Mitigation of Inelastic Structures. Buildings. 2025; 15(9):1402. https://doi.org/10.3390/buildings15091402
Chicago/Turabian StyleMunteanu, Ruben Iacob, Vasile Calofir, Karol-Cristian Lemnaru, and Cătălin Ponta. 2025. "Advanced Investigation into Active Control Force Requirements for Seismic Damage Mitigation of Inelastic Structures" Buildings 15, no. 9: 1402. https://doi.org/10.3390/buildings15091402
APA StyleMunteanu, R. I., Calofir, V., Lemnaru, K.-C., & Ponta, C. (2025). Advanced Investigation into Active Control Force Requirements for Seismic Damage Mitigation of Inelastic Structures. Buildings, 15(9), 1402. https://doi.org/10.3390/buildings15091402






