Overall Buckling Behavior and Design of Steel Stiffened Box Section Columns Under Axial Compression
Abstract
:1. Introduction
2. Experimental Design and Results
2.1. Specimen Design
2.2. Loading System and Scheme
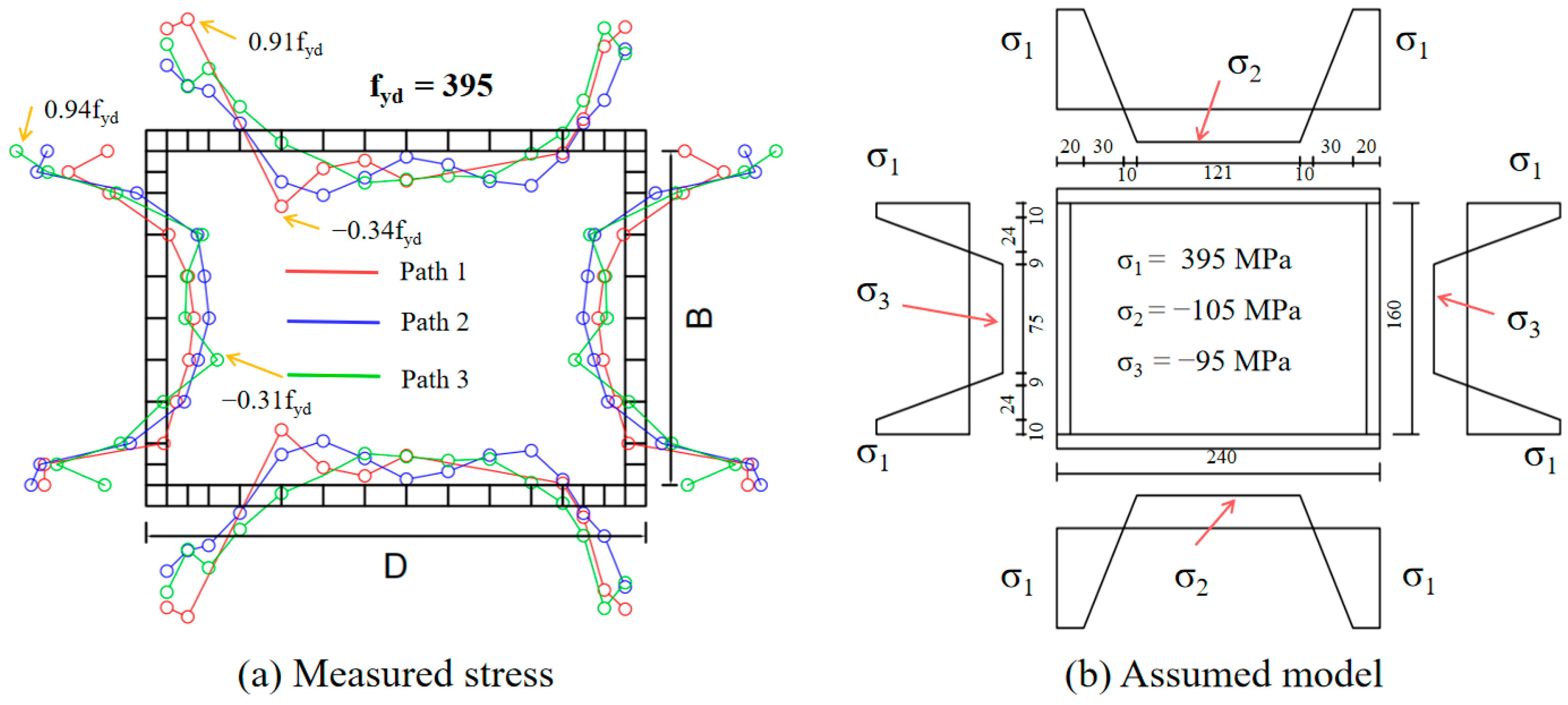
2.3. Initial Imperfections and Residual Stresses
2.3.1. Initial Geometric Imperfections
2.3.2. Residual Stresses
2.4. Experimental Results
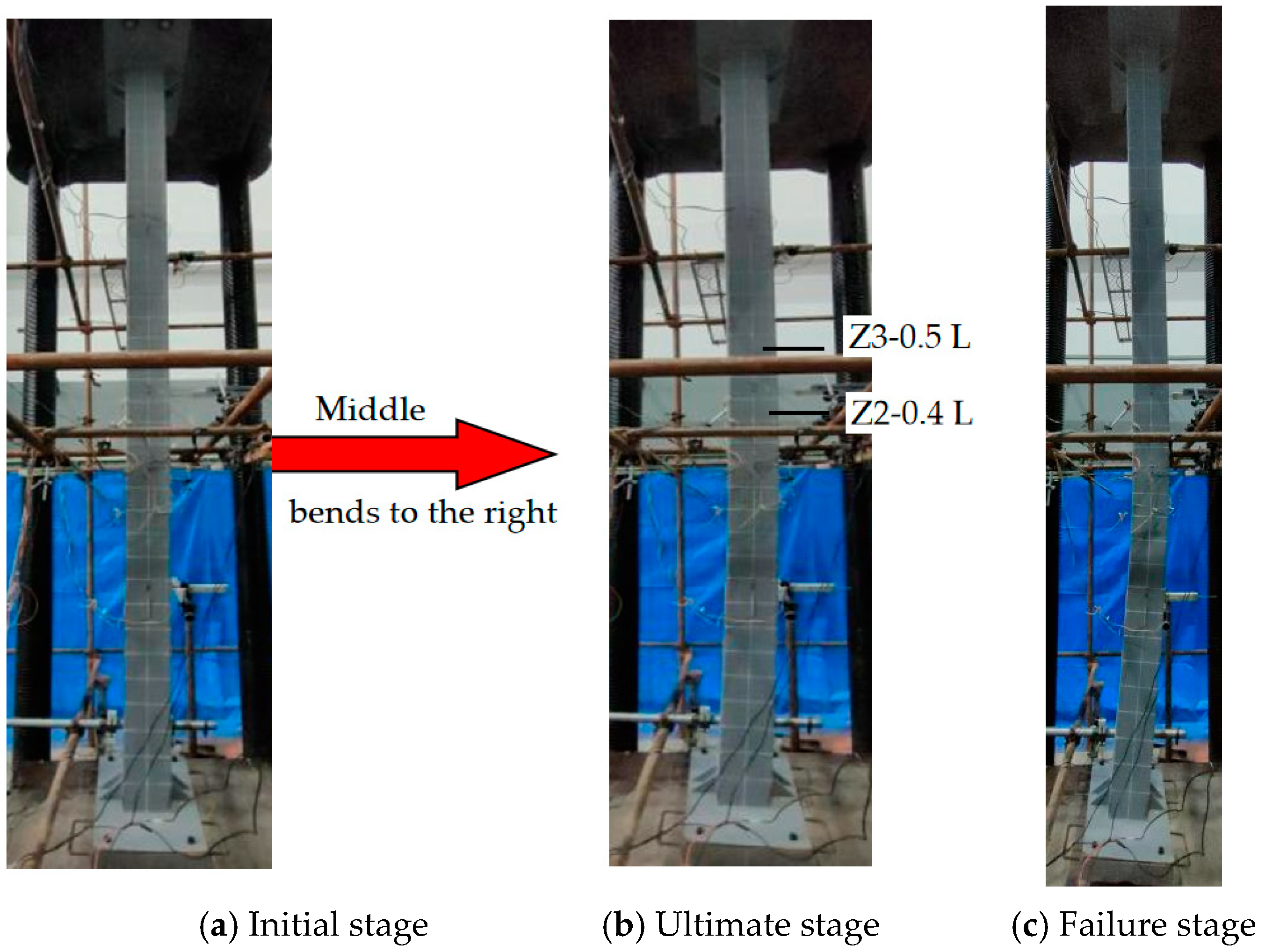
2.4.1. Experimental Phenomena
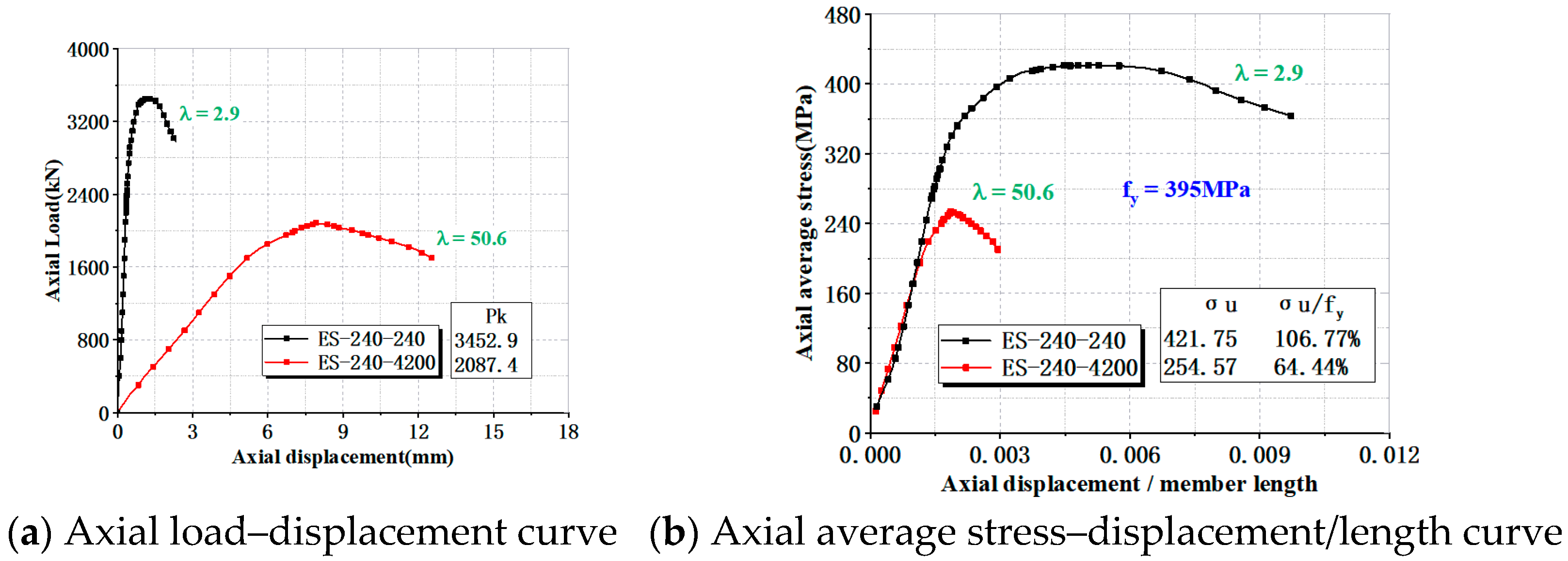
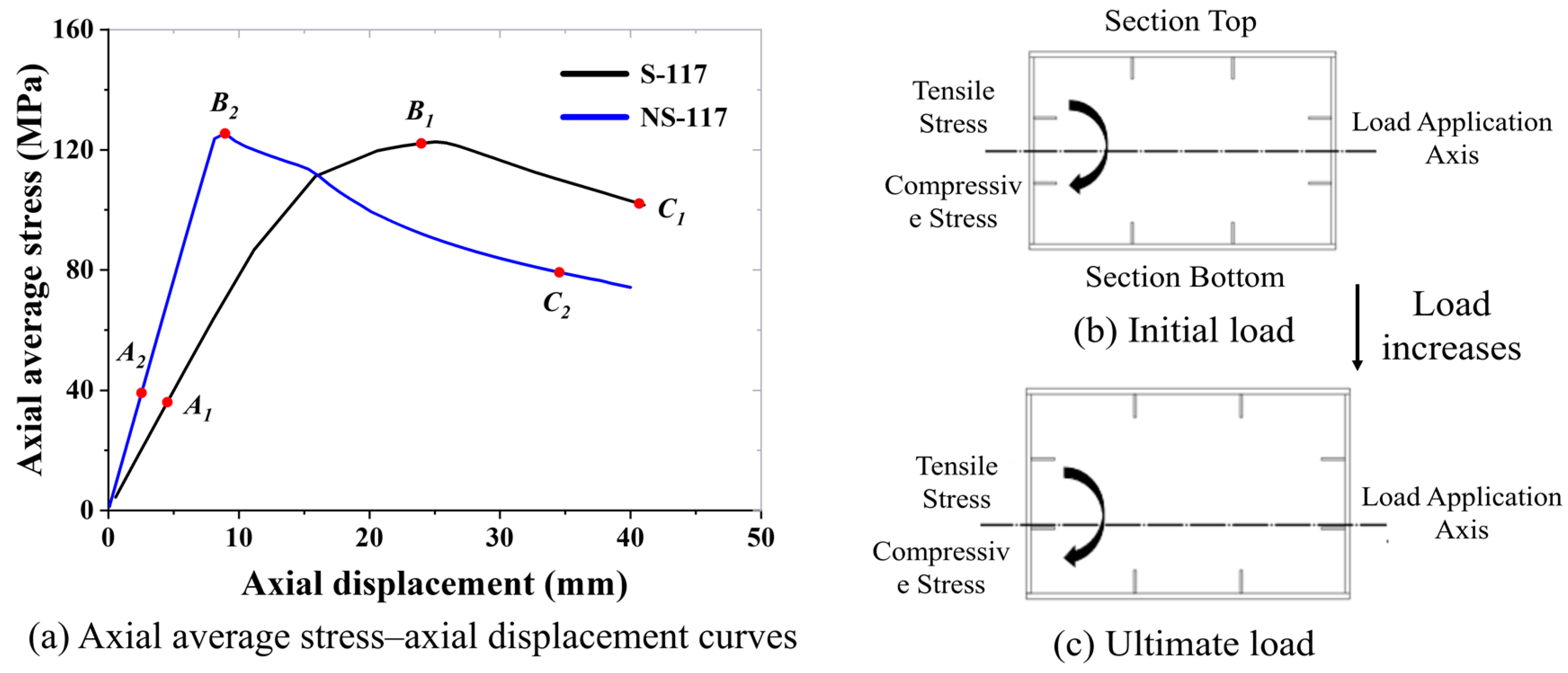
2.4.2. Load–Displacement Curve
3. Numerical Study
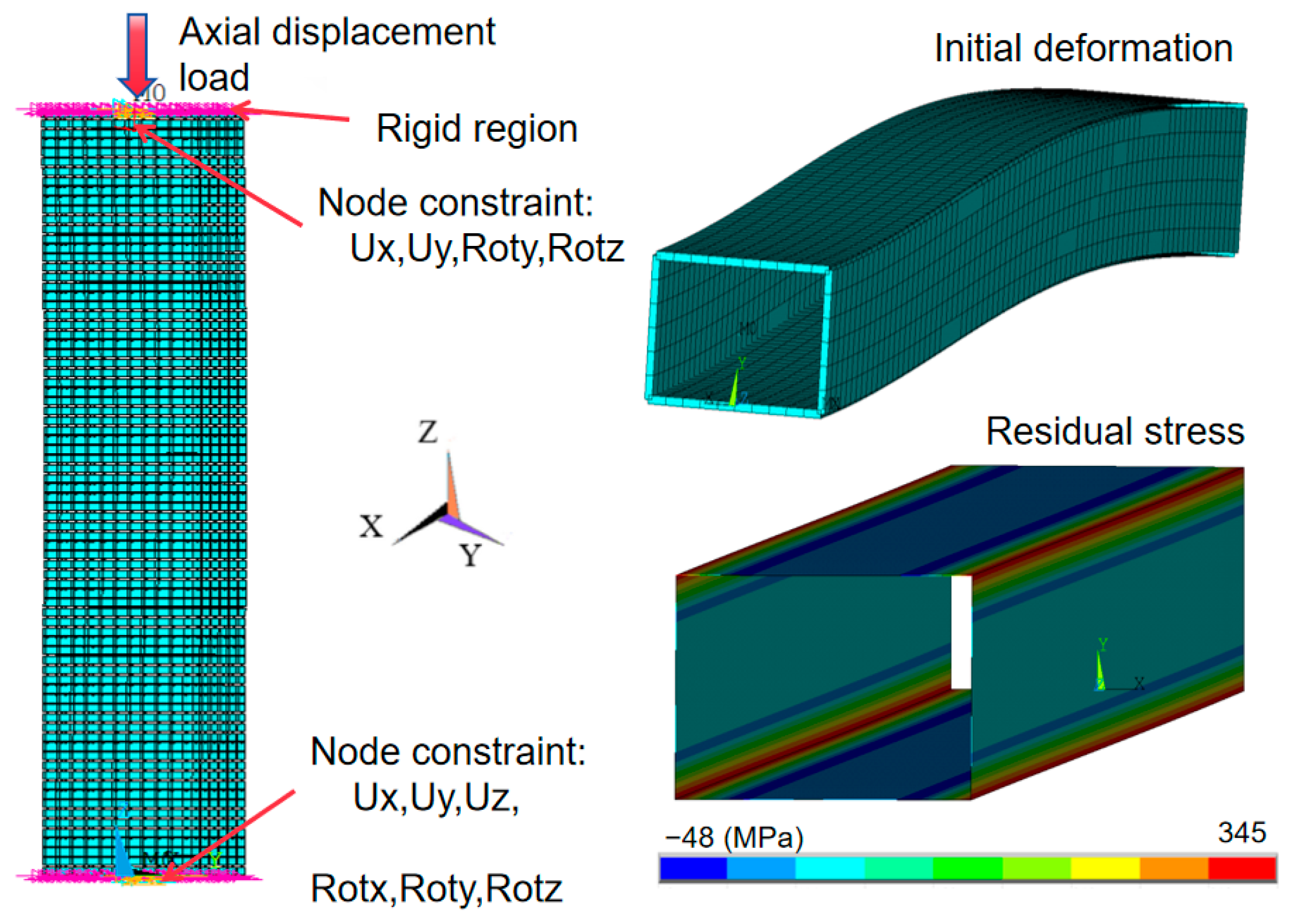
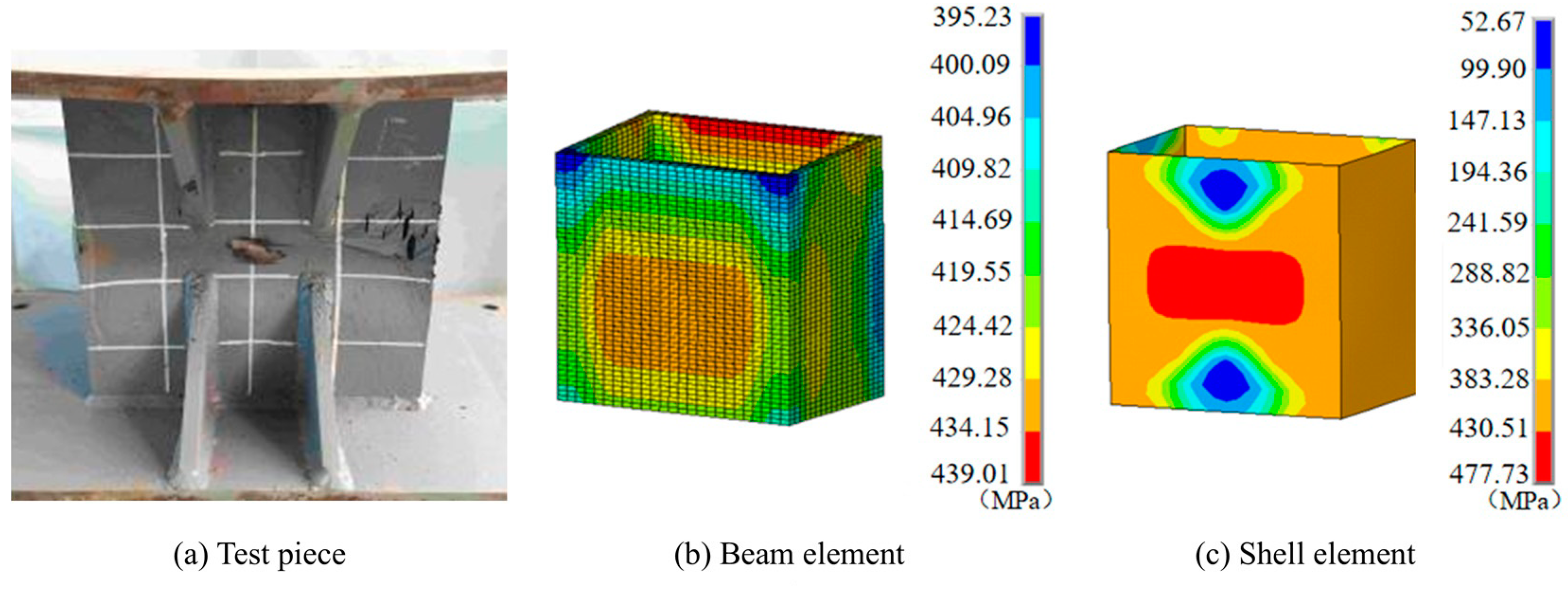
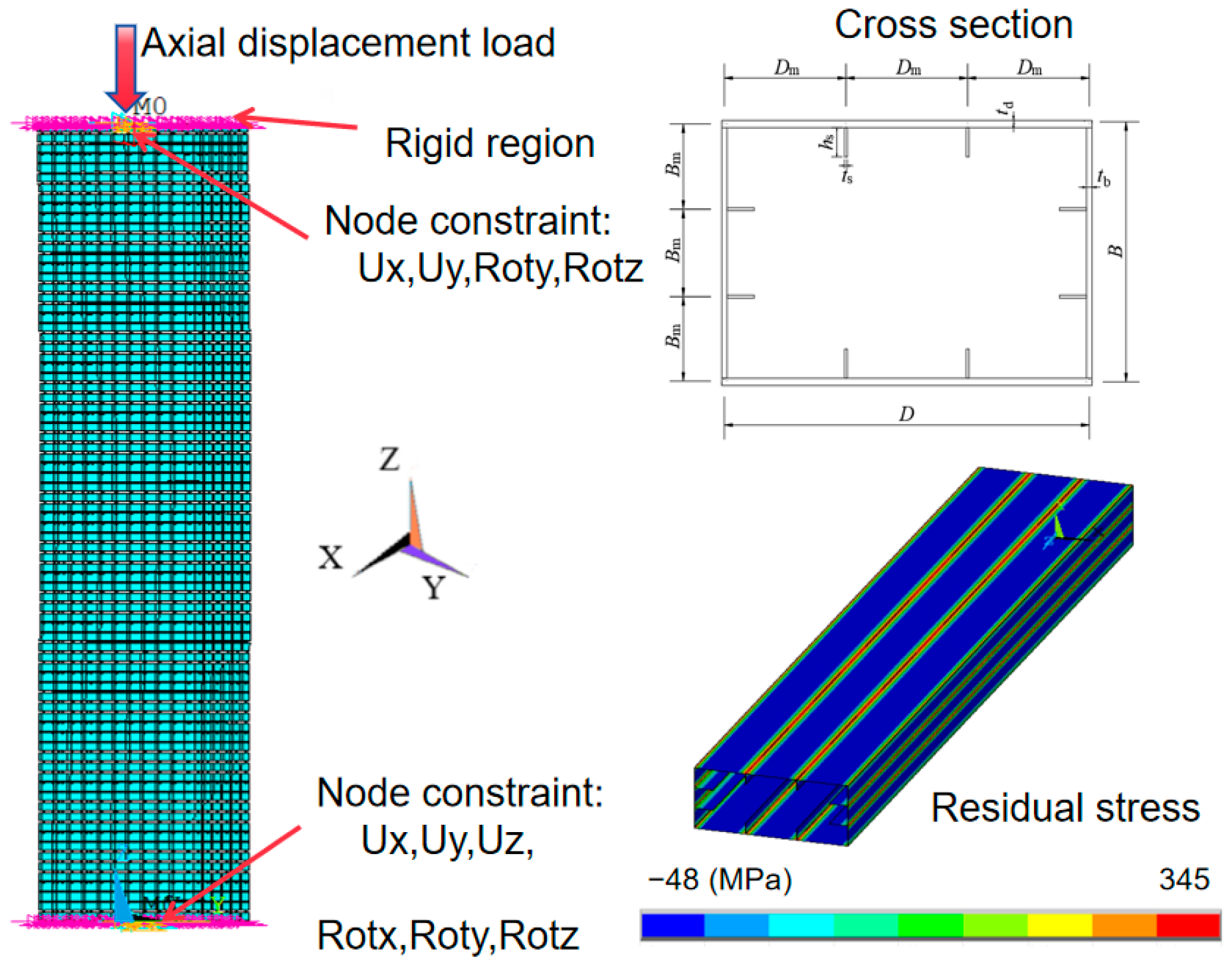
3.1. Finite Element Model
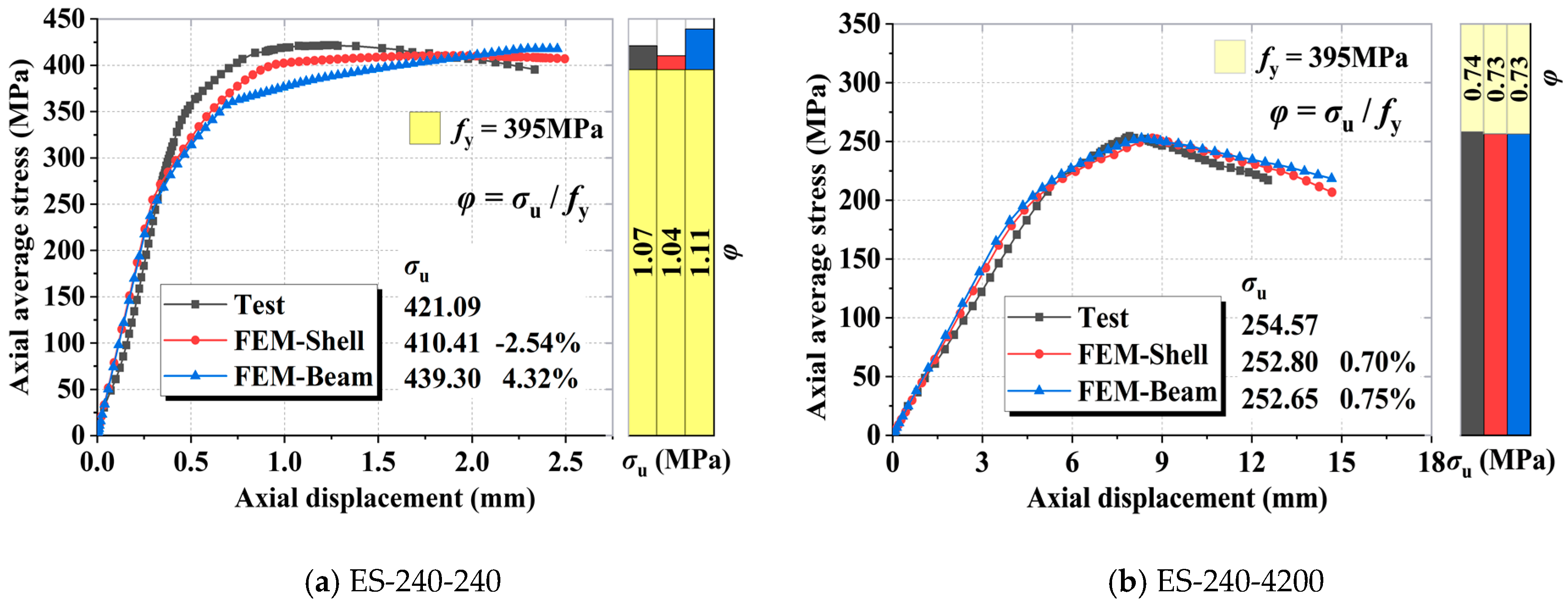
3.2. Finite Element Model Verification
3.3. Parametric Discussion
3.3.1. Influence of Initial Geometric Imperfections
- (1)
- Initial curvature
- (2)
- Initial eccentricity
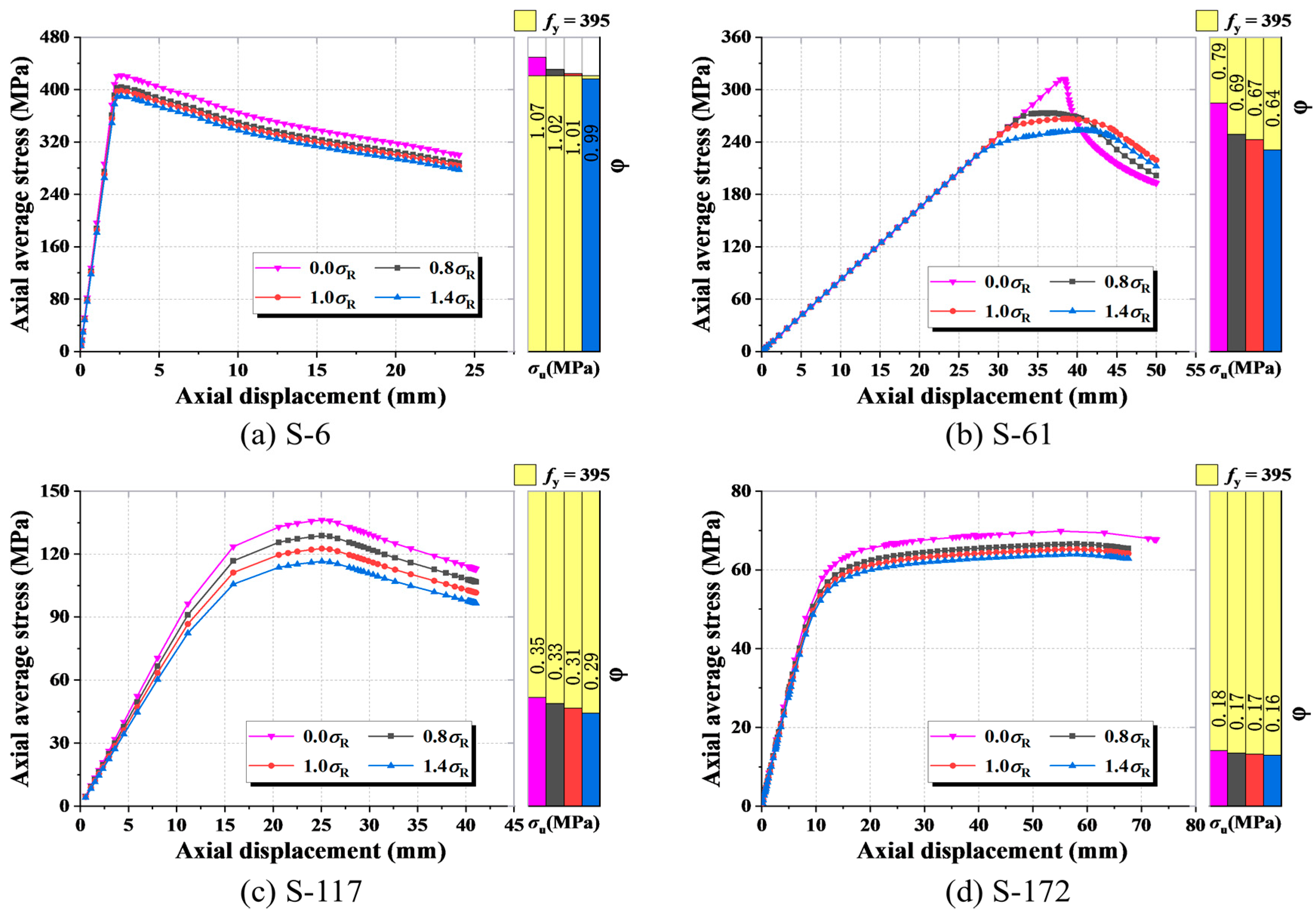
3.3.2. Influence of Residual Stresses
3.4. Force Mechanism of Box Section Columns
- (1)
- In the initial stage of loading, owing to the small out-of-plane initial deformation at the midsection, the model is in a state of axial compression, and the axial stress–displacement curves show a linear increase, as depicted in Figure 19a,b. As the load increased, the load application axis at the midsection of the member shifted in the direction opposite to the out-of-plane deformation, as shown in Figure 18b,c. At this point, the bottom of the section is compressed and subjected to a state in which the bending and axial compressive stresses were superimposed owing to the second-order effects of the model. The second-order effect of the model increases with the increase in the out-of-plane bending deformation of the model, resulting in the tensile side at the top of the section gradually changing from compression to tension.
- (2)
- As shown at point B in Figure 18a, most of the sections at the bottom of the model section reach the ultimate bearing capacity. The residual tensile stress area at the top of the section also exceeds the tensile yield strength under the combined effects of the bending tensile stress and axial compressive stress, as shown in Figure 19c,d. These results suggest that the bending tensile stress caused by the second-order effect is obviously higher than the axial compression stress and welding residual compressive stress of the model. Therefore, the influence of the second-order effect cannot be ignored.
- (3)
- When the model enters the load drop section, the out-of-plane deformation further increases, whereas the axial load decreases, making the bending tensile stress at the top of the section more pronounced. The area subjected to tensile yielding expanded rapidly from the weld locations to the surrounding plate, whereas the bottom of the section essentially reached the compressive yield strength, as shown in Figure 19e,f. The member ultimately failed, as indicated by point C in Figure 18a.
4. Proposed Stability Calculation Formulas for Stiffened Box Columns
4.1. Calculate the Construction Size of the Model
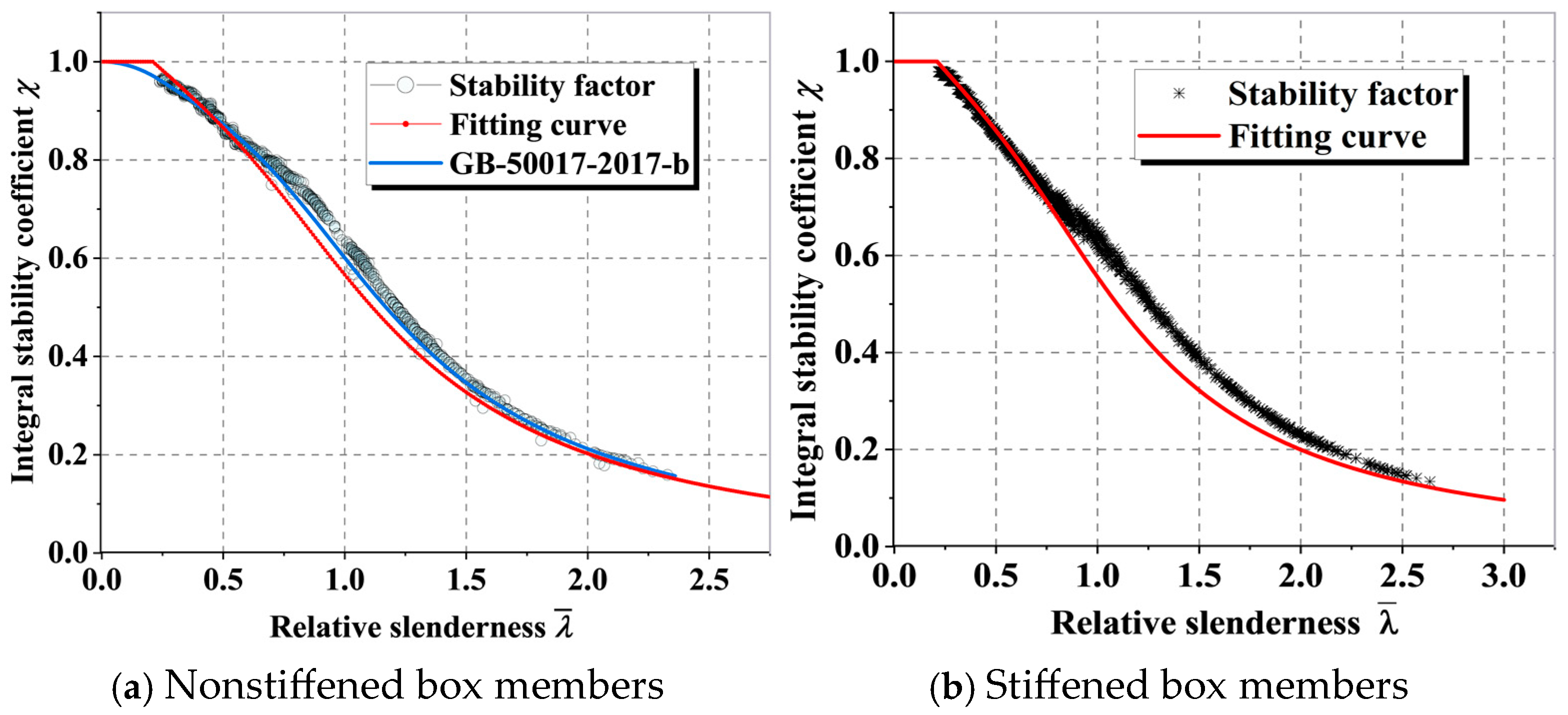
4.2. Calculation Formula for the Overall Stability Coefficient of Stiffened Box Columns
- (1)
- Batch calculation results
- (2)
- Calculation formula for the overall stability reduction factor.
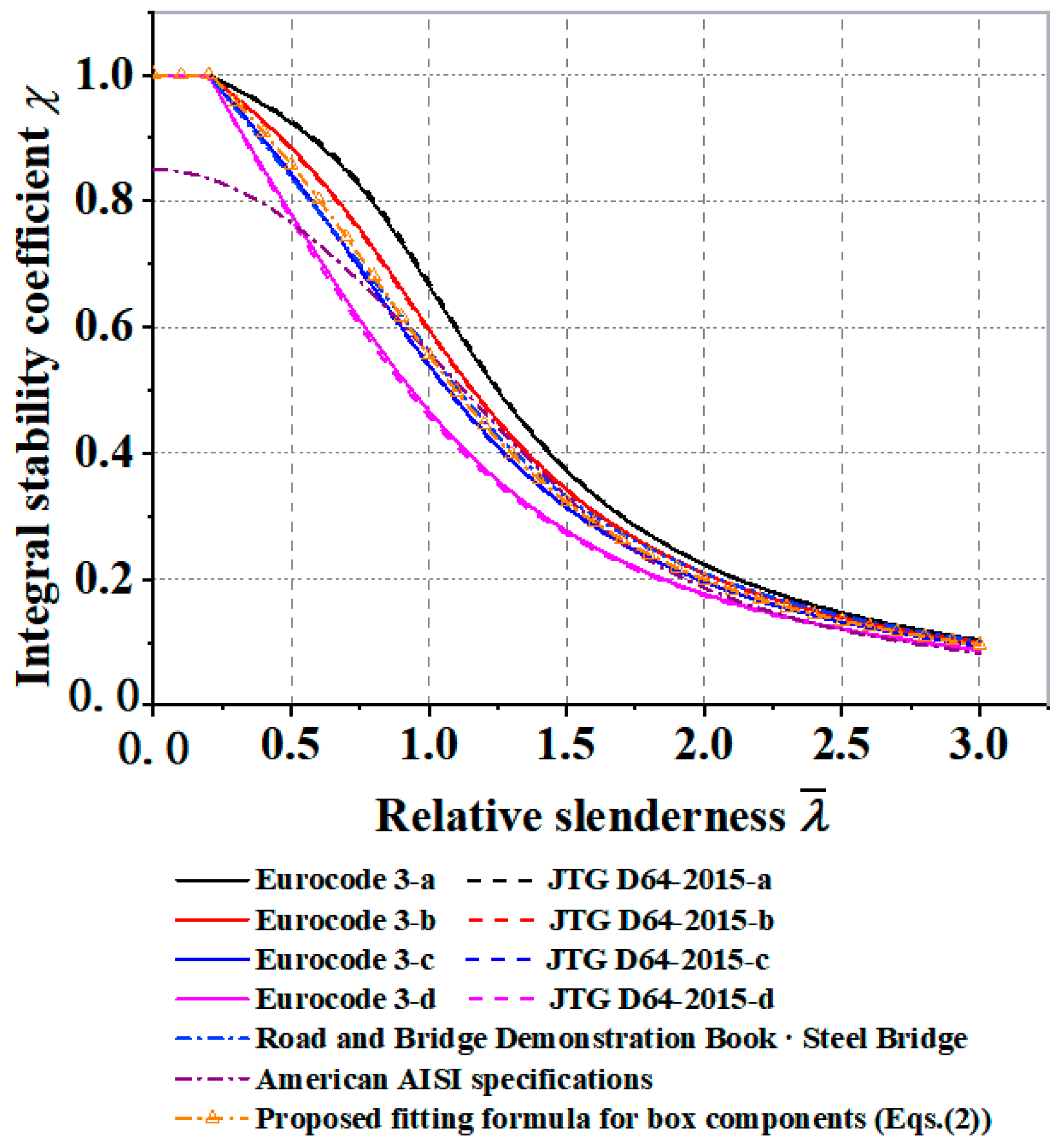
4.3. Comparative Analysis of the Overall Stability Coefficient
5. Conclusions
- (1)
- For box-shaped specimens in the overall stability tests, the experimental failure mode manifested as significant out-of-plane local bulging deformation of the wall plates in short column specimens and significant overall buckling deformation toward one side in the middles of the long column specimens. Short columns (λ = 2.9) exhibited a distinct yield plateau after the peak of the load curve, manifesting as strength failure, whereas long columns (λ = 50.6) demonstrated rapid post-peak load decline characteristic of buckling. The stability coefficients of the two columns are 1.07 and 0.64, respectively, indicating that increasing slenderness ratios reduce specimen load-carrying capacity and exacerbate buckling phenomena.
- (2)
- As the slenderness ratio increased, the influences of the initial geometric imperfections and residual stresses on the ultimate load-bearing capacities of the models showed a trend of first increasing and then decreasing. The initial curvature caused a maximum reduction in buckling strength of 5.2%, the initial eccentricity caused a maximum reduction in buckling strength of 4.7%, and the residual stresses caused a reduction in buckling strength of 6.52%.
- (3)
- Curves spanning a broad slenderness ratio range were calculated based on box-shaped specimens, and the Perry–Robertson formula was modified to derive fitted curves for two member categories. The curve for unstiffened members agreed well with the Class B column curves of China’s specifications, validating the formula’s accuracy. Since both member types exhibited consistent buckling modes, an overall stability modification formula for stiffened steel box columns was sestablished.
- (4)
- The modified formula in this study lies between the Class B and Class C column curves of Eurocode 3 and JTG D64-2015 [24] specifications (with an average 2.20% higher than Class C in JTG D64-2015 [24]) and is positioned between Japanese and U.S. specifications while being slightly lower than the Japanese code. Comparisons with various codes demonstrate the formula’s high accuracy, which can provide a reference for engineering applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Usami, T.; Zheng, Y.; Ge, H.B. Recent research developments in stability and ductility of steel bridge structures General Report. J. Constr. Steel Res. 2000, 55, 183–209. [Google Scholar] [CrossRef]
- Aboulella, F. Analysis of Cable stayed Bridges Supported by Flexible Towers. J. Struct. Eng. 1988, 12, 2741–2754. [Google Scholar] [CrossRef]
- Wang, P.; Yang, C.G. Parametric studies on cable stayed bridges. Comput. Struct. 1996, 60, 243–260. [Google Scholar] [CrossRef]
- Qu, Z. Research on Substructure Design and Construction Technology of Cross-Sea Bridge. Ph.D. Thesis, Tongji University, Shanghai, China, 2007. [Google Scholar]
- Susantha, K.; Aoki, T.; Kumano, T.; Yamamoto, K. Applicability of low-yield-strength steel for ductility improvement of steel bridge piers. Eng. Struct. 2005, 27, 1064–1073. [Google Scholar] [CrossRef]
- Ban, H.; Shi, G.; Shi, Y.; Wang, Y. Overall buckling behavior of 460 MPa high strength steel columns: Experimental investigation and design method. J. Constr. Steel. Res. 2012, 74, 140–150. [Google Scholar] [CrossRef]
- Ban, H.; Shi, G.; Shi, Y.; Bradford, M.A. Experimental investigation of the overall buckling behaviour of 960 MPa high strength steel columns. J. Constr. Steel. Res. 2013, 88, 256–266. [Google Scholar] [CrossRef]
- Ban, H.; Shi, G. Overall buckling behaviour and design of high-strength steel welded section columns. J. Constr. Steel. Res. 2018, 143, 180–195. [Google Scholar] [CrossRef]
- Gao, L.; Zheng, Y.Z.; Bai, L.Y.; He, X.H.; Ni, M. Research on overall stability of BS700 high-strength steel columns with box section. J. Constr. Steel Res. 2022, 189, 107090. [Google Scholar] [CrossRef]
- Radwan, M.; Kövesdi, B. Equivalent geometrical imperfections for local and global interaction buckling of welded square box section columns. Structures 2023, 48, 1403–1419. [Google Scholar] [CrossRef]
- Klitchieff, J.M.; Belgrade, Y. On the stability of plates reinforced by longitudinal ribs. J. Appl. Mech. 1949, 16, 74–76. [Google Scholar] [CrossRef]
- Cox, H.L. Computation of initial buckling stress of sheet stiffener combinations. J. R. Aeronaut. Soc. 1954, 58, 634–638. [Google Scholar] [CrossRef]
- Martin, D.W.; Cox, H.L. The buckling modes of longitudinally stiffened at panel. Aeronaut. Q. 1963, 14, 346–398. [Google Scholar] [CrossRef]
- Chen, N.-Z.; Soares, C.G. Reliability assessment of post-buckling compressive strength of laminated composite plates and stiffened panels under axial compression. Int. J. Solids Struct. 2007, 44, 7167–7182. [Google Scholar] [CrossRef]
- Khedmatia, M.R.; Edalat, P. A numerical investigation into the effects of parabolic curvature on the buckling strength and behaviour of stiffened plates under in-plane compression. Lat. Am. J. Solids Struct. 2010, 7, 249–264. [Google Scholar] [CrossRef]
- Liu, X.; Chung, K.-F.; Huang, M.; Wang, G.; Nethercot, D.A. Thermomechanical parametric studies on residual stresses in S355 and S690 welded H-sections. J. Constr. Steel Res. 2019, 160, 387–401. [Google Scholar] [CrossRef]
- Cao, X.; Wang, H.; Chen, Y.; Shen, S.; Tao, Z.; You, M.; Kim, S.-E.; Kong, Z. Experimental and numerical study of residual stresses in 550 MPa high strength steel welded angle sections. Structures 2023, 56, 104907. [Google Scholar] [CrossRef]
- Li, Y.; Xue, J.; Qi, L.; Wang, X.; Yuan, Z.; Xue, G. Residual stress model of welded steel L-shaped and T- shaped sections. J. Constr. Steel Res. 2024, 218, 108724. [Google Scholar] [CrossRef]
- Shin, D.K.; Van Dat, B.; Kim, K. Compressive strength of HPS box girder flanges stiffened with open ribs. J. Constr. Steel Res. 2014, 95, 230–241. [Google Scholar] [CrossRef]
- Rahbar-Ranji, A. Effective breadth/web concept for elastic coupled buckling analysis in flat-bar stiffened plates. Eng. Struct. 2014, 80, 316–322. [Google Scholar] [CrossRef]
- Rahbar-Ranji, A. Eigenvalue Analysis of Flexural-torsional Buckling of Angle-bar Stiffened Plates. Int. J. Steel Struct. 2016, 16, 823–830. [Google Scholar] [CrossRef]
- Sadamoto, S.; Tanaka, S.; Taniguchi, K.; Ozdemir, M.; Bui, T.Q.; Murakami, C.; Yanagihara, D. Buckling Analysis of Stiffened Plate Structures by an Improved Meshfree Flat Shell Formulation. Thinwalled Struct. 2017, 117, 303–313. [Google Scholar] [CrossRef]
- Khalaf, H.I.; Chodorowska, D.; Al-Sabur, R.; Kubit, A.; Macek, W. Comprehensive exploration of technological tensioning effects in welded thin plate girders: An in-depth investigation. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 572. [Google Scholar] [CrossRef]
- JTG D64-2015; Code for Design of Highway Steel Structure Bridge. China Communications Press: Beijing, China, 2015.
- Qingtian, S. Study on the Mechanical Characteristics and Failure Mechanism of Steel Pylon of Cable-Stayed Bridge. Ph.D. Thesis, Tongji University, Shanghai, China, 2003. [Google Scholar]
- Shi, G.; Ban, H.Y.; Bijlaard, F.S.K. Tests and numerical study of ultra-high strength steel columns with end restraints. J. Constr. Steel Res. 2012, 70, 236–247. [Google Scholar] [CrossRef]
- Ma, T.Y.; Hu, Y.F.; Liu, X.; Li, G.Q.; Chung, K.F. Experimental investigation into high strength Q690 steel welded H-sections under combined compression and bending. J. Constr. Steel Res. 2017, 138, 449–462. [Google Scholar] [CrossRef]
- Zhao, Q.; Chen, P.; Zhang, J. Local Stability Test and Design Method for Steel Bridge Plate Stiffeners. China J. Highw. Transp. 2022, 35, 49–61. [Google Scholar]
- Zhao, Q.; Chen, P.; Zhang, J. Experimental Study on Overall Stability of I-rib Stiffened Plate Under Compression. J. Basic Sci. Eng. 2023, 31, 1297–1311. [Google Scholar]
- GB 50017-2017; Steel Structure Design Standard. China Construction Industry Press: Beijing, China, 2017.
- Eurocode 3; Design of Steel Structures-Part 1–5: Plated Structural Elements. European Committee for Standardization (CEN): Brussels, Belgium, 2005.
- JRA-2017; Road and Bridge Demonstration Book-Tongjie (II Steel Bridge). March 14 Years of Pingcheng. Japan Road Association: Tokyo, Japan, 2017.
- Translation of Steel and Light Structure Laboratory, Tongji University. American Steel Structure Design Manual; Tongji University Press: Shanghai, China, 2006; Volume I. [Google Scholar]
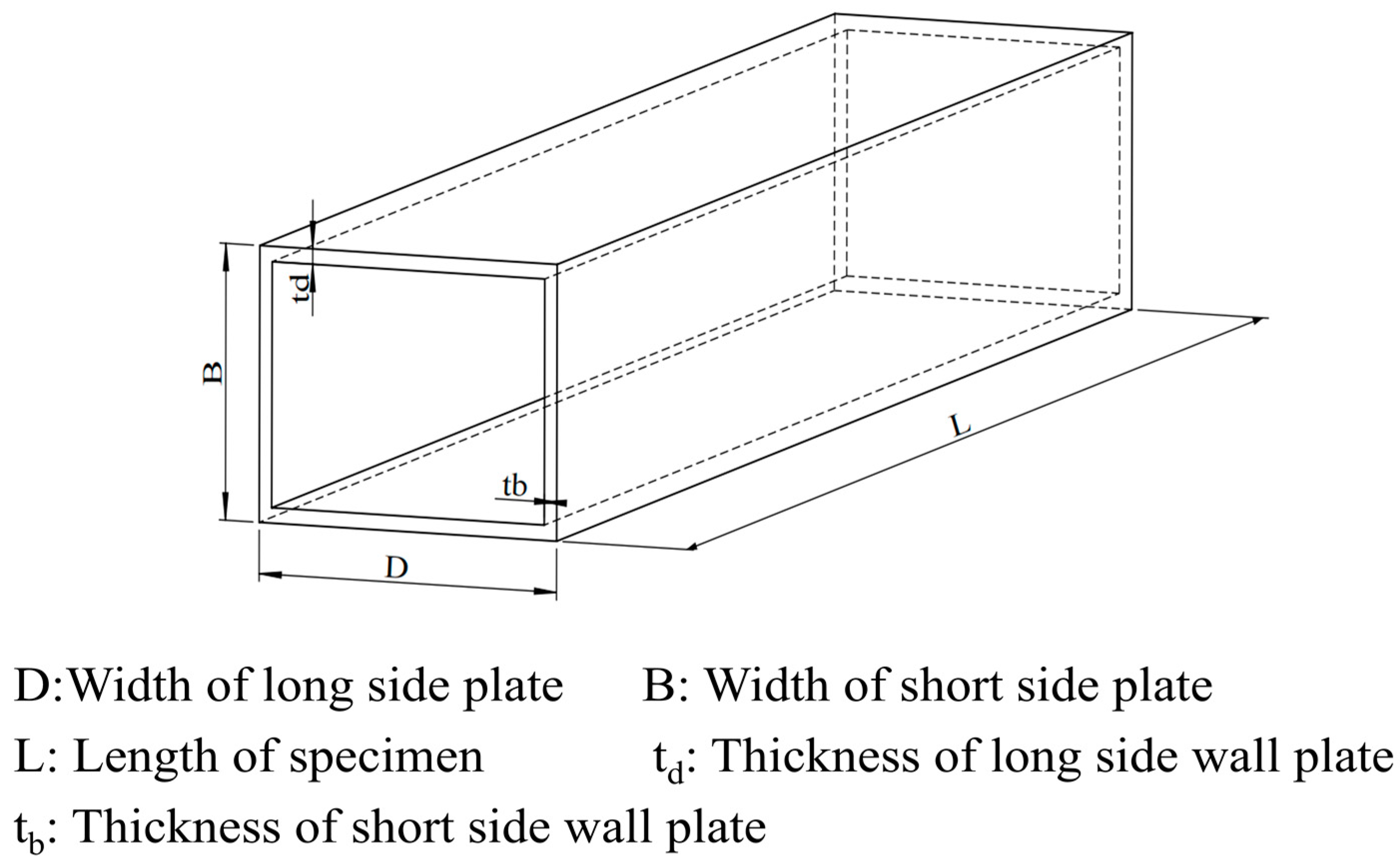
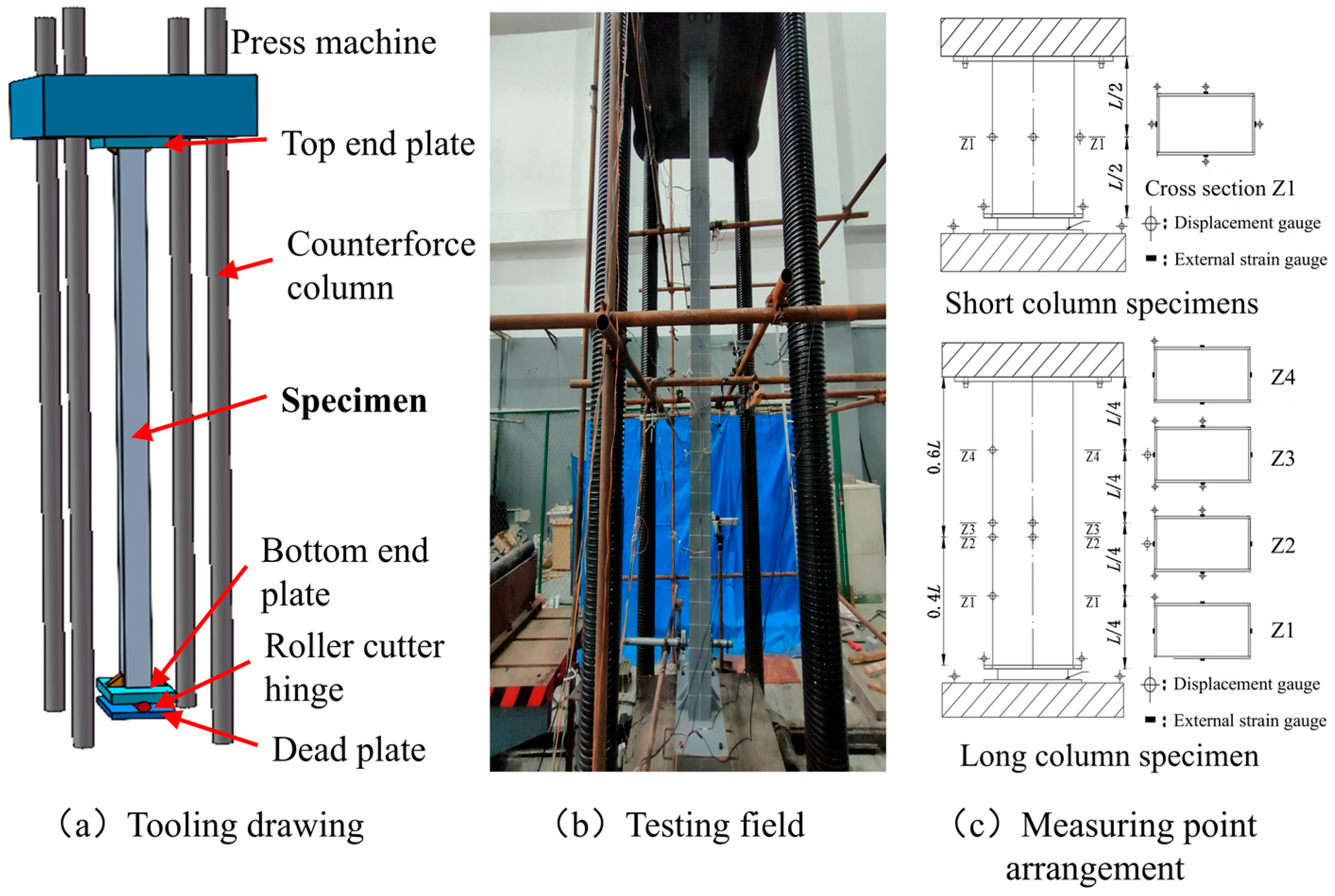
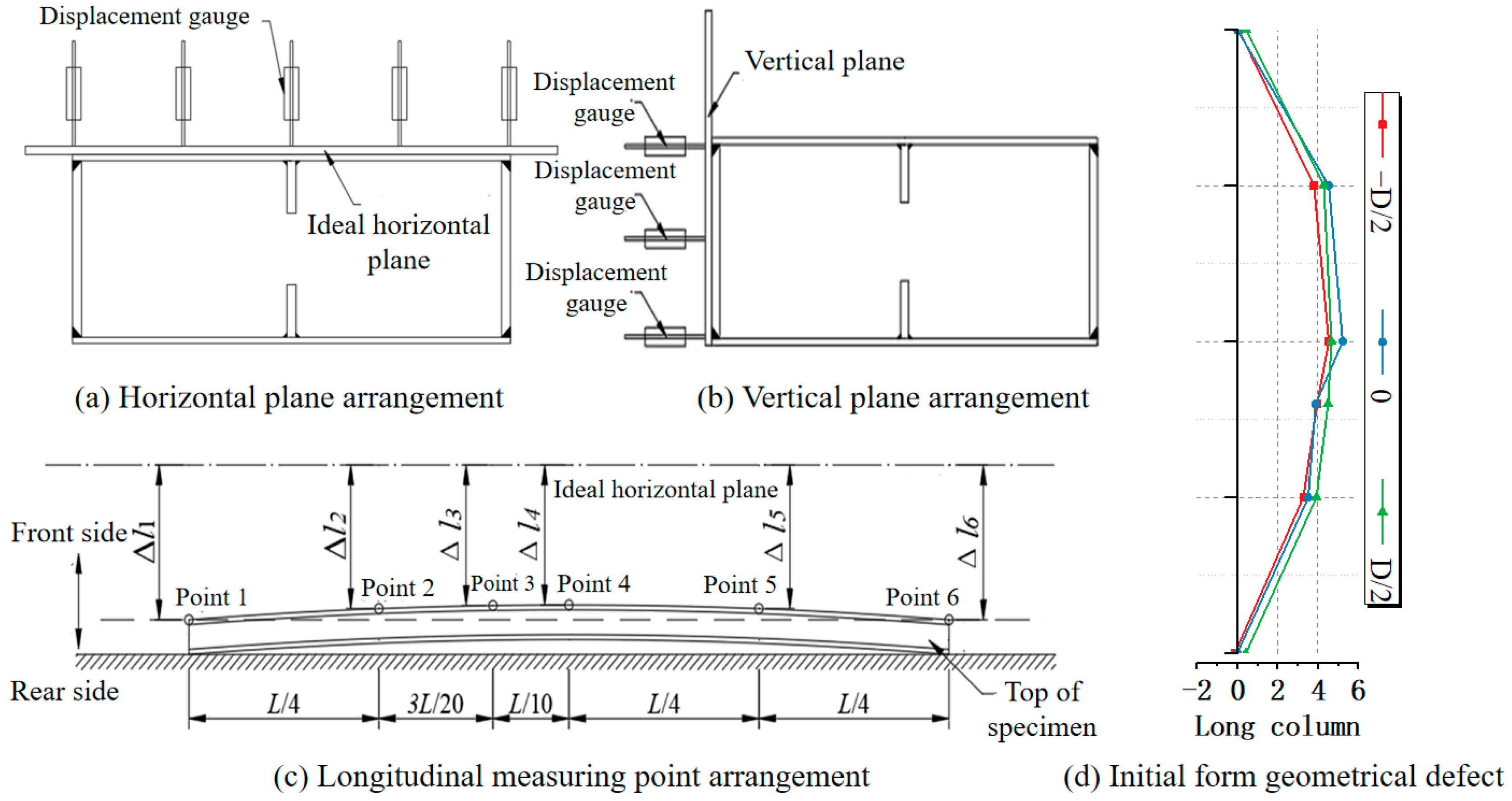
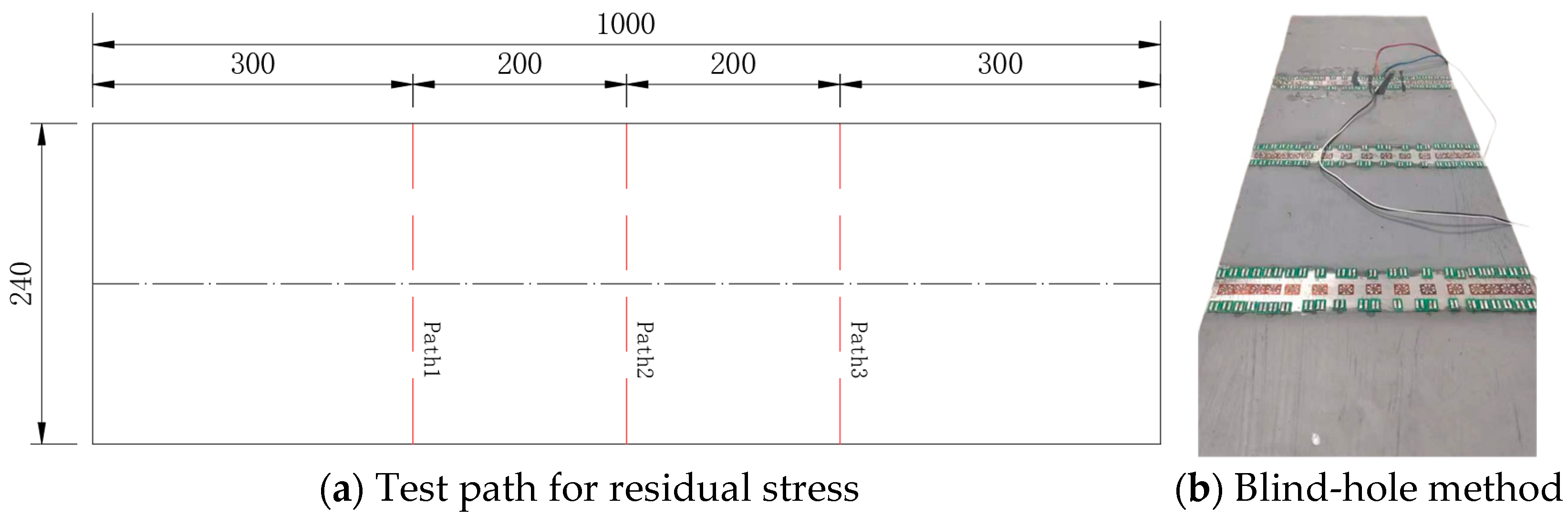






| Specimen | Length (mm) | D (mm) | B (mm) | td (mm) | tb (mm) |
|---|---|---|---|---|---|
| ES-240-240 | 240 | 240 | 160 | 10 | 10 |
| ES-240-4200 | 4200 | 240 | 160 | 10 | 10 |
| Model | Dm (mm) | td (mm) | Bm (mm) | tb (mm) | Rib Height (mm) | Rib Thickness (mm) | L (mm) | Slenderness Ratio |
|---|---|---|---|---|---|---|---|---|
| NS-6 | 240 | 10 | 160 | 10 | / | / | 400 | 6 |
| NS-61 | 240 | 10 | 160 | 10 | / | / | 4200 | 61 |
| NS-117 | 240 | 10 | 160 | 10 | / | / | 8000 | 117 |
| NS-172 | 240 | 10 | 160 | 10 | / | / | 11,800 | 172 |
| S-6 | 240 | 10 | 160 | 10 | 80 | 8 | 1200 | 6 |
| S-61 | 240 | 10 | 160 | 10 | 80 | 8 | 12,000 | 61 |
| S-117 | 240 | 10 | 160 | 10 | 80 | 8 | 23,000 | 117 |
| S-172 | 240 | 10 | 160 | 10 | 80 | 8 | 33,800 | 172 |
| tb (mm) | Bm (mm) | ts (mm) | hs (mm) | td (mm) | Dm (mm) | L × 10 (m) | Number |
|---|---|---|---|---|---|---|---|
| 10 | 160/200 | / | / | 10/12/16/18/20 | 200/250/300/350/400/500/600 | 0.25/0.3//0.4/0.45/0.75/0.9/1.05/1.2 | 396 |
| 12 | 250 | / | / | 10/12/16/18/20 | 250/300/350/400/500/600 | 0.25/0.3//0.4/0.45/0.75/0.9/1.05/1.2 | 225 |
| 16 | 300 | / | / | 10/12/16/18/20 | 300/350/400/500/600 | 0.25/0.3//0.4/0.45/0.75/0.9/1.05/1.2 | 162 |
| 20 | 300/350 | 12/16 | 120/160 | 20/25/30/36/40 | 400/500/600/700/800/900 | 0.25/0.3//0.4/0.45/0.75/0.9/1.05/1.2 | 468 |
| 25 | 400 | 20 | 200 | 20/25/30/36/40 | 400/500/600/700/800/900/1000 | 1/1.5/2/2.5/3/3.75/4.5/6/7.5 | 270 |
| 30 | 450 | 20 | 200 | 20/25/30/36/40 | 400/500/600/700/800/900/1000 | 1/1.5/2/2.5/3/3.75/4.5/6/7.5 | 270 |
| Grand total | 1791 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shangguan, B.; Li, J.; Zhao, Q.; Chen, P.; Ruan, F.; Pei, H. Overall Buckling Behavior and Design of Steel Stiffened Box Section Columns Under Axial Compression. Buildings 2025, 15, 1474. https://doi.org/10.3390/buildings15091474
Shangguan B, Li J, Zhao Q, Chen P, Ruan F, Pei H. Overall Buckling Behavior and Design of Steel Stiffened Box Section Columns Under Axial Compression. Buildings. 2025; 15(9):1474. https://doi.org/10.3390/buildings15091474
Chicago/Turabian StyleShangguan, Bing, Jie Li, Qiu Zhao, Peng Chen, Furong Ruan, and Huiteng Pei. 2025. "Overall Buckling Behavior and Design of Steel Stiffened Box Section Columns Under Axial Compression" Buildings 15, no. 9: 1474. https://doi.org/10.3390/buildings15091474
APA StyleShangguan, B., Li, J., Zhao, Q., Chen, P., Ruan, F., & Pei, H. (2025). Overall Buckling Behavior and Design of Steel Stiffened Box Section Columns Under Axial Compression. Buildings, 15(9), 1474. https://doi.org/10.3390/buildings15091474






