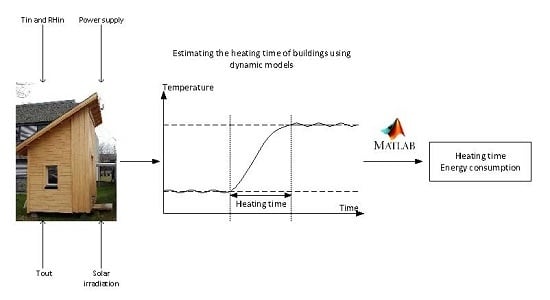
1. Introduction
Buildings account for more than one-third of the primary energy supply in the world, and the global contribution from buildings towards energy consumption has risen to 40%. Rising building service demand and enhanced comfort lifestyles along with the increased time spent in buildings have shown further increasing energy needs for the building sector. This has raised concerns over rapid energy resource depletion and, hence, alternative energy supplies. One main solution to cope with the rising energy demand is the energy efficiency of the buildings.
A Scandinavian country like Norway experiences cold climate conditions during about one-third of the year and, hence, requires high space heating energy demands during cold winter periods. In 2010, Norwegian household energy consumption was 34% of the total energy production, and space heating accounts for two-thirds out of that consumption [
1]. According to the Norwegian Building Code issued in 2010, all buildings must be heated to a thermally comfortable temperature when they are occupied. During the unoccupied periods, the temperature can be lowered to a predefined setpoint above 0
C, because lowering the temperature to sub-zero levels may cause a risk of condensation or frost with respect to the water sources. In that case, increasing the energy efficiency of the existing building stock is directed towards better heating control systems, and opportunely, at present, there is a trend towards better systems.
Building energy management systems (BEMS) are a rapidly expanding new technology that has recently gained attention as a standard way of controlling buildings [
2]. BEMS monitor and control the indoor climatic conditions while maintaining the operational performance along with the safety and comfort of the occupants [
3]. Usually, BEMS utilize classical control techniques, such as on-off control, P control, PI control, PID control and optimum start-stop routines, as the control algorithms. These control algorithms are normally good for single-input single-output systems. The heat dynamics associated with buildings show a multi-variable behavior owing to the thermal interactions amongst different zones and heating, ventilation and air-conditioning (HVAC) systems. Therefore, the buildings that have a multi-variable behavior cannot be perfectly controlled with classical controllers. This will result in high energy consumption and huge wastage owing to the abundant instabilities and frequent overshoot of the setpoints [
3]. Even though improvements to these systems have enhanced the system performance, improper gain selections can make the entire system unstable [
3]. According to these considerations, the use of advanced control techniques, such as predictive, adaptive and optimal controllers, which are integrated with a mathematical building heating model, may afford better control of building heating systems with energy savings and occupant comfort. The building heating model plays a vital role in addressing most of the insufficiencies present in the current control systems and, hence, increases the energy efficiency of buildings. Either dynamic, static or hybrid models can be integrated with BEMS.
In general, non-residential buildings, like schools and offices, have regular occupancy hours and are intermittently occupied. Further, most of the residential buildings can be admitted as intermittently occupied spaces, and also, they can be adjusted to have lower setpoint temperatures during the night. Comfortable temperatures need to be maintained only during the times that the spaces are occupied. The temperature drop during the non-occupied periods and nights along with the temperature recovery period of the heating system determine the possible amount of energy savings of the building. This control strategy is called weekend or night setback. Bloomfield and Fisk have shown that intermittent heating grants seasonal savings of 34% and 12% for lightweight and heavyweight office buildings [
4]. Unfortunately, the maximum amount of energy savings is not achieved from the buildings owing to the unavailability of suitable controllers for intermittent heating [
5]. Further, in most of the cases, for fear of ill-evaluation, lowering the temperature during non-occupancy is minimal, which reduces the energy savings.
As illustrated in
Figure 1, when the occupants are away or asleep, the temperature can be reduced to a value that will not affect the water sources inside the building. Prior to the occupants’ arrival or waking up, the heating systems must be switched on such that the comfortable temperature is approached at the right time. If the temperature is in the comfort range (also called the throttling range, where the room temperature lies between the lower and upper setpoint temperatures) before occupancy, energy is wasted, and conversely, if the temperature reaches the comfort range after occupancy starts, it may be uncomfortable for the occupants. Hence, there is a necessity for the “optimal start time” [
6]. There are many difficulties in determining the optimal start time of HVAC equipment, because the heating time of a building depends on the changing climatic conditions, building structure, HVAC system capacity,
etc. [
6].
It is difficult for the classical controllers in BEMS to ascertain the optimum point of heating restart time because of the strict non-linear characteristics of the HVAC system, changes in climate conditions and changes in heating loads. Hence, for an exact determination, the requirement of advanced control methods with a mathematical building heating model arises. However, this model should be able to predict the heating time within a short period. When applied to BEMS, the model will use looping to find the correct starting time. Therefore, the goal is to have a model such that it can predict the heating time in less than 10 min. Therefore, the model will perform a loop calculation every 10 min to find out when to start heating. It is possible to find literature addressing multiple techniques used to predict the heating restart time.
The artificial neural network (ANN) approach in building control has been used by Yang
et al. to determine the optimal start time of the building heating system [
6]. The programs for predicting the room air temperature and the training of the ANN model based on back propagation learning have been developed. The input and output architecture of the ANN has been constructed with the factors that affect the optimal start time of the system, and the optimized model has been shown to be capable of determining the accurate start time. Yang and Kim have developed an ANN model based on back propagation to predict the time for room air temperature descending for various buildings [
7]. Miller and Seem compare two techniques for estimating the start-up time required by a controller for returning building zones to the desired occupied room temperature after night or weekend setback [
8]. An ANN for calculating the start-up time was developed and compared to a state-of-the-art algorithm (recursive least squares) for heating [
8]. They have identified two advantageous of ANN over least squares methods. ANN requires less expertise, knowledge and experimentation, and the over-parameterization of ANN does not cause a significant degradation in performance [
8].
Different methods used for restart time optimization are discussed in [
9]. They explain classical methods, fuzzy logic-based methods and methods based on using a building heating model. These different approaches are compared by using an intermittent heating controller developed as a part of the TRNSYS software. The comparison is based on the restart precision, comfort conditions, the beginning of the occupancy and the energy consumption. A fuzzy logic method and a building model with two time constants were found to be sufficiently accurate and simple. They use inside and outside temperatures as inputs for the evaluations.
Seem
et al. [
10] present and compare seven different equations based on least squares techniques (including linear, quadratic, logarithmic and first order systems) for computing the return time from night or weekend setback. They discuss how to use these equations in the adaptive control strategy. The relationship between the return time, outdoor temperature and the indoor temperature is also discussed. However, the energy consumption and comfort levels are missing in the algorithms. Birtles and John [
11] derived an empirical curve of preheat time against preheat temperature difference. The curve is a logarithmic schedule, and it was proposed that it might be more appropriate than linear schedules for predicting the heating time. They use only the inside temperature of the building in determining the preheat time.
According to the available literature, most of the heating re-start time estimations are carried out using empirical methods either from ANN, Fuzzy Logic or regression models considering indoor and outdoor temperatures as the inputs. In this study, we strive towards more comprehensive heating time estimations based on a dynamic model that takes the indoor temperature, outdoor temperature, indoor humidity, solar irradiation, heat supply and the thermal mass of the building envelope into consideration. Both empirical and physical models have their advantages and drawbacks. Empirical models are more specific for different types of buildings and require more data for calibration and training. A physical model represents a general building and can be adapted to various types of buildings more efficiently. It is also easier to get information about the quality of windows and insulation out of a physical model. However, both models require data that cover the range for the weather conditions in the area.
In addition to the heating time, energy use of the building is estimated. Prediction of energy consumption becomes an important aspect when the energy tariffs are of interest. Different types of mathematical models have been used to estimate the space heating or space cooling energy consumption of buildings. In the literature, many statistical approaches can be found to be used for energy predictions, such as regression [
12,
13,
14], neural networks [
15] and support vector machines [
16]. A combined physical- and statistical-based technique has been used by [
17] for forecasting building energy use.
In Norway, it is planned to introduce advanced metering and management systems (AMS) by 1 January 2019 at each electricity customer point. AMS are more advanced in sending and receiving information as a two-way communication system. After launching this system, the energy consumption cost will be dependent on the time of usage. According to the preliminary information, there may be an option to divide the day into several sections and to assign a specific power price for each section per kWh; for example, a less expensive power price during the late night and the mid-day than morning and evening. The opportunities for reducing the energy use based on the new practice must be discussed in order to have lower energy tariffs. A study has been carried out to estimate the energy cost for two cases, including: (i) the heating system is switched on at the exact restart time to reach the higher setpoint on occupant arrival/wake up; and (ii) the heating system is switched on before the right time (during the low power price period) to reach the comfortable temperature before occupant arrival/wake up. The best way to cut-off the energy cost associated with heating while on AMS will be explained based on the results.
Owing to the lack of physical models for estimating particularly the heating time of buildings and also the energy use, this study could be of interest to many readers.
2. System Description
The building used for the experiments of heating time estimation is an experimental construction located at the University College of Southeast Norway in Porsgrunn, Norway, and was built in 2014. The test building has an approximate volume of 9.4 m
. An image of the test building is shown in
Figure 2, and the floor plan is presented in
Figure 3. The building is sealed, and no ventilation is provided other than possible infiltration.
The building envelope is constructed using layers of diverse materials, including wooden cladding, glass wool insulation, air fill, polyethylene vapor barriers, wood, cement chipboard, particle board and cardboard. There are three different types of walls in the test building: (i) Massive; (ii) Standard and; (iii) Bærekraftig (the Norwegian names are used for the walls); each having unique construction by compounding different materials. This implies different heat transfer characteristics through each component of the building envelope. The test building is constructed on support structures made out of concrete, and therefore, the floor of the building is not in contact with the ground. The outer surface of the roof is an asphalt coating, and the inside surface is wood. The experimental construction has three windows of each 60 × 90 cm in the south, east and west directions. The door is at the north side of the building and has dimensions of 90 × 120 cm . An electrical heater with a capacity of 375 W is used inside the building for heating with a thermostat controller. Furthermore, a computer is used inside the building for data logging, which contributes to using approximately 95–100 W.
The data required for model simulation and validation are collected from two different sensor setups. The weather station (art. 02049) [
19] consists of an indoor unit and an outdoor unit which measures the inside temperature, inside humidity and climate conditions at the building location. The measurements from the weather station are collected with 30-min sampling intervals. The energy supply to the building is measured by a power sensor connected to a data acquisition (DAQ) device and has a logging interval of 10 s. It is important to have a small sampling interval for capturing real heater dynamics associated with the on-off controller. At first, the building was allowed to cool down until it reached a steady low temperature. Then, the heater is switched on with the setpoint temperature specification until the inside temperature reaches contingently steady-state conditions.
3. The Model Development
To determine the heating restart time of a building, the knowledge of building heating time is important. A model that can predict the heating time from a low setpoint temperature to a high set point temperature is developed, and the heating time is computed based on that. The model is inherited from [
20], which is developed for typical Norwegian buildings associated with heat recovery ventilation. However, since the test building is not ventilated, the mass transfer terms are removed from the model to be suitable for the current application. Further, the model in [
20] is simplified in terms of representing the thermal mass of the building envelope by lumping the thermal properties of each layer to obtain uniform characteristics for each element. The new model for the building lab consists of ordinary differential equations describing the energy balances for inside air (Equation (
1)), energy balance for three different walls (Equations (
2)–(
4)), floor (Equation (
5)) and roof (Equation (
6)). The two last algebraic equations define the net heat flow (Equation (
7)) and heat loss through the components of the building envelope (Equation (
8)). The total energy use of the building can be estimated using Equation (
9). The nomenclature of the symbols is presented in
Table 1. The model has six state variables, and it takes most of the important heat transfer processes into account while providing a simple building heating model.
The heating restart time is affected by the weather conditions, such as outdoor temperature, solar irradiation, wind and humidity. However, the main variable affecting the preheat time is the power capacity of the heating system. Since one window of the test building is located on the south wall, solar irradiation directly affects the indoor temperature when it is sunny. Windows to the east and west do not create considerable solar irradiation disturbances, as they are usually covered by the shadows of other constructions adjacent to the test facility. Further, the walls and roof get heated by the Sun during the daytime in sunny weather. High wind speeds create increased heat losses from the wall surfaces due to forced convection conditions. Hence, the wind also plays a significant role in the heat dynamics of the building. The developed model only takes the outdoor temperature and the average sun irradiation for calculating the heating restart time. The experiments were conducted during the summer and autumn times. An average solar irradiation during the relevant time of the year was used during the experiments. Only the south-facing window is counted as receiving solar irradiation. However, the effect of wind speed is not addressed in the suggested approach.
Parameter identification for mechanistic models from test data has revealed that calibrating the parameters presented in the model to normal operating data may lead to grossly inaccurate estimates, which is the main limitation in physical modeling. The model parameters should be tuned to have a good match between the simulated results and measurements. The calibration of the model was performed by varying the most uncertain parameters, such as overall heat transfer coefficients and thermal diffusivities, as presented in
Table 2. Thermal parameters, such as overall heat transfer coefficients, may change their values depending on the weather conditions, and as a result, the dynamics of the system get affected. To cope with the changes, U
will get a variable value. The given thermal diffusivity values are estimated according to the thermal properties of composite walls.
The building heating time and energy usage prediction algorithm is given by
Figure 4. The model is implemented in MATLAB, and the ode23s solver is used for the simulations. The setpoint temperature of each simulation is regulated by adjusting the heater. The heater is modeled with an on-off controller having an operating bandwidth of ±0.5
C. To calculate the heating time, the algorithm evaluates the time required to achieve the setpoint temperature. Next, the total electric energy consumption to achieve the prescribed heating is determined.
4. Results
Table 3 summarizes the time duration and the conditions of four case studies used for predicting the heating time. The power consumption pattern of each case study is also presented in
Figure 5. The experiment conducted during the summer time has a quite high temperature setpoint compared to the autumn experiments. A high setpoint is used to obtain a good heating curve considering the outside temperature.
The predicted and measured inside temperature variation for Case 1 is presented in
Figure 6 with the outside temperature variation. According to the simulations, the predicted heating time is 20.3 h, while the measured heating time is 20.9 h. The simulation has overestimated the inside temperature of the building during the first 20 h. However, it closely follows the measured temperature profile. The function of the on-off controller is also clearly observed after reaching the setpoint. The power sensor in the test building measures the total electrical power consumption, which is the power consumed by the heater and the data logging computer. Most of the power supplied to the computer is converted to thermal energy, and that will also be used for heating the building. The predicted energy consumption for the simulated period calculates the total energy consumption, which is equal to 9.5 kWh. The estimated real energy consumption by the building for the same period is 9.6 kWh.
For the second case study, the simulated heating time is 19 h. According to
Figure 7, the measured heating time is approximately 18.8 h. From 5–15 h, the simulation has underestimated the inside temperature. This could be owed to the lower outside temperatures. However, the measured temperature may be affected by a large quantity of solar irradiation around 8:00 a.m. in the morning of 29 September after 14 h of simulation. For this case, the predicted energy consumption is around 9 kWh, while the measured energy consumption is 7.9 kWh.
In Case 3, the model predicts a heating time of 19 h, and the real heating time is 18.7 h, as presented in
Figure 8. Furthermore, in this case, inside temperatures are underestimated during the first 18 h. However, after reaching the setpoint, the two curves are overlapped. Total simulated energy consumption for Case 3 is 9 kWh, and total measured energy consumption is 7.8 kWh.
The simulated heating time of the building for Case 4 is 23 h, while the measured heating time is approximately 23.5 h (
Figure 9). In this simulation, we have used an average solar irradiation of 20 W/m
based on the few collected solar irradiation measurements during the period. The first day of the experiment was cloudy, and the second day was rainy, which causes very little solar irradiation to penetrate into the building. The predicted and measured energy consumptions are 10.9 and 9.4 kWh, respectively. In order to analyze the effect of solar irradiation on the model, the same simulation has been carried out with a solar irradiation of 150 W/m
instead of 20 W/m
, and the results are presented in the same figure. During heating, the inside temperature shows a slight increase, which causes the heating time to decrease up to 22.5 h. The predicted power consumption has also reduced by 0.2 kWh.
The prediction errors of the heating time for simulated case studies are presented in
Figure 10. According to the observations, the percentage of prediction error [prediction error % = (measured heating time − simulated heating time)/measured heating time] lies between 0% and 3%, which confirms that the model is able to estimate the heating time of single-zone buildings to an acceptable level. The highest prediction error is observed in Case 1, while the lowest error is observed for Case 2. Case 2 and Case 3 are overestimated, while the rest is underestimated.
The energy use for all cases with predicted and measured values is illustrated in
Figure 11. For the first case, the energy consumption estimation is quite accurate, and the highest error is observed in the last case.
Energy Cost
As explained in the Introduction, the usage of energy for space heating can play an important role in determining the energy cost after the launch of the AMS in Norway in 2019. Assume that the energy rates given in
Table 4 will be established by the energy service provider in the future. All rates are given in Norwegian krone per consumption of 1 kWh.
Based on the given rates, the cost of space heating will be estimated using the same model for the mentioned test building. Assume the building must be heated from 15
C–18
C by 8:00 in the morning with a constant outside temperature of 7
C and an inside relative humidity of 45%. Two scenarios for estimating the energy cost are illustrated in
Figure 12. With these conditions, the model predicts a heating time of 4.8 h with an energy use of 2.25 kWh, while 52% of it is used during the high price period. The building heating system must be switched on at least at 03:12 to reach the goal by 8:00 a.m. If the heating process has been carried out before 5:30, during the low price period, it has to be started at 00:42. In addition, the temperature should be maintained at 18
C for 2.5 h from 05:30–8:00, which costs an extra 0.78 kWh. For a fair comparison of both scenarios, the energy use of Scenario 1 is added with 0.54 kWh for maintaining the temperature at 15
C from 00:42–03:12. The cost estimations for both experiments are tabulated in
Table 5.
According to the estimations, the total costs for the first and second scenarios are 2.23 Nok and 2.25 Nok, respectively. For maintaining the temperature at the high setpoint, a considerable amount of energy has been used during the high price period that makes the concept of low-cost heating a faulty strategy.
5. Discussion
The computation of the temperature recovery duration was studied using a dynamic model for a simple single-zone pilot-scale experimental building. The primary heat transfer processes addressed in the model are the thermal mass of the building envelope, the effect of outdoor temperature, indoor temperature increase, indoor humidity and solar irradiation. The obtained results are sufficiently accurate and of great simplicity, and they show very close values to the measured figures. There are small deviations, which could be owed to the following reasons:
Even though the building is not officially ventilated, it may receive a small amount of air flow due to the opening of the building door, causing some amount of heat loss. Estimation of this heat loss becomes a tough task, because of the factors that influence it, such as the wind and how frequently the door is opened. Infiltration through the porous structures is beyond a certain lower limit for the mentioned test building, as it is constructed as a passive house.
The model is affected by the Sun on sunny days and wind on windy days [
21]. A constant solar radiation is included in the model depending on the sunrise and sunset times for each day. According to the simulation performed for Case 4, it was observed that increased solar irradiation has reduced the heating time by 1.8 h, while reducing the energy consumption. Solar irradiation has a prominent impact on the heating time of a building, as it supports raising the inside temperature without any power usage. Hence, for better results, the utilization of real solar irradiation measurements will be more powerful. The wind increases the heat transfer coefficient and, hence, the heat losses. However, the effect of wind is not addressed in the model.
The accuracy of the measured input variables, such as outside temperature, can cause deviations.
The calibrated model parameters may not be the optimum values.
The method claims the measurement of both inside and outside temperatures and only inside humidity for a non-ventilated building, for correctly evaluating the heating time. The sensitivity of the model to the outside temperature variations is very clear. Higher external temperatures will decrease the heating time and vice versa. However, a change in inside relative humidity does not cause substantial changes to the heating time.
As mentioned in the Introduction, the model should be able to estimate the heating time of a building within a short period, in order to apply it in BEMS for on-line control. According to the simulations, the time predictions can be obtained within 10 min for a 24-h simulation, which confirms that the model is fast enough for control applications.
The energy consumption of the building is estimated with a maximum deviation of 1.5 kWh for Case 4. Power consumption records of the building are measured with a 10-s sampling interval. During these 10 s, the heater can shift in between on-off conditions without the power sensor capturing that, which can also cause deviations in measured and predicted energy use. Further, a low pass filter has been used in the power measurement system, which causes a lag in power measurements.
A cost comparison of the building for two different heating scenarios has shown that heating the building during the low power price period does not give low energy cost. The result might be different with variable weather conditions and needs further assessments using real data.
For real residential buildings, the model for evaluating the heating time may have supplementary equations depending on the ventilation and the availability of furniture inside the building. Providing a ventilation air flow into the building lengthens the heating time due to the increased heat loss. This phenomenon is described by adding a mass balance equation to the model mentioned above and by adjusting the energy balance equation to represent ventilation heat loss as presented by Equation (
10) and Equation (
11). The same variable explanations given in
Table 2 apply.
and
represent inlet and outlet air flow rates, while
and
are the associated specific enthalpies.
The modeling of household furniture, including internal walls, is important when modeling the buildings. They act as either a heat sink or heat source depending on the temperature difference between themselves and surrounding air. The availability of furniture prolongs the heating and cooling times of buildings. To simplify the modeling approach of furniture, it is speculated as a spherical object with equal mass and equivalent average thermal diffusivity. The heat equation in spherical coordinates is discretized to develop a model for furniture as given by the Equation (
12).
is the temperature of furniture, and
r represents the radius of the sphere formed by furniture. Equation (
7) and Equation (
8) should be modified accordingly to represent the heat absorption or heat release by furniture.
For intermittently-occupied buildings, classical control options are not well suited, because they are not reflecting the thermal state of the building for determining energy requirements. When the controller does not perform well, it can influence the energy use and comfort. Hence, in real-world applications, the nature of the HVAC equipment, building properties, weather conditions and human factors should also be given special attention. Advanced control strategies, such as optimal control, adaptive control and predictive control techniques, combined with a dynamic building heating model, as presented above, may have the capability of addressing the constraints present in the classical control of intermittent buildings.