A Numerical Study on the Effect of Position and Number of Openings on the Performance of Composite Steel Shear Walls

Abstract

Use of composite steel shear walls (CSSW) in earthquake-resistant structures has grown in recent years. However, no thorough information exists on their performance, especially in cases where openings are present. In the present study, in order to first validate the analysis method, ABAQUS was used to model the studied composite shear wall with gap at UC-Berkeley, according to the results of which, a good agreement between the experimental and analytical models was observed. Then, the effect of the position and number of the openings on the performance of the walls was addressed. To this end, models with various openings, including openings close to the beam/column, horizontal/vertical openings and distributing opening, were prepared and analyzed. The results indicate that the maximum reduction in stiffness and strength occurred in walls with single openings. The size of opening and the opening’s area significantly affect shear wall performance. Ultimately, artificial neural network and fitness function tools were employed to obtain predictive models for shear wall performance. A neural network has proven an appropriate alternative method for predicting the displacement, stress, and strength of the composite shear wall.

1. Introduction

Reinforced concrete shear walls are amongst the most efficient seismic resistant systems in structures, which have also been manufactured using metallic materials in recent years. Steel plates resist earthquake loads initially through out-of-plane deformations and ultimately through diagonal buckling. Various methods have been proposed to reinforce steel shear walls, including the use of stiffeners, particularly in circumstances where architectural and installation concerns necessitate the use of openings in the walls. Nowadays, the use of composite shear walls is considered an alternative solution and different studies confirm their acceptable behavior [1,2]. The presence of the adjacent concrete plate alters the buckling mode of the steel plate, hence increasing its strength. Therefore, many researchers investigated the behavior of a concrete steel shear [1,2].

During 1998 to 2001, one of the major studies at UC-Berkeley was conducted by Astaneh et al. on the composite shear walls. The main objective of the study was to test the cyclic behavior of the two types of composite shear walls, namely walls with and without gap. The results indicated that the strength of the wall with no gap was slightly higher than the one with gap, and, additionally, the concrete panel of the composite wall with no gap was more prone to failure [1].

In an experimental study, Rahai and Hatami numerically investigated the effect of a wall stud spacing on the performance of the composite shear wall. According to the results, changes in wall stud spacing slightly affected the in-plane lateral displacement of the composite shear wall, but effectively controlled the out-of-plane displacement [3]. In 2012, Arabzadeh and Ahmadi conducted a study to evaluate the effects of the bolt’s distance on the performance of a composite steel shear wall. To this end, 14 single-story specimens of single span with various bolt spacings were modeled and analyzed in ABAQUS. As reported in the results, increases in the distance between bolts also improved the seismic performance of the system. However, the increase in bolt spacing should be limited, since an increased buckling chance of the steel plates in the subpanels between bolts does not lead to any improvements in the behavior of the shear walls [4].

Some researchers studied the influence of shape and size of the opening on the steel shear wall: Sabouri et al. numerically investigated the behavior of both reinforced and normal steel shear walls with rectangular openings in 2012. The specimens were selected with different dimensions as well as different opening positions. According to the results, the absorption level of the system in both reinforced and normal specimens linearly decreased as the aspect ratio of the opening increased. The decrease rate of absorbed energy in the reinforced specimen was lower than that of the normal specimen, and the opening with the least interference with the operation of the tension field was an ideal opening [5]. Hosseinzadeh and Tehranizadeh conducted a study on the steel shear wall specimens with and without openings in 2012. In this research, various single- and multi-story steel shear walls with different aspect ratios and opening attributes were studied and it was revealed that the ductility of steel shear walls always decreased with the introduction of reinforced openings, and type dimensions and the position of reinforced openings themselves did not affect the strength of the system [6]. In 2014, Mosoarca compared the failure behavior of concrete shear walls with regular and irregular openings. The results revealed that for a similar configuration of reinforcing bars, walls with irregular openings, compared to walls with regular openings, are more stiff, and under compression exhibit more bearing strength capacity [7]. Bhowmick et al. analytically studied the effect of circular openings on the behavior of single-story steel shear wall. In their work, a relation was proposed for calculating the shear strength of the steel plate with opening, which provides an appropriate prediction of the reduced shear strength of the steel shear wall with various opening patterns, their different diameters, and the aspect ratio of the steel plate [8]. Bahrebar et al. (2016) conducted an analytical study on the perforated, trapezoidally-corrugated steel shear walls, where the cyclic behavior and energy absorption ability of these type of walls were investigated. According to the results, parameters such as thickness and corrugation angle of the plate and the opening dimensions highly affect the hysteretic performance of these walls. Increasing opening dimensions leads to decreased energy absorption, and increasing the plate thickness improves the performance of the wall and increases energy absorption [9].

Neural networks have been previously applied to obtain predictive models for the mechanical properties of structure by some researchers such as:

Naseri (2017) conducted a study on the SVM-based prediction method to obtain an experimental result. In this paper, the impact of nano-CuO on the properties of polypropylene fibers reinforced self-compacting mortar was studied [10]. Ghanei et al. used ANFIS and PEGASOS to predict concrete properties like compressive strength and durability. The result shows that neural network and SVM can predict the laboratory result in the best way [11]. Johari et al. used the genetic algorithm to estimate the maximum lateral displacement of retaining wall. In this study, some parameters such as density, Young′s modulus, and friction angle of granular soil were used as input parameters and lateral displacement was used as lateral displacement. Authors who used finite element models were employed as database analysts to develop the neural network models. The result of this study shows that density has a strong influence on the lateral displacement [12]. Tohidi et al. investigated the buckling capacity of corroded web opening steel beams and used neural networks to estimate the ultimate capacities of steel I-beams. The influence of the different size of web opening on the buckling capacity was studied and the result shows that a neural network can predict the ultimate LTB moment in the web steel beam [13]. Koç et al. used the finite element method (FEM) and artificial neural network to reduce the cost of some experimental project. The authors of this research believed that using neural network and combining it with FEM can solve many complicated engineering problems. In this research, the nonlinear antiaircraft barrel’s behavior was obtained using a trained artificial neural network (ANN) and also FEM to show that the combination of these two methods can predict the structure’s behavior correctly [14]. Lai et al. used a neural network to estimate soil deformation in tunneling and they believed that the combination of the neural network with other research methods like FEM could solve many engineering problems [15].

According to the previous researchers, the size of opening has been studied in the steel shear wall; however, few pieces of research have been conducted to find out the effect of an opening that is necessary for the composite steel shear wall.In this paper, firstly, the validation of the analysis method is addressed and then the effect of the position and the number of the openings on the performance of composite shear walls is investigated. Another important innovation of this study is the use of neural network and fitness function tool in MATLAB [16] to predict shear wall performance. For this aim, after compiling the FEM model, neural network was used to predict the FEM result and the influence of the opening size and opening location on the shear wall performance was obtained. Ultimately, fit toolbox function was used to evaluate the ANN models.

2. Validation

Experimental Study and Modeling with ABAQUS

A laboratory test from UC-Berkeley was chosen to validate the software steel shear wall model [17,18]. This is a three-story model that has one span composite shear wall. Load-displacement diagram obtained from static nonlinear analysis was used to verify the models. Here, firstly, the experimental laboratory test was introduced and the result of ABAQUS was compared with the experimental result. The frame consists of three beams and two columns. A steel plate with one reinforced concrete wall was tied to one side of the steel plate. The steel plate shear wall is merged to the frame. Figure 1 shows one story of this frame and

Table 1. Properties of cross sections refer to the AISC Manuals (AISC).

Plate Thickness	Thickness	Rebar Diameter	Rebar Spacing	Reinforcement Ratio	Beam Section	Column Section
4.8 mm	76 mm	10 mm	102 mm	0.92%	W12*26	W12*120

shows the feature of composite steel sheer wall. In the experimental test, the authors discuss two types of steel shear wall (“traditional” and “innovative”) system. In the traditional system, the concrete wall is in contact with steel frame, while there is a gap in the innovation model (Astana [17]). This study was chosen for validation because it is one of the most famous steel composite shear wall studies [17,18]. Table 1 shows the approach used to model the frame and steel plate. Owing to this, all the dimensions were converted to centimeter and then introduced to ABAQUS software [19] in the menu.

According to the experimental result, the employed steel in the steel plates was of type ASTM A36 and ASTM A572 Grade 50, used for the beams and columns. Precast concrete was used for the walls, which was connected to the steel plate using ASTM A325 structural bolts or studs of 12.7 mm diameter. The characteristic of steel was entered into ABAQUS and stress-strain curve was used to show steel plastic behavior. Concrete damage plasticity was used to model a concrete plate. Here, a stress-strain curve for compressive and tensile behavior of concrete was calculated [19,20,21,22,23]. This model was also able to define the failure behavior of the concrete in the software.

The Young’s modulus and Poisson’s ratio for steel materials and concrete, with respect to its characteristic strength, were considered 206 GPa and 0.3 and 20.4 GPa and 0.2, respectively. The characteristic compressive strength of the employed concrete was 280 kg/cm² and tensile strength was 26 kg/cm². For all the studied specimens in the present research, steel plate, concrete panel, beams, and columns were modeled using an element type of Shell Homogeneous (S4R) and the structural stud was modeled using the wire element (Beam type).

Test Set-Up in Experimental Test

In the following, load and type of analyses are introduced into ABAQUS software. According to the laboratory test, the main components of the test set-up in the experimental study are actuator, top loading beam, bottom reaction beam, and R/C reaction blocks. After the design of this set-up, lateral displacement was applied to the steel shear wall. The lateral load was entered to the top beam and this test set-up has a certain place for boundary conditions. Figure 2 shows the location of load and boundary condition for ABAQUS models. Lateral and fixed supports were used to connect beam to column. The aforementioned specimen was modeled using ABAQUS [19]. This type of analyses should be introduced to ABAQUS software in this step. Therefore, static no linear analyses were chosen to obtain a force-displacement curve. To solve this problem, the maximum number of increment was chosen automatically using ABAQUS software. A load similar to the experimental study was applied to the specimen. The applied load to the specimen was defined by displacement control. The value of displacement is 0.06 × height according to the experimental test, that is, this displacement was entered into all the models for 50 cycles. Fixed supports were used in the column bases and the column webs and intermediate beam were constrained in an out-of-plane direction. Additionally, loads were applied to the upper end of the columns, as shown in Figure 2, this figure also shows steel shear wall after testing.

After analyzing the FEM model, the load-displacement envelope diagrams were obtained from the finite element software and the experimental results are shown and compared in Figure 3.

Figure 4 shows the stress and displacement for verification models. The result shows that the maximum stress occurred in the upper element where the maximum lateral displacement was entered, while the maximum stress occurred in the bottom element near to the base. Also, some elements reached the maximum stress near to the ultimate stress (572 MPa) and it is expected that this value remains of substance during the future models addressed in this paper. However, the number of elements that reaches the ultimate strength is different among diverse models.

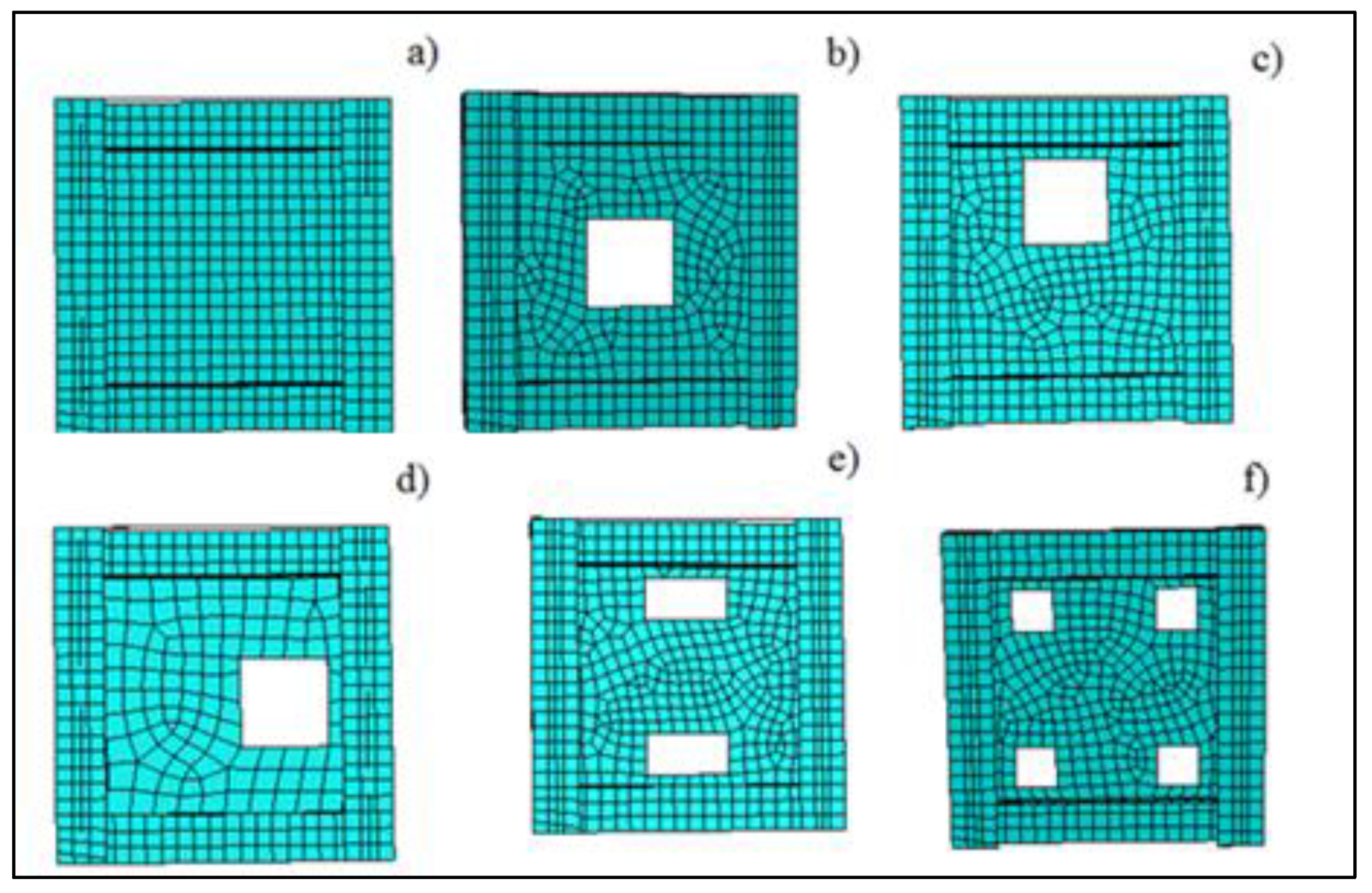
3. Introducing Models and Research Methodology

In the present research, in order to study the effect of openings, a single-story single-span composite shear wall with gap and dimensions, materials, and cross-sections similar to the experimental specimen mentioned in the validation section was considered. In the first stage, in order to investigate the effect of the opening position on the behavior of the composite shear wall, initially, a specimen was modeled, within the center of which an opening was created occupying 10% of the steel plate area; then, to investigate the effect of opening position, two other specimens were modeled, within which the opening position was moved near to the column and beam. Ultimately, two and four openings were created on the steel plate while the whole is 10% of the steel plate area in order to obtain the effect of opening number on the shear wall performance. Figure 5 shows all the models created in this part.

In group b, a specimen was modeled, within the center of which an opening was created, overall occupying 36% of the steel plate area; then, to investigate the effect of the number of openings on the behavior of the composite shear wall, another specimen was created with two horizontal openings, again occupying 36% of the wall area in total. This recent case was repeated with another specimen with two vertical openings of similar overall area as the previous case. Figure 6 shows all the models created in this part.

Ultimately, four and eight openings were created on the steel plate while the whole is 36% of the steel plate area. This action has been done to obtain the effect of the opening number on the shear wall performance.

4. Results

4.1. The Effect of Opening Position and Number of Opening for Model g–k (Group A)

Here, the effect of opening position on the behavior of composite shear wall is investigated. To this end, an opening of 10% area (the ratio of the opening area to the area of the steel plate is 0.1) was considered and its effect on the composite shear wall was investigated in scenarios where the opening is once positioned at 200 mm from the beam and column. The results were then compared with the central opening and without opening, and the load-displacement diagram for all the 6 specimens is as shown in Figure 7.

Figure 7 shows as the initial results, that the presence of opening results in decreased strength and stiffness of the wall as compared to specimen with no openings. The difference in the strength and stiffness of the specimens with a central opening and without an opening was 38% and 39%, respectively. The strength and stiffness of the wall for both cases where openings were positioned near the beam and column were lower than specimens with a central opening. In comparison between the specimen with opening near the beam (model c) and the specimen with a central opening (model b), strength reduction was extremely insignificant and the stiffness reduction was 5%. For the specimen with an opening near the column (model d), strength was reduced by 2.22% as compared to the specimen with a central opening, but no changes were sensed in the stiffness. The stiffness was increased by 7% for four and two openings (models f or e) as compared to the specimen with central opening. For a more accurate study of the effect of the openings, the effects of the tensile field, stresses, and out-of-plane displacements caused in the specimens are addressed in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15.

The followings are inferred from Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10:

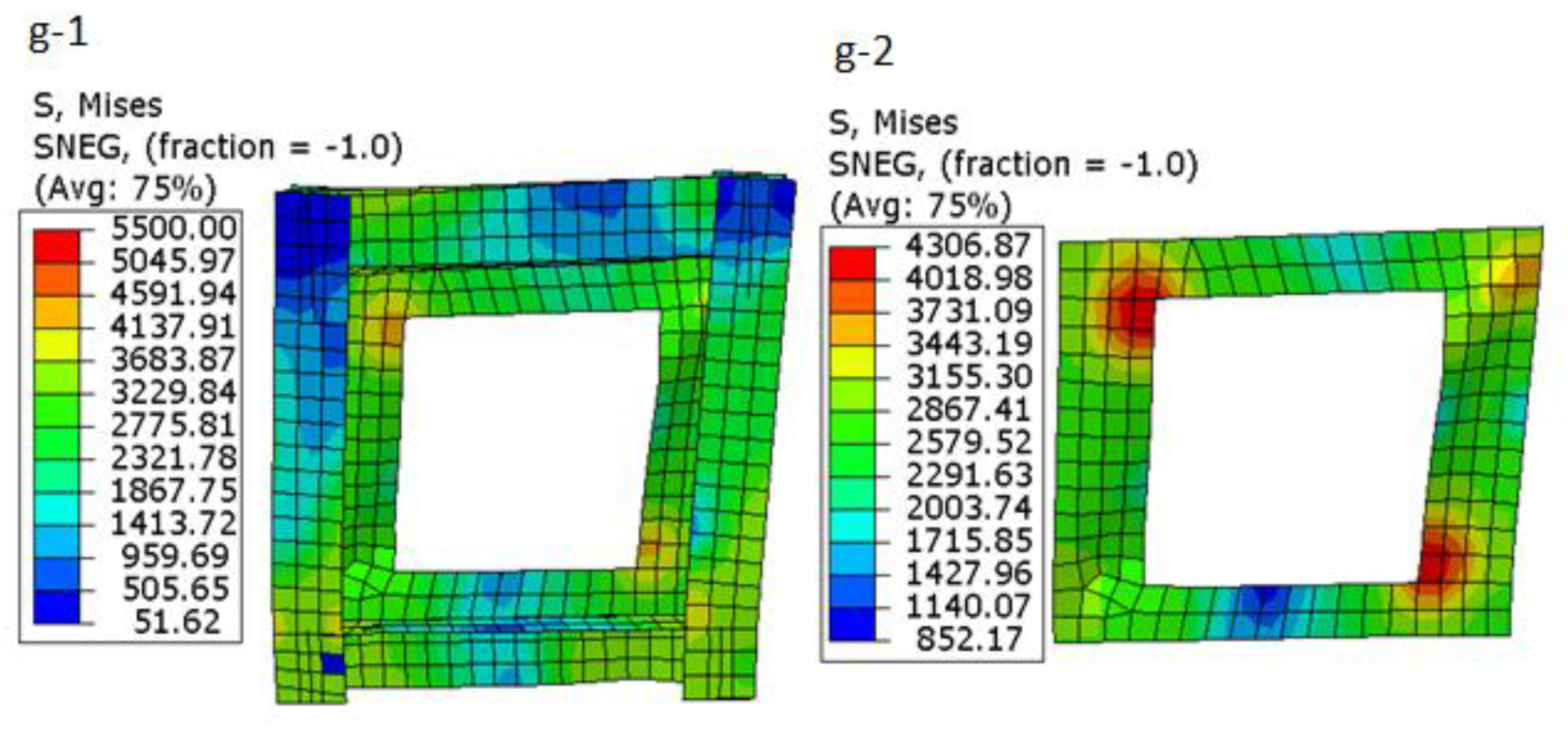
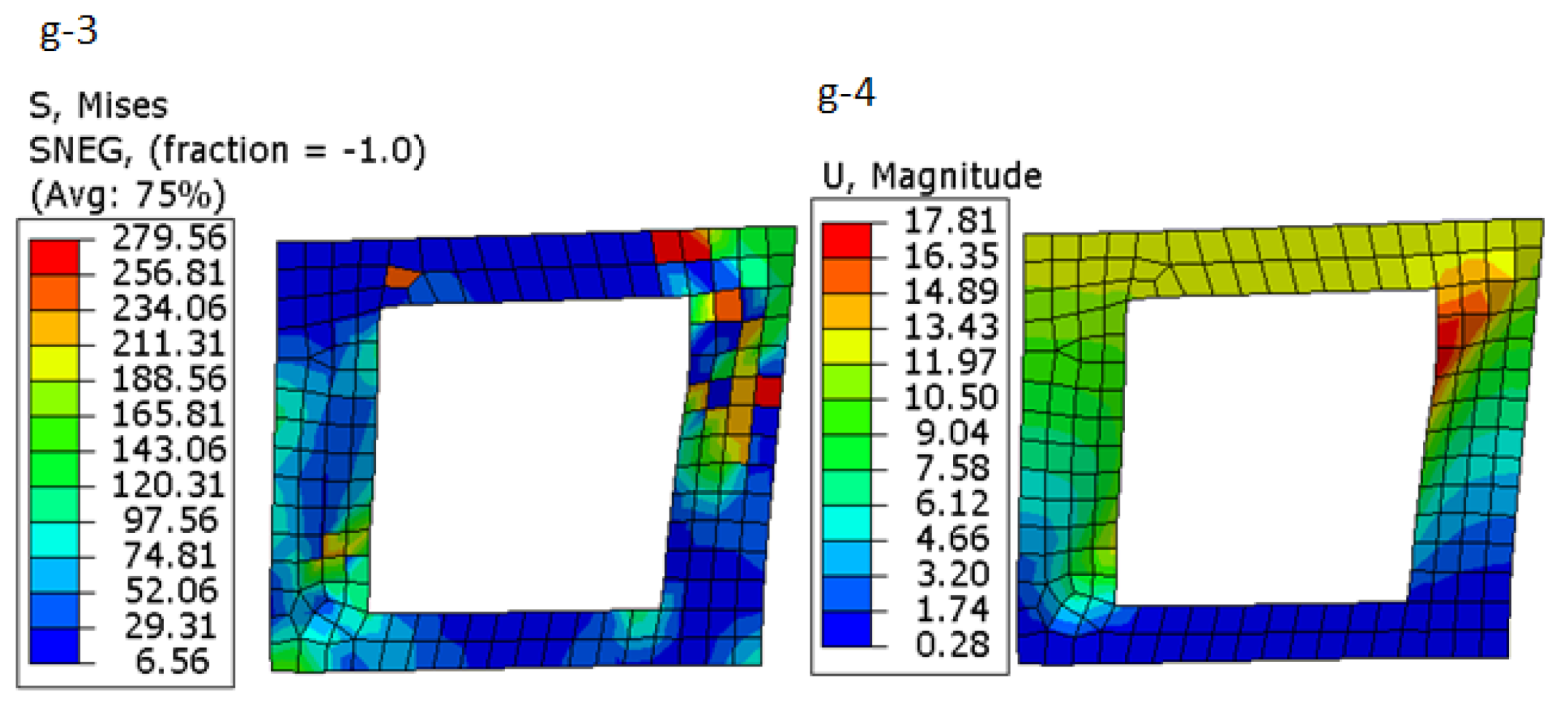
• In all models, some elements in the steel plate shear wall almost reached the near ultimate stress (4550 kg/cm³), however, the number of elements that reached the critical stress is different in different models. Figure 8 and Figure 9 show model a (shear wall without opening) has lower maximum stress and this stress is greater among elements; however, creating an opening increases stress and displacement in the concrete and steel plate. Moreover, the shear wall stiffness and stress uniformity decrease in all models with opening, especially for models with an opening near a column or beam.
• Figure 12 and Figure 14 show both specimens with openings near the beam and column, the formed corrugation in the steel plate exited along the main diagonal.
• The maximum stresses in the concrete layer in specimens without opening (Figure 10) and near the beam (Figure 13) were 18 MPa and 30 MPa, respectively, showing a 60% difference, due to decreases in steel plate performance.
• The maximum displacement in specimens without opening (Figure 9) and near the beams (Figure 13) was 13 cm and 17 cm, respectively, showing a 0.76% difference.
• In comparison with the two other samples shown in Figure 7 and Figure 8, stress distribution in the specimen with central opening (Figure 11) is more favorable and the number of elements reaching the ultimate strength is less compared to the models having an opening near the column or beam.
• Compared to the two other specimens, maximum displacement in specimen with an opening near the column was lower than the others, while the stiffness of wall decreases as compared to other models (model b and model c).
• In all the models, the elements located near the opening along the diagonal of the shear wall reached the ultimate strength and these elements have more displacement.
• In total, the performance of models (c) and (d) is similar to each other, but the number of elements reaching the ultimate stress in model (c) is higher than in model (b), so model (b) has the worst performance among all models in this group due to maximum displacement. Moreover, the number of elements reaching the ultimate stress are higher than others. In the following, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 show the stress and displacement for models 4 to 6.
• Figure 16, Figure 17, Figure 18 and Figure 19 show displacement, concrete and steel stress for models e and f. Figure 16 and Figure 18 show that the maximum stress in the steel plate in specimens with 4 openings is 439 MPa, which depicts the stress decrease as compared to model (e). Moreover, the stiffness of the shear wall increases with distributing opening.
• Figure 17 and Figure 19 show that the maximum displacement in the concrete layer in specimens with 4 and 2 openings is 14 cm, which shows displacement decreases as compared to other models with an opening. Moreover, the stiffness of the shear wall increases with distributing opening.
• The number of elements reaching maximum stresses around the opening near the beam was more than specimen with an opening near to column. The reason for the larger stress around the opening near beam as compared to the opening near column or central opening can be related to the out-of-plane displacement. When comparing the displacements in the two specimens, as shown in Figure 20, the displacement around the opening near the beam is larger than the opening near the column.

Figure 20 shows out of plane displacement for all the models, this figure shows the vertical opening (model b) has the maximum out of plane displacement (15.13 cm) as compared to others. Also, the stiffness of this shear wall is lower than others (models e and f). Therefore, model (c) has the maximum value (14.98 cm) as compared to others; moreover, the stiffness is the lowest value as compared to others. Model d has the best performance because the model has the minimum out of plane displacement (7.5 cm) and better stiffness as compared to models b and c.

By distributing opening (models f and i), the stiffness and out of plane displacement of composite steel shear wall increase as compared to model d, while the overall displacement (U) decreases in the steel plate.

In summary, the performance of models (b, c, and d) is similar to each other, but the out of plane displacement in model (d) is lower than models (b or c) and models (e) and (f) have the larger stiffness with lower overall displacement (U $\cong$ 14 cm).

4.2. The Effect of Number of Openings (Group B)

In this part, the effect of the opening size on the behavior of the composite shear wall is investigated. To this end, an opening of 36% of the area (the ratio of the opening area to the area of the steel plate is 0.1) was considered and its effect on the composite shear wall was evaluated. The load-displacement diagrams for these specimens are as shown in Figure 21.

According to Figure 21, model 4 is compared to the specimen with no openings, the strength and stiffness of the specimen with a single opening decreased by 75% and 70%, respectively. By transforming the single opening into two openings, the strength and stiffness of the specimen increased. In the case of specimens with distributed openings along the width of the wall (Figure 21), the strength and stiffness decreased by 66% and 65%, respectively and regarding the specimen with distributed openings along the height of the wall (Figure 15), the strength and stiffness decreased by 58% and 53% as compared to the specimen without opening. For a more accurate study of this issue, the effect of tensile field, stresses, and out-of-plane displacements caused in the specimens are as shown in Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28, Figure 29, Figure 30, Figure 31 and Figure 32. Figure 22, Figure 23, Figure 24, Figure 25, Figure 26 and Figure 27 show stress and displacement for models (g–i). All of these models show that the element near to opening has more stress than others.

The followings can be drawn from Figure 22, Figure 23, Figure 24, Figure 25, Figure 26 and Figure 27:

• Figure 26 and Figure 27 illustrates the maximum stress around the opening in specimens with horizontal openings (model i) and vertical openings was 443 MPa and 445 MPa, respectively, while this value was 430 MPa for specimen with a single opening, showing differences of 3% and 4% with the specimen with a single opening.
• The ratios of the maximum stress around the openings to the minimum stress for horizontal and vertical openings were 9.26% and 6.74%, respectively, signifying more uniform stress distribution around vertical openings.
• In both specimens, the formation of the diagonal field has been subject to interference.
• The maximum displacement in specimens with horizontal opening (Figure 25) and central openings (Figure 26) was 18.69 cm and 17 cm, respectively, showing a 9% difference in the maximum stresses of the two specimens.
• Compared to the specimen with horizontal openings (Figure 26), the maximum stress in the concrete layer of specimen with vertical openings in Figure 27 was larger by 11%.
• Figure 22 and Figure 23 show steel stress, concrete stress and stiffness in the single opening case was more favorable and lower than the other two specimens.
• Figure 28 and Figure 30 show that the maximum stress in the steel plate in specimens with 4 and 8 opening is decrease as compared to others. While, Figure 21 shows the stiffness of shear wall increases with distributing opening.
• Figure 29 and Figure 31 show that the maximum displacement in the steel plate in specimens with 4 and 8 opening is 15 cm and 13 cm repeatedly, which shows the displacement decrease as compared to other models in this group. Moreover, the stiffness of shear wall increases with distributing opening.
• Figure 23, Figure 25, Figure 27, Figure 29 and Figure 31 show that the average of maximum stress in the concrete plate in specimens is 29.4 MPa, which shows the maximum stress decrease in model (g) as compared to other models in this group because the stiffness of the shear wall decreases with a large single opening and the concrete panel cannot use its maximum capacity.

Figure 32 shows that the vertical opening (model h) has the maximum out of plane displacement (14.55 cm) as compared to others. Also, its stiffness of this shear wall is lower than others (models k, j and i). After that, model (g) has the maximum value (12.66 cm) as compared to others; moreover, the stiffness is the lowest value as compared to others. Model (i) has the best performance because this model has the minimum out of plane displacement (3.1 cm) and the maximum stiffness.

4.3. Average of Steel Stress

The value of stress in all elements has been obtained for each increment (0–6 s) and the average has been extracted for each steel frame ($\frac{\mathrm{sum}\left(\mathrm{stress}\right)\mathrm{for}\mathrm{elements}}{\mathrm{number}\mathrm{od}\mathrm{elements}}$). Figure 33 shows this value for all models.

The average stress shows that models with high stiffness have maximum stress as compared to others and creating holes increases average stress as compared to others and the average stress of the shear wall is raised by an increase in the number of holes in the section.

4.4. Modelling with Artificial Neural Networks

For the composite steel wall studied in this research, artificial neural network (ANN) was used to obtain predictive models. These models able to predict steel shear wall performance such as displacement, force, steel stress and concrete stress (output layers), by this way, the ability of the neural network for predicting steel shear wall performance is examined for the first time in this paper. The value of displacement, base shear, steel stress and concrete stress for 50 increments is extracted from an ABAQUS simulation for each model (730 points for each output ) and finally, the maximum value for each 10 elements at all models is obtained (73 points). Height, the opening’s location, the opening’s number, and time have been chosen as an input layer and the maximum value (73 points) for displacements, base shear, steel stress and concrete are assumed as an output layer. Finally, the values of the output layers have been predicted with MATLAB ANN- GUI. There are different types of ANNs of varying degrees of complexity and therefore with different levels of required computational capacity. In this paper, all models were based on a feed-forward neural network. This was the first and simplest kind of ANN devised, in which the information is processed in only one direction, from the input nodes through the hidden layer to the output nodes, using no cycles or loops [20]. The FEM data were split into three subsets (training data, testing data, and validating data). The input layer for each neural network included the variable (height, percentage of opening, location of opening and load), while the output layer for each neural network consisted of the FEM results. A Multilayer Perceptron (MLP) model was applied to predict the FEM results. MLP have one or more hidden layers, depending on the type and complexity of the problem that should be solved. A single hidden layer with a sufficient number of neurons is usually good enough to model many problems; this method, developed by Rosenblatt [21] has been used in different research studies. A graphical user interface (GUI) based workbench toolbox was used to generate the required MLP model. A sigmoid function was selected as the activation function. The training process was set for 7–10 epochs and the validation threshold was defined as 25 times (as in the majority of the models) and also the Lovenberg-Marquardt (LM) was used for a training network. This function is one of the fastest back propagation algorithms in the ANN neural network, and this is suggested as a first option supervised algorithm, while it does need more memory in comparison to other algorithms. Learngdm was used for training processes and this function was the gradient descent with momentum weight and bias learning function. Results from different neural network structures were evaluated based on two measures of accuracy [22]: The performances and accuracy of ANN models were evaluated according to statistical criteria, such as correlation coefficient (R2), and root mean square error (RMSE). Different researchers use these parameters for evaluating the efficiency of neural network models and the accuracy of ANN models [22]. Transfer function uses input to obtain output layers and TANSIG was used in this part to predict the output layers. Hidden layers are layers between input data and output data. In these layers, ANN assigns weights (W) and bias (b) to input layers and generates output layers by using learning and training function. Ten layers were also considered for each neural network. These models were obtained by minimizing the prediction error and therefore maximizing the correlation values for training, testing, and validating datasets. Different parameters were preliminarily evaluated and adjusted such as the overall architecture of the network (the hidden layers, the number of neurons in these networks), the number of training sets and the number of epochs. Figure 34 shows input and output layers for all neural network models.

4.4.1. Accuracy of Predicted Methods

Firstly, the neural network models predicted the output layer. Next, these values were compared to the FEM results for load-displacement curves in verification model (Figure 3), and it is presented in Figure 35. The predictions of the neural network were very close to the experimental values. In the following, the stress was considered as output layer for neural network and ${\mathrm{R}}^2$ value between FEM result and neural network was obtained and summarized in

Table 2. Accuracy parameters for each output.

Data Set	Accuracy Parameters		Relationship
Displacement	${\mathrm{R}}^2$	0.99	Y = 1.0019x − 0.063
	RRMSE	0.003
Concrete stress	${\mathrm{R}}^2$	0.98	Y = 0.99x − 0.0348
	RRMSE	0.0024
Steel stress	${\mathrm{R}}^2$	0.99	Y = 0.99x + 110.24
	RRMSE	0.0058
Force	${\mathrm{R}}^2$	0.90	Y = 0.85x + 328.54
	RRMSE	0.0048

. The prediction accuracy of this method is evaluated based on the relative root-mean-squared-error (RMSE) and the absolute fraction of variance (R²):

$$\mathrm{RRMSE}=\sqrt{\frac{{\mathrm{n}}_{\mathrm{t}}{{\displaystyle \sum }}_{\mathrm{i}=1}^{{\mathrm{n}}_{\mathrm{t}}}({\mathrm{y}}_{\mathrm{i}}-\overline{{\mathrm{y}}_{\mathrm{i}}{}^2)}}{({\mathrm{n}}_{\mathrm{t}}-1){{\displaystyle \sum }}_{\mathrm{i}=1}^{{\mathrm{n}}_{\mathrm{t}}}{\mathrm{y}}_{\mathrm{i}}{}^2}}$$

(1)

$${\mathrm{R}}^2=1-(\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{{\mathrm{n}}_{\mathrm{t}}}{\left({\mathrm{y}}_{\mathrm{i}}-\overline{{\mathrm{y}}_{\mathrm{i}}}\right)}^2}{{{\displaystyle \sum }}_{\mathrm{i}=1}^{{\mathrm{n}}_{\mathrm{t}}}{\overline{{\mathrm{y}}_{\mathrm{i}}}}^2}$$

(2)

In the above formulation, y and $\overline{\mathrm{y}}$ are FEM result and neural network values; and n is the number of points. The prediction accuracy was the highest value among models when the value of RRMSE is near to zero and the value of R² is near to 1. Figure 36 indicates the MSE of ANN model for training, validation (check), and test steps for force as an output sample of the neural network. This figure shows the least MSE in the validation step and occurred at epoch 8, which has the best validation performance, equal to 0.008. It should also be mentioned that model training keeps going as long as the error of the network on the validation vector is decreasing.

4.4.2. Prediction of the Surface of Stress and Displacement

Curve fitting is the GUI toolbox in MATLAB; users employed a mathematical function to obtain the best fit for a group of data. This method is employed as one of the most practical methods for interpreting data. This method has several functions and users can plot the predicted surface for output. On this note, users find the correlation between each input and output. Four standard models are available in this application. Moreover, users can estimate data between known (given, existent) and lost data. Polynomial, lowess, interpolation and a custom equation are four well-known models that are available in this application. Here, the curve fitting toolbox is employed to obtain the correlation of input and output data (predicting data with ANN) for the first time in the present study. The influences of the number of opening and their locations are shown as a surface plot of the predicting data, which is the maximum value for concrete stress, maximum value for steel stress, maximum value for load f and maximum value for displacement. As a result of this, after entering data (73 points) into the application, a variety of post-processing methods for plotting surface is employed and the best one is chosen according to ${\mathrm{R}}^2$ value and MSRE. Ultimately, polynomial is the best model for all outputs (base shear, displacement, the average of steel stress and concrete stress, because this model has the maximum value for ${\mathrm{R}}^2$ and the minimum value for MSRE).

Figure 37 shows the maximum (blue circle), minimum (red circle), and other points for steel stress, concrete stress, load and displacement for all models. Figure 37a shows the variation of displacement with the opening location and opening area. As clearly shown, applying an opening with 36% area has a positive influence on the increment of the displacement (models h to i) and model a has minimum displacement. The points that are related to model (v) have the highest value of the predicted surface and in contrast, the points that are related to model (a) have the minimum value of the predicted surface. Figure 37b shows the variation of concrete stress with the models. As shown, increasing the number of openings has a positive influence on the increase of the concrete stress (models f and j) and model (a) has the minimum stress value. Figure 37c shows that the higher the opening area (models h to i), the fewer the load capacity. Also, it shows that load surface is more affected by variation in the opening area instead of location of opening. Therefore, verification model and model a have the highest load capacity. Figure 37d shows the variation of steel stress with the models and location of opening. As shown, applying four openings with 10% area have a positive impact on the increase of the steel stress. Increase in the opening area led to decreased stress and model (i) has the minimum stress value. These graphs are practical for FEM results, because they can show which model has a more effective factor to promote the strength and to what extent the impact is on it. As clearly shown, the amount of area is more effective on the stress; however, the location of opening has less impact on the concrete stress (Figure 37).

5. Discussion and Conclusions

In this study, the effect of openings position and number of openings were investigated on the performance of composite shear walls. The following were investigated: load-displacement diagram, load-bearing capacity, stiffness, the stresses in the specimens particularly around the openings, and in some cases, the out-of-plane displacement. The maximum values for force, steel stress, concrete stress and displacement for all models were obtained and these values were divided by the maximum value for model (a). Figure 28 shows the ratios for all models.

The result shows that total displacement (U) decreases with distribution of openings while concrete stress, steel stress, strength, and stiffness increase. Compared to specimens in group B, concrete stress, strength, and stiffness are higher when opening area is 10%. By increasing the opening size (group B), the strength and stiffness decrease by 30% as compared to specimens in group A. In summary, model (g) has the worst performance among all the models, because it has the minimum strength and stiffness. Models (f) and (g) have the best performance among all models because these models have the maximum strength, stiffness, and the minimum displacement. All models are sensitive to change in an area of opening. The stiffness, strength, and performance of all farms depend on the area changes. To achieve this, the frame stiffness (K = E × A/L), depends directly on the area. Figure 38 shows that this diversity is considered as a sensitive factor (opening area). However, when the area is constant, the stiffness and the strength of the frames are a little close to each other, but it is not the same (Figure 12, Figure 13 and Figure 38) and these parameters reached an optimum point by finding the base place of opening. According to these investigations, the following was concluded:

• By creating openings, the strength and stiffness of the composite shear wall decrease and the opening position affects the reduction level in the wall stiffness, such that the stiffness reduction is larger than 20% when the openings move nearer to the boundary beams as compared to the case where openings are placed near the columns. Moreover, out of displacement is 25% lower when the openings move near to the boundary beam as compared to the state where openings are placed near the column. Compared to these two cases (c and d), the performance of central opening is near to the case b (opening near to the beam), but the maximum stress in concrete panels in case (c) is more than others.
• In group A, by transforming a single opening to four equivalent openings with an overall area equal to the initial one, the strength and stiffness of the wall increase by 7% and steel stress increases by 36%. However, as compared to these two cases (c and b), the overall displacement decreases by 11%.
• Compared to specimens with openings near the beams or columns, stress distribution was more favorable in specimen with central opening.
• Stress concentration is intensified as the opening position approaches the beam or column.
• In summary, changing the location of openings has strong influence on the steel shear wall performance, steel stress, concrete panel, and displacement.
• By increasing opening’s size, the strength and stiffness of the composite shear wall decrease, and the opening position affects the reduction level in the wall stiffness, such that the average of stiffness reduction is 60% for group B, however this value is 80% for group A. Steel stress, displacement and concrete stress are similar to the state where the opening size is 10%. As clearly shown in the neural network result (Figure 23, Figure 24, Figure 25, Figure 26 and Figure 27) and FEM result, the variation of strength and stiffness are 0.39% for the case where opening size is 36%; however, this value is 11% for the case where opening size is 10%. Therefore, as compared to specimens in group A, strength and stiffness variation is more intense for models in group B and changing opening place and opening size has strong influence on the composite shear wall stiffness.
• A strength and stiffness reduction is more intense for the case where horizontal openings are created instead of vertical openings.
• In group B, by moving openings near to the beam, the strength and stiffness of the wall increase 39% as compared to the central opening and this action does not have any fundamental impact on the steel and concrete stress. Therefore, this model has the best performance in this group, because the opening is near to the diagonal pattern and model g has the worst performance as compared to others due to its opening location.
• Displacement is lower in the case where openings are distributed in the plate (models f, e, g, and k) as compared to other models.
• Strength and stiffness increment is more intense in the case where openings are distributed in the plate (models f, e, g, and k).
• Compared to specimens with two openings (model i), stress was more conveniently distributed in specimens with a single opening (model g). This distribution is more uniform in the case of vertical openings (model i) as compared to horizontal cases (model h).
• The factors responsible for changing the wall stiffness, which are also observed in the load-displacement diagram, include the change in the stress distribution pattern in the wall, the commence of plastic yielding in some points in the wall, or the extreme increase in their numbers, which ultimately extend to the critical area such as the column base and/or the connection of the beams and columns, buckling, and corrugation in the steel plate.
• The results show that the neural network was successful in learning the relationship between the different input parameters and outputs. R value obtained for each output was higher than 90% and the ANN model was able to predict the properties of composite shear wall.