Analysis of the Thermal Characteristics of a Composite Ceramic Product Filled with Phase Change Material
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
- -
- variant I (V1)—no PCM, all slots filled with brick dust;
- -
- variant II (V2)—one row of slots filled with PCM, located on the outside air side, and the other slots filled with brick dust;
- -
- variant II (V3)—two rows of slots filled with PCM, located on the outside air side, and the other slots filled with brick dust;
2.2. Methods
- Experimental method (EM), in which the tests were carried out in a laboratory test chamber;
- Standardized calculation method (SCM), in which a spreadsheet was used to calculate the building component;
- Numerical simulation method (NSM), in which the ADINA computer program was used for thermal characteristics.
- In each of the above methods, the heat transfer coefficient U was determined for three variants V1, V2, and V3.
2.2.1. Experimental Method
- temperature stabilization in the chambers (warm and cold),
- placing the heat flow sensor in the central part of the tested surface,
- using a perforated metal curtain, whose task was to limit the forced air movement in the chambers (warm and cold).
2.2.2. Standard Calculation Method
- Rsi—heat transfer resistance on the inner surface;
- R1, R2, …, Rn—calculated thermal resistance of each layer;
- Rse—calculated thermal resistance of each layer.
- —upper limit of total thermal resistance;
- —lower limit of total thermal resistance.
- RTa, RTb, …, RTg—total thermal resistance of subsequent sections;
- fa, fb, …, fg—relative areas of successive slices.
- Σdj—sum of layer thicknesses (total thickness of the building component).
2.2.3. Numerical Simulation Method
3. Results and Discussion
3.1. Experimental Method
3.2. Standard Calculation Method
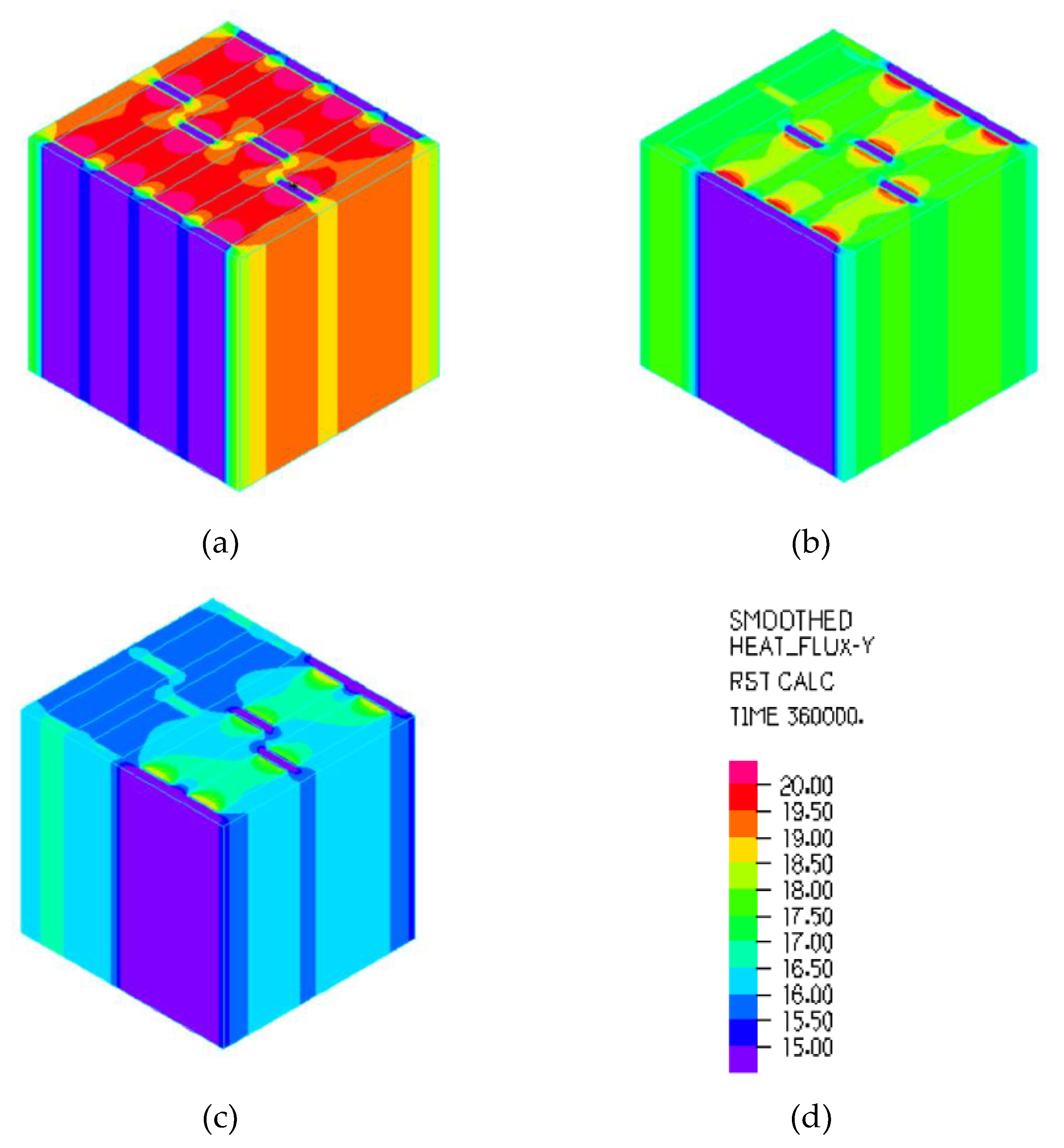
3.3. Numerical Simulation Method
3.4. Thermal Parameters of the Building Component Determined by Three Methods
4. Conclusions
- The calculations carried out indicate that the use of one of the three proposed methods for determining the thermal resistance of complex building structures allows obtaining results with an accuracy not exceeding the measurement errors of standard devices used to determine this value (5–6%).
- The standard method and numerical simulations can be used as part of checking the correctness of experimental tests.
- The convergence of the results obtained indicates the possibility of practical replacement of long-term experimental tests with simulation methods, which can be used to select the correct structural solutions from a group of many conceptual solutions.
- The use of the standard method or numerical simulation to determine the thermal parameters of complex building partitions allows cost reduction with respect to conducting experimental tests.
- The presented methods may be applied to other composite materials. However, the assessment of their effectiveness would require further experiments.
Author Contributions
Funding
Conflicts of Interest
References
- Entrop, A.G.; Brouwers, H.J.H.; Reinders, A.H.M.E. Experimental research on the use of micro-encapsulated Phase Change Materials to store solar energy in concrete floors and to save energy in Dutch houses. Sol. Energy 2011, 85, 1007–1020. [Google Scholar] [CrossRef]
- Alawadhi, E.M.; Hashem, J.A. Building roof with conical holes containing PCM to reduce the cooling load: Numerical study. Energy Convers. Manag. 2011, 52, 2958–2964. [Google Scholar] [CrossRef]
- Elarga, H.; Fantucci, S.; Serra, V.; Zecchin, R.; Benini, E. Experimental and numerical analyses on thermal performance of different typologies of PCMs integrated in the roof space. Energy Build. 2017, 150, 546–557. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Castellon, C.; Nogues, M.; Medrano, M.; Leppers, R.; Zubillaga, O. Use of microencapsulated PCM in concrete walls for energy savings. Energy Build. 2007, 39, 113–119. [Google Scholar] [CrossRef]
- Wang, X.; Yu, H.; Li, L.; Zhao, M. Experimental assessment on the use of phase change materials (PCMs)-bricks in the exterior wall of a full-scale room. Energy Convers. Manag. 2016, 120, 81–89. [Google Scholar] [CrossRef]
- Pomianowski, M.; Heiselberg, P.; Jensen, R.L.; Cheng, R.; Zhang, Y. A new experimental method to determine specific heat capacity of inhomogeneous concrete material with incorporated microencapsulated-PCM. Cement. Concr. Res. 2014, 55, 22–34. [Google Scholar] [CrossRef]
- Cheng, R.; Pomianowski, M.; Wang, X.; Heiselberg, P.; Zhang, Y. A new method to determine thermophysical properties of PCM-concrete brick. Appl. Energy 2013, 112, 988–998. [Google Scholar] [CrossRef]
- Silva, T.; Vicente, R.; Soares, N.; Ferreira, V. Experimental testing and numerical modelling of masonry wall solution with PCM incorporation: A passive construction solution. Energy Build. 2012, 49, 235–245. [Google Scholar] [CrossRef]
- Necib, H.; Settou, N.; Saifi, N.; Damene, D. Experimental and numerical study of a usual brick filled with PCM to improve the thermal inertia of buildings. Energy Procedia 2013, 36, 766–775. [Google Scholar] [CrossRef]
- Saxena, R.; Rakshit, D.; Kaushik, S.C. Phase change material (PCM) incorporated bricks for energy conservation in composite climate: A sustainable building solution. Sol. Energy 2019, 183, 276–284. [Google Scholar] [CrossRef]
- Kong, X.; Lu, S.; Huang, J.; Cai, Z.; Wei, S. Experimental research on the use of phase change materials in perforated brick rooms for cooling storage. Energy Build. 2013, 62, 597–604. [Google Scholar] [CrossRef]
- He, W.; Yu, C.; Yang, J.; Yu, B.; Hu, Z.; Shen, D.; Liu, X.; Qin, M.; Chen, H. Experimental study on the performance of a novel RC-PCM-wall. Energy Build. 2019, 199, 297–310. [Google Scholar] [CrossRef]
- Castell, A.; Martorell, I.; Medrano, M.; Perez, G.; Cabeza, L.F. Experimental study of using PCM in brick constructive solutions for passive cooling. Energy Build. 2010, 42, 534–540. [Google Scholar] [CrossRef]
- Lichołai, L.; Dębska, B.; Krasoń, J. Assessment of the applicability of a phase change material in horizontal building partitions. IOP Conf. Ser. Earth Environ. Sci. 2019, 214, 012042. [Google Scholar] [CrossRef]
- Errebaia, F.B.; Chikh, S.; Derradji, L. Experimental and numerical investigation for improving the thermal performance of a microencapsulated phase change material plasterboard. Energy Convers. Manag. 2018, 174, 309–321. [Google Scholar] [CrossRef]
- Kusamaa, Y.; Ishidoyaba, Y. Thermal effects of a novel phase change material (PCM) plaster under different insulation and heating scenarios. Energy Build. 2017, 141, 226–237. [Google Scholar] [CrossRef]
- Wang, X.; Yu, H.; Li, L.; Zhao, M. Research on temperature dependent effective thermal conductivity ofcomposite-phase change materials (PCMs) wall based on steady-state method in a thermal chamber. Energy Build. 2016, 126, 408–414. [Google Scholar] [CrossRef]
- Esteves, L.P.; Magalhães, A.; Ferreira, V.; Pinho, C. Evolution of global heat transfer coefficient on PCM energy storage cycles. Energy Procedia 2017, 136, 188–195. [Google Scholar] [CrossRef]
- Trgala, K.; Pavelek, M.; Wimmer, R. Energy performance of five different building envelope structures using a modified Guarded Hot Box apparatus—Comparative analysis. Energy Build. 2019, 195, 116–125. [Google Scholar] [CrossRef]
- Li, L.; Yu, H.; Liu, R. Research on composite-phase change materials (PCMs)-bricks in the west wall of room-scale cubicle: Mid-season and summer day cases. Build. Environ. 2017, 123, 494–503. [Google Scholar] [CrossRef]
- Lee, K.O.; Medina, M.A.; Sun, X.; Jin, X. Thermal performance of phase change materials (PCM)-enhanced cellulose insulation in passive solar residential building walls. Sol. Energy 2018, 163, 113–121. [Google Scholar] [CrossRef]
- Miąsik, P.; Krasoń, J. Thermal functioning of a transparent barrier equipped with a system of external thermal insulation shields. E3S Web Conf. 2018, 49, 00071. [Google Scholar] [CrossRef]
- Ramakrishnan, S.; Sanjayan, J.; Wang, X. Experimental Research on Using Form-stable PCM-Integrated Cementitious Composite for Reducing Overheating in Buildings. Buildings 2019, 9, 57. [Google Scholar] [CrossRef]
- Debska, B.; Lichołai, L.; Krasoń, J. Selected properties of epoxy mortars with perlite aggregate. J. Ecol. Eng. 2017, 18, 246–255. [Google Scholar] [CrossRef]
- Debska, B.; Lichołai, L. Long-term chemical resistance of ecological epoxy polymer composites. J. Ecol. Eng. 2018, 19, 204–212. [Google Scholar] [CrossRef]
- Heim, D. Isothermal storage of solar energy in building construction. Renew. Energy 2010, 35, 788–796. [Google Scholar] [CrossRef]
- Lichołai, L.; Miąsik, P.; Starakiewicz, A.; Krasoń, J. Analysis of the thermal characteristics of anti-icing driveway plates. IOP Conf. Ser. Earth Environ. Sci. 2019, 214, 012040. [Google Scholar] [CrossRef]
- Miąsik, P.; Lichołai, L. The influence of a thermal bridge in the corner of the walls on the possibility of water vapour condensation. E3S Web Conf. 2018, 49, 00072. [Google Scholar] [CrossRef]
- Dębska, B.; Lichołai, L.; Miąsik, P. Assessment of the Applicability of Sustainable Epoxy Composites Containing Waste Rubber Aggregates in Buildings. Buildings 2019, 9, 31. [Google Scholar] [CrossRef]
- Xie, J.; Wang, W.; Sang, P.; Liu, J. Experimental and numerical study of thermal performance of the PCM wall with solar radiation. Constr. Build. Mater. 2018, 177, 443–456. [Google Scholar] [CrossRef]
- Mehdaoui, F.; Hazami, M.; Messaouda, A.; Taghouti, H.; Guizania, A. Thermal testing and numerical simulation of PCM wall integrated inside a test cell on a small scale and subjected to the thermal stresses. Renew. Energy 2019, 135, 597–607. [Google Scholar] [CrossRef]
- PN-EN ISO. 6946:2017-10 Building Components and Building Elements–Thermal Resistance and Thermal Transmittance–Calculation Method; ISO: Warsaw, Poland, 2017. [Google Scholar]








| Material | Density (kg/m3) | Specific Heat Capacity (kJ/kgK) | Latent Heat (kJ/kg) | Melting Temperature (°C) | Solidification Temperature (°C) | Heat Conductivity (W/mK) |
|---|---|---|---|---|---|---|
| Ceramic body | 885 | 1.0 | – | – | – | 0.213 |
| RT25HC solid liquid | 880 770 | 2.0 | 230 | 22–26 | 26–22 | 0.200 |
| Brick dust | 1700 | – | – | – | – | 0.456 |
| Variant | Descriptive Statistics | ||
|---|---|---|---|
| Average Value of Heat Flux Density q | Standard Deviation s | Number of Measurements N | |
| (W/m2) | (W/m2) | – | |
| V1 | 17.42 | 2.00 | 864.0 |
| V2 | 16.07 | 1.86 | 864.0 |
| V3 | 14.74 | 1.84 | 864.0 |
| V1: 12 point moving average | 17.42 | 0.41 | 852.0 |
| V2: 12 point moving average | 16.07 | 0.38 | 852.0 |
| V3: 12 point moving average | 14.74 | 0.37 | 852.0 |
| Variant | Gradient Temperature on the Surface of the Partition ΔT | Resistance Thermal Component ΣRλ | Equivalent Heat Transfer Coefficient λequivalent |
|---|---|---|---|
| (°C) | (m2K/W) | (W/mK) | |
| V1 | 15.45 | 0.886 | 0.293 |
| V2 | 15.55 | 0.967 | 0.268 |
| V3 | 15.94 | 1.080 | 0.240 |
| Variant | Resistance Thermal Component ΣRλ | Equivalent Heat Transfer Coefficient λequivalent | Ratio of Heat Resistance Limits / | Maximum Error Due to Thermal Resistance e |
|---|---|---|---|---|
| (m2K/W) | (W/mK) | (–) | (%) | |
| V1 | 0.877 | 0.299 | 1.0140 | 0.70 |
| V2 | 0.977 | 0.268 | 1.0118 | 0.59 |
| V3 | 1.076 | 0.244 | 1.0087 | 0.43 |
| Variant | Emission Factor | Total Thermal Resistance RT | Heat Transfer Coefficient U |
|---|---|---|---|
| (m2·K/W) | (W/(m2·K)) | ||
| V1 | 0.85 | 1.060 | 0.943 |
| 0.95 | 1.050 | 0.952 | |
| V2 | 0.85 | 1.159 | 0.863 |
| 0.95 | 1.148 | 0.871 | |
| V3 | 0.85 | 1.257 | 0.796 |
| 0.95 | 1.247 | 0.802 |
| Method | Variant | Total Thermal Resistance RT | Heat Transfer Coefficient U |
|---|---|---|---|
| – | – | (m2·K/W) | (W/(m2·K)) |
| EM | V1 | 1.057 | 0.946 |
| SCM | 1.047 | 0.955 | |
| NSM | 1.050–1.060 | 0.943–0.952 | |
| EM | V2 | 1.137 | 0.879 |
| SCM | 1.147 | 0.872 | |
| NSM | 1.148–1.159 | 0.863–0.871 | |
| EM | V3 | 1.251 | 0.799 |
| SCM | 1.246 | 0.803 | |
| NSM | 1.247–1.257 | 0.796–0.802 |
| Variant | Total Thermal Resistance RMax | Total Thermal Resistance RMin | Maximum Error Due to Thermal Resistance eR | Heat Transfer Coefficient UMax | Heat Transfer Coefficient UMin | Maximum Error Due to Heat Transfer Coefficient eU |
|---|---|---|---|---|---|---|
| – | (m2K/W) | (W/m2K) | (%) | (W/(m2·K)) | (W/(m2·K)) | (%) |
| V1 | 1.060 | 1.047 | 1.24 | 0.955 | 0.943 | 1.27 |
| V2 | 1.159 | 1.137 | 1.93 | 0.879 | 0.863 | 1.85 |
| V3 | 1.257 | 1.246 | 0.88 | 0.803 | 0.796 | 0.88 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krasoń, J.; Miąsik, P.; Lichołai, L.; Dębska, B.; Starakiewicz, A. Analysis of the Thermal Characteristics of a Composite Ceramic Product Filled with Phase Change Material. Buildings 2019, 9, 217. https://doi.org/10.3390/buildings9100217
Krasoń J, Miąsik P, Lichołai L, Dębska B, Starakiewicz A. Analysis of the Thermal Characteristics of a Composite Ceramic Product Filled with Phase Change Material. Buildings. 2019; 9(10):217. https://doi.org/10.3390/buildings9100217
Chicago/Turabian StyleKrasoń, Joanna, Przemysław Miąsik, Lech Lichołai, Bernardeta Dębska, and Aleksander Starakiewicz. 2019. "Analysis of the Thermal Characteristics of a Composite Ceramic Product Filled with Phase Change Material" Buildings 9, no. 10: 217. https://doi.org/10.3390/buildings9100217
APA StyleKrasoń, J., Miąsik, P., Lichołai, L., Dębska, B., & Starakiewicz, A. (2019). Analysis of the Thermal Characteristics of a Composite Ceramic Product Filled with Phase Change Material. Buildings, 9(10), 217. https://doi.org/10.3390/buildings9100217





