Advanced Seismic Retrofit of a Mixed R/C-Steel Structure
Abstract
:1. Introduction
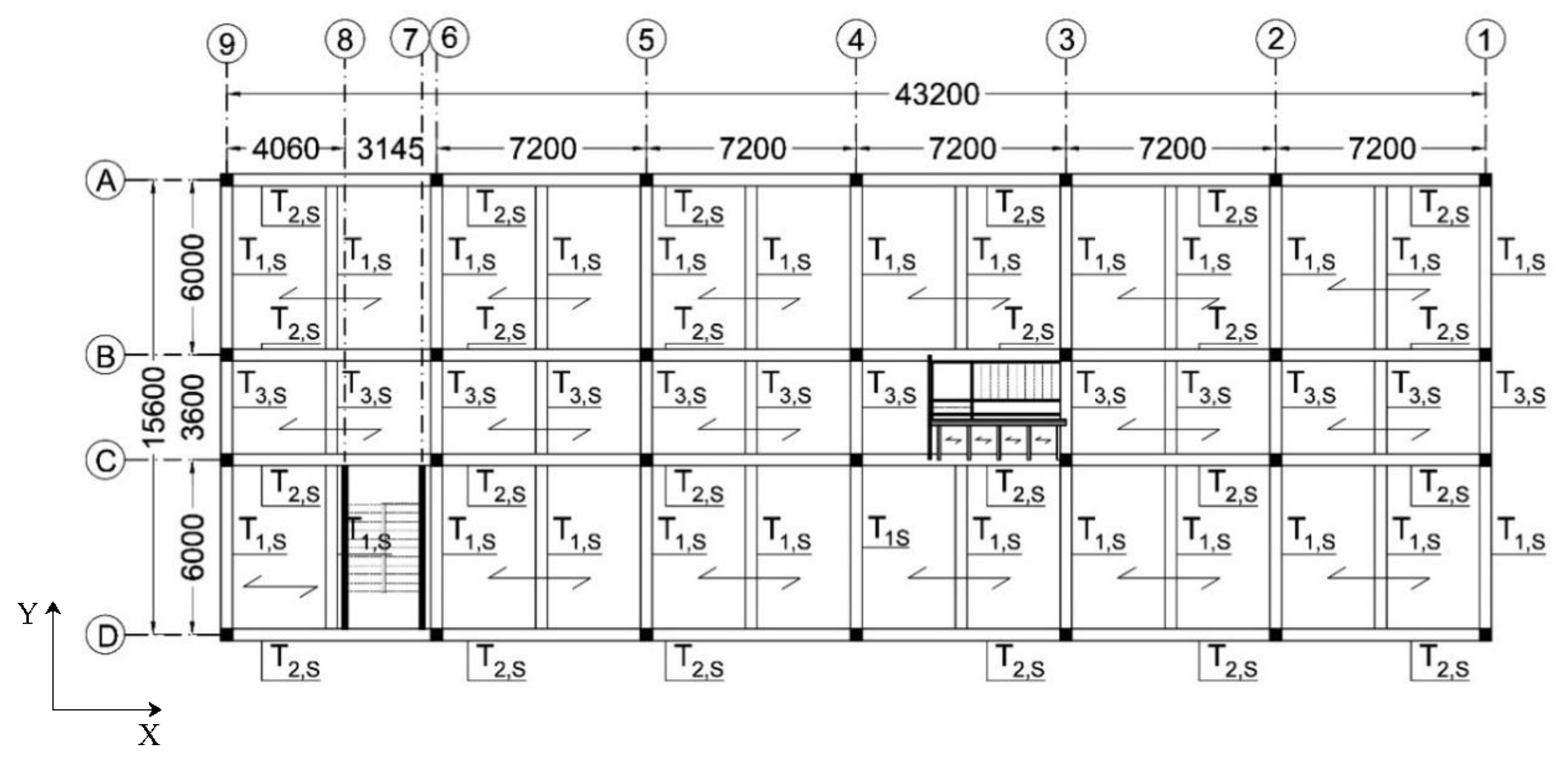
2. Case Study School Building
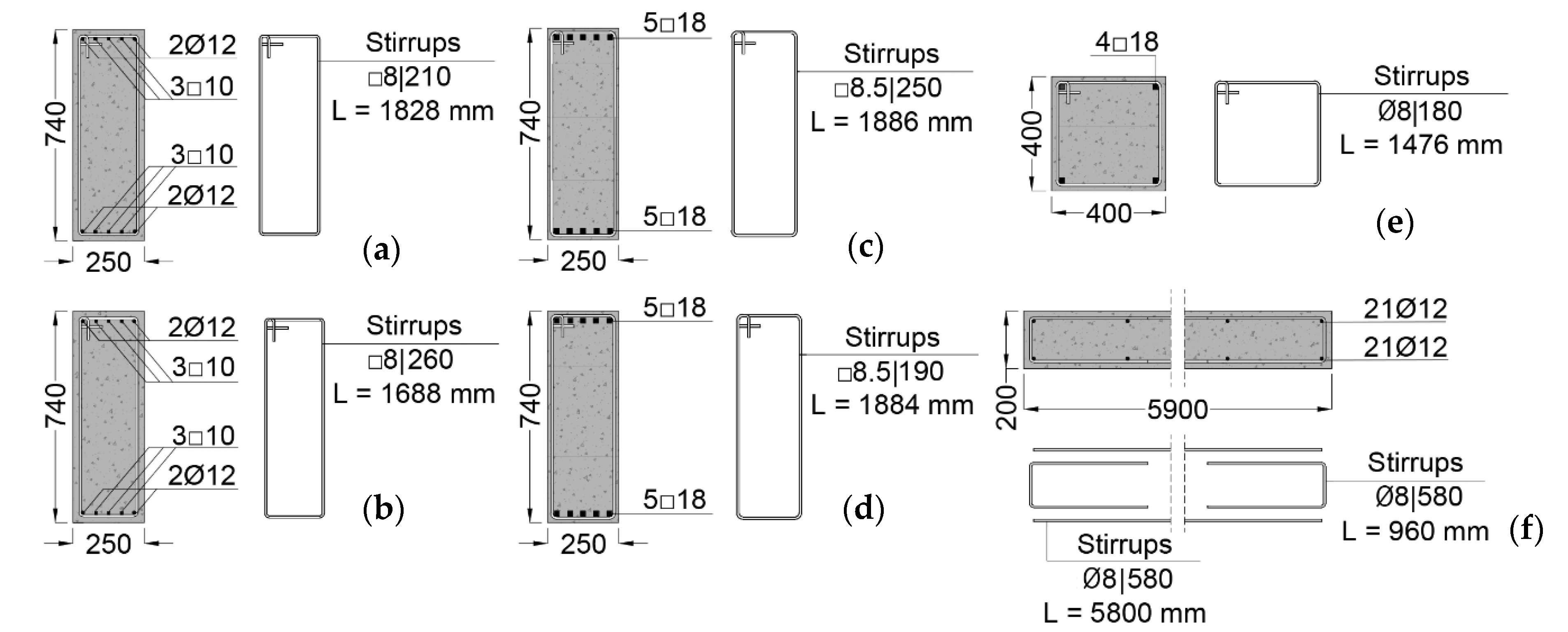
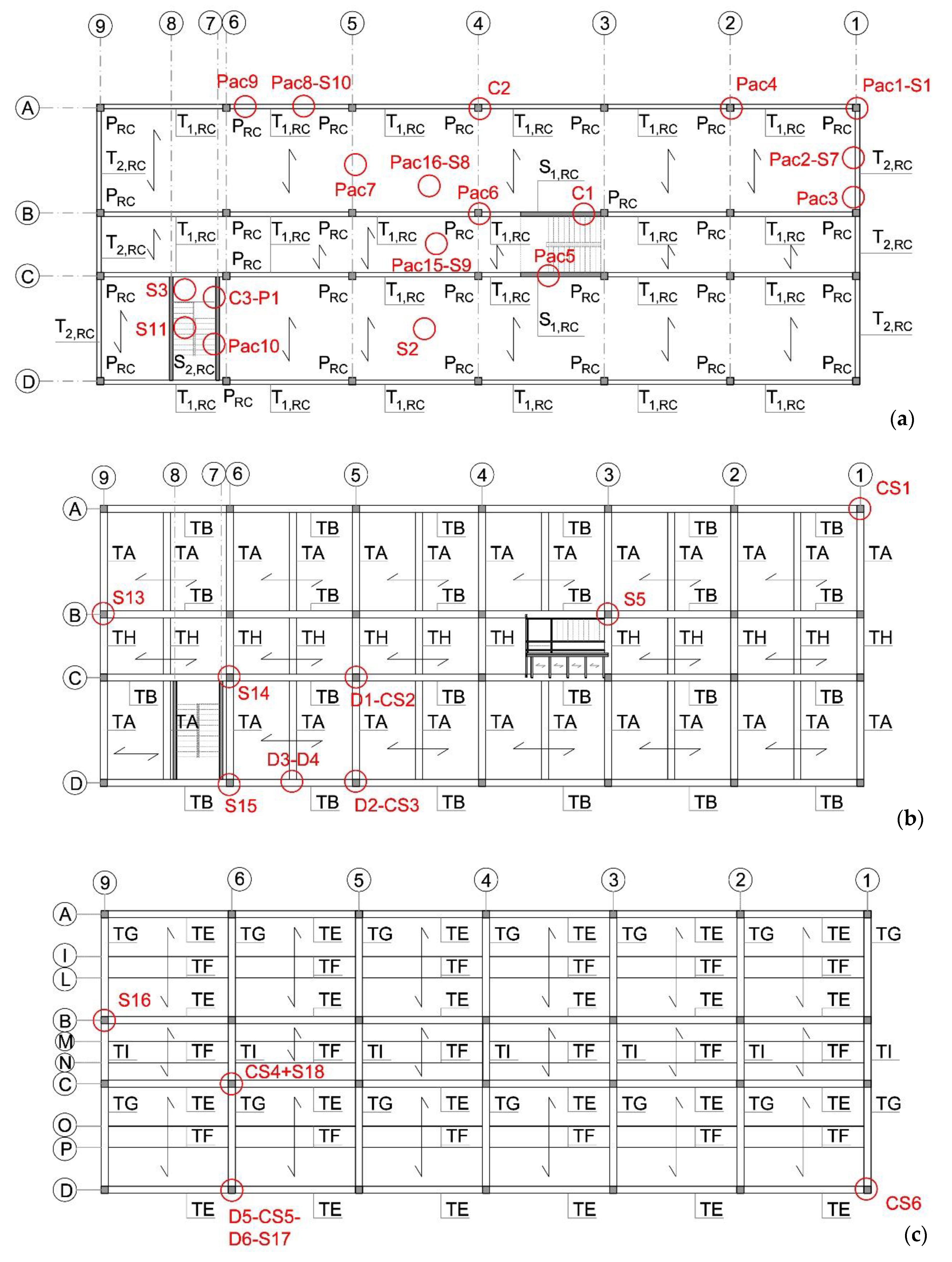
3. On-Site Testing Campaign
4. Assessment Analysis in Current Conditions
4.1. Modal Analysis
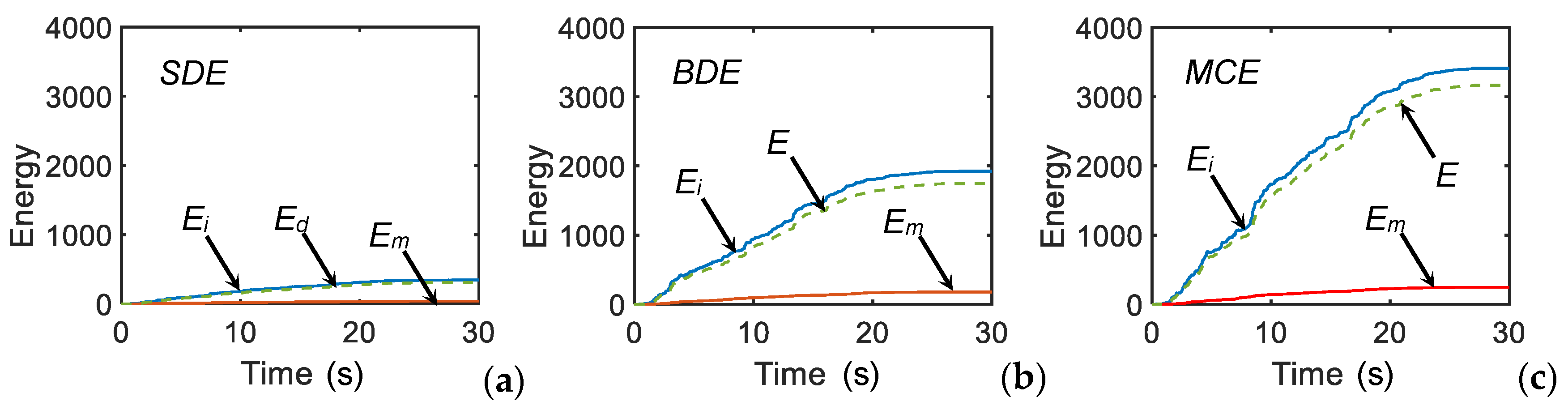
4.2. Time-History Verification and Performance Assessment Analysis
5. Retrofit Solution
5.1. Mechanical Characteristics of the FV Dampers
5.2. Sizing Design Procedure of FV Dampers and Performance Verification Analysis in Retrofitted Conditions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ministry of Public Works. Technical Provisions for Constructions, with Special Prescriptions for Seismic Zones; Law no. 64, 2 February 1974. Ordinary supplement to G.U. no. 76, 21 March 1974; Ministry of Public Works: Rome, Italy, 1974. (In Italian)
- Ministry of Public Works. Approval of Technical Standards for Constructions in Seismic Zones; Ministerial Decree, 3 March 1975. Ordinary supplement to G.U. no. 93, 8 April 1975; Ministry of Public Works: Rome, Italy, 1975. (In Italian)
- Terenzi, G.; Bazzani, C.; Costoli, I.; Sorace, S.; Spinelli, P. Seismic assessment and retrofit design of a school building in Florence. In IOP Conference Series: Materials Science and Engineering, Proceedings of the 4th World Multidisciplinary Civil Engineering-Architecture-Urban Planning Symposium, WMCAUS 2019, Prague, Czech Republic, 17–21 June 2019; IOP Publishing: Bristol, UK, 2019; Volume 603, Paper No. 032003. [Google Scholar]
- Ministry of Infrastructure and Transport. Guidelines for the Classification of Seismic Risk of Constructions and Relevant Annexes; Ministerial Decree no. 65, 7 March 2017, Ordinary supplement to G.U. no. 65, 18 March 2017; Ministry of Infrastructure and Transport: Rome, Italy, 2017. (In Italian)
- Di Ludovico, M.; Digrisolo, A.; Graziotti, F.; Moroni, C.; Belleri, A.; Caprili, S.; Ferracuti, B.; Ferretti, D.; Fiorentino, G.; Mannella, A.; et al. The contribution of ReLUIS to the usability assessment of school buildings following the 2016 central Italy earthquake. Boll. Geofis. Teor. Appl. 2017, 58, 353–376. [Google Scholar]
- Hwang, J.S.; Lin, W.C.; Wu, N.J. Comparison of distribution methods for viscous damping coefficients to buildings. Struct. Infrastruct. Eng. 2013, 9, 28–41. [Google Scholar] [CrossRef]
- Weng, D.G.; Zhang, C.; Lu, X.L.; Zeng, S.; Zhang, S.M. A simplified design procedure for seismic retrofit of earthquake-damaged RC frames with viscous dampers. Struct. Eng. Mech. 2013, 44, 611–631. [Google Scholar] [CrossRef]
- Palermo, M.; Muscio, M.; Silvestri, S.; Landi, L.; Trombetti, T. On the dimensioning of viscous dampers for the mitigation of the earthquake-induced effects in moment-resisting frame structures. Bull. Earthq. Eng. 2013, 11, 2429–2446. [Google Scholar] [CrossRef]
- Foti, D. Response of frames seismically protected with passive systems in near-field areas. Int. J. Struct. Eng. 2014, 5, 326–345. [Google Scholar] [CrossRef]
- Foti, D. Local ground effects in near-field and far-field areas on seismically protected buildings. Soil Dyn. Earthq. Eng. 2015, 74, 14–24. [Google Scholar] [CrossRef]
- Guo, T.; Xu, J.; Xu, W.; Di, Z. Seismic upgrade of existing buildings with fluid viscous dampers: Design methodologies and case study. J. Perform. Const. Facil. 2015, 29, 04014175. [Google Scholar] [CrossRef]
- Magar Patil, H.R.; Jangid, R.S. Numerical study of seismic performance of steel moment-resisting frame with buckling-restrained brace and viscous fluid damper. IES J. Part A Civ. Struct. Eng. 2015, 8, 165–174. [Google Scholar] [CrossRef]
- Mazza, F. Comparative study of the seismic response of RC framed buildings retrofitted using modern techniques. Earthq. Struct. 2015, 9, 29–48. [Google Scholar] [CrossRef]
- Dall’Asta, A.; Tubaldi, E.; Ragni, L. Influence of the nonlinear behavior of viscous dampers on the seismic demand hazard of building frames. Earthq. Eng. Struct. Dyn. 2016, 45, 149–169. [Google Scholar] [CrossRef]
- Dong, B.; Ricles, J.M.; Sause, R. Seismic performance of steel MRF building with nonlinear viscous dampers. Front. Struct. Civ. Eng. 2016, 10, 254–271. [Google Scholar] [CrossRef]
- Golzar, F.G.; Rodgers, G.W.; Chase, J.G. Design and experimental validation of a re-centring viscous dissipater. Structures 2016, 13, 193–200. [Google Scholar] [CrossRef]
- Impollonia, N.; Palmeri, A. Seismic performance of buildings retrofitted with nonlinear viscous dampers and adjacent reaction towers. Earthq. Eng. Struct. Dyn. 2018, 47, 1329–1351. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, Z.; Zhou, Y.; Lu, X. Nonlinear dissipative devices in structural vibration control: A review. J. Sound Vib. 2018, 423, 18–49. [Google Scholar] [CrossRef]
- Naeem, A.; Kim, J. Seismic performance evaluation of a spring viscous damper cable system. Eng. Struct. 2018, 176, 455–467. [Google Scholar] [CrossRef]
- Xu, L.-H.; Xie, X.-S.; Li, Z.-X. A self-centering brace with superior energy dissipation capability: Development and experimental study. Smart Mater. Struct. 2018, 27, 095017. [Google Scholar] [CrossRef]
- Bahmani, M.; Zahrai, S.M. Application of a comprehensive seismic retrofit procedure for steel buildings using nonlinear viscous dampers. Int. J. Civ. Eng. 2019, 17, 1261–1279. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G.; Takewaki, I. Design strategies of viscous dampers for seismic protection of building structures: A review. Soil Dyn. Earthq. Eng. 2019, 118, 144–165. [Google Scholar] [CrossRef]
- Dadkhah, H.; Mohebbi, M. Performance assessment of an earthquake-based optimally designed fluid viscous damper under blast loading. Adv. Struct. Eng. 2019, 22, 3011–3025. [Google Scholar] [CrossRef]
- Dadpour, O.; Banazadeh, M. Probabilistic seismic response models for risk assessment and design of steel moment frames with linear viscous dampers. Earthq. Spectra 2019, 55, 267–288. [Google Scholar] [CrossRef]
- Kariniotakis, K.; Karavasilis, T.L. Limits for the interstorey drift sensitivity coefficient θ of steel MRFs with viscous dampers designed according to Eurocode 8. Soil Dyn. Earthq. Eng. 2019, 117, 203–215. [Google Scholar] [CrossRef]
- Sonda, D.; Pollini, A.; Cossu, M. Seismic retrofit of an industrial building using damping devices. Struct. Eng. Int. 2019. [Google Scholar] [CrossRef]
- Xiang, N.; Alam, M.S. Displacement-based seismic design of bridge bents retrofitted with various bracing devices and their seismic fragility assessment under near-fault and far-field ground motions. Soil Dyn. Earthq. Eng. 2019, 119, 75–90. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G. Seismic protection of frame structures by fluid viscous damped braces. J. Struct. Eng. ASCE 2008, 134, 45–55. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G.; Fadi, F. Shaking table and numerical seismic performance evaluation of a fluid viscous-dissipative bracing system. Earthq. Spectra 2012, 28, 1619–1642. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G. Dissipative bracing-based seismic retrofit of R/C school buildings. Open Constr. Build. Technol. J. 2012, 6, 334–345. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G. Motion control-based seismic retrofit solutions for a R/C school building designed with earlier Technical Standards. Bull. Earthq. Eng. 2014, 12, 2723–2744. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G.; Mori, C. Passive energy dissipation-based retrofit strategies for R/C frame water storage tanks. Eng. Struct. 2016, 106, 385–398. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G. Existing prefab R/C industrial buildings: seismic assessment and supplemental damping-based retrofit. Soil Dyn. Earthq. Eng. 2017, 94, 193–203. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G.; Bertino, G. Viscous dissipative, ductility-based and elastic bracing design solutions for an indoor sports steel building. Adv. Steel Constr. 2012, 8, 295–316. [Google Scholar]
- Sorace, S.; Terenzi, G.; Licari, M. Traditional and viscous dissipative steel braced top addition strategies for a R/C building. Int. J. Struct. Eng. 2015, 6, 332–353. [Google Scholar] [CrossRef]
- Ministry of Infrastructure and Transport. Update of Technical Standards for Constructions; Ministerial Decree, 17 January 2018. Ordinary supplement to G.U. no. 42, 20 February 2018; Ministry of Infrastructure and Transport: Rome, Italy, 2018. (In Italian)
- Ministry of Infrastructure and Transport. Instructions for the Application of the Update of Technical Standards for Constructions; Circular no. 7, 21 January 2019. Ordinary supplement to G.U. no. 35; Ministry of Infrastructure and Transport: Rome, Italy, 2019. (In Italian)
- SAP2000NL. Theoretical and Users’ Manual; Release 20.05; Computers & Structures Inc.: Berkeley, CA, USA, 2019. [Google Scholar]
- Vanmarcke, E.H.; Fenton, G.A.; Heredia-Zavoni, E. SIMQKE-II—Conditioned Earthquake Ground Motion Simulator: User’s Manual, version 2.1; Princeton University: Princeton, NJ, USA, 1999; Available online: http://nisee.berkeley.edu/documents/SW/SIMQKE-II-V2-1.pdf (accessed on 22 June 2019).
- Sorace, S.; Terenzi, G. Non-linear dynamic modelling and design procedure of FV spring-dampers for base isolation. Eng. Struct. 2001, 23, 1556–1567. [Google Scholar] [CrossRef]
- Terenzi, G. Energy-based design criterion of dissipative bracing systems for seismic retrofit of framed structures. Appl. Sci. 2018, 8, 268. [Google Scholar] [CrossRef] [Green Version]
- Jarret, S.L. Shock-Control Technologies. 2019. Available online: http://www.introini.info (accessed on 5 July 2019).














© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terenzi, G.; Bazzani, C.; Costoli, I.; Sorace, S.; Spinelli, P. Advanced Seismic Retrofit of a Mixed R/C-Steel Structure. Buildings 2019, 9, 241. https://doi.org/10.3390/buildings9120241
Terenzi G, Bazzani C, Costoli I, Sorace S, Spinelli P. Advanced Seismic Retrofit of a Mixed R/C-Steel Structure. Buildings. 2019; 9(12):241. https://doi.org/10.3390/buildings9120241
Chicago/Turabian StyleTerenzi, Gloria, Caterina Bazzani, Iacopo Costoli, Stefano Sorace, and Paolo Spinelli. 2019. "Advanced Seismic Retrofit of a Mixed R/C-Steel Structure" Buildings 9, no. 12: 241. https://doi.org/10.3390/buildings9120241
APA StyleTerenzi, G., Bazzani, C., Costoli, I., Sorace, S., & Spinelli, P. (2019). Advanced Seismic Retrofit of a Mixed R/C-Steel Structure. Buildings, 9(12), 241. https://doi.org/10.3390/buildings9120241






