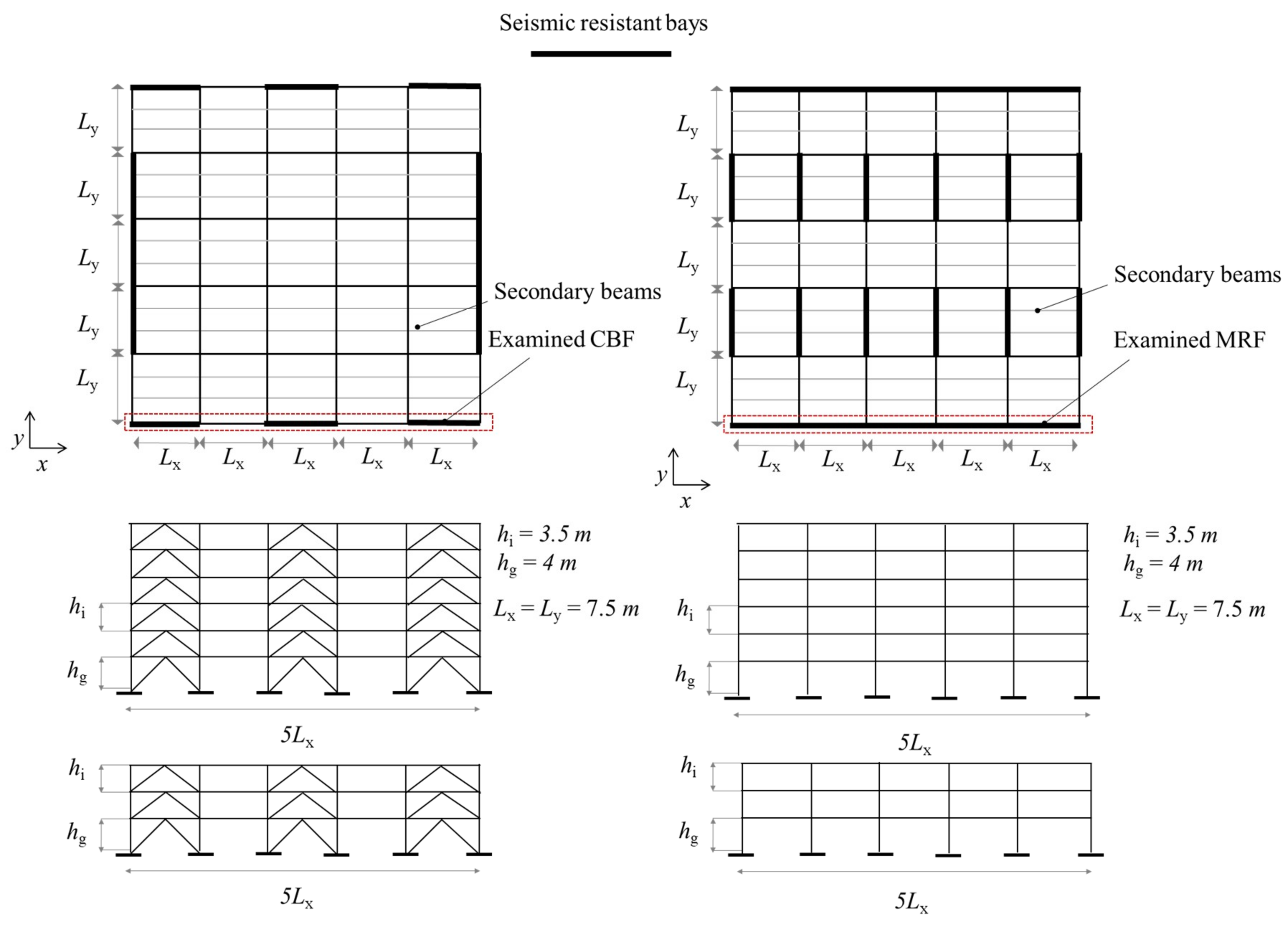
2.1. Moment resistring frames (MRF)
EC8 assigns a reference behaviour factor equal to 4 and 5 for ductility class medium (DCM) and high (DCH), respectively, where the ultimate-to-yielding capacity ratio accounts for the redundancy of the systems; it can be evaluated by performing a pushover analysis or otherwise it can be assumed equal to 1.3 for multi-storey multi-bay MRFs.
In MRFs with full strength and full rigid joints, the dissipative zones are located at the ends of the beams, where plastic hinges form. At the beam ends, the following inequality should be met:
where
MEd,
NEd and
VEd are the design forces, and
Mpl,Rd,
Npl,Rd and
Vpl,Rd are design resistances in accordance with EN 1993:1-1 [
25].
To achieve global ductile collapse, any plasticity should be avoided in the columns except at the base of the frame, at the top level of multi-storey buildings and for single storey buildings. This type of failure mode is generally referred as “weak beam/strong column” behaviour and it is guaranteed by meeting the following requirement:
where,
and
are the sum of the design values of the moments of resistance of the columns and beams, respectively, framing at a joint. This requirement is waived at the base of the frame on the top level of multi-storey buildings and for single storey buildings.
For steel MRFs, Eurocode 8 even mandates the following specific capacity design requirements as follows:
where:
NEd,G, MEd,G, VEd,G are the design forces in the column due to the non-seismic action included in the combination of actions for the seismic design situation;
NEd,E, MEd,E, VEd,E are the seismic induced effects;
γov is the overstrength factor accounting for randomness of yield strength according to EC8;
Ω is minimum of of all beams where dissipative zones are located;
Mpl,Rd,i is the plastic bending resistance of the i-th beam;
MEd,E,i is the bending moment due to the seismic loads in the i-th beam.
In addition, the column shear force
VEd resulting from the structural analysis should satisfy the following expression:
As observed by previous research [
2,
21,
24], capacity design requirement expressed by Equation (5) is inaccurate in the most of cases; indeed the beam overstrength factor
does not account for gravity loads. Therefore, the actual beam overstrength can be significantly larger than expected, even two or three times in gravity-ruled cases. Moreover, the minimum value of Ω evaluated according to Equation (5), considers the formation of the first plastic hinge and it does not correspond to the overall capacity of the structure. Depending on the frame redistribution capability, the column can be subjected to higher force than expected [
2,
21,
24].
Beside the capacity design rules, the deformation-related requirements stated by EC8 for both the serviceability and ultimate limit states play key role in the seismic design of MRFs and thus deserve proper consideration.
The lateral displacement should be controlled at the serviceability limit state, according to the following inequality:
where
dr is the design interstorey drift,
h is the story height, and
v is a reduction factor accounting for the lower return period of the seismic action associated with the serviceability limit state, even depending on the importance class of the building. The factor
K depends on the type of infill walls and it is equal to 0.05, 0.075, and 0.01 for brittle, ductile, and non-structural elements fixed in a way so as not to interfere with (or without) non-structural elements, respectively.
Moreover, EC8 stipulates that the influence of second order (namely, P-Δ) effect should be properly considered in the design at the ultimate limit state. With this regard, the Code defines an interstorey drift sensitivity coefficient as
where
Ptot is the total gravity load,
Vtot is the seismic shear at the storey under consideration,
dr is the interstorey drift (given by the elastic inter-storey drift by the behaviour factor), and
h is the storey height. If
, second order effects can be disregarded; conversely if
, the second-order effects may approximately be taken into account by multiplying the relevant seismic action effects by a factor equal to 1/(1–
θ). The value of the sensitivity coefficient
θ should not exceed 0.3.
The deformation related requirements rule the sizing of MRFs in the most of cases; indeed, to fulfil the drift limitation and to assure enough stability against second order effects, the designer is forced to oversize the structural members with respect to the relevant required strength, leading to massive and uneconomical systems characterized by large lateral overstrength and poor energy dissipation capacity. For instance, Tenchini et al. [
26] observed that for EC8 compliant MRFs, the overall overstrength factors are larger than the design behaviour factor owing to codified design procedure, which leads to increase member size to satisfy drift limitations. From nonlinear dynamic analyses, Tenchini et al. [
26] showed that MRFs have a seismic demand (namely, transient and residual drift ratios, beam ductility) fairly below the proposed limit for the damage limitation (DL), significant damage (SD), and near collapse (NC) limit states [
27]. In particular, in an SD limit state, most of frames behave in an elastic field due to the design being oversized. In addition, the elastic response of MRFs can be responsible for large non-structural damage of acceleration-sensitive components, since they obtained median peak storey accelerations ranging from two to three times the design PGA.
More recently, Tartaglia et al. [
2] investigated the influence of the P-Delta effect requirements in the design procedure of MRFs. In particular, they proposed to calculate the critical multiplier and the stability coefficients accounting for the design overstrength, thus using a secant stiffness of the non-linear equivalent structure larger than the value currently prescribed by EC8. This modification allowed the design of lighter and weaker MRFs that guaranteed an overall ductile response, while the EC8-compliant frames showed an elastic response up to a near collapse limit state.
In the light of these remarks and observations from previous studies, it can be argued that drift limitations and second order effect checks, as codified within EC8, are too stringent, even when compared with the corresponding rule provided by the US Code [
28], which defines the stability coefficient based solely on the elastic inter-storey drift, thus using the elastic stiffness of the structure and resulting in less stringent requirements [
21].
2.2. Chevron concentrically braced frames (CCBF)
The framework of EC8 bracings in chevron configuration are expected to provide limited ductility with respect to other concentric bracings types and a smaller value of behaviour factor is assigned. In detail, q equal to 2 and 2.5 is assumed in DCM and DCH, respectively, namely, smaller than value q = 4 is assumed for other bracing configurations.
The seismic design criteria codified within Eurocode 8 is aimed at guaranteeing an overall ductile performance with plastic deformations restrained into diagonal members, while the remaining structural members are kept in elastic range.
The required strength of diagonal members is evaluated by mean of elastic analysis and the bracings should be designed to fulfil the following inequality:
where
Npl,br,Rd is the plastic axial strength,
χ is the buckling reduction factor calculated according to EN 1993:1-1 [
25], and
NEd,br is the axial force acting on the element.
To prevent too severe a deterioration of bracing response, EC8 limits the diagonal normalized slenderness
, which should be smaller than 2.0. In addition, to avoid soft-storey mechanisms and to favour uniform distribution of plastic deformation along the building eight, the Code mandates to limit the variation of the diagonal capacity-to-demand ratios according to the following condition:
where
and
is the overstrength ratio at the
i-th storey. The rule expressed by Equation (10) leads to design systems characterized by significant lateral overstrength and very poor plastic engagement. Indeed, the seismic induced effect is generally lower at the roof storey, where the highest value of overstrength ratio is recognized due to need to contemporarily meet the maximum allowable slenderness ratio
; as a consequence, to limit the capacity-to-demand variation, the designer is forced to oversize the bracing cross-sections even at the intermediate and lower storeys. Moreover, as numerous research have report, the requirement expressed by Equation (10) is not adequate to assure uniform distribution of plasticity along the frame height and to prevent soft-storey mechanisms.
To avoid any nonlinearity into non-dissipative members (namely, beams and columns), capacity design criteria are applied.
The columns belonging to the braced bays are designed to withstand the following action:
where
Npl,Rd(
MEd) is the design resistance to axial force of the column calculated in accordance with EN 1993:1-1 [
25], taking into account the interaction with the design value of bending moment,
MEd, in the seismic design situation;
NEd,G is the axial force in the column due to the non-seismic actions included in the combination of actions for the seismic design situation;
NEd,E is the axial force in the column due to the design seismic action;
γov is the material overstrength factor;
Ω is the minimum overstrength ratio Ωi = Npl,bRd,i/NEd,br,i;
As highlighted by previous research [
17,
18,
19], the force transfer mechanism in the post-buckling range differs significantly from the elastic behavior and the columns are likely be subjected to a force significantly larger than that calculated according to Equation (11).
The seismic performance of chevron concentric bracings depends significantly on the behaviour of the brace-intercepted beam [
17,
29,
30]. Indeed, after the buckling of the compression diagonal, an unbalanced vertical force is applied at the brace-intercepting section, inducing high bending demand. Flexural yielding of the beam would result in sudden drop of the storey lateral capacity; thereby, to prevent such detrimental behaviour the beam in chevron configuration should be designed to withstand: (i) All non-seismic loads without considering the intermediate support given by diagonals; (ii) the unbalanced vertical force as result of vertical components transmitted by tension and compression braces in the nonlinear range. In this regard, the tension brace is assumed to attain its nominal plastic capacity, while the compression diagonal exhibits its post buckling capacity, evaluated as
It should be noted for diagonal members close to the maximum allowable slenderness ratio, the buckling reduction factor χ assumes values around 0.2 and thus the buckling capacity of the member results are smaller than the residual capacity evaluated according to Equation (12).
Several pieces of research have demonstrated that the capacity design requirements given by EC8 for brace-intercepted beams are not adequate to satisfactorily guarantee seismic behaviour [
17,
29,
30]. Indeed, the detailing rules current codified in EC8 focus solely on the beam strength, disregarding the deformation-related aspects. Conversely, as highlighted by [
17], the vertical deflection of the beam and the ductility demand on bracings are correlated phenomena, therefore frames with strong but flexible beams exhibit very poor seismic response. Shen et al. [
29] observed that the inelastic deformation in the middle spans of brace-intersected beams substantially increases ductility demands on braces and beam-to-column connections. Indeed, under this condition, the rotational demand on beam-to-column connection may be larger than 0.06 radians at the 0.02 story drift ratio response. Shen et al. [
29] also found that at 2% interstorey drift rotation, the ductility demand on diagonal bracings may significantly change from about eight times the yield displacement in CBF with stiff brace-intersected beams, up to more than 20 times the yield displacement in structures with weak and deformable brace-intersected beams.