Evaluating the Interaction of Emerging Diseases on White-Tailed Deer Populations Using an Agent-Based Modeling Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Agent-Based Model Framework
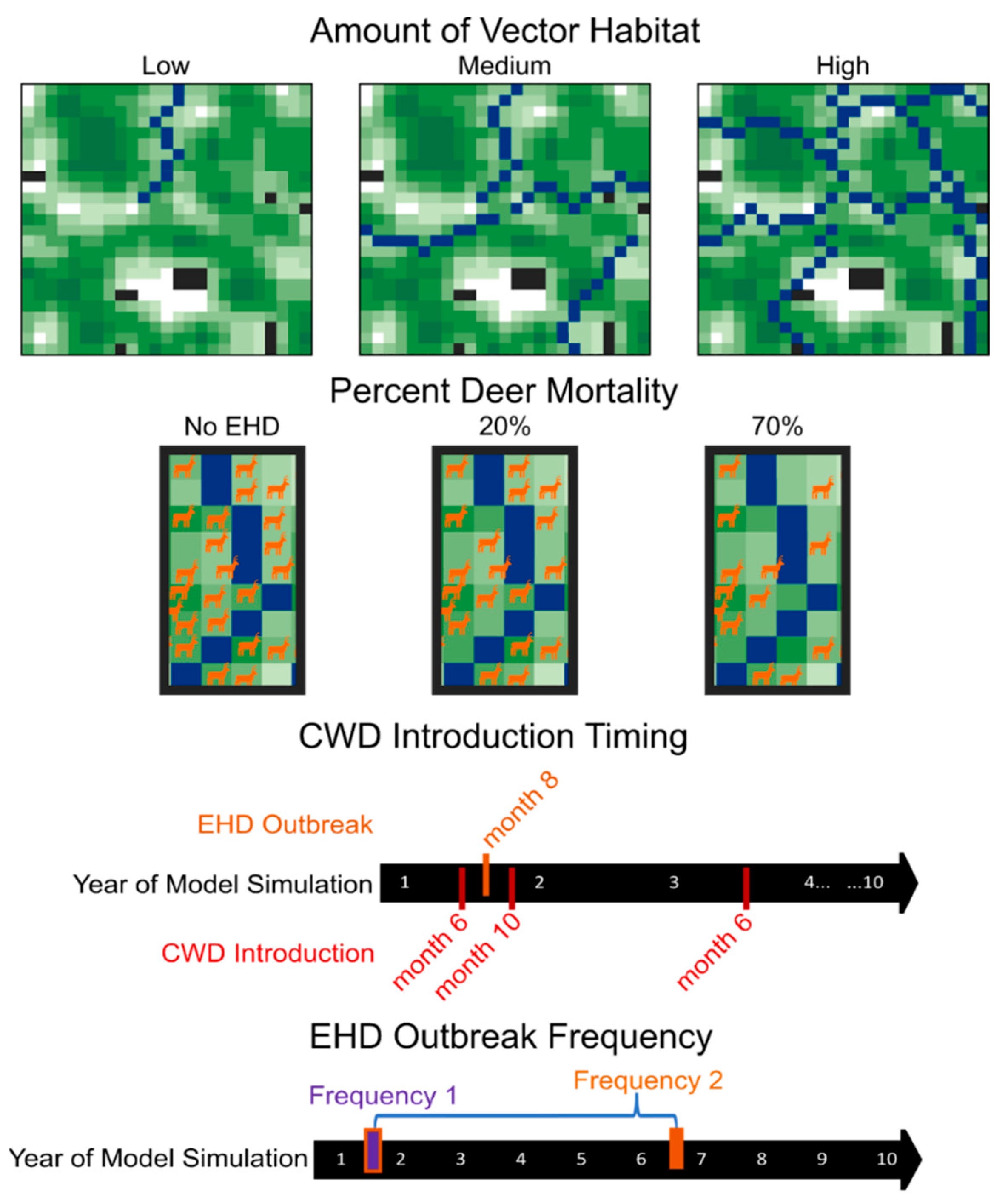
2.2. Experimental Design
2.3. Simulating HD Dynamics
2.4. Response Variables and Statistical Analysis
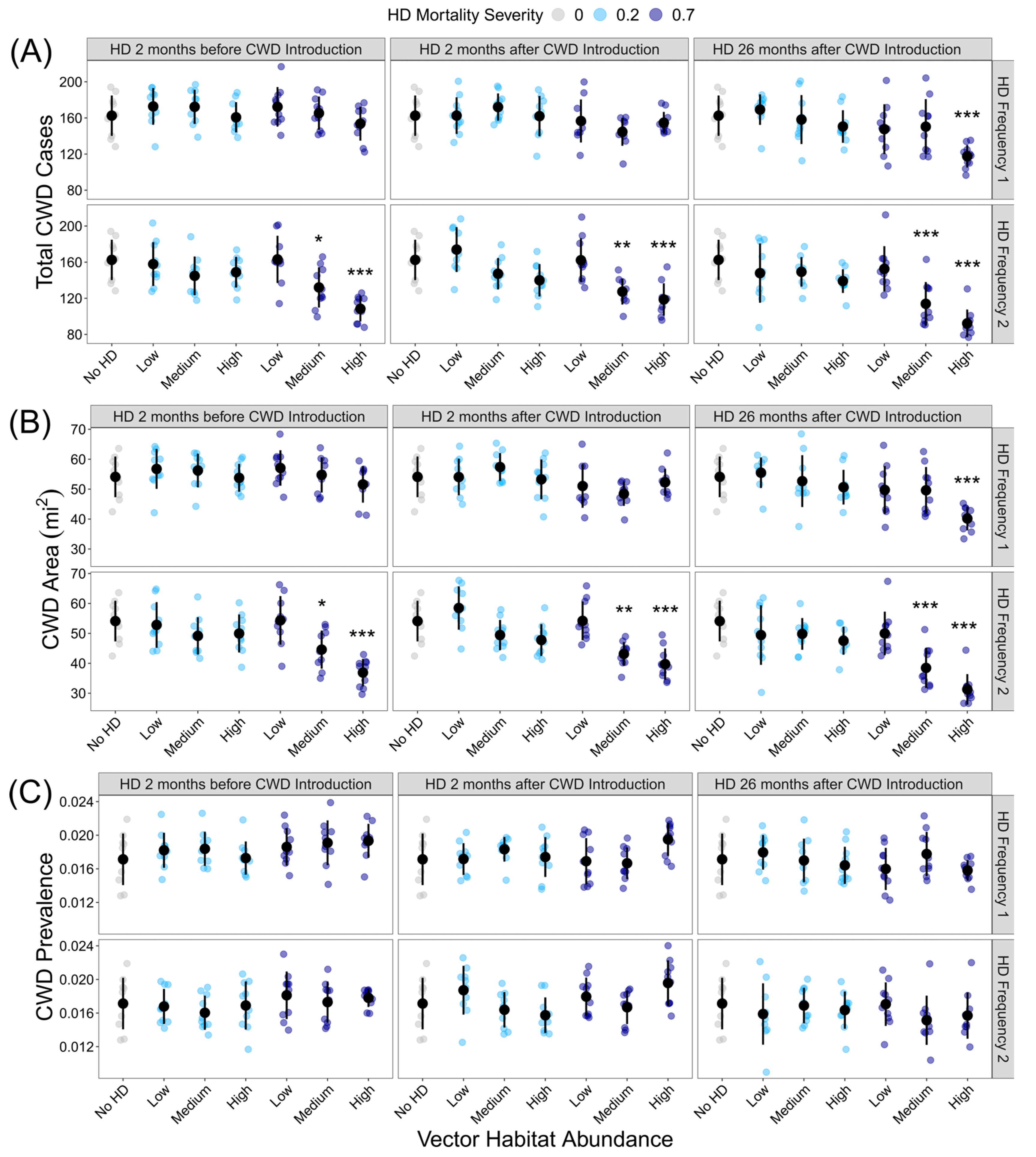
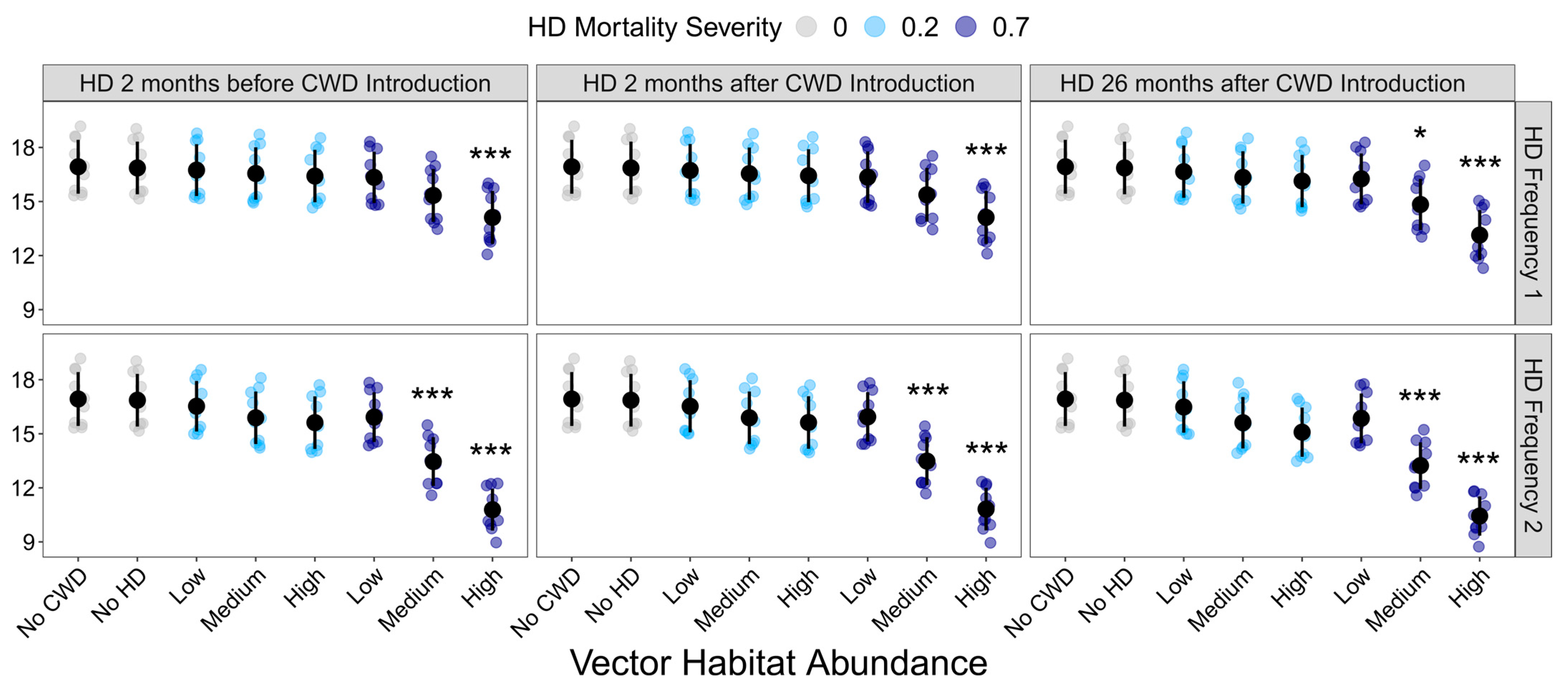
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moutailler, S.; Valiente Moro, C.; Vaumourin, E.; Michelet, L.; Tran, F.H.; Devillers, E.; Cosson, J.F.; Gasqui, P.; Van, V.T.; Mavingui, P.; et al. Co-infection of Ticks: The Rule Rather Than the Exception. PLoS Neglected Trop. Dis. 2016, 10, e0004539. [Google Scholar] [CrossRef] [PubMed]
- Petney, T.N.; Andrews, R.H. Multiparasite communities in animals and humans: Frequency, structure and pathogenic significance. Int. J. Parasitol. 1998, 28, 377–393. [Google Scholar] [CrossRef] [PubMed]
- Tompkins, D.M.; Dunn, A.M.; Smith, M.J.; Telfer, S. Wildlife diseases: From individuals to ecosystems. J. Anim. Ecol. 2011, 80, 19–38. [Google Scholar] [CrossRef] [PubMed]
- Russell, R.E.; DiRenzo, G.V.; Szymanski, J.A.; Alger, K.E.; Grant, E.H.C. Principles and Mechanisms of Wildlife Population Persistence in the Face of Disease. Front. Ecol. Evol. 2020, 8, 569016. [Google Scholar] [CrossRef]
- Daszak, P.; Cunningham, A.A.; Hyatt, A.D. Emerging infectious diseases of wildlife--threats to biodiversity and human health. Science 2000, 287, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Jones, K.E.; Patel, N.G.; Levy, M.A.; Storeygard, A.; Balk, D.; Gittleman, J.L.; Daszak, P. Global trends in emerging infectious diseases. Nature 2008, 451, 990–993. [Google Scholar] [CrossRef]
- Williams, E.S.; Miller, M.W.; Kreeger, T.J.; Kahn, R.H.; Thorne, E.T. Chronic Wasting Disease of Deer and Elk: A Review with Recommendations for Management. J. Wildl. Manag. 2002, 66, 551. [Google Scholar] [CrossRef]
- Stallknecht, D.E.; Allison, A.B.; Park, A.W.; Phillips, J.E.; Goekjian, V.H.; Nettles, V.F.; Fischer, J.R. Apparent increase of reported hemorrhagic disease in the midwestern and northeastern USA. J. Wildl. Dis. 2015, 51, 348–361. [Google Scholar] [CrossRef]
- Johnson, C.J.; Herbst, A.; Duque-Velasquez, C.; Vanderloo, J.P.; Bochsler, P.; Chappell, R.; McKenzie, D. Prion protein polymorphisms affect chronic wasting disease progression. PLoS ONE 2011, 6, e17450. [Google Scholar] [CrossRef]
- Shope, R.; MacNamara, L.; Mangold, R. A virus-induced epizootic hemorrhagic disease of the Virginia white-tailed deer (Odocoileus virginianus). J. Exp. Med. 2002, 11, 155–170. [Google Scholar] [CrossRef]
- Miller, M.W.; Williams, E.S.; Hobbs, N.T.; Wolfe, L.L. Environmental sources of prion transmission in mule deer. Emerg. Infect. Dis. 2004, 10, 1003–1006. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Madden, M.; Stallknecht, D.E.; Hodler, T.W.; Parker, K.C. Spatial-temporal model of haemorrhagic disease in white-tailed deer in south-east USA, 1983 to 2000. Vet. Rec. 2012, 170, 288. [Google Scholar] [CrossRef] [PubMed]
- Christensen, S.A.; Ruder, M.G.; Williams, D.M.; Porter, W.F.; Stallknecht, D.E. The role of drought as a determinant of hemorrhagic disease in the eastern United States. Glob. Chang. Biol. 2020, 26, 3799–3808. [Google Scholar] [CrossRef]
- Berry, B.S.; Magori, K.; Perofsky, A.C.; Stallknecht, D.E.; Park, A.W. Wetland cover dynamics drive hemorrhagic disease patterns in white-tailed deer in the United States. J. Wildl. Dis. 2013, 49, 501–509. [Google Scholar] [CrossRef] [PubMed]
- Christensen, S.A.; Williams, D.M.; Rudolph, B.A.; Porter, W.F. Spatial variation of white-tailed deer (Odocoileus virginianus) population impacts and recovery from epizootic hemorrhagic disease. J. Wildl. Dis. 2021, 57, 82–93. [Google Scholar] [CrossRef] [PubMed]
- Mellor, P.S.; Boorman, J.; Baylis, M. Culicoides biting midges: Their role as arbovirus vectors. Annu. Rev. Entomol. 2000, 45, 307–340. [Google Scholar] [CrossRef] [PubMed]
- Arnett, E.B.; Southwick, R. Economic and social benefits of hunting in North America. Int. J. Environ. Stud. 2015, 72, 734–745. [Google Scholar] [CrossRef]
- Rooney, T.P.; Waller, D.M. Direct and indirect effects of white-tailed deer in forest ecosystems. For. Ecol. Manag. 2003, 181, 165–176. [Google Scholar] [CrossRef]
- Belsare, A.V. MIOvCWD, version 1.0.0, CoMSES Computational Model Library: 2019. Available online: https://www.comses.net/codebases/31ff492f-bf2a-4b5c-8ebf-078d27579a9d/releases/1.0.0/ (accessed on 6 May 2024).
- Belsare, A.V. MiOVPop Version 1.1.0, CoMSES Computational Model Library: 2019. Available online: https://www.comses.net/codebases/7a376ee4-74db-4a84-924a-ecda12d6d839/releases/1.1.0/ (accessed on 6 May 2024).
- Belsare, A.V.; Stewart, C.M. Ov CWD: An agent-based modeling framework for informing chronic wasting disease management in white-tailed deer populations. Ecol. Solut. Evid. 2020, 1, e12017. [Google Scholar] [CrossRef]
- Long, E.S.; Diefenbach, D.R.; Rosenberry, C.S.; Wallingford, B.D. Multiple proximate and ultimate causes of natal dispersal in white-tailed deer. Behav. Ecol. 2008, 19, 1235–1242. [Google Scholar] [CrossRef]
- Long, E.S.; Diefenbach, D.R.; Rosenberry, C.S.; Wallingford, B.D.; Grund, M.D. Forest cover influences dispersal distance of white-tailed deer. J. Mammal. 2005, 86, 623–629. [Google Scholar] [CrossRef]
- Sciaini, M.; Fritsch, M.; Scherer, C.; Simpkins, C.E. NLMR and landscapetools: An integrated environment for simulating and modifying neutral landscape models in R. Methods Ecol. Evol. 2018, 9, 2240–2248. [Google Scholar] [CrossRef]
- Gardner, R.H.; Milne, B.T.; Turnei, M.G.; O’Neill, R.V. Neutral models for the analysis of broad-scale landscape pattern. Landsc. Ecol. 1987, 1, 19–28. [Google Scholar] [CrossRef]
- Rahimi, E.; Barghjelveh, S.; Dong, P. Estimating landscape structure effects on pollination for management of agricultural landscapes. Ecol. Process. 2021, 10, 59. [Google Scholar] [CrossRef]
- Keyser, P.D.; Guynn, D.C., Jr.; Hill, H.S., Jr. Density-dependent recruitment patterns in white-tailed deer. Wildl. Soc. Bull. 2005, 33, 222–232. [Google Scholar] [CrossRef]
- Hoarau, A.O.G.; Mavingui, P.; Lebarbenchon, C. Coinfections in wildlife: Focus on a neglected aspect of infectious disease epidemiology. PLoS Pathog. 2020, 16, 1–5. [Google Scholar] [CrossRef]
- Nieto, N.; Foley, J. Meta-Analysis of Coinfection and Coexposure with Borrelia burgdorferi and Anaplasma phagocytophilum in Humans, Domestic Animals, Wildlife and Ixodes ricinus-Comples Ticks. Vector-Borned Zoonotic Dis. 2009, 9, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Hoff, G.; Trainer, D. Observations of Bluetongue and Epizootic Hemorrhagic Disease Viruses in White-tailed deer: (1) Distribution of virus in the blood (2) Cross-challenge. J. Wildl. Dis. 1974, 10, 25–31. [Google Scholar] [CrossRef] [PubMed]
- Quist, C.; Howerth, E.; Stallknecht, D.; Brown, J.; Pisell, T.; Nettles, V. Host Defense Responses Associated with Experimental Hemorrhagic Disease in White-tailed deer. J. Wildl. Dis. 1997, 33, 584–599. [Google Scholar] [CrossRef]
- Ramsay, C.; Rohr, J. The application of community ecology theory to co-infections in wildlife hosts. Ecology 2021, 102, e03253. [Google Scholar] [CrossRef]
- Heberlein, T.A. “Fire in the Sistine Chapel”: How Wisconsin Responded to Chronic Wasting Disease. Hum. Dimens. Wildl. 2004, 9, 165–179. [Google Scholar] [CrossRef]
- Uehlinger, F.D.; Johnston, A.C.; Bollinger, T.K.; Waldner, C.L. Systematic review of management strategies to control chronic wasting disease in wild deer populations in North America. BMC Vet. Res. 2016, 12, 173. [Google Scholar] [CrossRef]
- Fischer, J.R.; Hansen, L.P.; Fales, W.H.; Gosser, H.S.; Turk, R.; Miller, A. An Epizootic of Hemorragic Disease in White-tailed Deer (Odocoileus virginianus) in Missouri: Necropsy Findings and Population Impact. J. Wildl. Dis. 1995, 31, 30–36. [Google Scholar] [CrossRef]
- Pybus, M.J.; Ravi, M.; Pollock, C.; Management, W. Epizootic Hemorrhagic Disease in Alberta, Canada. J. Wildl. Dis. 2014, 50, 720–722. [Google Scholar] [CrossRef] [PubMed]
- Roughton, R.D. An outbreak of a hemorrhagic disease in white-tailed deer in Kentucky. J. Wildl. Dis. 1975, 11, 177–186. [Google Scholar] [CrossRef]
- Sleeman, J.M.; Howell, J.E.; Knox, W.M.; Stenger, P.J. Incidence of Hemorrhagic Disease in White-Tailed Deer Is Associated with Winter and Summer Climatic Conditions. Ecohealth 2009, 6, 11–15. [Google Scholar] [CrossRef]
- Gaydos, J.K.; Davidson, W.R.; Elvinger, F.; Mead, D.G.; Howerth, E.W.; Stallknecht, D.E. Innate resistance to epizootic hemorrhagic disease in white-tailed deer. J. Wildl. Dis. 2002, 38, 713–719. [Google Scholar] [CrossRef] [PubMed]
- Stallknecht, D.E.; Luttrell, M.P.; Smith, K.E. Hemorrhagic Disease Enzootic Stability in White-tailed Deer in Texas: A Case for enzootic stability. J. Wildl. Dis. 1996, 32, 695–700. [Google Scholar] [CrossRef]
- Habib, T.J.; Merrill, E.H.; Pybus, M.J.; Coltman, D.W. Modelling landscape effects on density-contact rate relationships of deer in eastern Alberta: Implications for chronic wasting disease. Ecol. Model. 2011, 222, 2722–2732. [Google Scholar] [CrossRef]
- Storm, D.J.; Samuel, M.D.; Rolley, R.E.; Shelton, P.; Keuler, N.S.; Richards, B.J.; Van Deelen, T.R. Deer density and disease prevalence influence transmission of chronic wasting disease in white-tailed deer. Ecosphere 2013, 4, 1–14. [Google Scholar] [CrossRef]
- Belsare, A.; Gompper, M.; Keller, B.; Sumners, J.; Hansen, L.; Millspaugh, J. Size matters: Sample size assessments for chronic wasting disease surveillance using an agent-based modeling framework. MethodsX 2020, 7, 100953. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strasburg, M.; Christensen, S. Evaluating the Interaction of Emerging Diseases on White-Tailed Deer Populations Using an Agent-Based Modeling Approach. Pathogens 2024, 13, 545. https://doi.org/10.3390/pathogens13070545
Strasburg M, Christensen S. Evaluating the Interaction of Emerging Diseases on White-Tailed Deer Populations Using an Agent-Based Modeling Approach. Pathogens. 2024; 13(7):545. https://doi.org/10.3390/pathogens13070545
Chicago/Turabian StyleStrasburg, Miranda, and Sonja Christensen. 2024. "Evaluating the Interaction of Emerging Diseases on White-Tailed Deer Populations Using an Agent-Based Modeling Approach" Pathogens 13, no. 7: 545. https://doi.org/10.3390/pathogens13070545




