Conformational and Stability Analysis of SARS-CoV-2 Spike Protein Variants by Molecular Simulation
Abstract
1. Introduction
2. Materials and Methods
2.1. All-Atom Molecular Dynamics Simulation
2.2. Selection of Collective Variables
2.3. Probability Distribution of Conformational States
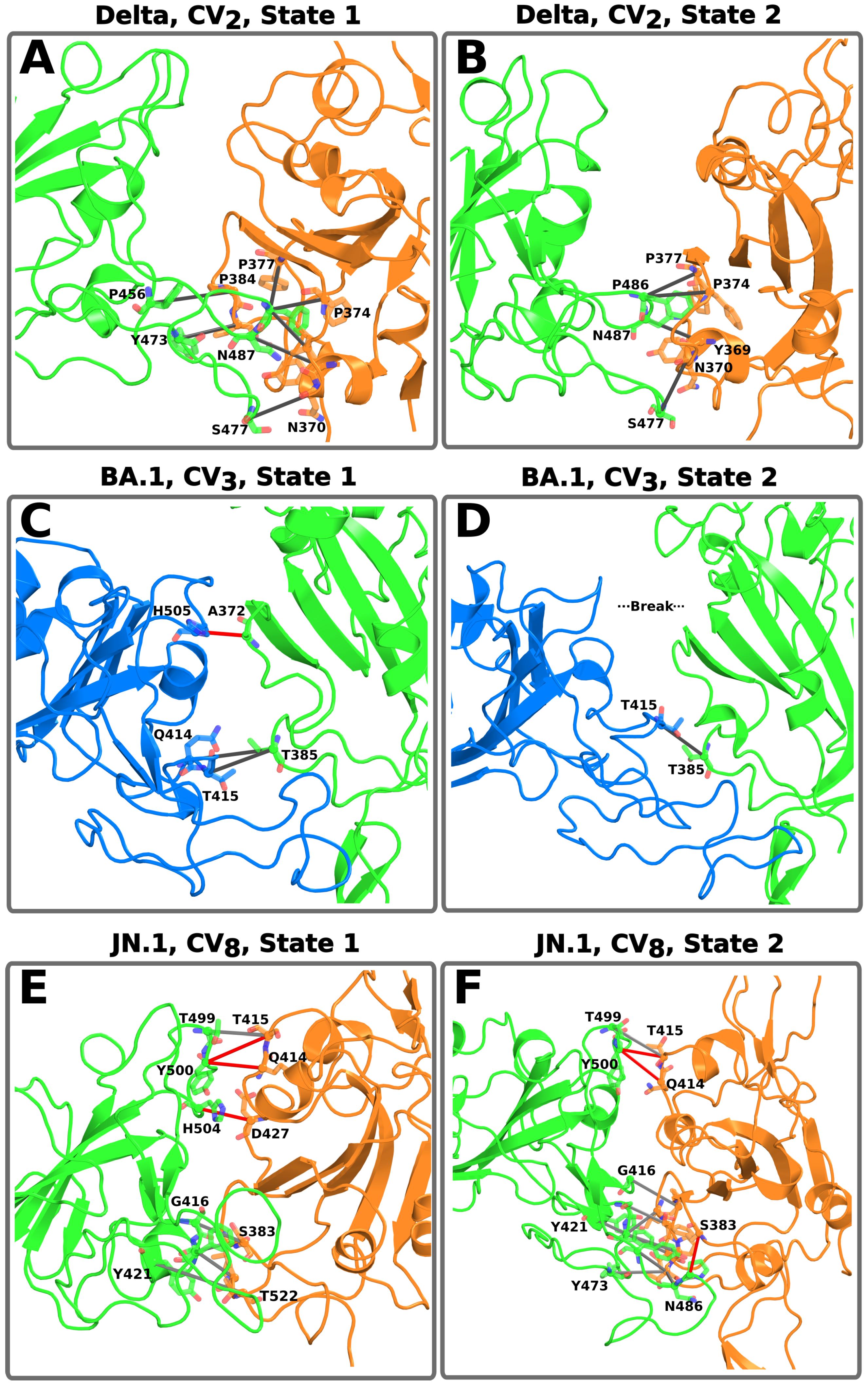
2.4. Calculation of Native Contacts in MD Simulation
3. Results and Discussion
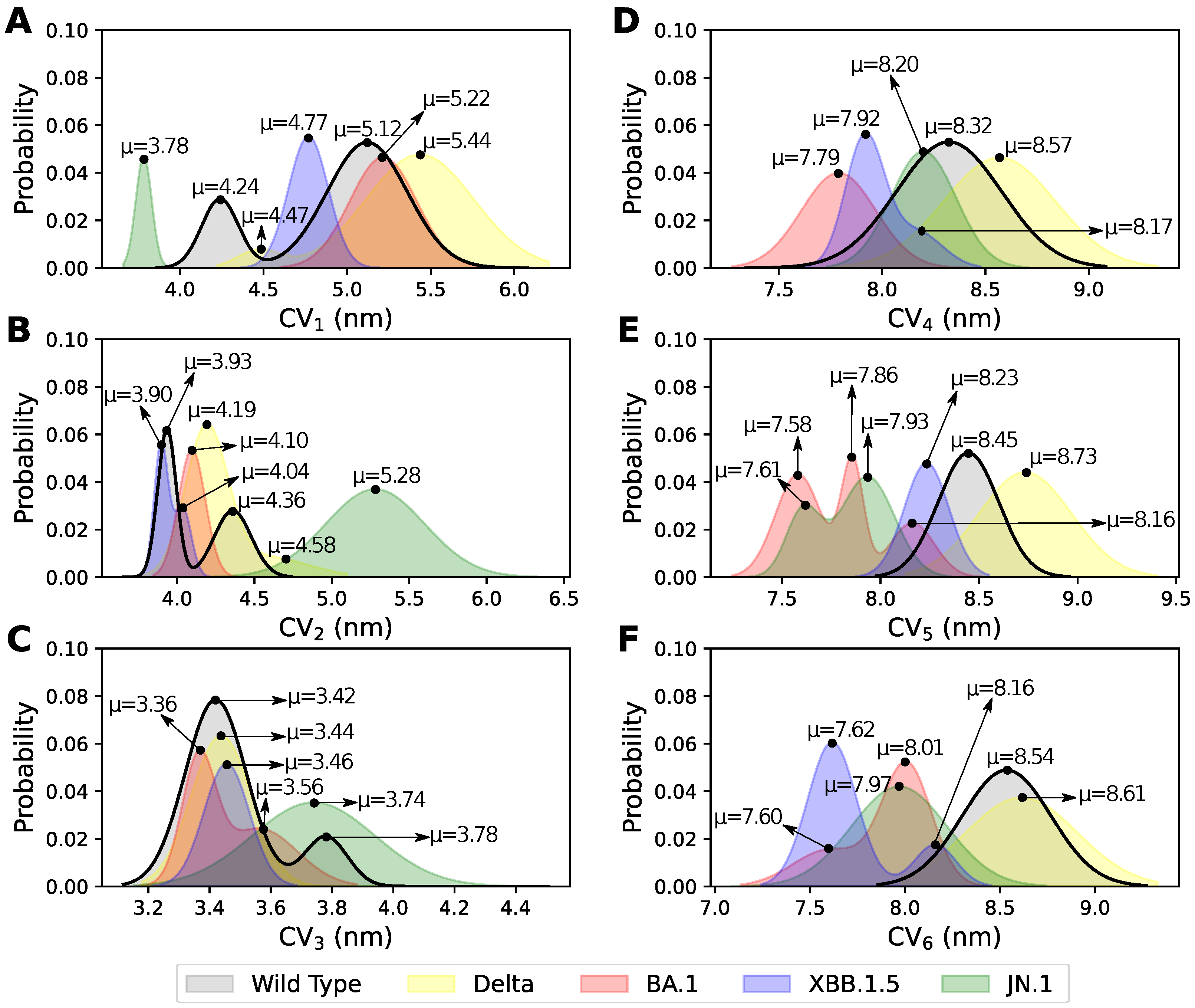
3.1. Elucidating the Conformational States Between Two RBDs
3.2. Conformational States and NCs Identified Between Two NTDs
3.3. Conformational States and NCs Identified with Angle Between RBD-HR1 Subunits
3.4. Role of the Mutations on the Conformational States of the S Protein
4. Conclusions and Perspectives
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Shaw, D.E. How fast-folding proteins fold. Science 2011, 334, 517–520. [Google Scholar] [CrossRef] [PubMed]
- Prašnikar, E.; Ljubič, M.; Perdih, A.; Borišek, J. Machine learning heralding a new development phase in molecular dynamics simulations. Artif. Intell. Rev. 2024, 57, 102. [Google Scholar] [CrossRef]
- Ramanathan, A.; Agarwal, P.K. Computational identification of slow conformational fluctuations in proteins. J. Phys. Chem. B 2009, 113, 16669–16680. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Prinz, J.H.; Wu, H.; Sarich, M.; Keller, B.; Senne, M.; Held, M.; Chodera, J.D.; Schütte, C.; Noé, F. Markov models of molecular kinetics: Generation and validation. J. Chem. Phys. 2011, 134, 174105. [Google Scholar] [CrossRef]
- Wang, W.; Cao, S.; Zhu, L.; Huang, X. Constructing Markov State Models to elucidate the functional conformational changes of complex biomolecules. WIREs Comput. Mol. Sci. 2018, 8, e1343. [Google Scholar] [CrossRef]
- Henderson, R.; Edwards, R.J.; Mansouri, K.; Janowska, K.; Stalls, V.; Gobeil, S.; Kopp, M.; Li, D.; Parks, R.; Hsu, A.; et al. Controlling the SARS-CoV-2 spike glycoprotein conformation. Nat. Struct. Mol. Biol. 2020, 27, 925–933. [Google Scholar] [CrossRef]
- Wrapp, D.; Wang, N.; Corbett, K.S.; Goldsmith, J.A.; Hsieh, C.L.; Abiona, O.M.; Graham, B.S.; McLellan, J.S. Cryo-EM structure of the 2019-nCoV spike in the prefusion conformation. Science 2020, 367, 1260–1263. [Google Scholar] [CrossRef]
- Moreira, R.A.; Chwastyk, M.; Baker, J.L.; Guzman, H.V.; Poma, A.B. Quantitative determination of mechanical stability in the novel coronavirus spike protein. Nanoscale 2020, 12, 16409–16413. [Google Scholar] [CrossRef]
- Ray, A.; Minh Tran, T.T.; Santos Natividade, R.d.; Moreira, R.A.; Simpson, J.D.; Mohammed, D.; Koehler, M.; L Petitjean, S.J.; Zhang, Q.; Bureau, F.; et al. Single-molecule investigation of the binding interface stability of SARS-CoV-2 variants with ACE2. ACS Nanosci. Au 2024, 4, 136–145. [Google Scholar] [CrossRef]
- Yan, R.; Zhang, Y.; Li, Y.; Xia, L.; Guo, Y.; Zhou, Q. Structural basis for the recognition of SARS-CoV-2 by full-length human ACE2. Science 2020, 367, 1444–1448. [Google Scholar] [CrossRef]
- Walls, A.C.; Park, Y.; Tortorici, M.A.; Wall, A.; McGuire, A.T.; Veesler, D. Structure, function, and antigenicity of the SARS-CoV-2 spike glycoprotein. Cell 2020, 181, 281–292.e6. [Google Scholar] [CrossRef] [PubMed]
- Klinakis, A.; Cournia, Z.; Rampias, T. N-terminal domain mutations of the spike protein are structurally implicated in epitope recognition in emerging SARS-CoV-2 strains. Comput. Struct. Biotechnol. J. 2021, 19, 5556–5567. [Google Scholar] [CrossRef] [PubMed]
- Ciccozzi, M.; Pascarella, S. Two sides of the same coin: The n-terminal and the receptor-binding domains of SARS-CoV-2 spike. Future Virol. 2023, 18, 75–78. [Google Scholar] [CrossRef]
- Pang, Y.T.; Acharya, A.; Lynch, D.L.; Pavlova, Á.; Gumbart, J.C. SARS-CoV-2 spike opening dynamics and energetics reveal the individual roles of glycans and their collective impact. Commun. Biol. 2022, 5, 1170. [Google Scholar] [CrossRef]
- Guruprasad, L.; Naresh, G.K.; Boggarapu, G. Taking stock of the mutations in human SARS-CoV-2 spike proteins: From early days to nearly the end of COVID-19 pandemic. Curr. Res. Struct. Biol. 2023, 6, 100107. [Google Scholar] [CrossRef] [PubMed]
- McCrone, J.; Hill, V.; Bajaj, S.; Pena, R.E.; Lambert, B.; Inward, R.; Bhatt, S.; Volz, E.; Ruis, C.; Dellicour, S.; et al. Context-specific emergence and growth of the SARS-CoV-2 Delta variant. Nature 2022, 610, 154–160. [Google Scholar] [CrossRef]
- Li, K.; Melnychuk, S.D.; Sandstrom, P.; Ji, H. Tracking the evolution of the SARS-CoV-2 delta variant of concern: Analysis of genetic diversity and selection across the whole viral genome. Front. Microbiol. 2023, 14, 1222301. [Google Scholar] [CrossRef]
- Zhang, L.; Jackson, C.B.; Mou, H.; Ojha, A.; Peng, H.; Quinlan, B.D.; Rangarajan, E.S.; Pan, A.; Vanderheiden, A.; Suthar, M.S.; et al. SARS-CoV-2 spike-protein D614G mutation increases virion spike density and infectivity. Nat. Commun. 2020, 11, 6013. [Google Scholar] [CrossRef]
- Dhawan, M.; Sharma, A.; Choudhary, P.; Thakur, N.; Rajkhowa, T.; Choudhary, O.P. Delta variant (B.1.617.2) of SARS-CoV-2: Mutations, impact, challenges and possible solutions. Hum. Vaccines Immunother. 2022, 18, 2068883. [Google Scholar] [CrossRef]
- Shrestha, L.B.; Foster, C.S.P.; Rawlinson, W.D.; Tedla, N.; Bull, R.A. Evolution of the SARS-CoV-2 omicron variants BA.1 to BA.5: Implications for immune escape and transmission. Rev. Med. Virol. 2022, 32, e2381. [Google Scholar] [CrossRef]
- Kumar, S.; Karuppanan, K.; Subramaniam, G. Omicron (BA.1) and sub-variants (BA.1.1, BA.2, and BA.3) of SARS-CoV-2 spike infectivity and pathogenicity: A comparative sequence and structural-based computational assessment. J. Med. Virol. 2022, 94, 4780–4791. [Google Scholar] [CrossRef] [PubMed]
- Parums, D.V. Editorial: The xbb.1.5 (‘kraken’) subvariant of omicron SARS-CoV-2 and its rapid global spread. Med. Sci. Monit. 2023, 29, e939580-1. [Google Scholar] [CrossRef]
- Satapathy, P.; Kumar, P.; Mehta, V.; Suresh, V.; Khare, A.; Rustagi, S.; Daulati, M.N.; Neyazi, M.; Najafi, E.; Neyazi, A. Global spread of COVID-19’s JN.1 variant: Implications and public health responses. New Microbes New Infect. 2024, 57, 101225. [Google Scholar] [CrossRef]
- Kaku, Y.; Okumura, K.; Padilla-Blanco, M.; Kosugi, Y.; Uriu, K.; Hinay, A.A.; Chen, L.; Plianchaisuk, A.; Kobiyama, K.; Ishii, K.J.; et al. Virological characteristics of the SARS-CoV-2 JN.1 variant. Lancet Infect. Dis. 2024, 24, e82. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Ao, D.; He, X.; Wei, X. The rising SARS-CoV-2 JN.1 variant: Evolution, infectivity, immune escape, and response strategies. MedComm 2024, 5, e675. [Google Scholar] [CrossRef] [PubMed]
- Haslwanter, D.; Dieterle, M.E.; Wec, A.Z.; O’Brien, C.M.; Sakharkar, M.; Florez, C.; Tong, K.; Rappazzo, C.G.; Lasso, G.; Vergnolle, O.; et al. A combination of receptor-binding domain and n-terminal domain neutralizing antibodies limits the generation of SARS-CoV-2 spike neutralization-escape mutants. mBio 2021, 12, e02473-21. [Google Scholar] [CrossRef]
- Barton, M.I.; MacGowan, S.A.; Kutuzov, M.A.; Dushek, O.; Barton, G.J.; Merwe, P.A.v.d. Effects of common mutations in the SARS-CoV-2 spike RBD and its ligand, the human ace2 receptor on binding affinity and kinetics. eLife 2021, 10, e70658. [Google Scholar] [CrossRef]
- Koehler, M.; Ray, A.; Moreira, R.A.; Juniku, B.; Poma, A.B.; Alsteens, D. Molecular insights into receptor binding energetics and neutralization of SARS-CoV-2 variants. Nat. Commun. 2021, 12, 6977. [Google Scholar] [CrossRef]
- Laffeber, C.; Koning, K.d.; Kanaar, R.; Lebbink, J.H. Experimental evidence for enhanced receptor binding by rapidly spreading SARS-CoV-2 variants. J. Mol. Biol. 2021, 433, 167058. [Google Scholar] [CrossRef]
- Sztain, T.; Ahn, S.; Bogetti, A.T.; Casalino, L.; Goldsmith, J.A.; Seitz, E.; McCool, R.S.; Kearns, F.L.; Acosta-Reyes, F.; Maji, S.; et al. A glycan gate controls opening of the SARS-CoV-2 spike protein. Nat. Chem. 2021, 13, 963–968. [Google Scholar] [CrossRef]
- Cofas-Vargas, L.; Moreira, R.; Poblete, S.; Chwastyk, M.; Poma, A. The Gōmartini approach: Revisiting the concept of contact maps and the modelling of protein complexes. Acta Phys. Pol. A 2024, 145, S9–S20. [Google Scholar] [CrossRef]
- Best, R.B.; Hummer, G.; Eaton, W.A. Native contacts determine protein folding mechanisms in atomistic simulations. Proc. Natl. Acad. Sci. USA 2013, 110, 17874–17879. [Google Scholar] [CrossRef] [PubMed]
- Duarte, J.M.; Sathyapriya, R.; Stehr, H.; Filippis, I.; Lappé, M. Optimal contact definition for reconstruction of contact maps. BMC Bioinform. 2010, 11, 283. [Google Scholar] [CrossRef] [PubMed]
- Noel, J.K.; Whitford, P.C.; Onuchic, J.N. The shadow map: A general contact definition for capturing the dynamics of biomolecular folding and function. J. Phys. Chem. B 2012, 116, 8692–8702. [Google Scholar] [CrossRef]
- Poupon, A. Voronoi and voronoi-related tessellations in studies of protein structure and interaction. Curr. Opin. Struct. Biol. 2004, 14, 233–241. [Google Scholar] [CrossRef]
- Tsai, J.; Taylor, R.; Chothia, C.; Gerstein, M. The packing density in proteins: Standard radii and volumes. J. Mol. Biol. 1999, 290, 253–266. [Google Scholar] [CrossRef]
- Sobolev, V.M.; Sorokin, A.; Prilusky, J.; Abola, E.E.; Edelman, M. Automated analysis of interatomic contacts in proteins. Bioinformatics 1999, 15, 327–332. [Google Scholar] [CrossRef]
- Woĺek, K.; Gómez-Sicilia, Á.; Cieplak, M. Determination of contact maps in proteins: A combination of structural and chemical approaches. J. Chem. Phys. 2015, 143, 243105. [Google Scholar] [CrossRef]
- Huang, E.S.; Subbiah, S.; Levitt, M. Recognizing native folds by the arrangement of hydrophobic and polar residues. J. Mol. Biol. 1995, 252, 709–720. [Google Scholar] [CrossRef]
- Gō, N. Protein folding as a stochastic process. J. Stat. Phys. 1983, 30, 413–423. [Google Scholar] [CrossRef]
- Pedersen, K.B.; Borges-Araújo, L.; Stange, A.D.; Souza, P.C.T.; Marrink, S.J.; Schiøtt, B. Olives: A gō-like model for stabilizing protein structure via hydrogen bonding native contacts in the Martini 3 coarse-grained force field. J. Chem. Theory Comput. 2024, 20, 8049–8070. [Google Scholar] [CrossRef] [PubMed]
- Souza, P.C.T.; Borges-Araújo, L.; Brasnett, C.; Moreira, R.A.; Grünewald, F.; Park, P.; Wang, L.; Razmazma, H.; Borges-Araújo, A.C.; Cofas-Vargas, L.F.; et al. Gōmartini 3: From large conformational changes in proteins to environmental bias corrections. BioRxiv 2024. [Google Scholar] [CrossRef]
- Moreira, R.A.; Chwastyk, M.; Baker, J.L.; Guzman, H.V.; Poma, A.B. All atom simulations snapshots and contact maps analysis scripts for SARS-CoV-2002 and SARS-CoV-2 spike proteins with and without ACE2 enzyme. Zenodo 2020. [Google Scholar] [CrossRef]
- Moreira, R.A.; Guzman, H.V.; Boopathi, S.; Baker, J.L.; Poma, A.B. Characterization of structural and energetic differences between conformations of the SARS-CoV-2 spike protein. Materials 2020, 13, 5362. [Google Scholar] [CrossRef] [PubMed]
- Maier, J.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.; Simmerling, C. Ff14sb: Improving the accuracy of protein side chain and backbone parameters from ff99sb. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef]
- Jorgensen, W.L. Quantum and statistical mechanical studies of liquids. 10. transferable intermolecular potential functions for water, alcohols, and ethers. application to liquid water. J. Am. Chem. Soc. 1981, 103, 335–340. [Google Scholar] [CrossRef]
- Åqvist, J.; Wennerström, P.; Nervall, M.; Bjelic, S.; Brandsdal, B.O. Molecular dynamics simulations of water and biomolecules with a monte carlo constant pressure algorithm. Chem. Phys. Lett. 2004, 384, 288–294. [Google Scholar] [CrossRef]
- Hopkins, C.W.; Grand, S.L.; Walker, R.C.; Roitberg, A.E. Long-time-step molecular dynamics through hydrogen mass repartitioning. J. Chem. Theory Comput. 2015, 11, 1864–1874. [Google Scholar] [CrossRef]
- Berman, H.M. The protein data bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef]
- Šali, A.; Blundell, T.L. Comparative protein modelling by satisfaction of spatial restraints. J. Mol. Biol. 1993, 234, 779–815. [Google Scholar] [CrossRef]
- Eastman, P.; Swails, J.M.; Chodera, J.D.; McGibbon, R.T.; Zhao, Y.; Beauchamp, K.A.; Wang, L.; Simmonett, A.C.; Harrigan, M.P.; Stern, C.; et al. Openmm 7: Rapid development of high performance algorithms for molecular dynamics. PLoS Comput. Biol. 2017, 13, e1005659. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Aktulga, H.M.; Belfon, K.; Cerutti, D.S.; Cisneros, G.A.; Cruzeiro, V.W.D.; Forouzesh, N.; Giese, T.J.; Götz, A.W.; Gohlke, H.; et al. Ambertools. J. Chem. Inf. Model. 2023, 63, 6183–6191. [Google Scholar] [CrossRef] [PubMed]
- Tian, C.; Kasavajhala, K.; Belfon, K.; Raguette, L.; Huang, H.; Migues, A.N.; Bickel, J.; Wang, Y.; Pincay, J.; Wu, Q.; et al. Ff19sb: Amino-acid-specific protein backbone parameters trained against quantum mechanics energy surfaces in solution. J. Chem. Theory Comput. 2019, 16, 528–552. [Google Scholar] [CrossRef]
- Salomón-Ferrer, R.; Götz, A.W.; Poole, D.; Grand, S.L.; Walker, R.C. Routine microsecond molecular dynamics simulations with Amber on GPUs. 2. Explicit solvent particle mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef]
- Izadi, S.; Anandakrishnan, R.; Onufriev, A.V. Building water models: A different approach. J. Phys. Chem. Lett. 2014, 5, 3863–3871. [Google Scholar] [CrossRef]
- Swails, J. ParmEd. 2024. Available online: https://github.com/ParmEd/ParmEd (accessed on 12 December 2024).
- Sindhikara, D.J.; Kim, S.; Voter, A.F.; Roitberg, A.E. Bad seeds sprout perilous dynamics: Stochastic thermostat induced trajectory synchronization in biomolecules. J. Chem. Theory Comput. 2009, 5, 1624–1631. [Google Scholar] [CrossRef]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Poma, A.B.; Thu, T.T.M.; Tri, L.T.M.; Nguyen, H.L.; Li, M.S. Nanomechanical stability of Aβ tetramers and fibril-like structures: Molecular dynamics simulations. J. Phys. Chem. B 2021, 125, 7628–7637. [Google Scholar] [CrossRef]
- Olivos-Ramirez, G.E.; Poma, A.; Cofas-Vargas, L.F. Conformational dynamics and stability analysis of SARS-CoV-2 Spike glycoprotein. Zenodo 2025. [Google Scholar] [CrossRef]
- Arbeitman, C.R.; Rojas, P.A.; Ojeda-May, P.; Garcia, M.E. The SARS-CoV-2 spike protein is vulnerable to moderate electric fields. Nat. Commun. 2021, 12, 5407. [Google Scholar] [CrossRef]
- Olukitibi, T.A.; Ao, Z.; Warner, B.M.; Unat, R.; Kobasa, D.; Yao, X. Significance of conserved regions in coronavirus spike protein for developing a novel vaccine against SARS-CoV-2 infection. Vaccines 2023, 11, 545. [Google Scholar] [CrossRef] [PubMed]
- Pondé, R.A.d.A. Physicochemical effect of the N501Y, E484K/Q, K417N/T, L452R and T478K mutations on the SARS-CoV-2 spike protein RBD and its influence on agent fitness and on attributes developed by emerging variants of concern. Virology 2022, 572, 44–54. [Google Scholar] [CrossRef] [PubMed]
- Goher, S.S.; Ali, F.; Amin, M. The delta variant mutations in the receptor binding domain of SARS-CoV-2 show enhanced electrostatic interactions with the ACE2. Med. Drug Discov. 2022, 13, 100114. [Google Scholar] [CrossRef]
- Zaheer, M.; Ali, N.S.; Javed, H.; Munir, R.; Jamil, N. Uncovering the impact of SARS-CoV-2 spike protein variants on human receptors: A molecular dynamics docking and simulation approach. J. Infect. Public Health 2023, 16, 1544–1555. [Google Scholar] [CrossRef]
- Cheng, Y.; Zheng, D.; Zhang, D.; Du, G.; Wang, Y.; Liu, W.; Liang, L.; Hu, J.; Luo, T. Molecular recognition of SARS-CoV-2 spike protein with three essential partners: Exploring possible immune escape mechanisms of viral mutants. J. Mol. Model. 2023, 29, 109. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.B.; Yang, B.; Lei, Z.H.; Zhang, X.F.; Li, J.; Li, S.S.; Dong, Z.; Liang, Y.; Li, Q.M.; Su, J.G. Identification of key mutations responsible for the enhancement of receptor-binding affinity and immune escape of SARS-CoV-2 omicron variant. J. Mol. Graph. Model. 2023, 124, 108540. [Google Scholar] [CrossRef]
- Božič, A.; Podgornik, R. Changes in total charge on spike protein of SARS-CoV-2 in emerging lineages. Bioinform. Adv. 2024, 4, vbae053. [Google Scholar] [CrossRef]
- Dokainish, H.; Re, S.; Mori, T.; Kobayashi, C.; Jung, J.; Sugita, Y. The inherent flexibility of receptor binding domains in SARS-CoV-2 spike protein. eLife 2022, 11, e75720. [Google Scholar] [CrossRef]
- Wu, Y.; Qian, R.; Yang, Y.; Sheng, Y.; Li, W.; Wang, W. Activation pathways and free energy landscapes of the SARS-CoV-2 spike protein. ACS Omega 2021, 6, 23432–23441. [Google Scholar] [CrossRef]
- Dommer, A.C.; Casalino, L.; Kearns, F.L.; Rosenfeld, M.A.; Wauer, N.; Ahn, S.; Russo, J.D.; Oliveira, A.S.F.; Morris, C.K.; Bogetti, A.T.; et al. #COVIDisairborne: AI-enabled multiscale computational microscopy of delta SARS-CoV-2 in a respiratory aerosol. Int. J. High Perform. Comput. Appl. 2022, 37, 28–44. [Google Scholar] [CrossRef]
- Springer, D.N.; Camp, J.V.; Aberle, S.W.; Deutsch, J.; Lammel, O.; Weseslindtner, L.; Stiasny, K.; Aberle, J.H. Neutralization of SARS-CoV-2 omicron XBB.1.5 and JN.1 variants after COVID-19 booster-vaccination and infection. J. Med. Virol. 2024, 96, e29801. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Guo, H.; Wang, A.; Cao, L.; Fan, Q.; Jiang, J.; Wang, M.; Lin, L.; Ge, X.; Wang, H.; et al. Structural basis for the evolution and antibody evasion of SARS-CoV-2 BA.2.86 and JN.1 subvariants. Nat. Commun. 2024, 15, 7715. [Google Scholar] [CrossRef]
- Tian, J.; Shang, B.; Zhang, J.; Guo, Y.; Li, M.; Hu, Y.; Bai, D.; She, J.; Han, Y.; Guo, P.; et al. T cell immune evasion by SARS-CoV-2 JN.1 escapees targeting two cytotoxic T cell epitope hotspots. Nat. Immunol. 2025, 26, 265–278. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Maurya, S.; Tripathi, T.; Padhi, A.K. Integrated all-atom and coarse-grained simulations uncover structural, dynamics and energetic shifts in SARS-CoV-2 JN.1 and BA.2.86 variants. Acta Trop. 2024, 260, 107444. [Google Scholar] [CrossRef]
- Paciello, I.; Maccari, G.; Pierleoni, G.; Perrone, F.; Realini, G.; Troisi, M.; Anichini, G.; Cusi, M.G.; Rappuoli, R.; Andreano, E. SARS-CoV-2 JN.1 variant evasion of IGHV3-53/3-66 B cell germlines. Sci. Immunol. 2024, 9, eadp9279. [Google Scholar] [CrossRef]
- Raisinghani, N.; Alshahrani, M.; Gupta, G.; Verkhivker, G.M. Alphafold2 modeling and molecular dynamics simulations of the conformational ensembles for the SARS-CoV-2 spike omicron JN.1, KP.2 and KP.3 variants: Mutational profiling of binding energetics reveals epistatic drivers of the ACE2 affinity and escape hotspots of antibody resistance. Viruses 2024, 16, 1458. [Google Scholar] [CrossRef]

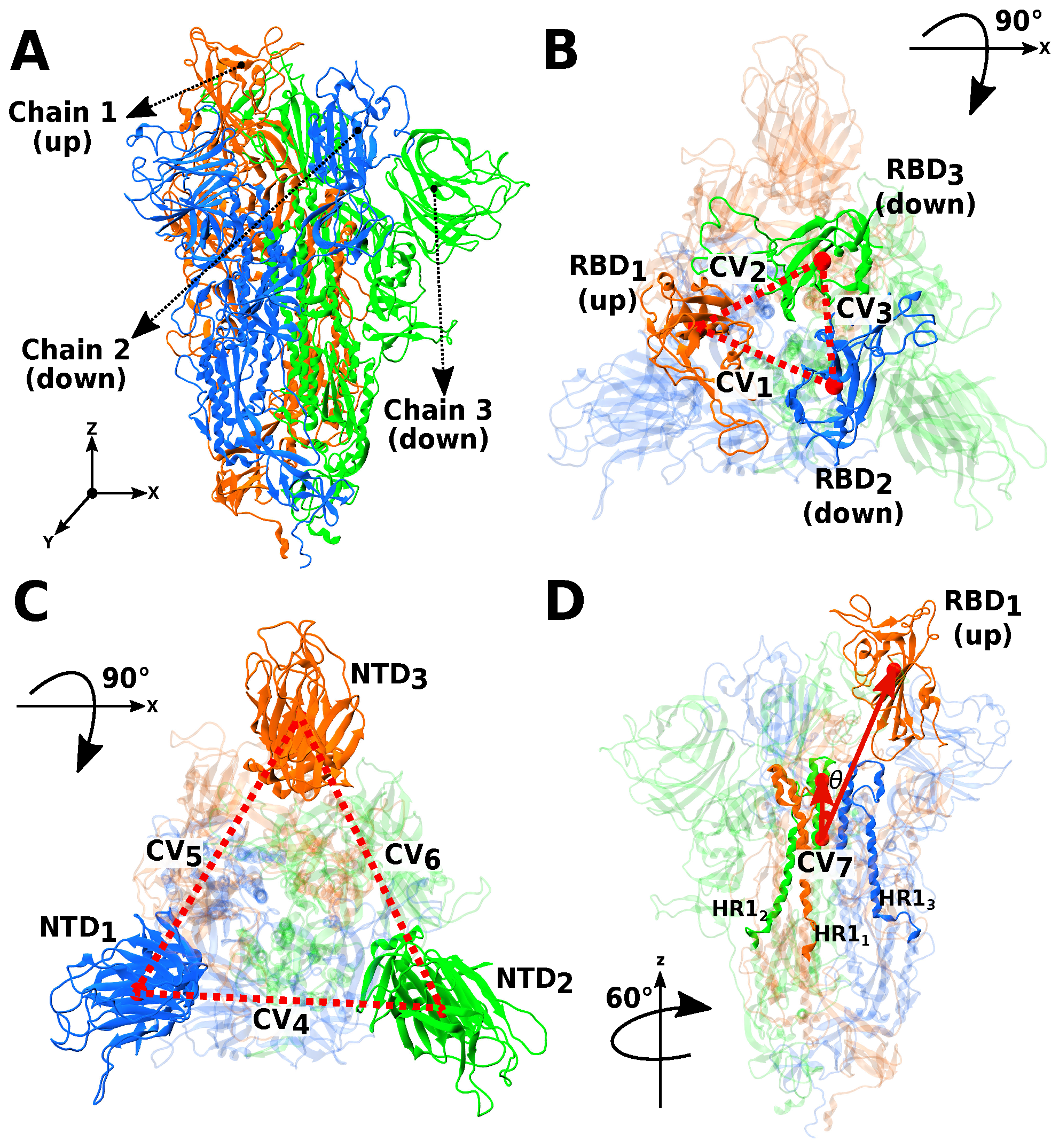

| CV | Measure | Index | Range of Residues Included in COM Calculations | |
|---|---|---|---|---|
| Type 1 | d | 1–3 | RBD1 (up): I338-W442 to Q512-G532 | RBD2 (down): I338-W442 to Q512-G532 |
| Type 2 | d | 4–6 | NTD1: A31 to F311 | NTD2: A31 to F311 |
| Type 3 | angle (°) | 7–9 | = RBD1 (up): I338-G532 and HR11– HR13: L943-Q1015 | = HR11–HR13: L943-Q1015 and HR11–HR13: S980-R1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olivos-Ramirez, G.E.; Cofas-Vargas, L.F.; Madl, T.; Poma, A.B. Conformational and Stability Analysis of SARS-CoV-2 Spike Protein Variants by Molecular Simulation. Pathogens 2025, 14, 274. https://doi.org/10.3390/pathogens14030274
Olivos-Ramirez GE, Cofas-Vargas LF, Madl T, Poma AB. Conformational and Stability Analysis of SARS-CoV-2 Spike Protein Variants by Molecular Simulation. Pathogens. 2025; 14(3):274. https://doi.org/10.3390/pathogens14030274
Chicago/Turabian StyleOlivos-Ramirez, Gustavo E., Luis F. Cofas-Vargas, Tobias Madl, and Adolfo B. Poma. 2025. "Conformational and Stability Analysis of SARS-CoV-2 Spike Protein Variants by Molecular Simulation" Pathogens 14, no. 3: 274. https://doi.org/10.3390/pathogens14030274
APA StyleOlivos-Ramirez, G. E., Cofas-Vargas, L. F., Madl, T., & Poma, A. B. (2025). Conformational and Stability Analysis of SARS-CoV-2 Spike Protein Variants by Molecular Simulation. Pathogens, 14(3), 274. https://doi.org/10.3390/pathogens14030274








