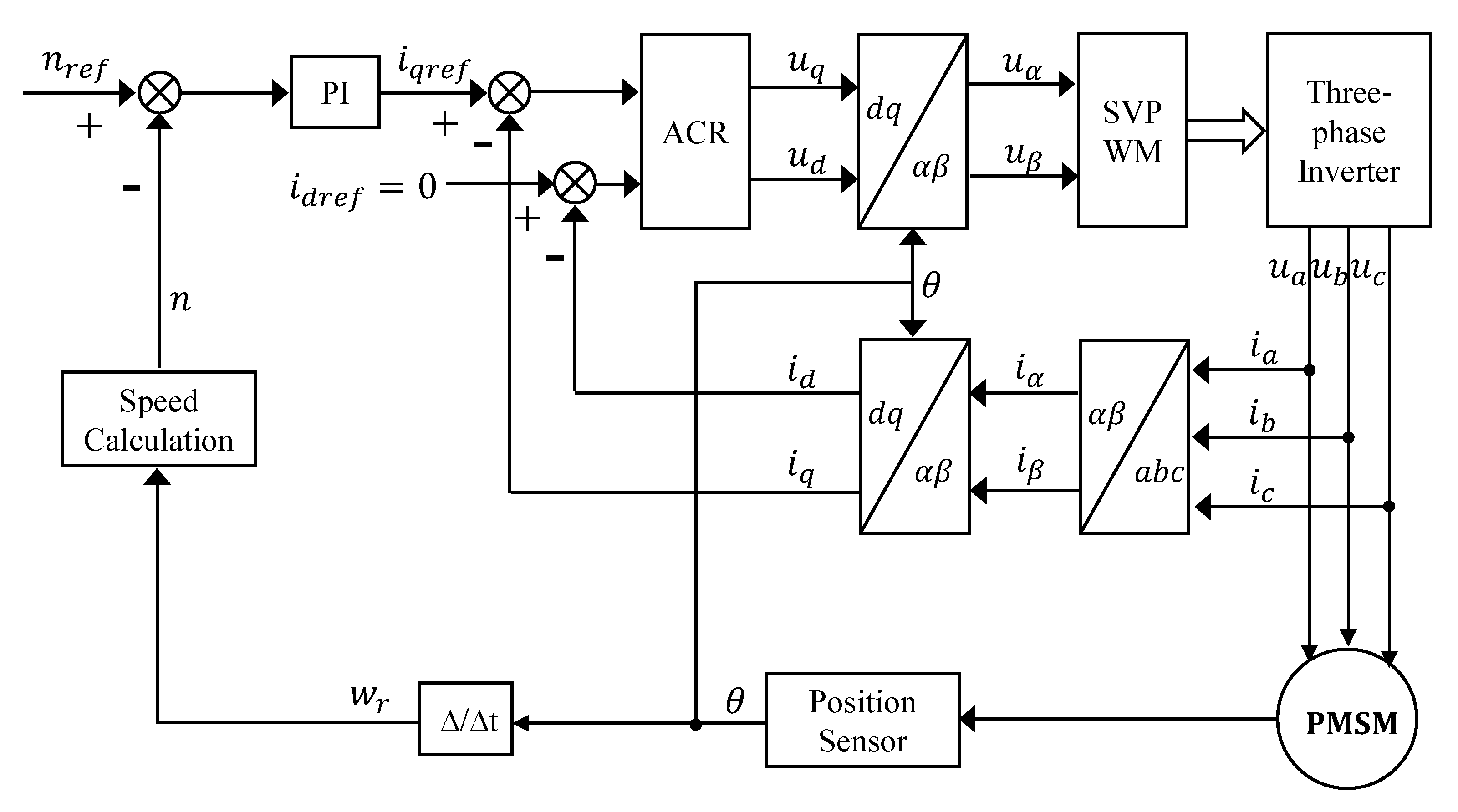
1. Introduction
The advantages of PMSM are small size, simple structure, light weight, low losses. It does not have commutator and brushes of DC motor, and it is characterized by high efficiency, high power factor, large torque inertia ratio, small current and resistance losses, high reliability and strong coupling [
1,
2,
3]. One of the more widely used control methods for these motors is the vector control method with rotor field orientation. The basic principle of operation is to decouple the magnetic field current and torque current of the motor on a synchronous coordinate system with rotor field orientation through coordinate transformation, so that it has the same operating performance as the conventional DC motor [
4,
5,
6]. The vector control system of PMSM can realize high precision, high dynamic performance, and wide range of speed regulation or positioning control, so the vector control system of PMSM has attracted a lot of attention from scholars at home and abroad [
7,
8,
9].
However, vector control only achieves the static decoupling of the two current components, not the dynamic decoupling, and the coupling voltage exists in the dynamic process, especially at high speed, the coupling voltage can even reach
of the stator voltage [
10], causing the two current components to affect each other, which makes the control performance of the system reduced. Dynamic decoupling is the compensation of coupling voltage to improve the control performance of the servo system based on the static decoupling. Here, feed-forward decoupling is used to compensate for the coupling voltage. By means of feed-forward decoupling, [
11] used a predictive current control method to improve the dynamic performance of the system, but the method is strongly influenced by the motor parameters and is not robust. Ref. [
12] applied a neural network decoupling control method, which required a large amount of experimental sample data for offline training and was relatively complicated to implement. Therefore, it is necessary to find a robust and easy-to-implement method, and high type control is such a method that meets the requirements.
High type control [
13] mainly refers to the parallel connection of one or more integrators in the forward path of the system to increase the system type and thus improve some aspect of the system performance. The integrator is an electronic component commonly used in control circuits, whose output signal is the time product of the input signal. From the physical point of view, it can convert acceleration signal into velocity signal and velocity signal into position signal, which is an essential device in the multi-closed loop system. According to the principle of automatic control, the greater the number of integrators in the forward path of a closed-loop control system, the higher the system type [
14]. Commonly used multi-closed-loop control systems are generally Type I or Type II systems. The higher the type, the smaller the steady-state error and the shorter the regulation time, but the system oscillation is also larger and extremely sensitive to disturbances, which can easily lead to system divergence [
13]. In order to overcome the instability of the high type system and retain its advantages of high accuracy, researchers have tried different approaches. Tang constructed a PID-I type system by adding an integrator to the PID controller to take advantage of the large closed-loop bandwidth of the PID so that the high-type system can accommodate more disturbances [
15]. Papadopoulos et al. designed an explicit analytical PID tuning rule for Type III control loop design based on the symmetric optimality criterion [
16]. However, this static way of increasing the system type has the pitfall that the integral satiation may occur when there is a large or high frequency sudden change in the system input, which may prevent the actuator from working properly. To solve the problem of integral saturation in high type systems, dynamic high type techniques using FLSs are proposed, adaptively turning on or off the integrator according to the system status to achieve dynamic switching type, which can improve the tracking performance of the system while avoiding the saturation of the integrator.
FLSs have an excellent ability in dealing with various uncertainties and interferences [
17,
18,
19]. At present, FLSs are mainly divided into type-1 FLSs (T1FLSs) and type-2 FLSs (T2FLSs). T1FLSs achieve a successful application in the area of fuzzy control because of its simple structure and convenient calculation. As the complexity and performance requirements of the control system increase, T1FLSs become increasingly inadequate to meet the control needs. Thus, T2FLSs, especially interval T2FLSs (IT2FLSs), have come into the limelight and are gradually being used in various fields [
20,
21,
22]. In IT2FLSs, the pros and cons of the membership parameters and the related parameters of the controller are directly reflected in the control effect. Especially for the nonlinear controlled system with high complexity and high precision, traditional parameter setting methods are often difficult to meet control requirements. In addition, because the dimension and complexity of IT2FLSs are higher than those of traditional T1FLSs, it is difficult for conventional optimization methods to obtain effective parameter configuration. Intelligent optimization algorithms [
23,
24,
25], as very popular methods in recent years, have been applied extensively for solving global optimization problems.
QPSO [
25] is an intelligent optimization algorithm based on conventional PSO idea. PSO [
24] was proposed on the basis of studies on the predatory behavior of birds. Although PSO has a wide range of applications, compared with QPSO, PSO has more parameters such as inertia weight
w, acceleration coefficient
c and scope of search space
to be set, which is not conducive to finding the global optimal solution, and for some complex nonlinear systems, the lack of randomness in particle position changes makes it easy to fall into the dilemma of local optimization. Combined quantum mechanics and PSO, QPSO improves on the shortcomings of PSO. Regarding the quantum behavior of a particle, its motion state can be described according to the quantum uncertainty principle and the global optimal solution is found throughout the feasible solution space. Therefore, QPSO is a strategy with better global convergence than PSO. Here, we employed QPSO to determine optimal parameters of FLSs.
In conclusion, in this article, based on feed-forward decoupling PI, an IT2FDHT control method using QPSO is proposed to improve dynamic performance of PMSM. The main contributions of this paper are briefly summarized as follows:
- (1)
Fuzzy dynamic high type methods are provided for the vector decoupling control of PMSM.
- (2)
Aiming at the problem that related parameters in the IT2FLSs are difficult to determine, QPSO is employed.
- (3)
In addition to the proposed method, PI, FDPI, FDPI-HT, FDPI-T1FDHT are also designed for simulations.
The remainder of the paper is structured as follows.
Section 2 introduces PMSM mathematical model and vector control in summary. Considering PMSM traditional control methods, conventional PI and FDPI are provided in
Section 3. Next, in
Section 4, we will focus on fuzzy dynamic high type methods for PMSM control. Then, in
Section 5, simulation analyses regarding PMSM are performed to demonstrate the excellence of FDPI-IT2FDHT method. Finally,
Section 6 provides the conclusion as well as future work.
4. Fuzzy Dynamic High Type Methods
In this section, firstly, we will present a detailed introduction of the QPSO algorithm. Then, the focus is the design of high type (HT) and fuzzy dynamic high type (T1FDHT and IT2FDHT).
4.1. QPSO Algorithm
For an
N-dimensional optimization problem, we assume that there are
M particles, and the position of each particle can represent a potential solution. In the
tth generation of the particle population, the
N-dimensional position of the
ith particle can be represented as
. Besides, the optimal positions of the
ith particle and the particle population are denoted as
and
, respectively.
is determined by the following equation
where the function
is the fitness function, and
is calculated by Equation (
21)
Since the position and velocity of a particle cannot be determined simultaneously in quantum space, by means of the wave function we can describe the quantum state of the particle. Finally, the improved expressions for the particle position are obtained by the Monte Carlo method
where
is the contraction-expansion coefficient,
u as well as
are random numbers between 0 and 1, and the mean optimal position
is
4.2. High Type
As mentioned in introduction, high type control is mainly a structure that improves the performance of a system in some way by adding one or more integrators to the forward path of the system.
Figure 4 illustrates the structure of high type based on feed-forward decoupling PI, where
e is speed error and
is the amplification factor of speed error.
In order to explore the impact of high type structure on the stability and rapidity of the system, the following simulation verification schemes are designed:
1. The structure of
Figure 4 is embedded in the simulation experiment of PMSM.
2. Simulation experiments are conducted with k of 10, 20, 30, 40 as well as 50 and the experimental results are compared.
The above steps are followed to simulate and collect the data, respectively, and
Figure 5 and
Table 1 are obtained. In
Table 1,
is the rise time and represents the time required for the response curve to go from 10% to 90% of the steady-state value;
is the regulation time, which indicates the time required for the response curve to start from zero and enter the 95–105% error band of the steady-state value;
is the overshoot, which indicates the maximum value of the response curve deviation from the steady-state value, often expressed as a percentage. Through the intuitive comparison of pictures and data, the following conclusions can be drawn.
1. The higher the system type will reduce the rise time (), and the larger the integration gain (), the smaller the rise time, and the faster the system will respond.
2. The higher the system type will increase the overshoot (), the larger the integral gain the larger the system overshoot will be, the more violent the oscillation will be, even leading to system divergence.
3. When the overshoot is small, the larger the integral gain, the smaller the regulation time (). When the overshoot is large, the larger the integral gain, the larger the oscillation, and the regulation time increases.
In summary, high type control can significantly improve the rapidity of the system, but can introduce oscillations into the system, which in turn lead to high overshoot and poor regulation time, so simply increasing the system type is not a perfect solution for improving control performance.
4.3. Type-1 Fuzzy Dynamic High Type
Since the high type structure alone can lead to oscillation and even divergence problems, the dynamic high type technique was proposed. However, most of the related researches simply control the integrator on or off, and do not realize the standard of automatic switching type. In addition, the jitter caused by the switching instant is also difficult to eliminate. In the context of modernization, high demands are placed on the degree of automation and performance of PMSM, and the development of intelligent control technologies brings new possibilities for this purpose. Fuzzy logic, as one of the widely used intelligent control technologies, in combination with high type control structures, allows for automated dynamic high type control.
As can be seen from
Figure 6, a T1FLS usually consists of four parts: fuzzifier, inference engine, rule base, and defuzzifier. First, the measurement inputs are processed by the fuzzifier to obtain type-1 fuzzy sets (T1FSs), and these T1FSs are mapped to all membership functions (MFs) to calculate the corresponding membership degrees. Next, the inference engine further determines the firing strengths of the rules based on the predefined rules in its rule base. After determining the membership degrees and firing strengths, the T1FSs can be calculated. Finally, a defuzzifier is used to process the output T1FSs to acquire the output of the system.
The FLS is implemented by monitoring the error and error change. So, the inputs of the FLS, i.e.,
E and
, can be of the form
where
k is the sampling moment,
and
are the scale coefficients of the two inputs.
So, the structure of the fuzzy dynamic high type (FDHT) based on feed-forward decoupling PI is designed in
Figure 7.
Where is the error change, U is the output of the FLS, and is the amplification factor of the output. By using the FLS, the oscillation problem caused by the high type structure can be handled and the dynamic switching of system types can be realized.
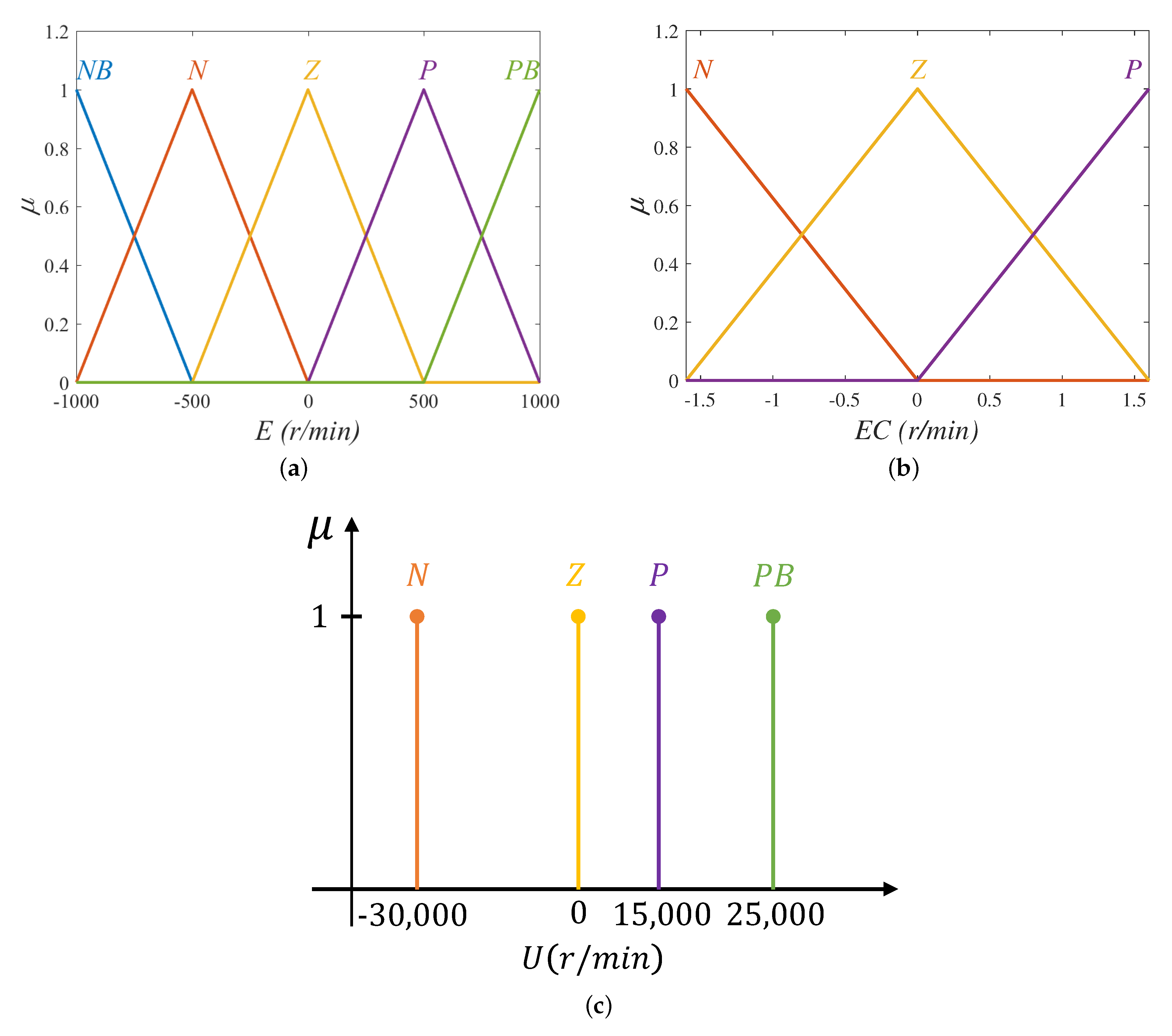
Here, we mainly describe the design of T1FLS.
Figure 8a,b, respectively, display MFs of input variable
E and
, and
Figure 8c shows MFs of output variable
U.
According to
Figure 8, the T-S T1FLS with two inputs and a single output has a total of 15 rules, and the
i-th rule has the following form
where
is the consequent,
and
are the antecedents of the
ith rule.
Through some simulations and analysis, it is found that when the output of the FLS and the error have the same sign, it will strengthen the current trend of error variation, and vice versa will weaken this trend. Thus, if
is
N, when
E is negative (
or
N), the amount of error will be increasing and we need to suppress this tendency, so the output of the FLS takes positive (
P or
), with the error difference sign. If
is
N, the amount of error gets smaller when
E is positive (
or
P), and this trend needs to be accelerated, but we find that the traditional FDPI method produces overshoot, and to avoid overshoot, the output is taken as
P or
Z. Similarly, to reduce overshoot or oscillation, the output of the FLS is
Z or
N when
E is
Z. For the sense of brevity, only the case where
is
N is described.
Table 2 lists the specific fuzzy rules of the T-S T1FLS.
By means of T1FLS, the T1FDHT based on FDPI, i.e., FDPI-T1FDHT, not only has a faster dynamic response, but can also handle a wide range of loads and perturbations. Nevertheless, faced with higher performance requirements and more load devices of PMSM, FDPI-T1FDHT is hardly perfect for the job.
4.4. Interval Type-2 Fuzzy Dynamic High Type
Figure 9 is the structure diagram of an IT2FLS. Compared with T1FLS in
Figure 6, the main difference is that IT2FLS has an additional step of type-reduction. The role of type-reduction is to transform the T2FSs into T1FSs. Here, we use the common type-reduction inference approach, namely center-of-set (COS) type-reduction [
30], to acquire T1FSs.
The input to the IT2FLS has the same form as the input to the T1FLS in Equation (
25), and the only difference is the MFs of the input and output.
Figure 10a,b present MFs of input variable
E and
in the IT2FLS, respectively.
Table 3 shows consequent MFs of output variable
U in the IT2FLS.
Regarding the rules, IT2FLS and T1FLS have the same design, as shown in
Table 2. Eventually, we provide the structure of the PMSM vector control system applying FDPI-FDHT (FDPI-T1FDHT and FDPI-IT2FDHT) methods. The dashed box at the top of
Figure 11 describes the design of FDHT, while the dashed box at the bottom of the
Figure 11 shows the structure of the classic PI current regulator.
and
are the voltage feed-forward coupling compensation terms analyzed earlier.
and
are, respectively, the current sampling filter time constant and the speed sampling filter time constant [
31].
Although the IT2FLS has better performance than T1FLS, the superiority of IT2FLS cannot be guaranteed if the appropriate parameters are not taken. Therefore, the relevant parameters () of the IT2FLS are optimized by the QPSO algorithm introduced earlier, while the same optimization process is adopted for the T1FLS for the sake of the reasonableness of the comparison. In the next section, we will demonstrate the excellence of FDPI-FDHT, especially FDPI-IT2FDHT, through simulation analyses.
6. Conclusions and Future Work
In this paper, a FDPI-IT2FDHT is proposed for PMSM to enhance the ability of dynamic response. Furthermore, to show the superiority of the designed method, PI, FDPI, FDPI-HT, and FDPI-T1FDHT are provided as well. Numerous comparative simulations suggest that FDPI with dynamic high type structure, especially FDPI-IT2FDHT, is superior to other methods in terms of dynamic characteristics and disturbance rejection, both under no-load and load conditions of the motor.
Future work will focus on improvement of FLS. Although the dynamic performance of FDPI-IT2FDHT is better than that of FDPI-T1FDHT at no load, the load oscillation of FDPI-IT2FDHT is more intense than that of FDPI-T1FDHT when a load is added, which indicates that the IT2FDHT designed in this paper is not superior to T1FDHT in all aspects and needs to be improved. Besides, we will regard experimental verification as the core of our future work.