Prescribed Performance Active Braking Control with Reference Adaptation for High-Speed Trains
Abstract
:1. Introduction
2. Problem Formulation
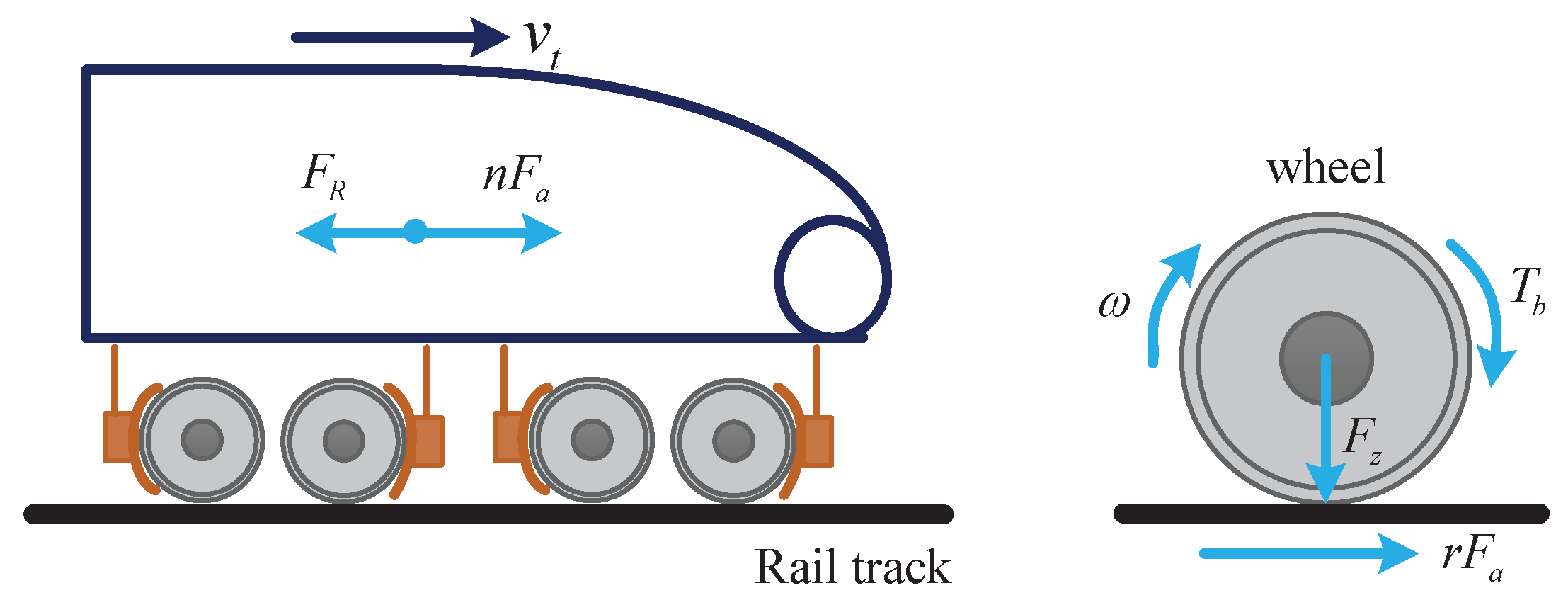
2.1. High-Speed Train Model
2.2. Active Braking Control Approach
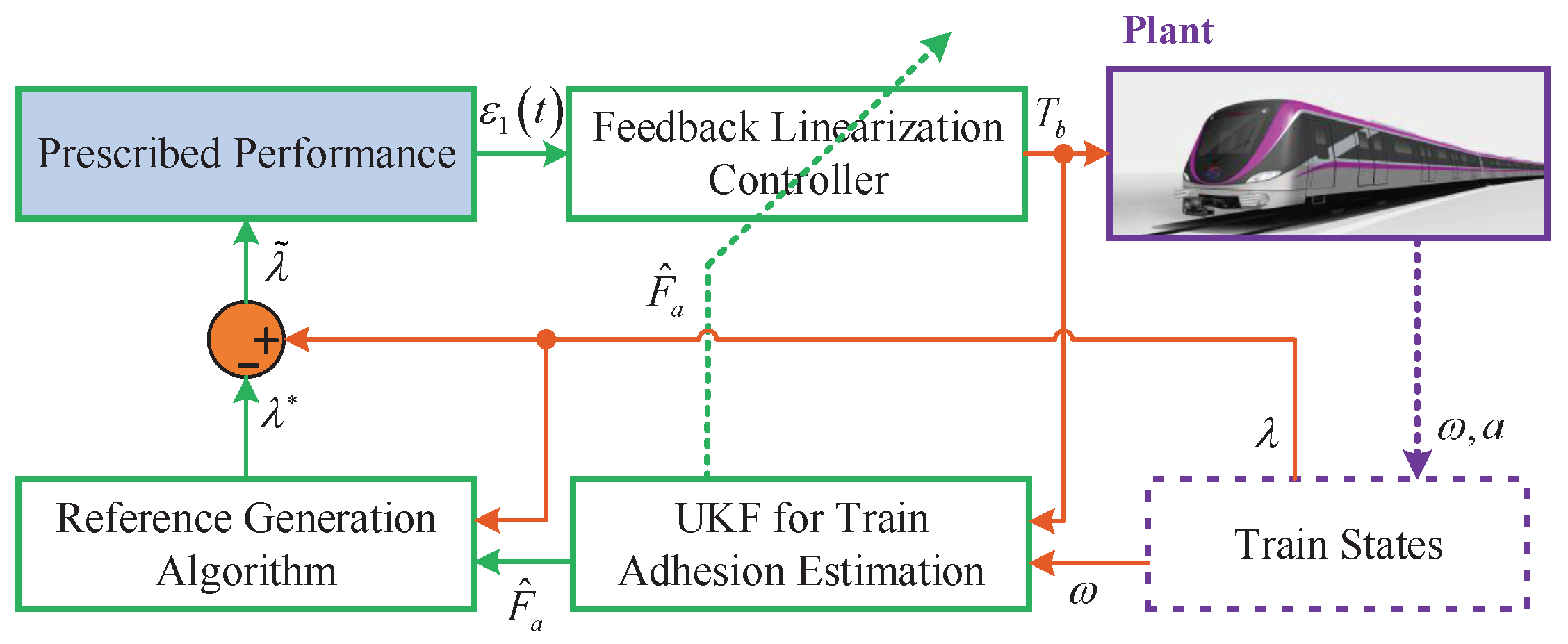
3. Prescribed Performance Feedback Linearization Controller with Adhesion Estimation
3.1. Wheel Slip Dynamics
3.2. Prescribed Performance
3.2.1. Prescribed Performance Function
3.2.2. Error Transformation
3.3. Unscented Kalman Filter-Based Feedback Linearization Controller
3.3.1. Feedback Linearization Controller
3.3.2. Unscented Kalman Filter for Adhesion Estimation
3.3.3. Stability Analysis
4. Reference Slip Ratio Generation Algorithm
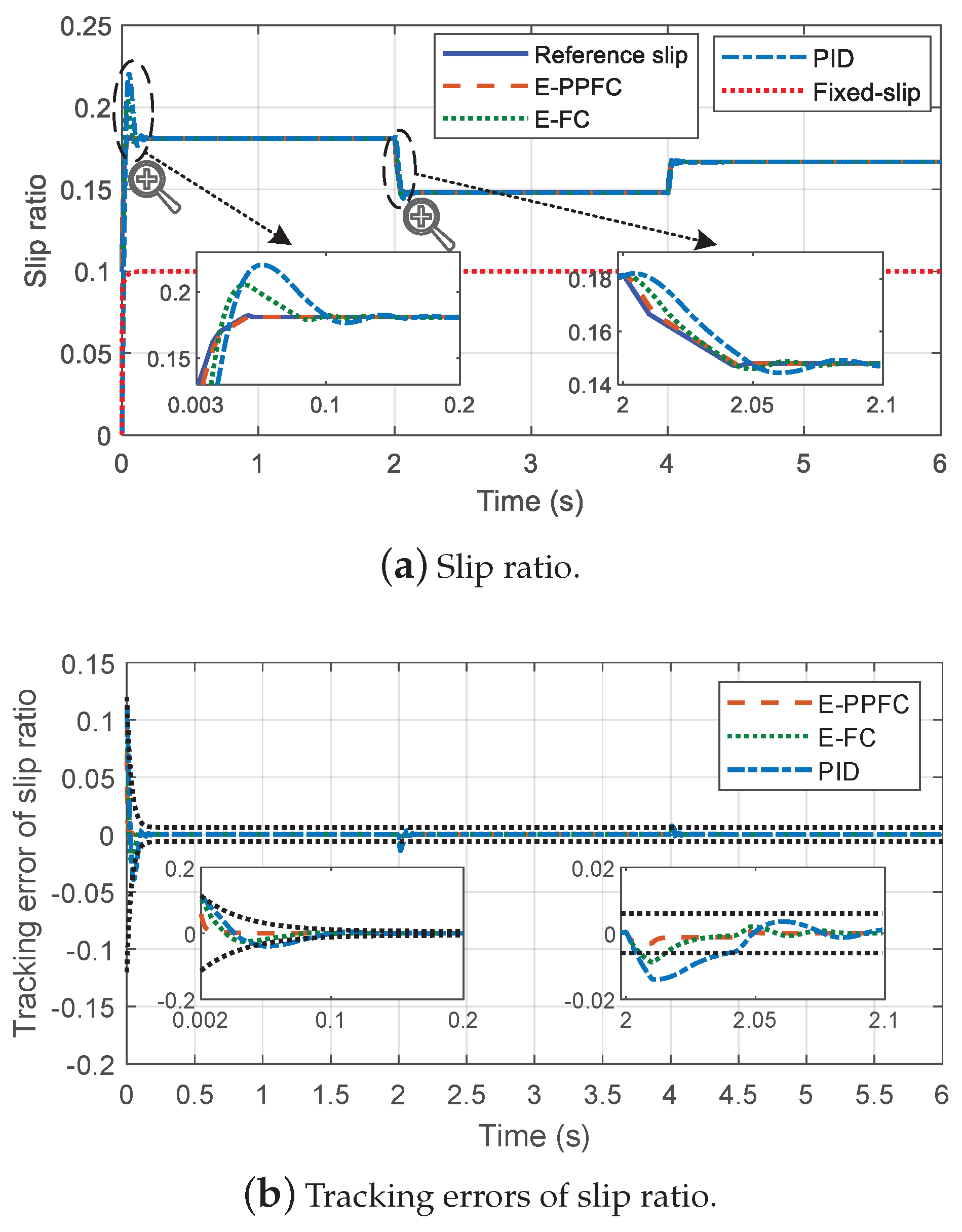
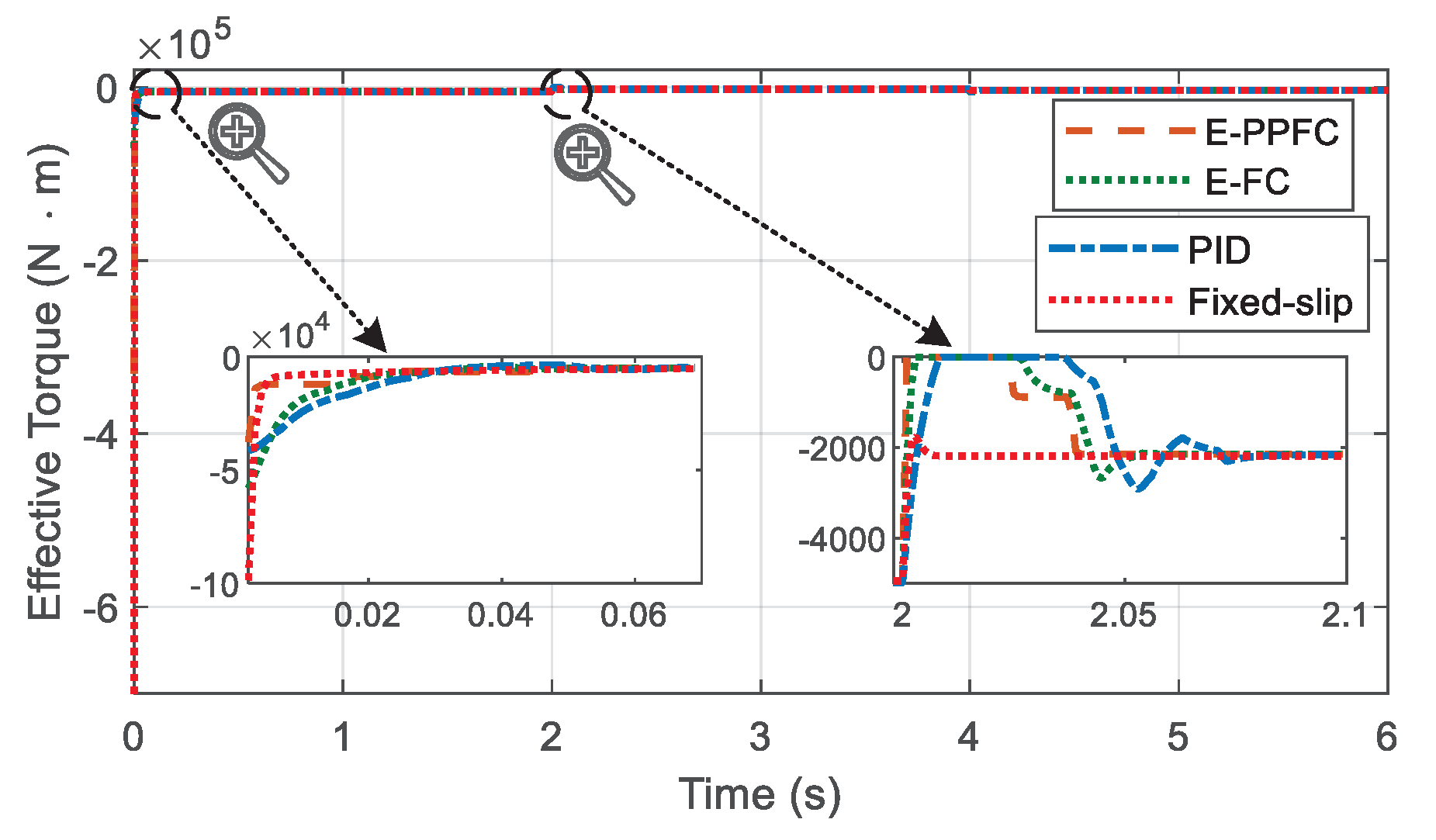
5. Experimental Validation
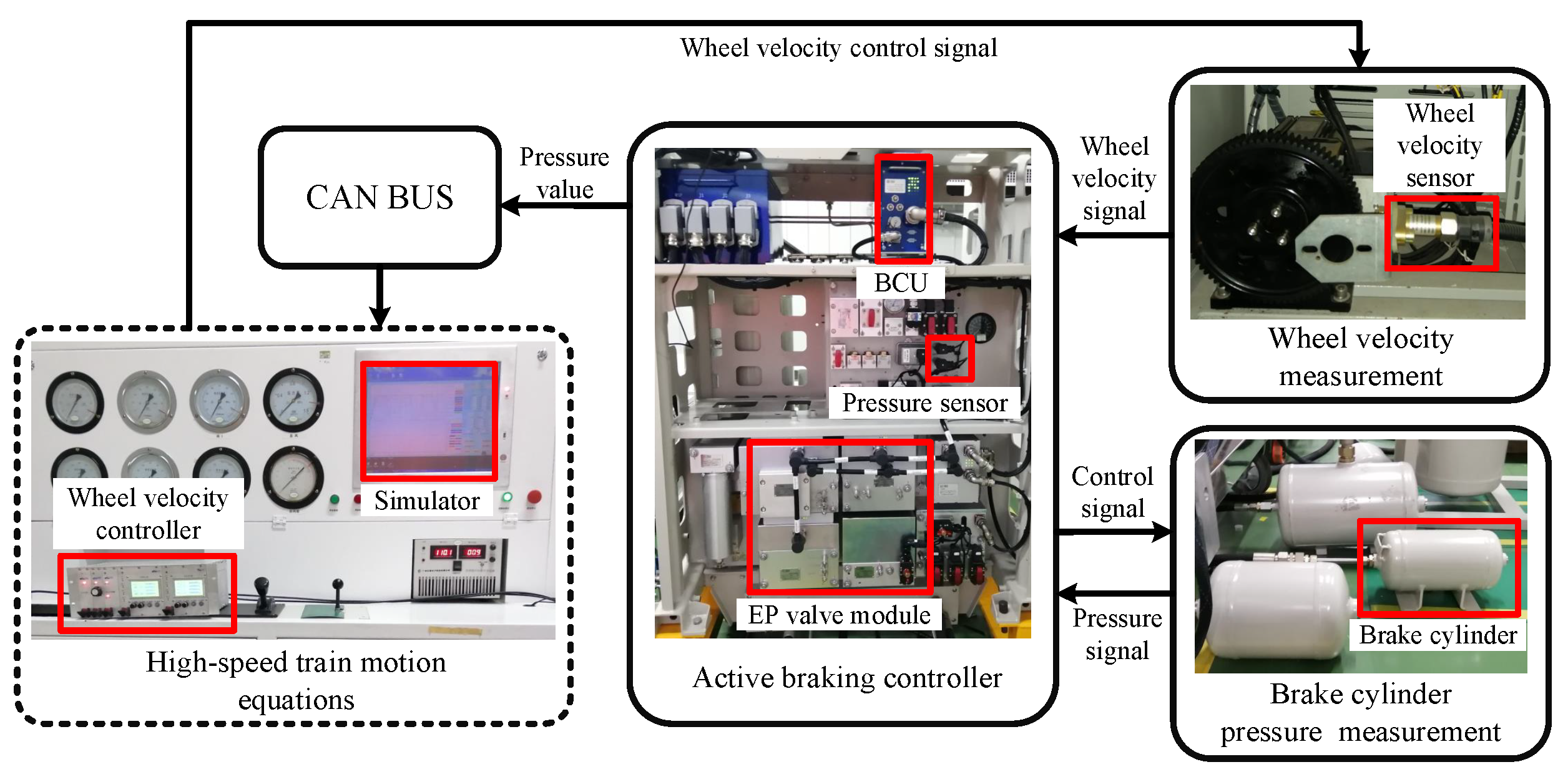
5.1. Experimental Setup
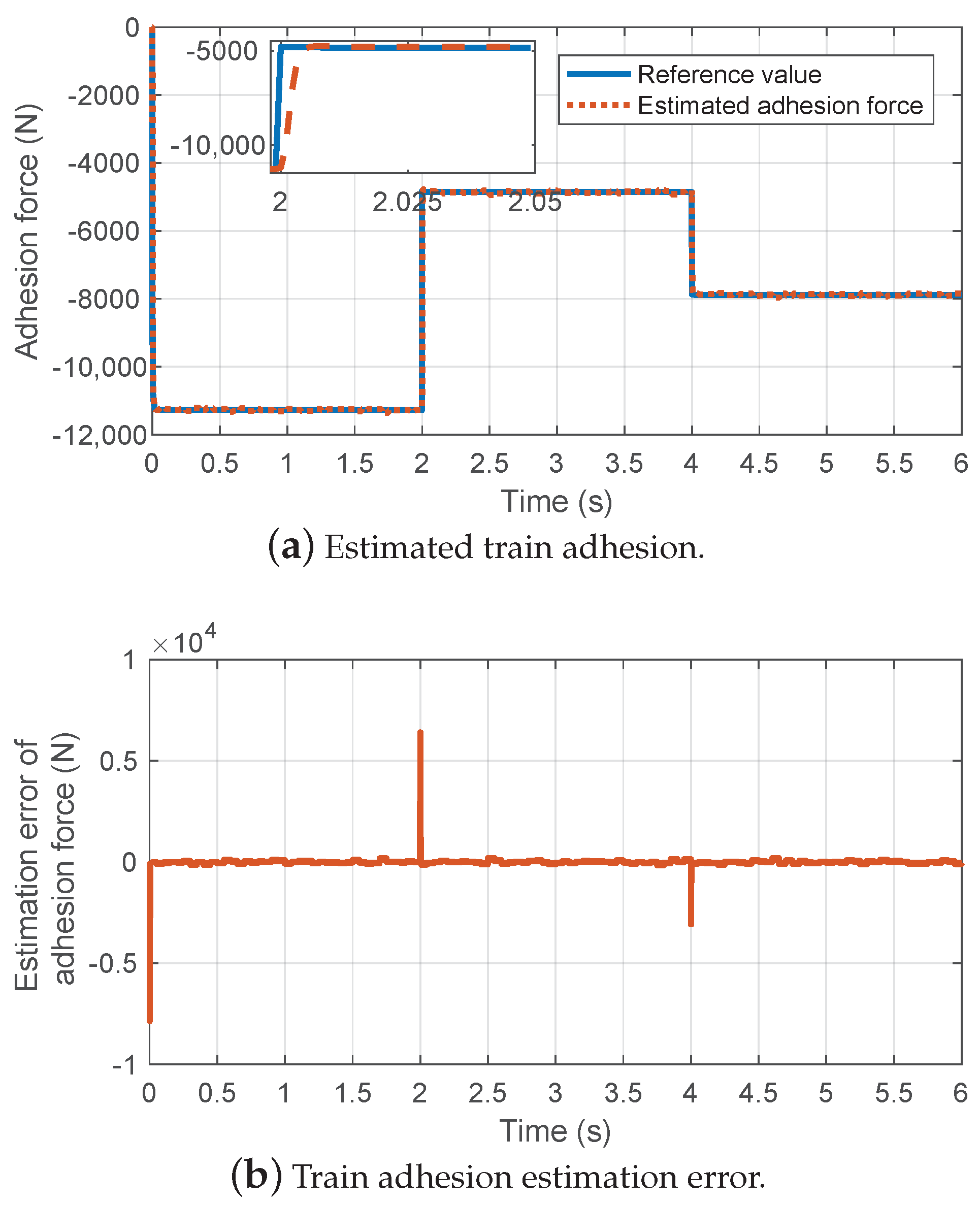
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Picasso, B.; Caporale, D.; Colaneri, P. Braking control in railway vehicles: A distributed preview approach. IEEE Trans. Autom. Control 2018, 63, 189–195. [Google Scholar] [CrossRef]
- Chen, B.; Huang, Z.; Zhang, R.; Jiang, F.; Liu, W.; Li, H.; Wang, J.; Peng, J. Adaptive slip ratio estimation for active braking control of high-speed trains. ISA Trans. 2021, 112, 302–314. [Google Scholar] [CrossRef]
- Cai, W.; Li, D.; Song, Y. A novel approach for active adhesion control of high-speed trains under antiskid constraints. IEEE Trans. Intell. Transp. Syst. 2015, 16, 3213–3222. [Google Scholar] [CrossRef]
- Lee, N.J.; Kang, C.G. Wheel slide protection control using a command map and Smith predictor for the pneumatic brake system of a railway vehicle. Veh. Syst. Dyn. 2016, 54, 1491–1510. [Google Scholar] [CrossRef]
- Chen, E.P.; Cheng, J.; Tu, J.H.; Lin, C.L. Sensorless Driving/Braking Control for Electric Vehicles. Actuators 2020, 9, 22. [Google Scholar] [CrossRef] [Green Version]
- Tavernini, D.; Vacca, F.; Metzler, M.; Savitski, D.; Ivanov, V.; Gruber, P.; Karci, A.E.H.; Dhaens, M.; Sorniotti, A. An explicit nonlinear model predictive ABS controller for electro-hydraulic braking systems. IEEE Trans. Ind. Electron. 2020, 67, 3990–4001. [Google Scholar] [CrossRef]
- Savaresi, S.M.; Tanelli, M. Active Braking Control Systems Design for Vehicles; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Diao, L.; Zhao, L.; Jin, Z.; Wang, L.; Sharkh, S.M. Taking traction control to task: High-adhesion-point tracking based on a disturbance observer in railway vehicles. IEEE Ind. Electron. Mag. 2017, 11, 51–62. [Google Scholar] [CrossRef]
- Aksjonov, A.; Augsburg, K.; Vodovozov, V. Design and simulation of the robust ABS and ESP fuzzy logic controller on the complex braking maneuvers. Appl. Sci. 2016, 6, 382. [Google Scholar] [CrossRef]
- Pichlik, P.; Zdenek, J. Locomotive Wheel Slip Control Method Based on an Unscented Kalman Filter. IEEE Trans. Veh. Technol. 2018, 67, 5730–5739. [Google Scholar] [CrossRef]
- Formentin, S.; Novara, C.; Savaresi, S.M.; Milanese, M. Active Braking Control System Design: The D2-IBC Approach. IEEE/ASME Trans. Mechatronics 2015, 20, 1573–1584. [Google Scholar] [CrossRef]
- Radac, M.B.; Precup, R.E. Data-driven model-free slip control of anti-lock braking systems using reinforcement Q-learning. Neurocomputing 2018, 275, 317–329. [Google Scholar] [CrossRef]
- Sun, J.; Xue, X.; Cheng, K.W.E. Fuzzy Sliding Mode Wheel Slip Ratio Control for Smart Vehicle Anti-Lock Braking System. Energies 2019, 12, 2501. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Dong, H.; Lü, J.; Sun, X.; Guo, L. A super-twisting-like algorithm and its application to train operation control with optimal utilization of adhesion force. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3035–3044. [Google Scholar] [CrossRef]
- de Jesús Rubio, J. Robust feedback linearization for nonlinear processes control. ISA Trans. 2018, 74, 155–164. [Google Scholar] [CrossRef]
- Yang, S.; Wang, P.; Tang, Y. Feedback Linearization-Based Current Control Strategy for Modular Multilevel Converters. IEEE Trans. Power Electron. 2018, 33, 161–174. [Google Scholar] [CrossRef]
- Lascu, C.; Jafarzadeh, S.; Fadali, M.S.; Blaabjerg, F. Direct Torque Control With Feedback Linearization for Induction Motor Drives. IEEE Trans. Power Electron. 2017, 32, 2072–2080. [Google Scholar] [CrossRef]
- Poursamad, A. Adaptive feedback linearization control of antilock braking systems using neural networks. Mechatronics 2009, 19, 767–773. [Google Scholar] [CrossRef]
- Wu, Y.; Isidori, A.; Lu, R.; Khalil, H.K. Performance Recovery of Dynamic Feedback-Linearization Methods for Multivariable Nonlinear Systems. IEEE Trans. Autom. Control 2020, 65, 1365–1380. [Google Scholar] [CrossRef]
- Sariyildiz, E.; Oboe, R.; Ohnishi, K. Disturbance Observer-based Robust Control and Its Applications: 35th Anniversary Overview. IEEE Trans. Ind. Electron. 2020, 67, 2042–2053. [Google Scholar] [CrossRef] [Green Version]
- Chaudhari, S.; Shendge, P.; Phadke, S.B. Dynamic Nonlinear Gradient Observer based Extremum Seeking Control for Optimum Braking. IEEE Trans. Ind. Electron. 2021. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, Z.; Zhou, G.; Liu, S.; Zhou, D.; Chen, S.; Zhang, X. Adaptive Fuzzy Active-Disturbance Rejection Control-Based Reconfiguration Controller Design for Aircraft Anti-Skid Braking System. Actuators 2021, 10, 201. [Google Scholar] [CrossRef]
- Patil, A.; Ginoya, D.; Shendge, P.; Phadke, S. Uncertainty-estimation-based approach to antilock braking systems. IEEE Trans. Veh. Technol. 2015, 65, 1171–1185. [Google Scholar] [CrossRef]
- Vafamand, N.; Arefi, M.M.; Khayatian, A. Nonlinear system identification based on Takagi-Sugeno fuzzy modeling and unscented Kalman filter. ISA Trans. 2018, 74, 134–143. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Tian, X.; Zhou, L.; Li, Y. A decision-tree based multiple-model UKF for attitude estimation using low-cost MEMS MARG sensor arrays. Measurement 2019, 135, 355–367. [Google Scholar] [CrossRef]
- Uyulan, C.; Gokasan, M.; Bogosyan, S. Comparison of the re-adhesion control strategies in high-speed train. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2018, 232, 92–105. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Xu, C.; Li, H.; Jiang, K.; Wang, K. State of charge and online model parameters co-estimation for liquid metal batteries. Appl. Energy 2019, 250, 677–684. [Google Scholar] [CrossRef]
- Li, D.; Yu, Y.; Jin, Q.; Gao, Z. Maximum power efficiency operation and generalized predictive control of PEM (proton exchange membrane) fuel cell. Energy 2014, 68, 210–217. [Google Scholar] [CrossRef]
- Bruce, A.L.; Goel, A.; Bernstein, D.S. Convergence and consistency of recursive least squares with variable-rate forgetting. Automatica 2020, 19, 109052. [Google Scholar] [CrossRef]
- Sadr, S.; Khaburi, D.A.; Rodríguez, J. Predictive slip control for electrical trains. IEEE Trans. Ind. Electron. 2016, 63, 3446–3457. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Adaptive control with guaranteed transient and steady state tracking error bounds for strict feedback systems. Automatica 2009, 45, 532–538. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust Adaptive Control of Feedback Linearizable MIMO Nonlinear Systems With Prescribed Performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Jing, C.; Xu, H.; Niu, X. Adaptive sliding mode disturbance rejection control with prescribed performance for robotic manipulators. ISA Trans. 2019, 91, 41–51. [Google Scholar] [CrossRef] [PubMed]
- Na, J.; Huang, Y.; Wu, X.; Gao, G.; Herrmann, G.; Jiang, J.Z. Active Adaptive Estimation and Control for Vehicle Suspensions With Prescribed Performance. IEEE Trans. Control Syst. Technol. 2018, 26, 2063–2077. [Google Scholar] [CrossRef] [Green Version]
- Hu, Q.; Shao, X.; Guo, L. Adaptive Fault-Tolerant Attitude Tracking Control of Spacecraft With Prescribed Performance. IEEE/ASME Trans. Mechatronics 2018, 23, 331–341. [Google Scholar] [CrossRef]
- Ivanov, V.; Savitski, D.; Shyrokau, B. A survey of traction control and antilock braking systems of full electric vehicles with individually controlled electric motors. IEEE Trans. Veh. Technol. 2014, 64, 3878–3896. [Google Scholar] [CrossRef]
- Sarkka, S. On unscented Kalman filtering for state estimation of continuous-time nonlinear systems. IEEE Trans. Autom. Control 2007, 52, 1631–1641. [Google Scholar] [CrossRef] [Green Version]
- Maree, J.P.; Imsland, L.; Jouffroy, J. On convergence of the unscented Kalman–Bucy filter using contraction theory. Int. J. Syst. Sci. 2016, 47, 1816–1827. [Google Scholar] [CrossRef]
- Barahanov, N.; Ortega, R. Necessary and sufficient conditions for passivity of the LuGre friction model. IEEE Trans. Autom. Control 2000, 45, 830–832. [Google Scholar] [CrossRef]



| Symbol | Definition |
|---|---|
| The slip ratio | |
| The desired slip ratio | |
| The adhesion coefficient | |
| The maximum adhesion coefficient | |
| The adhesion force | |
| The estimated adhesion force | |
| The wheel angular velocity | |
| The vehicle velocity | |
| The velocity difference | |
| The total effective torque acting on the wheel | |
| The wheel moment of inertia | |
| m | The total mass of the high-speed train |
| n | The numbers of wheels |
| The wheel vertical load | |
| The total wind resistance | |
| Davis resistance coefficients | |
| r | The wheel rolling radius |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| m | 13,800 kg | 60.35 kg·m | |
| r | 0.43 m | n | 4 |
| 50 m/s | - | - |
| Methods | Parameters | Values | Parameters | Values |
|---|---|---|---|---|
| UKF | 0.5 | 0.23 | ||
| 2 | 1 | |||
| 2 | - | - | ||
| RSRGA | 0.01 | 0.7 | ||
| 1 | 1 | |||
| - | - | |||
| E-PPFC | 0.1 | 1.2 | ||
| 0.005 | 1.2 | |||
| k | 30 | 100 |
| Methods | Braking Distances (m) | Acceleration Variances (m/s) |
|---|---|---|
| Fixed-slip | 256.8391 | — |
| PID | 254.4313 | 0.0679 |
| E-FC | 254.1955 | 0.0637 |
| E-PPFC | 254.0479 | 0.0564 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Peng, J.; Chen, B.; Gao, K.; Yang, Y.; Huang, Z. Prescribed Performance Active Braking Control with Reference Adaptation for High-Speed Trains. Actuators 2021, 10, 313. https://doi.org/10.3390/act10120313
Zhang R, Peng J, Chen B, Gao K, Yang Y, Huang Z. Prescribed Performance Active Braking Control with Reference Adaptation for High-Speed Trains. Actuators. 2021; 10(12):313. https://doi.org/10.3390/act10120313
Chicago/Turabian StyleZhang, Rui, Jun Peng, Bin Chen, Kai Gao, Yingze Yang, and Zhiwu Huang. 2021. "Prescribed Performance Active Braking Control with Reference Adaptation for High-Speed Trains" Actuators 10, no. 12: 313. https://doi.org/10.3390/act10120313






