Multifunctional Cantilevers as Working Elements in Solid-State Cooling Devices
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fabrication and Characterization of Bulk Ceramic Disc Samples
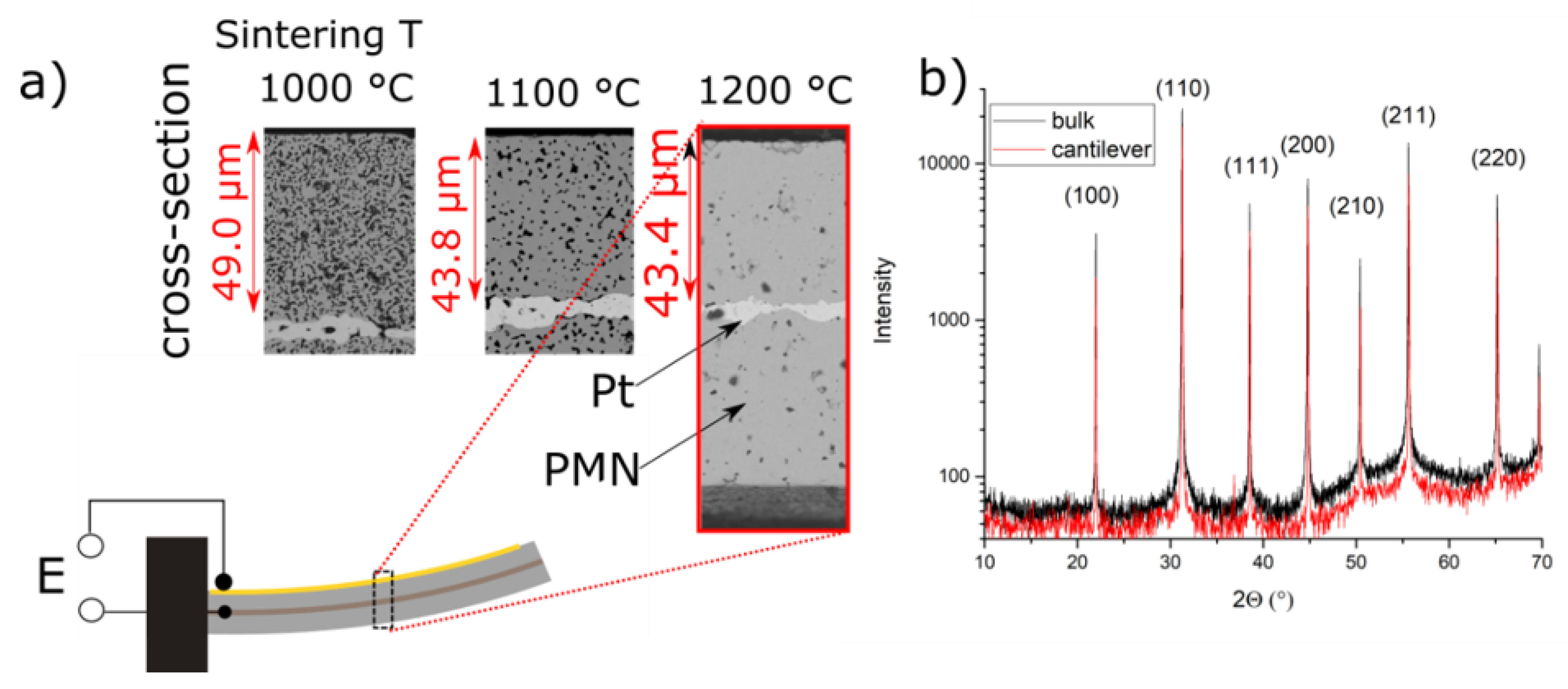
2.2. Fabrication and Characterization of Cantilever Elements
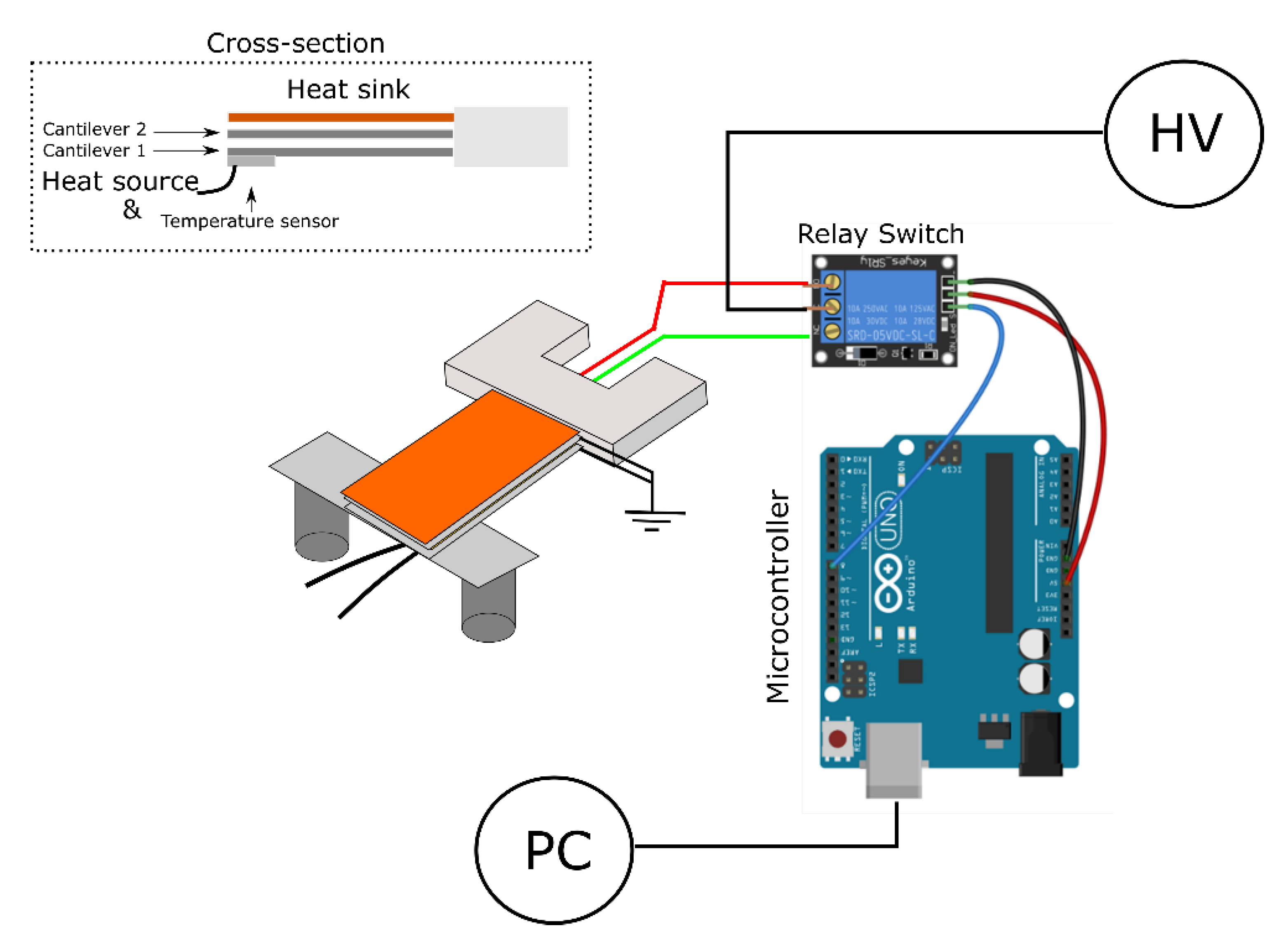
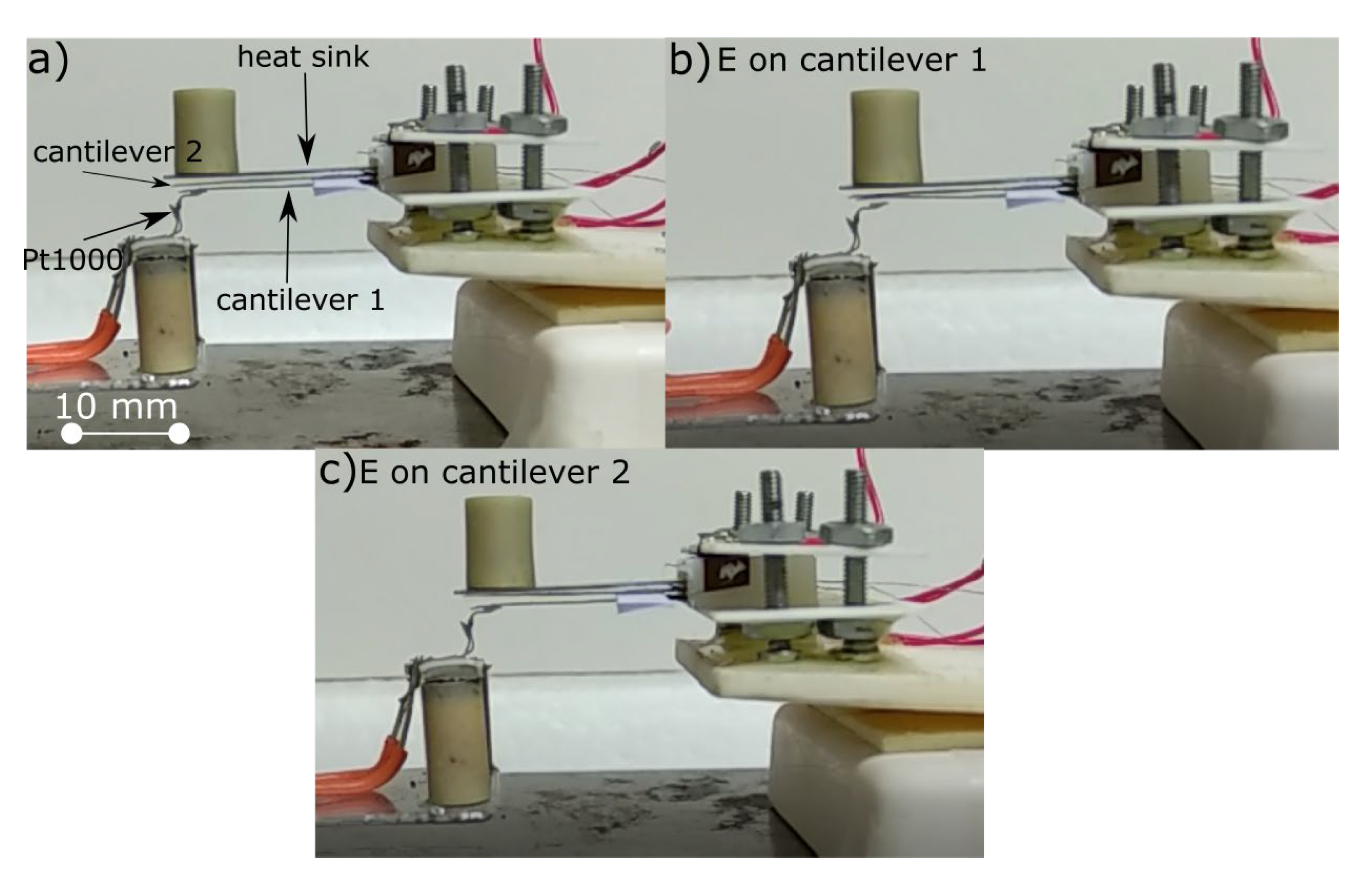
2.3. Building the Proof-of-Concept Device
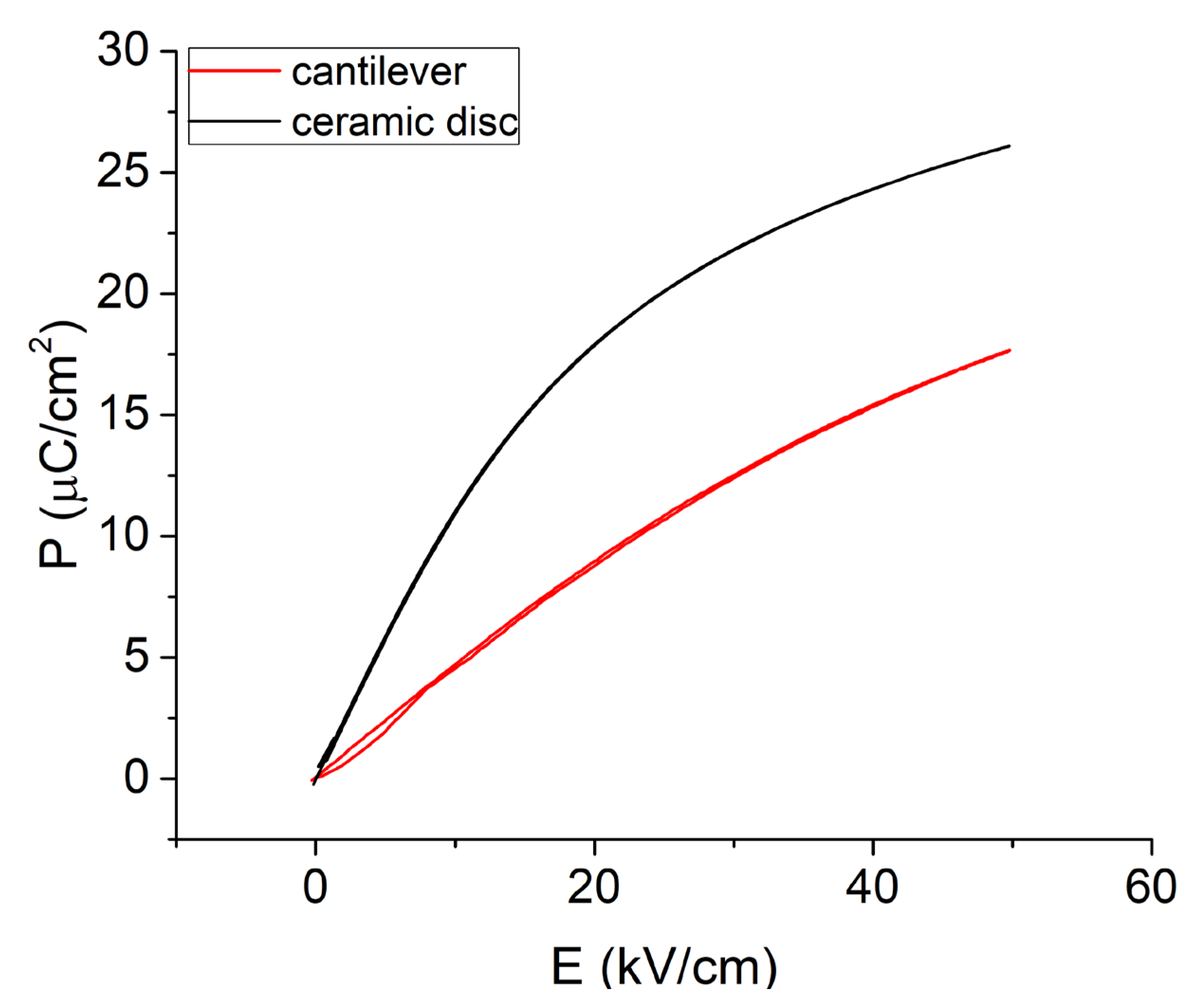
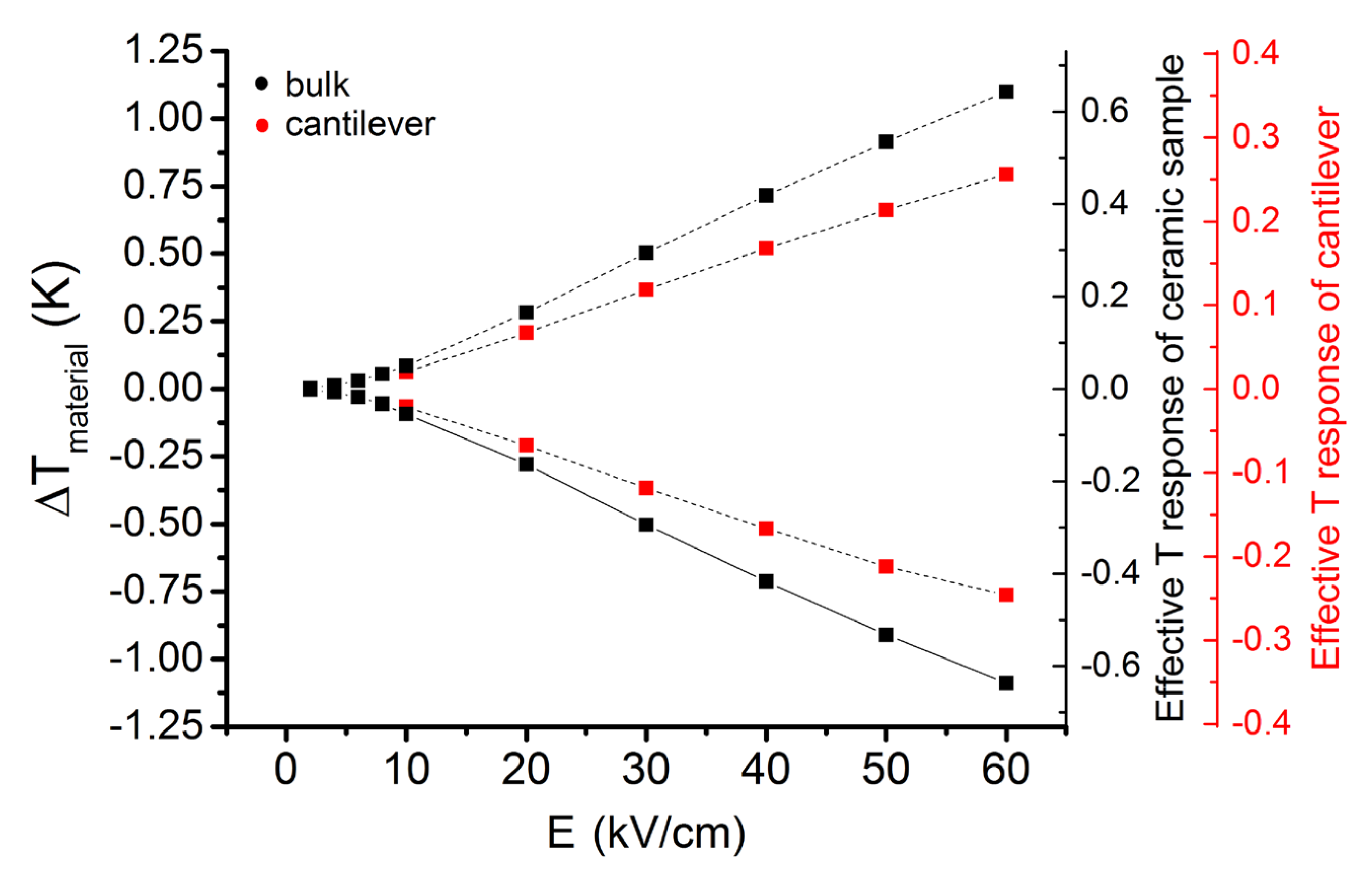
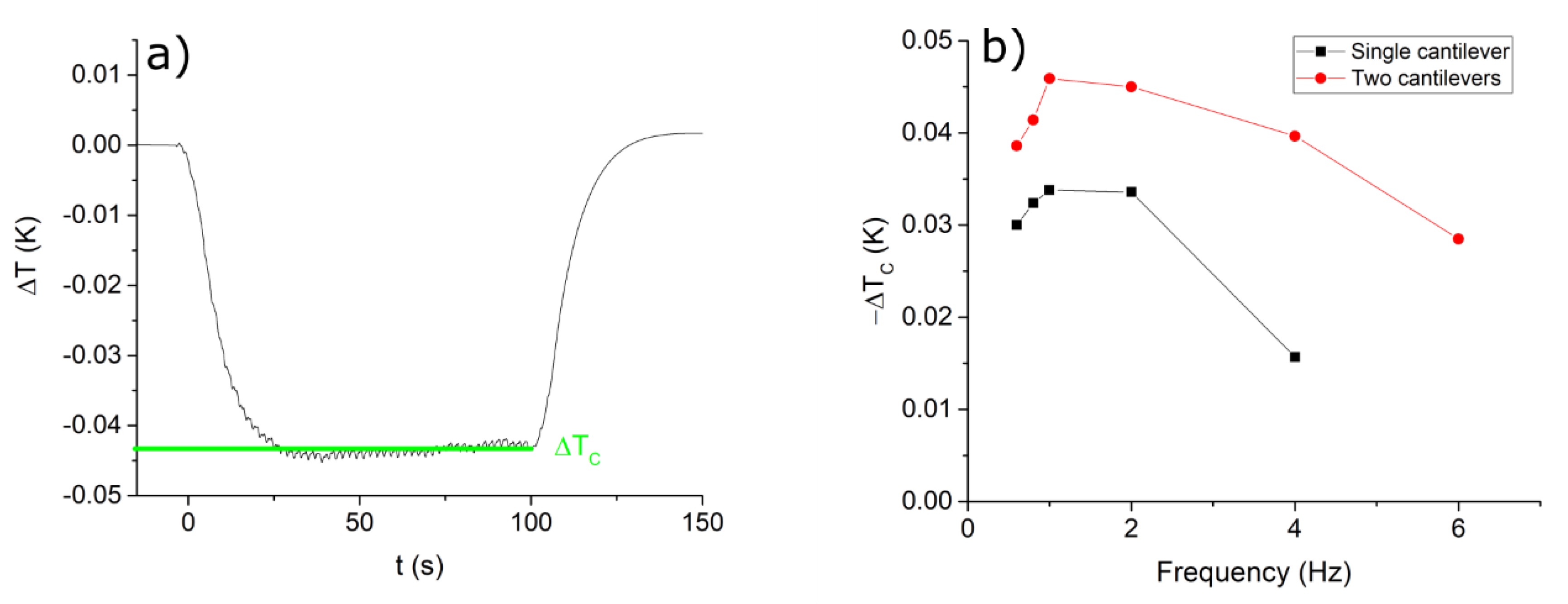
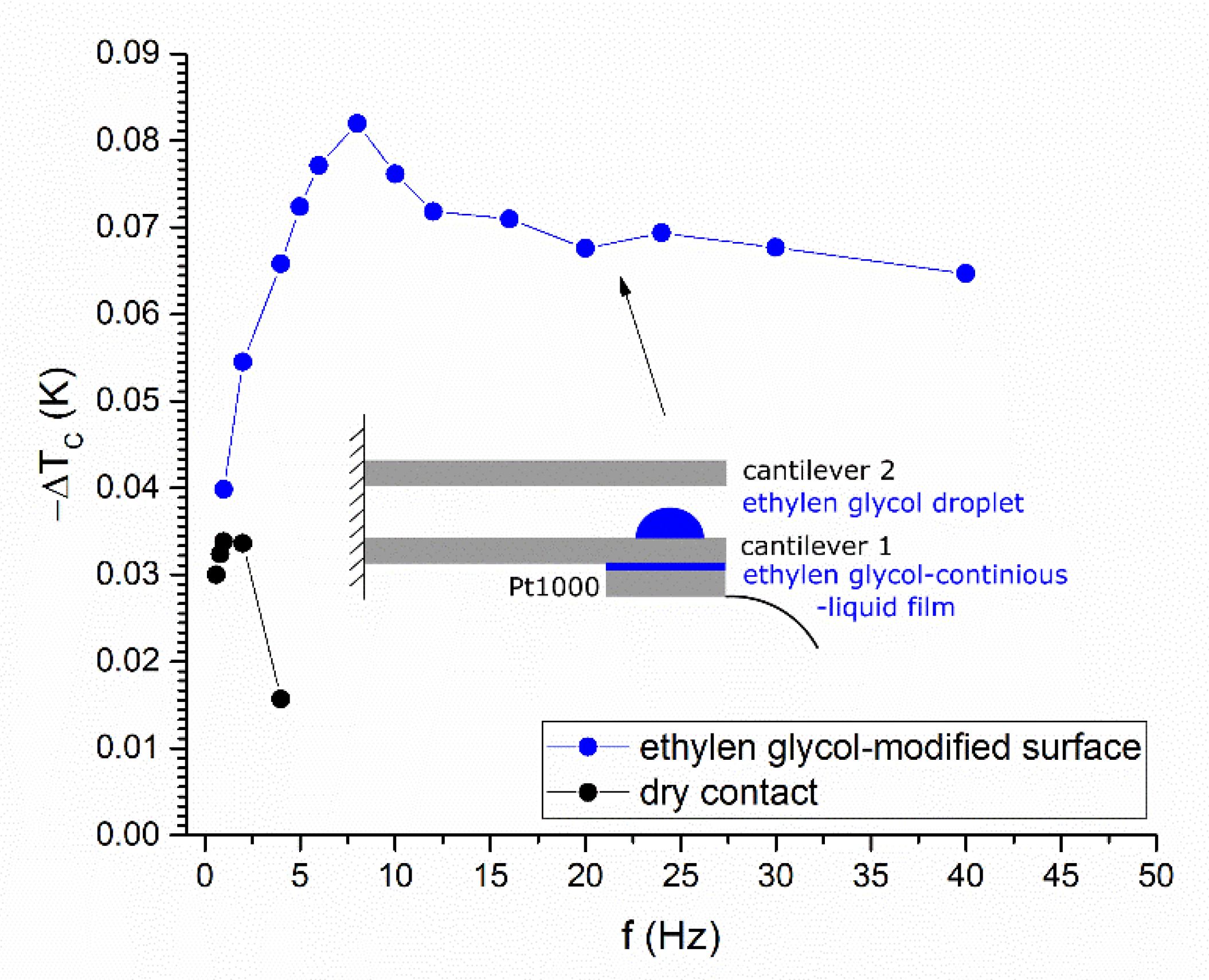
3. Results
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Kutnjak, Z.; Rožič, B.; Pirc, R. Electrocaloric Effect: Theory, Measurements, and Applications. In Wiley Encyclopedia of Electrical and Electronics Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; pp. 1–19. [Google Scholar]
- Scott, J.F. Electrocaloric Materials. Annu. Rev. Mater. Res. 2011, 41, 229–240. [Google Scholar] [CrossRef]
- Mischenko, A.S.; Zhang, Q.; Scott, J.F.; Whatmore, R.W.; Mathur, N.D. Giant electrocaloric effect in thin-film PbZr0.95Ti0.05O3. Science 2006, 311, 1270–1271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Correia, T.; Zhang, Q. Electrocaloric Materials; Correia, T., Zhang, Q., Eds.; Engineering Materials; Springer: Berlin/Heidelberg, Germany, 2014; Volume 34, ISBN 978-3-642-40263-0. [Google Scholar]
- Lu, S.G.; Rožič, B.; Zhang, Q.M.; Kutnjak, Z.; Li, X.; Furman, E.; Gorny, L.J.; Lin, M.; Malič, B.; Kosec, M.; et al. Organic and inorganic relaxor ferroelectrics with giant electrocaloric effect. Appl. Phys. Lett. 2010, 97, 162904. [Google Scholar] [CrossRef]
- Nair, B.; Usui, T.; Crossley, S.; Kurdi, S.; Guzmán-Verri, G.G.; Moya, X.; Hirose, S.; Mathur, N.D. Large electrocaloric effects in oxide multilayer capacitors over a wide temperature range. Nature 2019, 575, 468–472. [Google Scholar] [CrossRef]
- Neusel, C.; Schneider, G.A. Size-dependence of the dielectric breakdown strength from nano- to millimeter scale. J. Mech. Phys. Solids 2014, 63, 201–213. [Google Scholar] [CrossRef] [Green Version]
- Otoničar, M.; Bradeško, A.; Fulanović, L.; Kos, T.; Uršič, H.; Benčan, A.; Cabral, M.J.; Henriques, A.; Jones, J.L.; Riemer, L.; et al. Connecting the Multiscale Structure with Macroscopic Response of Relaxor Ferroelectrics. Adv. Funct. Mater. 2020, 30, 2006823. [Google Scholar] [CrossRef]
- Fu, D.; Taniguchi, H.; Itoh, M.; Mori, S. Pb(Mg1/3Nb2/3)O3 (PMN) Relaxor: Dipole Glass or Nano-Domain Ferroelectric? In Advances in Ferroelectrics; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Bokov, A.A.; Ye, Z.-G. Recent progress in relaxor ferroelectrics with perovskite structure. J. Mater. Sci. 2006, 41, 31–52. [Google Scholar] [CrossRef]
- Härdtl, K.H. Electrical and mechanical losses in ferroelectric ceramics. Ceram. Int. 1982, 8, 121–127. [Google Scholar] [CrossRef]
- Uchino, K.; Zheng, J.H.; Chen, Y.H.; Du, X.H.; Ryu, J.; Gao, Y.; Ural, S.; Priya, S.; Hirose, S. Loss mechanisms and high power piezoelectrics. J. Mater. Sci. 2006, 41, 217–228. [Google Scholar] [CrossRef]
- Zheng, J.; Takahashi, S.; Yoshikawa, S.; Uchino, K.; de Vries, J.W.C. Heat Generation in Multilayer Piezoelectric Actuators. J. Am. Ceram. Soc. 1996, 79, 3193–3198. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, S.; Jiang, W.; Cao, W. Losses in ferroelectric materials. Mater. Sci. Eng. R Rep. 2015, 89, 1–48. [Google Scholar] [CrossRef] [Green Version]
- Bradeško, A.; Hedl, A.; Fulanović, L.; Novak, N.; Rojac, T. Self-heating of relaxor and ferroelectric ceramics during electrocaloric field cycling. APL Mater. 2019, 7, 071111. [Google Scholar] [CrossRef] [Green Version]
- Plaznik, U.; Vrabelj, M.; Kutnjak, Z.; Malič, B.; Poredoš, A.; Kitanovski, A. Electrocaloric cooling: The importance of electric-energy recovery and heat regeneration. Europhys. Lett. 2015, 111, 57009. [Google Scholar] [CrossRef]
- Shi, J.; Han, D.; Li, Z.; Yang, L.; Lu, S.G.; Zhong, Z.; Chen, J.; Zhang, Q.M.; Qian, X. Electrocaloric Cooling Materials and Devices for Zero-Global-Warming-Potential, High-Efficiency Refrigeration. Joule 2019, 3, 1200–1225. [Google Scholar] [CrossRef]
- Plaznik, U.; Kitanovski, A.; Rožič, B.; Malič, B.; Uršič, H.; Drnovšek, S.; Cilenšek, J.; Vrabelj, M.; Poredoš, A.; Kutnjak, Z. Bulk relaxor ferroelectric ceramics as a working body for an electrocaloric cooling device. Appl. Phys. Lett. 2015, 106, 043903. [Google Scholar] [CrossRef]
- Blumenthal, P.; Molin, C.; Gebhardt, S.; Raatz, A. Active electrocaloric demonstrator for direct comparison of PMN-PT bulk and multilayer samples. Ferroelectrics 2016, 497, 1–8. [Google Scholar] [CrossRef]
- Torelló, A.; Lheritier, P.; Usui, T.; Nouchokgwe, Y.; Gérard, M.; Bouton, O.; Hirose, S.; Defay, E. Giant temperature span in electrocaloric regenerator. Science 2020, 370, 125–129. [Google Scholar] [CrossRef]
- Gu, H.; Qian, X.; Li, X.; Craven, B.; Zhu, W.; Cheng, A.; Yao, S.C.; Zhang, Q.M. A chip scale electrocaloric effect based cooling device. Appl. Phys. Lett. 2013, 102, 122904. [Google Scholar] [CrossRef]
- Gu, H.; Qian, X.S.; Ye, H.J.; Zhang, Q.M. An electrocaloric refrigerator without external regenerator. Appl. Phys. Lett. 2014, 105, 162905. [Google Scholar] [CrossRef]
- Wang, Y.; Schwartz, D.E.; Smullin, S.J.; Wang, Q.; Sheridan, M.J. Silicon Heat Switches for Electrocaloric Cooling. J. Microelectromech. Syst. 2017, 26, 580–587. [Google Scholar] [CrossRef]
- Jia, Y.; Ju, Y.S. A solid-state refrigerator based on the electrocaloric effect. Appl. Phys. Lett. 2012, 100, 242901. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Usui, T.; Benedict, M.; Hirose, S.; Lee, J.; Kalb, J.; Schwartz, D. A high-performance solid-state electrocaloric cooling system. Science 2020, 370, 129–133. [Google Scholar] [CrossRef] [PubMed]
- Bradeško, A.; Juričić, Đ.; Santo Zarnik, M.; Malič, B.; Kutnjak, Z.; Rojac, T.; Juričić, D.; Santo Zarnik, M.; Malič, B.; Kutnjak, Z.; et al. Coupling of the electrocaloric and electromechanical effects for solid-state refrigeration. Appl. Phys. Lett. 2016, 109, 143508. [Google Scholar] [CrossRef]
- Ma, R.; Zhang, Z.; Tong, K.; Huber, D.; Kornbluh, R.; Ju, Y.S.; Pei, Q. Highly efficient electrocaloric cooling with electrostatic actuation. Science 2017, 357, 1130–1134. [Google Scholar] [CrossRef] [Green Version]
- Meng, Y.; Zhang, Z.; Wu, H.; Wu, R.; Wu, J.; Wang, H.; Pei, Q. A cascade electrocaloric cooling device for large temperature lift. Nat. Energy 2020, 5, 996–1002. [Google Scholar] [CrossRef]
- Uršič, H.; Vrabelj, M.; Fulanović, L.; Bradeško, A.; Drnovsek, S.; Malič, B. Specific heat capacity and thermal conductivity of the electrocaloric (1 − x)Pb(Mg1/3Nb2/3)O3–xPbTiO3 ceramics between room temperature and 300 °C. J. Microelectron. Electron. Compon. Mater. 2015, 45, 260–265. [Google Scholar]
- Lide, D. CRC Handbook of Chemistry and Physics, 84th ed.; CRC Press: Boca Raton, FL, USA, 2005; Volume 86. [Google Scholar]
- Wang, Q.-M.; Cross, L.E. Performance analysis of piezoelectric cantilever bending actuators. Ferroelectrics 1998, 215, 187–213. [Google Scholar] [CrossRef]
- Ealey, M.A. Standard SELECT electrostrictive lead magnesium niobate actuators for active and adaptive optical components. Opt. Eng. 1990, 29, 1373. [Google Scholar] [CrossRef]
- Uršič, H.; Hrovat, M.; Holc, J.; Zarnik, M.S.; Drnovšek, S.; Maček, S.; Kosec, M. A large-displacement 65Pb(Mg1/3Nb2/3)O3–35PbTiO3/Pt bimorph actuator prepared by screen printing. Sens. Actuators B Chem. 2008, 133, 699–704. [Google Scholar] [CrossRef]
- Arduino Uno. Available online: https://www.arduino.cc/ (accessed on 23 December 2020).
- Vrabelj, M.; Uršič, H.; Kutnjak, Z.; Rožič, B.; Drnovšek, S.; Benčan, A.; Bobnar, V.; Fulanović, L.; Malič, B. Large electrocaloric effect in grain-size-engineered 0.9Pb(Mg1/3Nb2/3)O3–0.1PbTiO3. J. Eur. Ceram. Soc. 2016, 36, 75–80. [Google Scholar] [CrossRef]
- Dragomir, M.; Otoničar, M.; Vrabelj, M.; Fulanović, L.; Drnovšek, S.; Rojac, T.; Malič, B. Seeding effects on the mechanochemical synthesis of 0.9Pb(Mg1/3Nb2/3)O3–0.1PbTiO3. J. Eur. Ceram. Soc. 2019, 39, 1837–1845. [Google Scholar] [CrossRef]
- Pirc, R.; Kutnjak, Z.; Blinc, R.; Zhang, Q.M. Upper bounds on the electrocaloric effect in polar solids. Appl. Phys. Lett. 2011, 98, 4–7. [Google Scholar] [CrossRef]
- Griggio, F.; Jesse, S.; Kumar, A.; Ovchinnikov, O.; Kim, H.; Jackson, T.N.; Damjanovic, D.; Kalinin, S.V.; Trolier-Mckinstry, S. Substrate clamping effects on irreversible domain wall dynamics in lead zirconate titanate thin films. Phys. Rev. Lett. 2012, 108, 157604. [Google Scholar] [CrossRef] [PubMed]
- Ihlefeld, J.F.; Harris, D.T.; Keech, R.; Jones, J.L.; Maria, J.P.; Trolier-McKinstry, S. Scaling Effects in Perovskite Ferroelectrics: Fundamental Limits and Process-Structure-Property Relations. J. Am. Ceram. Soc. 2016, 99, 2537–2557. [Google Scholar] [CrossRef]
- Lee, H.J.; Zhang, S.; Luo, J.; Li, F.; Shrout, T.R. Thickness-dependent properties of relaxor-PbTiO3 ferroelectrics for ultrasonic transducers. Adv. Funct. Mater. 2010, 20, 3154–3162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leite, E.R.; Scotch, A.M.; Khan, A.; Li, T.; Chan, H.M.; Harmer, M.P.; Liu, S.-F.; Park, S.-E. Chemical Heterogeneity in PMN-35PT Ceramics and Effects on Dielectric and Piezoelectric Properties. J. Am. Ceram. Soc. 2004, 85, 3018–3024. [Google Scholar] [CrossRef]
- Nomura, S.; Uchino, K. Electrostrictive effect in Pb(Mg 1/3 Nb 2/3)O 3 -type materials. Ferroelectrics 1982, 41, 117–132. [Google Scholar] [CrossRef]
- Greiner, A.; Molin, C.; Neubert, H.; Gebhardt, S.E.; Neumeister, P. Direct Measurement of the Electrocaloric Temperature Change in Multilayer Ceramic Components using Resistance-Welded Thermocouple Wires. Energy Technol. 2018, 6, 1535–1542. [Google Scholar] [CrossRef]
- Wu, C.C.M.; Kahn, M.; Moy, W. Piezoelectric Ceramics with Functional Gradients: A New Application in Material Design. J. Am. Ceram. Soc. 2005, 79, 809–812. [Google Scholar] [CrossRef]
- Uchino, K.; Yoshizaki, M.; Kasai, K.; Yamamura, H.; Sakai, N.; Asakura, H. “Monomorph Actuators” Using Semiconductive Ferroelectrics. Jpn. J. Appl. Phys. 1987, 26, 1046–1049. [Google Scholar] [CrossRef]
- Jia, Y.; Cha, G.; Ju, Y.S. Switchable Thermal Interfaces Based on Discrete Liquid Droplets. Micromachines 2012, 3, 10–20. [Google Scholar] [CrossRef] [Green Version]
- Almanza, M.; Depreux, L.; Parrain, F.; Lobue, M. Electrostatically actuated thermal switch device for caloric film. Appl. Phys. Lett. 2018, 112, 083901. [Google Scholar] [CrossRef] [Green Version]
- Dos Santos, W.N.; Iguchi, C.Y.; Gregorio, R. Thermal properties of poly(vinilidene fluoride) in the temperature range from 25 to 210 °C. Polym. Test. 2008, 27, 204–208. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bradeško, A.; Fulanović, L.; Vrabelj, M.; Matavž, A.; Otoničar, M.; Koruza, J.; Malič, B.; Rojac, T. Multifunctional Cantilevers as Working Elements in Solid-State Cooling Devices. Actuators 2021, 10, 58. https://doi.org/10.3390/act10030058
Bradeško A, Fulanović L, Vrabelj M, Matavž A, Otoničar M, Koruza J, Malič B, Rojac T. Multifunctional Cantilevers as Working Elements in Solid-State Cooling Devices. Actuators. 2021; 10(3):58. https://doi.org/10.3390/act10030058
Chicago/Turabian StyleBradeško, Andraž, Lovro Fulanović, Marko Vrabelj, Aleksander Matavž, Mojca Otoničar, Jurij Koruza, Barbara Malič, and Tadej Rojac. 2021. "Multifunctional Cantilevers as Working Elements in Solid-State Cooling Devices" Actuators 10, no. 3: 58. https://doi.org/10.3390/act10030058
APA StyleBradeško, A., Fulanović, L., Vrabelj, M., Matavž, A., Otoničar, M., Koruza, J., Malič, B., & Rojac, T. (2021). Multifunctional Cantilevers as Working Elements in Solid-State Cooling Devices. Actuators, 10(3), 58. https://doi.org/10.3390/act10030058





