Active Loading Control Design for a Wearable Exoskeleton with a Bowden Cable for Transmission
Abstract
1. Introduction
2. Mathematical Modeling of the System
3. Controller Design
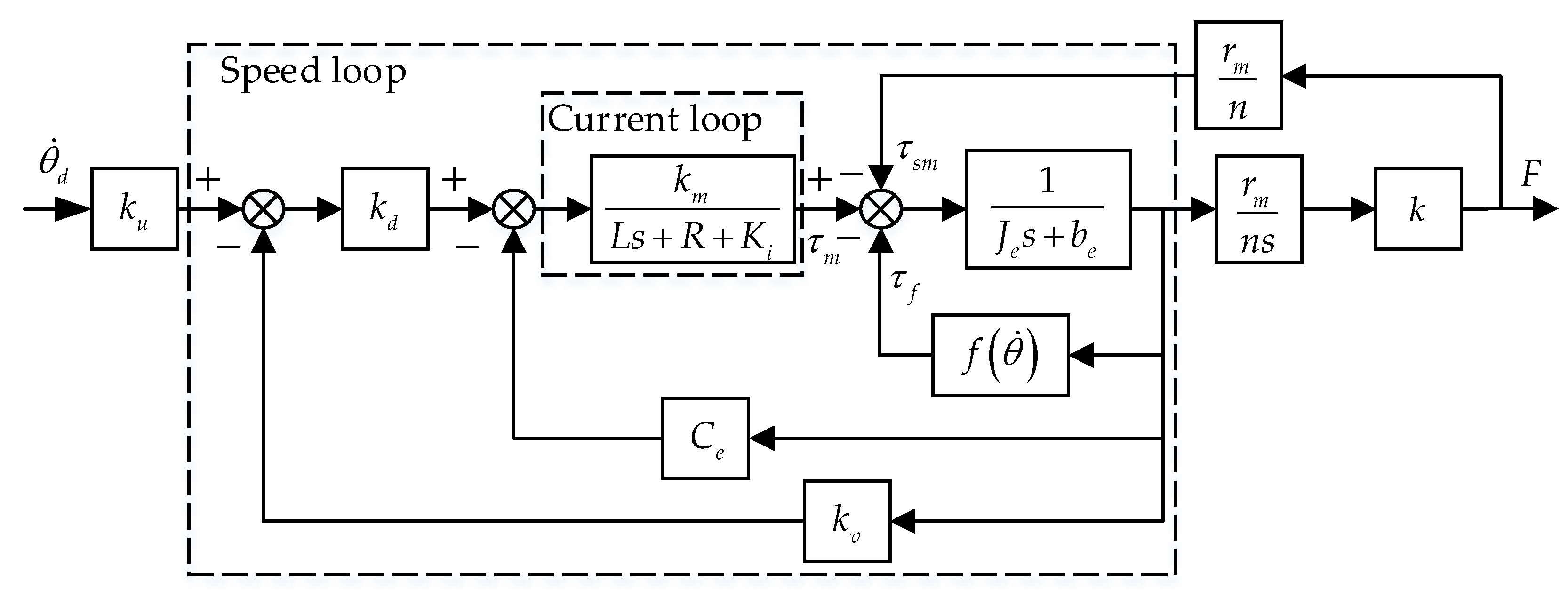
3.1. Design of the Inner-Loop Controller
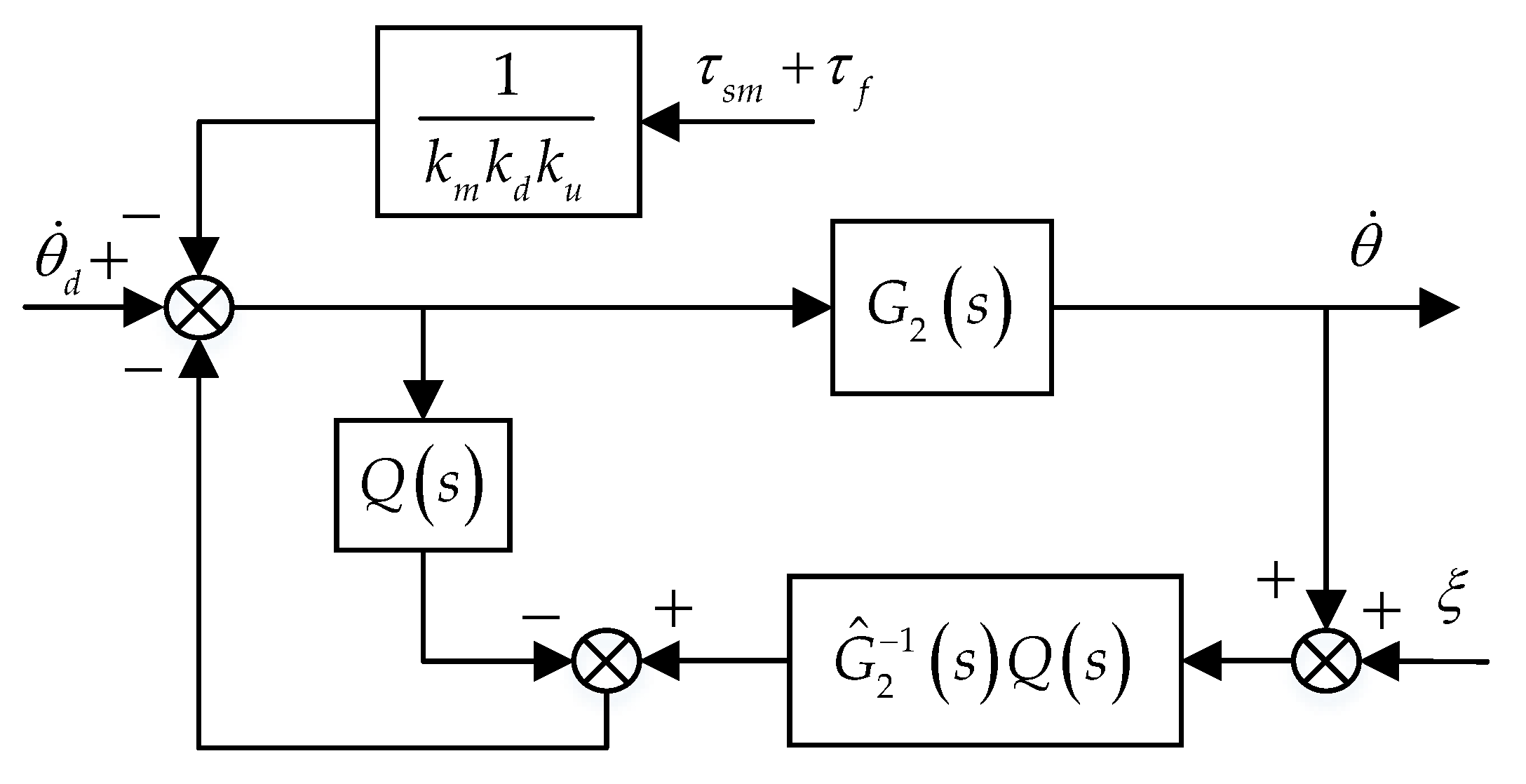
3.2. Design of the Oute-Loop Controller
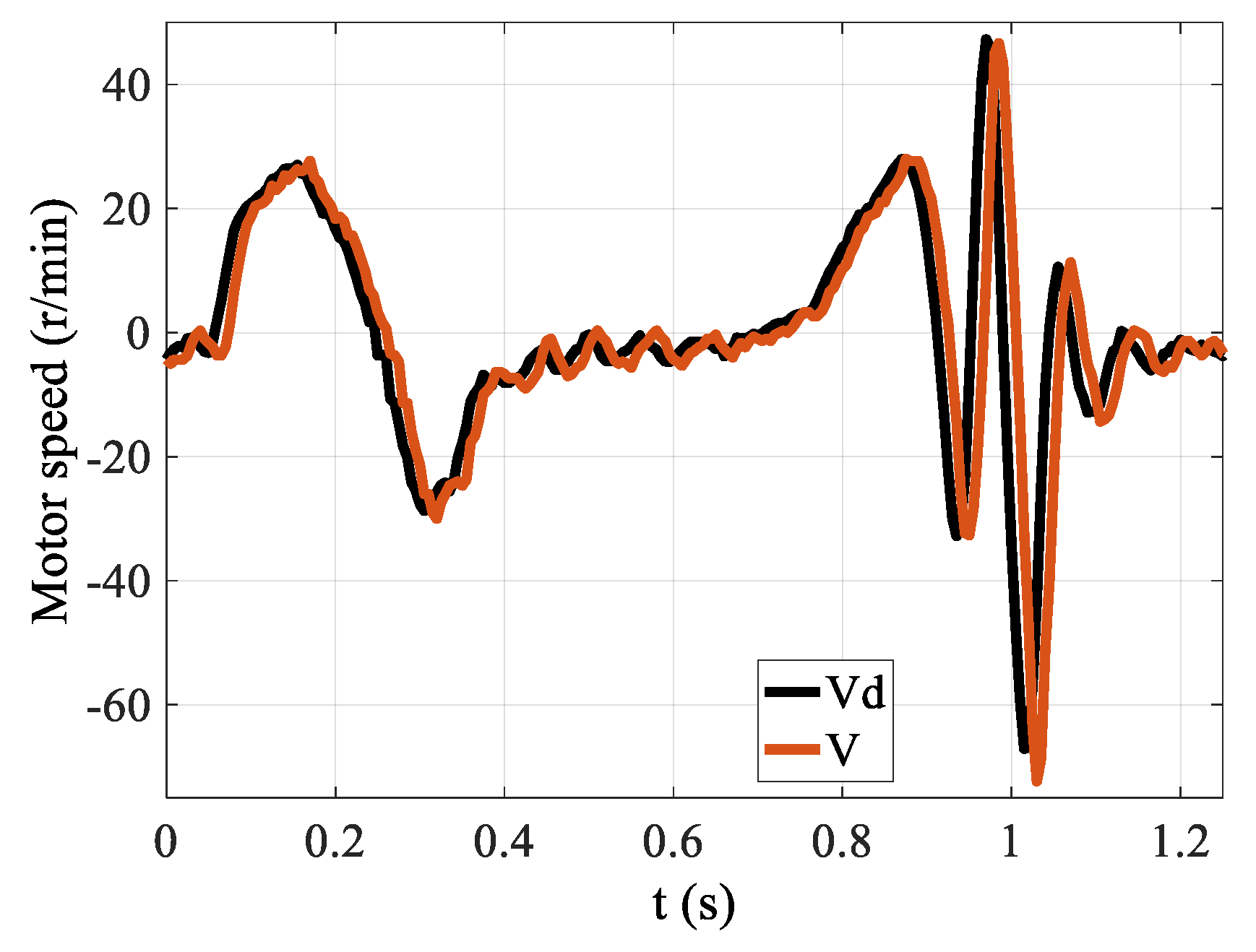
4. Results
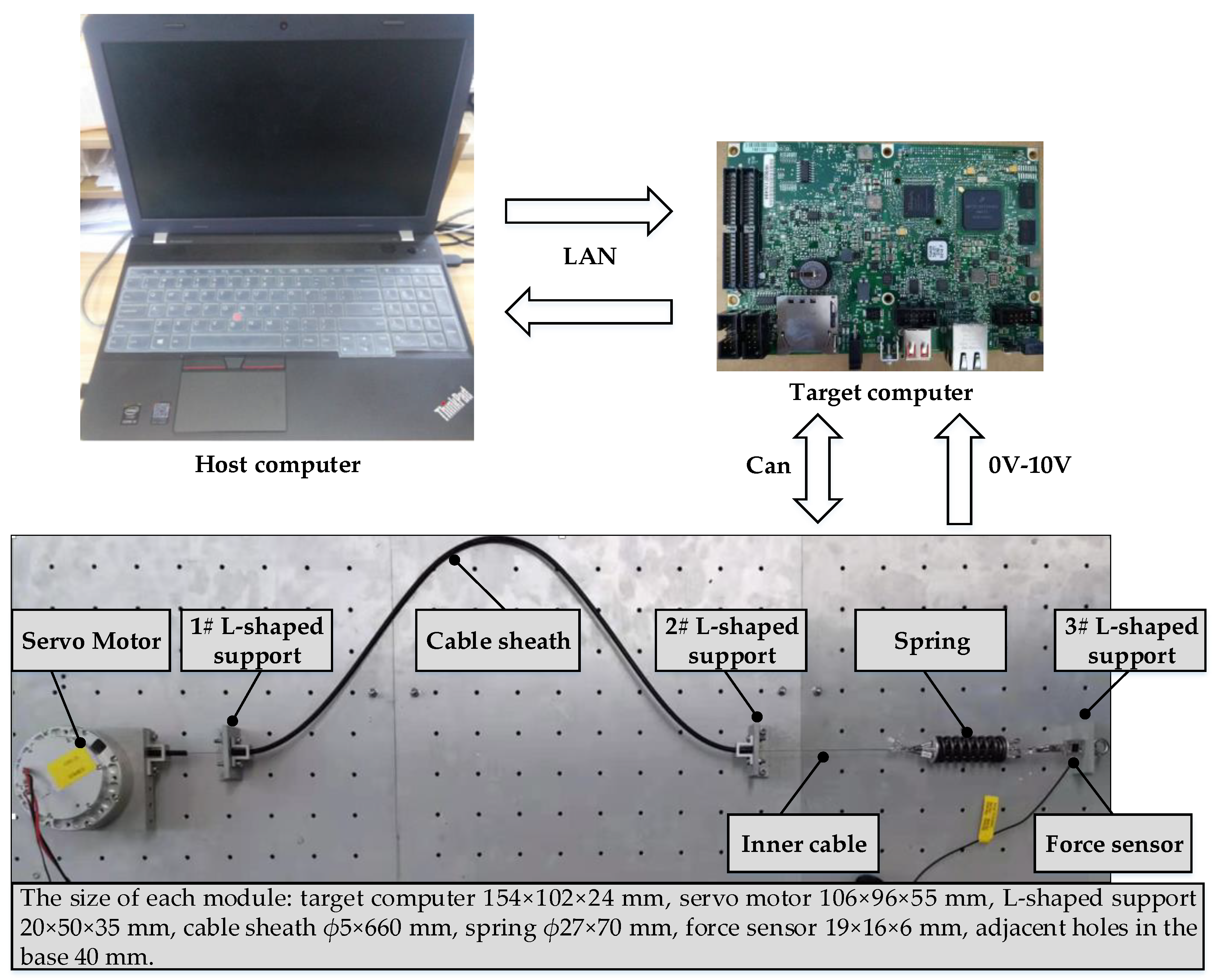
4.1. Test Setup
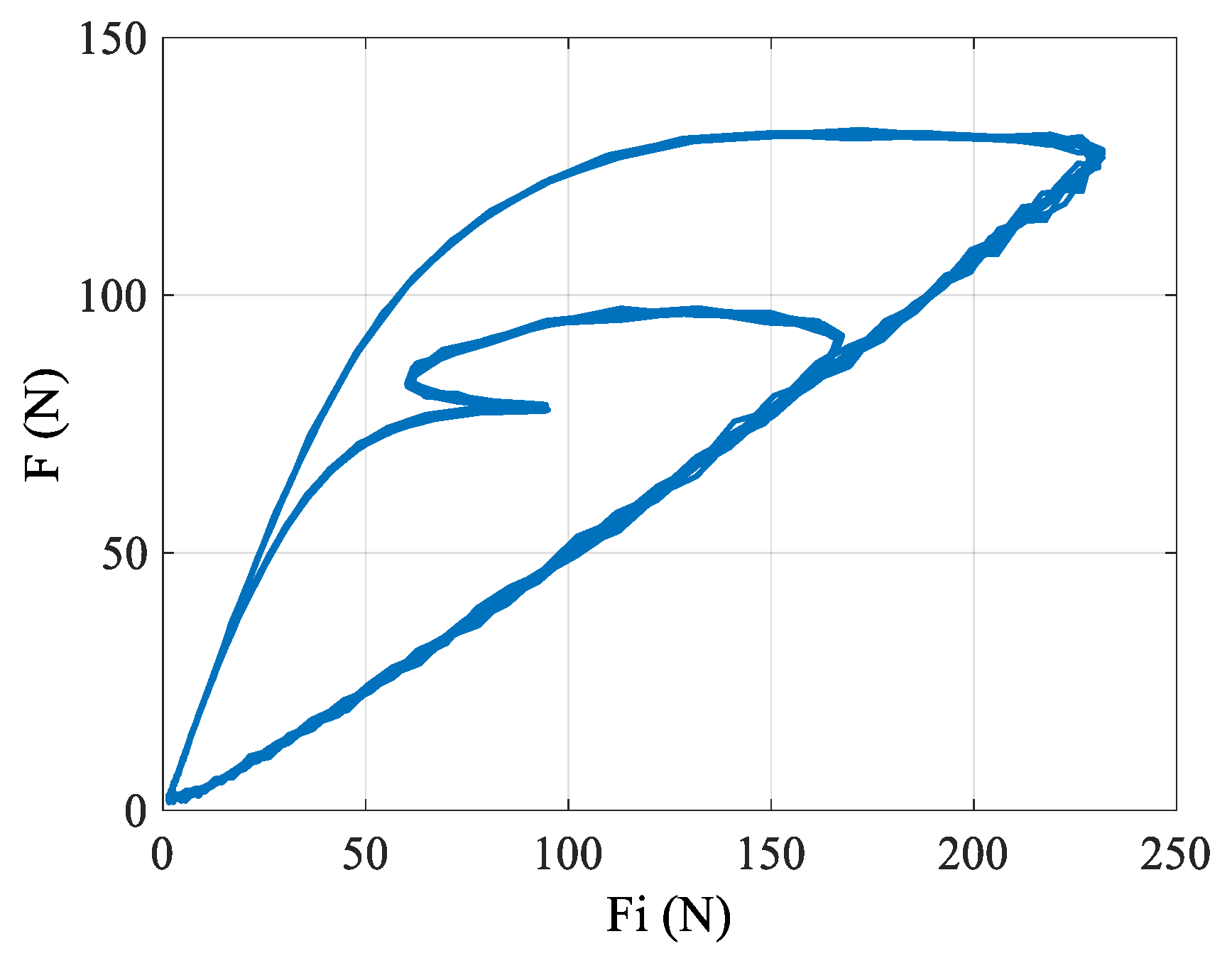
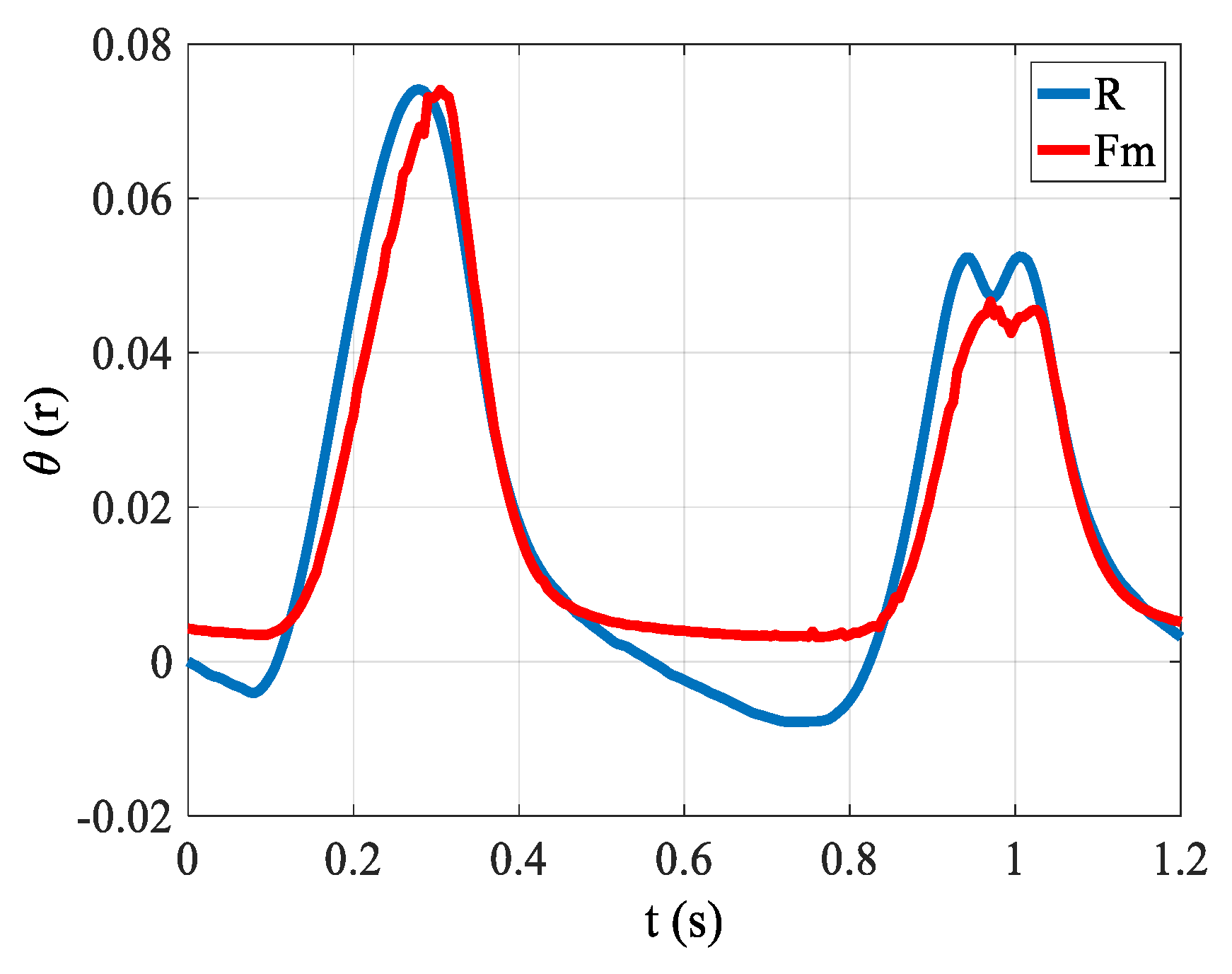
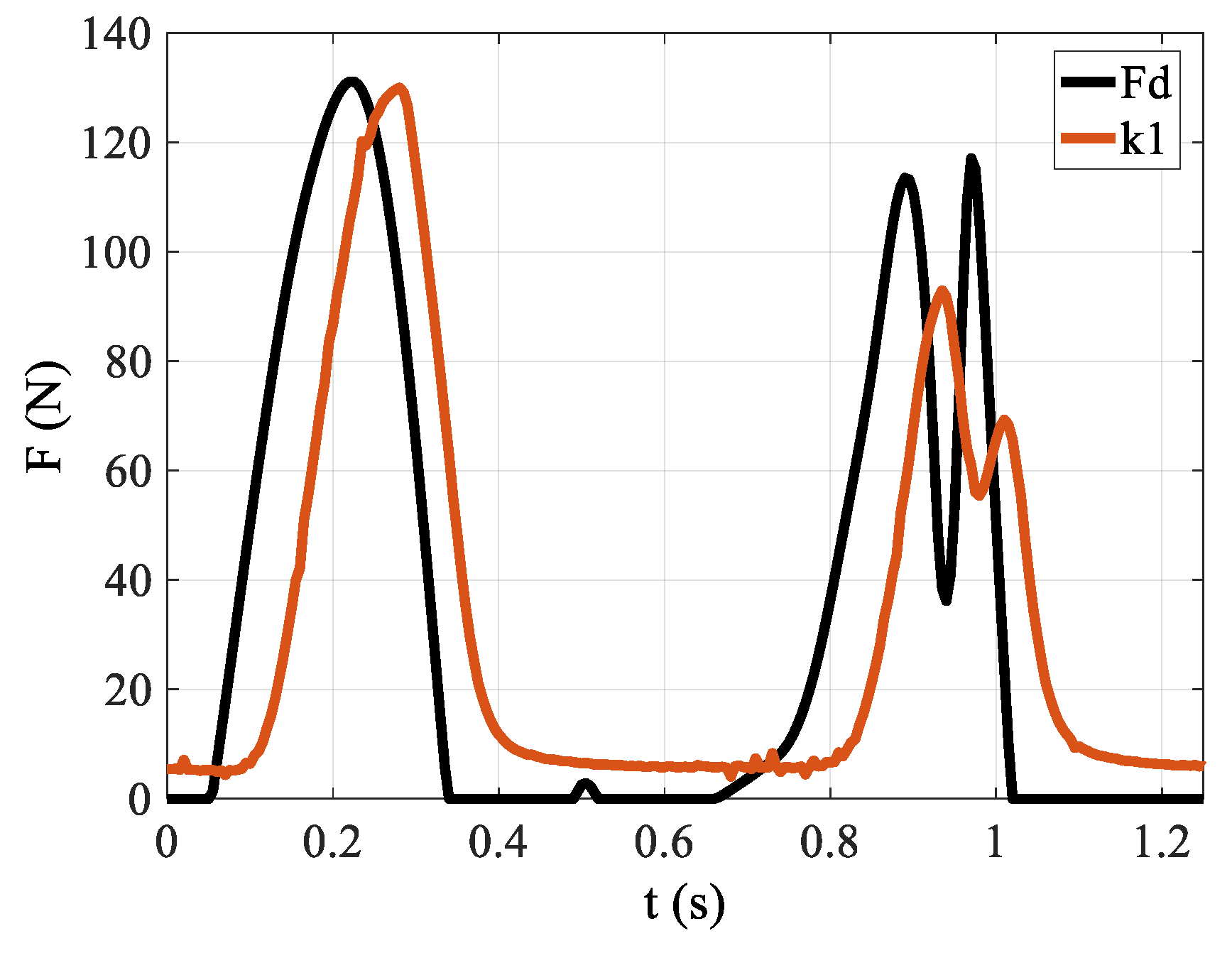
4.2. Friction Verification of the Bowden Cable
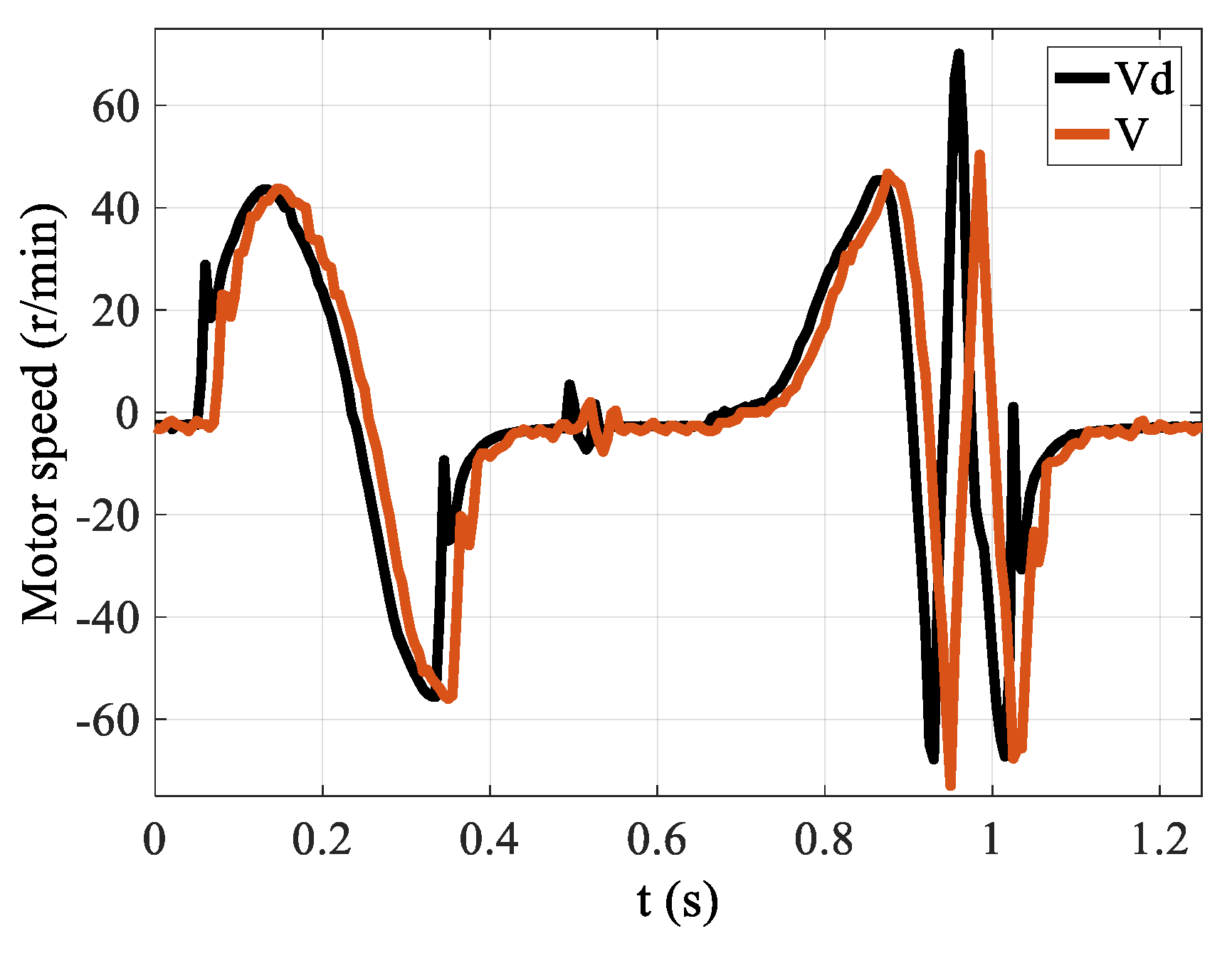
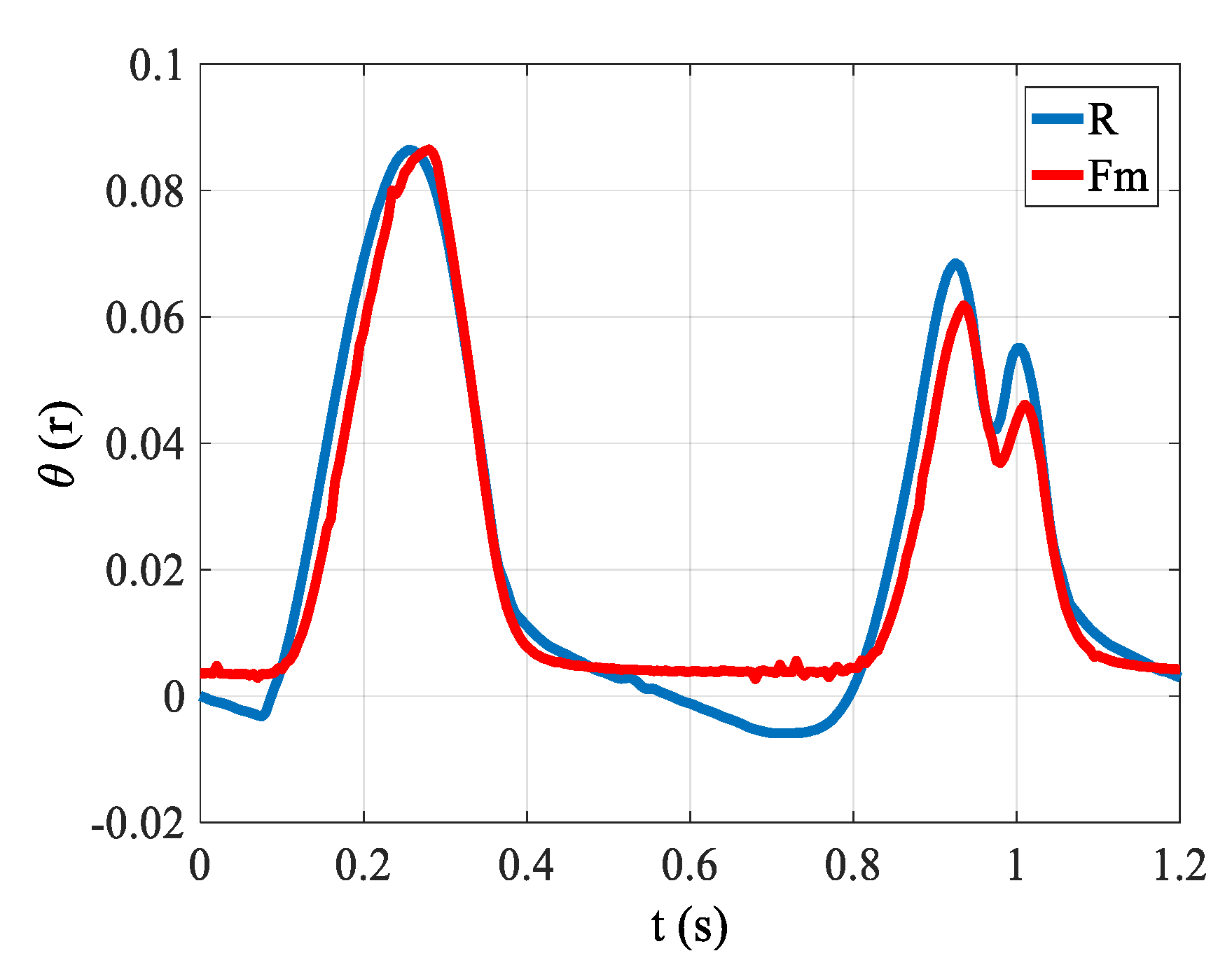
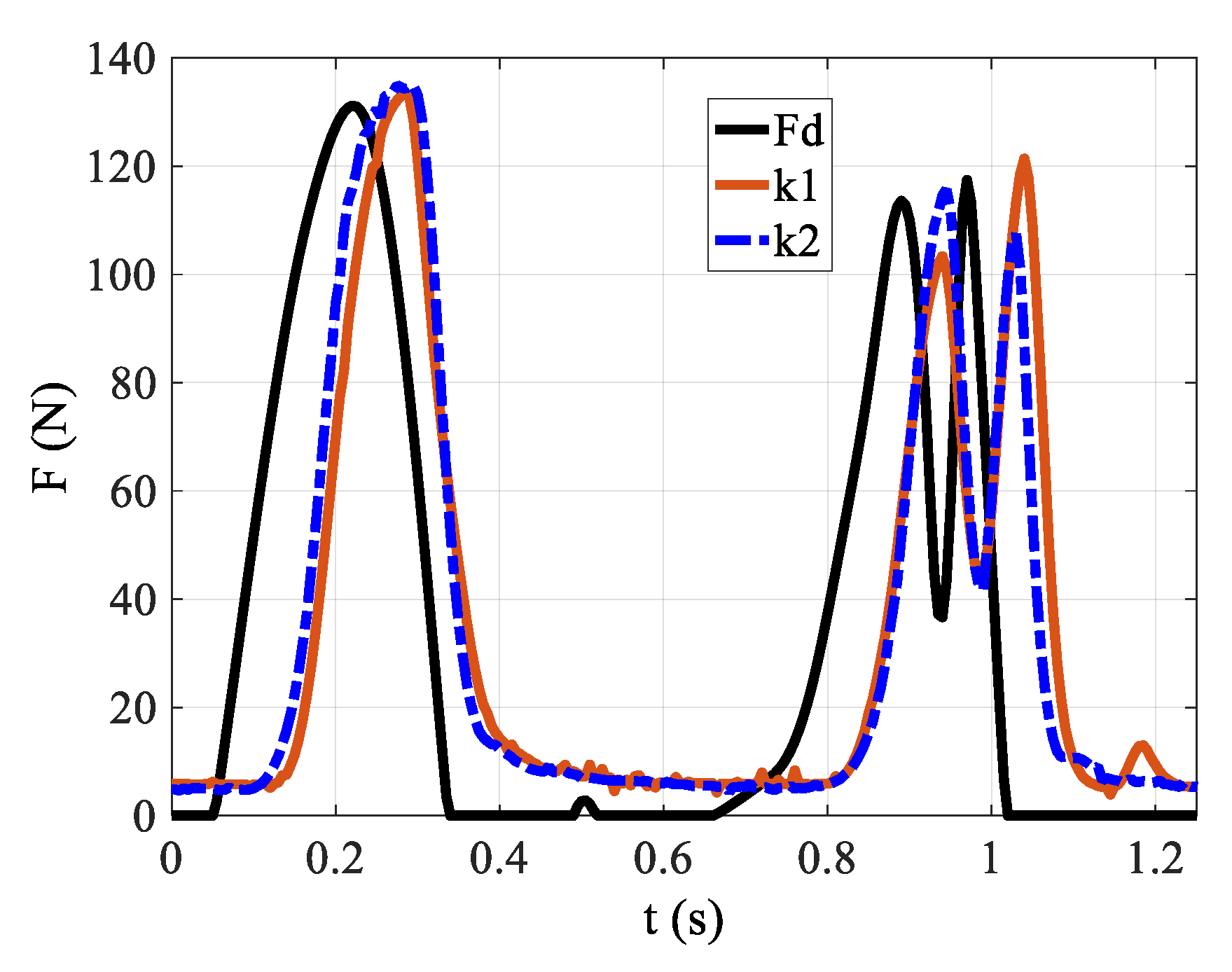
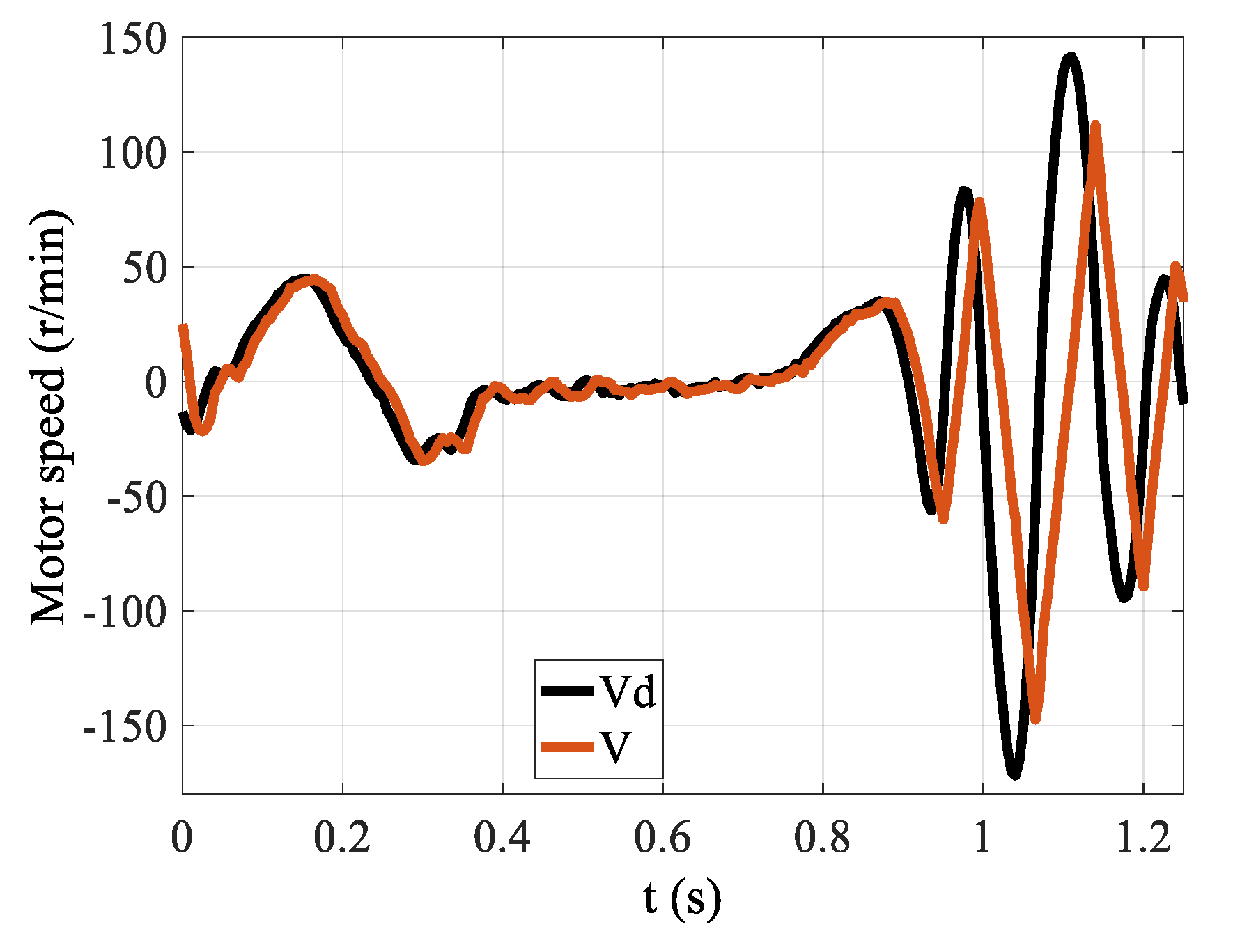
4.3. PID Control in Both the Inner and Outer Loop
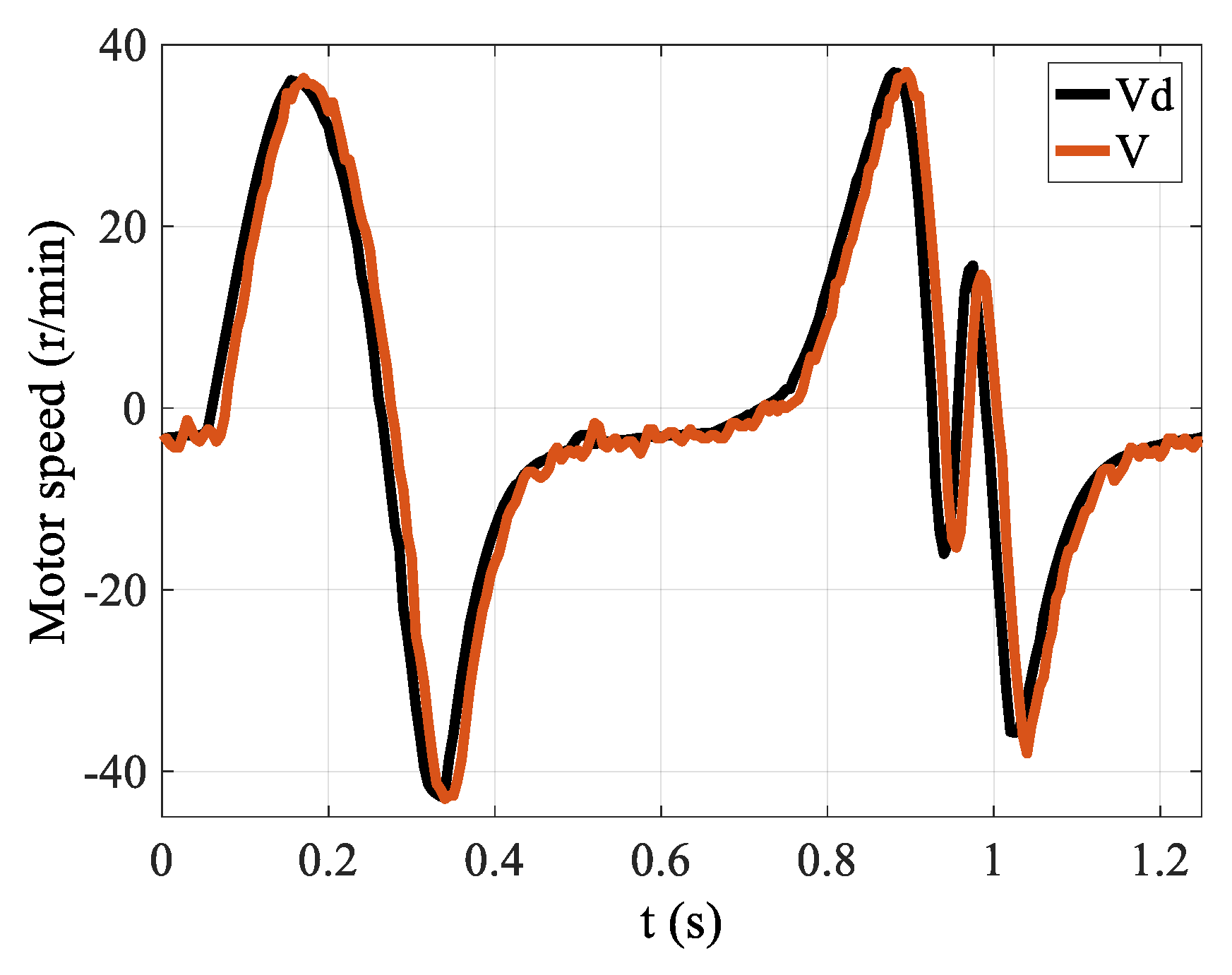
4.4. The FFPD in the Outer Loop
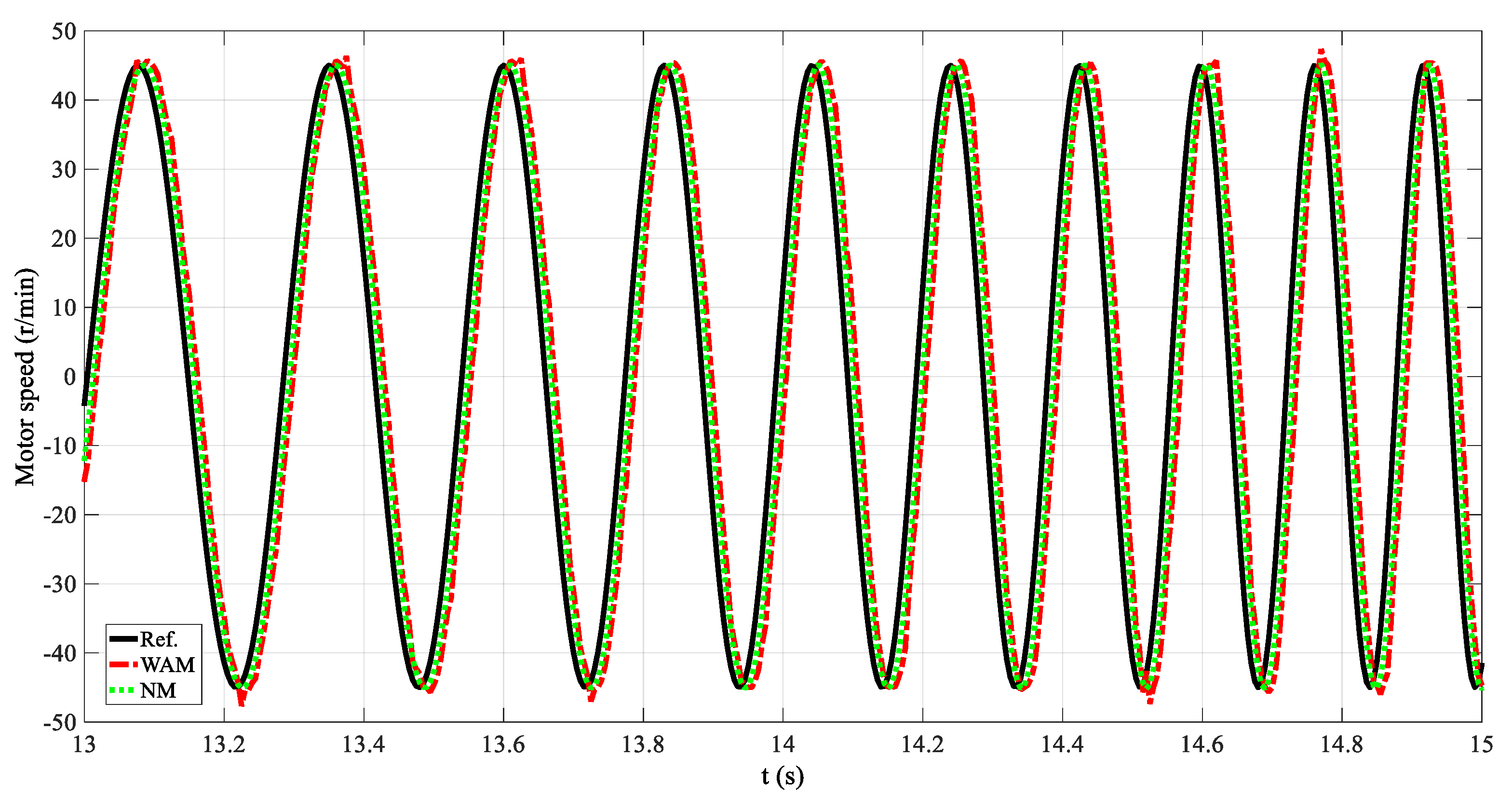
4.5. The FFPD in the Outer Loop and the DOB in the Inner Loop
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FFPD | Feedforward-feedback PD controller |
| DOB | Disturbance observer |
References
- Choi, B.; Seo, C.; Lee, S.; Kim, B. Control of power-augmenting lower extremity exoskeleton while walking with heavy payload. Int. J. Adv. Robot. Syst. 2019, 16, 1–16. [Google Scholar] [CrossRef]
- Song, G.K.; Huang, R.; Qiu, J.; Cheng, H.; Fan, S. Model-based Control with Interaction Predicting for Human-coupled Lower Exoskeleton Systems. J. Intell. Robot. Syst. 2020, 100, 389–400. [Google Scholar] [CrossRef]
- Sulzer, J.S.; Roiz, R.A.; Peshkin, M.A.; Patton, J.L. A highly backdrivable, lightweight knee actuator for investigating gait in stroke. IEEE Trans. Robot. 2009, 25, 539–548. [Google Scholar] [CrossRef] [PubMed]
- Dawson-Elli, A.R.; Adamczyk, P.G. Design and Validation of a Lower-Limb Haptic Rehabilitation Robot. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1584–1594. [Google Scholar] [CrossRef] [PubMed]
- Lippi, V.; Mergner, T. A Challenge: Support of Standing Balance in Assistive Robotic Devices. Appl. Sci. 2020, 10, 5240. [Google Scholar] [CrossRef]
- Wu, Y.N.; Hwang, M.; Ren, Y.; Gaebler-Spira, D.; Zhang, L.Q. Combined passive stretching and active movement rehabilitation of lower-limb impairments in children with cerebral palsy using a portable robot. Neurorehabilit. Neural Repair. 2011, 25, 378–385. [Google Scholar] [CrossRef]
- Zhang, T.; Tran, M.; Huang, H. Admittance shaping-based assistive control of SEA-driven robotic hip exoskeleton. IEEE/ASME Trans. Mechatron. 2019, 24, 1508–1519. [Google Scholar] [CrossRef]
- Huo, W.G.; Mohammed, S.; Amirat, Y. Impedance reduction control of a knee joint human-exoskeleton system. IEEE Trans. Control Syst. Technol. 2019, 27, 2541–2556. [Google Scholar] [CrossRef]
- Asbeck, A.T.; De Rossi, S.M.; Galiana, I.; Ding, Y.; Walsh, C.J. Stronger, Smarter, Softer: Next-Generation Wearable Robots. IEEE Robot. Autom. Mag. 2014, 21, 22–33. [Google Scholar] [CrossRef]
- Wu, Q.C.; Wang, X.S.; Chen, B.; Wu, H.G. Development of an RBFN-based neural-fuzzy adaptive control strategy for an upper limb rehabilitation exoskeleton. Mechatronics 2018, 53, 85–94. [Google Scholar] [CrossRef]
- Xiloyannis, M.; Annese, E.; Canesi, M.; Kodiyan, A.; Bicchi, A.; Micera, S.; Ajoudani, A.; Masia, L. Design and Validation of a Modular One-To-Many Actuator for a Soft Wearable Exosuit. Front. Neurorobot. 2019, 13, 39. [Google Scholar] [CrossRef]
- Nycz, C.J.; Butzer, T.; Lambercy, O.; Arata, J.; Fischer, G.S.; Gassert, R. Design and Characterization of a Lightweight and Fully Portable Remote Actuation System for Use with a Hand Exoskeleton. IEEE Robot. Autom. Lett. 2016, 1, 976–983. [Google Scholar] [CrossRef]
- Zhang, F.H.; Hua, L.; Fu, Y.L.; Chen, H.W.; Wang, S.G. Design and development of a hand exoskeleton for rehabilitation of hand injuries. Mech. Mach. Theory 2016, 73, 103–116. [Google Scholar] [CrossRef]
- Pinto-Fernandez, D.; Torricelli, D.; Sanchez-Villamanan, M.D.; Aller, F.; Mombaur, K.; Conti, R.; Vitiello, N.; Moreno, J.C.; Pons, J.L. Performance Evaluation of Lower Limb Exoskeletons: A Systematic Review. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1573–1583. [Google Scholar] [CrossRef] [PubMed]
- Bryan, G.M.; Franks, P.W.; Klein, S.C.; Peuchen, R.J.; Collins, S.H. A hip–knee–ankle exoskeleton emulator for studying gait assistance. Int. J. Robot. Res. 2020, 40, 1–25. [Google Scholar] [CrossRef]
- Yu, S.Y.; Huang, T.H.; Wang, D.P.; Lynn, B.; Sayd, D.; Silivanov, V.; Park, Y.S.; Tian, Y.L.; Su, H. Design and Control of a High-Torque and Highly-Backdrivable Hybrid Soft Exoskeleton for Knee Injury Prevention during Squatting. IEEE Robot. Autom. Lett. 2019, 4, 4579–4586. [Google Scholar] [CrossRef]
- Chen, D.Y.; Yun, Y.; Deshpande, A.D. Experimental characterization of Bowden cable friction. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 5927–5933. [Google Scholar] [CrossRef]
- Li, J.T.; Zheng, R.Y.; Zhang, Y.R.; Yao, J.C. iHandRehab: An interactive hand exoskeleton for active and passive rehabilitation. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics (ICORR), Zurich, Switzerland, 27 June–1 July 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Do, T.N.; Tjahjowidodo, T.; Lau, M.W.; Phee, S.J. Adaptive Control of Position Compensation for Cable-Conduit Mechanisms Used in Flexible Surgical Robots. In Proceedings of the 2014 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO), Vienna, Austria, 1–3 September 2014; pp. 110–117. [Google Scholar] [CrossRef]
- Ding, Y.; Galiana, I.; Asbeck, A.; Quinlivan, B.; Rossi, S.M.; Walsh, C. Multi-joint actuation platform for lower extremity soft exosuits. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 1327–1334. [Google Scholar] [CrossRef]
- Li, P.; Zhu, G.L.; Zhang, M.M. Linear Active Disturbance Rejection Control for Servo Motor Systems with Input Delay via Internal Model Control Rules. IEEE Trans. Ind. Electron. 2021, 68, 1077–1086. [Google Scholar] [CrossRef]
- Lee, G.; Ding, Y.; Bujanda, I.G.; Karavas, N.; Zhou, Y.M.; Walsh, C.J. Improved assistive profile tracking of soft exosuits for walking and jogging with off-board actuation. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1699–1706. [Google Scholar] [CrossRef]
- Kesner, S.B.; Howe, R.D. Position control of motion compensation cardiac catheters. IEEE Trans. Robot. 2011, 27, 1045–1055. [Google Scholar] [CrossRef]
- Palli, G.; Borghesan, G.; Melchiorri, C. Modeling, Identification, and Control of Tendon-Based Actuation Systems. IEEE Trans. Robot. 2012, 28, 277–290. [Google Scholar] [CrossRef]
- Jeong, U.; Cho, K.J. A novel low-cost, large curvature bend sensor based on a Bowden-cable. Sensors 2016, 16, 961. [Google Scholar] [CrossRef]
- Palli, G.; Melchiorri, C. Model and control of tendon-sheath transmission systems. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 988–993. [Google Scholar] [CrossRef]
- Kuan, J.Y.; Pasch, K.A.; Herr, H.M. A High-Performance Cable-Drive Module for the Development of Wearable Devices. IEEE/ASME Trans. Mechatron. 2018, 23, 1238–1248. [Google Scholar] [CrossRef]
- Carlson, L.E.; Veatch, B.D.; Frey, D.D. Efficiency of Prosthetic Cable and Housing. JPO J. Prosthet. Orthot. 1995, 7, 96–99. [Google Scholar] [CrossRef]
- Jeong, U.; Cho, K.J. Control of a Bowden-Cable Actuation System with Embedded BoASensor for Soft Wearable Robots. IEEE Trans. Ind. Electron. 2019, 67, 7669–7680. [Google Scholar] [CrossRef]
- Jeong, U.; Cho, K. Feedforward friction compensation of Bowden-cable transmission via loop routing. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 5948–5953. [Google Scholar] [CrossRef]
- Wang, W.J.; Yu, L.T.; Yang, J. Toward force detection of a cable-driven micromanipulator for a surgical robot based on disturbance observer. Mech. Sci. 2017, 8, 323–335. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S.H. Disturbance-Observer-Based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Zhao, J.S.; Wang, Z.P.; Yang, T.; Xu, J.X.; Ma, Z.L.; Wang, C.F. Design of a novel modal space sliding mode controller for electro-hydraulic driven multi-dimensional force loading parallel mechanism. ISA Trans. 2020, 99, 374–386. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Rho, S.; Yang, C.; Jiang, F.; Ding, Z.; Yi, C.; Wei, B. Active Loading Control Design for a Wearable Exoskeleton with a Bowden Cable for Transmission. Actuators 2021, 10, 108. https://doi.org/10.3390/act10060108
Wang Z, Rho S, Yang C, Jiang F, Ding Z, Yi C, Wei B. Active Loading Control Design for a Wearable Exoskeleton with a Bowden Cable for Transmission. Actuators. 2021; 10(6):108. https://doi.org/10.3390/act10060108
Chicago/Turabian StyleWang, Zhipeng, Seungmin Rho, Chifu Yang, Feng Jiang, Zhen Ding, Chunzhi Yi, and Baichun Wei. 2021. "Active Loading Control Design for a Wearable Exoskeleton with a Bowden Cable for Transmission" Actuators 10, no. 6: 108. https://doi.org/10.3390/act10060108
APA StyleWang, Z., Rho, S., Yang, C., Jiang, F., Ding, Z., Yi, C., & Wei, B. (2021). Active Loading Control Design for a Wearable Exoskeleton with a Bowden Cable for Transmission. Actuators, 10(6), 108. https://doi.org/10.3390/act10060108






