Effects of Ferroelectric Fillers on Composite Dielectric Elastomer Actuator
Abstract
:1. Introduction
2. Materials and Methods
- PDMS, Sylgard 184 (Dow Inc., Midland, MI, USA, part #4019862), number average molecular weight of 27,000 [35], elastomer matrix of dielectric composites. As a widely used commercial PDMS for DEA application, Sylgard 184 was chosen due to its moderate dielectric and mechanical properties, low polydispersity and branching, low pre-cured viscosity (3.5 Pa-s), and fast curing in the presence of temperature. The latter two properties allow to disperse particles using simple fabrication methods and prevent particles from settling down during the curing process, respectively.
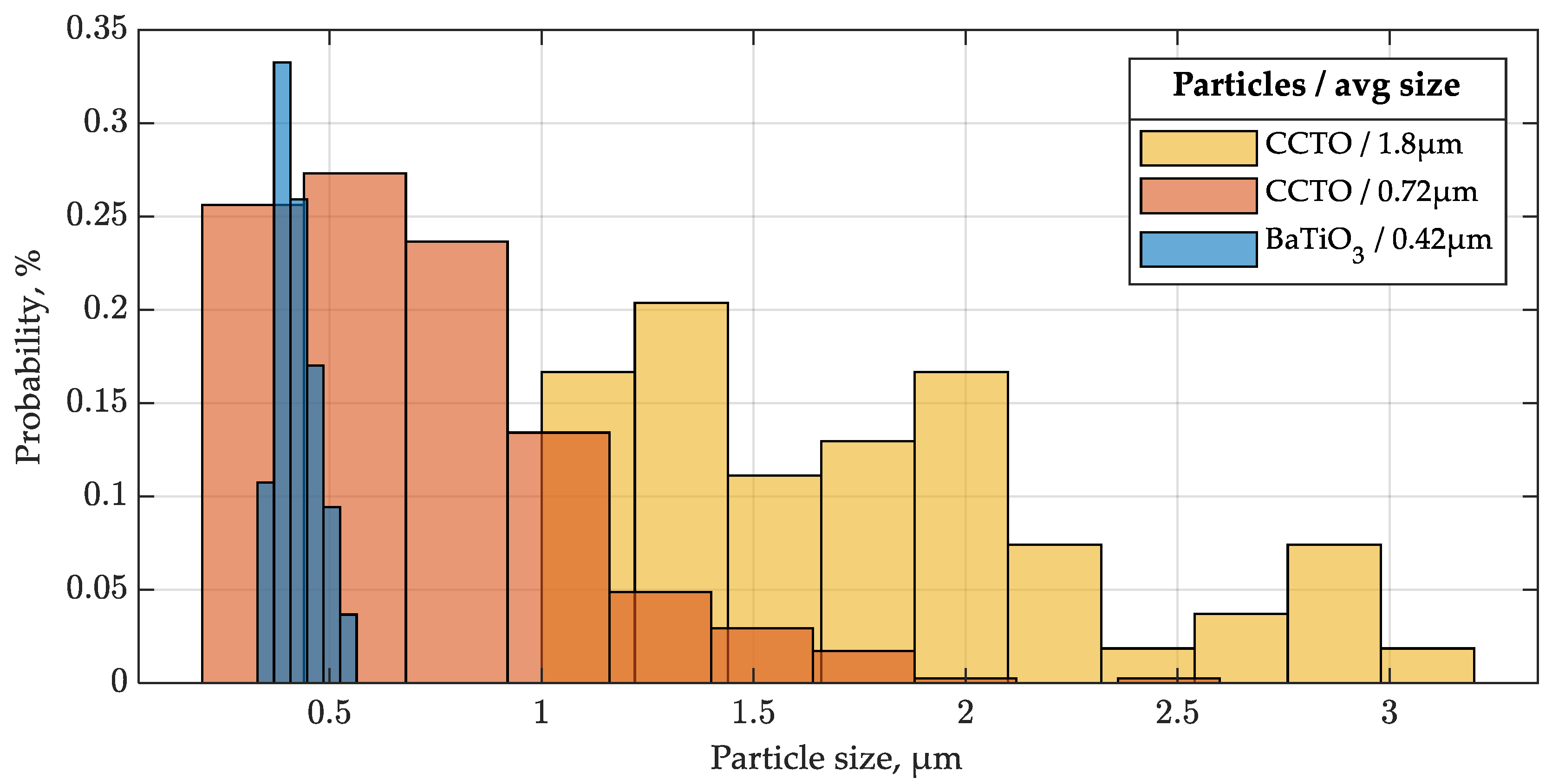
- BaTiO3 (TPL Inc., Albuquerque, NM, USA, HPB-4000), near-spherical particles with a mean diameter of 0.42 μm and tightly packed size distribution (Figure 1a), specific surface area of 4 m2/g, density of 6 g/cm3, purity of 99.5%, and permittivity of 6000.
- CCTO_#1 (Stanford Advanced Materials Corp., Lake Forest, CA, USA, part #19185478), random morphology, low aspect ratio particles, with a mean effective diameter of 0.72 μm (Figure 1b), specific surface area of 1.74 m2/g, density of 4.7 g/cm3, purity of 99.5%, and permittivity range of 9600–12,000.
- CCTO_#2 (Bonding Chemical, Katy, TX, USA, part #535616), random morphology, low aspect ratio particles, with a mean effective diameter of 1.8 μm (Figure 1c), specific surface area of 0.28 m2/g, density of 4.7 g/cm3, purity of 98.2%, and permittivity range of 9600–12,000.
2.1. Composites Mixtures and Film Preparation
2.2. Material Characterization
2.2.1. Permittivity
2.2.2. Mechanical Testing
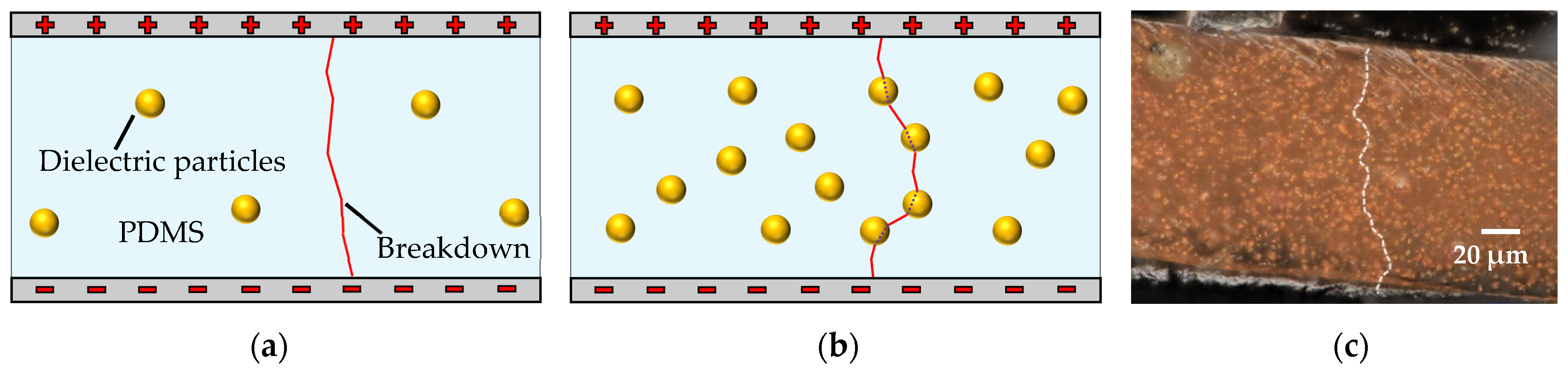
2.2.3. Breakdown Strength
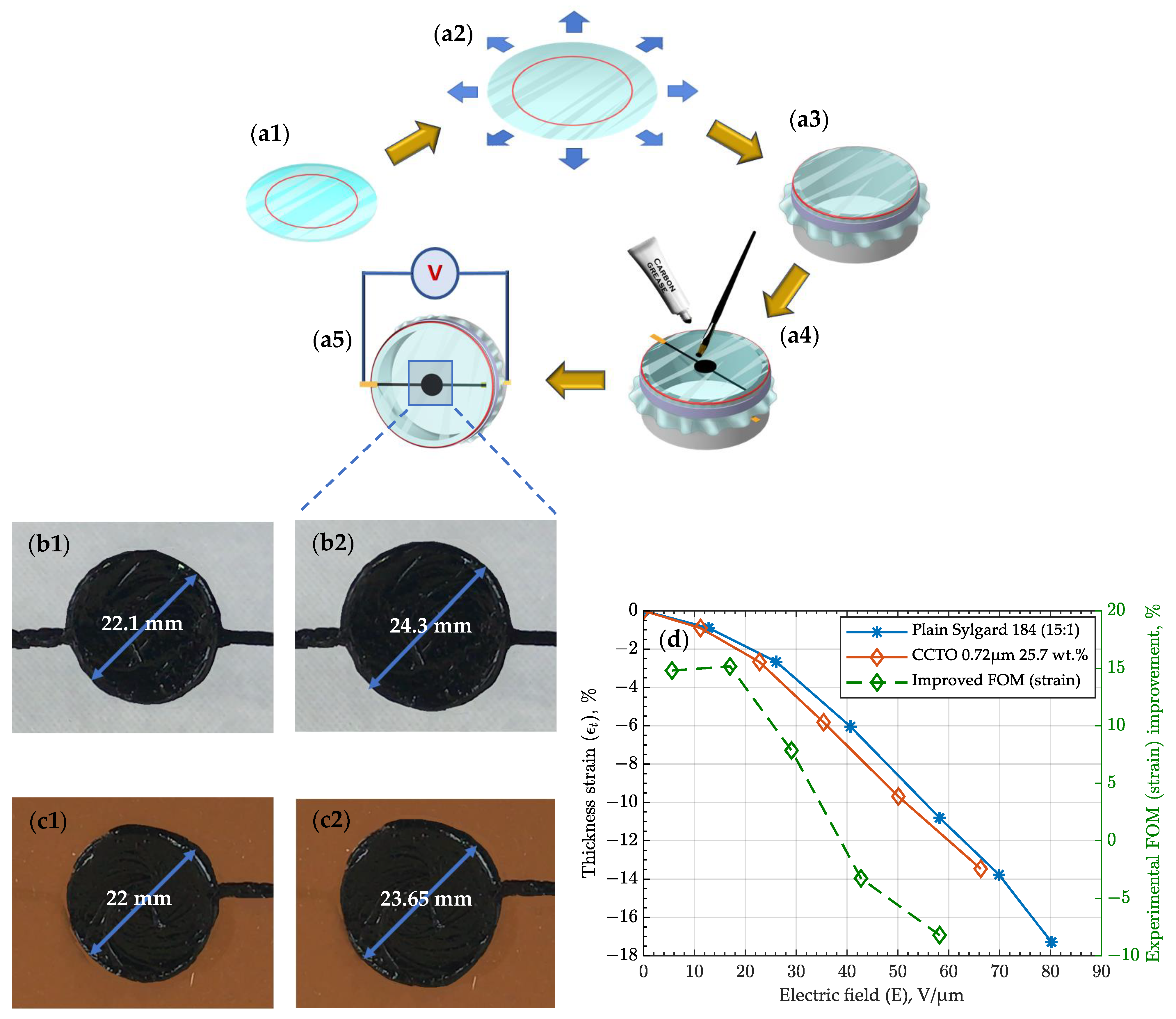
2.2.4. Pre-Stretched DEA Testing
3. Results and Discussion
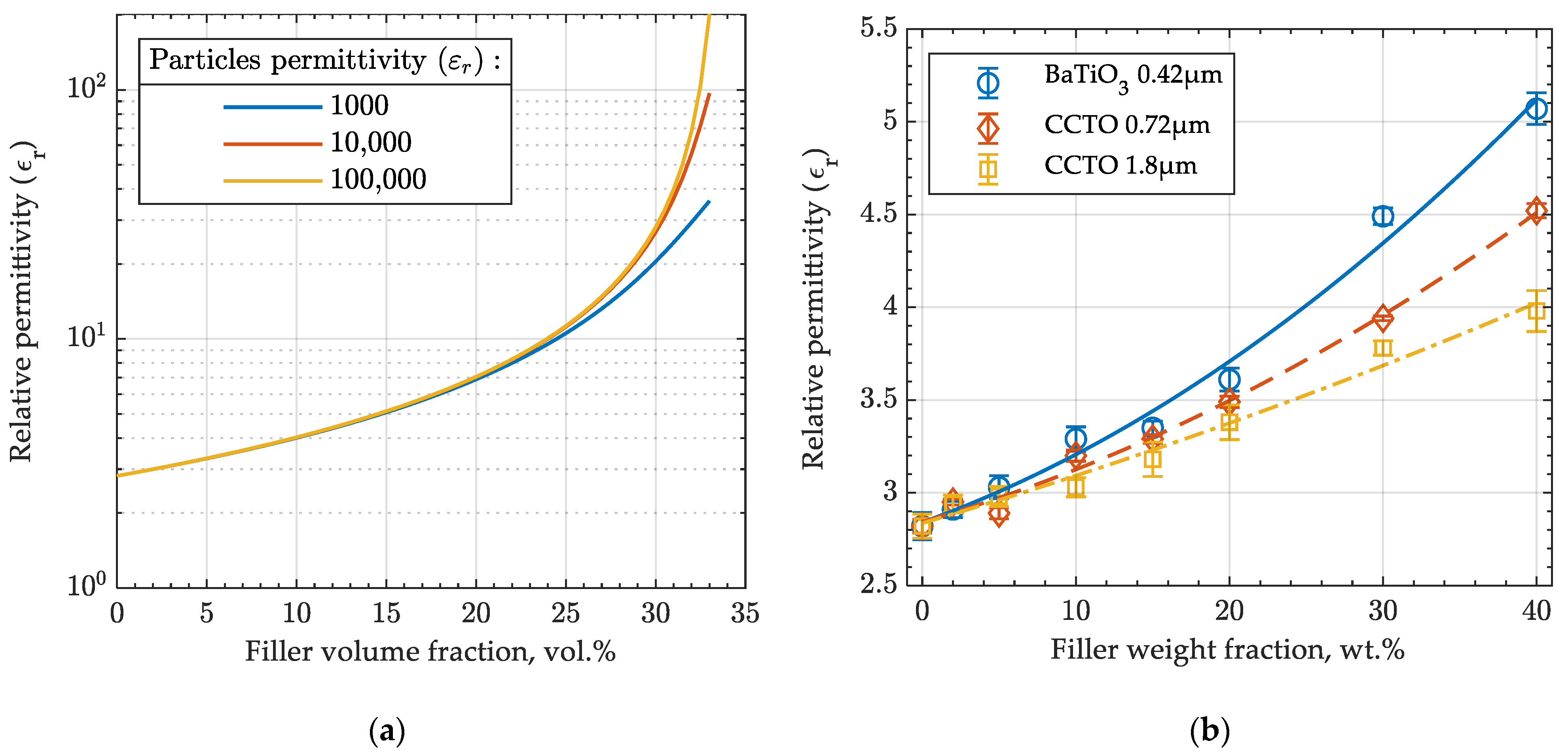
3.1. Permittivity
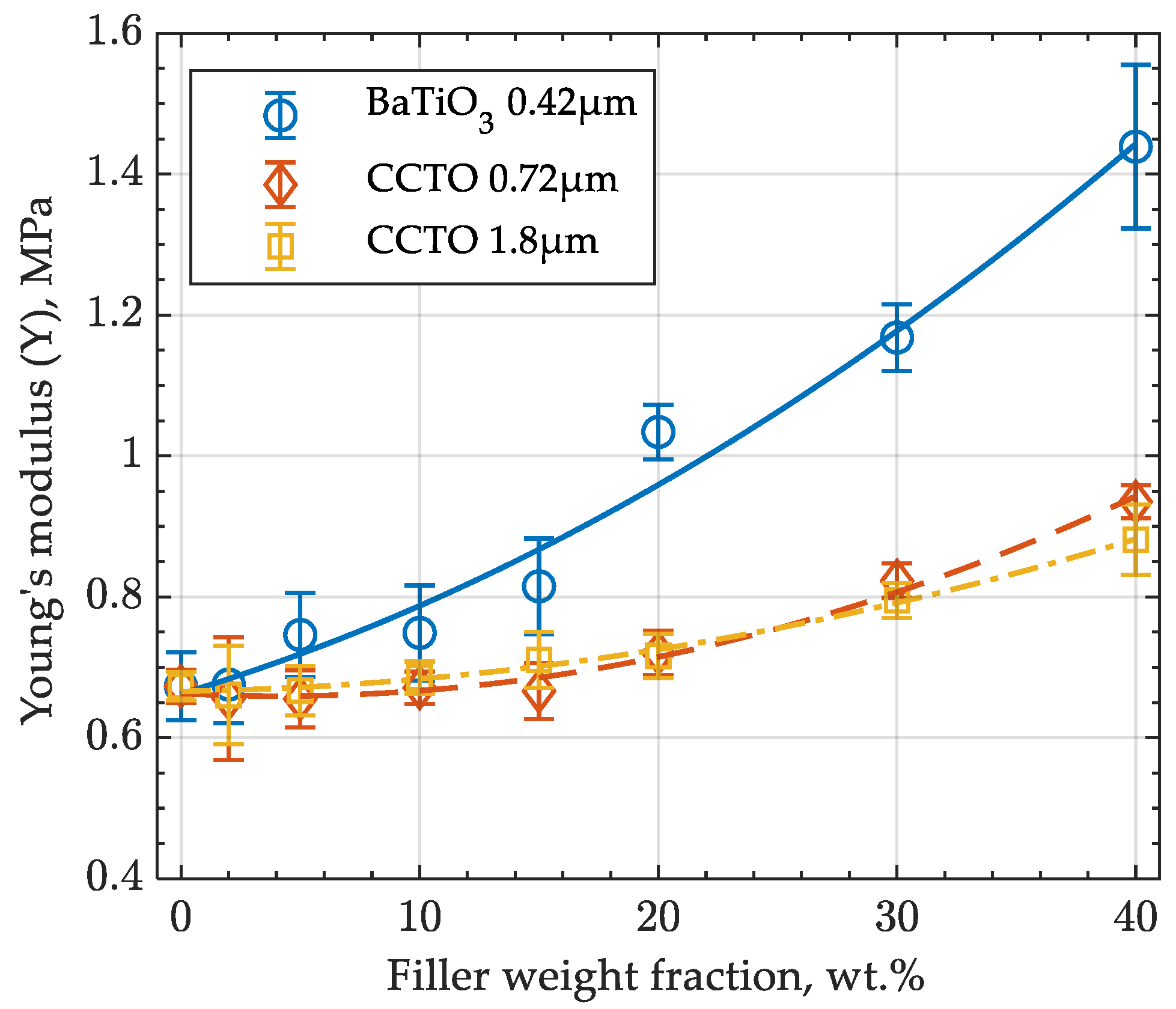
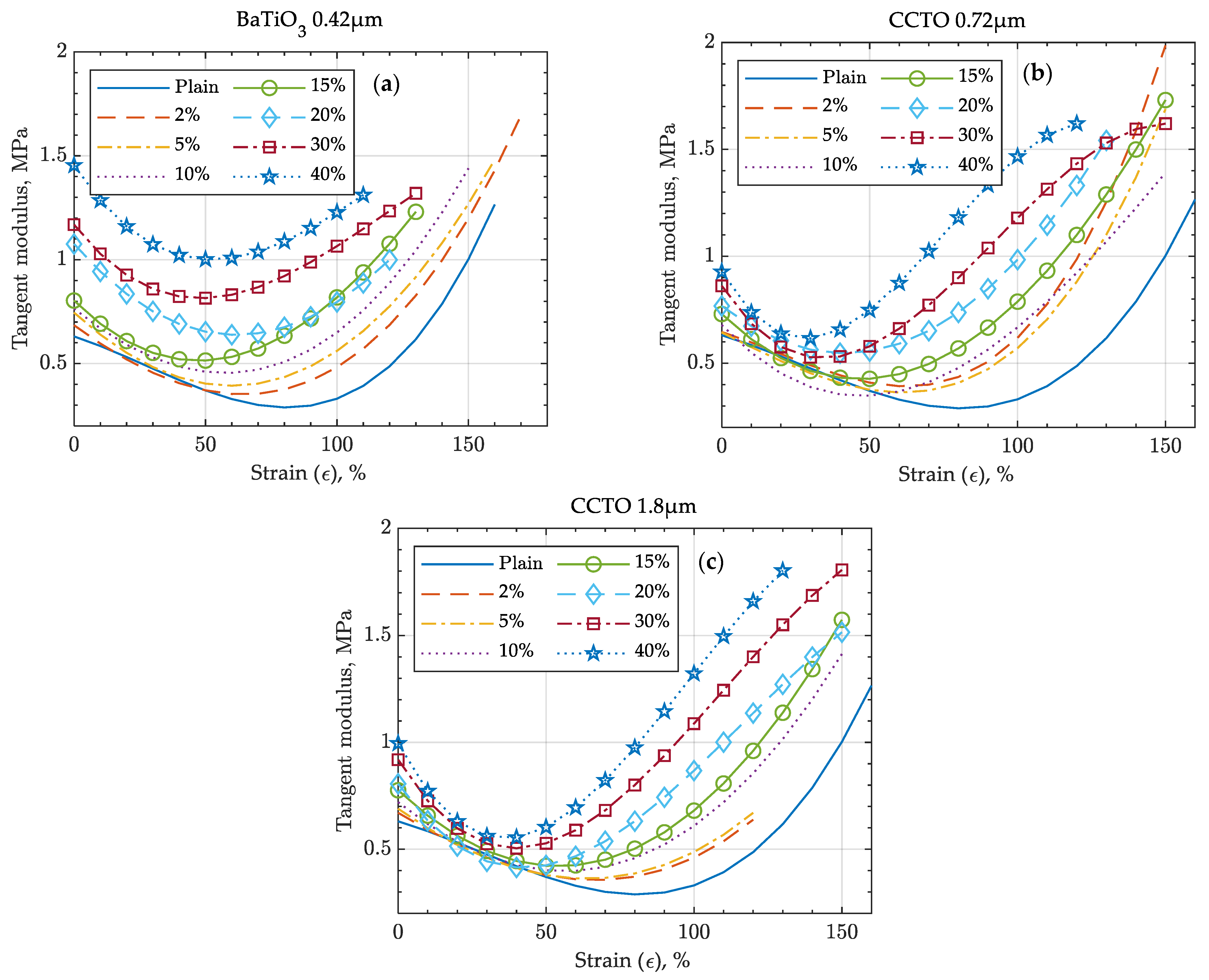
3.2. Mechanical Testing of Dielectrics
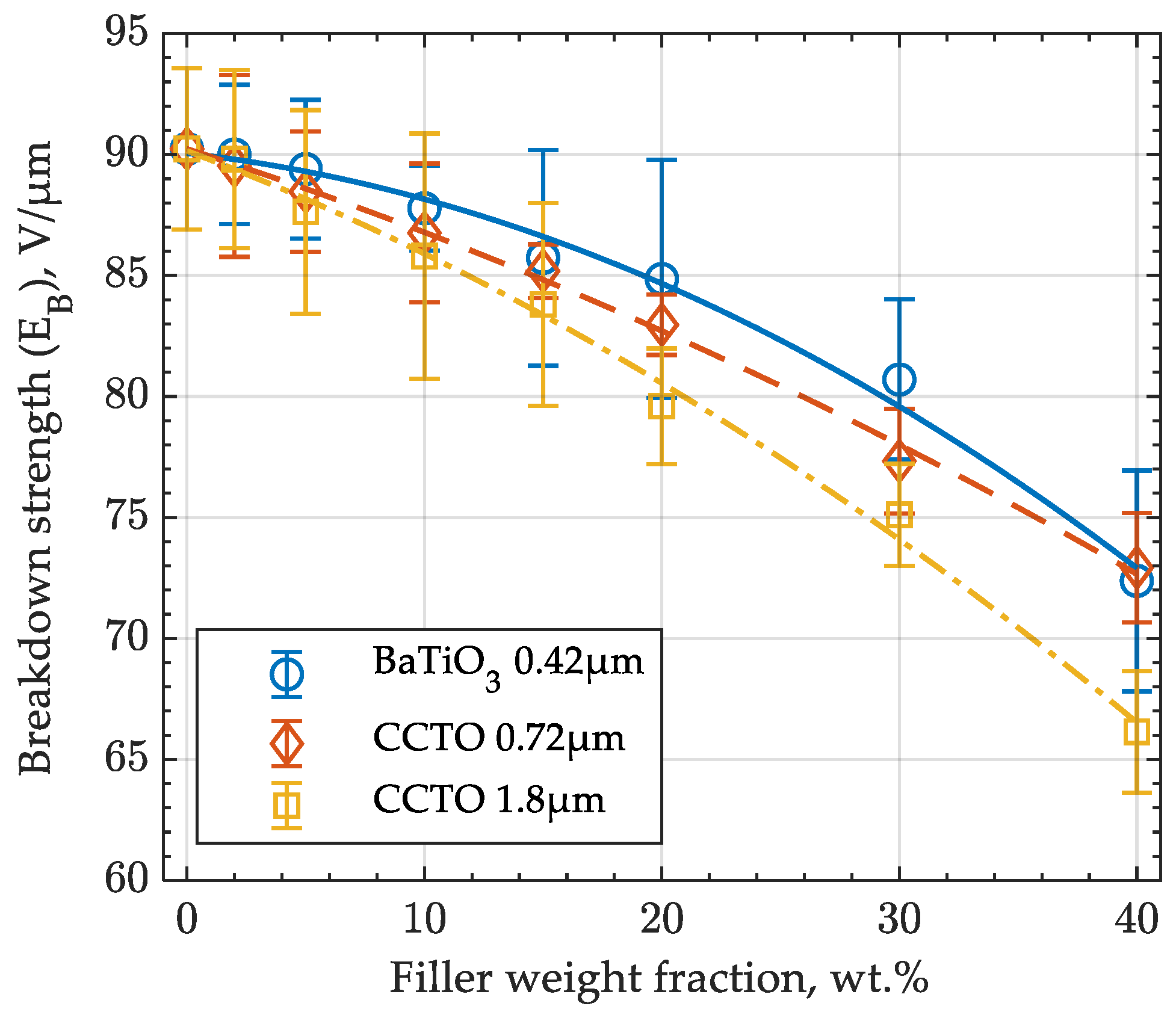
3.3. Breakdown Strength
| Material Composition | (MPa) | Tensile Strength | Maximum Strain | Maximum Actuaction Thickness Strain | |||||
|---|---|---|---|---|---|---|---|---|---|
| Sylgard 184 (15:1 mix ratio) | 2.82 | 0.673 | 90.3 | 1 | 1 | 0.984 | 174 | 30.8 | |
| BaTiO3 0.42 μm | 2% | 2.91 | 0.676 | 90.0 | 0.986 | 0.992 | 1.18 | 172 | 30.3 |
| 5% | 3.03 | 0.746 | 89.4 | 0.961 | 0.977 | 1.04 | 156 | 29.6 | |
| 10% | 3.29 | 0.749 | 87.8 | 0.912 | 0.951 | 0.999 | 147 | 28 | |
| 15% | 3.35 | 0.815 | 85.7 | 0.857 | 0.926 | 1.06 | 139 | 26.3 | |
| 20% | 3.61 | 1.03 | 84.9 | 0.798 | 0.903 | 1.06 | 133 | 24.5 | |
| 30% | 4.49 | 1.17 | 80.7 | 0.673 | 0.862 | 1.32 | 134 | 20.7 | |
| 40% | 5.07 | 1.44 | 72.4 | 0.543 | 0.829 | 1.43 | 125 | 16.7 | |
| CCTO 0.72 μm | 2% | 2.95 | 0.656 | 89.5 | 1.01 | 1.02 | 1.06 | 152 | 31.1 |
| 5% | 2.89 | 0.655 | 88.5 | 1.02 | 1.05 | 1.06 | 154 | 31.3 | |
| 10% | 3.2 | 0.671 | 86.8 | 1.02 | 1.09 | 1.09 | 154 | 31.3 | |
| 15% | 3.29 | 0.666 | 85.2 | 0.998 | 1.12 | 1.16 | 149 | 30.7 | |
| 20% | 3.49 | 0.720 | 83.0 | 0.964 | 1.14 | 1.18 | 141 | 29.6 | |
| 30% | 3.94 | 0.823 | 77.3 | 0.86 | 1.15 | 1.58 | 140 | 26.4 | |
| 40% | 4.52 | 0.935 | 72.9 | 0.728 | 1.12 | 1.49 | 131 | 22.4 | |
| CCTO 1.8 μm | 2% | 2.94 | 0.661 | 89.8 | 0.995 | 1.01 | 0.628 | 132 | 30.6 |
| 5% | 2.98 | 0.667 | 87.6 | 0.987 | 1.03 | 0.676 | 133 | 30.3 | |
| 10% | 3.03 | 0.686 | 85.8 | 0.962 | 1.06 | 1.06 | 154 | 29.6 | |
| 15% | 3.18 | 0.711 | 83.8 | 0.922 | 1.08 | 1.04 | 147 | 28.3 | |
| 20% | 3.38 | 0.716 | 79.6 | 0.87 | 1.09 | 1.16 | 148 | 26.7 | |
| 30% | 3.78 | 0.795 | 75.1 | 0.736 | 1.09 | 1.31 | 143 | 22.6 | |
| 40% | 3.98 | 0.881 | 66.1 | 0.582 | 1.07 | 1.42 | 138 | 17.9 | |
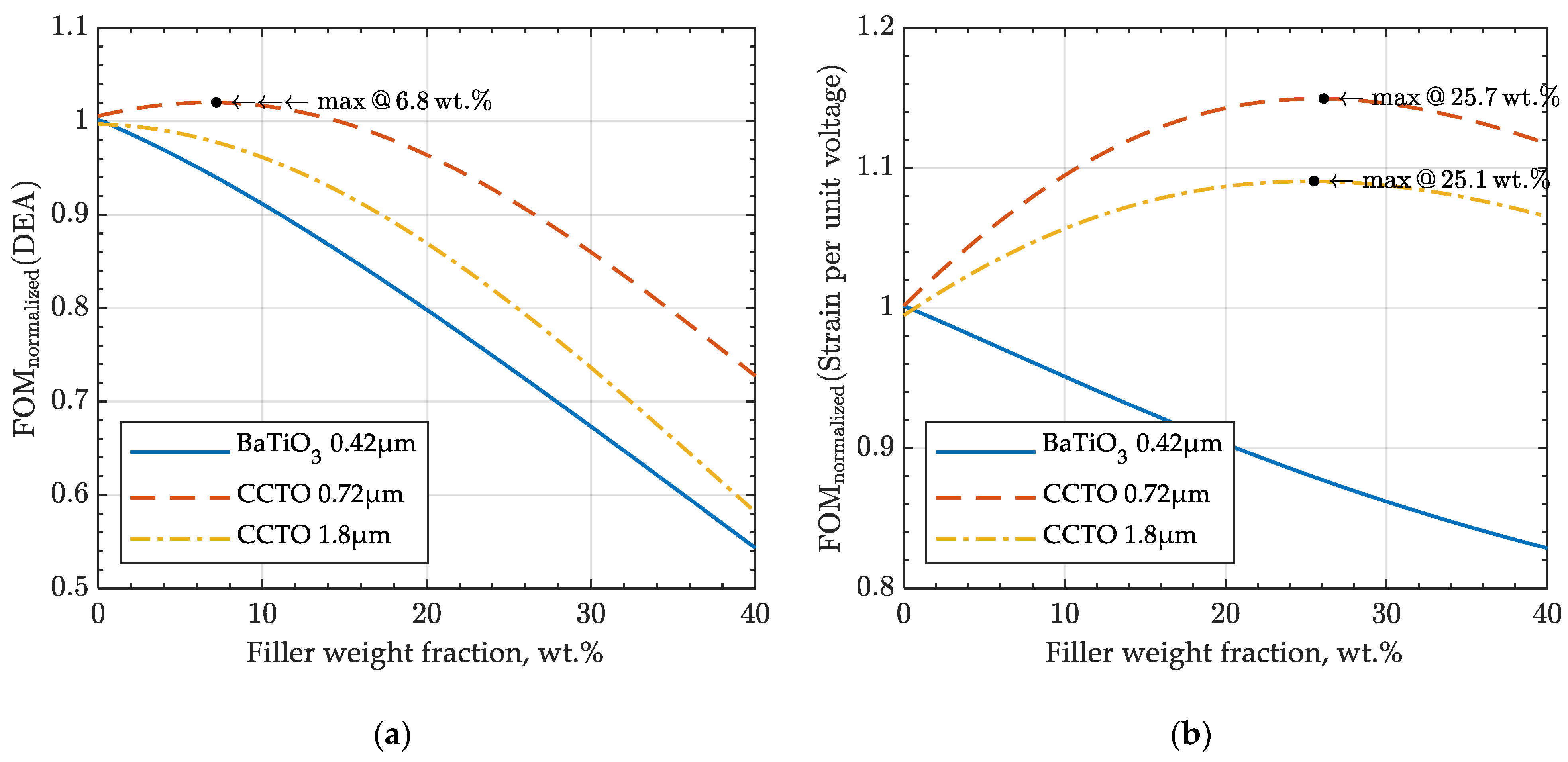
3.4. Figure of Merit (FOM)
3.5. Pre-Stretched DEA Testing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

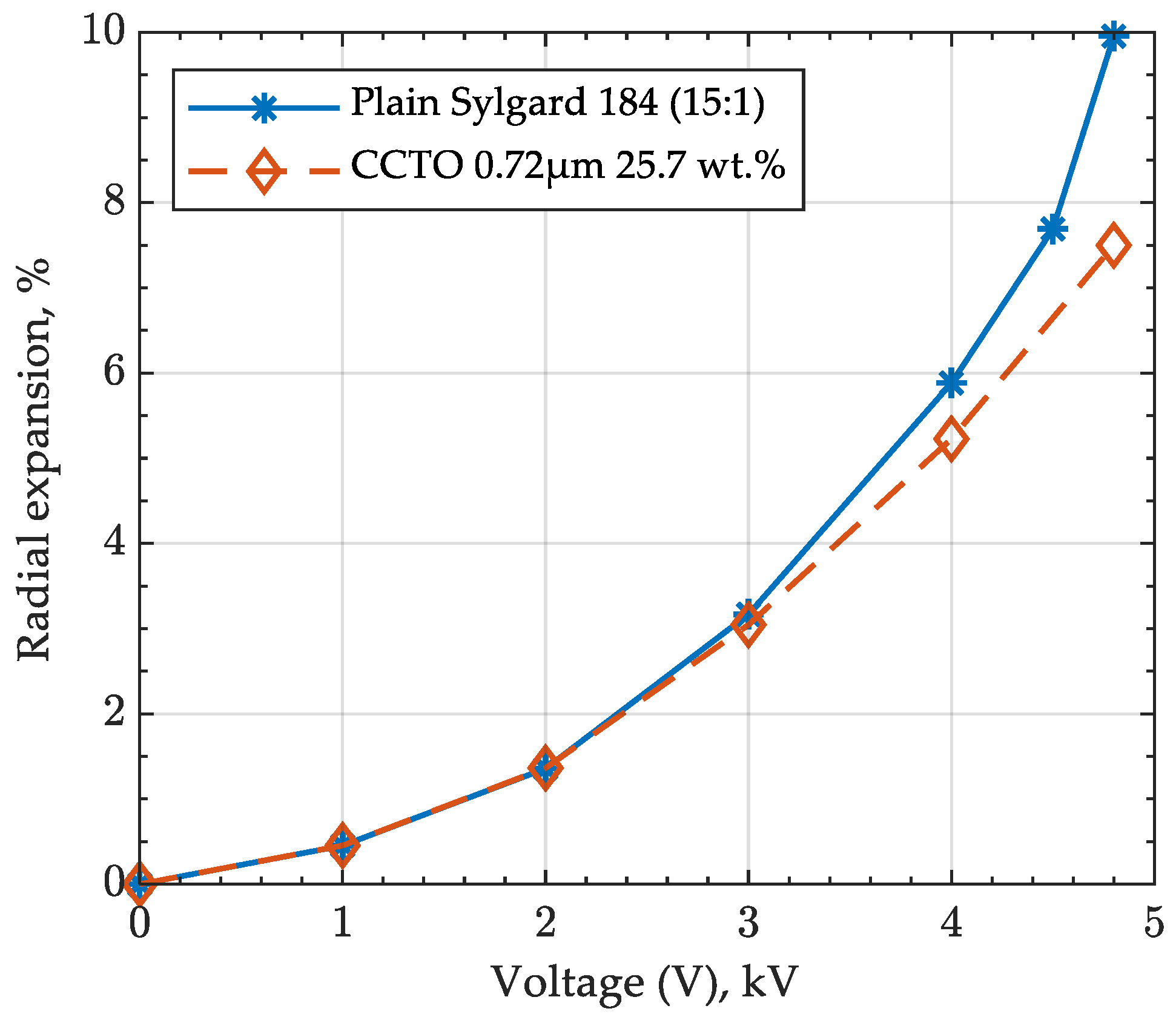
| Material Composition | Thickness t (μm) | (V/μm) and | Max Thickness Actuation |
|---|---|---|---|
| Sylgard 184 (15:1 mix ratio) | 78.6 | 80.2 (88.8%) | −17.3 |
| CCTO 0.72 μm 25.7 wt.% | 89.6 | 66.3 (83.0%) | −13.5 |
Appendix B
- Poly(acrylic acid) (MilliporeSigma, Burlington, MA, USA, part #523925) aqueous 35 wt.% solution of poly(acrylic acid) used for a sacrificial layer in the film preparation procedure.
- Isopropanol (M.G. Chemicals Ltd., Burlington, ON, Canada, part #824) used for dissolving poly(acrylic acid).
- Carbon conductive grease (M.G. Chemicals Ltd., part #846) used as pre-stretched DEA electrode material with a resistivity of 117 Ω·cm.
- 1.
- 125 μm PET films were placed on a vacuum plate to ensure their flatness.
- 2.
- A sacrificial layer was applied using an applicator Zehntner ZUA2000 (Zurich, Switzerland) on each PET film. A 35 wt.% aqueous solution of poly(acrylic acid) was mixed with isopropanol in a 1:6 ratio to reach a 5 wt.% concentration of poly(acrylic acid) in the sacrificial solution.
- 3.
- As the sacrificial layer dried out, material compositions were applied by manually operating the applicator. By setting the applicator to 500 μm, films with thicknesses of about 320 μm (thick film) were produced for mechanical and dielectric permittivity testing. For breakdown strength and biaxial electromechanical tests, 100 μm thick films (thin film) were produced by setting the applicator to 200 μm. It was noticed that higher application speed for the manually operated applicator provided better thickness evenness of the film.
- 4.
- Finally, samples were cured in a Grieve SA-550 air furnace (Round Lake, IL, USA) at 100 °C for 45 min and cut into testing coupons.
References
- Hines, L.; Petersen, K.; Lum, G.Z.; Sitti, M. Soft Actuators for Small-Scale Robotics. Adv. Mater. 2017, 29, 1603483. [Google Scholar] [CrossRef] [PubMed]
- Sommer-Larsen, P.; Larsen, A. Materials for dielectric elastomer actuators. In Proceedings of the SPIE Smart Structures and Materials, San Diego, CA, USA, 27 July 2004; pp. 67–77. [Google Scholar]
- Madsen, F.B.; Daugaard, A.E.; Hvilsted, S.; Skov, A.L. The Current State of Silicone-Based Dielectric Elastomer Transducers. Macromol. Rapid Commun. 2016, 37, 378–413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barber, P.; Balasubramanian, S.; Anguchamy, Y.; Gong, S.; Wibowo, A.; Gao, H.; Ploehn, H.J.; zur Loye, H.-C. Polymer Composite and Nanocomposite Dielectric Materials for Pulse Power Energy Storage. Materials 2009, 2, 1697–1733. [Google Scholar] [CrossRef]
- Zhou, L.; Jiang, Y. Recent progress in dielectric nanocomposites. Mater. Sci. Technol. 2020, 36, 1–16. [Google Scholar] [CrossRef]
- Panahi-Sarmad, M.; Zahiri, B.; Noroozi, M. Graphene-based composite for dielectric elastomer actuator: A comprehensive review. Sens. Actuators A Phys. 2019, 293, 222–241. [Google Scholar] [CrossRef]
- Vaicekauskaite, J.; Mazurek, P.; Vudayagiri, S.; Ladegaard Skov, A. Silicone elastomer map: Design the ideal elastomer. In Proceedings of the SPIE Smart Structures + Nondestructive Evaluation, Denver, CO, USA, 13 March 2019. [Google Scholar]
- Shintake, J.; Matsuno, K.; Baba, K.; Takeuchi, H. Characterization of dielectric elastomer actuators made of slide ring materials. In Proceedings of the SPIE Smart Structures + Nondestructive Evaluation, Denver, CO, USA, 13 March 2019. [Google Scholar]
- Yu, L.; Madsen, F.; Hvilsted, S.; Skov, A. Dielectric elastomers, with very high dielectric permittivity, based on silicone and ionic interpenetrating networks. RSC Adv. 2015, 5. [Google Scholar] [CrossRef] [Green Version]
- Yoon, J.R.; Han, J.-W.; Lee, K.-M. Dielectric Properties of Polymer-ceramic Composites for Embedded Capacitors. Trans. Electr. Electron. Mater. 2009, 10, 116–120. [Google Scholar] [CrossRef] [Green Version]
- Lotz, P.; Matysek, M.; Lechner, P.; Hamann, M.; Schlaak, H. Dielectric elastomer actuators using improved thin film processing and nanosized particles. In Proceedings of the SPIE Smart Structures + Nondestructive Evaluation, San Diego, CA, USA, 10 April 2008. [Google Scholar] [CrossRef]
- Ahmadipour, M.; Ain, M.F.; Ahmad, Z.A. A Short Review on Copper Calcium Titanate (CCTO) Electroceramic: Synthesis, Dielectric Properties, Film Deposition, and Sensing Application. Nano Micro Lett. 2016, 8, 291–311. [Google Scholar] [CrossRef] [Green Version]
- Romasanta, L.; Leret, P.; Casaban, L.; Hernández, M.; Rubia, M.; Fernández, J.; Kenny, J.; Lopez-Manchado, M.; Verdejo, R. Towards materials with enhanced electro-mechanical response: CaCu3Ti4O12–polydimethylsiloxane composites. J. Mater. Chem. 2012, 22, 24705–24712. [Google Scholar] [CrossRef] [Green Version]
- Vudayagiri, S.; Zakaria, S.; Yu, L.; Hassouneh, S.; Benslimane, M.; Skov, A. High breakdown-strength composites from liquid silicone rubbers. Smart Mater. Struct. 2014, 23, 105017. [Google Scholar] [CrossRef]
- Wan, W.; Luo, J.; Huang, C.-E.; Yang, J.; Feng, Y.; Yuan, W.-X.; Ouyang, Y.; Chen, D.; Qiu, T. Calcium copper titanate/polyurethane composite films with high dielectric constant, low dielectric loss and super flexibility. Ceram. Int. 2017. [Google Scholar] [CrossRef]
- Wang, J.; Chao, X.; Li, G.; Feng, L.; Zhao, K. Fabrication and enhanced characterization of copper powder filled copper calcium titanate/poly(vinylidene difluoride) composite. J. Mater. Sci. Mater. Electron. 2016, 28, 1–5. [Google Scholar] [CrossRef]
- Duan, L.; Wang, G.; Zhang, Y.; Zhang, Y.; Wei, Y.; Wang, Z.; Zhang, M. High dielectric and actuated properties of silicone dielectric elastomers filled with magnesium-doped calcium copper titanate particles. Polym. Compos. 2016. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Wang, G.L.; Zhang, J.; Ding, K.H.; Wang, Z.F.; Zhang, M. Preparation and properties of core-shell structured calcium copper titanate@ polyaniline/silicone dielectric elastomer actuators. Polym. Compos. 2019, 40, E62–E68. [Google Scholar] [CrossRef]
- Babu, S.; Singh, K.; Govindan, A. Dielectric properties of CaCu3Ti4O12—Silicone resin composites. Appl. Phys. A 2012, 107. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Zhang, Y.; Duan, L.; Ding, K.; Wang, Z.; Zhang, M. Property reinforcement of silicone dielectric elastomers filled with self-prepared calcium copper titanate particles. J. Appl. Polym. Sci. 2015, 132. [Google Scholar] [CrossRef]
- Zhang, Y.-Y.; Min, Y.; Wang, G.-L.; Wang, Z.-F.; Junliang, L.; Luo, Z.-W.; Zhang, M. Design and properties of calcium copper titanate/poly(dimethyl siloxane) dielectric elastomer composites. Rare Met. 2019. [Google Scholar] [CrossRef]
- Fralick, B.S.; Gatzke, E.P.; Baxter, S.C. Three-dimensional evolution of mechanical percolation in nanocomposites with random microstructures. Probabilistic Eng. Mech. 2012, 30, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Sakakibara, T.; Izu, H.; Kura, T.; Shinohara, W.; Iwata, H.; Kiyama, S.; Tsuda, S. High-voltage photovoltaic micro-devices fabricated by a new laser-processing. In Proceedings of the IEEE 5th International Symposium on Micro Machine and Human Science, Nagoya, Japan, 2–4 October 1994; p. 75. [Google Scholar]
- Tunkasiri, T.; Rujijanagul, G. Dielectric strength of fine grained barium titanate ceramics. J. Mater. Sci. Lett. 1996, 15, 1767–1769. [Google Scholar] [CrossRef]
- Branwood, A.; Hurd, J.D.; Tredgold, R.H. Dielectric breakdown in barium titanate. Br. J. Appl. Phys. 1962, 13, 528. [Google Scholar] [CrossRef]
- Scott, J.F.; Azuma, M.; Paz de Araujo, C.A.; McMillan, L.D.; Scott, M.C.; Roberts, T. Dielectric breakdown in high-ε films for ULSI DRAMs: II. barium-strontium titanate ceramics. Integr. Ferroelectr. 1994, 4, 61–84. [Google Scholar] [CrossRef]
- Ertuğ, B. The Overview of the Electrical Properties of Barium Titanate. Am. J. Eng. Res. 2013, 2, 1–7. [Google Scholar]
- Ertuğ, B. Electrical Conductivity and Hysteresis Characteristic of BaTiO3-Based Sensors with Polymethyl metacrylate (PMMA) Pore Former. Sens. Mater. 2013, 25, 309–321. [Google Scholar]
- Subramanian, M.; Li, D.; Duan, N.; Reisner, B.; Sleight, A. High dielectric constant in a ACu3Ti4O12 and ACu3Ti3FeO12 phases. J. Solid State Chem. 2000, 151, 323–325. [Google Scholar] [CrossRef]
- Ramírez, M.; Parra, R.; Reboredo, M.; Varela, J.; Castro, M.M.; Ramajo, L. Elastic modulus and hardness of CaTiO3, CaCu3Ti4O12 and CaTiO3/CaCu3Ti4O12 mixture. Mater. Lett. 2010, 64, 1226–1228. [Google Scholar] [CrossRef]
- Li, T.; Chen, Z.; Chang, F.; Hao, J.; Zhang, J. The effect of Eu2O3 doping on CaCu3Ti4O12 varistor properties. J. Alloy. Compd. 2009, 484, 718–722. [Google Scholar] [CrossRef]
- Cheng, B.; Lin, Y.-H.; Deng, W.; Cai, J.; Lan, J.; Nan, C.-W.; Xiao, X.; He, J. Dielectric and nonlinear electrical behaviors of Ce-doped CaCu3Ti4O12 ceramics. J. Electroceram. 2012, 29, 250–253. [Google Scholar] [CrossRef]
- Tang, Z.; Wu, K.; Huang, Y.; Li, J. High Breakdown Field CaCu3Ti4O12 Ceramics: Roles of the Secondary Phase and of Sr Doping. Energies 2017, 10, 1031. [Google Scholar] [CrossRef] [Green Version]
- Samarakoon, D.P.; Govindaraju, N.; Singh, R.N. Dielectric Properties of Calcium Copper Titanate Ceramics Exposed to Air and Dry Nitrogen Atmospheres. Trans. Indian Inst. Met. 2019, 72, 2035–2041. [Google Scholar] [CrossRef]
- Santiago-Alvarado, A.; Cruz-Felix, A.; Iturbide, F.; Licona-Morán, B. Physical-chemical properties of PDMS samples used in tunable lenses. Int. J. Eng. Sci. Innov. Technol. 2014, 3, 563–571. [Google Scholar]
- Fu, S.-Y.; Feng, X.-Q.; Lauke, B.; Mai, Y.-W. Effects of particle size, particle/matrix interface adhesion and particle loading on mechanical properties of particulate–polymer composites. Compos. Part. B Eng. 2008, 39, 933–961. [Google Scholar] [CrossRef]
- Wang, Z.; Keith Nelson, J.; Hillborg, H.; Zhao, S.; Schadler, L.S. Dielectric constant and breakdown strength of polymer composites with high aspect ratio fillers studied by finite element models. Compos. Sci. Technol. 2013, 76, 29–36. [Google Scholar] [CrossRef]
- Rosset, S.; Araromi, O.; Schlatter, S.; Shea, H. Fabrication Process of Silicone-based Dielectric Elastomer Actuators. J. Vis. Exp. 2015, 2016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carpi, F.; Anderson, I.; Bauer, S.; Frediani, G.; Gallone, G.; Gei, M.; Graaf, C.; Jean-Mistral, C.; Kaal, W.; Kofod, G.; et al. Standards for dielectric elastomer transducers. Smart Mater. Struct. 2015, 24, 105025. [Google Scholar] [CrossRef] [Green Version]
- Nawanil, C.; Makcharoen, W.; Khaosa-Ard, K.; Maluangnont, T.; Vittayakorn, W.; Isarakorn, D.; Vittayakorn, N. Electrical and dielectric properties of barium titanate—Polydimethylsiloxane nanocomposite with 0–3 connectivity modified with carbon nanotube (CNT). Integr. Ferroelectr. 2019, 195, 46–57. [Google Scholar] [CrossRef]
- Sappati, K.k.; Bhadra, S. 0–3 Barium Titanate-PDMS Flexible Film for Tactile Sensing. In Proceedings of the 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25–28 May 2020; pp. 1–6. [Google Scholar]
- Hosford, W.F. Mechanical Behavior of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Dandan Satia, M.S.; Jaafar, M.; Julie, M. Properties of calcium copper titanate and barium titanate filled epoxy composites for electronic applications: Effect of filler loading and hybrid fillers. J. Mater. Sci. Mater. Electron. 2014, 25, 4923–4932. [Google Scholar] [CrossRef]
- Teng, H. Stiffness properties of particulate composites containing debonded particles. Int. J. Solids Struct. 2010, 47, 2191–2200. [Google Scholar] [CrossRef] [Green Version]
- Molberg, M.; Crespy, D.; Rupper, P.; Nüesch, F.; Månson, J.-A.E.; Löwe, C.; Opris, D.M. High Breakdown Field Dielectric Elastomer Actuators Using Encapsulated Polyaniline as High Dielectric Constant Filler. Adv. Funct. Mater. 2010, 20, 3280–3291. [Google Scholar] [CrossRef]
- Yang, X.; Hu, J.; Chen, S.; Jinliang, H. Understanding the Percolation Characteristics of Nonlinear Composite Dielectrics. Sci. Rep. 2016, 6, 30597. [Google Scholar] [CrossRef] [Green Version]
- Cai, Z.; Wang, X.; Luo, B.; Hong, W.; Wu, L.; Li, L. Dielectric response and breakdown behavior of polymer-ceramic nanocomposites: The effect of nanoparticle distribution. Compos. Sci. Technol. 2017, 145, 105–113. [Google Scholar] [CrossRef]
- Wissler, M.; Mazza, E. Modeling of a pre-strained circular actuator made of dielectric elastomers. Sens. Actuators A Phys. 2005, 120, 184–192. [Google Scholar] [CrossRef]

| Filler | Relative Permittivity (−) | Young’s Modulus (GPa) | Breakdown Strength (V/μm) | Electrical Conductivity (S/cm) |
|---|---|---|---|---|
| BaTiO3 | 6000 [3] | 67 [23] | 2–24 1 [24,25,26] | 1–2.5 × 10−9 [27,28] |
| CCTO | 10,000–100,000 [12,29] | 256 [30] | 0.05–0.2 1 [31,32,33] | 5 × 10−8 2 |
| Material Composition | (−) | (MPa) | (V/μm) | Tensile Strength | Maximum Strain | Maximum Actuaction Thickness Strain | ||
|---|---|---|---|---|---|---|---|---|
| Sylgard 184 (15:1 mix ratio) | 2.82 | 0.673 | 90.3 | 1 | 1 | 0.984 | 174 | 30.8 |
| CCTO 0.72 μm 6.8 wt.% | 3.02 | 0.666 | 88.0 | 1.015 | 1.07 | 1.07 | 154 | 31.4 |
| CCTO 0.72 μm 25.7 wt.% | 3.75 | 0.761 | 80.2 | 0.905 | 1.15 | 1.41 | 146 | 28 |
| CCTO 1.8 μm 25.1 wt.% | 3.53 | 0.756 | 77.5 | 0.802 | 1.09 | 1.23 | 145 | 24.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sikulskyi, S.; Mekonnen, D.T.; El Atrache, A.; Divo, E.; Kim, D. Effects of Ferroelectric Fillers on Composite Dielectric Elastomer Actuator. Actuators 2021, 10, 137. https://doi.org/10.3390/act10070137
Sikulskyi S, Mekonnen DT, El Atrache A, Divo E, Kim D. Effects of Ferroelectric Fillers on Composite Dielectric Elastomer Actuator. Actuators. 2021; 10(7):137. https://doi.org/10.3390/act10070137
Chicago/Turabian StyleSikulskyi, Stanislav, Danayit T. Mekonnen, Abdullah El Atrache, Eduardo Divo, and Daewon Kim. 2021. "Effects of Ferroelectric Fillers on Composite Dielectric Elastomer Actuator" Actuators 10, no. 7: 137. https://doi.org/10.3390/act10070137
APA StyleSikulskyi, S., Mekonnen, D. T., El Atrache, A., Divo, E., & Kim, D. (2021). Effects of Ferroelectric Fillers on Composite Dielectric Elastomer Actuator. Actuators, 10(7), 137. https://doi.org/10.3390/act10070137







