Fluid-Structure Interaction Modelling of a Soft Pneumatic Actuator
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fluid-Structure Interaction
- Navier–Stokes equations for the laminar, incompressible fluid flow:where u is the fluid velocity, ρ is the fluid density, p is the fluid pressure, I is the identity matrix, μ is the dynamic fluid viscosity, F is the volume force, and g is the gravity acceleration.
- Equations of solid mechanics given by Newton’s second law:where u is the displacement in the solid body, ρ is the body’s structural density, S is the 2nd Piola-Kirchhoff stress tensor, F is the deformation gradient, and Fv is the body force.
2.2. Hyperelastic Material Model
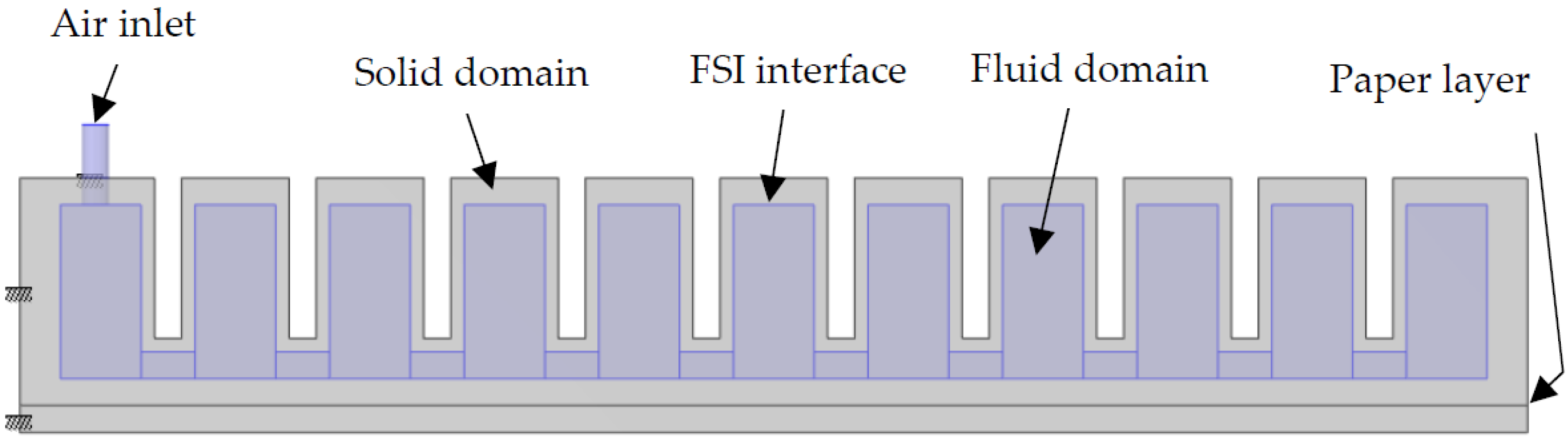
2.3. PneuNets Bending Actuator
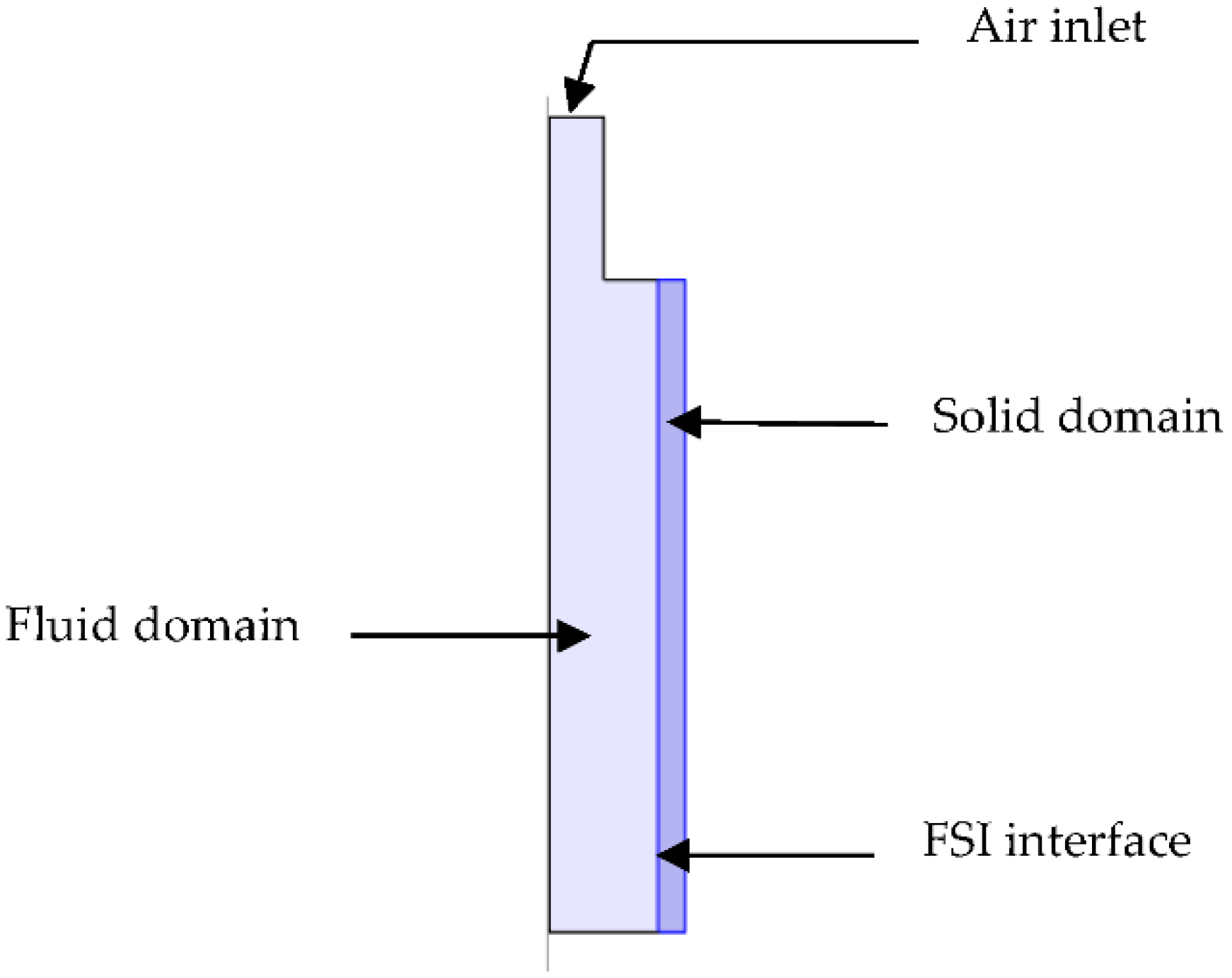
2.4. Coupled 2D FSI Modelling and Simulation
2.5. Coupled 3D FSI Modelling and Simulation
3. Results and Discussion
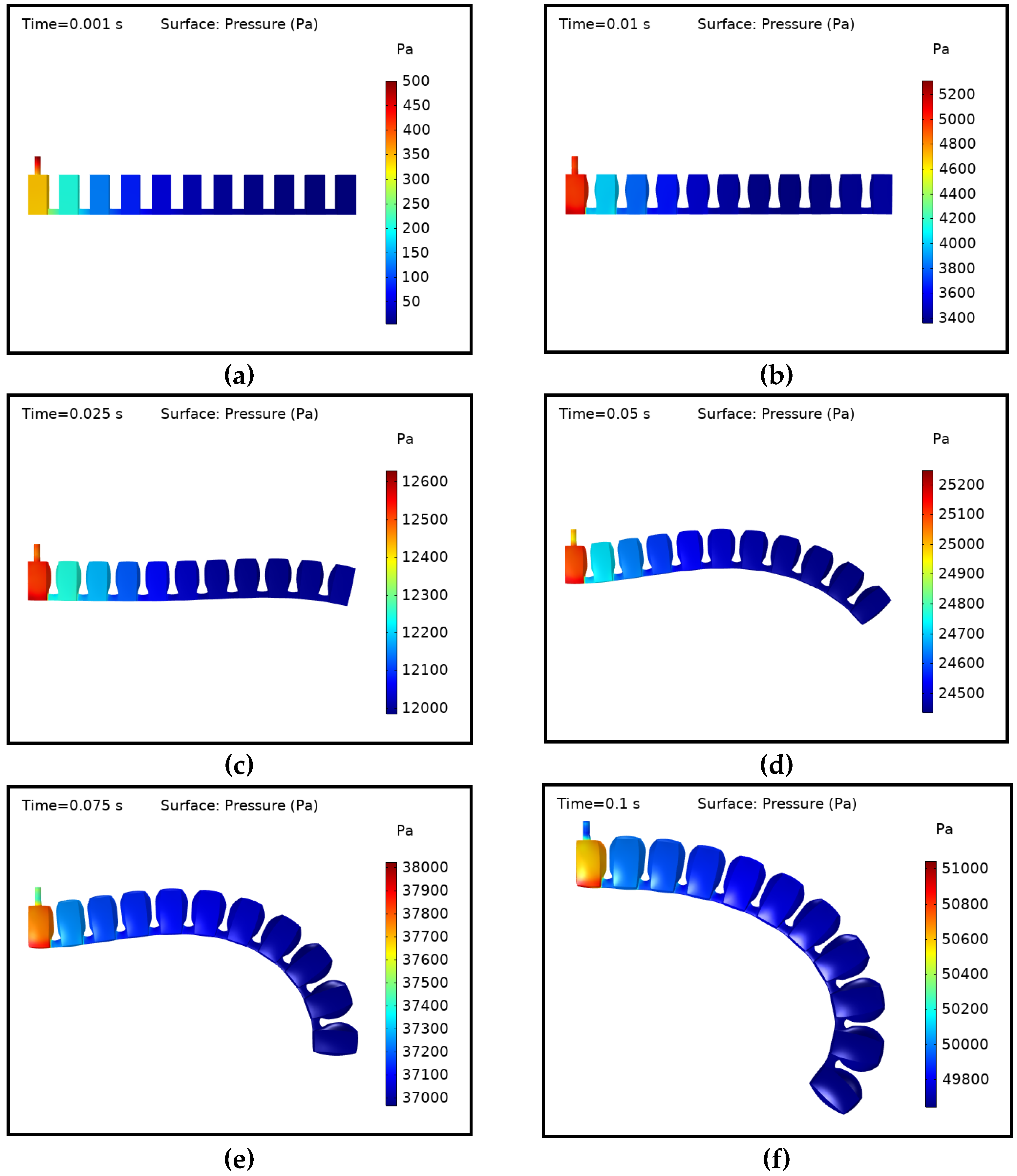
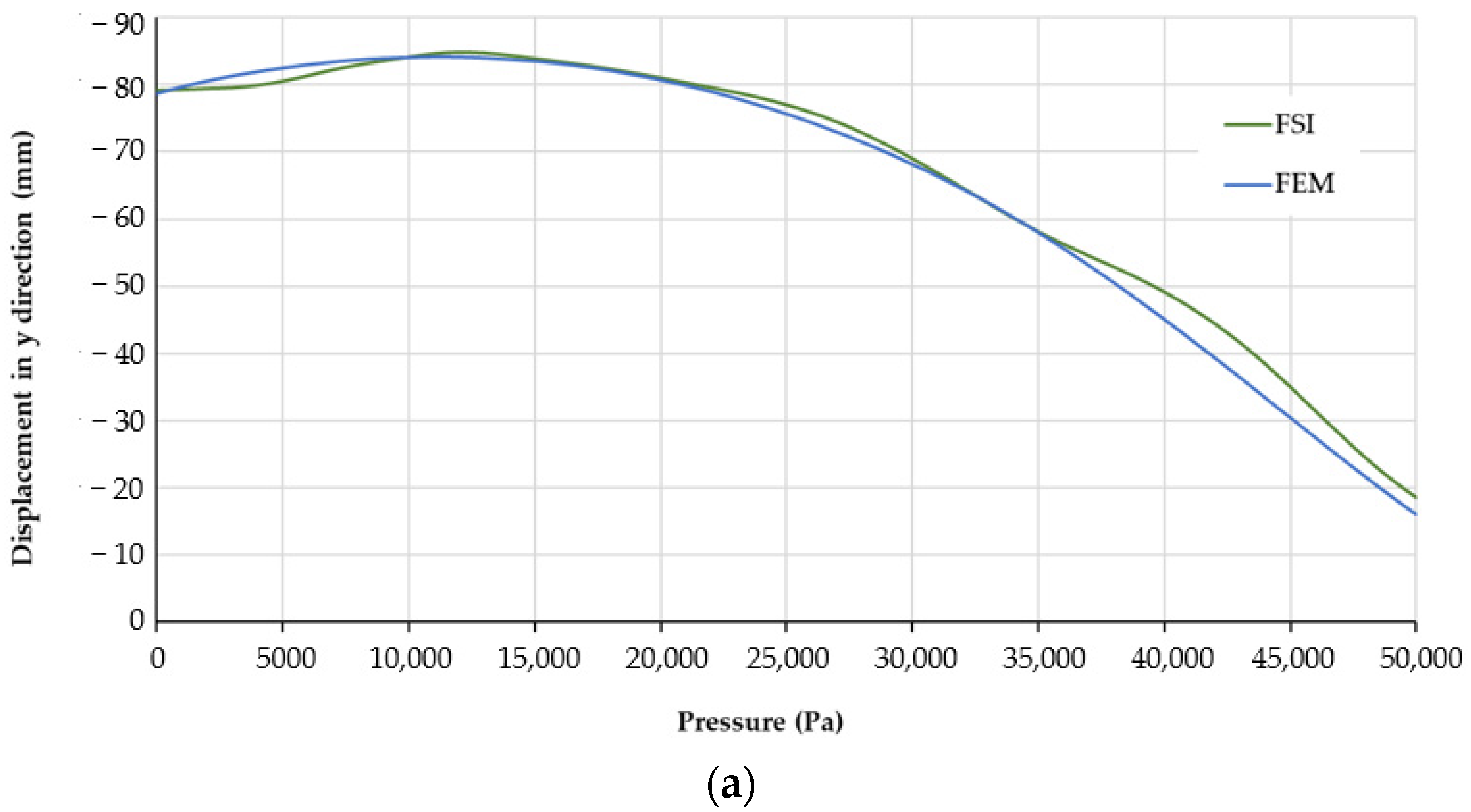
3.1. Deformation and Comparison with FEM Model
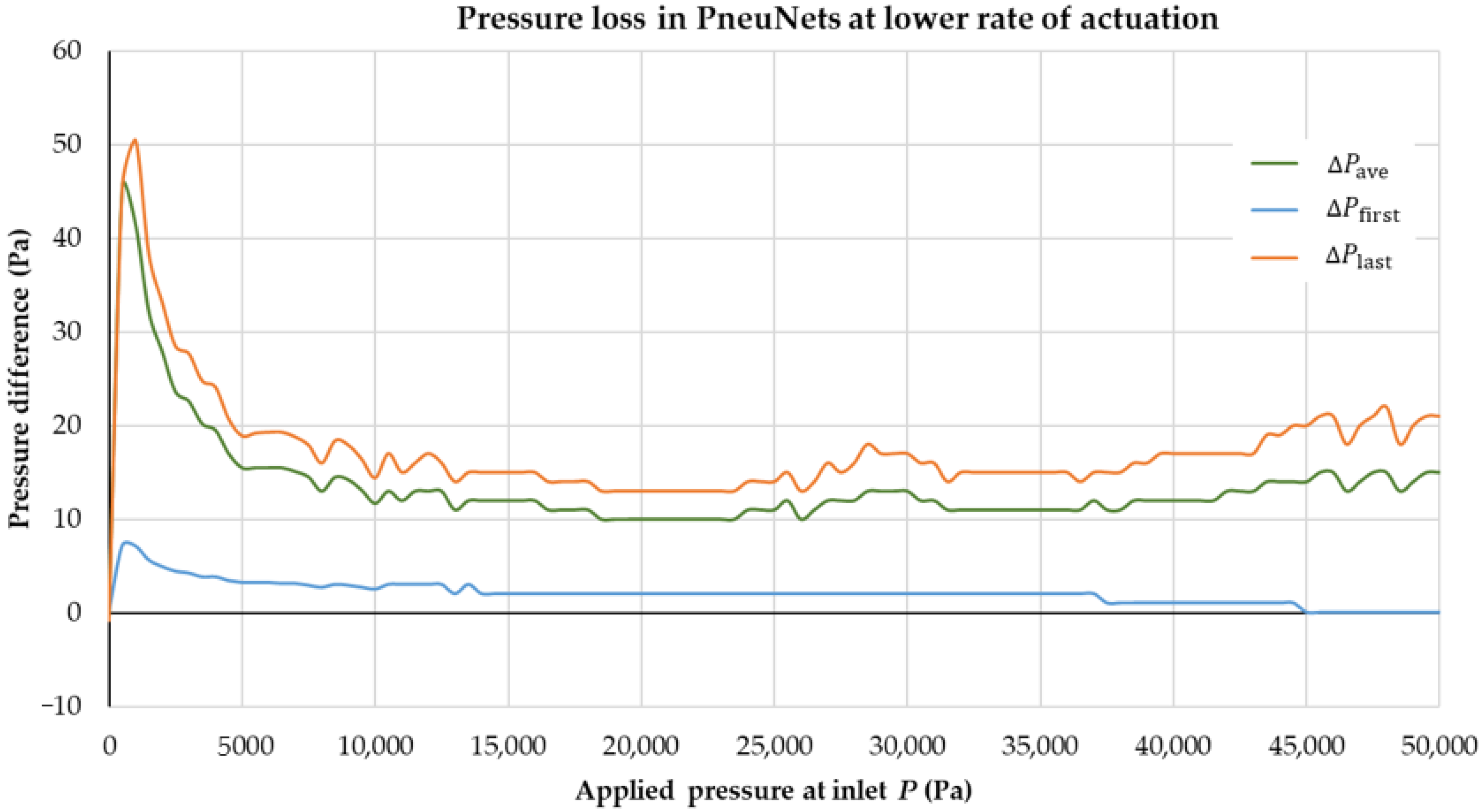
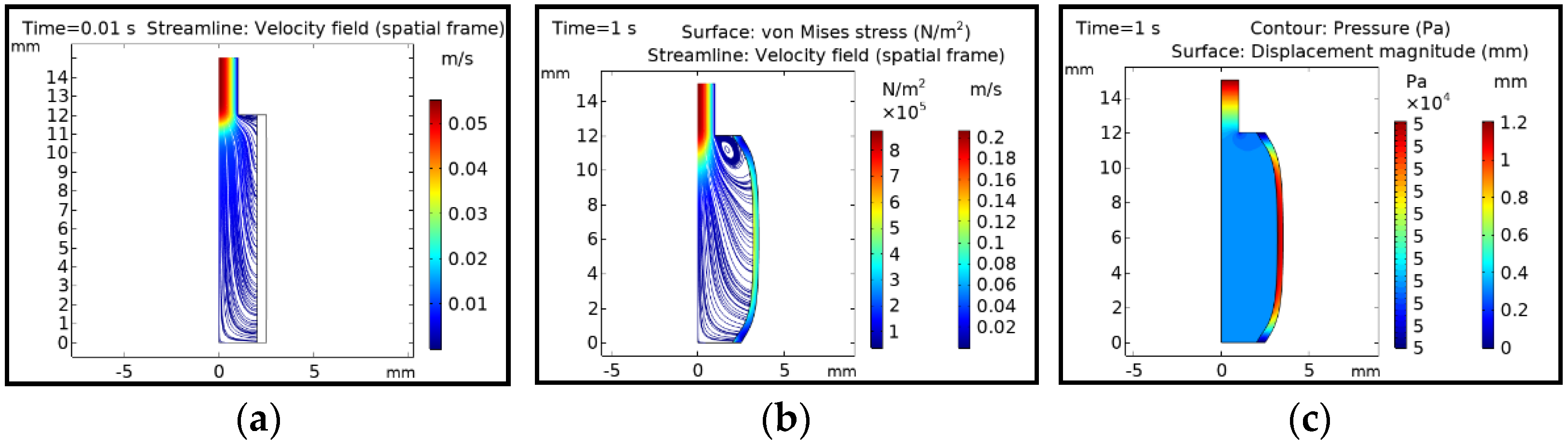
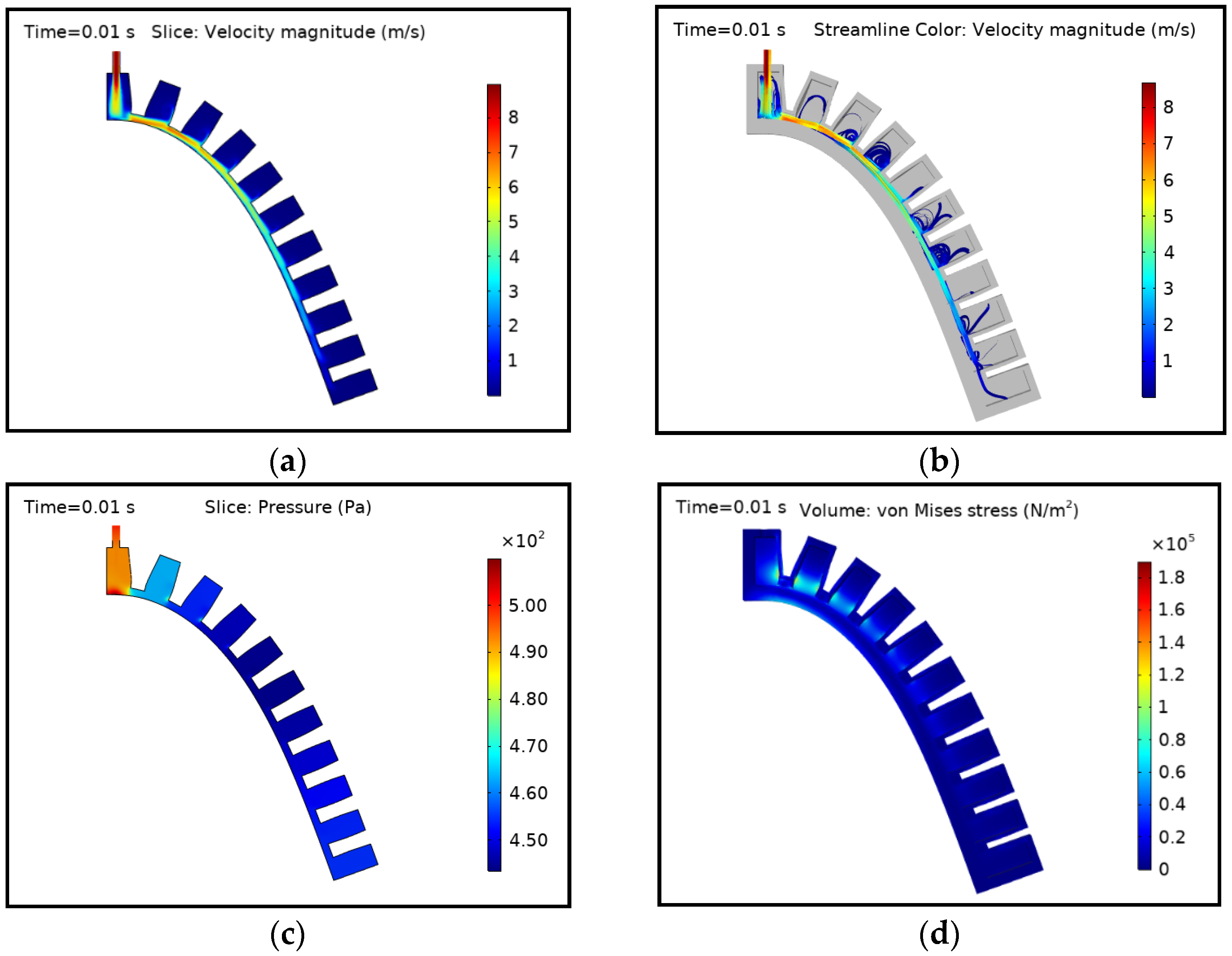
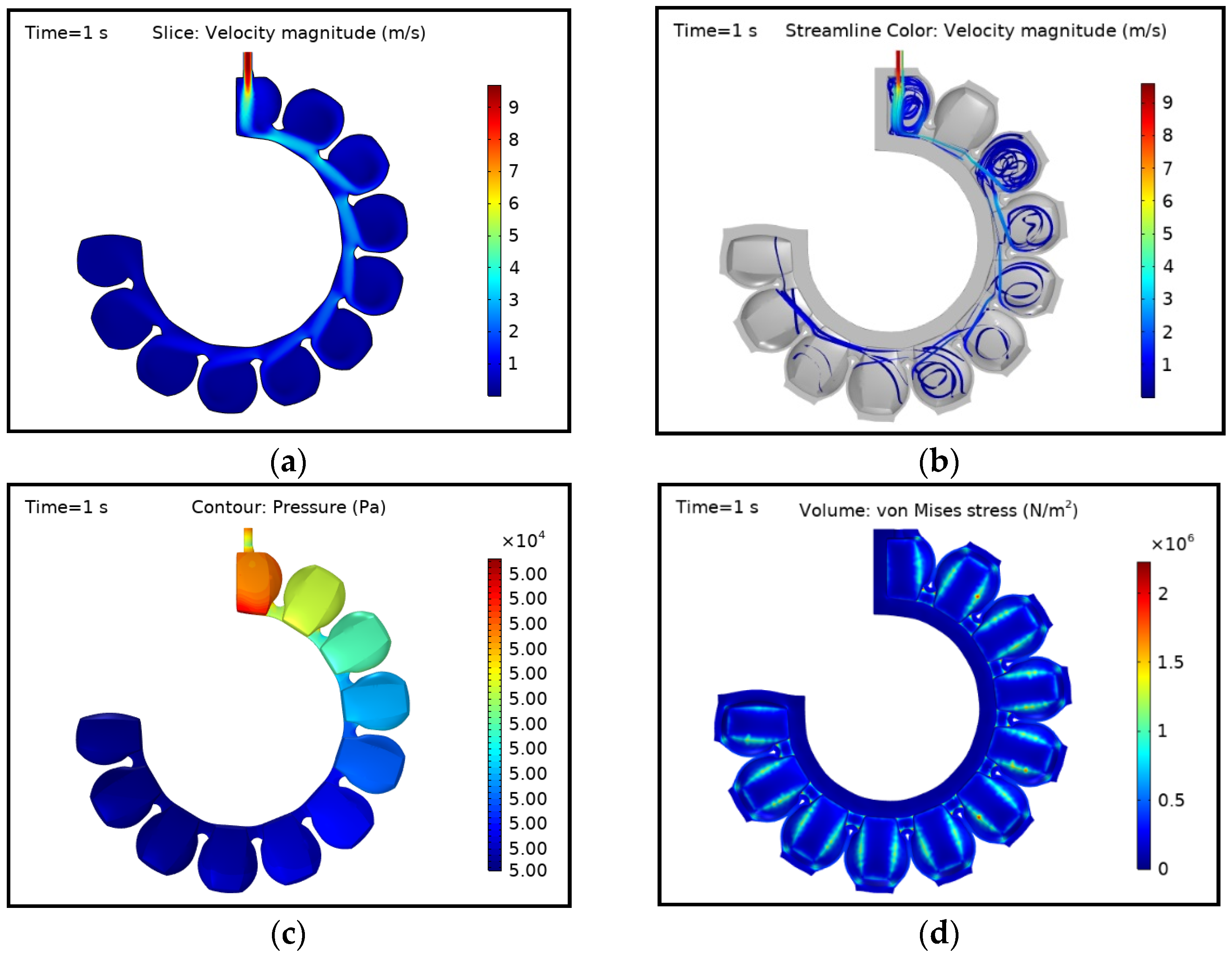
3.2. Initial Time Step Condition
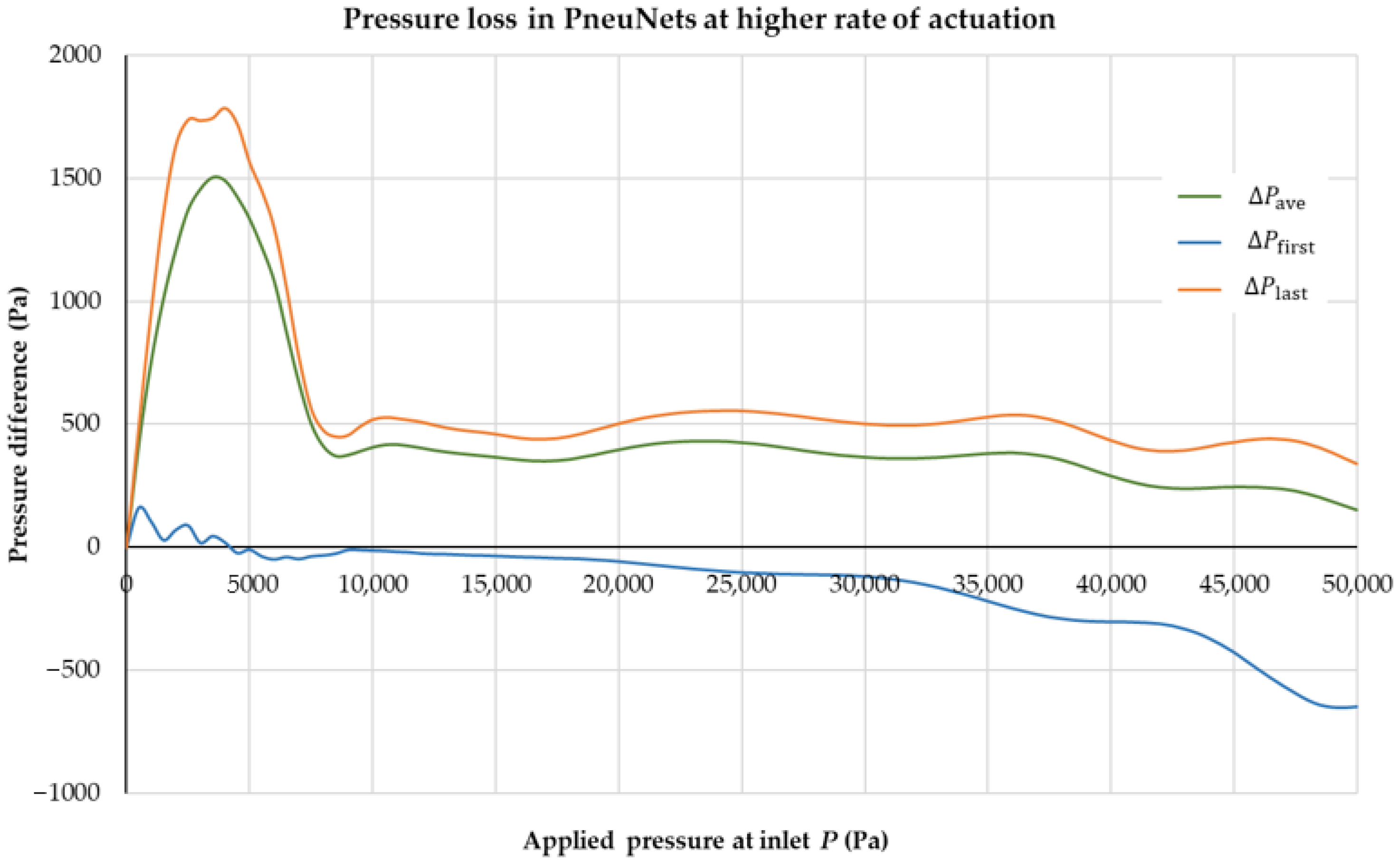
3.3. Middle and Last Time Step Condition
3.4. Average Velocity of Fluid Domain
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Required modules in COMSOL: COMSOL Multiphysics Module, Structural Mechanics/MEMS Module, Nonlinear Structural Materials Module, CFD Module, and CAD Import Module
- Space dimension: three-dimensional model
- Physics: fluid–solid interaction
- Study type: stationary (gravity) and time-dependent (air pressure)
- Fluid mechanics: Air is chosen as material. Incompressible and laminar flow are selected. Gravity is included. Walls are treated with no slip condition. Material properties like dynamic viscosity and density of air are considered using a built-in function in COMSOL.
- Solid mechanics:
- ○
- Elastomer: Elastosil is assigned to the top and bottom parts, which is created as user-defined material with a density of 1130 kg/m3. The Yeoh hyperelastic material model is assigned using the model parameters given in Section 2.2.
- ○
- Paper: Paper is assigned to the interface boundary, and linear elastic material behaviour is applied. Paper is created as user defined material with required material properties of density = 750 kg/m3, Poisson’s ratio = 0.2, and Young’s modulus = 6.5 GPa [54].
- ○
- Contacts: The sidewalls of the chambers (except the left sidewall of the first chamber and the right sidewall of the last chamber) are assigned as contact pairs for the deformed configuration. All the left sidewalls are considered as source and the right sidewalls as destination for contact modelling. For the thin paper layer, another contact pair is created for the initial configuration. Contacts are modelled using the penalty condition.
- Moving mesh: The fluid domain is selected as deforming domain under a moving mesh. The Navier–Stokes equations given in (1) and (2) are solved in the deforming domain using Yeoh smoothing with C2 = 10. The prescribed mesh displacement of zero in all directions is applied to the inlet and the wall boundaries of the air supply tube above the first chamber.
- Boundary conditions: An inlet air pressure of 0.5 bar is applied at the inlet boundary. The pressure is applied using the ramp function, gradually increasing the pressure from 0 bar to 0.5 bar from t = 0 s to t = 1 s. The side and top walls of the first chamber are fixed, hence there is no displacement in all directions.
- Gravity is taken into account for the solid domain, and it acts in negative y direction.
- Fluid–structure interaction: The fluid domain is selected as deforming domain under a moving mesh and the walls of the fluid chambers are automatically assigned as the interface for fluid and solid. The fully coupled solver is selected for simulating fluid and solid domains.
- Mesh: The physics-controlled mesh is selected. The fine mesh is created predominantly with tetrahedral elements. The mesh is generated specifically in each domain and FSI interface. The total number of mesh elements is 1,022,609, in which 598,947 elements represent the fluid domain and are calibrated for fluid mechanics and 311,810 elements represent the solid domains. The minimum element quality based on skewness is 0.06.
- Study: Two study steps are implemented. Study Step 1 denotes a stationary study, which solves the model for gravity. Regarding this, the parameter t is defined with value zero in global definition. Study Step 2 denotes the time-dependent study, in which the inlet pressure is applied in time steps. The time steps are given as 0, 0.01, and 1 s. The inlet pressure increases for each time step by 500 Pa.
- Solver: The segregated solver is selected for the time-dependent study. Compared to the fully coupled solver, the segregated solver approach requires less memory and computation time.
- Cluster specifications: The model is computed on 24 cores running at 2.5 GHz. It takes 18 h and 43 min to compute.
Appendix B
References
- Laschi, C.; Mazzolai, B.; Cianchetti, M. Soft robotics: Technologies and systems pushing the boundaries of robot abilities. Sci. Robot. 2016, 1, eaah3690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marchese, A.D.; Katzschmann, R.K.; Rus, D. Whole arm planning for a soft and highly compliant 2D robotic manipulator. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 554–560. [Google Scholar]
- Burgner-Kahrs, J.; Rucker, D.C.; Choset, H. Continuum robots for medical applications: A survey. IEEE Trans. Robot. 2015, 31, 1261–1280. [Google Scholar] [CrossRef]
- Kim, D.H.; Heo, S.H.; Park, H.S. Biomimetic finger extension mechanism for soft wearable hand rehabilitation devices. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; pp. 1326–1330. [Google Scholar]
- Maeder-York, P.; Clites, T.; Boggs, E.; Neff, R.; Polygerinos, P.; Holland, D.; Stirling, L.; Galloway, K.; Wee, C.; Walsh, C. Biologically inspired soft robot for thumb rehabilitation. J. Med. Devices 2014, 8, 020933. [Google Scholar] [CrossRef] [Green Version]
- Polygerinos, P.; Lyne, S.; Wang, Z.; Nicolini, L.F.; Mosadegh, B.; Whitesides, G.M.; Walsh, C.J. Towards a soft pneumatic glove for hand rehabilitation. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1512–1517. [Google Scholar]
- Villoslada, A.; Flores, A.; Copaci, D.; Blanco, D.; Moreno, L. High-displacement flexible shape memory alloy actuator for soft wearable robots. Robot. Auton. Syst. 2015, 73, 91–101. [Google Scholar] [CrossRef]
- Copaci, D.; Cano, E.; Moreno, L.; Blanco, D. New design of a soft robotics wearable elbow exoskeleton based on shape memory alloy wire actuators. Appl. Bionics Biomech. 2017, 2017, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oguntosin, V.; Harwin, W.S.; Kawamura, S.; Nasuto, S.J.; Hayashi, Y. Development of a wearable assistive soft robotic device for elbow rehabilitation. In Proceedings of the 2015 IEEE International Conference on Rehabilitation Robotics (ICORR), Singapore, 11–14 August 2015; pp. 747–752. [Google Scholar]
- Manfredi, L.; Capoccia, E.; Ciuti, G.; Cuschieri, A. A Soft Pneumatic Inchworm Double balloon (SPID) for colonoscopy. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Jianfei, C.; Xingsong, W. Conception of a tendon-sheath and pneumatic system driven soft rescue robot. In Robot Intelligence Technology and Applications 3; Springer: Cham, Switzerland, 2015; pp. 475–481. [Google Scholar]
- Tolley, M.T.; Shepherd, R.F.; Mosadegh, B.; Galloway, K.C.; Wehner, M.; Karpelson, M.; Wood, R.J.; Whitesides, G.M. A resilient, untethered soft robot. Soft Robot. 2014, 1, 213–223. [Google Scholar] [CrossRef]
- Shintake, J.; Cacucciolo, V.; Floreano, D.; Shea, H. Soft robotic grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar] [CrossRef] [Green Version]
- Dong, W.; Wang, Y.; Zhou, Y.; Bai, Y.; Ju, Z.; Guo, J.; Gu, G.; Bai, K.; Ouyang, G.; Chen, S.; et al. Soft human–machine interfaces: Design, sensing and stimulation. Int. J. Intell. Robot. Appl. 2018, 2, 313–338. [Google Scholar] [CrossRef] [Green Version]
- Serchi, F.G.; Arienti, A.; Baldoli, I.; Laschi, C. An elastic pulsed-jet thruster for Soft Unmanned Underwater Vehicles. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 5103–5110. [Google Scholar]
- Hines, L.; Petersen, K.; Lum, G.Z.; Sitti, M. Soft actuators for small-scale robotics. Adv. Mater. 2017, 29, 1603483. [Google Scholar] [CrossRef]
- Boyraz, P.; Runge, G.; Raatz, A. An overview of novel actuators for soft robotics. Actuators 2018, 7, 48. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Sheng, J.; O’Neill, C.T.; Walsh, C.J.; Wood, R.J.; Ryu, J.H.; Desai, J.P.; Yip, M.C. Robotic artificial muscles: Current progress and future perspectives. IEEE Trans. Robot. 2019, 35, 761–781. [Google Scholar] [CrossRef]
- Adami, M.; Seibel, A. On-board pneumatic pressure generation methods for soft robotics applications. Actuators 2019, 8, 2. [Google Scholar] [CrossRef] [Green Version]
- Seibel, A.; Schiller, L. Systematic engineering design helps creating new soft machines. Robot. Biomim. 2018, 5, 5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manfredi, L.; Putzu, F.; Guler, S.; Huan, Y.; Cuschieri, A. 4 DOFs hollow soft pneumatic actuator–HOSE. Mater. Res. Express 2019, 6, 045703. [Google Scholar] [CrossRef] [Green Version]
- Suzumori, K.; Iikura, S.; Tanaka, H. Flexible microactuator for miniature robots. In Proceedings of the IEEE Micro Electro Mechanical Systems, Nara, Japan, 30 December 1990–2 January 1991; pp. 204–209. [Google Scholar]
- Suzumori, K.; Iikura, S.; Tanaka, H. Development of flexible microactuator and its applications to robotic mechanisms. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; pp. 1622–1627. [Google Scholar]
- Manfredi, L.; Yue, L.; Zhang, J.; Cuschieri, A. A 4 DOFs variable stiffness soft module. In Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, 24–28 April 2018; pp. 94–99. [Google Scholar]
- Cianchetti, M.; Laschi, C.; Menciassi, A.; Dario, P. Biomedical applications of soft robotics. Nat. Rev. Mater. 2018, 3, 143–153. [Google Scholar] [CrossRef]
- Mosadegh, B.; Polygerinos, P.; Keplinger, C.; Wennstedt, S.; Shepherd, R.F.; Gupta, U.; Shim, J.; Bertoldi, K.; Walsh, C.J.; Whitesides, G.M. Pneumatic networks for soft robotics that actuate rapidly. Adv. Funct. Mater. 2014, 24, 2163–2170. [Google Scholar] [CrossRef]
- Polygerinos, P.; Wang, Z.; Overvelde, J.T.; Galloway, K.C.; Wood, R.J.; Bertoldi, K.; Walsh, C.J. Modeling of soft fiber-reinforced bending actuators. IEEE Trans. Robot. 2015, 31, 778–789. [Google Scholar] [CrossRef] [Green Version]
- Connolly, F.; Walsh, C.J.; Bertoldi, K. Automatic design of fiber-reinforced soft actuators for trajectory matching. Proc. Natl. Acad. Sci. USA 2017, 114, 51–56. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Kang, R.; Branson, D.T.; Chen, L.; Dai, J.S. Kinematics and statics of eccentric soft bending actuators with external payloads. Mech. Mach. Theory 2019, 139, 526–541. [Google Scholar] [CrossRef]
- Gu, G.; Wang, D.; Ge, L.; Zhu, X. Analytical Modeling and Design of Generalized PneuNet Soft Actuators with Three-Dimensional Deformations. Soft Robot. 2020. [Google Scholar] [CrossRef]
- Breitman, P.; Matia, Y.; Gat, A.D. Fluid mechanics of pneumatic soft robots. Soft Robot. 2020. [Google Scholar] [CrossRef] [PubMed]
- Wikipedia. Fluid-Structure Interaction. Available online: https://en.wikipedia.org/wiki/Fluid%E2%80%93structure_interaction (accessed on 6 July 2021).
- Moon, D.H.; Shin, S.H.; Na, J.B.; Han, S.Y. Fluid-structure interaction based on meshless local Petrov-Galerkin method for worm soft robot Analysis. Int. J. Precis. Eng. Manuf. Green Technol. 2020, 7, 727–742. [Google Scholar] [CrossRef]
- Gul, J.Z.; Kim, K.H.; Lim, J.H.; Doh, Y.H.; Choi, K.H. FSI modeling of frog inspired soft robot embedded with ALD encapsulated flex sensor for underwater synchronous swim. In Proceedings of the 2017 IEEE International Symposium on Robotics and Intelligent Sensors (IRIS), Ottawa, ON, Canada, 5–7 October 2017; pp. 255–259. [Google Scholar]
- Bao, G.; Fang, H.; Chen, L.; Wan, Y.; Xu, F.; Yang, Q.; Zhang, L. Soft robotics: Academic insights and perspectives through bibliometric analysis. Soft Robot. 2018, 5, 229–241. [Google Scholar] [CrossRef] [PubMed]
- COMSOL Application Gallery. Fluid-Structure Interaction. Available online: https://www.comsol.com/model/fluid-structure-interaction-361 (accessed on 3 May 2021).
- Multiphysics Cyclopedia. Fluid-Structure Interaction. Available online: https://www.comsol.com/multiphysics/fluid-structure-interaction (accessed on 5 May 2021).
- Fras, J.; Glowka, J.; Althoefer, K. Instant soft robot: A simple recipe for quick and easy manufacturing. In Proceedings of the 2020 3rd IEEE International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 15 May–15 July 2020; pp. 482–488. [Google Scholar]
- Gul, J.Z.; Sajid, M.; Rehman, M.M.; Siddiqui, G.U.; Shah, I.; Kim, K.H.; Lee, J.W.; Choi, K.H. 3D printing for soft robotics—A review. Sci. Technol. Adv. Mater. 2018, 19, 243–262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wallin, T.J.; Pikul, J.; Shepherd, R.F. 3D printing of soft robotic systems. Nat. Rev. Mater. 2018, 3, 84–100. [Google Scholar] [CrossRef]
- Gent, A.N. Engineering with Rubber: How to Design Rubber Components, 2nd ed.; Hanser: Munich, Germany, 2001. [Google Scholar]
- Mullins, L. Effect of stretching on the properties of rubber. Rubber Chem. Technol. 1948, 21, 281–300. [Google Scholar] [CrossRef]
- Cantournet, S.; Desmorat, R.; Besson, J. Mullins effect and cyclic stress softening of filled elastomers by internal sliding and friction thermodynamics model. Int. J. Solids Struct. 2009, 46, 2255–2264. [Google Scholar] [CrossRef]
- Ali, A.; Hosseini, M.; Sahari, B.B. A review of constitutive models for rubber-like materials. Am. J. Eng. Appl. Sci. 2010, 3, 232–239. [Google Scholar] [CrossRef] [Green Version]
- Treloar, L.R.G. The elasticity of a network of long-chain molecules. i. Trans. Faraday Soc. 1943, 39, 36–41. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The elasticity of a network of long-chain molecules. ii. Trans. Faraday Soc. 1943, 39, 241–246. [Google Scholar] [CrossRef]
- Rivlin, R. Large elastic deformations of isotropic materials. i. Fundamental concepts. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 240, 459–490. [Google Scholar]
- Rivlin, R.S. Large elastic deformations of isotropic materials. iv. Further developments of the general theory. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 241, 379–397. [Google Scholar]
- Ogden, R.W. Large deformation isotropic elasticity–on the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. London. A. Math. Phys. Sci. 1972, 326, 565–584. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef] [Green Version]
- Behroozi, M.; Olatunbosun, O.A.; Ding, W. Finite element analysis of aircraft tyre–effect of model complexity on tyre performance characteristics. Mater. Des. 2012, 35, 810–819. [Google Scholar] [CrossRef]
- Xavier, M.S.; Fleming, A.J.; Yong, Y.K. Finite element modeling of soft fluidic actuators: Overview and recent developments. Adv. Intell. Syst. 2021, 3, 2000187. [Google Scholar] [CrossRef]
- Soft Robotics Toolkit. PneuNets Modeling. Available online: https://softroboticstoolkit.com/book/pneunets-modeling (accessed on 5 September 2020).
- Utkan, D.; Maruthavanan, D.; Schimanowski, A.; Seibel, A. Compression behavior of typical silicone rubbers for soft robotic applications at elevated temperatures. In Proceedings of the 2021 4th IEEE International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 12–16 April 2021; pp. 539–542. [Google Scholar]




| Sylgard | Elastosil | Ecoflex | |
|---|---|---|---|
| Manufacturer | Dow Corning | Wacker Chemie | Smooth-On |
| Type | 184 | M4601 | 00–30 |
| Colour | transparent | reddish brown | translucent |
| Shore hardness | 50 A | 28 A | 00–30 |
| Tensile strength | 6.76 MPa | 6.50 MPa | 1.38 MPa |
| Density | 1.04 g/cm3 | 1.13 g/cm3 | 1.07 g/cm3 |
| Elongation at break | 150% | 700% | 900% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maruthavanan, D.; Seibel, A.; Schlattmann, J. Fluid-Structure Interaction Modelling of a Soft Pneumatic Actuator. Actuators 2021, 10, 163. https://doi.org/10.3390/act10070163
Maruthavanan D, Seibel A, Schlattmann J. Fluid-Structure Interaction Modelling of a Soft Pneumatic Actuator. Actuators. 2021; 10(7):163. https://doi.org/10.3390/act10070163
Chicago/Turabian StyleMaruthavanan, Duraikannan, Arthur Seibel, and Josef Schlattmann. 2021. "Fluid-Structure Interaction Modelling of a Soft Pneumatic Actuator" Actuators 10, no. 7: 163. https://doi.org/10.3390/act10070163






