Development of a Bionic Dolphin Flexible Tail Experimental Device Driven by a Steering Gear
Abstract
:1. Introduction
2. Design of Flexible Tail Structure of Bionic Dolphin Driven by Steering Gear
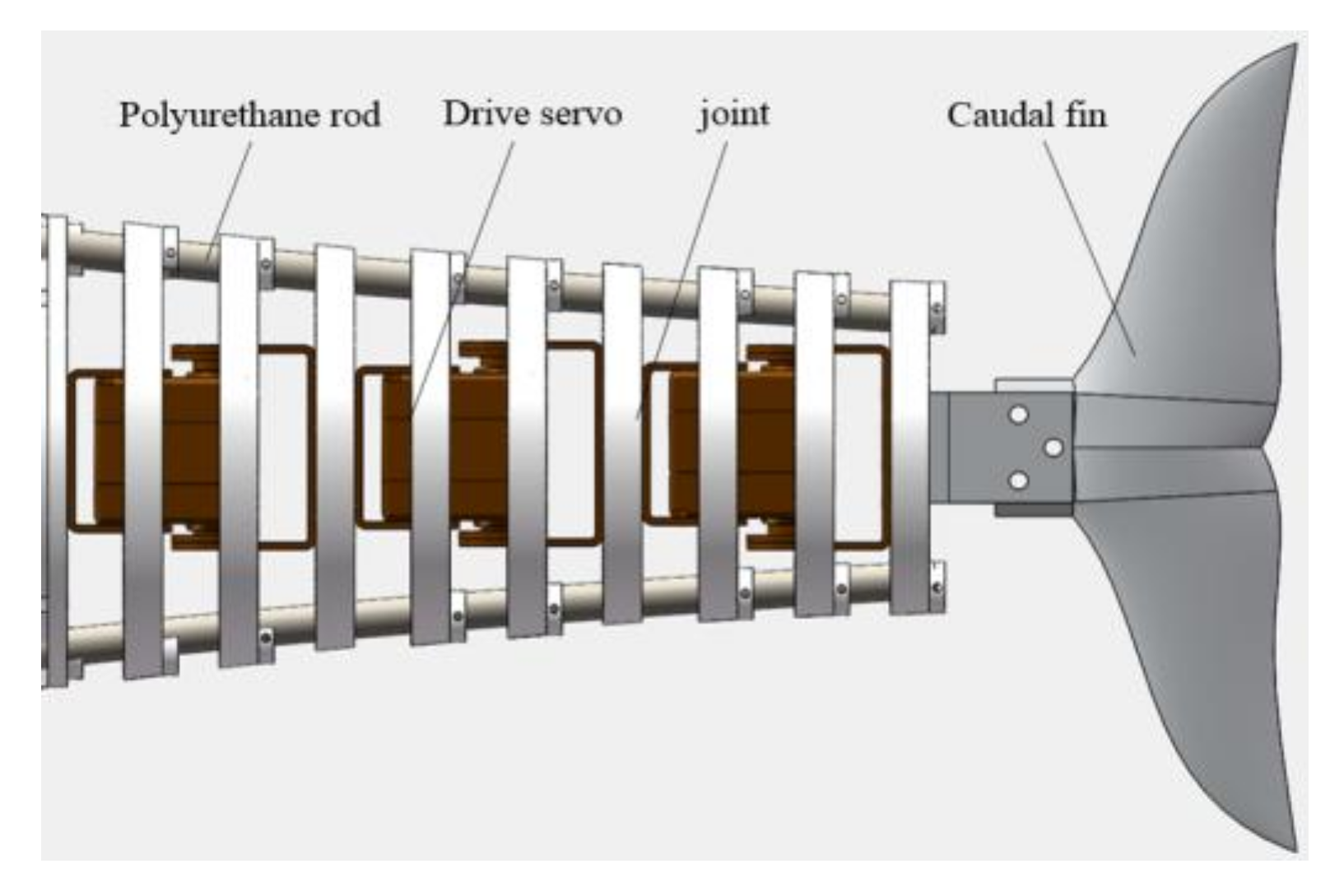
2.1. Tail Swing Mechanism Design
- Spring: Spring has good elasticity and flexibility. However, it is difficult to control the spring when it deforms in the axial direction;
- Silicone tube: The elasticity of silicone tube is good, but its flexibility is insufficient, and it is easy to break;
- Polyurethane rod: Polyurethane rod is a new type of polymer material with good elasticity and flexibility. When the polyurethane rod deforms, the axial deformation is small and easy to control.
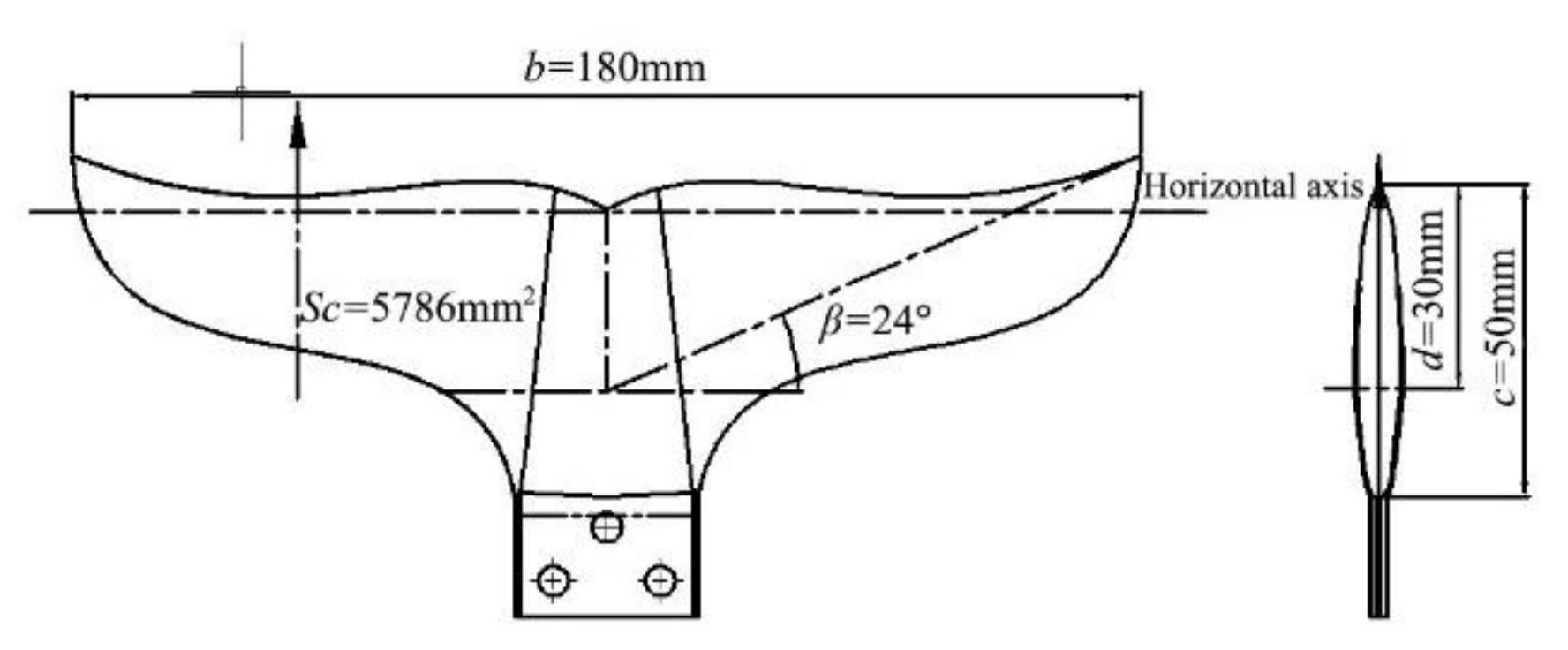
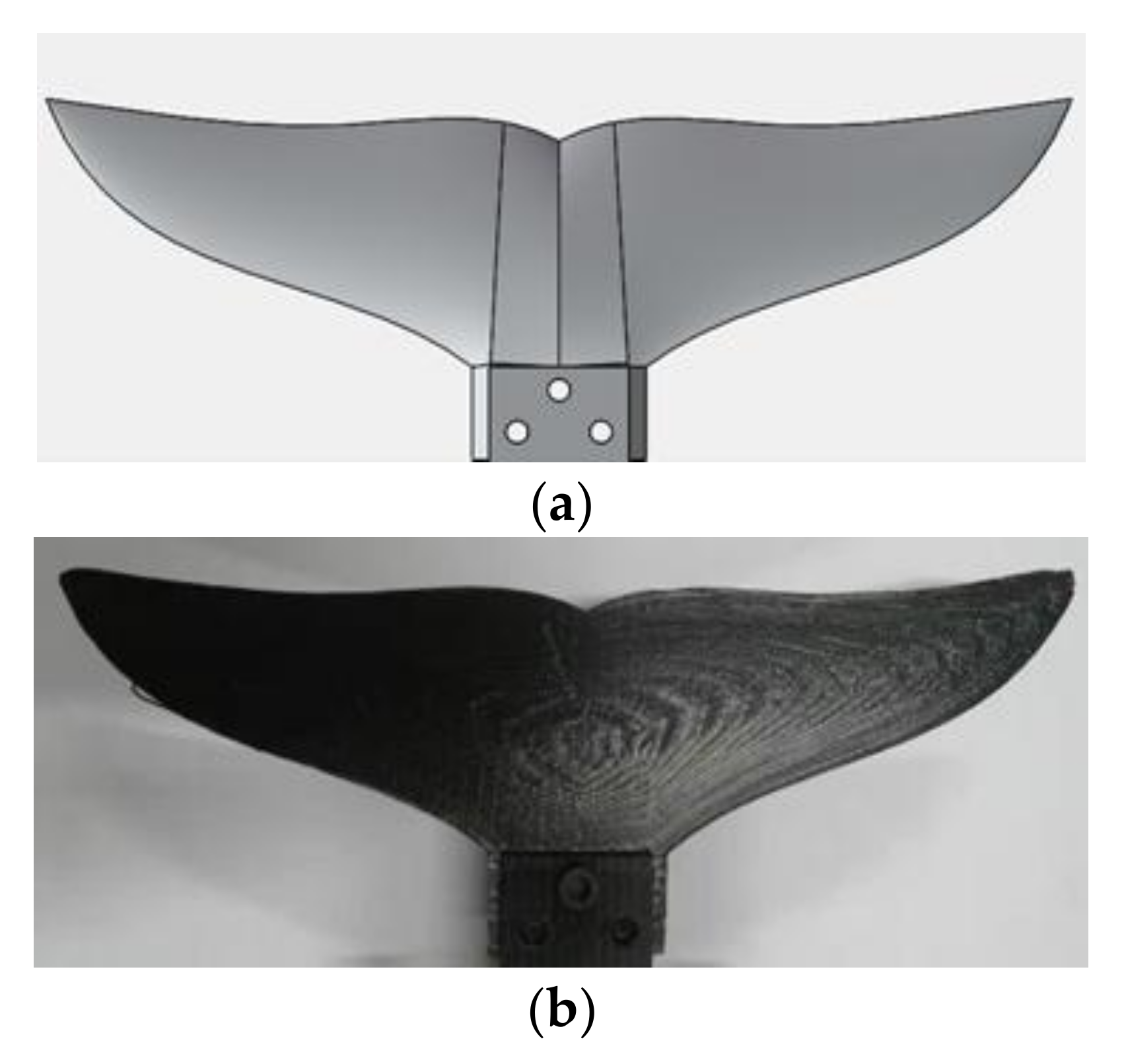
2.2. Bionic Dolphin Tail Fin Structure Design
- Aspect ratio . The aspect ratio mainly affects the efficiency of the swing and propulsion of the bionic dolphin’s tail, and its calculation formula is shown in Equation (1). The aspect ratio of the tail fin of different species is slightly different, and the aspect ratio of the dolphin is between 4.5 and 7.2. Through considering the relationship between the propulsion efficiency and the propulsion force, the aspect ratio of the bionic dolphin is selected as 5.6.where is the tail fin spread in millimeters and is the caudal fin area in square millimeters.
- Swept angle . In theory, it can be known that the sharper the trailing edge of the tail fin, the easier it is for the tail vortex to fall off. While the bionic dolphin is swimming, the drag on the tail fin decreases as decreases. Through considering the shape of the actual dolphin tail fin and the tail fin’s area, the value of the swept angle is selected as 24°.
- Tail fin’s stiffness . As the stiffness increases, the propulsion efficiency and propulsion force generated by the tail fin swing are greater. Because the designed tail fin shape is a curved shape, it was decided to use 3D printing technology to process it. The material used for the tail fin is photosensitive resin, which has very high strength and rigidity. But the disadvantage is that the cost is relatively high.
- Strouhal number . This parameter affects the motion posture of the dolphin’s tail wake, and its specific formula is shown in Equation (2). When the propulsion efficiency is the highest, it is between 0.3 and 0.4.where is the caudal fin swing frequency around the sagittal axis in Hertz, is the trailing edge swing of caudal fin in millimeters and is the average speed of fish in meters per second.
3. Kinematic Analysis and Swing Curve Simulation of Bionic Dolphin Tail Mechanism Driven by Servos
3.1. Kinematic Analysis of Bionic Dolphin Tail Mechanism Driven by Servos
3.2. Kinetic Energy Mapping Principle and Kinematic Nonlinear Characteristic Equation
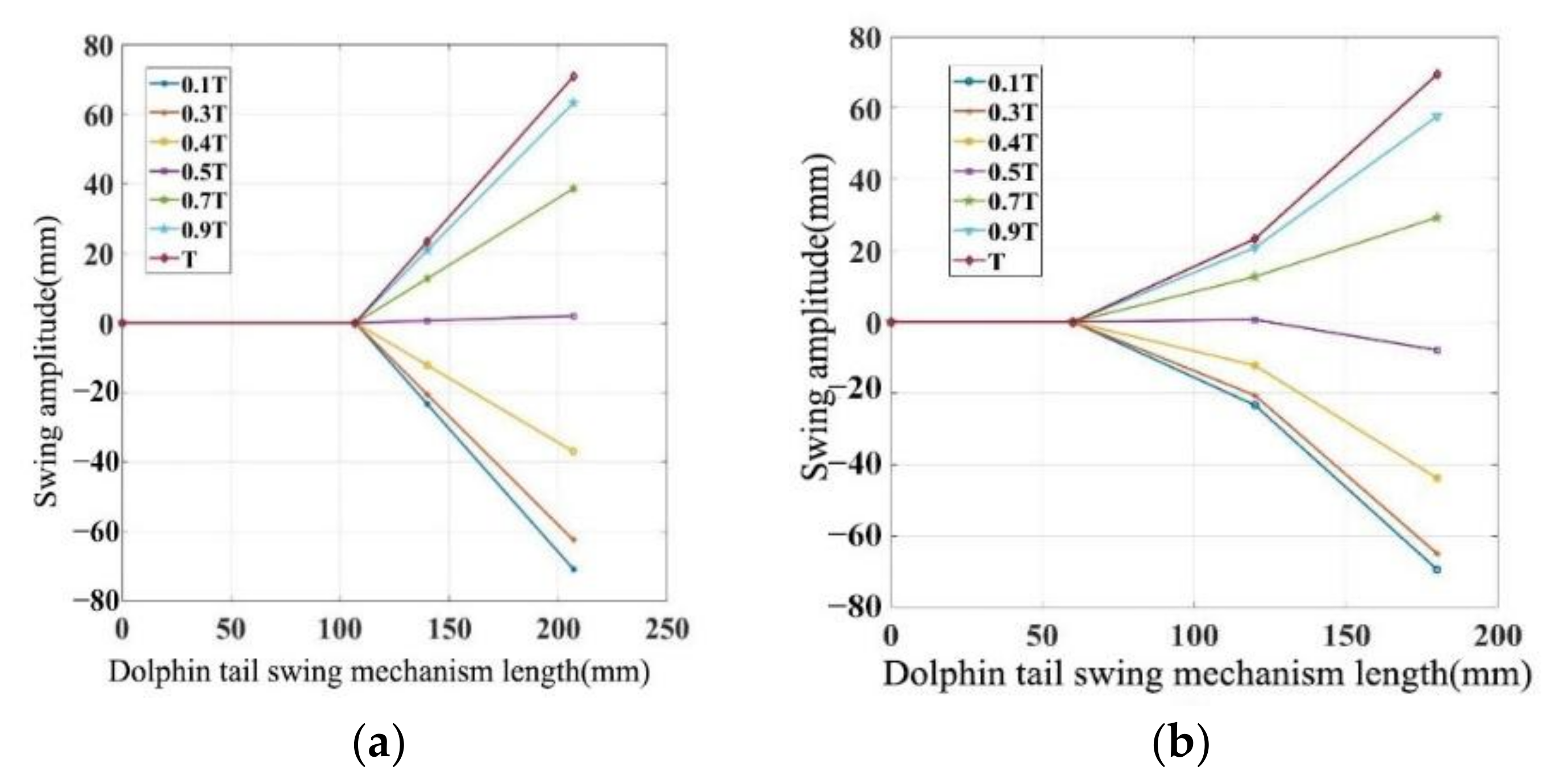
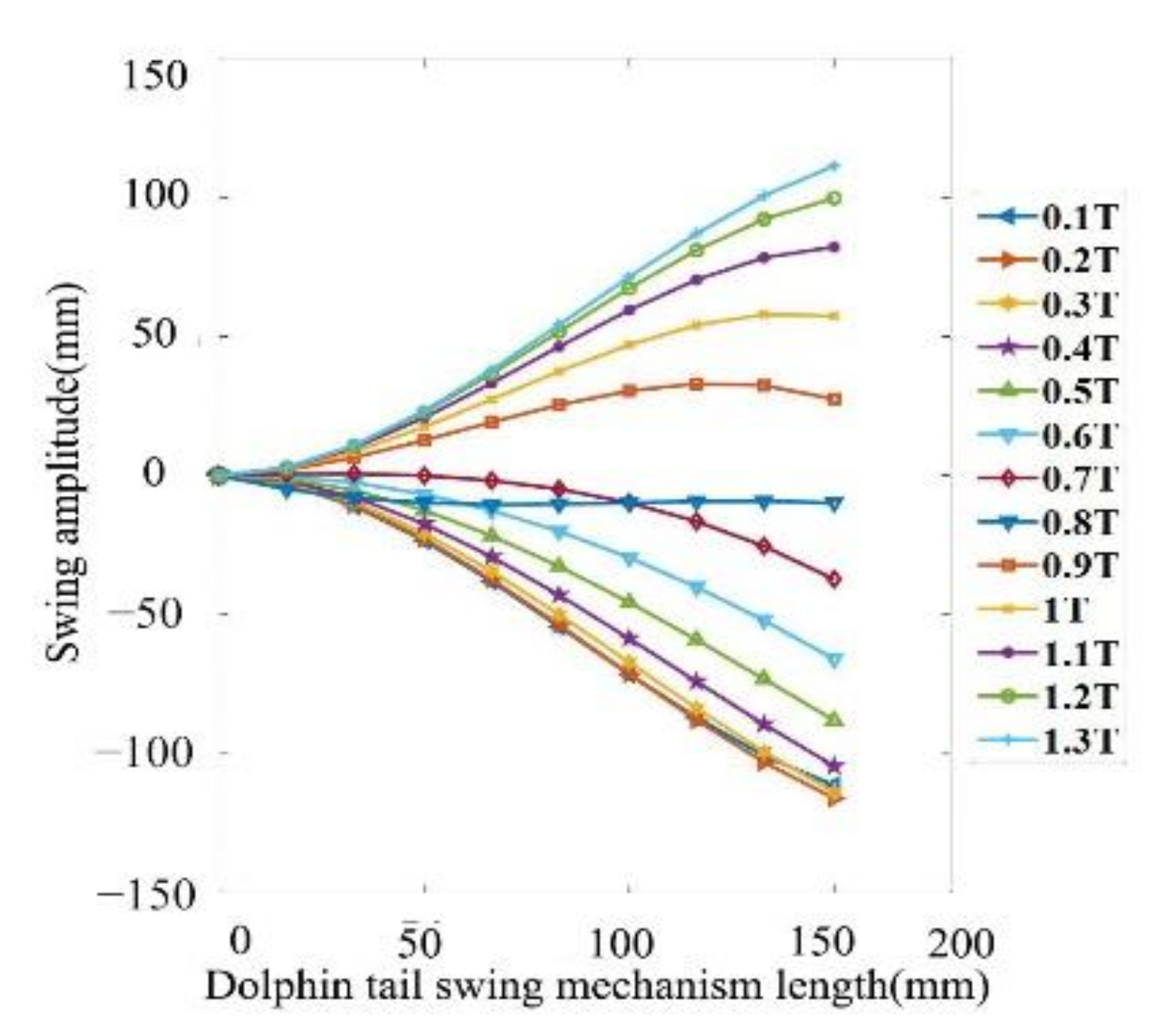
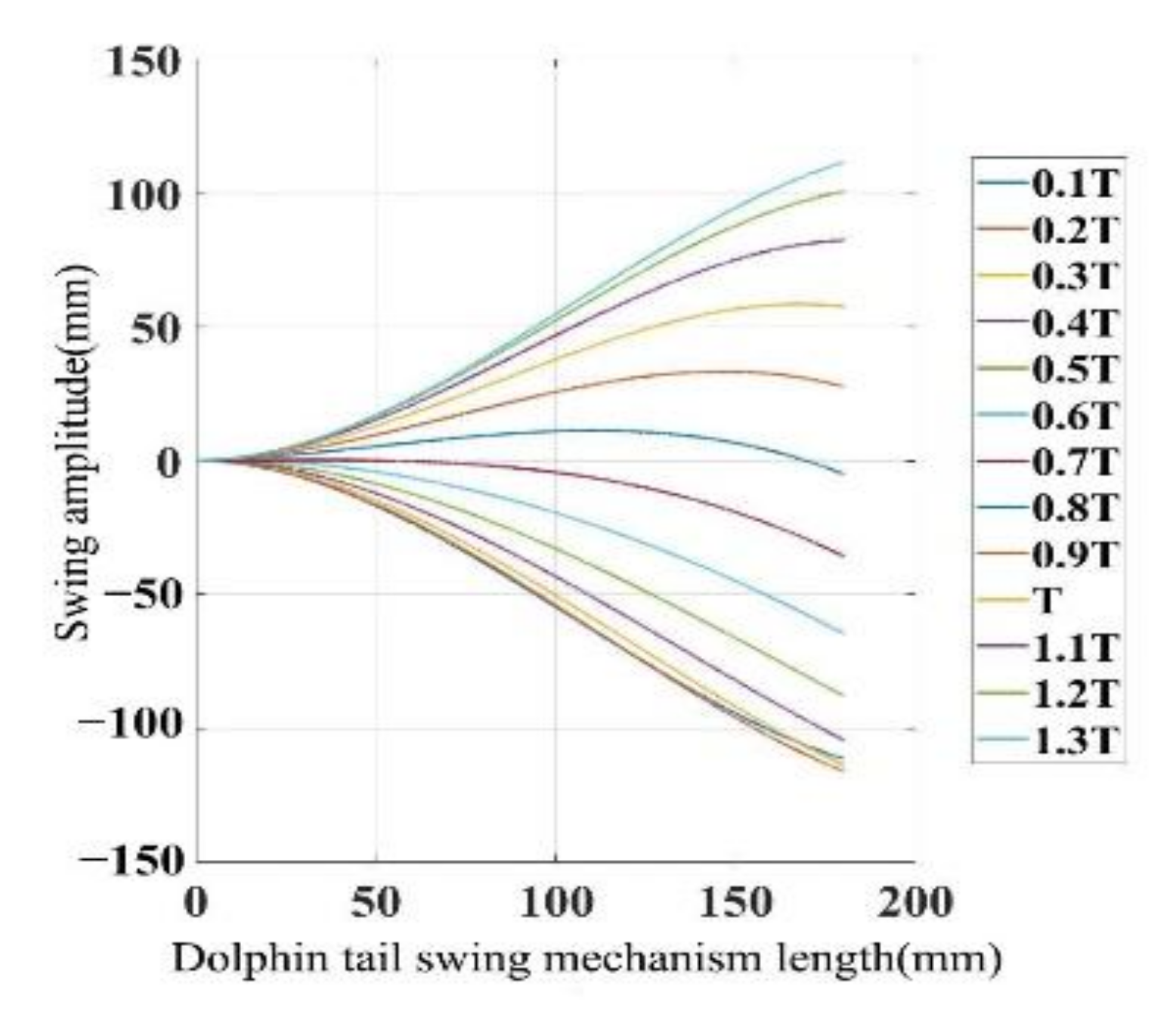
3.3. Simulation of Tail Swing Curve of Bionic Dolphin by Servos
4. Experimental Study
4.1. CPG Control Analysis of Bionic Dolphins Based on Kane Dynamic Model
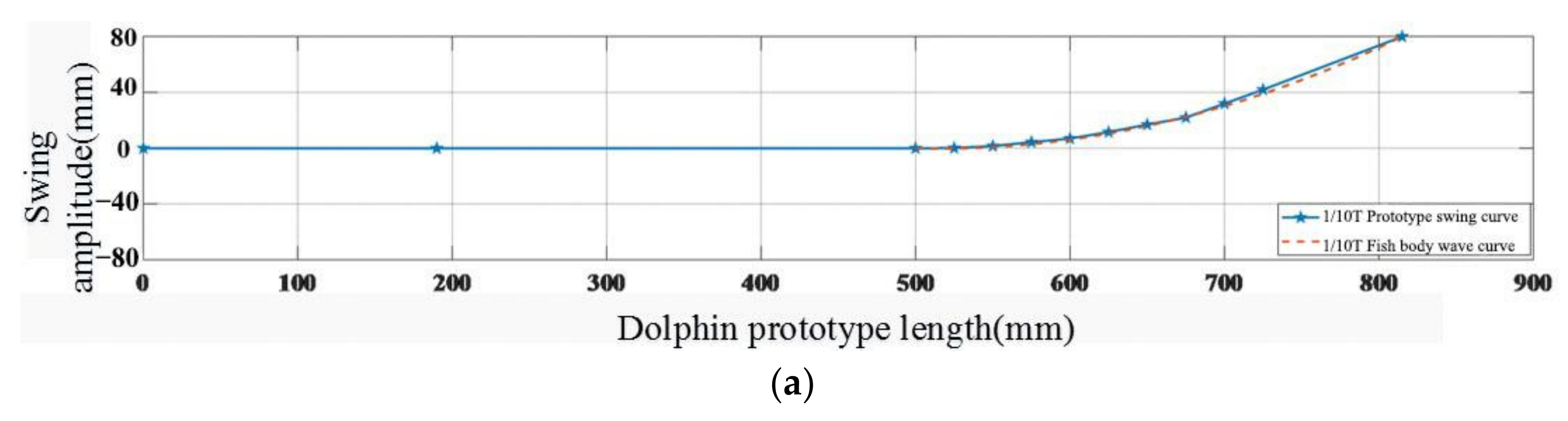
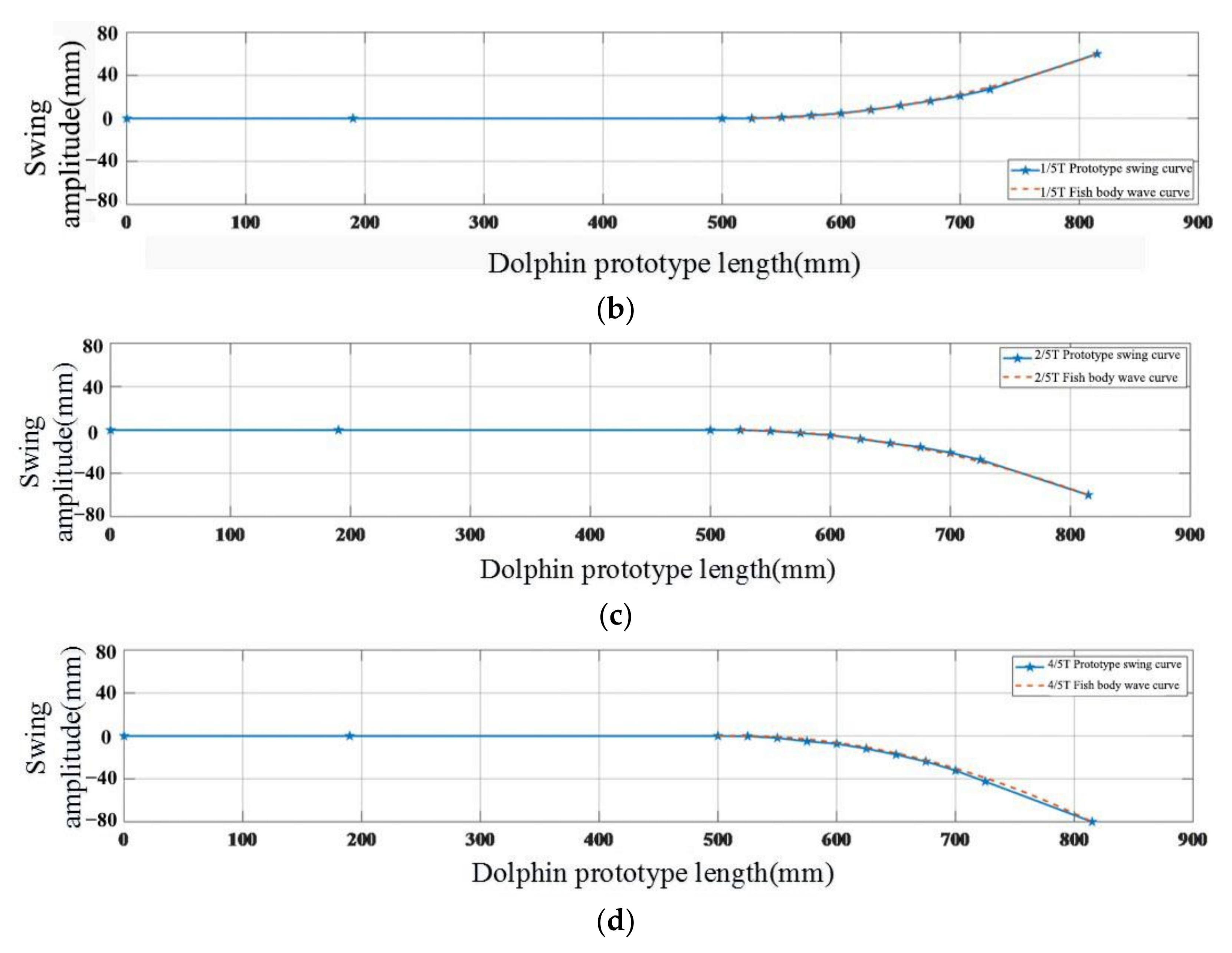
4.2. Curve Fitting Experiment of Bionic Dolphin Tail Based on Steering Gear Drive
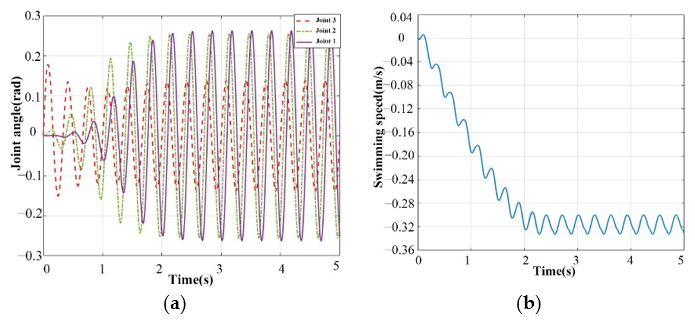
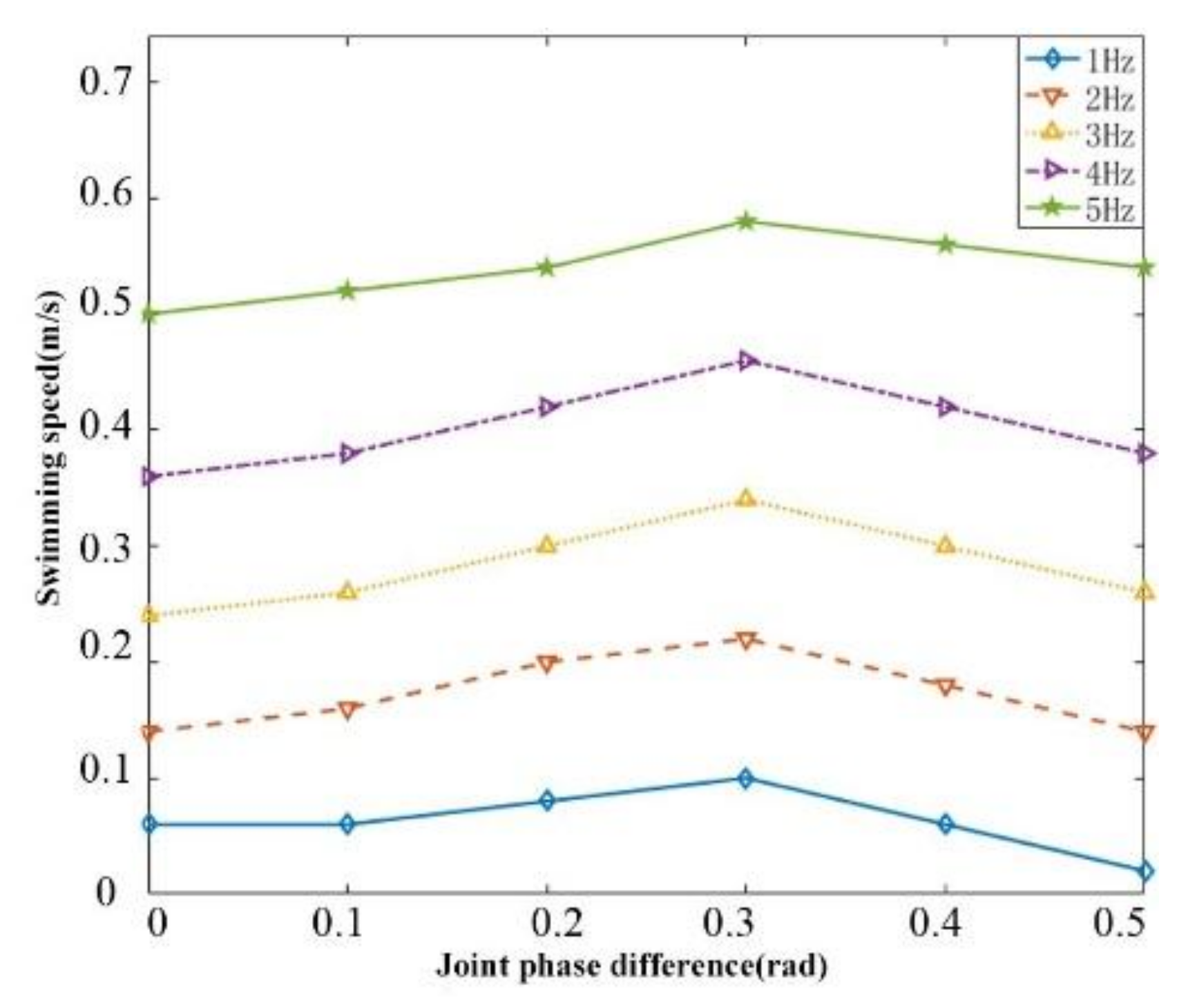
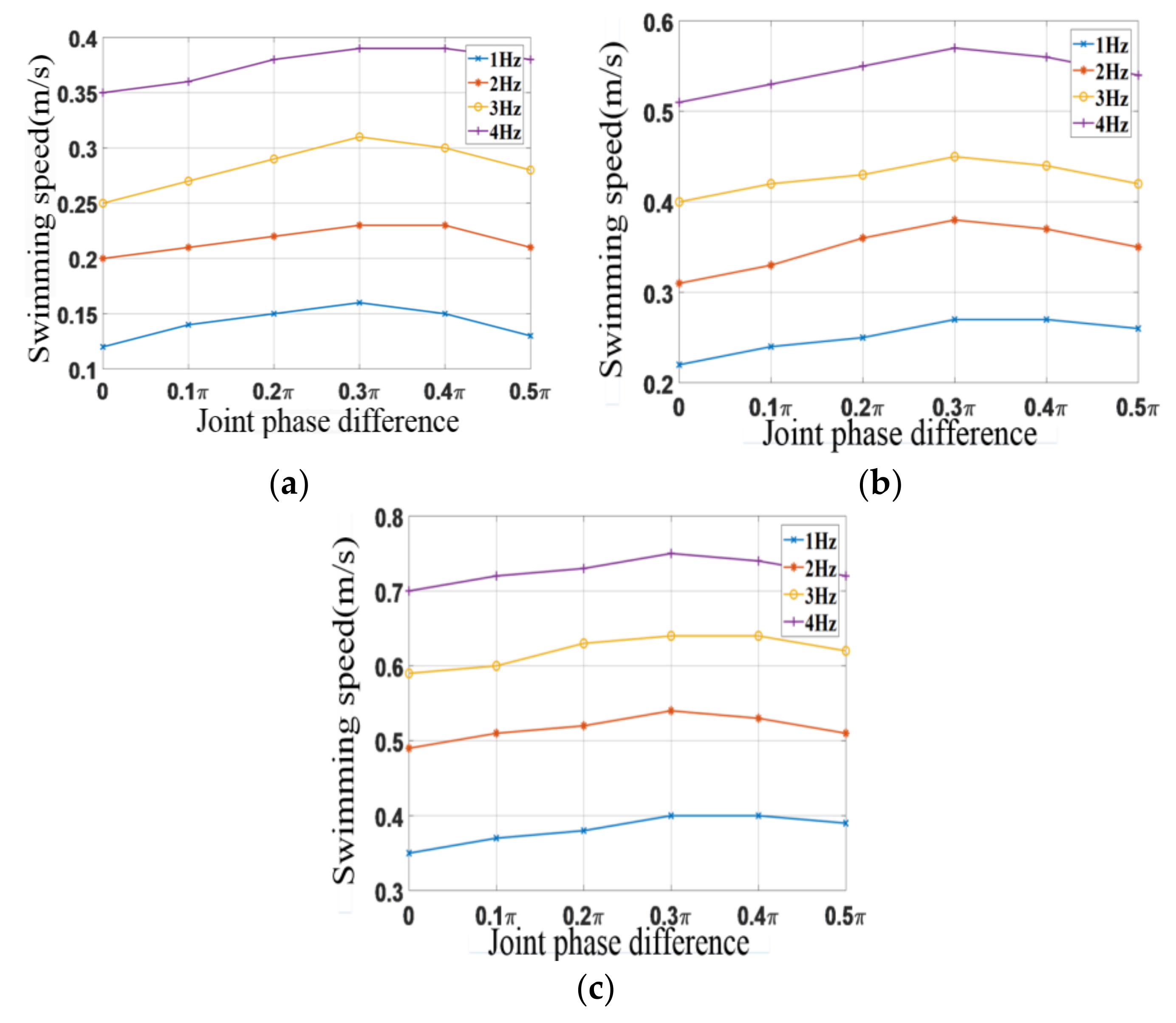
4.3. Underwater Tail Swing Experiment Based on Steering Gear Drive
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, Y.; Huang, Y. The significance of protecting the marine environment in the exploitation of marine resources. Chin. Market 2018, 1, 233–234. [Google Scholar]
- Moynihan, R.; Magsig, B.O. The role of international regimes and courts in clarifying prevention of harm in freshwater and marine environmental protection. Int. Environ. Agreem. Polit. Law Econ. 2020, 20, 649–666. [Google Scholar] [CrossRef]
- Gao, S.; Zhao, L.; Sun, H.H.; Cao, G.X.; Liu, W. Evaluation and Driving Force Analysis of Marine Sustainable Development Based on the Grey Relational Model and Path Analysis. J. Resour. Ecol. 2020, 11, 570–579. [Google Scholar]
- Zheng, Y.H.; Guo, H.D.; Wu, S.C. Analysis of my country’s energy status and its development strategy. City 2018, 1, 35–42. [Google Scholar]
- Zhang, S.; Zhang, A.M.; Cui, P.; Li, T. Simulation of air gun bubble motion in the presence of air gun body based on the finite volume method. Appl. Ocean Res. 2020, 97, 102095. [Google Scholar] [CrossRef]
- Wang, J.C.; Jing, C.L.; Tian, X. The operation and maintenance status of large-scale marine equipment in the United States and its enlightenment to my country. Mar. Sci. 2018, 44, 171–179. [Google Scholar]
- Ren, Y.G.; Liu, B.H.; Ding, Z.J.; Li, Y.; Yang, L.; Hu, X.H. Development status and trends of manned submersibles. J. Ocean Technol. 2018, 37, 114–122. [Google Scholar]
- Liang, J.; Wang, T.; Wen, L. Development of a two-joint robotic fish for real-world exploration. J. Field Robot. 2011, 28, 70–79. [Google Scholar] [CrossRef]
- Hu, Y.Y. Research on the Control System of High-Mobility Bionic Robotic Dolphin Based on STM32. Master’s Thesis, Shenzhen University, Shenzhen, China, 2018. [Google Scholar]
- Xu, D.; Zeng, H.N.; Peng, X. A Stiffness Adjustment Mechanism Based on Negative Work for High-efficient Propulsion of Robotic Fish. J. Bionic Eng. 2018, 15, 270–282. [Google Scholar] [CrossRef]
- Shen, F. Modeling and Control of Bionic Robotic Dolphin and Its Application in Water Quality Monitoring. Master’s Thesis, Graduate School of Chinese Academy of Sciences, Beijing, China, 2012. [Google Scholar]
- Wang, M.; Zhang, Y.L.; Dong, H.F.; Yu, J.Z. Trajectory tracking control of a bionic robotic fish based on iterative learning. Sci. China Inf. Sci. 2020, 63, 505–518. [Google Scholar] [CrossRef]
- Wang, S.Y.; Zhu, J.; Wang, X.J.; Li, Q.F.; Zhu, H.Y.; Zhou, R. Optimization and simulation of a bionic fish tail driving system based on linear hypocycloid with hydrodynamics. Adv. Mech. Eng. 2017, 9, 975–991. [Google Scholar] [CrossRef] [Green Version]
- Techet, A.H.; Hover, F.S.; Triantafyllou, M.S. Separation and Turbulence Control in Biomimetic Flows. Flow Turbul. Combust. 2003, 71, 105–118. [Google Scholar] [CrossRef]
- Liu, J.; Hu, H. Biological Inspiration: From Carangiform Fish to Multi-Joint Robotic Fish. J. Bionic Eng. 2010, 7, 35–48. [Google Scholar] [CrossRef]
- Wang, Y.W.; Yu, K.; Yan, Y.C. Research status and development trend of BCF propulsion model bionic robotic fish. Micro Special Motor 2016, 44, 75–80. [Google Scholar]
- Peng, Z.C. Motion Simulation of Fish-Like Robot. Master’s Thesis, Harbin Engineering University, Harbin, China, 2003. [Google Scholar]
- Liu, Y.X.; Liu, J.K.; Chen, W.S. Development and experimental study of a new type of two-joint robotic fish. Ship Eng. 2008, 30, 28–31. [Google Scholar]
- Yang, Y.; Wang, J.; Wu, Z. Fault-Tolerant Control of a CPG-Governed Robotic Fish. Engineering 2018, 4, 861–869. [Google Scholar] [CrossRef]
- Osama, E.; Christopher, H.; Darryl, W.H. Characterization of acoustic detection efficiency using a gliding robotic fish as a mobile receiver platform. Anim. Biotelem. 2020, 8, 260–272. [Google Scholar]
- Ren, G. Research on Kinematics and Control Method of Robot Dolphin Propulsion System. Master’s Thesis, Beijing Institute of Technology, Beijing, China, 2015. [Google Scholar]
- Xie, F.G.; Zhong, Y.; Du, R.X. Central Pattern Generator (CPG) Control of a Biomimetic Robot Fish for Multimodal Swimming. J. Bionic Eng. 2019, 16, 222–234. [Google Scholar] [CrossRef]
- Sheng, F.; Cao, Z.Q.; Xu, D.; Zhou, C. Dynamic modeling and speed optimization method of robotic dolphin based on Kane method. Acta Autom. Sin. 2012, 38, 1247–1256. [Google Scholar] [CrossRef]













| Drive Servo Quantity/Piece | Serial Number | Description |
|---|---|---|
| 1 | 001 | Servo 1 drive |
| 2 | 010 | Servo 2 drive; Servo 1 follow |
| 011 | Servos 1, 2 have phase difference drive | |
| 3 | 100 | Servo 3 drive; Servo 1, 2 follow |
| 101 | Servos 1, 3 have phase difference drive; Servo 2 follow | |
| 110 | Servos 2, 3 have phase difference drive; Servo 1 follow | |
| 111 | Servo 1, 2, 3 have phase difference drive |
| Cycle/T | Servo 1 Displacement | Servo 2 Displacement | Servo 3 Displacement |
|---|---|---|---|
| 0.1 | −23.33 | −71.40 | −111.36 |
| 0.2 | −22.69 | −71.32 | −115.98 |
| 0.3 | −20.71 | −67.10 | −113.69 |
| 0.4 | −17.30 | −58.55 | −104.40 |
| 0.5 | −12.45 | −45.57 | −87.96 |
| 0.6 | −6.71 | −29.46 | −65.92 |
| 0.7 | 0.00 | −9.77 | −37.23 |
| 0.8 | −9.77 | −9.77 | −9.77 |
| 0.9 | 12.72 | 30.46 | 27.49 |
| 1 | 17.50 | 47.03 | 57.40 |
| 1.1 | 20.84 | 59.54 | 82.21 |
| 1.2 | 22.69 | 67.36 | 99.76 |
| 1.3 | 23.33 | 71.40 | 111.36 |
| Cycle/T | Joint 1 | Joint 2 | Joint 3 | Joint 4 | Joint 5 | Joint 6 | Joint 7 | Joint 8 | Joint 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | −2.92 | −10.89 | −23.33 | −38.00 | −54.18 | −71.40 | −87.03 | −100.62 | −111.36 |
| 0.2 | −2.76 | −10.48 | −22.69 | −37.27 | −53.59 | −71.32 | −87.89 | −102.98 | −115.98 |
| 0.3 | −2.41 | −9.43 | −20.71 | −34.36 | −49.89 | −67.10 | −83.63 | −99.28 | −113.69 |
| 0.4 | −1.85 | −7.69 | −17.30 | −29.16 | −42.91 | −58.55 | −74.05 | −89.37 | −104.40 |
| 0.5 | −1.11 | −5.28 | −12.45 | −21.61 | −32.60 | −45.57 | −59.03 | −73.09 | −87.96 |
| 0.6 | −0.29 | −2.49 | −6.71 | −12.53 | −20.00 | −29.46 | −40.04 | −52.02 | −65.92 |
| 0.7 | 0.59 | 0.70 | 0.00 | −1.75 | −4.83 | −9.77 | −16.45 | −25.33 | −37.23 |
| 0.8 | −4.89 | −8.01 | −9.77 | −10.37 | −10.26 | −9.77 | −9.29 | −9.16 | −9.77 |
| 0.9 | 2.04 | 6.50 | 12.72 | 19.25 | 25.41 | 30.46 | 33.03 | 32.44 | 27.49 |
| 1 | 2.51 | 8.57 | 17.50 | 27.40 | 37.49 | 47.03 | 54.07 | 57.94 | 57.40 |
| 1.1 | 2.79 | 9.97 | 20.84 | 33.24 | 46.37 | 59.54 | 70.41 | 78.35 | 82.21 |
| 1.2 | 2.93 | 10.71 | 22.69 | 36.62 | 51.70 | 67.36 | 81.03 | 92.17 | 99.76 |
| 1.3 | 2.92 | 10.89 | 23.33 | 38.00 | 54.18 | 71.40 | 87.03 | 100.62 | 111.36 |
| Parameter | ||||
|---|---|---|---|---|
| head | 0.8 | 0.172 | 0.018258 | 0.036296 |
| Joint 1 | 0.6 | 0.074 | 0.006576 | 0.011864 |
| Joint 2 | 0.5 | 0.074 | 0.002515 | 0.006076 |
| Joint 3 | 0.4 | 0.074 | 0.00387 | 0.0061 |
| Caudal fin | 0.1 | 0.128 | 0.000372 | 0.00692 |
| Coordinate | 525 | 550 | 575 | 600 | 625 | 650 | 675 | 700 | 725 | 815 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cycle | |||||||||||
| 0.1 T | 0.2 | 1.6 | 4.4 | 7.0 | 10.6 | 17 | 22 | 32 | 42 | 80 | |
| 0.2 T | 0 | 1.0 | 2.8 | 4.8 | 8 | 12 | 16.2 | 21 | 27 | 60 | |
| 0.4 T | 0 | −0.9 | −2.9 | −5 | −8.3 | −12 | −16 | −22 | −28 | −59 | |
| 0.8 T | −0.2 | −1.8 | −5 | −7.2 | −11.8 | −17.4 | −23.8 | −32.2 | −42.4 | −79 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Li, Q.; Wang, T.; Wang, Z. Development of a Bionic Dolphin Flexible Tail Experimental Device Driven by a Steering Gear. Actuators 2021, 10, 167. https://doi.org/10.3390/act10070167
Zhang B, Li Q, Wang T, Wang Z. Development of a Bionic Dolphin Flexible Tail Experimental Device Driven by a Steering Gear. Actuators. 2021; 10(7):167. https://doi.org/10.3390/act10070167
Chicago/Turabian StyleZhang, Bo, Qingxiang Li, Tao Wang, and Zhuo Wang. 2021. "Development of a Bionic Dolphin Flexible Tail Experimental Device Driven by a Steering Gear" Actuators 10, no. 7: 167. https://doi.org/10.3390/act10070167
APA StyleZhang, B., Li, Q., Wang, T., & Wang, Z. (2021). Development of a Bionic Dolphin Flexible Tail Experimental Device Driven by a Steering Gear. Actuators, 10(7), 167. https://doi.org/10.3390/act10070167






