Design and Optimal Control of a Multistable, Cooperative Microactuator
Abstract
:1. Introduction
2. Methods
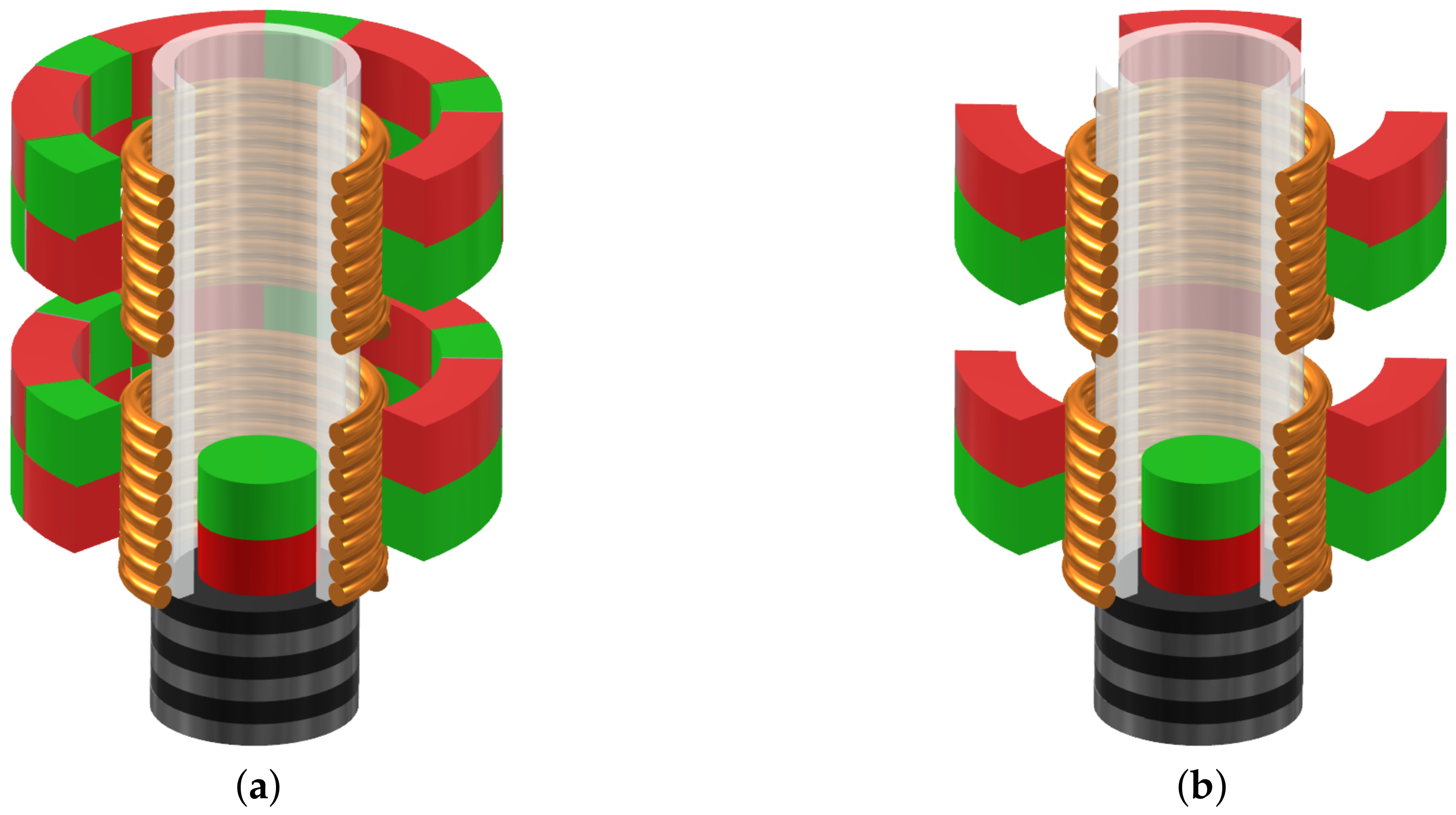
2.1. Modeling
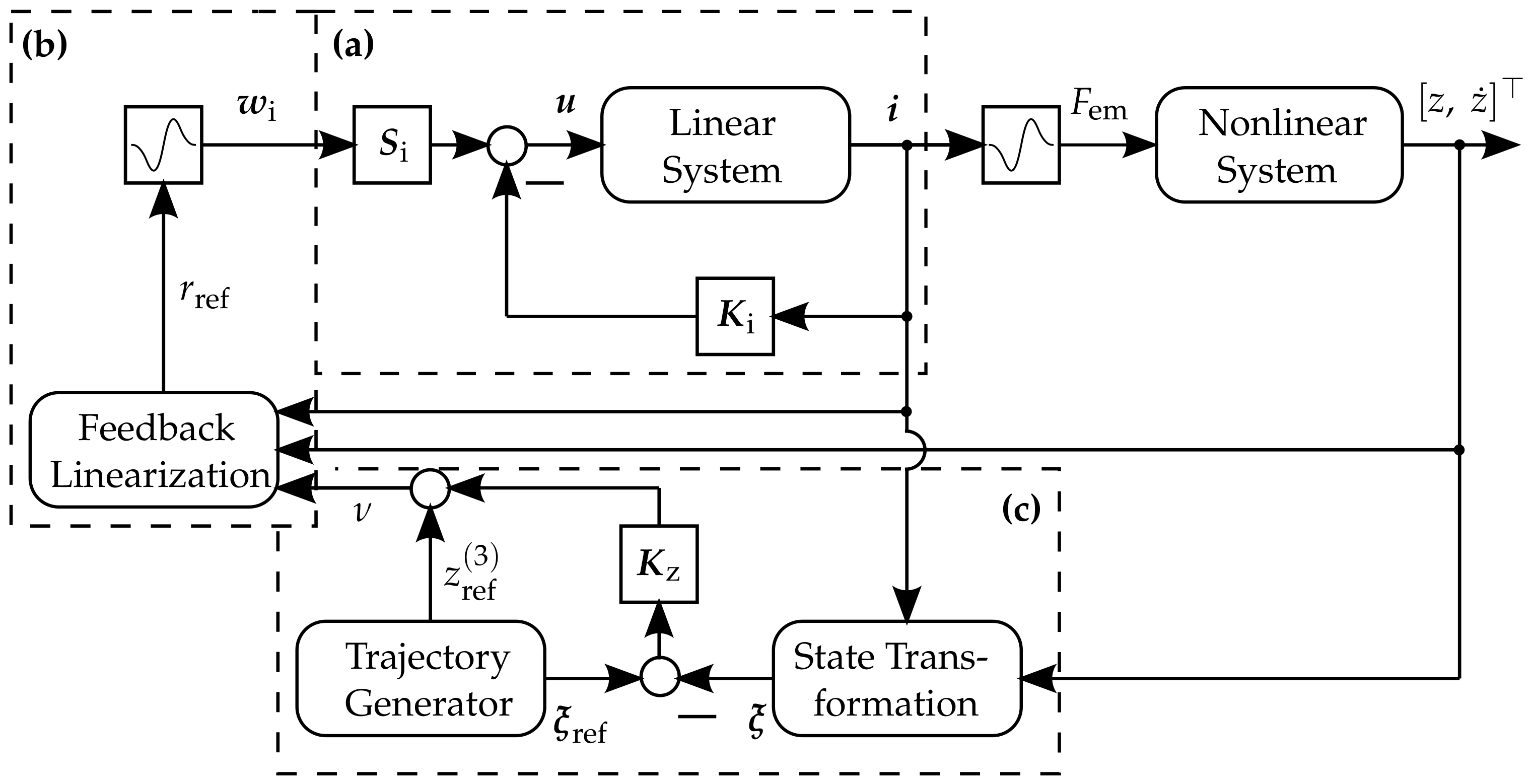
2.2. Trajectory Planning and Control
2.2.1. Piezoelectric Kick
2.2.2. Flatness-Based Control
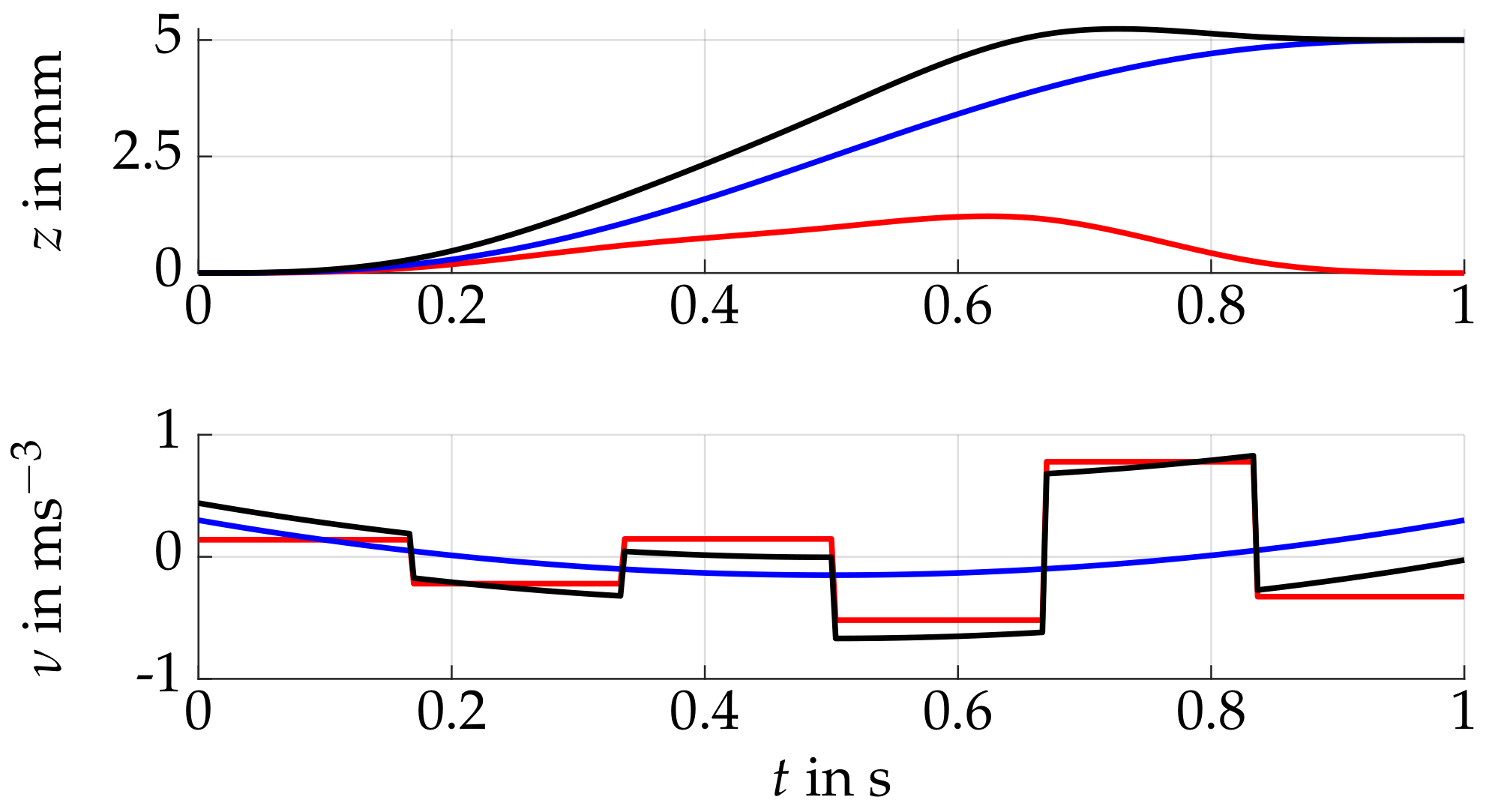
2.2.3. Optimal Trajectory Planning
3. Results
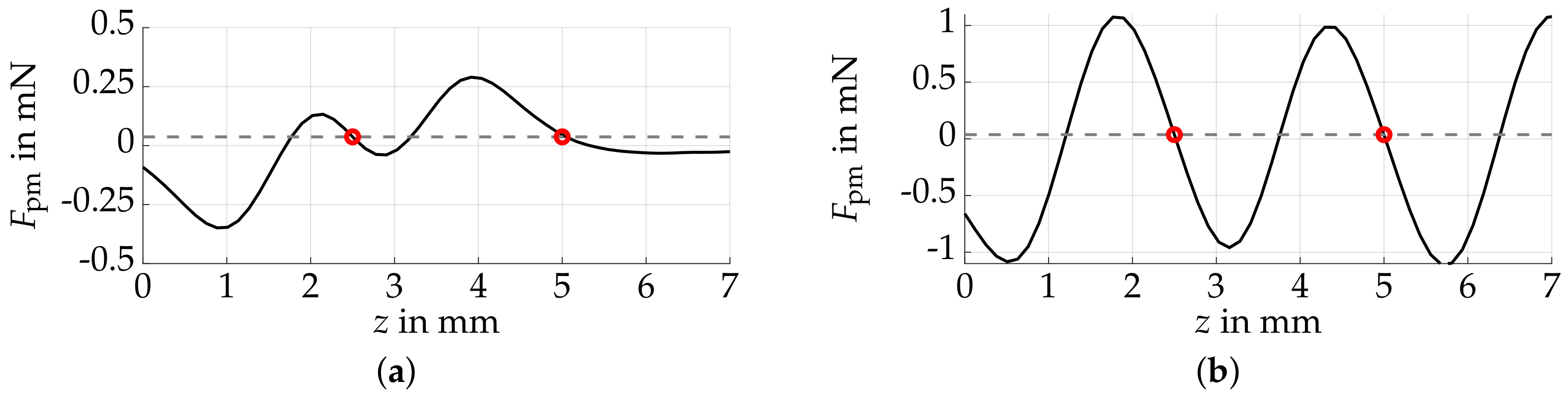
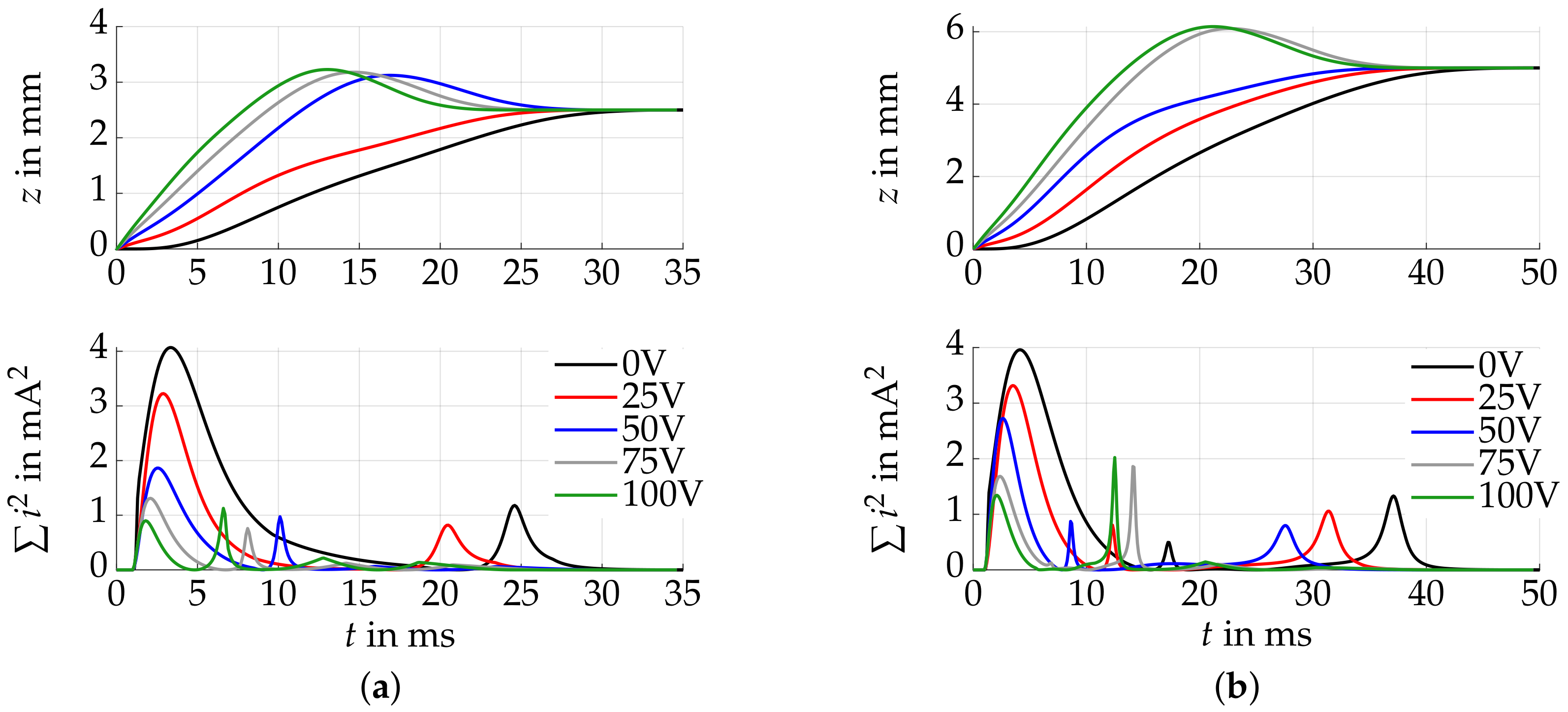
3.1. Multistability Consideration
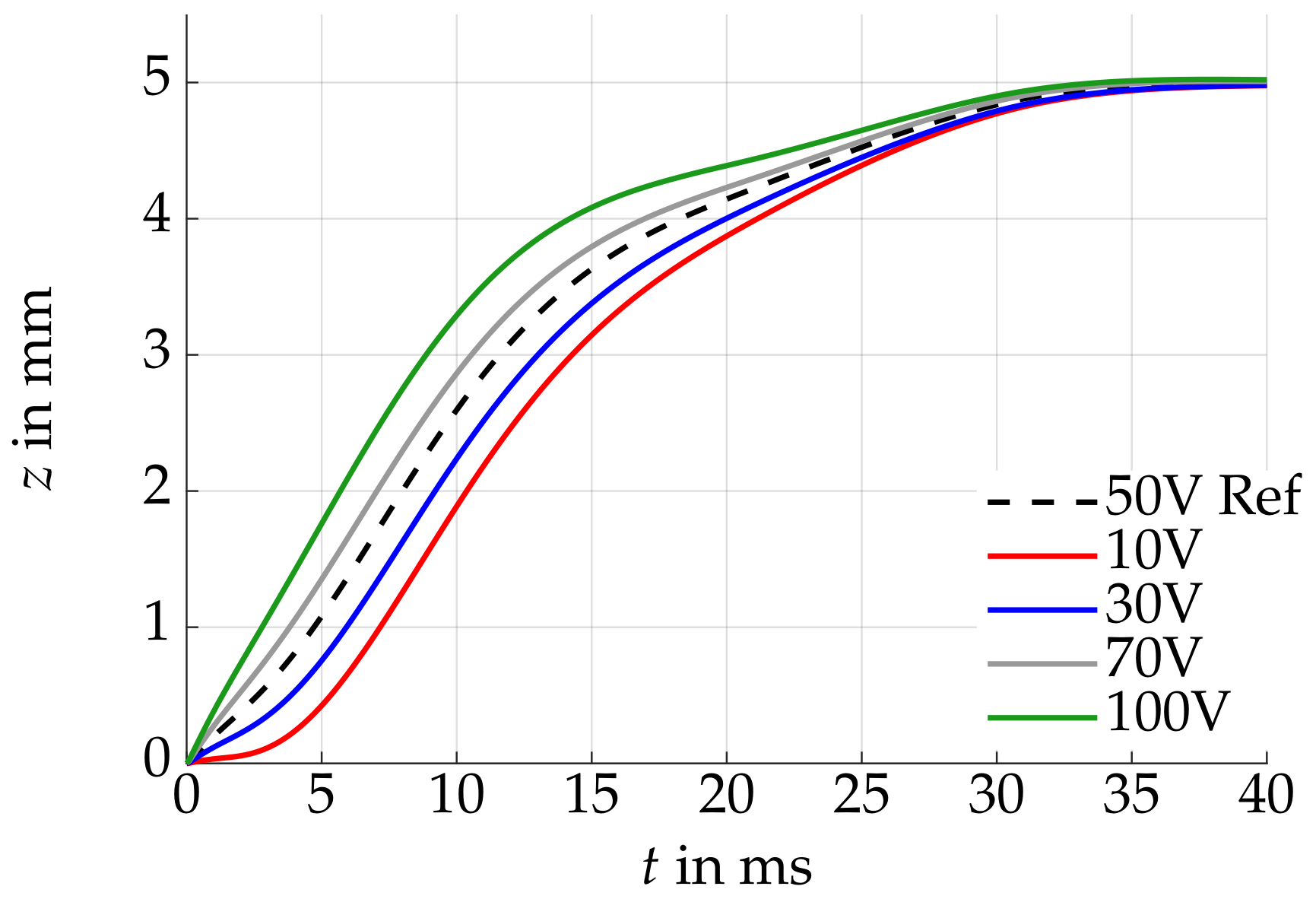
3.2. Simulation Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mita, M.; Arai, M.; Tensaka, S.; Kobayashi, D.; Fujita, H. A Micromachined Impact Microactuator Driven by Electrostatic Force. J. Microelectromech. Syst. 2003, 12, 37–41. [Google Scholar] [CrossRef]
- Min, H.J.; Lim, H.J.; Kim, S.H. A new impact actuator using linear momentum exchange of inertia mass. J. Med. Eng. Technol. 2002, 26, 265–269. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, L.; Zhang, Y.; Cao, J.; Cheng, Y.; Wang, J. A smooth impact drive mechanism actuation method for flapping wing mechanism of bio-inspired micro air vehicles. Microsyst. Technol. 2018, 24, 935–941. [Google Scholar] [CrossRef]
- Huang, W.; Sun, M. Design, Analysis, and Experiment on a Novel Stick-Slip Piezoelectric Actuator with a Lever Mechanism. Micromachines 2019, 10, 863. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Breguet, J.M.; Pérez, R.; Bergander, A.; Schmitt, C.; Clavel, R.; Bleuler, H. Piezoactuators for Motion Control from Centimeter to Nanometer. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Takamatsu, Japan, 31 October–5 November 2000; pp. 492–497. [Google Scholar]
- Hernando-García, J.; García-Caraballo, J.L.; Ruiz-Díez, V.; Sánchez-Rojas, J.L. Motion of a Legged Bidirectional Miniature Piezoelectric Robot Based on Traveling Wave Generation. Micromachines 2020, 11, 321. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ruiz-Díez, V.; Hernando-García, J.; Sánchez-Rojas, J.L. Linear motors based on piezoelectric MEMS. Proceedings 2020, 64, 9. [Google Scholar] [CrossRef]
- Floyd, S.; Pawashe, C.; Sitti, M. An Untethered Magnetically Actuated Micro-Robot Capable of Motion on Arbitrary Surfaces. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 419–424. [Google Scholar] [CrossRef]
- Dieppedale, C.; Desloges, B.; Rostaing, H.; Delamare, J.; Cugat, O.; Meunier-Carus, J. Magnetic bistable micro-actuator with integrated permanent magnets. In Proceedings of the IEEE Sensors, Vienna, Austria, 24–27 October 2004; pp. 493–496. [Google Scholar] [CrossRef]
- Stepanek, J.; Rostaing, H.; Lesecq, S.; Delamare, J.; Cugat, O. Position Control of a Levitating Magnetic Actuator Applications to Microsystems. In Proceedings of the 16th Triennial World Congress, Prague, Czech Rebublic, 4–8 July 2005; pp. 85–90. [Google Scholar] [CrossRef] [Green Version]
- Ruffert, C.; Gehrking, R.; Ponick, B.; Gatzen, H.H. Magnetic Levitation Assisted Guide for a Linear Micro-Actuator. IEEE Trans. Magn. 2006, 42, 3785–3787. [Google Scholar] [CrossRef]
- Ruffert, C.; Li, J.; Denkena, B.; Gatzen, H.H. Development and Evaluation of an Active Magnetic Guide for Microsystems With an Integrated Air Gap Measurement System. IEEE Trans. Magn. 2007, 43, 2716–2718. [Google Scholar] [CrossRef]
- Laurent, G.J.; Delettre, A.; Zeggart, R.; Yahiaoui, R.; Manceau, J.F.; Le Fort-Piat, N. Micropositioning and Fasst Transport Using a Contactless Micro-Conveyor. Micromachines 2014, 5, 66–80. [Google Scholar] [CrossRef] [Green Version]
- Poletkin, K.; Lu, Z.; Wallrabe, U.; Korvink, J.G.; Badilita, V. Stable dynamics of micro-machined inductive contactless suspensions. Int. J. Mech. Sci. 2017, 131, 753–766. [Google Scholar] [CrossRef] [Green Version]
- Olbrich, M.; Schütz, A.; Kanjilal, K.; Bechtold, T.; Wallrabe, U.; Ament, C. Co-Design and Control of a Magnetic Microactuator for Freely Moving Platforms. Proceedings 2020, 64, 23. [Google Scholar] [CrossRef]
- Schütz, A.; Hu, S.; Rudnyi, E.B.; Bechtold, T. Electromagnetic System-Level Model of Novel Free Flight Microactuator. In Proceedings of the 21st International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems, Cracow, Poland, 5–8 July 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Schütz, A.; Olbrich, M.; Hu, S.; Ament, C.; Bechtold, T. Parametric system-level models for position-control of novel electromagnetic free flight microactuator. Microelectron. Reliab. 2021, 119, 1–9. [Google Scholar] [CrossRef]
- Goldfarb, M.; Celanovic, N. A lumped parameter electromechanical model for describing the nonlinear behavior of piezoelectric actuators. J. Dyn. Sys. Meas. Control 1997, 119, 478–485. [Google Scholar] [CrossRef]
- Gomis-Bellmunt, O.; Ikhouane, F.; Castell-Vilanova, P.; Bergas-Jane, J. Modeling and validation of a piezoelectric actuator. Electr. Eng. 2007, 89, 629–638. [Google Scholar] [CrossRef]
- Richter, H.; Misawa, E.A.; Lucca, D.A.; Lu, H. Modeling nonlinear behavior in a piezoelectric actuator. Precis. Eng. 2001, 25, 128–137. [Google Scholar] [CrossRef] [Green Version]
- Main, J.A.; Garcia, E. Piezoelectric Stack Actuators and Control System Design: Strategies and Pitfalls. J. Guid. Control Dynam. 1997, 20, 478–485. [Google Scholar] [CrossRef]
- Agashe, J.S.; Arnold, D.P. A study of scaling and geometry effects on the forces between cuboidal and cylindrical magnets using analytical force solutions. J. Phys. D Appl. Phys. 2008, 41, 1–9. [Google Scholar] [CrossRef]
- Ravaud, R.; Lemarquand, G.; Babic, S.; Lemarquand, V.; Akyel, C. Cylindrical Magnets and Coils: Fields, Forces, and Inductances. IEEE Trans. Magn. 2010, 46, 3585–3590. [Google Scholar] [CrossRef]
- Ansys Inc. ANSYS Electronics Desktop, Release 2020 R1; Ansys Inc.: Washington County, PA, USA, 2020. [Google Scholar]
- Specker, T.; Buchholz, M.; Dietmayer, K. Dynamical Modeling of Constraints with Friction in Mechanical Systems. In Proceedings of the 8th Vienna International Conference on Mathematical Modelling, Vienna, Austria, 18–20 February 2015; pp. 514–519. [Google Scholar]
- Fliess, M.; Lévine, J.; Martin, P.; Rouchon, P. Flatness and defect of non-linear systems: Introductory theory and examples. Int. J. Control 1995, 61, 1327–1361. [Google Scholar] [CrossRef] [Green Version]
- Mackenroth, U. Basic Properties of Multivariable Feedback Systems. In Robust Control Systems: Theory and Case Studies, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Charlet, B.; Lévine, J. On dynamic feedback linearization. Syst. Control Lett. 1989, 13, 143–151. [Google Scholar] [CrossRef]
- Bergman, K.; Ljungqvist, O.; Linder, J.; Axehill, D. An Optimization-Based Motion Planner for Autonomous Maneuvering of Marine Vessels in Complex Environments. In Proceedings of the 59th IEEE Conference on Decision and Control, Jeju Island, Korea, 14–18 December 2020; pp. 5283–5290. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, H.; Zhang, B.; Du, K.L. Using Radial Basis Function Networks for Function Approximation and Classification. ISRN Appl. Math. 2012, 2012, 1–34. [Google Scholar] [CrossRef] [Green Version]
- The MathWorks Inc. MATLAB (R2019a); The MathWorks Inc.: Natick, MA, USA, 2019. [Google Scholar]
- Andersson, J. A General-Purpose Software Framework for Dynamic Optimization. Ph.D. Thesis, Department of Electrical Engineering (ESAT/SCD) and Optimization in Engineering Center, Heverlee, Belgium, October 2013. [Google Scholar]
- Wächter, A.; Biegler, L.T. On the implementation of a primal-dual interior point filter line search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Halbach, K. Design of permanent multipole magnets with oriented rare Earth cobalt material. Nucl. Instrum. Methods 1980, 169, 1–10. [Google Scholar] [CrossRef] [Green Version]




| Component | Height in mm | Inner Radius in mm | Outer Radius in mm | Mass in mg |
|---|---|---|---|---|
| Proof mass | 1 | – | ||
| Ring magnet | – |
| Setup | Magnet | Remanence in T | Position in mm |
|---|---|---|---|
| 1 | 0.1 | – | |
| 0.12 | 1.592 | ||
| 0.1 | 3.296 | ||
| 2 | 0.2 | – | |
| 0.2 | 1.225 | ||
| 0.2 | 3.746 | ||
| 0.2 | 6.338 | ||
| 3 | 0.2 | – | |
| 0.2 | 1.143 | ||
| 0.2 | 3.807 | ||
| 0.2 | 6.223 | ||
| 0.2 | 8.868 | ||
| 4 | 0.2 | – | |
| 0.2 | 1.283 | ||
| 0.2 | 3.670 | ||
| 0.2 | 6.344 | ||
| 0.2 | 8.701 | ||
| 0.2 | 11.42 |
| Description | Value | Description | Value |
|---|---|---|---|
| Inner radius (solenoid) | 0.8 mm | Resistance (solenoid) | 281 Ω |
| Outer radius (solenoid) | 1.2 mm | (piezo) | 360 N |
| Height (solenoid) | 1.5 mm | (piezo) | 100 V |
| Wire diameter (solenoid) | 25 μm | (piezo) | 1.1 MNm−1 |
| Specific resistance (solenoid) | 18 nΩm | M (piezo) | 1.8 g |
| Number of turns (solenoid) | 1222 | (piezo) | 25 |
| Inductance (solenoid) | 3.9 mH | (proof mass) | 2.5 × 10−4 |
| Mutual inductance (solenoid) | 2.0 mH | (contact) | 4.5 × 106 |
| Position (solenoid 1) | 2.2 mm | (contact) | |
| Position (solenoid 2) | 4.7 mm | (contact) | 3 |
| Description | Value |
|---|---|
| 1 ms | |
| 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olbrich, M.; Schütz, A.; Bechtold, T.; Ament, C. Design and Optimal Control of a Multistable, Cooperative Microactuator. Actuators 2021, 10, 183. https://doi.org/10.3390/act10080183
Olbrich M, Schütz A, Bechtold T, Ament C. Design and Optimal Control of a Multistable, Cooperative Microactuator. Actuators. 2021; 10(8):183. https://doi.org/10.3390/act10080183
Chicago/Turabian StyleOlbrich, Michael, Arwed Schütz, Tamara Bechtold, and Christoph Ament. 2021. "Design and Optimal Control of a Multistable, Cooperative Microactuator" Actuators 10, no. 8: 183. https://doi.org/10.3390/act10080183
APA StyleOlbrich, M., Schütz, A., Bechtold, T., & Ament, C. (2021). Design and Optimal Control of a Multistable, Cooperative Microactuator. Actuators, 10(8), 183. https://doi.org/10.3390/act10080183






