On the Lightweight Truss Structure for the Trash Can-Handling Robot †
Abstract
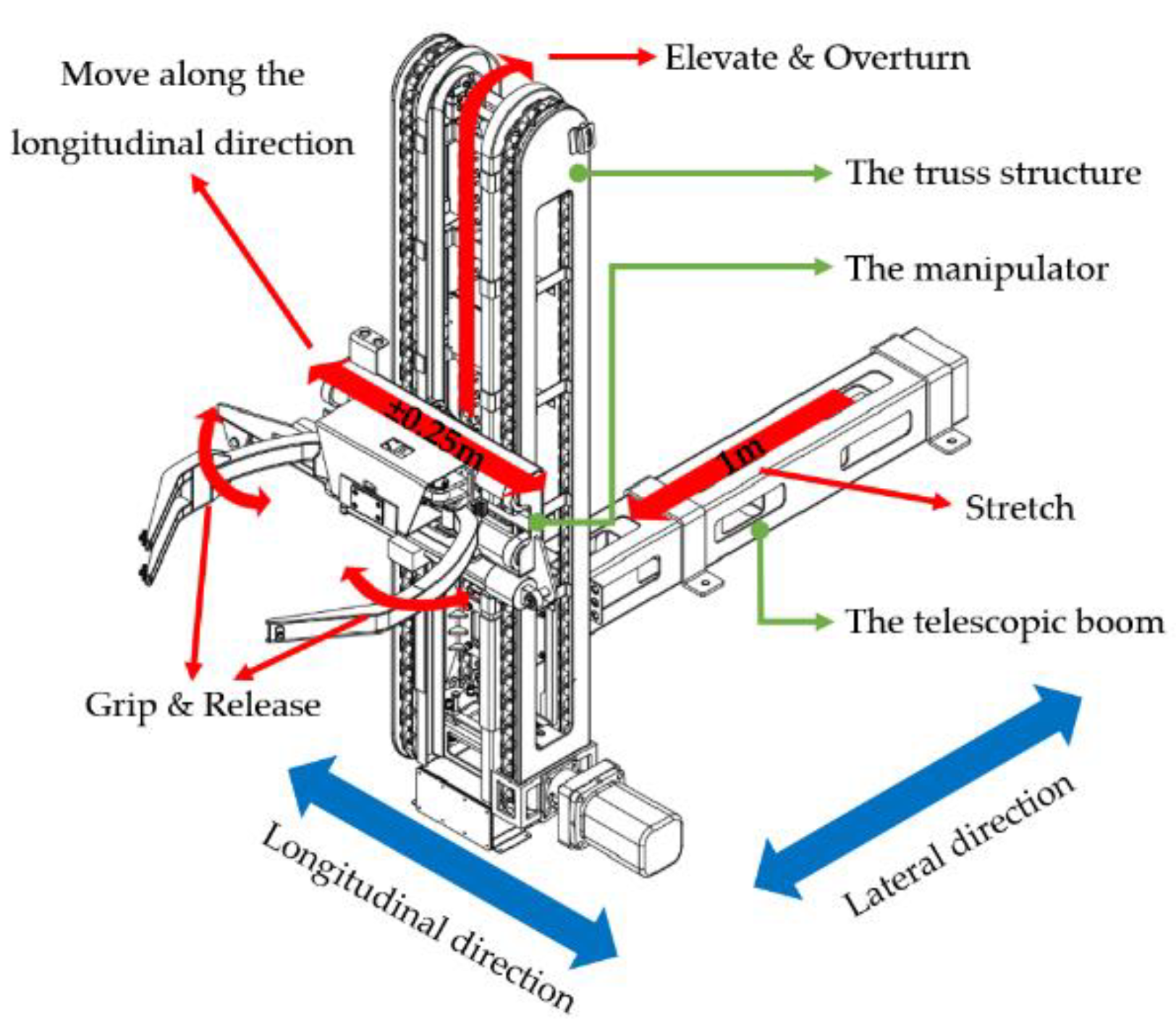
:1. Introduction
- 1
- After the driver parks the sanitation vehicle next to the trash can, the perception system sequentially detects the type of the trash can, the relative position of the trash can, pedestrians and obstacles. If the position of the trash can is beyond the working range of the robot, the driver will be prompted to make adjustments;
- 2
- The perception system converts the relative position information of the trash can into control data and then sends it to the control system;
- 3
- According to the preset control strategy, the control system controls the manipulator through the hydraulic components to complete the garbage loading operation.
2. Multi-Objective Optimization of Parameters Related to Robot Load
2.1. Establishment of Kinematic Equation
- There is no relative displacement between the manipulator and the trash can;
- The garbage in the trash can does not move during the whole operation, and the position of the center of mass remains unchanged;
2.2. Establishment of Dynamic Equation
2.3. Mathematical Model of the Multi-Objective Optimization of the Load-Related Parameters
- 1
- Design variables: this paper takes the arc radius , the center distance and the time consumption of the dumping action as the design variables;
- 2
- Constraints: to ensure that the manipulator can dump garbage smoothly, the pitch angle of the manipulator must be greater than 135°;
- 3
- Optimization objective: the purpose of parameter optimization is to reduce the load on the truss structure. Therefore, the optimization objective is to minimize the maximum instantaneous power , the average power , the maximum change of the instantaneous driving force and the time consumption of the dumping action.
2.4. Results of the Multi-Objective Optimization of the Load-Related Parameters
3. Topology Optimization of the Truss Structure under Multiple Load Cases
3.1. Analysis of the Load on the Truss Structure
3.2. Topology Optimization under Multiple Load Cases
3.2.1. Determination of Load Cases
3.2.2. Mathematical Model of Topology Optimization under Multiple Load Cases
3.2.3. Results of Topology Optimization under Multiple Load Cases
4. Discrete Optimization of the Truss Structure under Multiple Load Cases
4.1. Mathematical Model of Discrete Optimization under Multiple Load Cases
4.2. Results of Discrete Optimization under Multiple Load Cases
5. Lightweight Design Method of the Robot Truss Structure
- 1
- This paper first established the kinematic and dynamic equations of the manipulator (load). Then the variables that are related to the load were optimized through the particle swarm algorithm to reduce the load of the truss structure;
- 2
- This paper then determined the typical load cases of the truss structure. The topology optimization under multiple load cases was carried out to optimize the material distribution of the truss structure. The conceptual configuration model was established through model reconstruction method;
- 3
- Based on the conceptual configuration model, this paper finally reduced the dimensions of the optimization variables according to the technological conditions and processing efficiency. The sequential quadratic programming solver was applied to optimize the thickness of the truss structure parts under multiple load cases.
6. Conclusions
- 1
- In this paper, the kinematic and dynamic equations of the manipulator was established through the complex interpolation method and the theorem of kinetic energy. The particle swarm algorithm was used to optimize the load-related parameters. This provides a new method for the optimization of the equipment moving along the guide rail in the future. After the optimization, the maximum instantaneous power required by the robot for dumping garbage is reduced by 48.55%, the average power is reduced by 38.60%, and the maximum change of the instantaneous driving force is reduced by 85.70%;
- 2
- By analyzing the load of the truss structure during the operation, the states when the manipulator is in the acceleration lifting movement, the transition movement, and on standby are regarded as three typical load cases in this paper. Combined with practical engineering experience, due to the significant increase of the driving force, the transition movement needs special attention in the design and optimization of the equipment with similar structure;
- 3
- In this paper, three kinds of discrete optimization of the truss structure with different preference were carried out. According to the optimization results, the optimization scheme with no preference best meets the actual needs of the project. In this optimization scheme, the mass of the truss structure is reduced by 8.72%, the inherent frequency is increased by 61.08%, and the maximum stress is reduced by 10.98%;
- 4
- The lightweight design method proposed in this paper is a new optimization method as it includes load optimization. The results show that the method is effective for the optimization of the robot’s truss structure. This method can also be applied to the forward design or lightweight design of the actuators with similar structure, such as the column of vertical drilling machine. So, this method gives a reference value for actual projects.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, W.; Dong, Z. Analysis of Influencing Factors and Scale Prediction of Garbage Production in Shanghai - Research Based on Grey System Theory. Available online: https://oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2020&filename=ZSZY202005005&v=EBMK4Zr%25mmd2Fj8q0NJrqqoPvvXols3NuLzWluZqj8%25mmd2F%25mmd2FbI4rnr3%25mmd2FfcufjH4WFSksEXEB2 (accessed on 30 August 2021).
- Chu, X. Evaluation Research on the Implementation Effect of the Current Municipal Household Waste Classification Policy in Shanghai. Master’s Thesis, Harbin Engineering University, Harbin, China, June 2020. [Google Scholar]
- Wei, M. Performance Study and Improved Design of the Leakage-Free Lifting Mechanism for Garbage Truck. Master’s Thesis, Yangzhou University, Yangzhou, China, June 2020. [Google Scholar]
- Yin, C. Simulation Analysis and Key Components Lightweight of Food Garbage Truck Lifting Mechanism. Master’s Thesis, Yangzhou University, Yangzhou, China, June 2021. [Google Scholar]
- Yang, Q.; Xue, B. Kinematics and Dynamics Analysis of the Lifting Mechanism of the New-Type Sugarcane Harvester. Available online: https://oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&dbname=CJFDAUTO&filename=GXJX202105001&v=oOprQCOQxw%25mmd2F0om%25mmd2BakEi8%25mmd2B1vKqhiUVfZfmaW4Qlc6wJn4L8fA%25mmd2BhDhI16AKb7EK7qH (accessed on 30 August 2021).
- Wang, B. Coupling Characteristics Analysis and Structure Optimization of Truss Robot. Master’s Thesis, Hefei University of Technology, Hefei, China, April 2017. [Google Scholar]
- Wang, J.; Wang, X.; Fu, J.; Lu, G.; Jin, C.; Chen, Y. Static and dynamic characteristic analysis and structure optimization for crossbeam structure of heavy-duty truss robot. J. Zhejiang Univ. Eng. Sci. 2021, 55, 124–134. [Google Scholar]
- Li, Z.; Li, D.; Song, Y. Finite Element Analysis of Law of Thermo Mechanical Coupling Deformation and Dynamic Characteristics of Rail Beam of Truss Pipe Pulling Robot. Available online: https://oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2021&filename=JXQD202103029&v=Ldfdhg%25mmd2F21Z8X%25mmd2BOmhufPrWhMdseEIy8%25mmd2B40uPDb2asqtIjdi%25mmd2Fn57dALYr4myuf%25mmd2BD0m (accessed on 30 August 2021).
- Yuan, B. Analysis and Optimization of Truss Structure Based on Finite Element Method. Master’s Thesis, Yangzhou University, Yangzhou, China, December 2018. [Google Scholar]
- Shi, G.; Chen, Y.; Yang, Y.; Jiang, X.; Song, Z. BIW architecture multidisciplinary light weight optimization design. J. Mech. Eng. 2012, 48, 110–114. [Google Scholar] [CrossRef]
- Xu, X.; Chen, X.; Liu, Z.; Xu, Y.; Zhang, Y. Reliability-based design for lightweight vehicle structures with uncertain manufacturing accuracy. Appl. Math. Model. 2021, 95, 22–37. [Google Scholar] [CrossRef]
- Xu, X.; Chen, X.; Liu, Z.; Yang, J.; Xu, Y.; Zhang, Y.; Zhang, Y. Multi-Objective Reliability-Based Design Optimization for the Reducer Housing of Electric Vehicles. Available online: https://www.tandfonline.com/doi/abs/10.1080/0305215X.2021.1923704 (accessed on 30 August 2021).
- Wang, J.; Zhang, P.; Wang, C.; Han, S. Lightweight Optimization Design of the Flat Transport Vehicle’s Loading Platform Based on the high-Strength Steel. Available online: https://www.webofscience.com/wos/alldb/full-record/CSCD:6967249 (accessed on 30 August 2021).
- Li, Y.; Xu, Z.; Zhang, L.; Du, J.; Jiang, Y. Light Weight Design of Chassis Frame for a Soybean Harvester. Available online: https://www.webofscience.com/wos/alldb/full-record/CSCD:6600797 (accessed on 30 August 2021).
- Huang, W.; Huang, L.; Peng, T.; Liang, Q.; Luo, L. Comprehensive Optimal Design of the Column of Double Spindle Horizontal Machining Center. Available online: https://www.webofscience.com/wos/alldb/full-record/CSCD:6841618 (accessed on 30 August 2021).
- Gao, Y.; Ma, C.; Liu, Z.; Duan, Y.; Tian, L. Optimization of Multi-Material and Beam Cross-Sectional Shape and Dimension of Skeleton-Type Body. Available online: https://oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CAPJ&dbname=CAPJLAST&filename=JLGY20201216006&v=yiDx1rS1Ygw5mkOLat4bs%25mmd2BGYRDj9LAxCGX6WtMshjMK9bIGGSEc5LzRR634jCfOf (accessed on 17 December 2020).
- Cheng, M.; Prayogo, D.; Wu, Y.; Lukito, M. A hybrid harmony search algorithm for discrete sizing optimization of truss structure. Autom. Constr. 2016, 69, 21–33. [Google Scholar] [CrossRef]
- Yoshimura, M.; Nishiwaki, S.; Izui, K. A multiple cross-sectional shape optimization method for automotive body frames. J. Mech. Des. 2005, 127, 49–57. [Google Scholar] [CrossRef]
- Hou, W.; Wang, Z.; Zhang, W.; Zhang, H. Optimization design for auto-body beam section based on complex engineering constraints. J. Mech. Eng. 2014, 50, 127–133. [Google Scholar] [CrossRef]
- Cui, X.; Zhang, H.; Wang, S.; Zhang, L.; Ko, J. Design of lightweight multi-material automotive bodies using new material performance indices of thin-walled beams for the material selection with crashworthiness consideration. Mater. Des. 2011, 32, 815–821. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, Z.; Zhou, C.; Wang, W. Optimization of circular-axis flexure hinge by considering material selection and geometrical configuration simultaneously. J. Mech. Eng. 2017, 53, 46–57. [Google Scholar] [CrossRef]
- Cui, A.; Zhang, H.; Yu, D.; Zhang, S.; Yang, Y. A study on material selection for multi-material autobody components based on PSI method. Automot. Eng. 2018, 40, 239–244+233. [Google Scholar]
- Zhao, Y.; Li, Y.; Chen, D.; Hou, W. Optimization Design Method of Multi-Material Car Body Structure Based on Modified Graphic Decomposition. Available online: https://www.webofscience.com/wos/alldb/full-record/CSCD:6721999 (accessed on 30 August 2021).
- Hou, Y.; Zhang, Y.; Liu, T. Optimization of standard cross-section type selection in steel frame structures based on gradient methods. Eng. Mech. 2013, 30, 454–462. [Google Scholar]
- Kaveh, A.; Hosseini, S.M.; Zaerreza, A. Improved shuffled Jaya algorithm for sizing optimization of skeletal structures with discrete variables. Structures 2021, 29, 107–128. [Google Scholar] [CrossRef]
- Degertekin, S.O.; Minooei, M.; Santoro, L.; Trentadue, B.; Lamberti, L. Large-scale truss-sizing optimization with enhanced hybrid HS algorithm. Appl. Sci. 2021, 11, 3270. [Google Scholar] [CrossRef]
- Xing, G.; Sun, Z.; Cui, X.; Wu, W.; Jia, P.; Jia, Z. Topological Optimization Design of Aero-Engine Support Structure under Multiple Loading Conditions. Available online: https://www.webofscience.com/wos/alldb/full-record/CSCD:6884473 (accessed on 30 August 2021).
- Ding, M.; Geng, D.; Zhou, M.; Lai, X. Topology optimization strategy of structural strength based on variable density method. J. Shanghai Jiaotong Univ. 2021, 55, 764–773. [Google Scholar]
- Picelli, R.; Townsend, S.; Brampton, C.; Norato, J.; Kim, H. Stress-based shape and topology optimization with the level set method. Comput. Meth. Appl. Mech. Eng. 2018, 329, 1–23. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, X.; Wang, F. Topology optimization design of the bracket of a special vehicle based on FEA method. In Proceedings of the 2010 Second International Conference on Computational Intelligence and Natural Computing (CINC 2010), Wuhan, China, 13–14 September 2010; pp. 352–355. [Google Scholar]
- Chen, X.; Zhao, K.; Shen, C.; Zheng, K.; Lü, W. Topological Analysis and a Parametric Optimization Method for Aluminum Alloy Frame Body of Electric Vehicle. Available online: https://www.webofscience.com/wos/alldb/full-record/CSCD:6824257 (accessed on 30 August 2021).
- Kober, M.; Kühhorn, A.; Rademann, J.; Mück, B. Nonlinear topology optimization of centrifugally loaded aero-engine part with newly developed optimality-criteria based algorithm. Aerosp. Sci. Technol. 2014, 39, 705–711. [Google Scholar] [CrossRef]
- Yang, J.G.; Zhang, W.H.; Zhu, J. Optimal design of aero-engine stator structure with combined shape and topology optimization method. Mater. Sci. Forum. 2012, 1441, 623–626. [Google Scholar] [CrossRef]
- Tong, X.; Ge, W.; Gao, X.; Li, Y. Optimization of combining fiber orientation and topology for constant-stiffness composite laminated plates. J. Optim. Theory Appl. 2019, 181, 653–670. [Google Scholar] [CrossRef]
- Zhan, J.; Qin, Y.; Liu, M. Topological Design of Orthotropic Material Compliant Mechanisms Considering Variable Fiber Angle. Available online: https://oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CAPJ&dbname=CAPJLAST&filename=JXKX2021061000H&v=71l%25mmd2FrpOgPQe%25mmd2FKnRykBkh6qlngqWHUPsifvaU%25mmd2F6hoRHnoSON5jHQ3OqbSY%25mmd2Bd8QFdF (accessed on 30 August 2021).
- Chen, F.; Zhang, W.; Ye, D. Typical additive manufacturing joint design in civil aircrafts. Available online: https://oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2021&filename=YYLX202103028&v=rZj4GQjzvwxqTa%25mmd2BL4M4l9ZW0Xl%25mmd2Fi3K6bYFFr5QEPPM4D3aWKWJn6DLYj3Wi5ZAwc (accessed on 30 August 2021).
- Yan, M.; Tian, X.; Peng, G.; Li, D.; Yao, R.; Zhang, W.; Bai, R.; Meng, W. Performance Study of Lightweight Composites Equipment Section Support Fabricated by Selective Laser Sintering. Available online: http://www.cjmenet.com.cn/CN/Y2019/V55/I13/144 (accessed on 30 August 2021).
- Zhang, X. The Complex Interpolation Approach to Analysis of the Planar Motion of Rigid Bodies. Available online: https://oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2019&filename=DXWL201901002&v=oJ4RN9i2Lsp399gicG4Y20zdGmxcL4SLG%25mmd2B5zFM81vwlOaVKM%25mmd2FTal3kN3CZh6Rl9L (accessed on 30 August 2021).
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Fuzzy adaptive particle swarm optimization. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001; pp. 101–106. [Google Scholar]
- Wang, D.; Shen, H.; Sun, Y.; Dong, H.; Ma, Y. A novel approach for conceptual structural design of complex machine elements. J. Mech. Eng. 2016, 52, 152–163. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Lü, X. Control and Simulation of Robotic Arm System of Intelligent Sanitation Vehicle. Available online: https://oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CPFD&dbname=CPFDLAST2021&filename=ZGZN202011001048&v=Q7FS4XFR%25mmd2BG4Tb7oQsGIvtVN8qh5towQwpfrJytHAoT4%25mmd2BgRst1wWVbxKOAKiDukwEHtdAwf%25mmd2FRmMU%3d (accessed on 30 August 2021).
- Zhang, Z.; Li, H. The method of truss structure layout discrete variable optimization based on ant colony optimization. Chin. J. Comput. Mech. 2013, 30, 336–342. [Google Scholar]
- Liu, D.; Wang, Y.; Tong, Y.; Tong, Y.; Luo, Y.; Chen, W.; Tan, Z. Properties and disposal countermeasures of sorting waste. Environ. Sanitation Eng. 2013, 21, 27–30. [Google Scholar]













| Parameter | Initial Design Scheme 1 | Optimization Scheme A 2 | Optimization Scheme B 3 |
|---|---|---|---|
| (mm) | 120 | 130 | 148 |
| (mm) | 150 | 157 | 210 |
| (s) | 2 | 3.45 | 3.36 |
| (W) | 3764.17 | 2028.33 | 1936.71 |
| (W) | 1817.43 | 1028.25 | 1115.82 |
| (N) | 2442.92 | 722.22 | 349.32 |
| Load | Definition |
|---|---|
| , | The force of the driven sprocket assembly acting on the truss structure. |
| , | The force of the groove wheels acting on the track. |
| , | The friction force of the groove wheels acting on the track. |
| , | The force of the drive sprocket assembly acting on the truss structure. |
| The gravity of the hydraulic motor. | |
| The torque of the hydraulic motor acting on the truss structure. |
| (kg) | |||||||
|---|---|---|---|---|---|---|---|
| 148 | 210 | 68.5 | 383.65 | 308.84 | 1720 | 320.35 | 0.1 |
| Load Case | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Load case A | 5160.07 | 5160.07 | 3379.75 | 337.97 | 337.97 | 3379.75 | 2335.97 | 2335.97 | 342.02 | 716.12 |
| Load case B | 15,041.05 | 15,041.05 | 5721.5 | 572.15 | 57.08 | 570.75 | 7276.46 | 7276.46 | 342.02 | 2178.05 |
| Load case C | 3620.2 | 3620.2 | 2169.76 | 0 | 0 | 280.14 | 2149.46 | 2149.46 | 342.02 | 660.46 |
| Part Number | Initial Design Scheme 1 (mm) | Optimization Scheme A (mm) | Optimization Scheme B (mm) | Optimization Scheme C (mm) |
|---|---|---|---|---|
| 1 | 5.0 | 5.0 | 5.0 | 5.0 |
| 2 | 5.0 | 1.0 | 1.0 | 1.0 |
| 3 | 4.0 | 1.5 | 10.0 | 10.0 |
| 4 | 5.0 | 1.0 | 2.0 | 2.0 |
| 5 | 3.0 | 1.0 | 1.0 | 1.0 |
| 6 | 4.0 | 10.0 | 10.0 | 10.0 |
| 7 | 5.0 | 1.5 | 10.0 | 9.0 |
| 8 | 3.0 | 2.0 | 10.0 | 10.0 |
| 9 | 4.0 | 1.0 | 10.0 | 10.0 |
| 10 | 3.0 | 1.0 | 1.0 | 1.0 |
| 11 | 4.0 | 4.5 | 9.5 | 10.0 |
| 12 | 4.0 | 1.0 | 10.0 | 5.5 |
| 13 | 5.0 | 3.0 | 8.0 | 4.5 |
| 14 | 5.0 | 4.5 | 4.5 | 4.5 |
| 15 | 5.0 | 1.0 | 1.0 | 1.0 |
| 16 | 5.0 | 1.0 | 6.0 | 5.0 |
| 17 | 4.0 | 2.5 | 10.0 | 10.0 |
| 18 | 5.0 | 3.5 | 3.0 | 3.0 |
| 19 | 5.0 | 1.0 | 9.5 | 1.5 |
| 20 | 5.0 | 2.0 | 9.5 | 1.5 |
| 21 | 5.0 | 3.5 | 3.0 | 4.0 |
| 22 | 5.0 | 2.5 | 6.0 | 5.5 |
| 23 | 3.0 | 3.0 | 2.5 | 3.5 |
| Performance | Initial Design Scheme | Optimization Scheme A | Optimization Scheme B | Optimization Scheme C |
|---|---|---|---|---|
| (kg) | 72.05 | 58.37 | 71.72 | 65.77 |
| (Hz) | 10.20 | 10.38 | 16.92 | 16.43 |
| (mm) | 1.10 | 1.75 | 0.93 | 1.08 |
| (mm) | 2.19 | 3.41 | 1.98 | 2.39 |
| (mm) | 0.77 | 1.51 | 0.64 | 0.77 |
| (MPa) | 218.16 | 273.30 | 216.47 | 222.75 |
| (MPa) | 646.09 | 666.74 | 573.67 | 575.12 |
| (MPa) | 202.37 | 322.62 | 128.29 | 226.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Li, Y.; Xu, X.; Chen, X. On the Lightweight Truss Structure for the Trash Can-Handling Robot. Actuators 2021, 10, 214. https://doi.org/10.3390/act10090214
Chen J, Li Y, Xu X, Chen X. On the Lightweight Truss Structure for the Trash Can-Handling Robot. Actuators. 2021; 10(9):214. https://doi.org/10.3390/act10090214
Chicago/Turabian StyleChen, Jiawei, Yan Li, Xiang Xu, and Xinbo Chen. 2021. "On the Lightweight Truss Structure for the Trash Can-Handling Robot" Actuators 10, no. 9: 214. https://doi.org/10.3390/act10090214
APA StyleChen, J., Li, Y., Xu, X., & Chen, X. (2021). On the Lightweight Truss Structure for the Trash Can-Handling Robot. Actuators, 10(9), 214. https://doi.org/10.3390/act10090214





