Segment Drift Control with a Supervision Mechanism for Autonomous Vehicles
Abstract
:1. Introduction
- (1)
- A segment drift control strategy is designed. The depot approach section ensures that the vehicle enters the drift state when it reaches the drift trigger point. Drift in depot ensures that vehicles can complete the drift in operation with high precision.
- (2)
- The drift monitoring strategy is proposed, including a path planning monitoring strategy, a drift-triggered state monitoring strategy, and a drift process monitoring strategy. Since the drift results are greatly affected by external disturbance factors, the proposed monitoring strategy can increase the success rate of drifts and ensure the safety and integrity of the test.
- (3)
- Based on Simulink and CarSim, simulation experiments are carried out to verify the drift parking and monitoring strategy. Actual vehicle verification is carried out to provide the basis for the research under typical limit conditions.
2. The Location Approaching Process
2.1. Path Planning
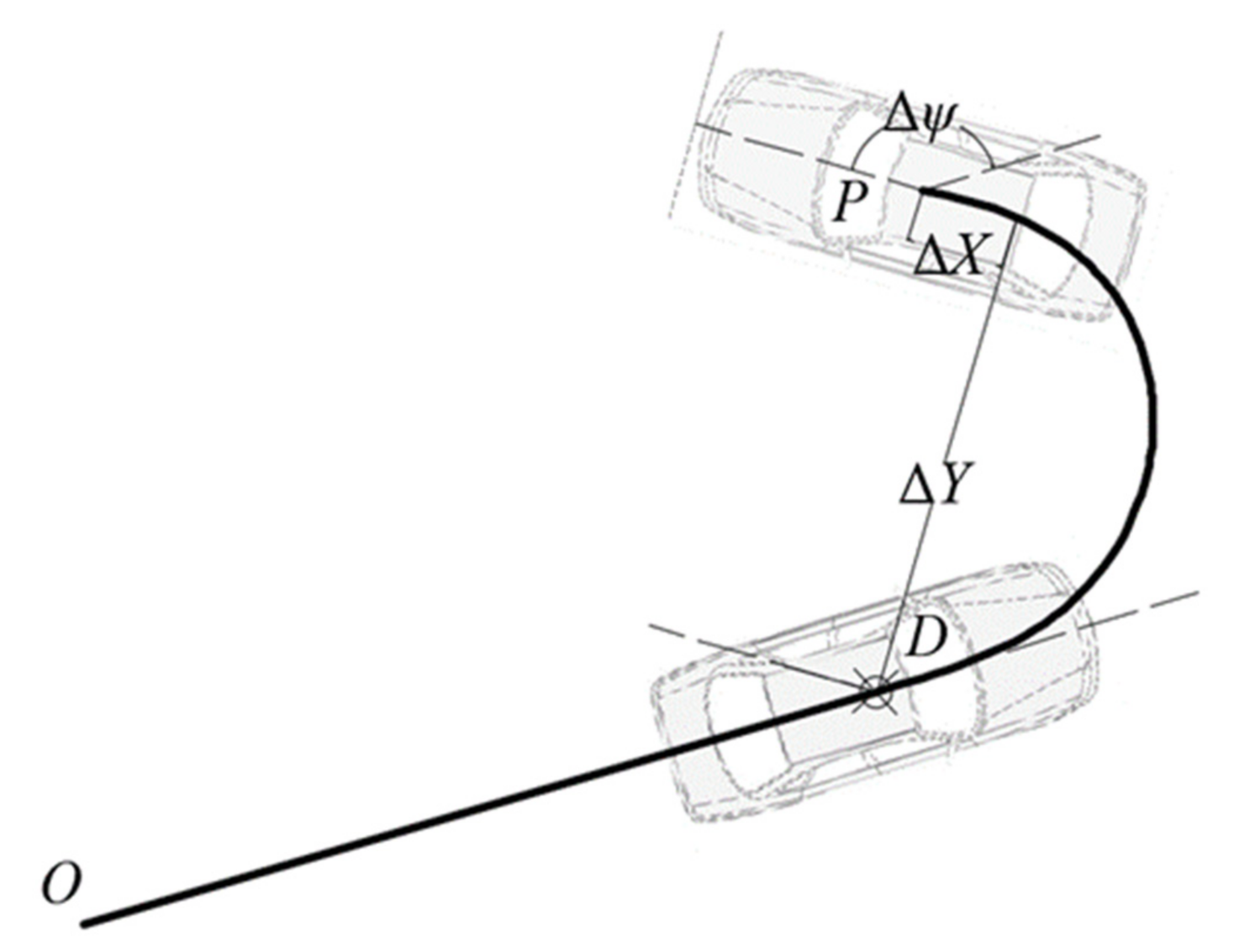
2.2. Trajectory Tracking
3. The Process of Drift Parking
3.1. Drift Open-Loop Control
3.2. Design of Drift Trigger Conditions
- (1)
- Begin by calculating the distance between the current vehicle position coordinates and the drift trigger point , . Compare this with the distance obtained previously, to determine if , and . The result indicates whether the vehicle meets the position condition triggered by drift.
- (2)
- Calculate whether the difference between the actual speed and the expected speed, is less than . If , the vehicle meets the speed condition triggered by a drift.
- (3)
- Calculate whether the difference between the actual heading angle and the expected heading angle, is less than . If , the vehicle meets the heading angle condition triggered by drift.
- (4)
- Judge whether the current steering wheel angle exceeds the limit value. If , it means that the vehicle meets the yaw motion condition triggered by drift.
4. Monitoring Strategy
4.1. Supervision Strategy of the Path Planning Algorithm
- (1)
- Maximum curvature constraint: The minimum radius of the path should be greater than the minimum turning radius of the vehicle while satisfying the corner constraint of the path-following controller.
- (2)
- Maximum attachment constraint: The tire force should be less than the maximum tire force provided by the road surface at the maximum curvature of the constrained path, and also less than the tire force provided at the larger curvature when running at the maximum speed, so as to avoid wheel slip.
- (3)
- Longitudinal velocity constraint: The planned path should be long enough to allow the vehicle to accelerate at the maximum acceleration and reach the desired drift longitudinal speed at the drift trigger point.
4.2. Drift Process Monitoring Strategy
- (1)
- Tire characteristics: Tire wear occurs in the process of lock slip, which leads to the change of tire characteristics. The change of tire force will directly affect the corresponding relationship between the steering wheel angle input and the drift trajectory output, so that the actual drift trajectory does not match the expected trajectory.
- (2)
- Road conditions: Due to the influence of temperature and humidity, the adhesion condition of the road surface may differ between the tail-flick test and the drift test, which changes the tire force under the same load and slip rate.
- (3)
- Vehicle status: Changes in the vehicle load size and distribution lead to changes in vehicle mass and the centroid position, which affects the tire force.
5. Simulation and Ground Test
5.1. Simulation Test of Drift Whole Process Control
- (1)
- Working condition setting:
- (2)
- Parameter setting:
- (3)
- Simulation test results:
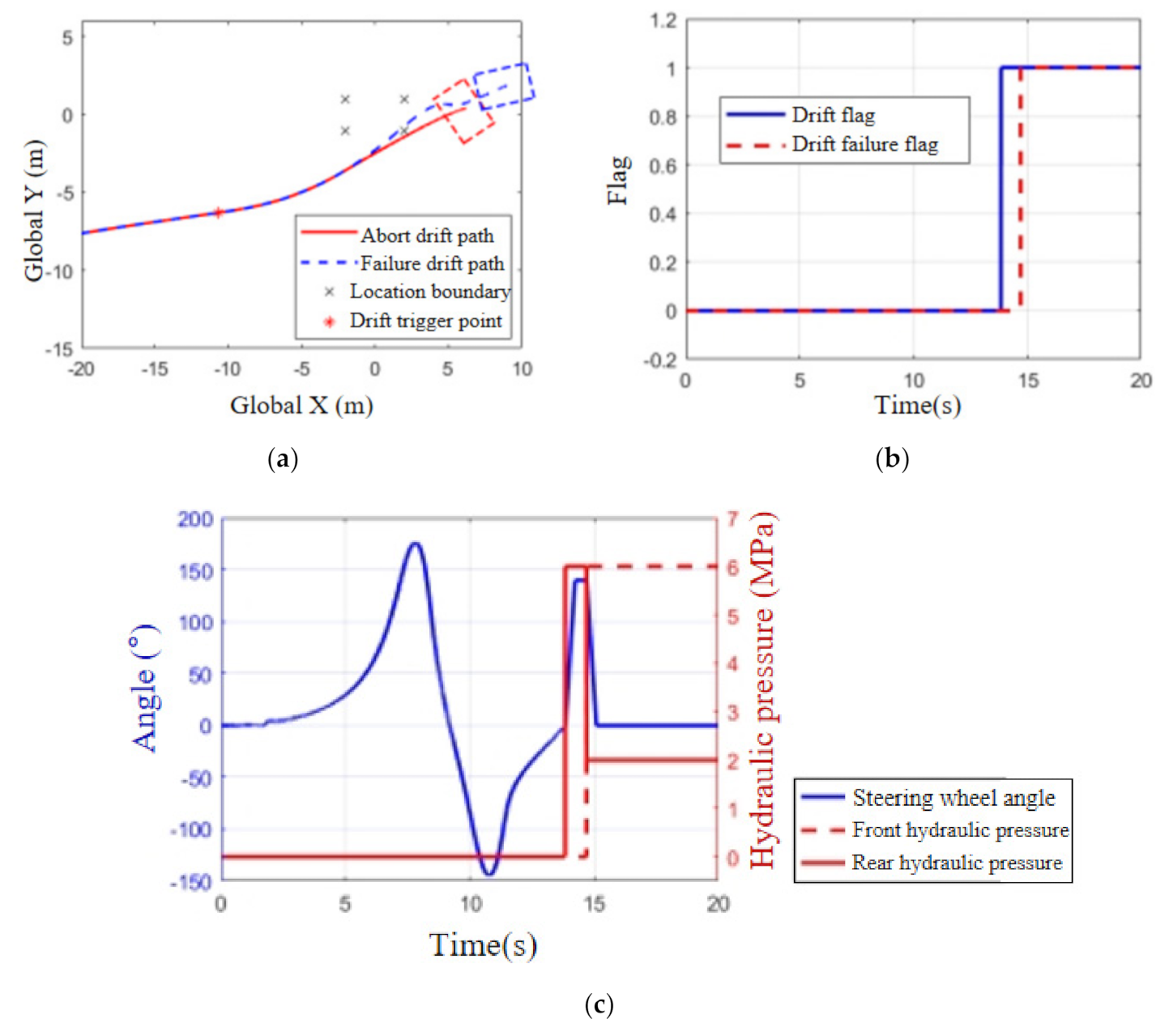
5.2. Function Verification of Monitoring Strategy
5.3. Ground Test
6. Discussion and Conclusions
- (1)
- Through the combination of path planning, path tracking, and an open-loop control algorithm, it can realize the action of the driverless vehicle drifting into the warehouse, which demonstrates the potential of further research on driverless vehicle under extreme conditions.
- (2)
- The segmented drift control strategy is designed to make the vehicle complete a drift during its approach of the warehouse. In order to ensure that there are no major changes to the vehicle road system, the open-loop control rate can effectively complete the drift.
- (3)
- The realization of the whole drift process requires the initial state of the vehicle and the vehicle path system to be consistent with the acquisition path, which leads to the low success rate of drift parking. Constraints on the planned path and drift trigger state can significantly improve the success rate of drift storage. The monitoring strategy of the drift process can also ensure the integrity and safety of the test.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, F. Trajectory Planning and Motion Control for Extreme Maneuvers of Autonomous Vehicles. Ph.D. Thesis, Tsinghua University, Beijing, China, 2018. [Google Scholar]
- Goh, J.Y.; Goel, T.; Gerdes, J.C. A controller for automated drifting along complex trajectories. In Proceedings of the 14th International Symposium on Advanced Vehicle Control (AVEC 2018), Beijing, China, 14–18 September 2018; pp. 1–6. [Google Scholar]
- Alcala, E.; Puig, V.; Quevedo, J.; Escobet, T.; Comasolivas, R. Autonomous vehicle control using a kinematic Lyapunov-based technique with LQR-LMI tuning. Control Eng. Pract. 2018, 73, 1–12. [Google Scholar] [CrossRef]
- Tagne, G.; Talj, R.; Charara, A. Higher-order sliding mode control for lateral dynamics of autonomous vehicles, with experimental validation. In Proceedings of the IEEE Intelligent Vehicles Symposium, Gold Coast, QLD, Australia, 23–26 June 2013; pp. 678–683. [Google Scholar]
- Hu, C.; Wang, R.; Yan, F. Integral Sliding Mode-Based Composite Nonlinear Feedback Control for Path Following of Four-Wheel Independently Actuated Autonomous Vehicles. IEEE Trans. Transp. Electrif. 2016, 2, 221–230. [Google Scholar] [CrossRef]
- Funke, J.; Brown, M.; Erlien, S.M.; Gerdes, J.C. Collision Avoidance and Stabilization for Autonomous Vehicles in Emergency Scenarios. IEEE Trans. Control Syst. Technol. 2017, 25, 1204–1216. [Google Scholar] [CrossRef]
- Liu, K.; Gong, J.; Kurt, A.; Chen, H.; Ozguner, U. Dynamic Modeling and Control of High-Speed Automated Vehicles for Lane Change Maneuver. IEEE Trans. Intell. Veh. 2018, 3, 329–339. [Google Scholar] [CrossRef]
- Guo, J.; Luo, Y.; Li, K.; Dai, Y. Coordinated path-following and direct yaw-moment control of autonomous electric vehicles with sideslip angle estimation. Mech. Syst. Signal Process. 2018, 105, 183–199. [Google Scholar] [CrossRef]
- Kim, E.; Kim, J.; Sunwoo, M. Model predictive control strategy for smooth path tracking of autonomous vehicles with steering actuator dynamics. Int. J. Automot. Technol. 2014, 15, 1155–1164. [Google Scholar] [CrossRef]
- Velenis, E.; Katzourakis, D.; Frazzoli, E.; Tsiotras, P.; Happee, R. Steady-state drifting stabilization of RWD vehicles. Control Eng. Pract. 2011, 19, 1363–1376. [Google Scholar] [CrossRef]
- Nakano, H.; Kinugawa, J.; Kosuge, K. Control of a four-wheel independently driven electric vehicle with a large sideslip angle. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics (ROBIO 2014), Bali, Indonesia, 5–10 December 2014; pp. 265–270. [Google Scholar]
- Goh, J.Y.; Gerdes, J.C. Simultaneous stabilization and tracking of basic automobile drifting trajectories. In Proceedings of the IEEE Intelligent Vehicles Symposium, Gothenburg, Sweden, 19–22 June 2016; pp. 597–602. [Google Scholar]
- Jelavic, E.; Gonzales, J.; Borrelli, F. Autonomous Drift Parking using a Switched Control Strategy with Onboard Sensors. IFAC-PapersOnLine 2017, 50, 3714–3719. [Google Scholar] [CrossRef]
- Kolter, J.Z.; Plagemann, C.; Jackson, D.T.; Ng, A.; Thrun, S. A probabilistic approach to mixed open-loop and closed-loop control, with application to extreme autonomous driving. In Proceedings of the IEEE International Conference on Robotics Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 839–845. [Google Scholar]
- Kolter, J.Z. Learning and Control with Inaccurate Models; Stanford University: San Francisco, CA, USA, 2010. [Google Scholar]
- Sakurama, K.; Nakano, K. Path tracking control of Lagrange systems with obstacle avoidance. Int. J. Control Autom. Syst. 2012, 10, 50–60. [Google Scholar] [CrossRef]
- Rosolia, U.; De Bruyne, S.; Alleyne, A.G. Autonomous vehicle control: A nonconvex approach for obstacle avoidance. IEEE Trans. Control Syst. Technol. 2016, 25, 469–484. [Google Scholar] [CrossRef]
- Gong, J.; Liu, K.; Qi, J. Model Predictive Control for Self-Driving Vehicles, 2nd ed.; Beijing Institute of Technology Press: Beijing, China, 2019; pp. 89–90. [Google Scholar]
- Zhang, F.; Gonzales, J.; Li, S.; Borrelli, F.; Li, K. Drift control for cornering maneuver of autonomous vehicles. Mechatronics 2018, 54, 167–174. [Google Scholar] [CrossRef]
- Gonzales, J.M. Planning and Control of Drift Maneuvers with the Berkeley Autonomous Race Car. Ph.D. Thesis, University of California, Berkeley/San Francisco, CA, USA, 2018. [Google Scholar]
- Lau, T.K. Learning autonomous drift parking from one demonstration. In Proceedings of the 2011 IEEE International Conference on Robotics Biomimetics, Karon Beach, Thailand, 7–11 December 2011; pp. 1456–1461. [Google Scholar]






| Symbols | Definitions |
|---|---|
| Vehicle heading angle | |
| Vehicle front wheel angle | |
| Vehicle speed | |
| Wheel base | |
| System reference input | |
| Vehicle reference status | |
| Sampling time | |
| Weight matrix | |
| Weight matrix | |
| Prediction time domain | |
| Control time domain | |
| Weight coefficient | |
| Relaxation factor | |
| Dimension of state quantity | |
| System reference input minimum | |
| System reference input maximum | |
| Drift trigger point position | |
| Heading angle of drift trigger point | |
| Drift trigger distance threshold | |
| Drift trigger heading angle threshold | |
| Drift trigger speed threshold | |
| Distance from centroid to front axle | |
| Distance from centroid to rear axle |
| Parameter | Unit | Value | Parameter | Unit | Value |
|---|---|---|---|---|---|
| Vehicle mass | kg | 1412 | Vehicle length | m | 4.025 |
| Yaw moment of inertia | kg m2 | 1536.7 | Vehicle width | m | 1.916 |
| Wheel radius | m | 0.325 | Steering ratio | - | 2.91 |
| Centroid height | m | 0.54 | Wheelbase | m | 2.91 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Leng, B.; Xiong, L.; Yu, Y.; Yang, X. Segment Drift Control with a Supervision Mechanism for Autonomous Vehicles. Actuators 2021, 10, 219. https://doi.org/10.3390/act10090219
Liu M, Leng B, Xiong L, Yu Y, Yang X. Segment Drift Control with a Supervision Mechanism for Autonomous Vehicles. Actuators. 2021; 10(9):219. https://doi.org/10.3390/act10090219
Chicago/Turabian StyleLiu, Ming, Bo Leng, Lu Xiong, Yize Yu, and Xing Yang. 2021. "Segment Drift Control with a Supervision Mechanism for Autonomous Vehicles" Actuators 10, no. 9: 219. https://doi.org/10.3390/act10090219
APA StyleLiu, M., Leng, B., Xiong, L., Yu, Y., & Yang, X. (2021). Segment Drift Control with a Supervision Mechanism for Autonomous Vehicles. Actuators, 10(9), 219. https://doi.org/10.3390/act10090219






