A New Positioning Strategy Based on Parameter Tuning and Optimal Control Technique for Pneumatic Control Valve
Abstract
:1. Introduction
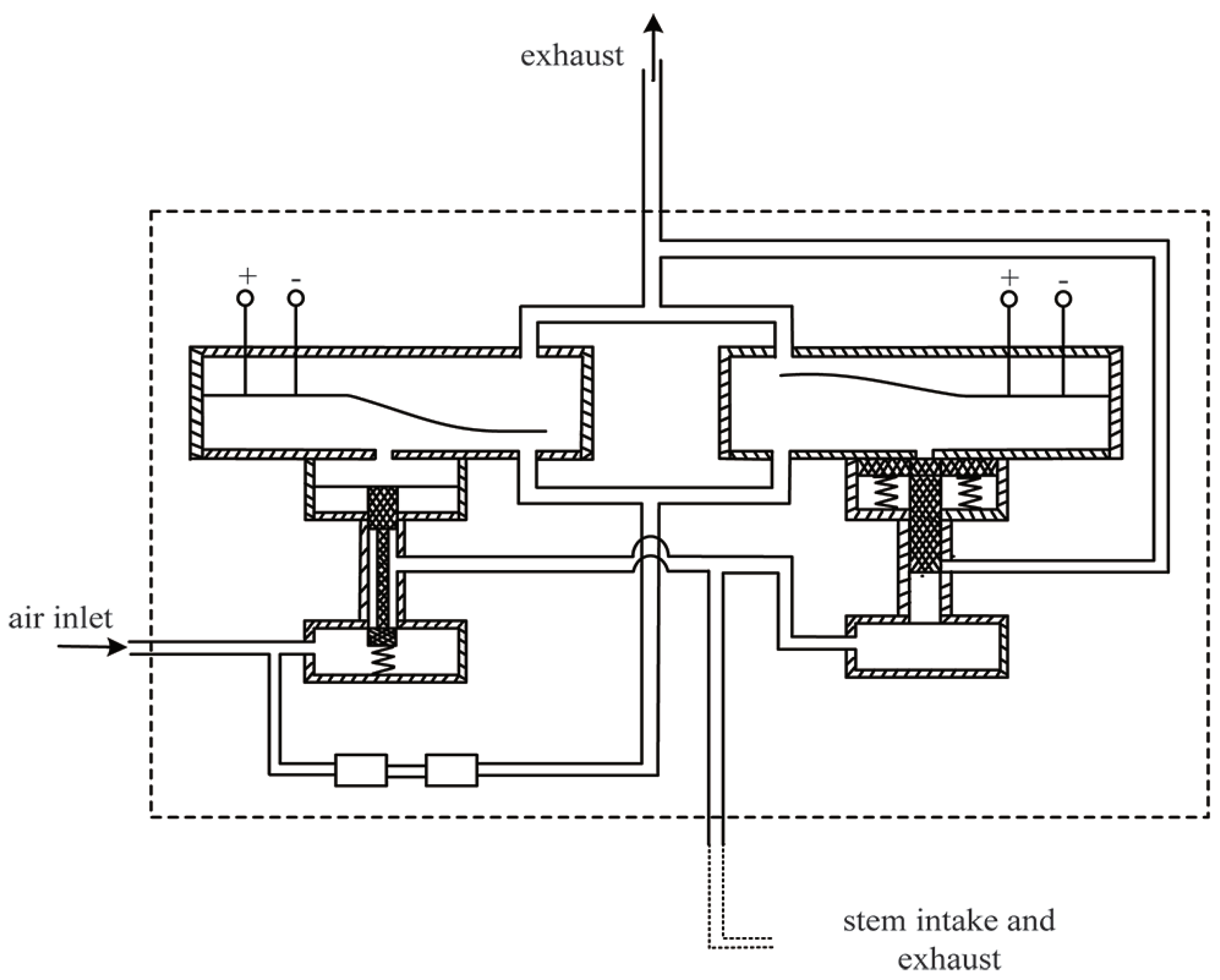
2. Modeling and Optimization Analysis of the Dynamics of Pneumatic Control Process
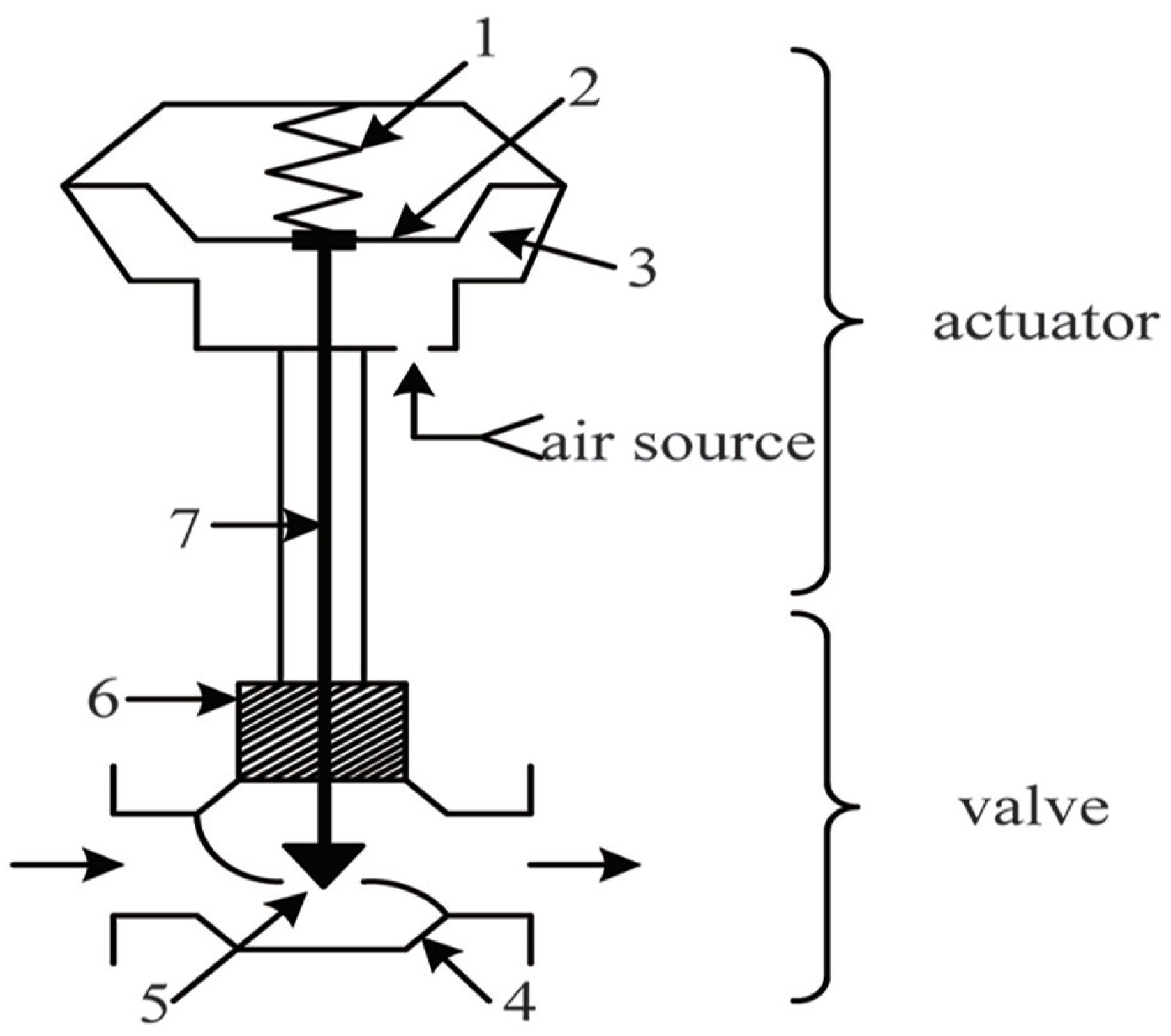
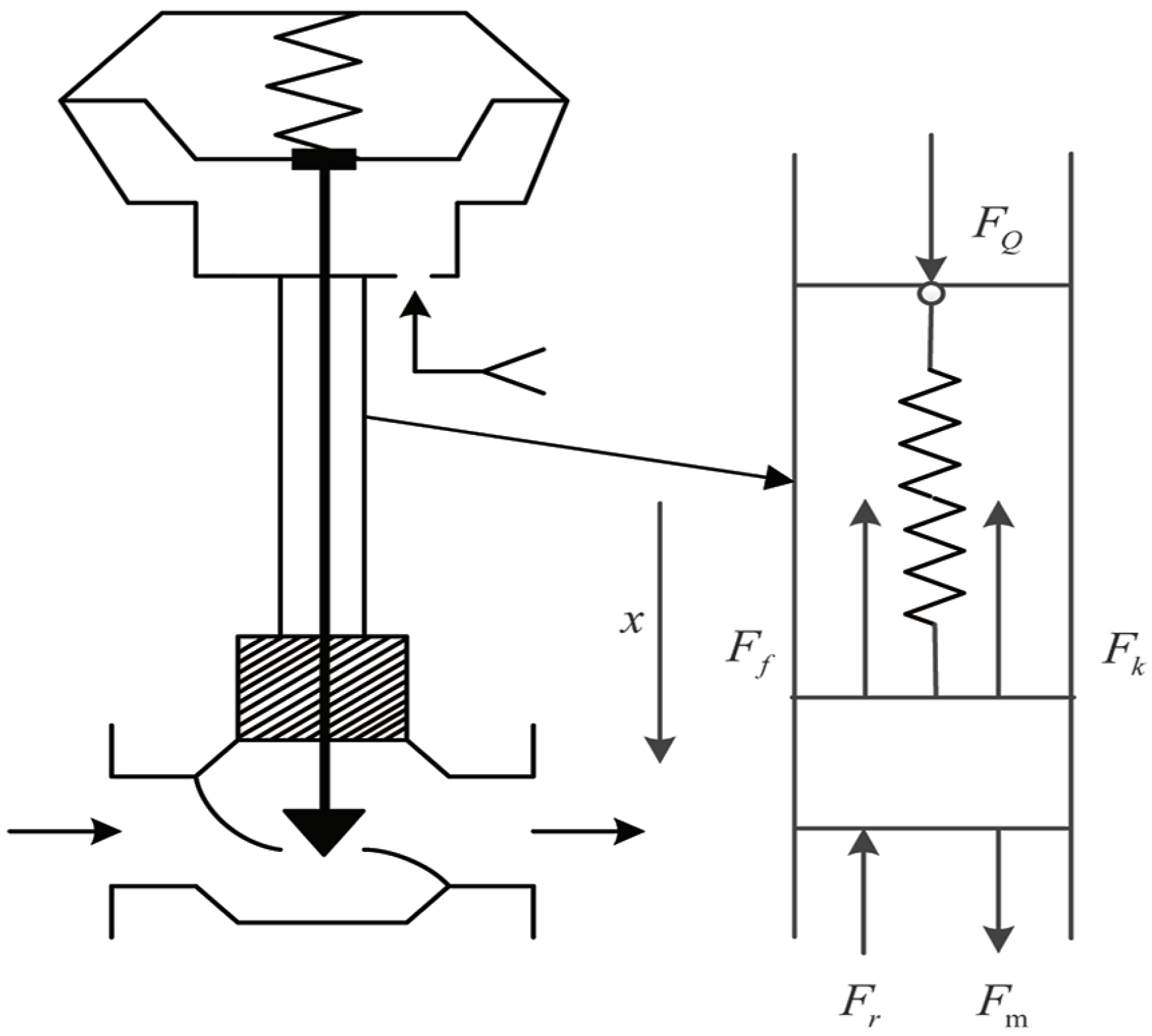
2.1. Dynamic Modeling of a Control Valve Pneumatic Actuator
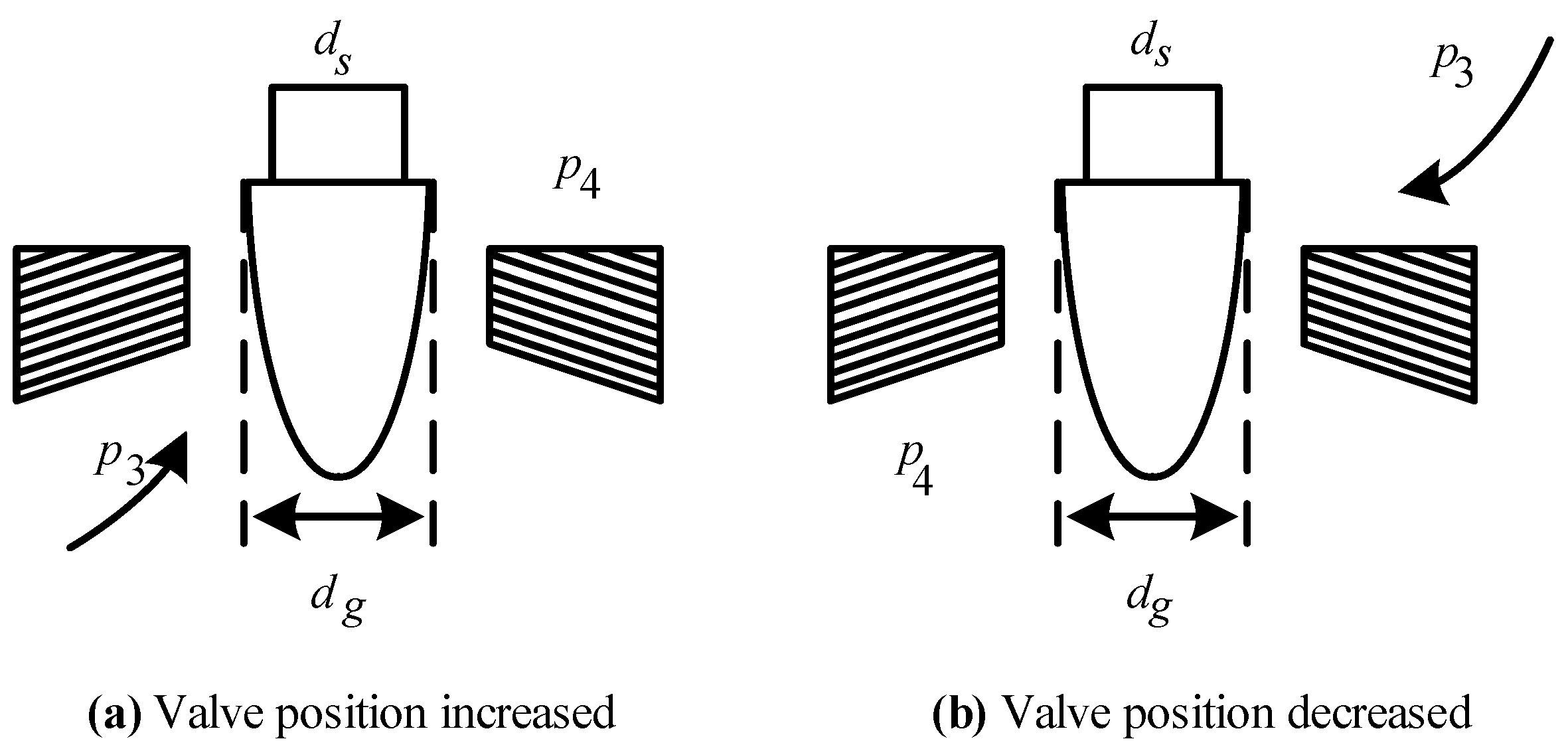
2.2. Optimization Analysis of the Dynamic Model
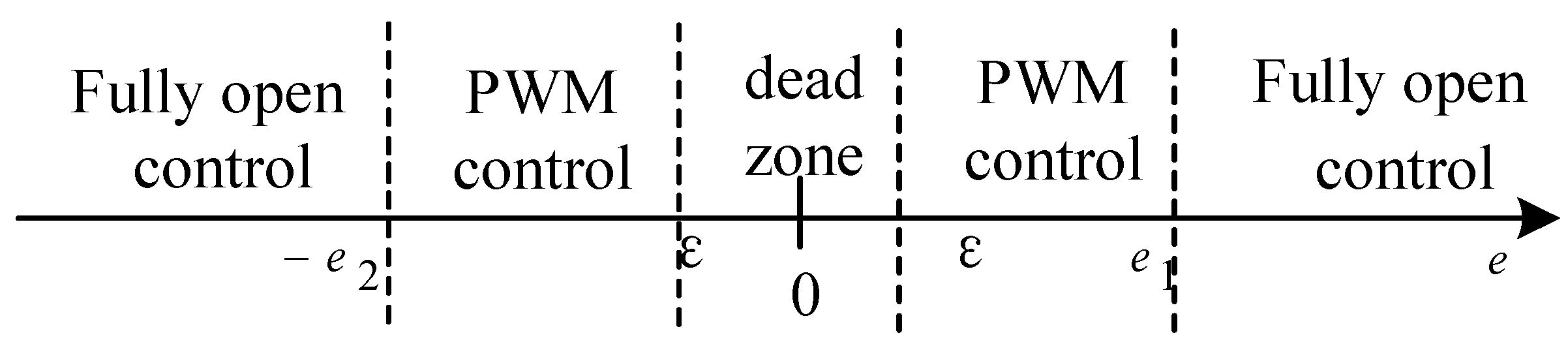
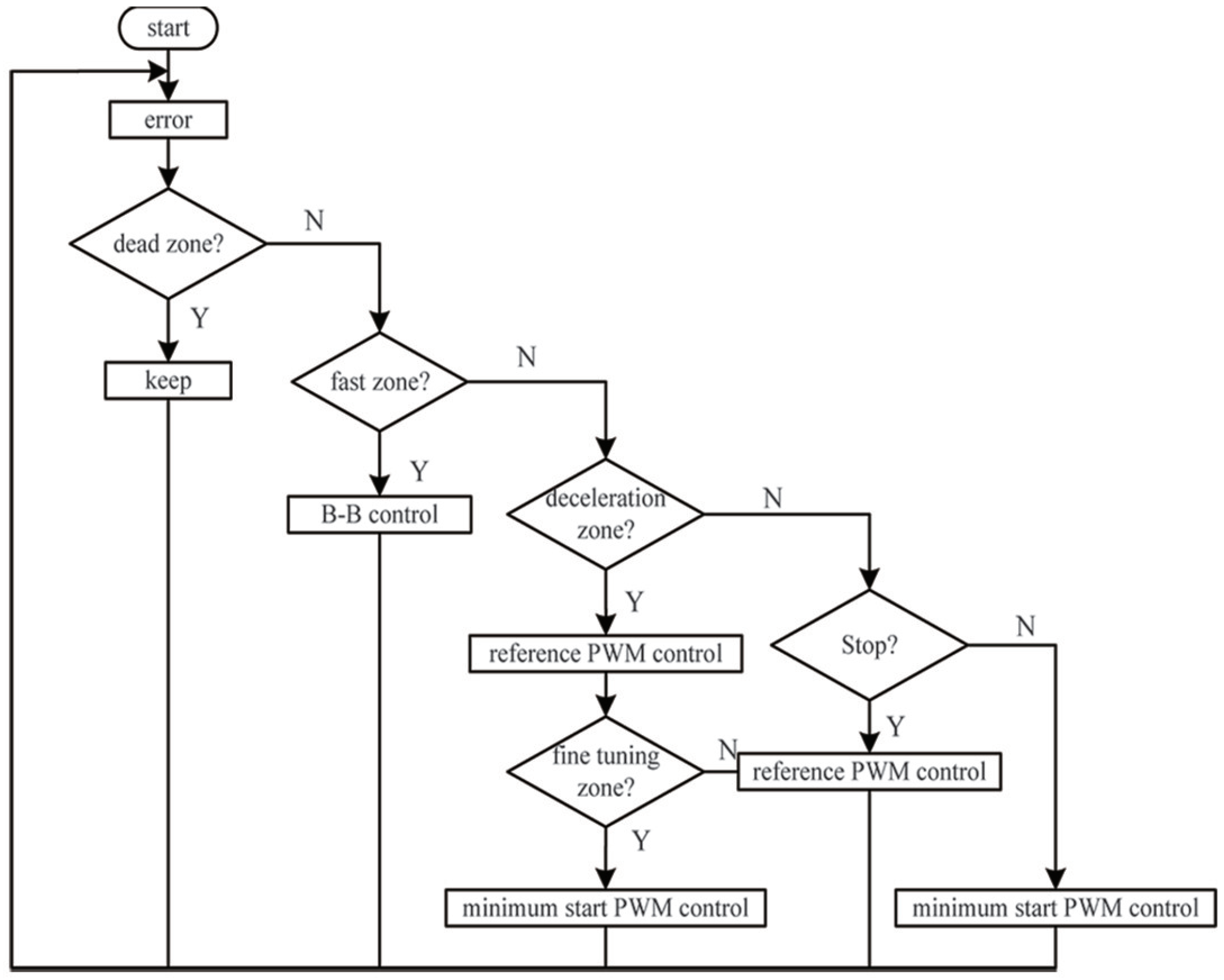
3. Five-Step Switch Control Strategy
- (1)
- When or , the valve positioner is controlled via the fully open intake valve or fully open exhaust valve. This can quickly intake or exhaust, and quickly reduce the error.
- (2)
- When or , the valve positioner uses the PWM control method. It adopts a suitable period and duty cycle to output the PWM. In this way, the actuator can be adjusted in a small range, and the error value can be slowly reduced.
- (3)
- When , the piezoelectric valve of the valve positioner is in a static state.
4. A Positioning Strategy Combining Parameter Tuning and Optimal Control
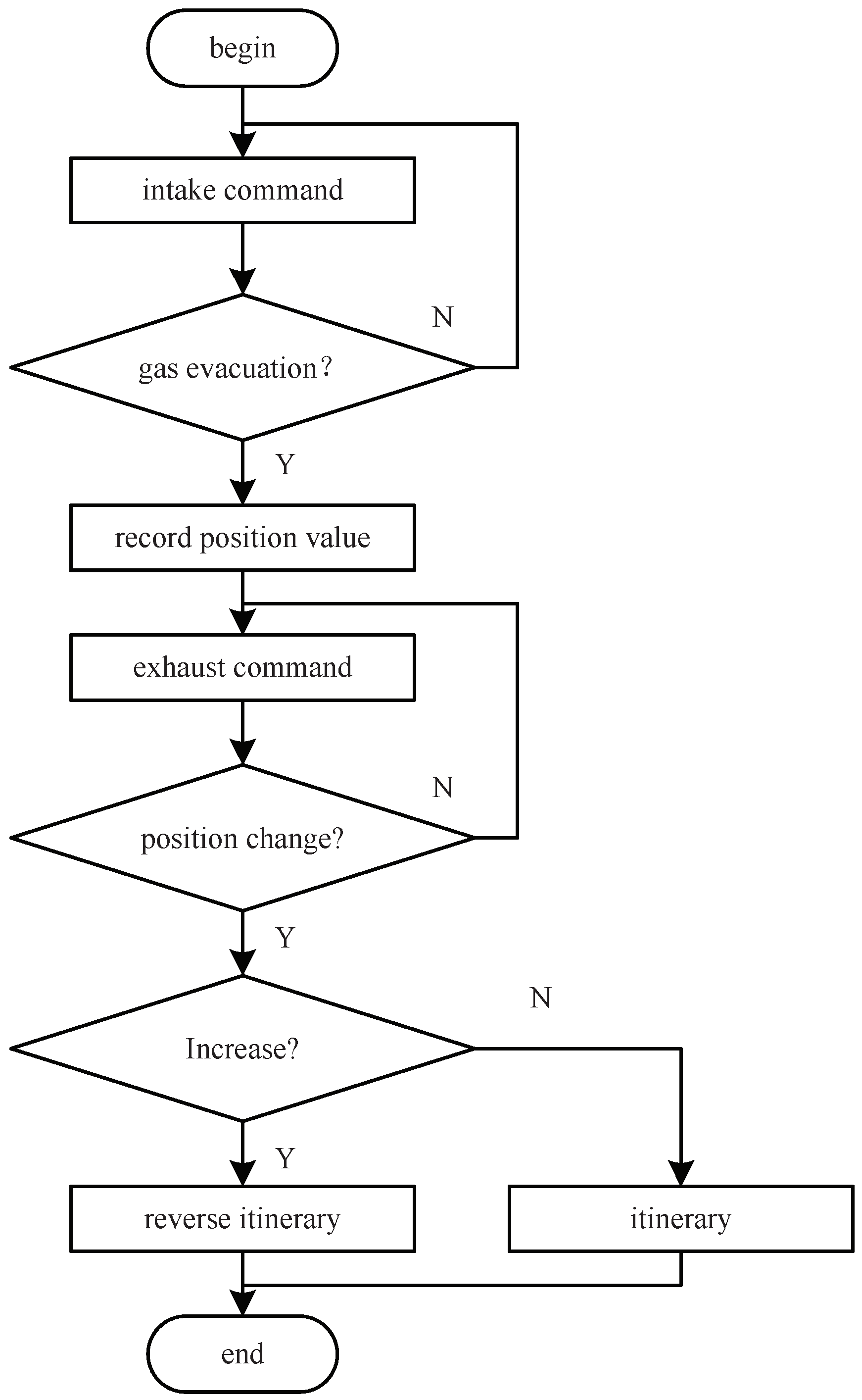
4.1. Self-Tuning of Pneumatic Control Valve Parameters
- Pneumatic control valve, stroke type;
- Minimal start pwm for pneumatic control valve;
- Maximum speed of the pneumatic control valve and its overshoot;
- Reference speed and reference speed pwm for the pneumatic control valve.
4.1.1. Pneumatic Control Valve—Stroke Type
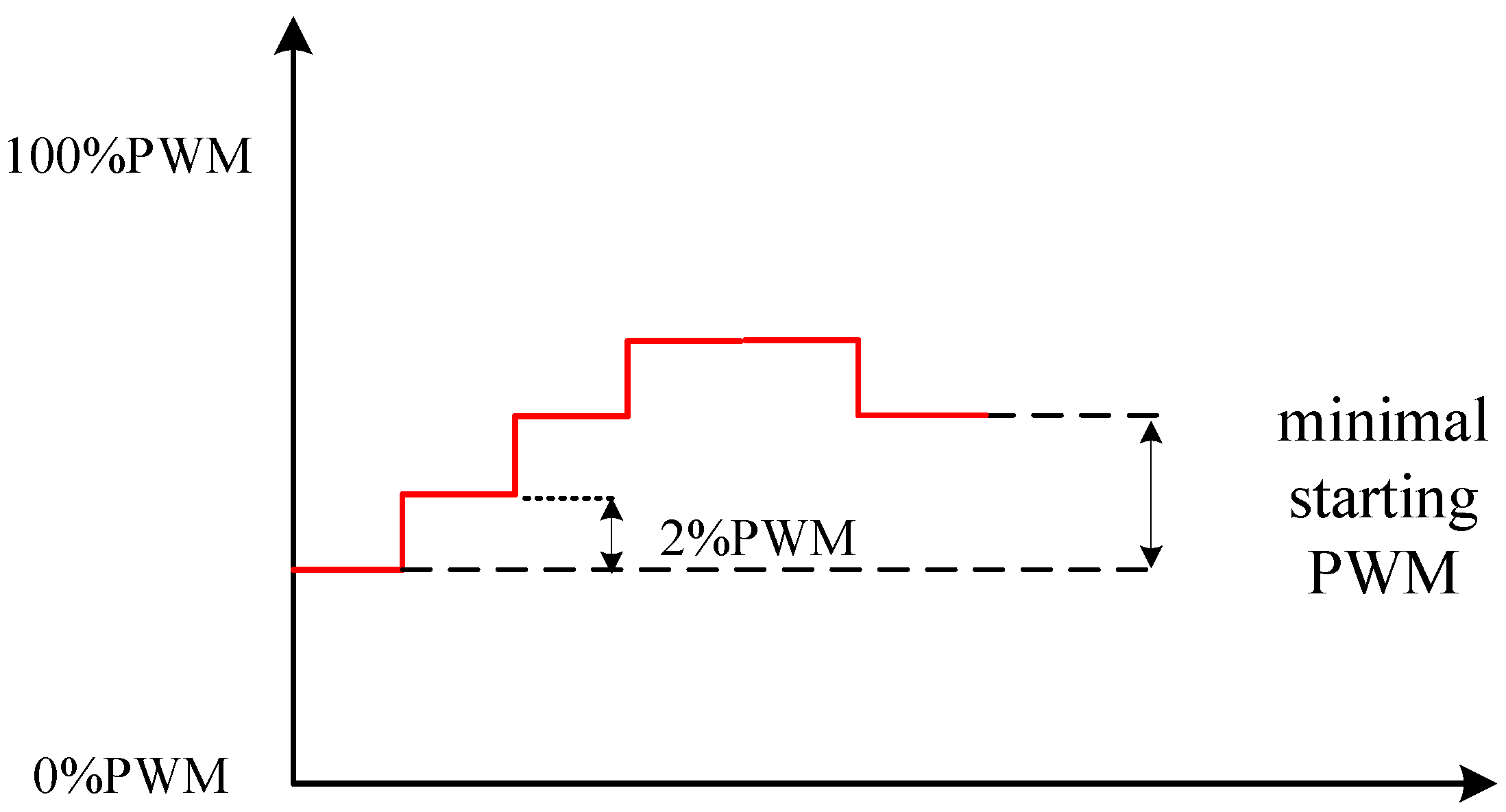
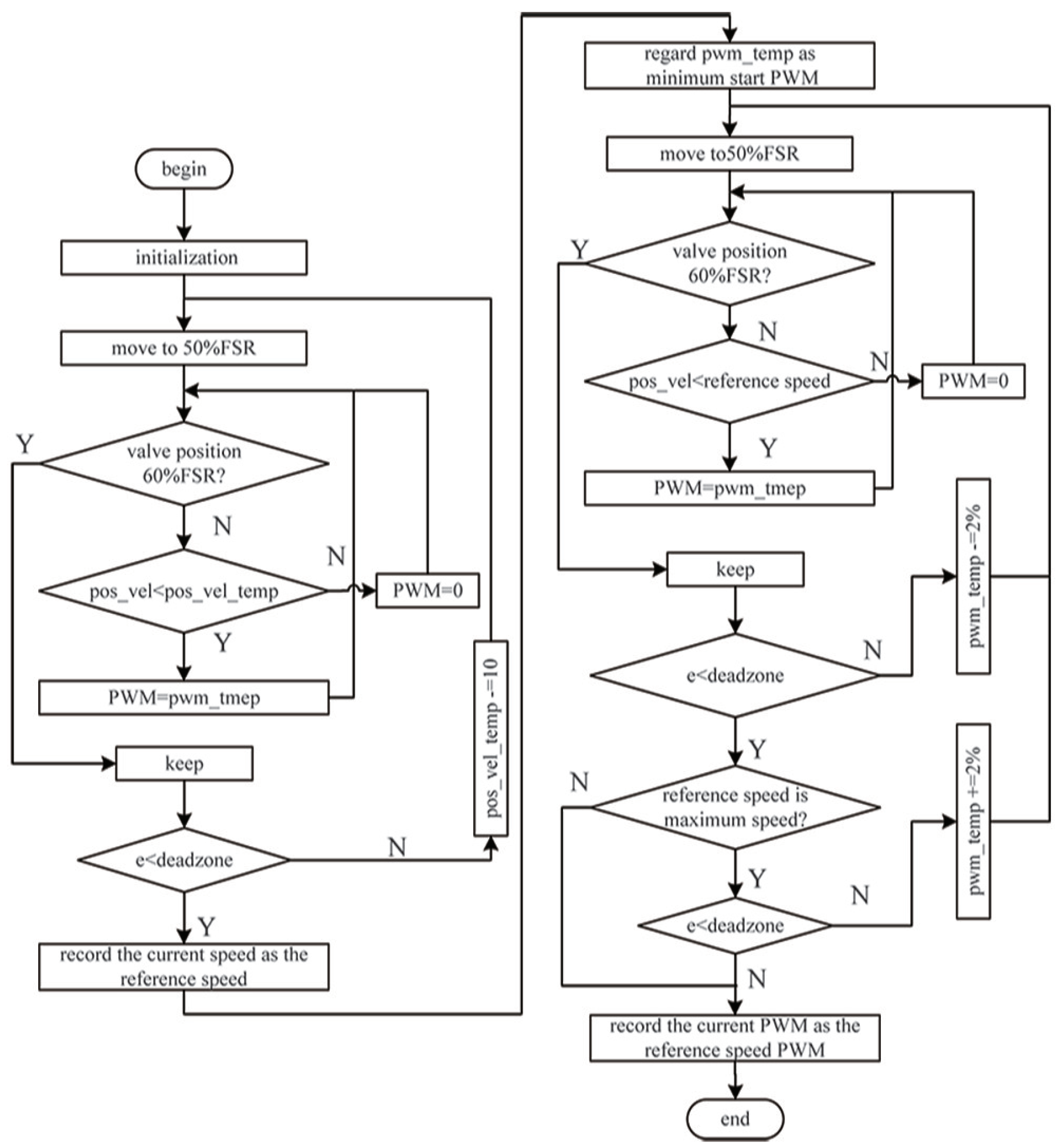
4.1.2. Minimal Start PWM for Pneumatic Control Valve
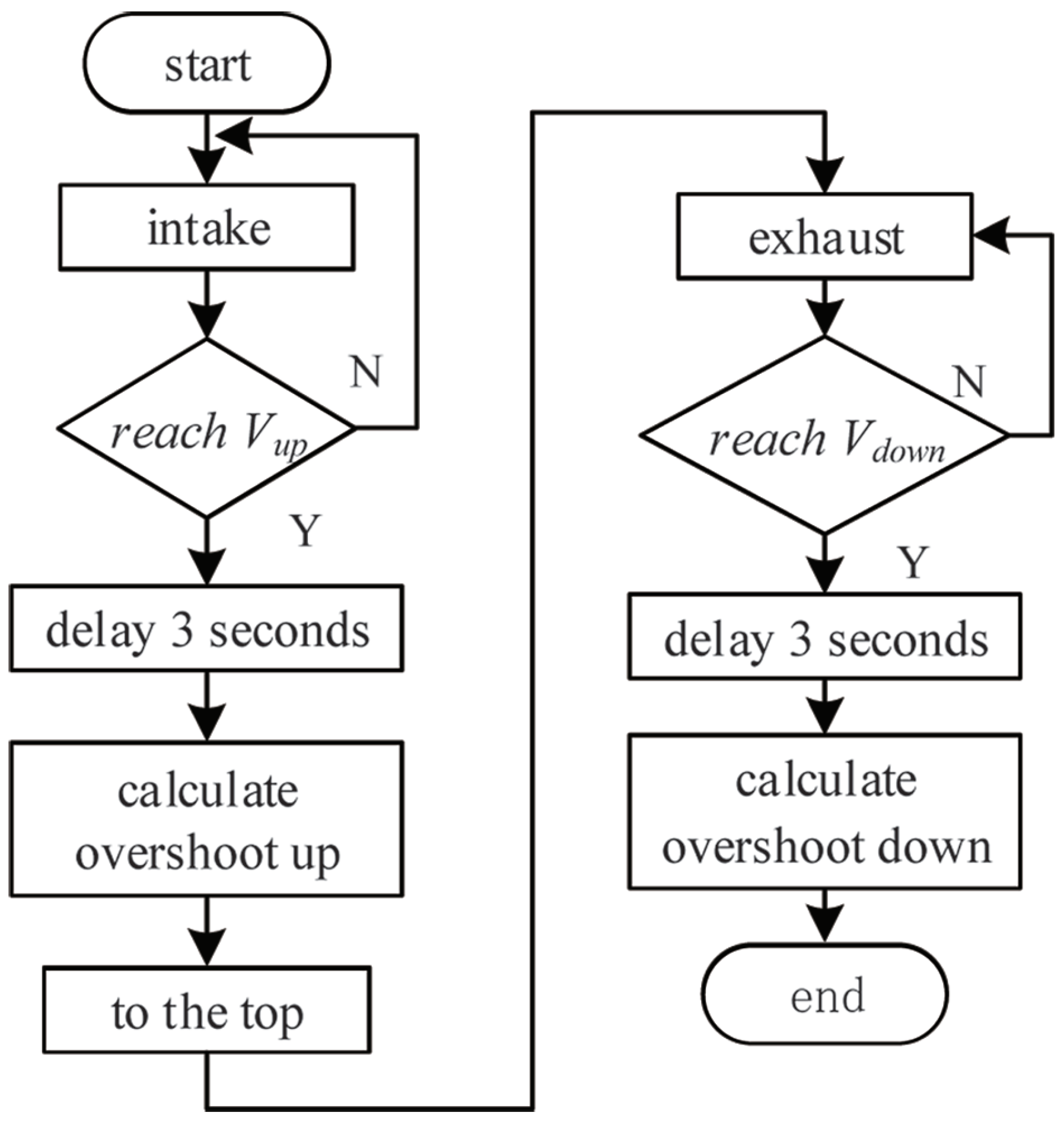
4.1.3. Maximum Speed of Pneumatic Control Valve and Its Overshoot
4.1.4. Reference Speed and Reference Speed PWM for Pneumatic Control Valve
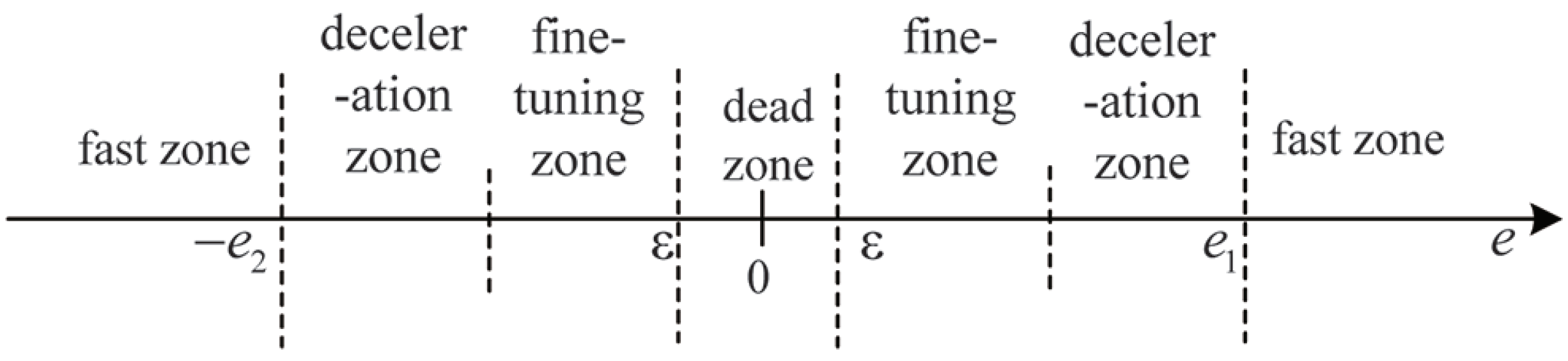
4.2. Optimal Control Strategy Based on Parameter Self-Tuning
- When the valve position error is in the fast zone, the fully open control is adopted; it can quickly reduce the error. The fully open control can meet the adjustment time and avoid the influence of static friction of the valve stem during the transition from static to moving, as shown in Equation (24).
- When e is in the deceleration zone within the range of and , the reference speed PWM control is used, and the valve position speed is detected.
- When is less than the reference speed, the valve position enters the fine-tuning zone. It not only satisfies the constraint condition and , but also avoids the vibration of the valve position. With the minimum start PWM control, the PWM starts to decrease by 4%, and the lower limit is the minimum start PWM, which achieves the purpose of slowly entering the dead zone of the valve position.
- When the valve position enters the dead zone range, , keep the piezoelectric valve in steady state.
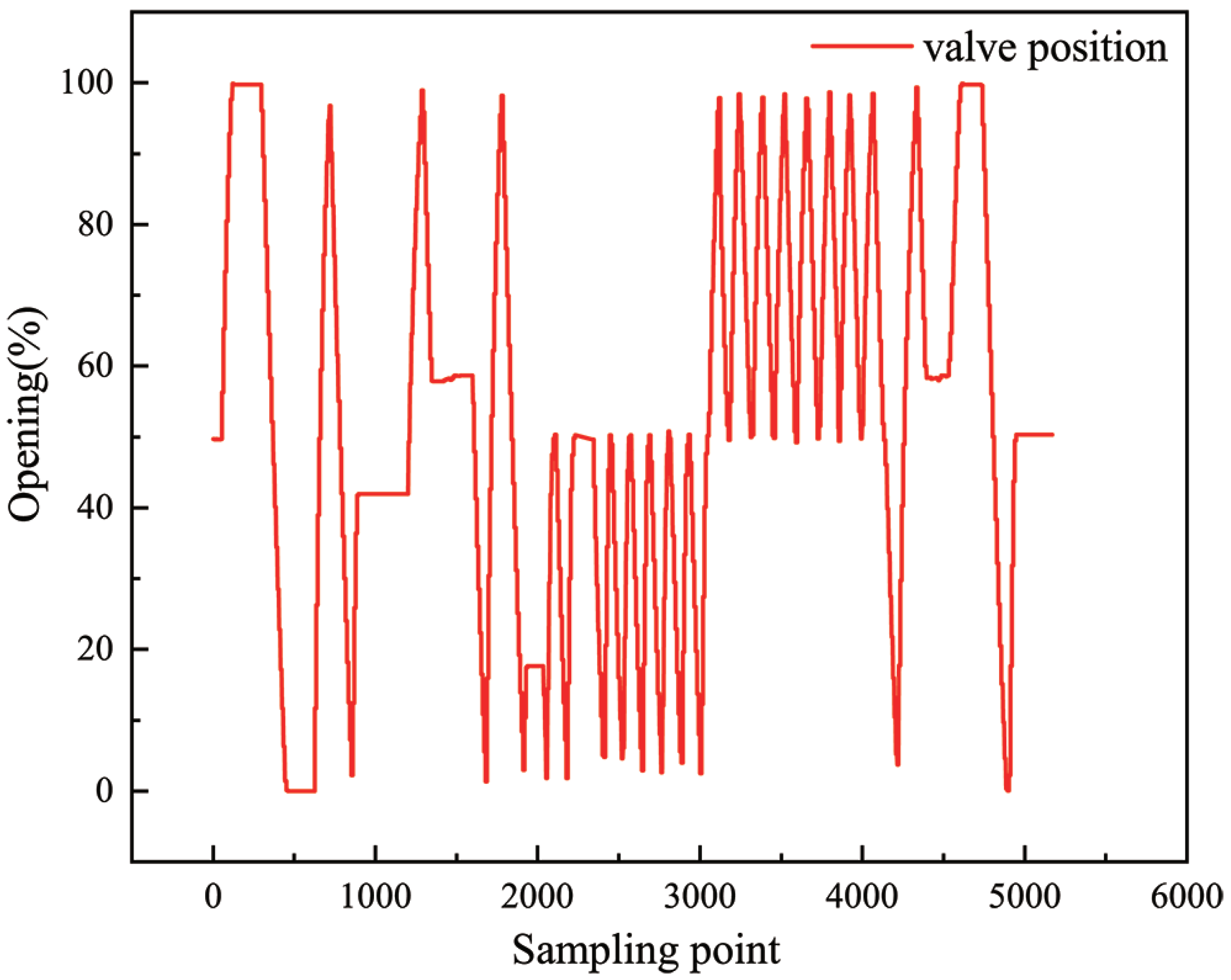
5. Experimental Analysis and Comparison
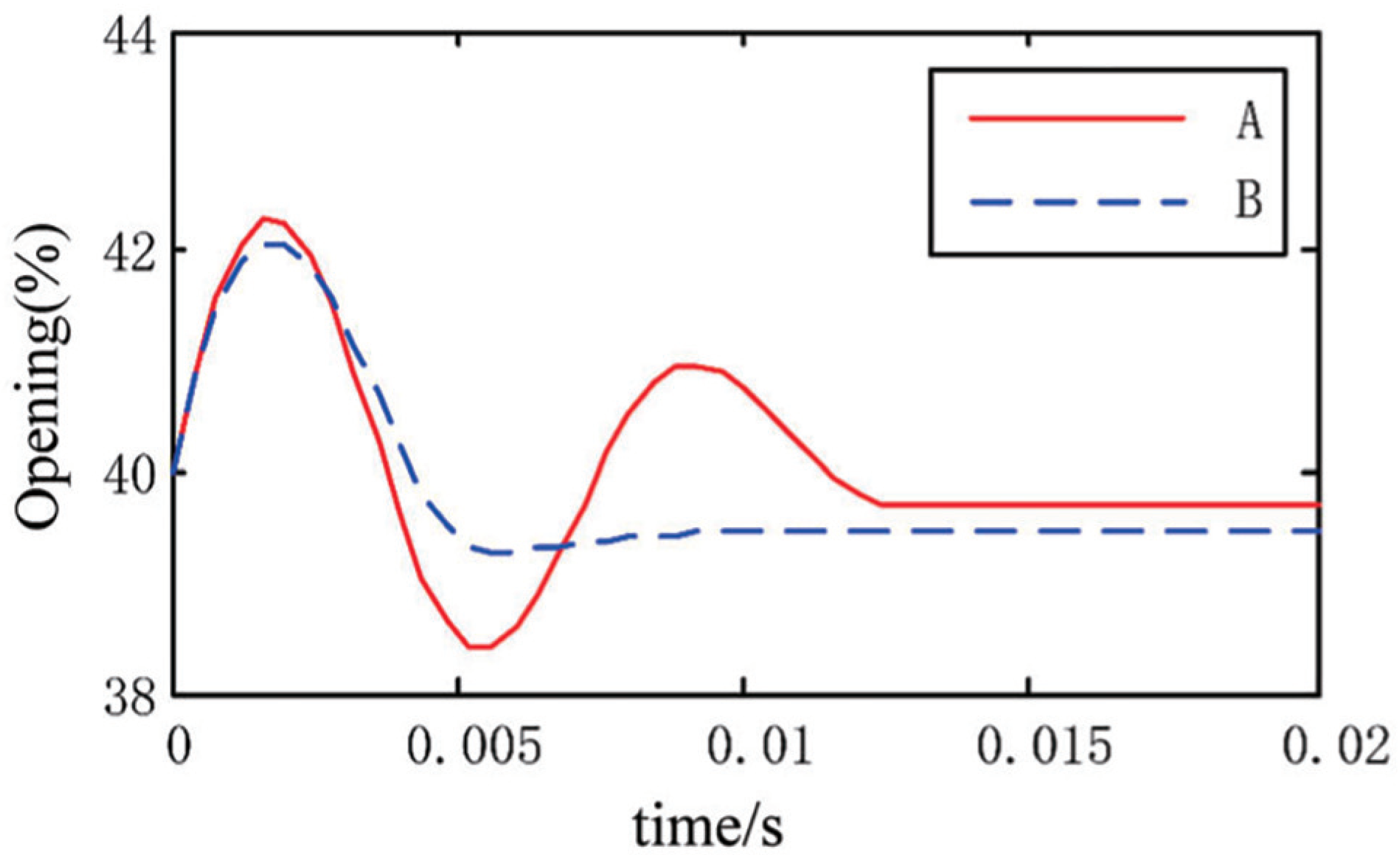
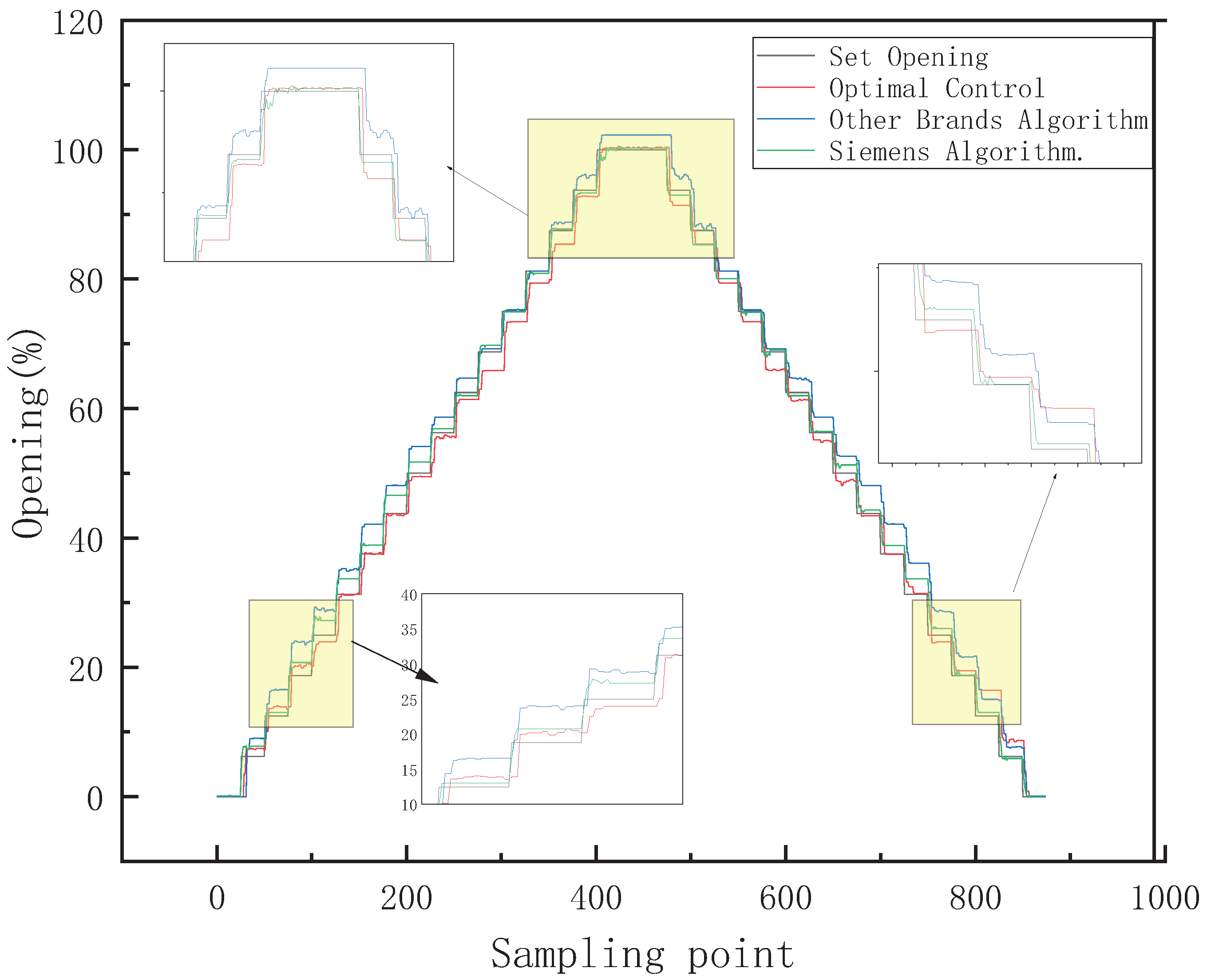
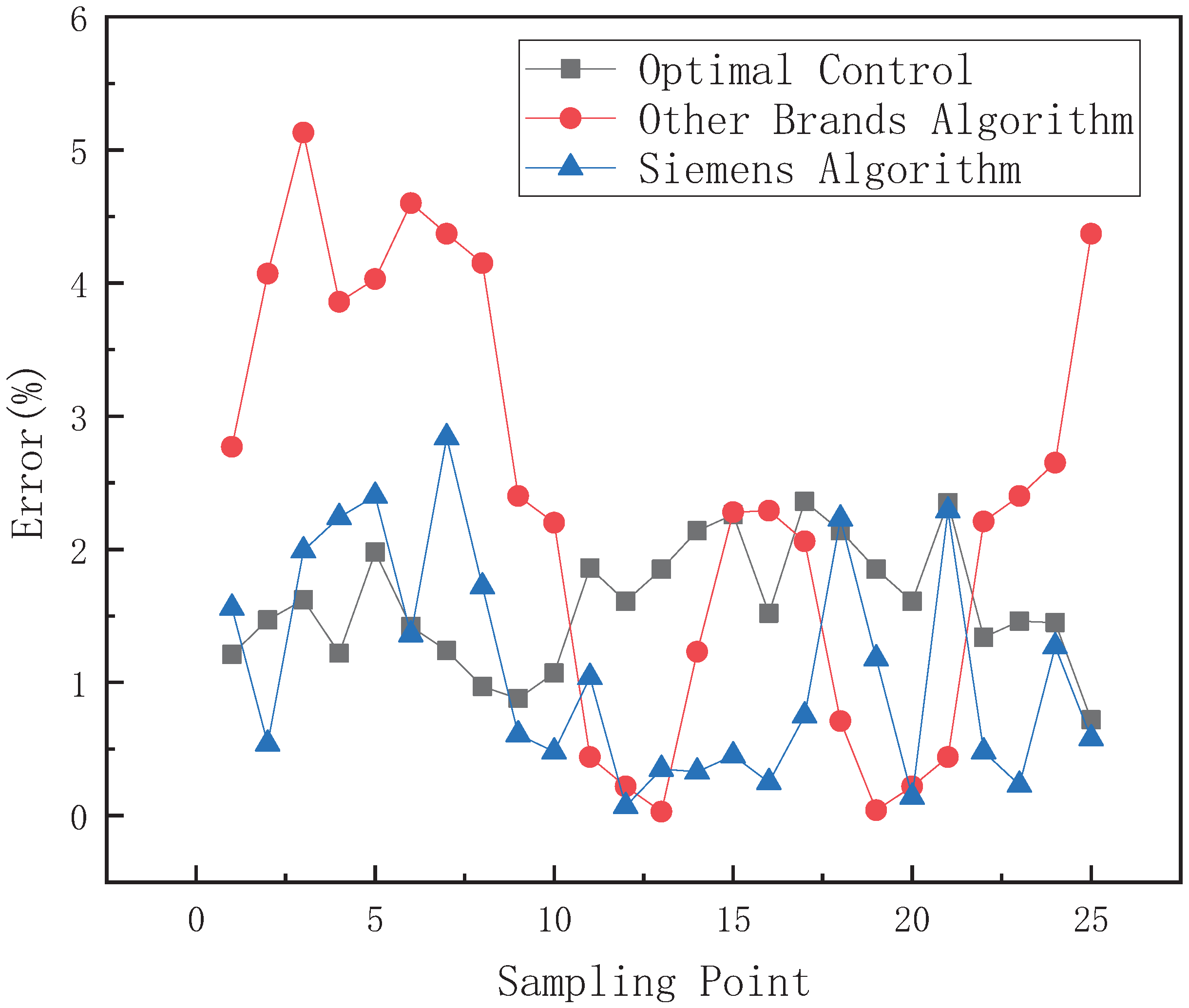
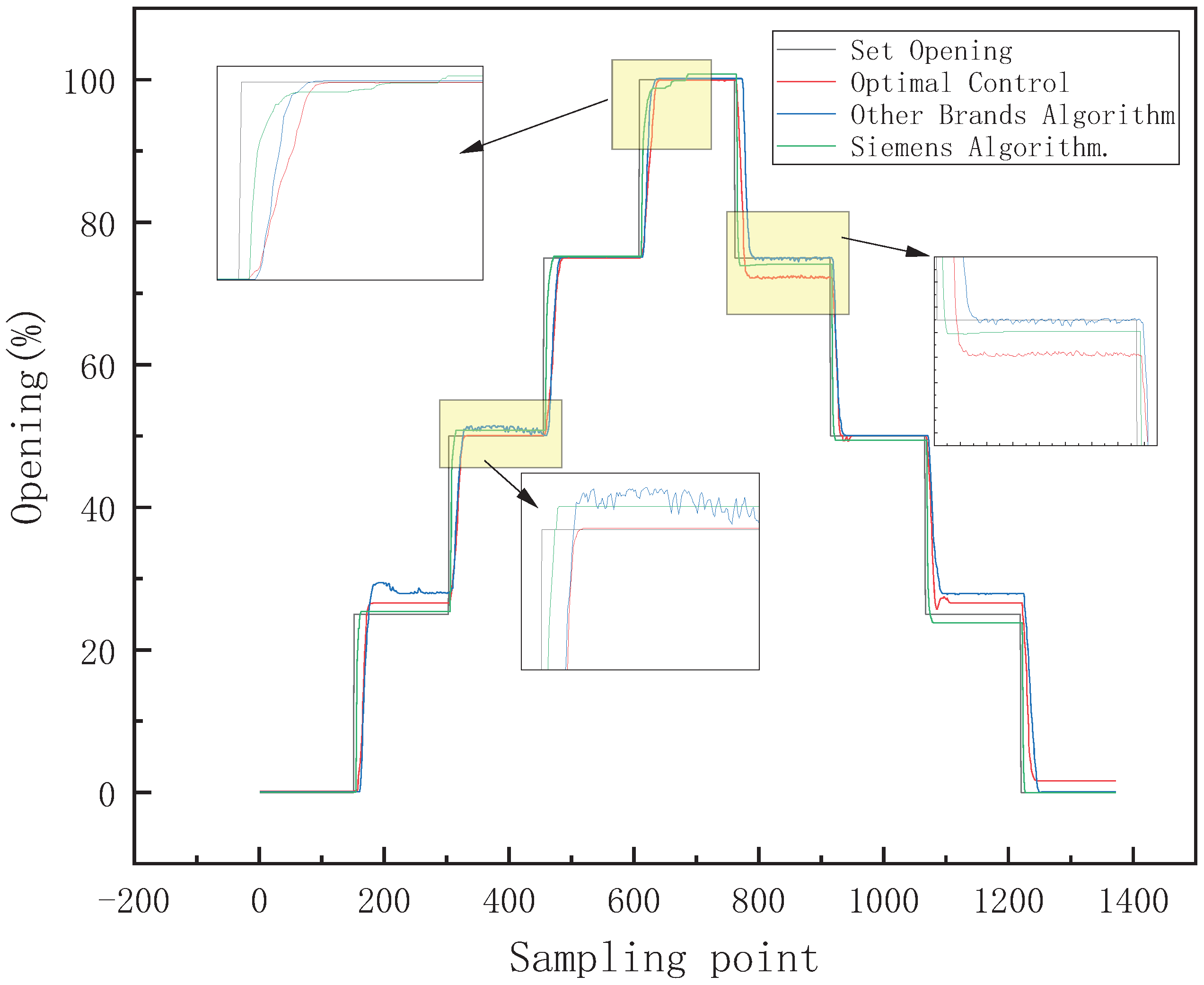
5.1. Small-Range Control Effect Comparison
5.2. Large-Range Control Effect Comparison
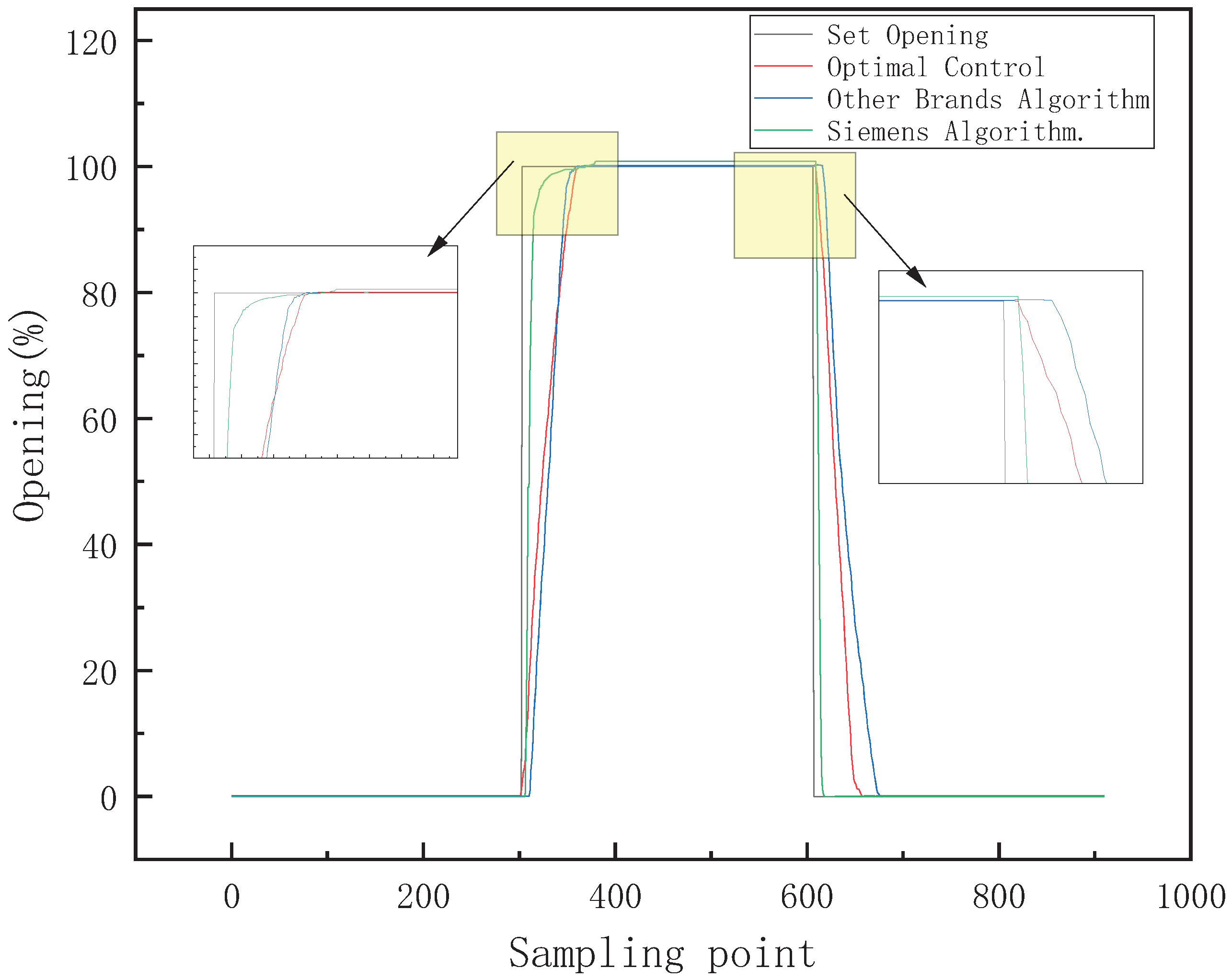
5.3. Full-Stroke Control Effect Comparison
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gu, L.H.; Ge, X.Y.; Yao, X.D.; Jiang, B. Design of Intelligent Valve Positioner. Appl. Mech. Mater. 2013, 241, 552–556. [Google Scholar] [CrossRef]
- Mandali, A.; Dong, L. Modeling and Cascade Control of a Pneumatic Positioning System. J. Dyn. Syst. Meas. Control 2022, 144, 061004. [Google Scholar] [CrossRef]
- Cheng, Q.; Liu, Z.; Jiang, A.; Jiang, E.; Xiao, Y.; Li, F.; Jiang, J. Research on control algorithm of intelligent valve positioner based on parameter self-tuning. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 1380–1385. [Google Scholar]
- Jiang, E. Intelligent Control and Analysis of Piezoelectric Switch Valve Positioner. Master’s Thesis, Hangzhou Dianzi University, Hangzhou, China, 2020. [Google Scholar]
- Wu, J. Research on Output Feedback H Control for Offshore Platforms. Master’s Thesis, China Jiliang University, Hangzhou, China, 2017. [Google Scholar]
- Wang, C. Design of Intelligent Valve Positioner Control System. Process. Autom. Instrum. 2020, 41, 77–79. [Google Scholar]
- Shi, G. Research on Intelligent Control Tactic in Smart Electro-Pneumatic Valve Positioner. Ph.D. Dissertation, Chongqing University, Chongqing, China, 2011. [Google Scholar]
- Yan, B. Developing Trend and Product Planning of Intelligent Valve Positioner Technology. Instrum. Cust. 2015, 22, 23–25. [Google Scholar]
- Wang, K. Research on Control Algorithm of Intelligent Electric Valve Positioner. Master’s Thesis, Zhejiang University of Technology, Hangzhou, China, 2018. [Google Scholar]
- Fei, L.; You, J.F.; Hua, T.Z. The Research of a Piezoelectric Valve Positioner Control Algorithm. Adv. Mater. Res. 2014, 1030, 1565–1569. [Google Scholar]
- Lv, Y. Research on Nonlinear Characteristics and Algorithm of Intelligent Valve Positioner. Master’s Thesis, Zhejiang University of Technology, Hangzhou, China, 2020. [Google Scholar]
- Casas, J.; Quetsch, J.M. Radiation Hardness of the Siemens SIPART intelligent valve positioner. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Kazimierz Dolny, Poland, 21–23 November 2019; p. 012196. [Google Scholar]
- McCormick, J.; Hagen, S. Leveraging Smart Valve Positioners. Chem. Eng. Prog. 2017, 113, 48–51. [Google Scholar]
- Papadopoulos, K.G.; Margaris, N.I. Optimal automatic tuning of active damping PID regulators. J. Process. Control 2013, 23, 905–915. [Google Scholar] [CrossRef]
- Hidalgo, M.C.; Garcia, C.; Angélico, B.A.; Tannuri, E.A. Embedded sliding mode controller applied to control valves with high friction. J. Control. Autom. Electr. Syst. 2019, 30, 677–687. [Google Scholar] [CrossRef]
- Li, X.; Chen, S.-L.; Teo, C.S.; Tan, K.K.; Lee, T.H. Data-driven modeling of control valve stiction using revised binary-tree structure. Ind. Eng. Chem. Res. 2015, 54, 330–337. [Google Scholar] [CrossRef]
- Khadim, Q.; Kiani-Oshtorjani, M.; Jaiswal, S.; Matikainen, M.K.; Mikkola, A. Estimating the Characteristic Curve of a Directional Control Valve in a Combined Multibody and Hydraulic System Using an Augmented Discrete Extended Kalman Filter. Sensors 2021, 21, 5029. [Google Scholar] [CrossRef]
- Muftah, M.N.; Faudzi, A.A.M.; Sahlan, S. Modeling and fuzzy FOPID controller tuned by PSO for pneumatic positioning system. Energies 2022, 15, 3757. [Google Scholar] [CrossRef]
- Xavier, M.S.; Fleming, A.J.; Yong, Y.K. Nonlinear Estimation and Control of Bending Soft Pneumatic Actuators Using Feedback Linearization and UKF. IEEE/ASME Trans. Mechatron. 2022, 27, 1919–1927. [Google Scholar] [CrossRef]
- Agh, S.M.; Pirkandi, J.; Mahmoodi, M.; Jahromi, M. Development of a novel rotary flow control valve with an electronic actuator and a pressure compensator valve for a gas turbine engine fuel control system. Flow Meas. Instrum. 2020, 74, 101759. [Google Scholar] [CrossRef]
- Chen, H.; Chang, S.; Fan, A. Model-based control of electromagnetic valve actuators for engine speed control. Int. J. Automot. Technol. 2019, 20, 127–135. [Google Scholar] [CrossRef]
- Liang, K.; Zhang, Y.; Jiang, X.; Chen, Z. Apery Integral Rule Self-study Fuzzy Control Arithmetic of Intelligent Valve Localizer. China Instrum. 2004, 8, 4–6. [Google Scholar]
- Jin, X. Research on Self-Tuning Algorithm of Intelligent Valve Positioner. Master’s Thesis, Zhejiang University, Hangzhou, China, 2013. [Google Scholar]
- Ma, Z.; Hu, E.; Mao, L.; Zhu, Z.; Liu, R. Design of Valve Positioner Based on Adaptive Fuzzy Immune PID. Comput. Meas. Control 2021, 29, 6. [Google Scholar]
- Yang, Q.; Xu, K.; Ren, B. Control method of piezoelectric valve positioner with variable PWM duty cycle. J. Electron. Meas. Instrum. 2014, 28, 424–433. [Google Scholar]
- Zhong, S.; Liu, Y. Piezoelectric valve type I/P conversion unit in intelligent valve positioner. Autom. Instrum. 2002, 79, 44–46. [Google Scholar]
- Liu, G.; Liao, X.; Hu, R. Control Algorithm Improvement for Intelligent Valve Positioner. Control Instrum. Chem. Ind. 2012, 39, 515–517. [Google Scholar]
- Wang, Q.; Xu, K.; Jiang, P. Parameter optimization self-tuning method of piezoelectric valve positioner. J. Electron. Meas. Instrum. 2011, 25, 612–619. [Google Scholar] [CrossRef]
- Liu, J.; Feng, Y.; Wang, J. Research on the Algorithm of Valve Position Adaptive Control for Intelligent Electro-pneumatic Valve Positioner. Instrum. Tech. Sens. 2012, 12, 151–152+155. [Google Scholar]
- Li, Y.; Zhang, L.; Siqin, P. Control Algorithm esearch of Hydraulic AGC System Based on High-speed On-off Valve. Mach. Tool Hydraul. 2016, 44, 135–139. [Google Scholar]



| Control Signal | Other Brand Control Algorithm | Siemens Control Algorithm | Optimal Control Strategy | |||
|---|---|---|---|---|---|---|
| Adjustment Time/s | Error/% | Adjustment Time/s | Error/% | Adjustment Time/s | Error/% | |
| 4∼5 | 1.73 | 2.77 | 0.56 | 1.56 | 0.96 | 1.21 |
| 5∼6 | 1.34 | 4.07 | 0.56 | 0.54 | 1.53 | 1.47 |
| 6∼7 | 1.73 | 5.13 | 0.56 | 1.99 | 1.15 | 1.62 |
| 7∼8 | 0.96 | 3.86 | 0.56 | 2.24 | 0.77 | 1.22 |
| 8∼9 | 1.15 | 4.03 | 0.56 | 2.40 | 1.15 | 1.98 |
| 9∼10 | 0.96 | 4.6 | 0.56 | 1.36 | 0.96 | 1.42 |
| 10∼11 | 1.15 | 4.37 | 1.11 | 2.84 | 0.58 | 1.24 |
| 11∼12 | 0.96 | 4.15 | 1.11 | 1.72 | 0.96 | 0.97 |
| 12∼13 | 0.77 | 2.4 | 0.56 | 0.61 | 0.77 | 0.88 |
| 13∼14 | 0.96 | 2.2 | 0.56 | 0.48 | 0.97 | 1.07 |
| 14∼15 | 0.77 | 0.44 | 0.56 | 1.04 | 0.77 | 1.86 |
| 15∼16 | 0.97 | 0.22 | 0.56 | 0.07 | 0.96 | 1.61 |
| 16∼17 | 0.77 | 0.03 | 0.56 | 0.35 | 0.77 | 1.85 |
| 17∼18 | 3.07 | 1.23 | 1.11 | 0.33 | 1.15 | 2.14 |
| 18∼19 | 3.26 | 2.28 | 2.78 | 0.4519 | 0.77 | 2.26 |
| 19∼20 | 0.97 | 2.29 | 6.21 | 0.25 | 1.15 | 1.52 |
| Control Signal | Other Brand Control Algorithm | Siemens Control Algorithm | Optimal Control Strategy | |||
|---|---|---|---|---|---|---|
| Adjustment Time/s | Error/% | Adjustment Time/s | Error/% | Adjustment Time/s | Error/% | |
| 20∼19 | 3.46 | 2.06 | 1.88 | 0.75 | 1.15 | 2.36 |
| 19∼18 | 0.97 | 0.71 | 1.11 | 2.23 | 0.97 | 2.14 |
| 18∼17 | 0.97 | 0.04 | 0.56 | 1.18 | 1.15 | 1.85 |
| 17∼16 | 0.97 | 0.22 | 0.56 | 0.14 | 0.97 | 1.61 |
| 16∼15 | 0.97 | 0.44 | 0.56 | 2.29 | 1.34 | 2.35 |
| 15∼14 | 0.97 | 2.21 | 1.11 | 0.48 | 1.15 | 1.34 |
| 14∼13 | 0.97 | 2.4 | 0.56 | 0.23 | 0.77 | 1.46 |
| 13∼12 | 1.34 | 2.65 | 0.56 | 1.27 | 0.58 | 1.45 |
| 12∼11 | 0.97 | 4.37 | 0.56 | 0.58 | 0.97 | 0.72 |
| 11∼10 | 1.15 | 4.61 | 1.11 | 1.28 | 1.15 | 4.61 |
| 10∼9 | 1.53 | 4.82 | 0.56 | 4.2 | 1.53 | 4.82 |
| 9∼8 | 1.25 | 3.63 | 1.67 | 3.34 | 1.25 | 3.63 |
| 8∼7 | 1.34 | 2.84 | 1.11 | 2.67 | 1.34 | 2.84 |
| 7∼6 | 1.34 | 2.57 | 1.11 | 2.7 | 1.34 | 2.57 |
| 6∼5 | 1.53 | 1.45 | 1.11 | 1.22 | 1.53 | 1.45 |
| 5∼4 | 0.76 | 0.03 | 2.22 | 0.0 | 0.76 | 0.03 |
| Control Signal | Other Brand Control Algorithm | Siemens Control Algorithm | Optimal Control Strategy | |||
|---|---|---|---|---|---|---|
| Adjustment Time/s | Error/% | Adjustment Time/s | Error/% | Adjustment Time/s | Error/% | |
| 4∼8 | 4.67 | 2.94 | 0.8 | 0.37 | 1.60 | 1.56 |
| 8∼12 | 2 | 0.83 | 0.73 | 0.81 | 1.73 | 0.05 |
| 12∼16 | 2.33 | 0.1 | 1 | 0.18 | 1.46 | 0.01 |
| 16∼20 | 2.1 | 0.15 | 5.33 | 0.81 | 1.87 | 0.08 |
| Control Signal | Other Brand Control Algorithm | Siemens Control Algorithm | Optimal Control Strategy | |||
|---|---|---|---|---|---|---|
| Adjustment Time/s | Error/% | Adjustment Time/s | Error/% | Adjustment Time/s | Error/% | |
| 20∼16 | 1.87 | 0.02 | 1.53 | 0.93 | 1.13 | 0.01 |
| 16∼12 | 1.6 | 0.05 | 0.46 | 0.56 | 0.93 | 0.05 |
| 12∼8 | 1.73 | 2.94 | 0.8 | 1.18 | 1.11 | 0.66 |
| 8∼4 | 0.22 | 0.08 | 0.47 | 0 | 1.53 | 0.78 |
| Control Signal | Other Brand Control Algorithm | Siemens Control Algorithm | Optimal Control Strategy | |||
|---|---|---|---|---|---|---|
| Adjustment Time/s | Error/% | Adjustment Time/s | Error/% | Adjustment Time/s | Error/% | |
| 4∼20 | 4.20 | 0.15 | 6.72 | 4∼20 | 4.20 | 0.15 |
| 20∼4 | 4.80 | 0.08 | 1.45 | 20∼4 | 4.80 | 0.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Jiang, A.; Jiang, J.; Qi, Y.; Xue, L.; Wang, Y. A New Positioning Strategy Based on Parameter Tuning and Optimal Control Technique for Pneumatic Control Valve. Actuators 2022, 11, 279. https://doi.org/10.3390/act11100279
Zhang B, Jiang A, Jiang J, Qi Y, Xue L, Wang Y. A New Positioning Strategy Based on Parameter Tuning and Optimal Control Technique for Pneumatic Control Valve. Actuators. 2022; 11(10):279. https://doi.org/10.3390/act11100279
Chicago/Turabian StyleZhang, Bo, Aipeng Jiang, Jiaji Jiang, Yanying Qi, Li Xue, and Yan Wang. 2022. "A New Positioning Strategy Based on Parameter Tuning and Optimal Control Technique for Pneumatic Control Valve" Actuators 11, no. 10: 279. https://doi.org/10.3390/act11100279
APA StyleZhang, B., Jiang, A., Jiang, J., Qi, Y., Xue, L., & Wang, Y. (2022). A New Positioning Strategy Based on Parameter Tuning and Optimal Control Technique for Pneumatic Control Valve. Actuators, 11(10), 279. https://doi.org/10.3390/act11100279







